Výpis souhrnů
Elementární algebra
Podtémata
- Elementární algebra
- Přímá a nepřímá úměrnost
- Trojčlenka
- Poměry
- Poměry: základy
- Poměry: změna a rozdělení čísla
- Poměry: výpočty
- Poměry: měřítko mapy
- Algebraické výrazy a jejich úpravy
- Dosazování do výrazů
- Úpravy výrazů s jednou proměnnou
- Úpravy výrazů s více proměnnými
- Úpravy výrazů se zlomky
- Lomené výrazy
- Podmínky lomených výrazů
- Lomené výrazy: úpravy a výpočty
- Rovnice
- Jednokrokové rovnice
- Základní rovnice s jednou neznámou
- Rovnice se závorkami
- Rovnice s neznámou ve jmenovateli
- Rovnice se zlomky
- Rovnice s desetinnými čísly
- Pokročilé rovnice
- Rovnice s lomenými výrazy
- Dvě rovnice o dvou neznámých
- Kvadratické rovnice
- Exponenciální rovnice
- Logaritmické rovnice
- Goniometrické rovnice
- Úlohy s rovnicemi
- Vyjádření neznámé z rovnice
- Myslím si číslo
- Úlohy o směsích
- Společná práce
- Nerovnice
- Aritmetická a geometrická posloupnost
- Zápis posloupností
Elementární algebra
Elementární algebra rozšiřuje aritmetiku („počítání s čísly“, např. 3+5\cdot8) o práci s neznámými veličinami (např. x-4\cdot y). Tato oblast má uplatnění nejen v mnoha dalších částech matematiky, ale je klíčová třeba i pro porozumění fyzice.
| téma | ukázky pojmů a příkladů |
|---|---|
| Úměrnosti | přímá a nepřímá úměrnost, trojčlenka |
| Poměry | měřítko mapy, poměry surovin v jídle |
| Algebraické výrazy a jejich úpravy | 3x - (x+2), (a+b)^2 |
| Rovnice | 4x + 3 = 27 |
| Pokročilé rovnice | 2x^2+6x=20 |
| Úlohy s rovnicemi | úlohy o směsích, společná práce |
| Nerovnice | 2x + 5 \leq 8 |
| Posloupnosti a řady | aritmetická a geometrická posloupnost |
Přímá a nepřímá úměrnost
Přímá úměrnost
Přímá úměrnost je závislost veličiny y na druhé veličině x, kdy se při zvýšení veličiny x zvýší poměrně i hodnota veličiny y. Přímou úměrnost tedy můžeme popsat vztahem y=k\cdot x, kde k je koeficient úměrnosti. Grafem přímé úměrnosti je přímka, která prochází počátkem souřadnic (bodem [0, 0]).
Názorné příklady přímé úměrnosti
- Nákup: Čím víc rohlíků koupím, tím víc zaplatím (koeficient úměrnosti je cena rohlíku).
- Práce a plat: Čím více hodin pracuji, tím víc peněz vydělám (koeficient úměrnosti je hodinová mzda).
- Čas a vzdálenost: Čím déle se pohybuji, tím větší vzdálenost urazím (koeficient úměrnosti je rychlost, o přímou úměrnost se jedná pouze při pohybu konstantní rychlostí)
- Obvod: Čím delší strana čtverce, tím delší obvod čtverce (koeficient úměrnosti je 4).
Příklad výpočtu přímé úměrnosti
- Osm dračích vajec stojí 40 zlaťáků. Kolik stojí dvacet dračích vajec?
- Vypočítáme cenu za jedno vejce (koeficient úměrnosti k):
40:8 = 5 zlaťáků. - Celkovou cenu vypočítáme prostým násobením (k\cdot x):
5\cdot 20 = 100 zlaťáků.
Nepřímá úměrnost
Nepřímá úměrnost je závislost veličiny y na druhé veličině x, kdy se při zvýšení veličiny x sníží poměrně hodnota veličiny y. Nepřímou úměrnost tedy můžeme popsat vztahem y=\frac{k}{x}. Grafem nepřímé úměrnosti je hyperbola.
Názorné příklady nepřímé úměrnosti
- Doba práce a počet lidí: Čím více lidí pracuje na natírání plotu, tím rychleji je plot natřený.
- Dort a děti: Čím více dětí je na oslavě, tím menší kus dortu každé z nich dostane.
- Obdélník: Pokud uvažujeme obdélníky se stejným obsahem, pak mezi šířkou a výškou obdélníku platí nepřímá úměrnost.
- Rychlost a čas: Čím rychleji jedu na kole, tím kratší dobu mi zabere dostat se do cíle.
Příklad výpočtu nepřímé úměrnosti
- Pětihlavý drak sní všechny zásoby na hradě za 12 dní. Za kolik dní sní zásoby šestihlavý drak?
- Nejdříve určíme, jak dlouho by jedla zásoby jedna hlava:
5\cdot 12=60 dní. - Tento počet podělíme počtem hlav v otázce:
60:6 = 10 dní.
Trojčlenka
Trojčlenka je grafický zápis výpočtu neznámého členu přímé nebo nepřímé úměry.
Na první řádek napíšeme dvě známé hodnoty, na druhý známou hodnotu a neznámou (např. x). První šipka povede od neznámé nahoru. Druhá šipka povede pro přímou úměru stejným směrem jako první a pro nepřímou úměru opačným směrem než první šipka.
Příklad: trojčlenka pro přímou úměru
Zadání: 10\,000 lumíků má dohromady stejnou hmotnost jako dva medvědi, kolik medvědů má dohromady stejnou hmotnost jako 40\,000 lumíků?
Na první řádek si zapíšeme, že 10\,000 lumíků odpovídá hmotnostně dvěma medvědům. Větší počet lumíků bude odpovídat většímu počtu medvědů, takže jde o přímou úměru. Obě šipky ukazují nahoru.

Zapíšeme dvě strany rovnice jako zlomky podle směru šipek a vypočítáme x.
První šipka vede od 40\,000 k 10\,000, druhá šipka vede od x k 2. Rovnice tedy je \frac{40\,000}{10\,000}=\frac{x}{2}.
Zjednodušený způsob, jak přímo zapsat výsledek: $x=2 $ zlomek zapsaný ve směru šipky na levé straně, tedy: x= 2 \cdot \frac{40\,000}{10\,000} = 2\cdot 4 = 8
Výsledek je: 8 medvědů má dohromady stejnou hmotnost jako 40\,000 lumíků.
Příklad: trojčlenka pro nepřímou úměru
Zadání: 100 mravenců sní bonbón za tři dny. Jak dlouho by stejný bonbón jedlo 500 mravenců?
Na první řádek si zapíšeme, že 100 mravenců potřebuje ke snědení bonbónu 3 dny. Čím víc je mravenců, tím kratší čas potřebují na snědení bonbónu, takže jde o nepřímou úměru. Šipka od neznámé ukazuje nahoru a druhá šipka opačným směrem.

Zapíšeme dvě strany rovnice jako zlomky vytvořené podle směru šipek a vypočítáme x.
První šipka vede od 100 k 500, druhá od x k 3. Rovnice je \frac{100}{500}=\frac{x}{3}.
Zjednodušený zápis výsledku: x = 3 \cdot zlomek zapsaný podle směru šipky na levé straně, tedy: x= 3 \cdot \frac{100}{500} = 3 \cdot \frac{1}{5} = 0{,}6
Výsledek je: 500 mravenců bude jíst bonbón 0{,}6 dne.
Poměr dvou nebo více čísel vyjadřuje vztah jejich velikostí – tedy kolikrát je jedno číslo větší (nebo menší) než druhé. S poměry se setkáváme v běžném životě i v matematice: určují například poměr stran obrazovky (16 : 9), měřítko mapy (1 : 50 000) nebo směs dvou látek v určitém poměru. Poměry úzce souvisejí se zlomky nebo pojmem podobnost v geometrii.
- Základy poměrů – zápis poměru, základní tvar, postupný a převrácený poměr, vztah ke zlomkům
- Změna a rozdělení čísla – zvětšení nebo zmenšení čísla v daném poměru, rozdělení čísla v poměru (např. rozdělit 12 v poměru 1 : 3 na 3 a 9)
- Výpočty s poměry – výpočty při znalosti součtu nebo rozdílu částí, příklady s poměry a rovnicemi
- Měřítko mapy – použití poměrů při práci s mapami, plány nebo modely, převody skutečných a zmenšených vzdáleností
Poměry: základy
Poměr dvou kladných hodnot, např. 2:4, vyjadřuje vztah jejich velikostí.
Dědeček našel 10 hřibů a 1 bedlu. Poměr počtu hřibů ku počtu bedel v dědečkově košíku je 10:1.
Podobně jako u zlomků můžeme poměry krátit a rozšiřovat kladnými čísly.
Poměr počtu hřibů ku počtu bedel 10:1 může být zrovna tak vyjádřen jako 20:2 nebo 1:0{,}1.
Poměr, který je vyjádřen dvěma celými čísly a nejde už víc zkrátit, je v základním tvaru.
Základní tvar poměru 2:4 je 1:2.
Lze zapsat i poměr více než dvou hodnot, pak jde o postupný poměr.
Kedlubny, ředkvičky a mrkve nám na zahrádce vyrostly v poměru 2 : 10 : 11.
Převráceným poměrem k poměru a:b myslíme poměr b:a.
Poměr objemů sirupu a vody v nápoji je 1:10, převrácený poměr 10:1 značí poměr objemů vody ku sirupu.
Jaký je rozdíl mezi poměrem a zlomkem? Poměr popisuje vztah dvou částí. Zlomek je část z celku.

Poměry: změna a rozdělení čísla
Změna čísla
Změna čísla v zadaném poměru a:b je vynásobení čísla odpovídajícím zlomkem \frac{a}{b}.
- Pokud je a \lt b a tedy \frac{a}{b} \lt 1, budeme číslo zmenšovat.
- Pokud je a > b a tedy \frac{a}{b}>1, budeme číslo zvětšovat.

Příklad: změna čísla v zadaném poměru
Změna čísla 10 v poměru 2:5 znamená vynásobení čísla 10 zlomkem \frac{2}{5}. Vyjde nám číslo 4.
Rozdělení čísla
Rozdělení čísla v zadaném poměru a:b znamená rozdělení čísla na dvě části, které jsou v poměru a:b.
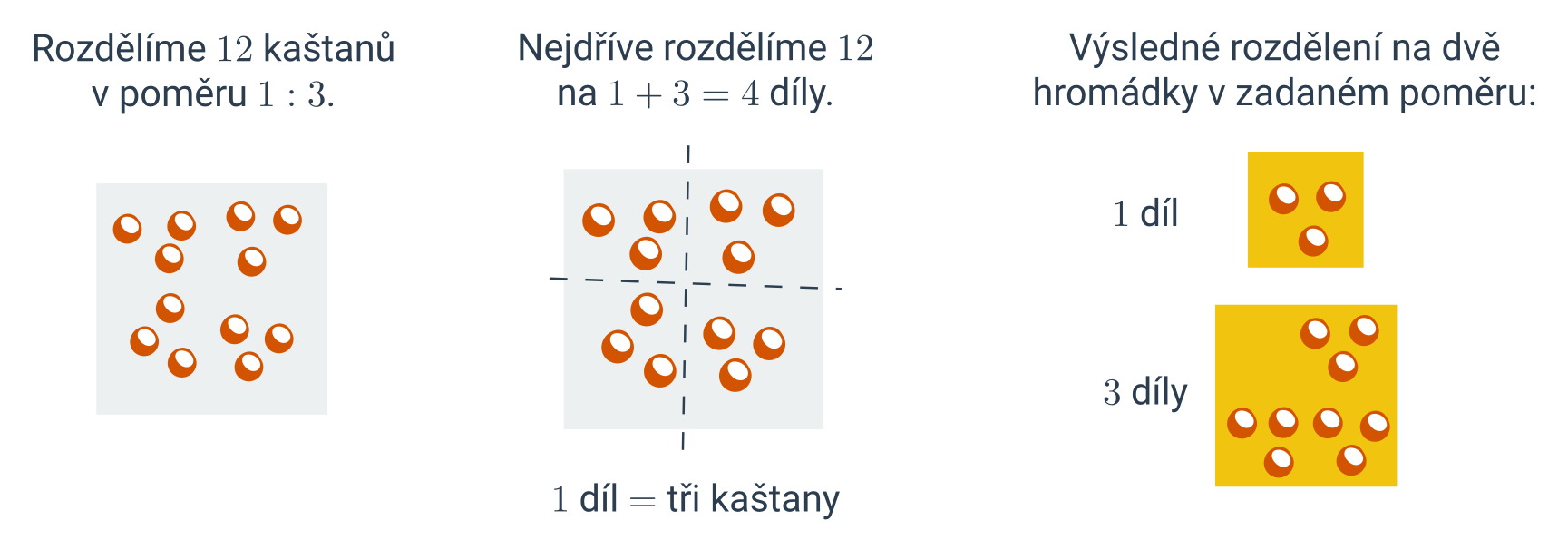
Příklad: rozdělení čísla v zadaném poměru
Rozdělte číslo 30 v poměru 2:3. Celkem budeme rozdělovat na 2+3=5 dílů. Jeden díl je tedy roven \frac{30}{5}=6.
Výsledná čísla jsou rovna 2 dílům, tj. 2\cdot 6= 12, a 3 dílům, tj. 3\cdot 6=18. Rozdělili jsme číslo 30 v poměru 2:3 na 12 a 18.
Poměry: výpočty
Výpočty při znalosti součtu (rozdílu)
Hledáme dvě čísla, když známe jejich poměr a známe jejich součet (případně rozdíl, součin, nebo nějaký jiný výraz). V takovém případě nám většinou pomůže spočítat si nejdříve čemu odpovídá jeden díl v poměru. Pokračujeme obvykle výpočtem hledaných čísel podle toho, kolika dílům v poměru odpovídá první a druhé číslo.
Příklad: výpočet čísel, když známe jejich poměr
Poměr nabitých a vybitých baterií v Gargamelově detektoru šmoulů je 1:4. Vybitých baterií je přitom o 6 více než nabitých. Jaké jsou počty nabitých a vybitých baterií?
Nejdříve si spočítáme, kolika bateriím odpovídá jeden díl. Víme, že vybitých baterií je o 6 více než nabitých. Vybitých baterií jsou přitom 4 díly a nabitých 1 díl, takže vybitých je o 4-1=3 díly více než nabitých. Takže 3 díly odpovídají 6 bateriím. Jeden díl odpovídá \frac{6}{3}=2 bateriím. Gargamel tedy má 2 nabité baterie a 4 \cdot 2 = 8 vybitých baterií.
Výsledek: Gargamel má dvě nabité a osm vybitých baterií.
Výpočty pomocí rovnic
Pokud už se vyznáme v řešení rovnic, můžeme při řešení využít zápisu pomocí dvou rovnic pro dvě neznámé.
- První rovnici zapíšeme ze známého poměru.
- Druhou rovnici zapíšeme z informace o hodnotě součtu (nebo rozdílu, součinu, atd.).
Těžší příklad pro ty, kteří už znají rovnice a obvod kruhu
Víme, že poloměry dvou kruhů jsou v poměru 2 : 5 a že součet jejich obvodů je 70 \pi. O jaké poloměry jde?
Označíme si poloměry a a b a zapíšeme si rovnice. Známe poměr a : b = 2 : 5, takže máme první rovnici \frac{a}{b}=\frac{2}{5}. Součet obvodů kruhů o poloměrech a,b je roven 2a\cdot \pi + 2b\cdot \pi. Tento součet známe, takže druhá rovnice zní 2(a+b)\cdot\pi = 70 \pi.
Řešíme soustavu rovnic. První rovnici vynásobíme 5b (má smysl pro b\neq 0) a dostaneme 5a=2b. Vydělíme druhou rovnici kladným číslem 2\pi a dostaneme a+b=35. Vyjádříme a z druhé rovnice a dosadíme do první. 5\cdot(35-b)=2b. Zjednodušíme a vypočítáme b. 175= 7b, tedy b=25. Spočítáme druhý poloměr a=35-b=10.
Výsledné poloměry kruhů jsou a=10,b=25.
Poměry: měřítko mapy
Měřítko mapy, plánku, zmenšeného modelu
Měřítko mapy je speciální případ poměru. Jde o poměr, ve kterém je obraz krajiny na mapě ku krajině ve skutečnosti.
Příklady
- Mapa s měřítkem 1 : 10\,000. Centimetr na této mapě odpovídá 10\,000\ \text{cm} = 100\ \text{m} ve skutečnosti.
- Nákres, na kterém je délka pětimetrové sochy 2\ \text{cm}, má měřítko 2 : (100\cdot 5) = 2 : 500 = 1 : 250.
Měřítko zvětšeného modelu
Podobně u zvětšeného modelu hodně malé věci nebo tvora použijeme opět poměr velikosti obrazu ku velikosti ve skutečnosti.
Příklady
- Model lidského neuronu v kabinetu biologie má šířku 20 \ \text{cm}. Skutečný motoneuron, který byl inspirací pro tento model, má velikost 80\ \mu \text{m} = 0{,}000\,08 \ \text{m}= 0{,}008 \ \text{cm}. Měřítko modelu je 20 : 0{,}008 = 20\,000 : 8 = 2\,500 : 1.
- Pojďme si ještě určit, čemu odpovídá 1\ \text{cm} na tomto modelu neuronu. Centimetr na modelu odpovídá \frac{1}{2\,500}\ \text{cm} ve skutečnosti, tedy 1\ \text{cm} na modelu neuronu odpovídá 0{,}000\,4\ \text{cm} = 0{,}000\,004\ \text{m} = 4\ \mu \text{m} ve skutečnosti.
Algebraické výrazy a jejich úpravy
Algebraický výraz je tvořen z konstant („čísla“) a proměnných („písmenka“), které jsou dohromady spojeny pomocí algebraických operací (např. sčítání, násobení) a závorek. Proměnná zastupuje čísla z určitého oboru hodnot. Pomocí algebraických výrazů můžeme provádět obecné výpočty.
Příklad: počet noh zvířat
- Sedlák Sedloň má na dvorku p prasat a s slepic.
- Výraz 4\cdot p + 2 \cdot s vyjadřuje celkový počet nohou, která zvířata na dvorku mají.
- V tomto výrazu jsou čísla 4 a 2 konstanty, písmena p a s jsou proměnné, jejichž oborem jsou přirozená čísla.
- Výraz můžeme upravit do tvaru 2(2p+s). Tato úprava zachovává hodnotu výrazu pro všechna možná přiřazení hodnot proměnných.
| téma | příklad (zadání) | příklad (výsledek) |
|---|---|---|
| Dosazování do výrazů | dosadit x = 3 do výrazu 2x + 5 | 11 |
| Zápis pomocí výrazů | „O 5 větší než dvojnásobek čísla x“ | 2x + 5 |
| Úpravy výrazů s jednou proměnnou | 3x - 2 \cdot(3+x) | x - 6 |
| Úpravy výrazů s více proměnnými | 2a + 3b - a + 4b | a + 7b |
| Úpravy výrazů se zlomky | \frac{x}{2} + \frac{x}{3} | \frac{5x}{6} |
| Lomené výrazy | \frac{x^2 - 9}{x - 3} | x + 3 pro x \ne 3 |
| Dělení mnohočlenu mnohočlenem | \frac{2x^4 + x + 4}{x^2 + 2} | 2x^2 - 4, zbytek x+12 |
| Výrazy s faktoriálem a kombinačními čísly | \frac{n!}{(n+1)!} | \frac{1}{n+1} |
Dosazování do výrazů
Základní krok pro práci s algebraickými výrazy je dosazení hodnoty za proměnnou. Častým zdrojem chyb při dosazování jsou „mínuska“, dáváme si na ně tedy obzvlášť pozor (počítání se zápornými čísly může být užitečné zopakovat před dosazováním těchto čísel do výrazů).
Příklad:
| Výraz | Hodnoty proměnných | Dosazení |
|---|---|---|
| 14-3n | n=2 | 14-3\cdot 2 = 8 |
| 3x-y | x=2, y=4 | 3\cdot2 - 4 = 2 |
| 2a+3b | a=5, b=-1 | 2\cdot 5 + 3\cdot(-1) = 7 |
| 1-x-2y | x=-5, y=7 | 1-(-5)-2\cdot 7 = 1+5-14=-8 |
Úpravy výrazů s jednou proměnnou
Provádíme takové úpravy výrazů, které zachovávají hodnotu výrazu pro všechna možná dosazení za proměnné. Příklady úprav:
| Popis | Výraz | Upravený výraz |
|---|---|---|
| Sečtení členů s proměnnou | 3x+4+6x | =9x+4 |
| Roznásobení závorky | 3(x+2) | =3x+6 |
| Odečtení závorky | 1-(x-2) | =1-x+2 =3-x |
| Vytknutí proměnné | x^2+2x+3 | =x\cdot x +2x+3=x(x+2)+3 |
| Umocnění | (x+1)^2 | =(x+1)(x+1)=x^2+2x+1 |
Pozor na častou chybu v případě odečtení závorky: nesmíme zapomenout, že „mínus a mínus dává plus“.
NahoruÚpravy výrazů s více proměnnými
Provádíme takové úpravy výrazů, které zachovávají hodnotu výrazu pro všechna možná dosazení za proměnné. Příklady úprav:
| Popis | Výraz | Upravený výraz |
|---|---|---|
| Sečtení členů se stejnou proměnnou | 3x+2y+4x | =7x+2y |
| Roznásobení závorky | x(y-2) | =xy-2x |
| Vytknutí | 4x-x^2y+3 | =x(4-xy)+3 |
| Umocnění | (a+b)^2 | =(a+b)(a+b)=a^2+2ab+b^2 |
| Roznásobení dvou závorek | (a+b)(a-b) | =(a+b)(a-b)=a^2+ab-ab-b^2 = a^2-b^2 |
Úpravy výrazů se zlomky
Úpravy výrazů se zlomky provádíme stejnými základními postupy jako ostatní úpravy výrazů, pouze při tom používáme navíc operace specifické pro zlomky, např. krácení zlomků, sčítání a odčítání zlomků, násobení a dělení zlomků. Příklady úprav:
| Popis | Výraz | Upravený výraz |
|---|---|---|
| Krácení zlomku | \frac{3x+6}{15} | =\frac{x+2}{5} |
| Součet zlomků | \frac{x}{2}+\frac{x}{3} | =\frac{3x}{6}+\frac{2x}{6} = \frac{5x}{6} |
| Násobení zlomků | \frac{x+1}{2} \cdot \frac{1}{3} | =\frac{x+1}{6} |
Lomené výrazy
Lomený výraz je podíl dvou mnohočlenů. Zapisujeme většinou jako zlomek, například \frac{x+2}{x^2-1}. Toto téma dělíme na dvě podtémata:
- Podmínky lomených výrazů – Přesněji řečeno jde o „podmínky, za kterých má daný lomený výraz smysl“. Musíme se jimi zabývat, protože pro takové hodnoty proměnných, pro které výraz ve jmenovateli lomeného výrazu nabývá hodnoty nula, nemá celý lomený výraz smysl.
- Výpočty s lomenými výrazy a jejich úpravy – Ty provádíme podobně, jako když pracujeme se zlomky, jenom musíme mít na paměti, že čitatelé a jmenovatelé jsou u lomených výrazů mnohočleny.
Podmínky lomených výrazů
U lomených výrazů je potřeba brát v potaz podmínky, za kterých má smysl. Lomený výraz má smysl pro všechny hodnoty proměnných, pro něž je výraz ve jmenovateli různý od nuly. Příklady:
- Výraz \frac{x+5}{x-3} má smysl pro x \neq 3.
- Výraz \frac{x^3}{x^2-1} má smysl pro x \in \mathbb{R} \setminus \{-1, 1\}, protože x^2-1 = 0 pro hodnoty -1 a 1.
- Výraz \frac{x^3}{x^2+1} má smysl pro všechna reálná čísla, protože x^2+1 je vždy větší než nula.
Určit, kdy je výraz různý od nuly nemusí být úplně snadné. Pro ilustraci uveďme těžší příklad výrazu s obecným kvadratickým jmenovatelem (mohou se hodit poznatky z kvadratických rovnic a grafy kvadratických funkcí).
Určení podmínek lomeného výrazu \frac{1}{x^2+kx+3}
- Výraz má smysl pokud x^2+kx+3 \neq 0.
- Diskriminant kvadratické rovnice x^2+kx+3 = 0 pro proměnnou x je k^2-12.
- Uvedená kvadratická rovnice má jedno nebo dvě řešení x_1=\frac{-k+\sqrt{k^2-12}}{2}, x_2=\frac{-k-\sqrt{k^2-12}}{2} pro k^2-12 \geq 0, tedy pro k \leq -\sqrt{12} nebo k \geq \sqrt{12}.
- Lomený výraz má smysl, když jeho jmenovatel není roven nule, tedy když kvadratická rovnice nemá žádné řešení nebo x není rovno řešení této rovnice.
- Celkově má výraz \frac{1}{x^2+kx+3} smysl pokud k \in (-\sqrt{12},\sqrt{12}) nebo x \notin \{ x_1,x_2\}.
Určení podmínek lomeného výrazu \frac{1}{\frac{x-3}{x}}
- Výraz má smysl, pokud žádný zlomek nemá nulový jmenovatel.
- Jedná se o zlomek \frac{1}{\frac{x-3}{x}} se jmenovatelem \frac{x-3}{x} a také o zlomek \frac{x-3}{x} se jmenovatelem x.
- \frac{x-3}{x} by bylo rovno nule pro x=3.
- x by bylo rovno nule přímo pro x=0.
- Takže celkově podmínky, za kterých má smysl výraz ze zadání, jsou: x \neq 3, x \neq 0
Lomené výrazy: úpravy a výpočty
S lomenými výrazy počítáme podobně jako se zlomky, pouze musíme úpravy provádět s mnohočleny. Při úpravách často využíváme úpravy algebraických výrazů.
Krácení lomených výrazů
- Když je čitatel i jmenovatel lomeného výrazu vynásobený stejným výrazem, můžeme tento výraz zkrátit.
- Pozor, krátíme jen při násobení.
Příklad: úprava výrazu \frac{x+y}{x^2-y^2}
- Jmenovatel rozepíšeme pomocí vzorce: x^2-y^2=(x+y)(x-y)
- Dostáváme: \frac{\textcolor{#3498db}{x+y}}{\textcolor{#3498db}{(x+y)}(x-y)}
- Pokrátíme na: \frac{1}{x-y}
Příklad: nesprávná úprava výrazu \frac{x-2}{x^2-4}
- Nesprávným krokem by bylo vykrácení x, tedy například \frac{x-2}{x^{2}-4} nelze upravit na \frac{-2}{x-4}, protože x zde nemůžeme z čitatele a jmenovatele vytknout.
- Správným postupem je rozložení jmenovatele na součin \frac{x-2}{(x-2)(x+2)} a dále pokrácení \frac{\textcolor{#3498db}{x-2}}{\textcolor{#3498db}{(x-2)}(x+2)}=\frac{1}{x+2}.
Sčítání a odčítání lomených výrazů
- Při sčítání a odčítání lomených výrazů převedeme jmenovatele výrazů na společného jmenovatele.
- Výhodné je najít nejmenšího společného jmenovatele.
Příklad: úprava výrazu \frac{3}{4x} + \frac{2}{3x}
- Převedeme oba výrazy na společný jmenovatel: \frac{9}{12x} + \frac{8}{12x}
- Sečteme: \frac{9+8}{12x} = \frac{17}{12x}
Násobení lomených výrazů
Při násobení vynásobíme čitatele mezi sebou a jmenovatele mezi sebou.
Příklad: násobení \frac{x}{x+1}\cdot\frac{x-1}{x^3}
- vynásobíme čitatele původních lomených výrazů a získáme čitatele výsledku: x \cdot (x-1)
- vynásobíme jmenovatele původních lomených výrazů a získáme jmenovatele výsledku: (x+1) \cdot x^3
- celkově máme: \frac{x}{x+1}\cdot\frac{x-1}{x^3} = \frac{x (x-1)}{x^3 (x+1)}
- což ještě můžeme zkrátit na: \frac{x-1}{x^2 (x+1)}
Dělení lomených výrazů
Dělení lomeným výrazem převádíme na násobení převráceným lomeným výrazem.
Příklad: úprava výrazu \frac{1-x}{x}:\frac{x-1}{3x^2}
- Dělení převedeme na násobení převrácenou hodnotou \frac{1-x}{x}\cdot\frac{3x^2}{x-1}
- Vykrátíme \frac{1-x}{\textcolor{#3498db}{x}}\cdot\frac{3x^{\textcolor{#3498db}{2}}}{x-1}= \frac{(1-x)\cdot 3x}{x-1}
- A opět vykrátíme, protože výrazy 1-x a x-1 se liší pouze znaménkem
\frac{(1-x) \cdot 3x}{(x-1)}=\frac{\textcolor{#3498db}{(1-x)} \cdot3x}{\textcolor{#3498db}{(1-x)}\cdot(-1)}=-3x
Rovnice s neznámou x je zápis ve tvaru L(x) = P(x), kde L(x), P(x) jsou výrazy s proměnnou x. L(x) je levá strana rovnice, P(x) je pravá strana rovnice. Řešit rovnici znamená najít všechny hodnoty proměnné x, pro které výrazy L(x) a P(x) nabývají stejné hodnoty. Tato čísla nazýváme kořeny rovnice. Výpočet hodnot L(x) a P(x) pro konkrétní x se nazývá zkouška.
Příklad: 2x-7 = 5-4x
| levá strana | L(x) = 2x - 7 |
| pravá strana | P(x) = 5-4x |
| kořen (řešení) rovnice | x=2 |
| zkouška | L(x) = 2x-7 = 2\cdot 2 - 7= -3 |
| P(x) = 5-4x = 5 - 4\cdot 2 = -3 |
Řešení rovnic
Rovnice řešíme ekvivalentními úpravami, což jsou úpravy, které nemění množinu kořenů rovnice. Mezi takové úpravy patří například:
- výměna levé a pravé strany rovnice,
- přičtení nebo odečtení stejného výrazu k oběma stranám rovnice,
- vynásobení nebo vydělení obou stran rovnice nenulovým číslem.
Řešený příklad: 7x-1=4x+20
| Od obou stran rovnice odečteme 4x. | 7x-1-4x=4x+20-4x |
| 3x - 1 = 20 | |
| K oběma stranám rovnice přičteme 1. | 3x - 1 + 1 = 20 + 1 |
| 3x = 21 | |
| Obě strany rovnice vydělíme číslem 3. | 3x : 3 = 21 : 3 |
| x = 7 | |
| Řešení rovnice je x=7. |
Typy rovnic
Základní lineární rovnice obsahují pouze konstanty a násobky proměnné. Pro důkladné procvičení je v dělíme do několika skupin:
| podtéma | příklad |
|---|---|
| Jednokrokové rovnice | x + 2 = 5 |
| Základní rovnice s jednou neznámou | 2x - 7 = 5 -4x |
| Rovnice se závorkami | 2(x+3) = 12 -x |
| Rovnice se zlomky | \frac{x}{2} - \frac{x}{3} = 2 |
| Rovnice s neznámou ve jmenovateli | \frac{20}{x} + 2 = 7 |
| Rovnice s desetinnými čísly | 0{,}2x = 4{,}6 - 2{,}1x |
Další typy rovnic jsou pak uvedeny v sekci Pokročilé rovnice, jde například o rovnice s lomenými výrazy, soustavy dvou rovnic, kvadratické rovnice, exponenciální rovnice a logaritmické rovnice.
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 7.–9. ročník | základní práce s algebraickými výrazy, řešení jednoduchých lineárních rovnic | |
| 8.–9. ročník | složitější rovnice, použití rovnic pro řešení problémů |
Jednokrokové rovnice
Nejjednodušší rovnice jako x+2 = 5 nebo 3x = 15 vedou na jednokrokové řešení, tj. stačí provést jednu úpravu rovnice (např. odečtení čísla 2 od obou stran rovnice v prvním případě). Tyto rovnice lze vesměs řešit snadno i intuitivní úvahou (pro jaké číslo platí, že když k němu přičtu dvojku, dostanu pětku?). Slouží tak jako dobrý výchozí bod pro seznámení s tématem rovnic.
NahoruZákladní rovnice s jednou neznámou
Nejjednodušší rovnice obsahují pouze lineární výrazy, tj. vyskytují se v nich pouze konstanty a násobky proměnné x. Rovnici upravujeme pomocí ekvivalentních úprav: přičítání a odčítání stejného výrazu k oběma stranám rovnice, úpravy výrazů na levé a pravé straně. Pomocí takových úprav ji převedeme do tvaru x = a, kde a je řešení.
Řešený příklad: 3x-1=2x+5
| Od obou stran rovnice odečteme 2x. | 3x-1-2x=2x+5-2x |
| x-1=5 | |
| K oběma stranám rovnice přičteme 1. | x-1+1=5+1 |
| x=6 | |
| Řešení rovnice je x=6. |
Řešený příklad: 2x-7 = 5-4x
| K oběma stranám rovnice přičteme 4x. | 2x - 7 + 4x = 5 - 4x + 4x |
| 6x - 7 = 5 | |
| K oběma stranám rovnice přičteme 7. | 6x - 7 + 7 = 5 + 7 |
| 6x = 12 | |
| Obě strany rovnice vydělíme číslem 6. | 6x : 6 = 12 : 6 |
| x = 2 | |
| Řešení rovnice je x=2. |
Počet řešení
U základních lineárních rovnic mohou nastat tři případy:
- Rovnice nemá žádné řešení, např. x+2=x+3.
- Rovnice má nekonečně mnoho řešení, např. u rovnice x+1+x = 2x+1 je řešením rovnice je libovolné číslo.
- Rovnice má právě jedno řešení, např. výše uvedená rovnice 2x-7 = 5-4x má jediné řešení x=2.
Časté chyby
Mezi časté chyby při řešení rovnic patří:
- provedení úpravy (přičtení čísla, vydělení čísel) pouze na jedné straně rovnice,
- chybné zkombinování konstant a výrazů s proměnnou x, např. úprava 3x + 2 na 5x,
- špatné znaménko u výrazu při převádění z jedné strany rovnice na druhou.
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření

Rovnice se závorkami
Rovnice se závorkami můžeme řešit stejným způsobem jako základní rovnice, pouze jako první krok odstraníme závorky.
Řešený příklad: 2(x+3) = 12 - x
| Zadání: | 2(x+3) = 12 - x |
| Roznásobíme závorku na levé straně: | 2x+6 = 12 - x |
| Následně řešíme stejně jako základní rovnici: | 3x+6 = 12 |
| 3x = 6 | |
| x = 2 |
V některých případech si však můžeme ušetřit práci, pokud závorky neroznásobíme. Například v rovnici 3(x+1) = 18 je výhodnější nejdříve rovnici podělit číslem 3, čímž dostaneme x+1 = 6, z čehož již snadno dostaneme x=5.
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruRovnice s neznámou ve jmenovateli
Pokud rovnice obsahuje zlomek, ve kterém se vyskytuje neznámá ve jmenovateli, musíme rovnici nejdříve vynásobit jmenovatelem (případně společným násobkem všech jmenovatelů). Tím rovnici převedeme na základní rovnici, kterou řešíme běžným postupem.
Řešený příklad
| Zadání: | \frac{20}{x} +2 = 7 |
| Vynásobíme obě strany rovnice jmenovatelem x: | 20 + 2x = 7x |
| Dále řešíme běžnými úpravami: | 20 = 5x |
| x = 4 |
Rovnice se zlomky
Rovnice se zlomky řešíme stejnými postupy jako základní rovnice, pouze při tom používáme operace se zlomky.
Často se můžeme operacím se zlomky vyhnout tak, že celou rovnici nejprve roznásobíme společným násobkem všech jmenovatelů zlomků.
Řešený příklad
| Zadání: | \frac{x}{2} - \frac{x}{3} = 2 |
| Jmenovatelé ve zlomcích jsou 2 a 3, společný násobek je 6. Roznásobíme tedy rovnici číslem 6: | 3x - 2x = 12 |
| Řešení: | x=12 |
Rovnice s desetinnými čísly
Rovnice s desetinnými čísly řešíme stejnými postupy jako základní rovnice, pouze při tom máme na paměti pravidla pro sčítání, odčítání, násobení a dělení desetinných čísel. Často si můžeme řešení usnadnit tím, že celou rovnici vynásobíme deseti (případně vyšší mocninou desítky).
Řešený příklad
| Zadání: | 0{,}2x+2{,}1x=4{,}6 |
| Vynásobíme deseti: | 2x+21x=46 |
| Řešíme jako základní rovnici: | 23x = 46 |
| x = 2 |
Pokročilé rovnice
Nejjednodušším typem rovnic jsou lineární rovnice, které obsahují pouze konstanty a násobky jedné proměnné. Ty jsou důkladně pokryty v základním tématu o rovnicích. Zde jsou pokryty rovnice složitějších typů:
| téma | příklad |
|---|---|
| Rovnice s lomenými výrazy | \frac{-1}{2} = \frac{x+1}{1-x} |
| Dvě rovnice o dvou neznámých | \begin{array}{lll}x+y &=&8\\2x-y &=&1\end{array} |
| Kvadratické rovnice | 2x^2+6x-20 = 0 |
| Exponenciální rovnice | 3^{2x}-3^x=6 |
| Logaritmické rovnice | 2 \cdot \log_6(x-2) = \log_6(14-x) |
| Goniometrické rovnice | \cos^2 x -6\cos x+5=0 |
Rovnice s lomenými výrazy
Rovnice s lomenými výrazy řešíme stejnými postupy jako základní rovnice.
Užitečným (avšak ne vždy nezbytným) prvním krokem bývá roznásobení obou stran rovnice společným násobkem všech jmenovatelů lomených výrazů.
Podmínky řešitelnosti
Aby lomený výraz dával smysl, nesmí být jmenovatel roven nule. Po vyřešení rovnice tedy musíme zkontrolovat, že výsledné řešení tuto podmínku splňuje pro všechny jmenovatele v rovnici.
Řešený příklad
| Zadání: | \frac{-1}{2} = \frac{x+1}{1-x} |
| Jmenovatelé jsou 2 a 1-x, společný násobek je 2(1-x). Roznásobíme tedy rovnici 2(1-x). | \frac{-1}{2}\cdot 2(1-x) = \frac{x+1}{1-x} \cdot 2(1-x) |
| Pokrátíme obě strany. | (-1)\cdot (1-x) = (x+1)\cdot 2 |
| Roznásobíme obě strany. | x-1 = 2x +2 |
| Převedeme x na jednu stranu, konstanty na druhou. | x = -3 |
Dvě rovnice o dvou neznámých
Soustava dvou rovnic o dvou neznámých je podobná jako základní rovnice, jen máme místo jedné proměnné x navíc i proměnnou y a rovnice jsou dvě. Podobně jako rovnice o jedné proměnné může mít celou řadu různých typů, i dvě rovnice o dvou neznámých mohou být lineární, kvadratické, logaritmické a jiné. Většinou se však procvičují pouze základní lineární rovnice. Pokud totiž dobře zvládneme jejich řešení, můžeme naučené postupy použít i na složitější rovnice. Základní metody řešení soustavy dvou rovnic jsou dosazovací metoda a sčítací metoda.
| Příklad soustavy dvou rovnic o dvou neznámých: | x+y=8 |
| 2x-y=1 |
Dosazovací metoda
Při řešení dosazovací metodou vyjádříme z jedné rovnice jednu neznámou pomocí druhé. Toto vyjádření pak dosadíme do druhé rovnice, čímž dostaneme obyčejnou jednu rovnici o jedné neznámé. Ukázka postupu na uvedeném příkladě:
| Z první rovnice vyjádříme y: | y = 8 -x |
| Dosadíme do druhé rovnice: | 2x - y = 1 |
| 2x - (8-x) = 1 | |
| Řešíme jako obyčejnou rovnici: | 3x = 9 |
| x = 3 | |
| Nalezenou hodnotu dosadíme do výrazu pro y: | y = 8 - x = 8 - 3 = 5 |
Sčítací metoda
Při řešení sčítací metodou sečteme (či odečteme) odděleně levé a pravé strany obou rovnic. Tato úprava vede k cíli, pokud nám při této operaci jedna z proměnných vypadne. V některých případech je proto nutné nejdříve jednu z rovnic vynásobit vhodným číslem. V případě naší ukázkové soustavy stačí rovnice prostě sečíst. Tím dostaneme 3x = 9, odtud x=3 a dosazením pak již dopočítáme y.
NahoruKvadratické rovnice
Pojmy
Kvadratická rovnice je rovnice, ve které se vyskytuje jedna neznámá ve druhé mocnině. Základní tvar kvadratické rovnice je: ax^2+bx+c=0, kde a, b, c jsou reálná čísla a a\neq 0. Pro kvadratické rovnice používáme následující názvosloví:
- ax^2 je kvadratický člen,
- bx je lineární člen,
- c je absolutní člen.
Příklad: 2x^2+6x-20 = 0
| kvadratický člen | 2x^2 |
| lineární člen | 6x |
| absolutní člen | -20 |
| řešení rovnice | x=2 a x=-5 |
Speciální typy kvadratických rovnic:
- Pokud je b=0 nazýváme rovnici ryze kvadratickou: ax^2+c=0.
- Pokud je c=0 mluvíme o rovnici bez absolutního členu: ax^2+bx=0.
Řešení kvadratické rovnice
Každou kvadratickou rovnici lze řešit pomocí výpočtu diskriminantu D. Pro něj platí: D=b^2-4\cdot a\cdot c. Mohou nastat 3 situace:
- D \lt 0 – rovnice nemá v reálných číslech řešení.
- D = 0 – rovnice má jeden dvojnásobný kořen.
- D \gt 0 – rovnice má dva různé reálné kořeny.
Pro kořeny rovnice platí:
- x_1=\frac{-b+\sqrt{D}}{2a}
- x_2=\frac{-b-\sqrt{D}}{2a}
Řešený příklad: x^2+2x-3=0
- Pro tuto rovnici a=1, b=2, c=-3.
- Diskriminant D=b^2-4ac = 2^2-4\cdot 1\cdot(-3) = 4+12=16.
- D>0, rovnice má tedy dvě řešení.
- x_1 = \frac{-b+\sqrt{D}}{2a} = \frac{-2+\sqrt{16}}{2\cdot 1} = 1
- x_2 = \frac{-b-\sqrt{D}}{2a} = \frac{-2-\sqrt{16}}{2\cdot 1} = -3
- Řešení rovnice jsou tedy hodnoty 1 a -3.
Vietovy vzorce
Kvadratické rovnice můžeme řešit i bez počítání diskriminantu za využití Vietových vzorců. Pro kořeny rovnice platí: x_1+x_2=-\frac{b}{a}, x_1\cdot x_2=\frac{c}{a}. V případě a=1: x_1+x_2=-b, x_1\cdot x_2=c.
NahoruExponenciální rovnice
Exponenciální rovnice má neznámou v exponentu (mocniteli), např. 3^{2x}-3^x=6.
Exponenciální rovnice lze řešit různými způsoby. Nejjednodušší je řešení rovnice se stejnými základy. Pokud se nám podaří rovnici převést na tvar a^{f(x)} = a^{g(x)}, můžeme se zbavit exponenciální funkce a řešit f(x) = g(x). Složitější způsoby řešení exponenciálních rovnic jsou logaritmování a substituce.
NahoruLogaritmické rovnice
Logaritmická rovnice je taková, kde neznámá vystupuje jako argument logaritmické funkce, např. 2 \cdot \log_6(x-2) = \log_6(14-x).
U logaritmických rovnic musíme dávat pozor na podmínky řešení. Argument každého logaritmu totiž musí být vždy kladné číslo. V uvedeném příkladě tedy musí platit x-2>0 a současně 14-x > 0.
Logaritmické rovnice řešíme za využití vlastností logaritmické funkce a jejího vztahu k exponenciální funkci. Dílčí způsoby, jak řešit logaritmické rovnice:
- Převedeme rovnici na tvar \log_a f(x) = c. Pak musí platit f(x) = a^c.
- Převedeme rovnici na tvar \log_a f(x) = \log_a g(x). Pak musí platit f(x) = g(x).
Goniometrické rovnice
V goniometrických rovnicích se neznámá objevuje v argumentu goniometrických funkcí, např. \sin x = 2 \cos (x+\pi). Pokud není uvedeno jinak, předpokládáme, že jsou argumenty goniometrických funkcí v radiánech.
Zápis výrazů s goniometrickými funkcemi a priorita operací
V zápisu výrazů s goniometrickými funkcemi často vynecháváme závorky okolo argumentu (píšeme \sin x místo \sin(x)), pokud je jasné, co je argumentem goniometrické funkce.
Je důležité si při čtení výrazů s goniometrickými funkcemi uvědomit, která operace se bude provádět dříve. Například \cos x + 2 není totéž jako \cos(x+2), protože funkci \cos aplikujeme u výrazu bez závorek dříve než sčítání nebo odčítání. Zvyklost je chápat \sin 2x jako \sin (2x), ale když máme výraz \sin x \sin x, chápeme jej jako \sin (x) \cdot \sin (x).
Mocniny hodnot goniometrických funkcí také mají svůj speciální zápis.
| \sin^2 x | druhá mocnina výrazu \sin x |
| \sin x + 1 | součet \sin x a 1 |
| \sin (x+1) | sinus součtu x+1 |
| \sin 3y | sinus součinu 3\cdot y |
| \sin x \tan y | součin výrazů \sin x a \tan y |
Tipy pro řešení goniometrických rovnic
Můžou se kromě znalostí o hodnotách, vlastnostech a grafech goniometrických funkcí hodit také
- goniometrické vzorce,
- tzv. goniometrická jednička – vztah \sin^2 x + \cos^2 x = 1 platí pro libovolné reálné x,
- substituce, např. \cos^2 x -2 \cos x +1 = 0 můžeme nejdříve řešit jako kvadratickou rovnici t^2 -2t +1 pro t=\cos x, a teprve pro známé hodnoty řešení t hledat odpovídající hodnoty x.
Úlohy s rovnicemi
Rovnice jsou velmi obecný nástroj, kterým v matematice řešíme spoustu problémů. V tomto tématu nabízíme procvičení některých obecných dovedností souvisejících s využitím rovnic při řešení problémů. Dále pak nabízíme procvičení na několika klasických typech slovních úloh.
| téma | popis typu úloh / ilustrační příklad |
|---|---|
| Zápis zadání pomocí rovnice | rozcvička na řešení úloh: přepis textu zadání do tvaru rovnice |
| Vyjádření neznámé z rovnice | trénink obecného postupu, jak ze zápisu rovnice dostat to, co nás zajímá |
| Myslím si číslo | Myslím si číslo. Když od něj odečtu 6 a výsledek vydělím dvěma, dostanu 2… |
| Úlohy o směsích | Teta dělá tyčinky vážící 9 gramů a kuličky vážící 6 gramů, celkem udělala 300 kusů vážích 2400 gramů… |
| Společná práce | Petr a Pavel společně natírají plot, Petr by plot sám natřel za 6 hodin… |
| Úlohy s pohybem | Jana vyrazila pěšky za babičkou, Alena o hodinu později na kole… |
Vyjádření neznámé z rovnice
Často máme rovnici s několika neznámými a potřebujeme vyjádřit jednu z nich. Typicky na takovou situaci narazíme ve fyzice. Máme třeba vzorec pro výpočet dráhy na základě času: s = \frac{1}{2}gt^2. Z této rovnice chceme vyjádřit čas v závislosti na dráze, tj. t = \sqrt{\frac{2s}{g}}.
Při řešení tohoto problému používáme stejné postupy jako při řešení rovnic s číselnými koeficienty, pouze místo přímých výpočtů provádíme úpravy výrazů.
Řešený příklad
| Máme vyjádřit a z rovnice: | c-(a+b)=2b |
| Zbavíme se závorky: | c-a-b=2b |
| Převedeme všechny proměnné krom a na druhou stranu: | -a=3b-c |
| Vynásobíme -1: | a=c-3b |
Myslím si číslo
Slovní úlohy typu „myslím si číslo“ spočívají v tom, že si vypravěč myslí tajné číslo, řekne nám o něm informaci a my musíme číslo odhalit.
Příklad: jaké číslo si myslím?
Myslím si číslo. Když od něj odečtu 6 a výsledek vydělím dvěma, dostanu 2. Jaké číslo si myslím?
Řešení:
- v tomto příkladu můžeme k původnímu myšlenému číslu dojít tak, že postupně odebereme provedené operace (začneme od nejpozdější, tj. dělení dvěma)
- před dělením dvěma jsme měli číslo 2\cdot 2 = 4
- číslo 4 vzniklo jako výsledek odečtení čísla 6 od myšleného čísla ? - 6 = 4
- takže myšlené číslo bylo 10
Jednoduché úlohy tohoto typu lze řešit úvahou z hlavy. Pro složitější úlohy se hodí zapsat úlohu pomocí rovnice.
NahoruÚlohy o směsích
Úlohy o směsích jsou speciální typ slovních úloh, ve kterých pracujeme se směsí dvou (nebo více) typů objektů, které mají trochu jiné vlastnosti. Může jít o směs roztoků, čokolád, zeleniny nebo třeba tučňáků.
Příklad úlohy o směsích: tučňáci
V Antarktidě žijí vedle sebe tučňáci císařští, kteří váží 35 kilogramů, a menší tučňáci kroužkoví, ti váží pouze 5 kilogramů. Včera objevilo 60 tučňáků obrovskou starou váhu ze ztroskotané nákladní obchodní lodi. Když na ni všichni vlezli, váha ukázala 840 kilogramů. Kolik bylo v objevitelské tučňáčí bandě tučňáků kroužkových?
Řešení:
- označíme si počet tučňáků císařských x
- počet tučňáků kroužkových je pak 60-x
- napíšeme si rovnici pro celkovou váhu tučňáků na váze v kg: 35 \cdot x + 5 \cdot (60-x) = 840
- levou stranu rovnice upravíme: 30x + 300 = 840
- odečteme od obou stran 300 a potom obě strany vydělíme 30, dostaneme: x = 18
- takže tučňáků císařských je 18 a tučňáků kroužkových je 60-18=42
Úlohy o směsích řešíme pomocí rovnic.
NahoruSpolečná práce
Úlohy o společné práci jsou speciální typ slovních úloh, ve kterých typicky vystupuje několik pracantů a máme za úkol určit, jak dlouho by jim trvala práce společně.
Příklad: okopávání záhonu
Na hodině bylinkářství v kouzelnické škole v Bradavicích žáci okopávali záhony s mandragorami. Nevillovi trvalo okopání záhonu 40 minut, Draco Malfoy zvládl stejně velký záhon za 24 minut. Kolik minut by jim trvalo okopání záhonu, kdyby na něm pracovali společně?
Řešení:
- označme si počet minut, který by jim společně trvalo okopat záhon x
- rychlost Nevilla v okopávání záhonů je \frac{1}{40} (1 záhon za 40 minut)
- rychlost Draca v okopávání záhonů je \frac{1}{24} (1 záhon za 24 minut)
- jejich společná rychlost je \frac{1}{40} + \frac{1}{24} (což odpovídá 1 záhonu za x minut)
- máme tedy rovnici: \frac{1}{40} + \frac{1}{24} = \frac{1}{x}
- na levé straně je po převedení na společného jmenovatele 120 a sečtení zlomek \frac{3+5}{120}, tedy \frac{8}{120}, to je \frac{1}{15}.
- je tedy \frac{1}{15} = \frac{1}{x}, tj. x=15
- společně by Neville a Draco okopali záhon za 15 minut
Úlohy o společné práci řešíme za využití nepřímé úměry a zlomků.
NahoruNerovnice
Rovnice s neznámou x zapisujeme ve tvaru L(x) = P(x), kde L(x), P(x) jsou výrazy s proměnnou x. Nerovnice jsou podobné, jen v nich je mezi levou a pravou stranou místo rovnosti = některá z nerovností \lt, \leq, \gt, \geq.
| podtéma | příklady, pojmy |
|---|---|
| Nerovnice: zápis řešení | zápis řešení pomocí intervalů, např. (-\infty, 3) |
| Lineární nerovnice | x + 5 \leq 12 |
| Nerovnice: ekvivalentní úpravy | postupné kroky při řešení nerovnic, násobení záporným číslem |
| Nerovnice s absolutní hodnotou | |x-2| > 4 - x |
| Kvadratické nerovnice | -x^2+x \geq -2 |
Aritmetická a geometrická posloupnost
Aritmetická a geometrická posloupnost jsou posloupnosti čísel, jejichž členy – čísla a_1, a_2, \ldots, a_n, \ldots se dají všechny odvodit z prvního členu podle jednoduchých pravidel zahrnujících sčítání (aritmetická posloupnost), resp. násobení (geometrická posloupnost).
Aritmetická posloupnost
V aritmetické posloupnosti je stálý rozdíl mezi dvěma po sobě jdoucími členy. Tento rozdíl se obvykle značí d a nazývá diference.
- rekurentní vzorec: a_n = a_{n-1} + d
- vzorec pro n-tý člen: a_n = a_1+ (n-1)\cdot d
Příklady aritmetických posloupností
| posloupnost | a_1 | d |
| 1, 3, 5, 7, 9, 11, \ldots | 1 | 2 |
| 20, 17, 14, 11, 8, \ldots | 20 | -3 |
| 300, 305, 310, 315, 320, \ldots | 300 | 5 |
Geometrická posloupnost
V geometrické posloupnosti je stálý poměr mezi dvěma po sobě jdoucími členy. Jejich podíl se obvykle značí q a nazývá kvocient.
- rekurentní vzorec: a_n = q \cdot a_{n-1}
- vzorec pro n-tý člen: a_n = q^{n-1}\cdot a_1
Příklady geometrických posloupností
| posloupnost | a_1 | q |
| 1, 2, 4, 8, 16, 32, \ldots | 1 | 2 |
| 1000, 100, 10, 1, 0{,}1, 0{,}01, \ldots | 1000 | 0{,}1 |
| 5, 15, 45, 135, 405, \ldots | 5 | 3 |
| 8, -8, 8, -8, 8, -8, \ldots | 8 | -1 |
Zápis posloupností
Posloupnost je sada objektů, ve kterých závisí na pořadí a objekty se mohou opakovat. Posloupnost může být konečná i nekonečná. Členy posloupnosti typicky zapisujeme pomocí indexů: a_n značí n-tý člen posloupnosti a.
Posloupnosti můžeme zapsat různými způsoby:
- výčtem členů: a = (7, 10, 13, 16, 19, 22)
- vzorcem pro n-tý člen: a_n = 4 + 3\cdot n
- rekurentně (začátek posloupnosti a způsob výpočtu dalších členů z předchozích): a_1 = 7, a_n = a_{n-1} + 3
Příklady:
- 8, 18, 28, 38, 48, 58, … (aritmetická posloupnost s počáteční hodnotou 8 a diferencí 10)
- 3, 6, 12, 24, 48, 96, … (geometrická posloupnost s počáteční hodnotou 3 a kvocientem 2)
- 1, 1, 2, 3, 5, 8, 13, 21, 34, … (Fibonacciho posloupnost, a_n = a_{n-1} + a_{n-2})
- 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, … (periodická posloupnost)
Existuje celá řada zajímavých posloupností. Mají dokonce svoji vlastní encyklopedii.
Nahoru
