Hodnoty goniometrických funkcí

umime.to/F1F

Často používané hodnoty goniometrických funkcí ilustruje tento obrázek jednotkové kružnice:

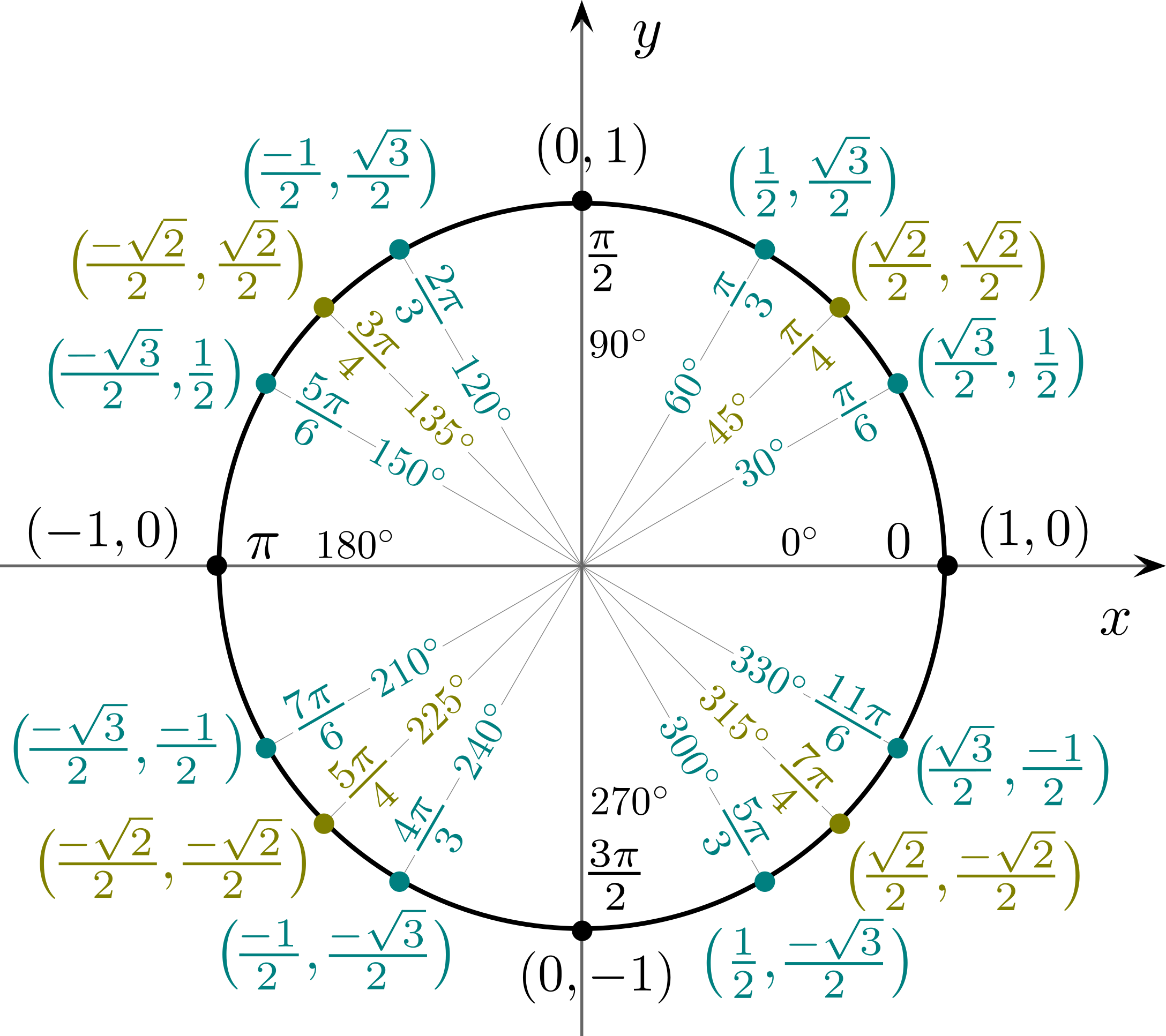
Polopřímka, která svírá úhel \alpha s kladnou částí osy x a začíná v počátku souřadnic, protíná jednotkovou kružnici v bodě se souřadnicemi [\cos \alpha; \sin \alpha], neboli:

x-ová souřadnice bodu odpovídá hodnotě \cos daného úhlu,
y-ová souřadnice bodu odpovídá hodnotě \sin daného úhlu.

Příklad: sinus a kosinus úhlu 30°

Polopřímka, která svírá s kladnou částí osy x úhel 30° (to je \frac{\pi}{6} radiánů), protíná jednotkovou kružnici v bodě [\frac{\sqrt{3}}{2}; \frac12]. Takže máme:

\cos 30^{\circ} = \frac{\sqrt{3}}{2}
\sin 30^{\circ} = \frac12

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Hodnoty goniometrických funkcí

Rozhodovačka • těžké

Pexeso

Hledání dvojic, které k sobě patří.

Hodnoty goniometrických funkcí

Pexeso • těžké

Předcházející

Navazující

Cvičení

Hodnoty goniometrických funkcí

umime.to/F1F

Rozhodovačka