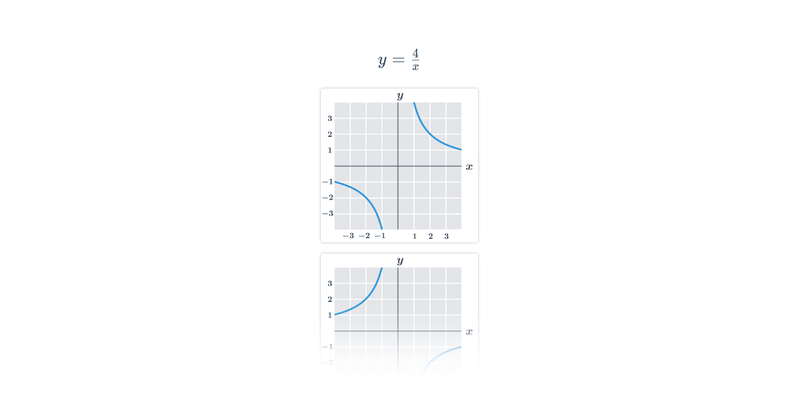
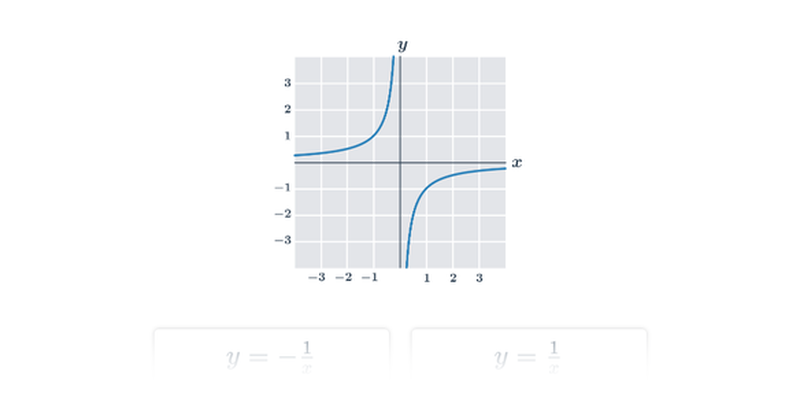
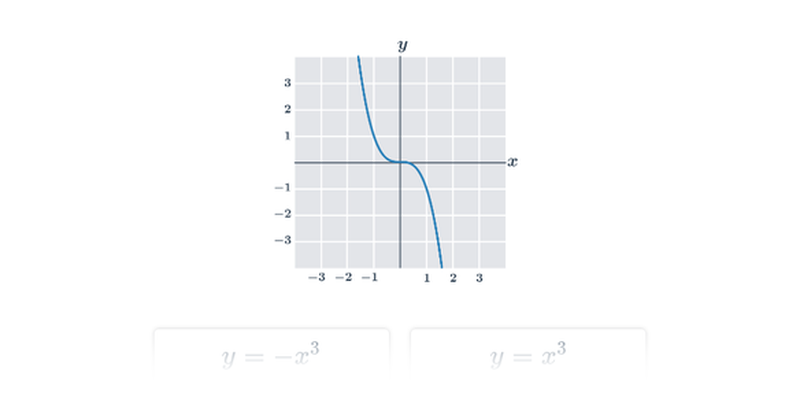
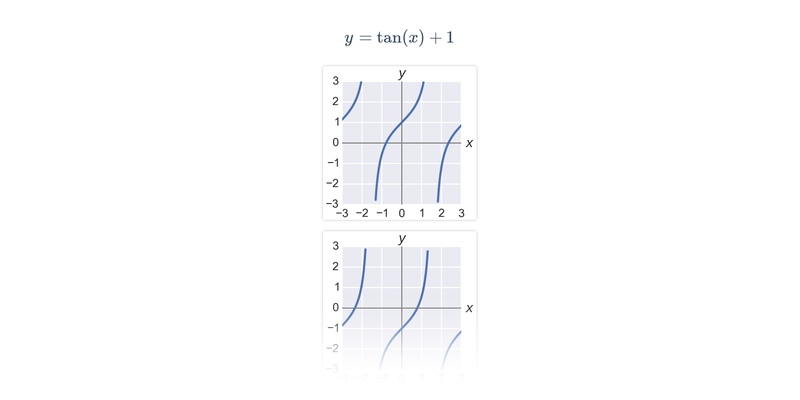
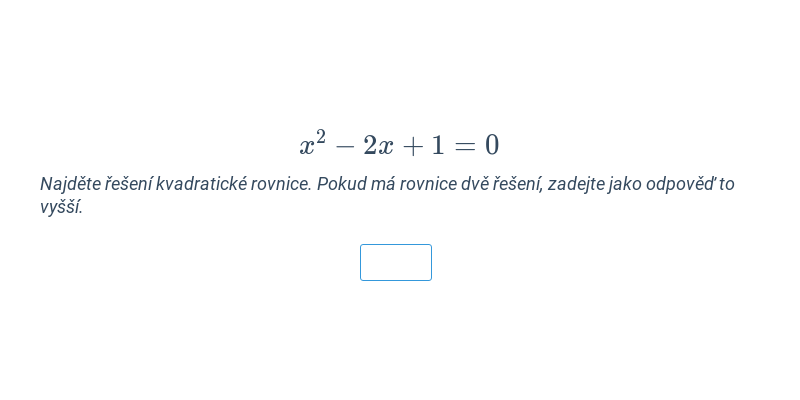
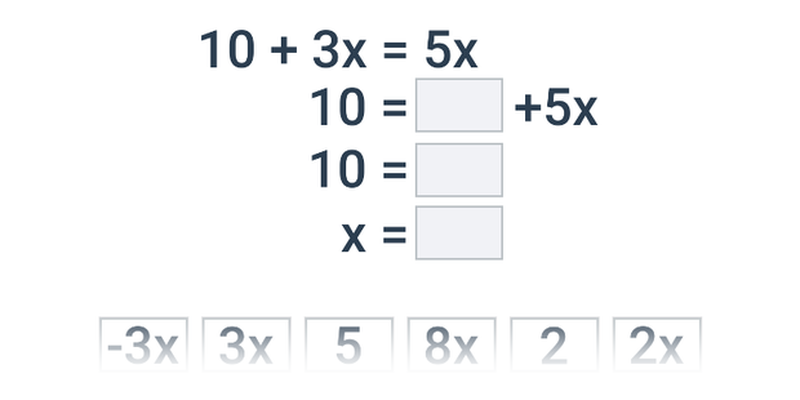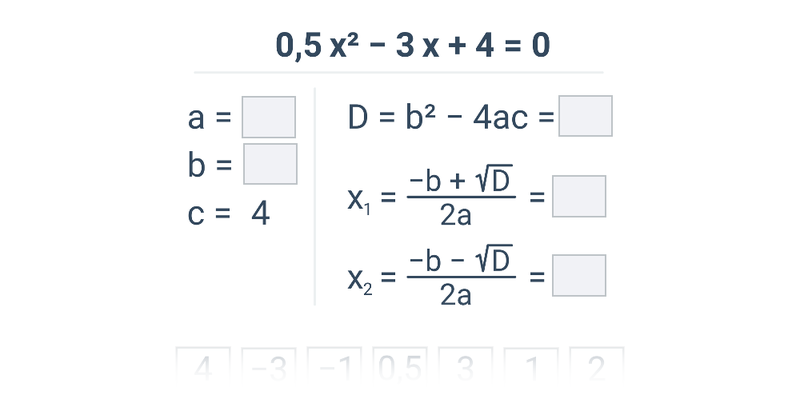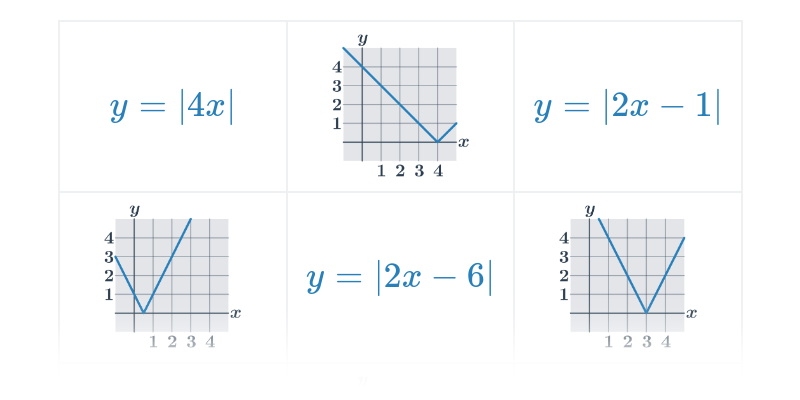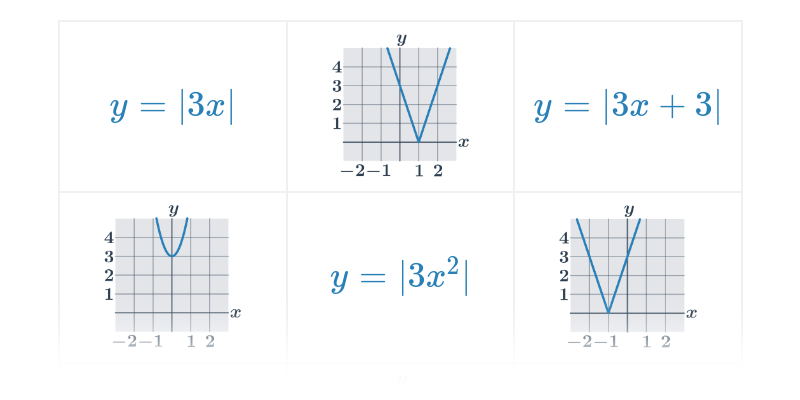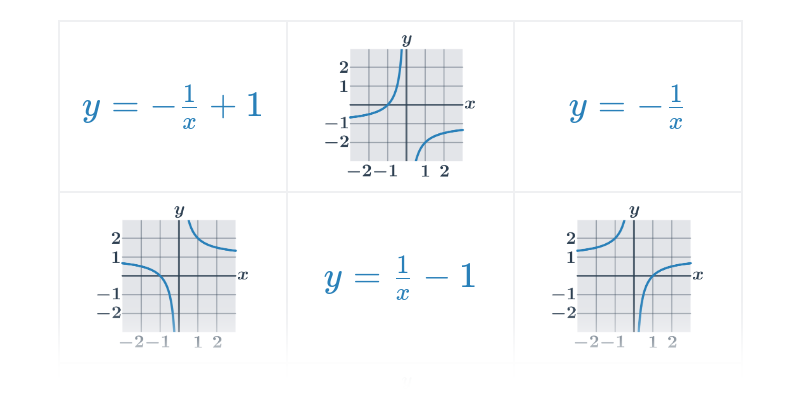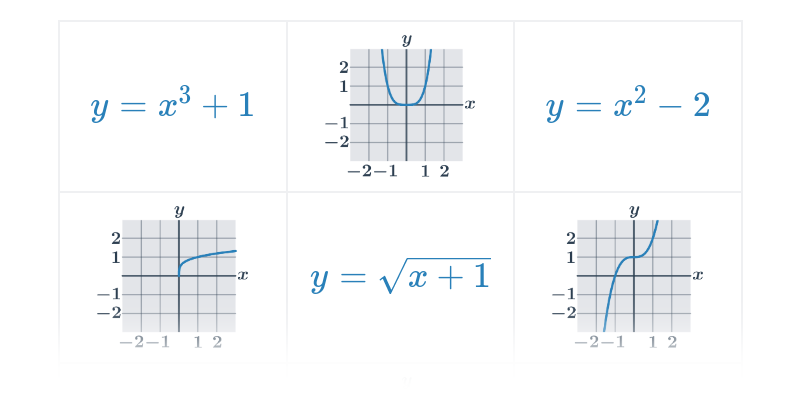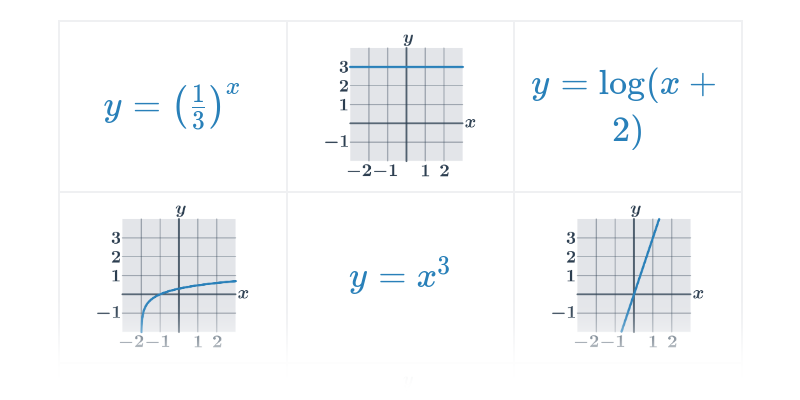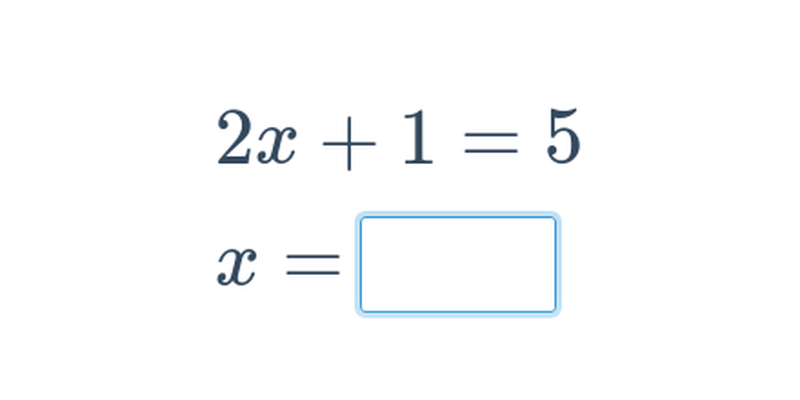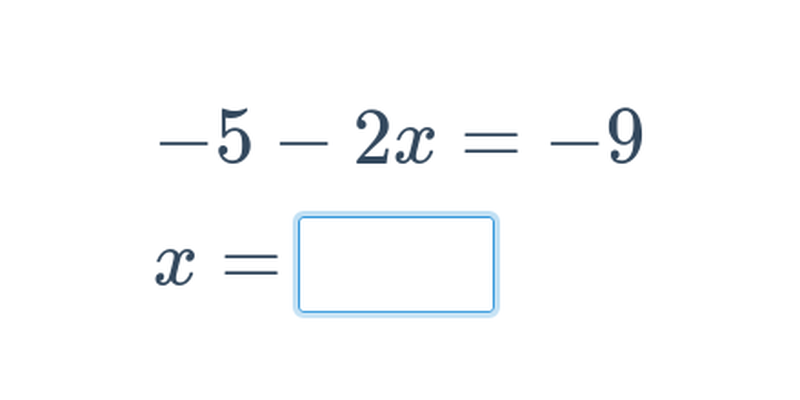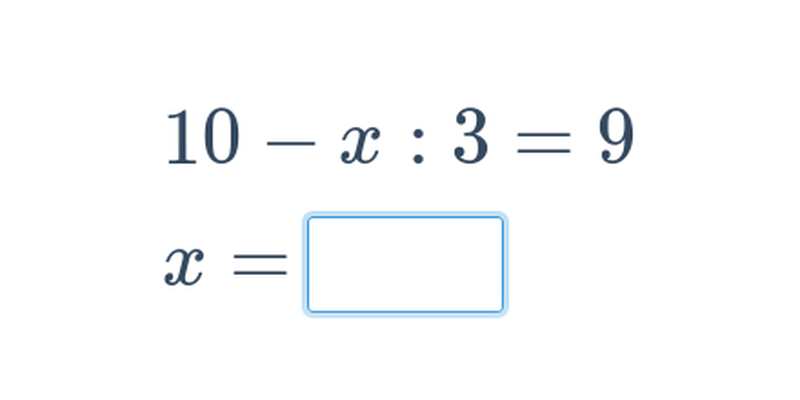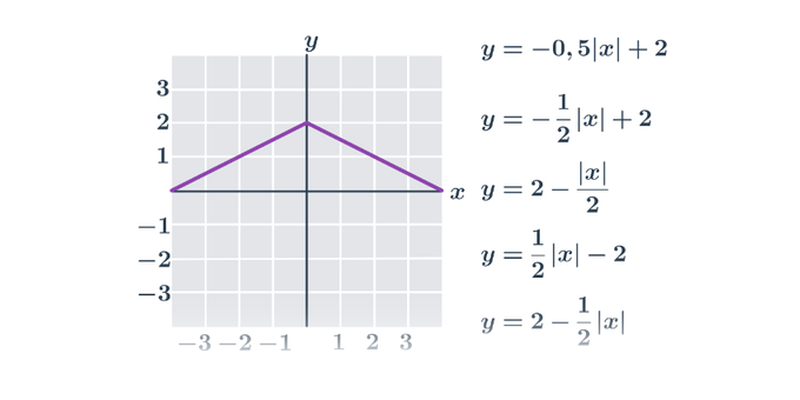Funkce
F21Funkce je speciální typ závislosti, při které je každé hodnotě z jedné množiny (definičního oboru funkce) přiřazena právě jedna hodnota z druhé množiny (oboru hodnot).
V matematice obvykle pracujeme s funkcemi nad množinami čísel, kde vztah mezi x a y popisuje matematický výraz, píšeme ve tvaru y=f(x). Definiční obor je množina všech hodnot x, které uvažujeme (např. množina všech x pro která má výraz f(x) smysl), označujeme D(f). Obor hodnot je množina všech funkčních hodnot y, označujeme H(f).
Procvičit si Co je funkce? lze v tématu Funkce: základy.
Mezi základní typy funkcí, se kterými se v matematice setkáme, patří:
| Typ | Příklad |
|---|---|
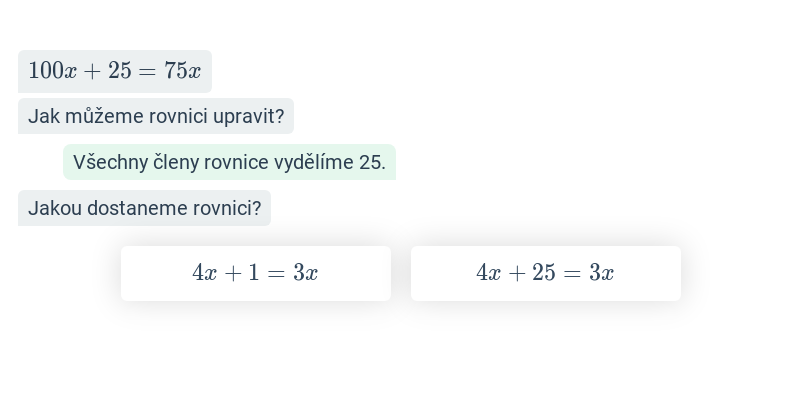
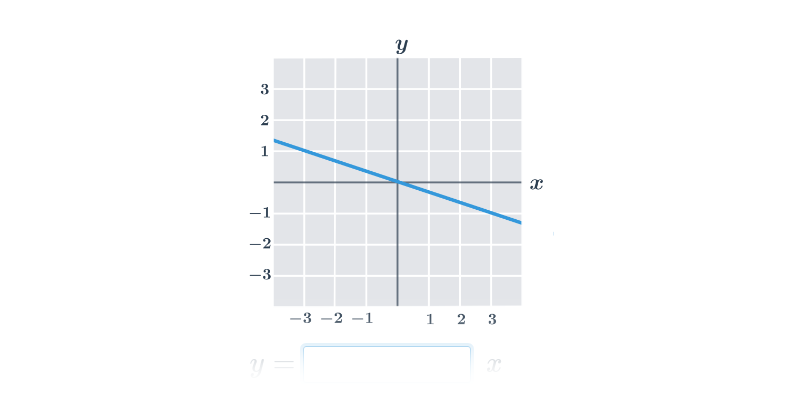
| Lineární funkce | f(x) = 3x + 1 |
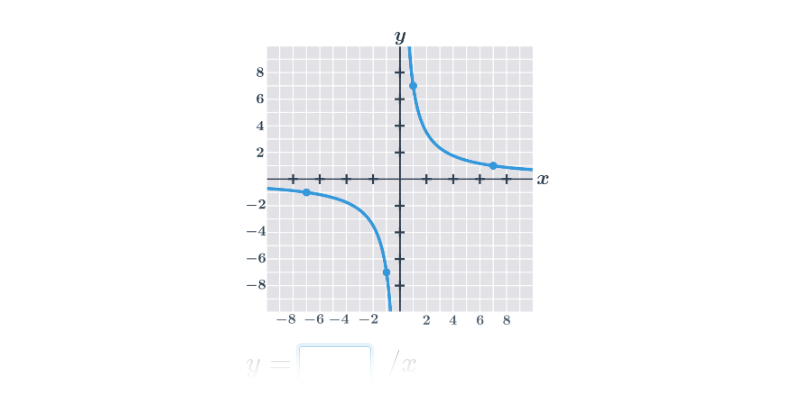
| Lineární lomené funkce | f(x) = \frac{2x -4}{x+3} |
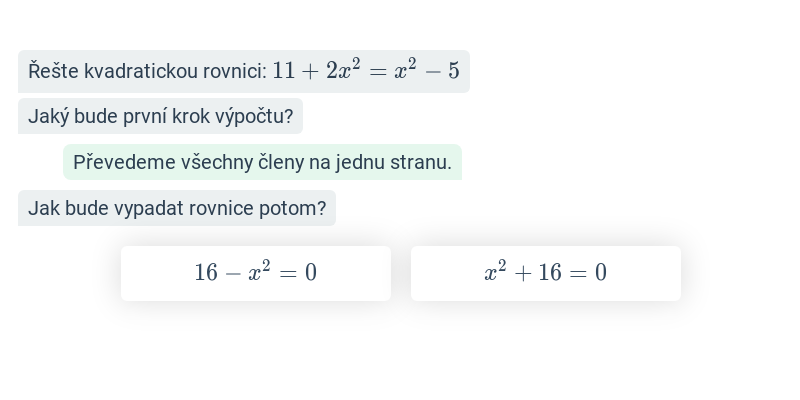
| Kvadratické funkce | f(x) = x^2 - 4x + 3 |
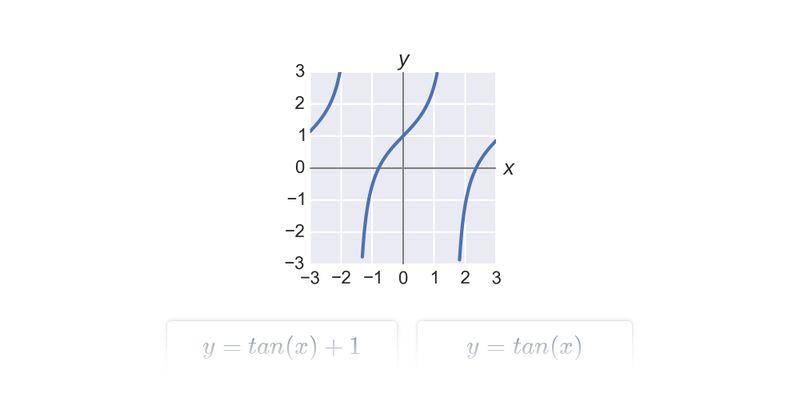
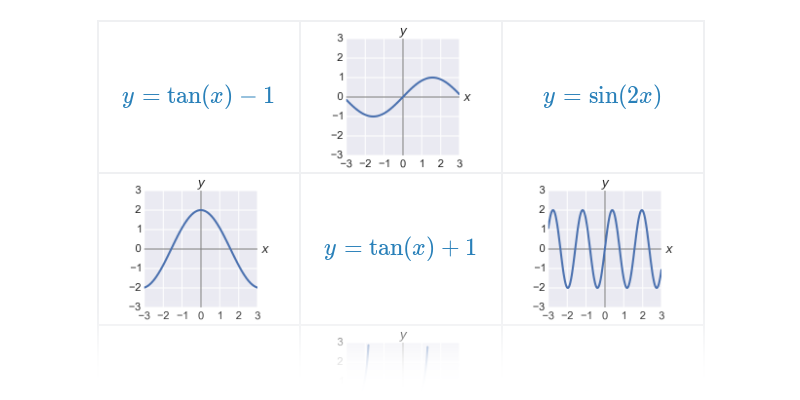
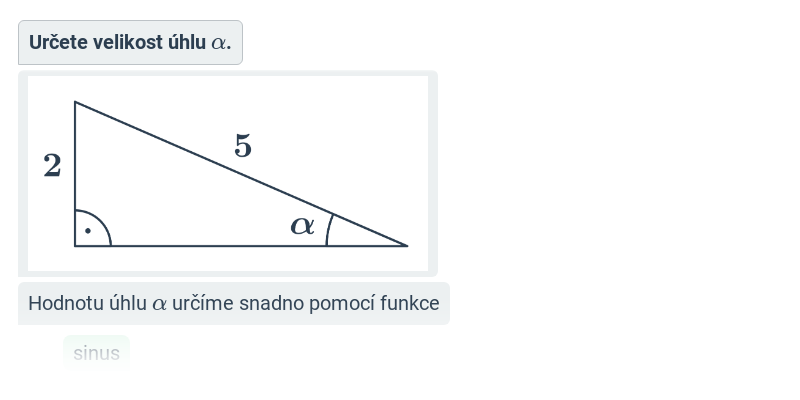
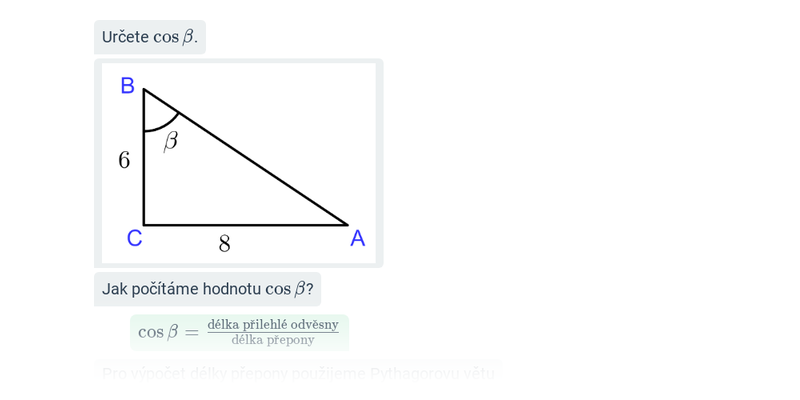
| Goniometrické funkce | f(x) = \sin x |
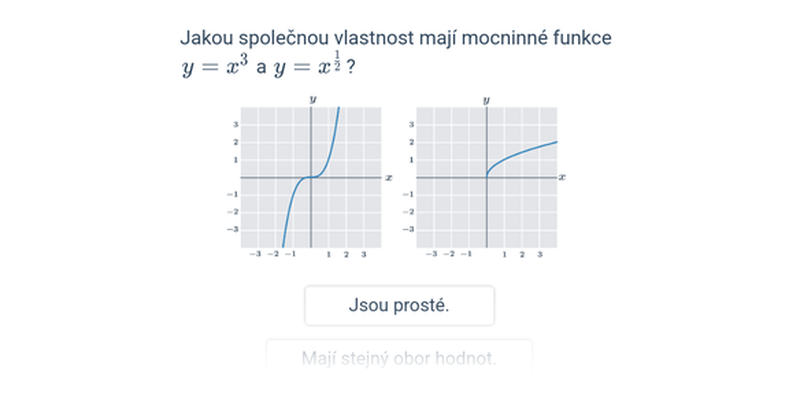
| Mocninné funkce | f(x) = x^3, f(x) = \sqrt{x} |
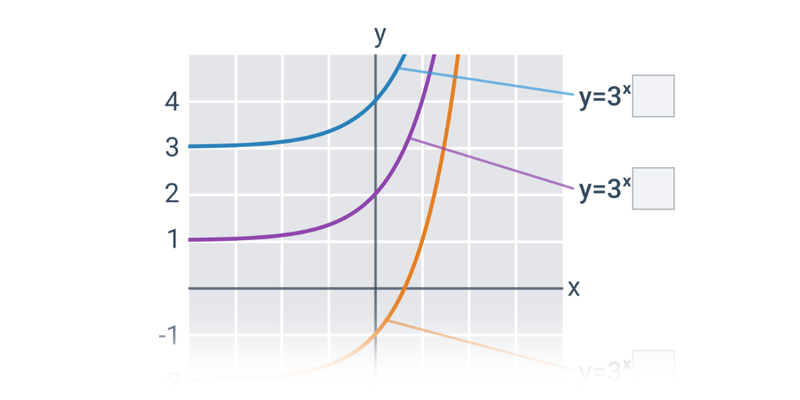
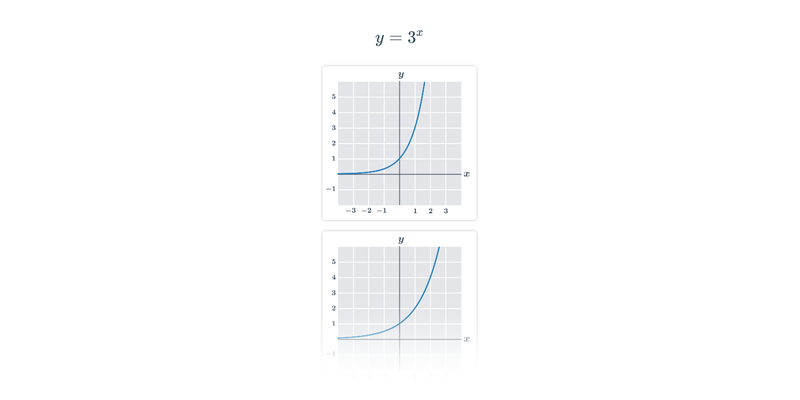
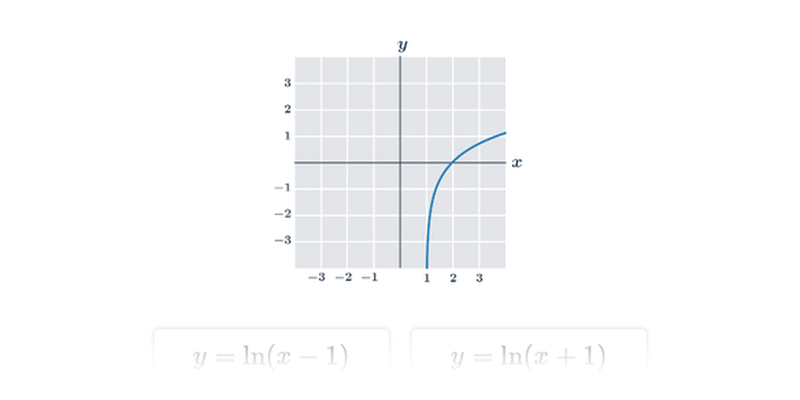
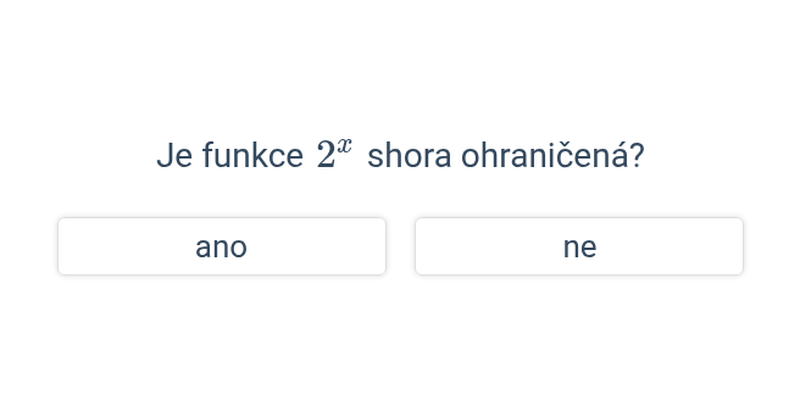
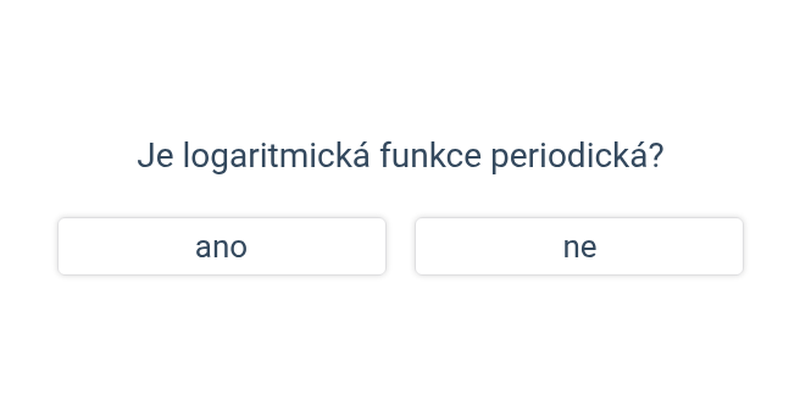
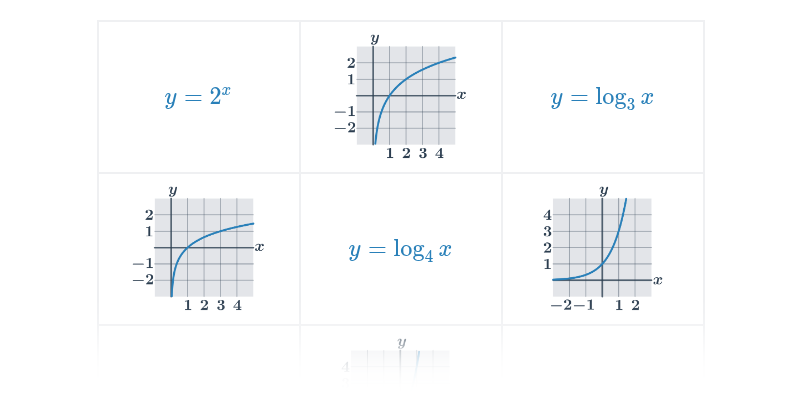
| Exponenciální a logaritmické funkce | f(x) = 2^x, f(x) = \log x |
Téma typy a vlastnosti funkcí se zabývá podrobnějším rozlišováním mezi jednotlivými typy funkcí a jejich vlastnostmi, jako jsou periodičnost či omezenost.
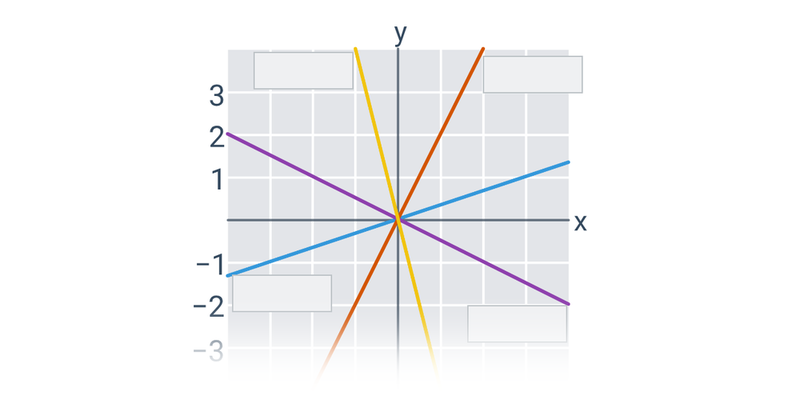
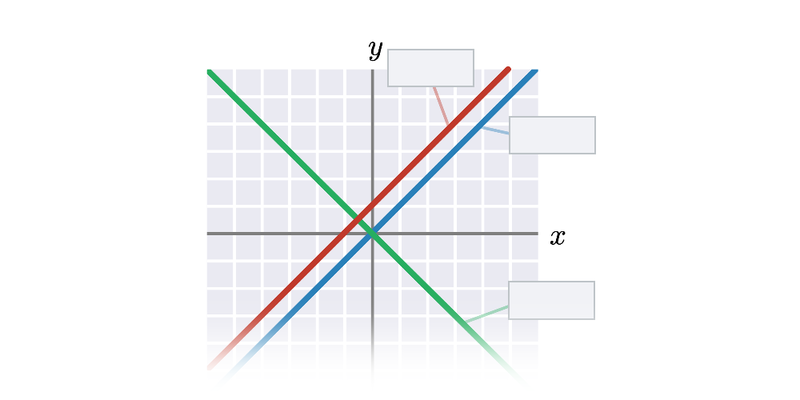
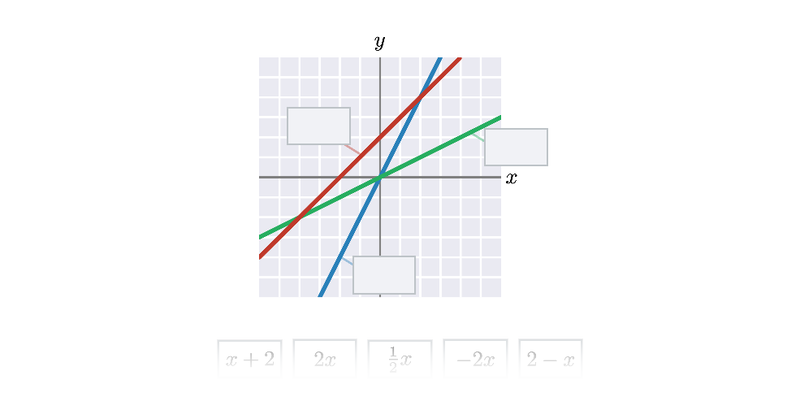
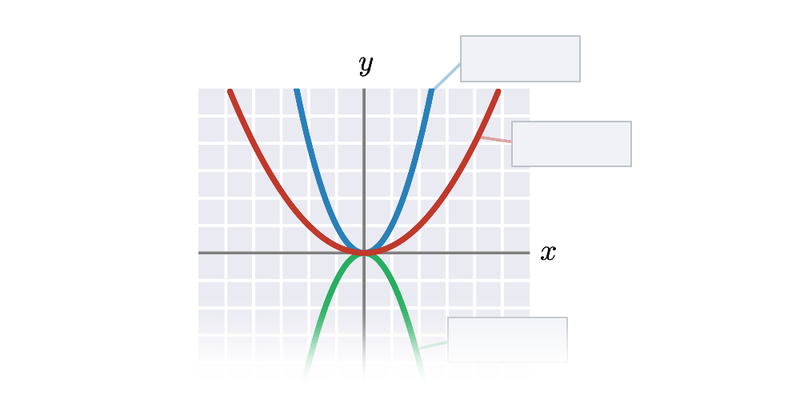
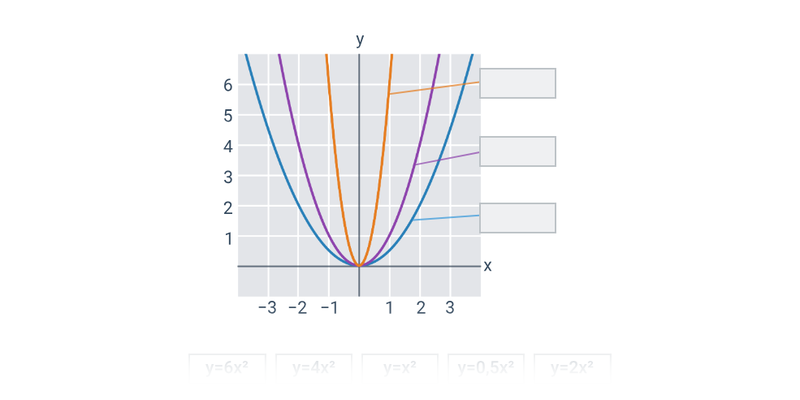
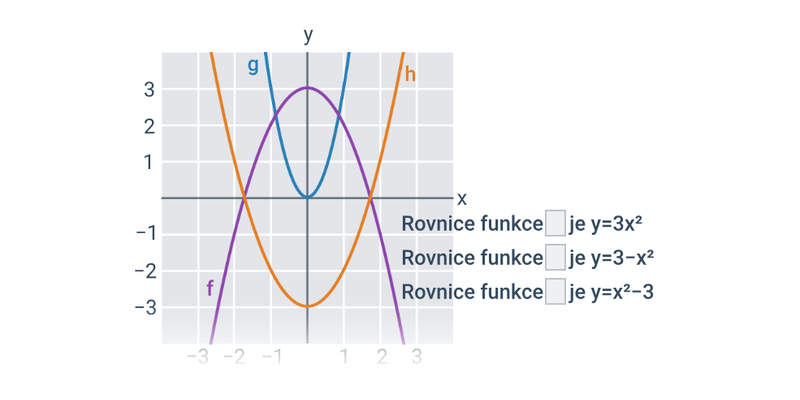
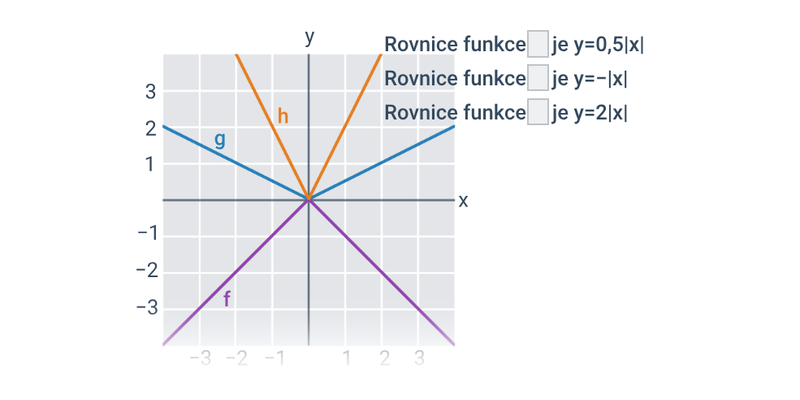
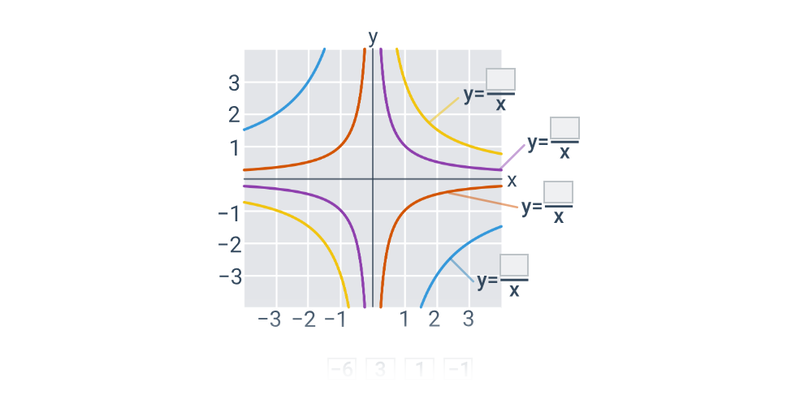
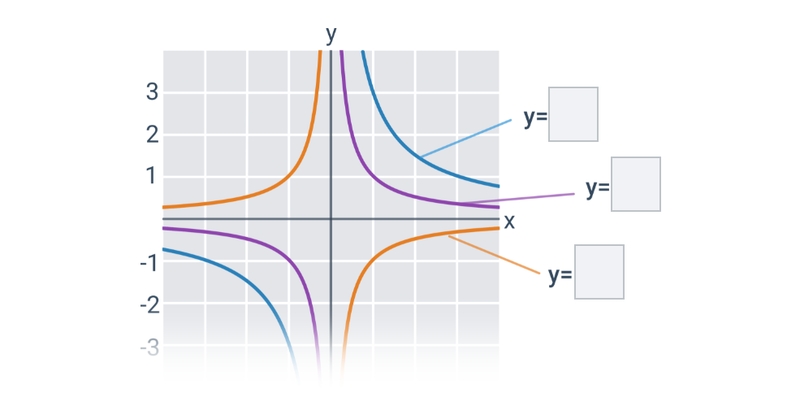
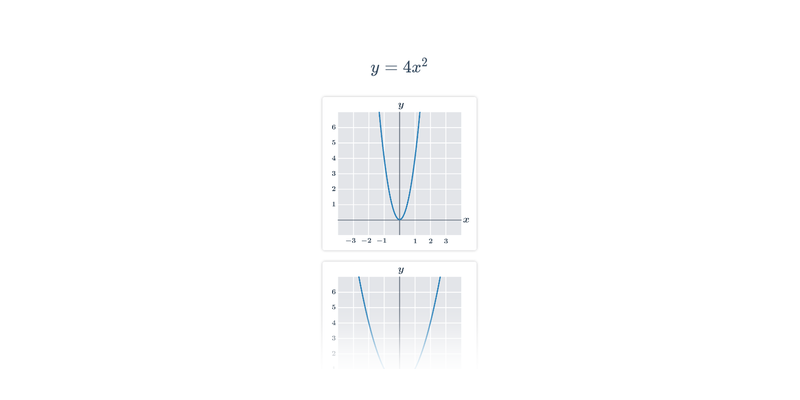
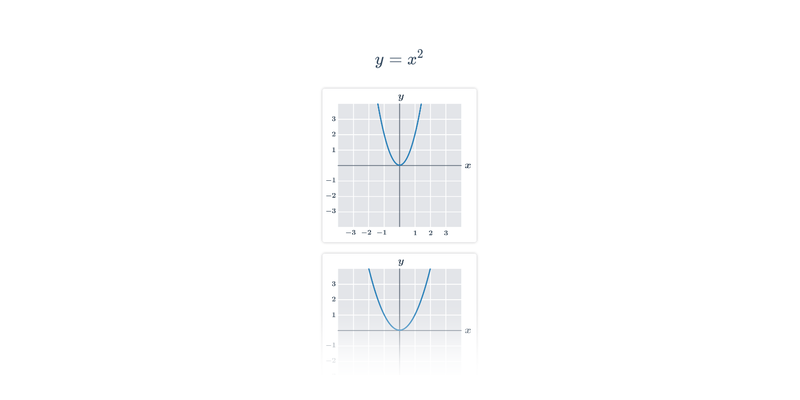
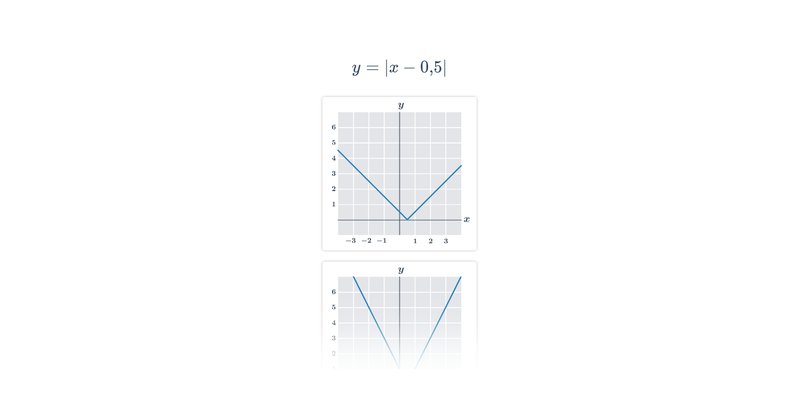
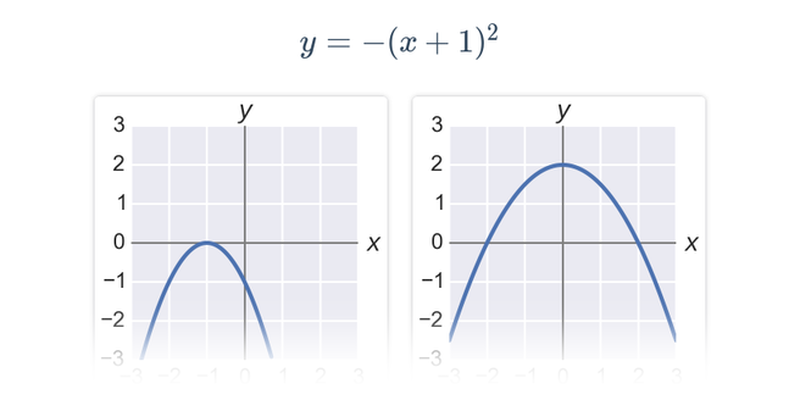
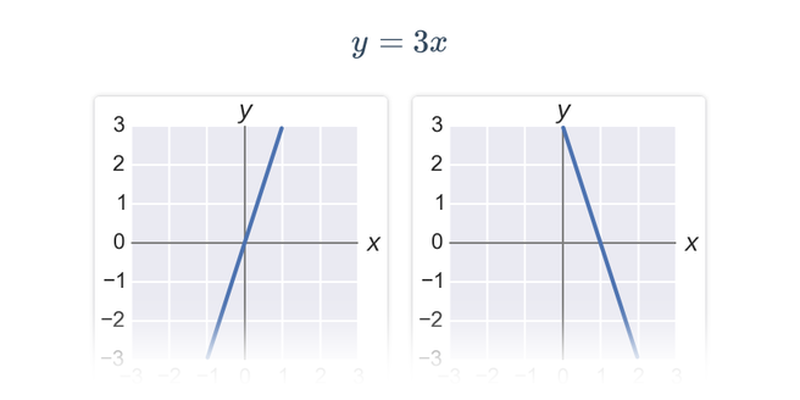
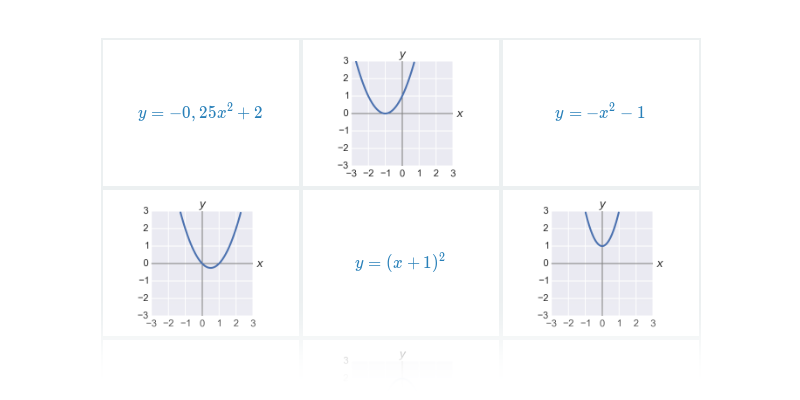
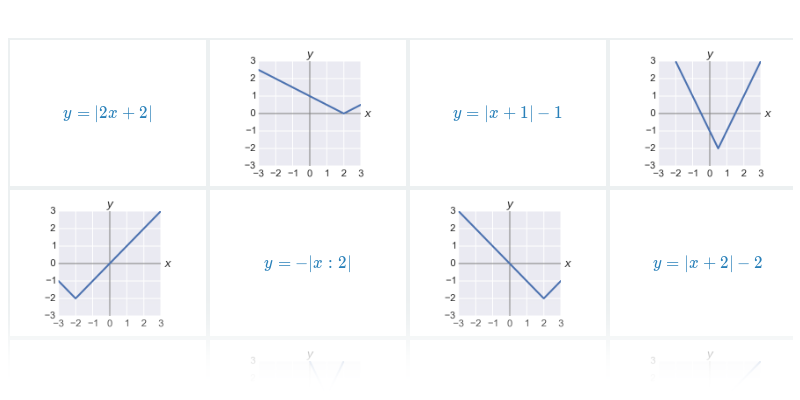
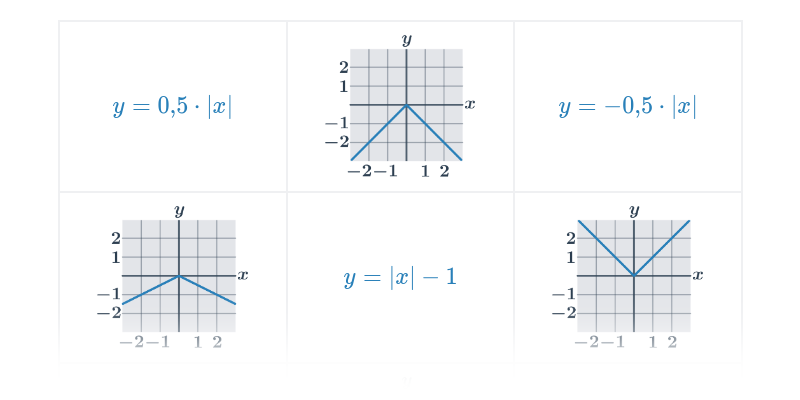
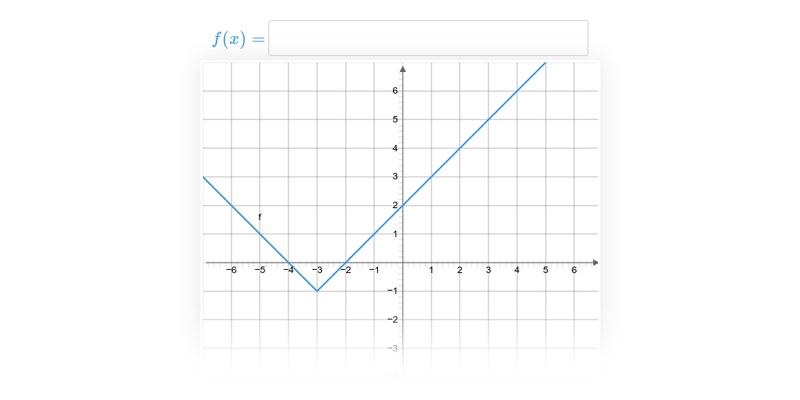
Funkce pro lepší pochopení často zakreslujeme graficky, což nám umožňuje lépe vidět vztah mezi x a f(x). Téma grafy funkcí zastřešuje procvičování v tomto ztvárnění.
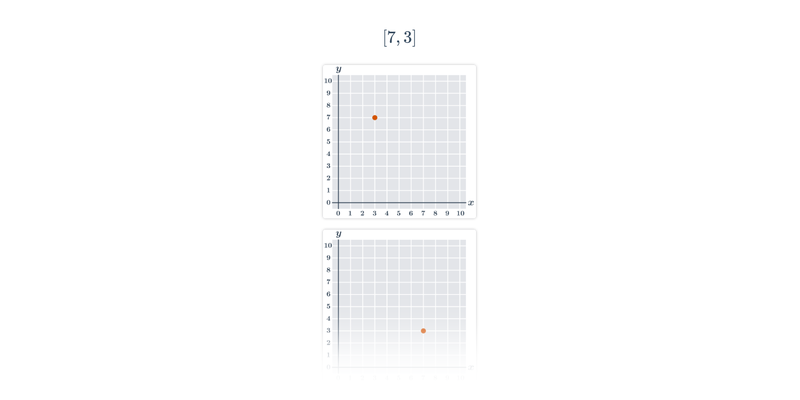
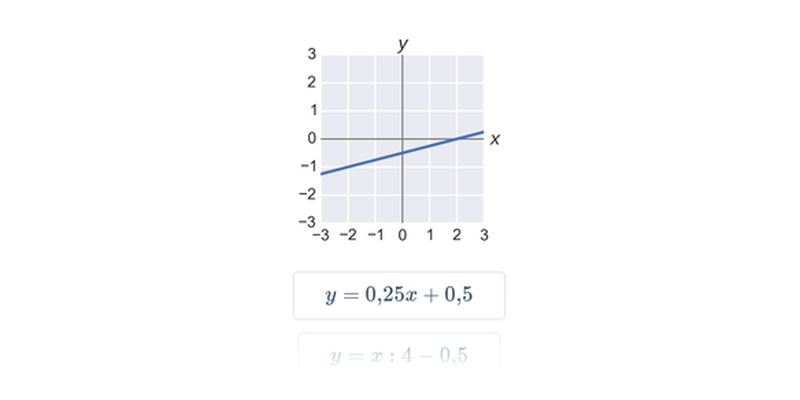
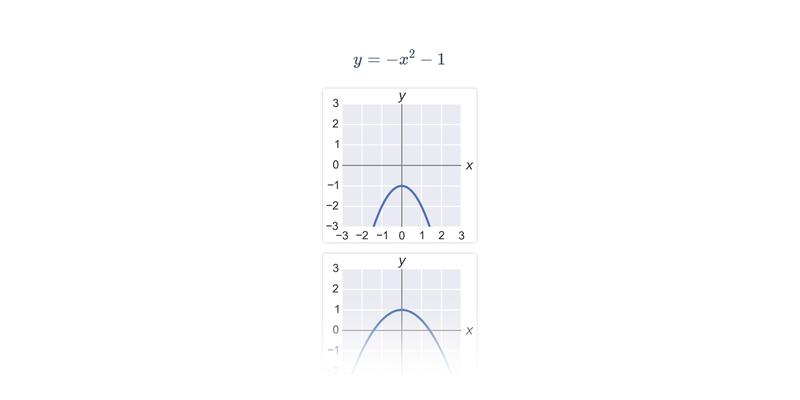
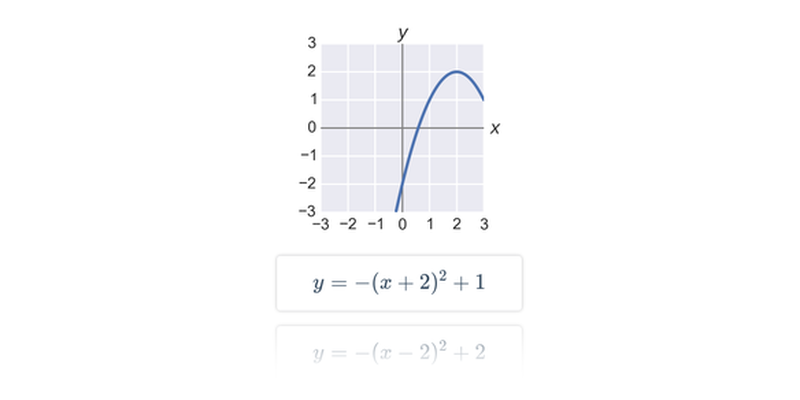
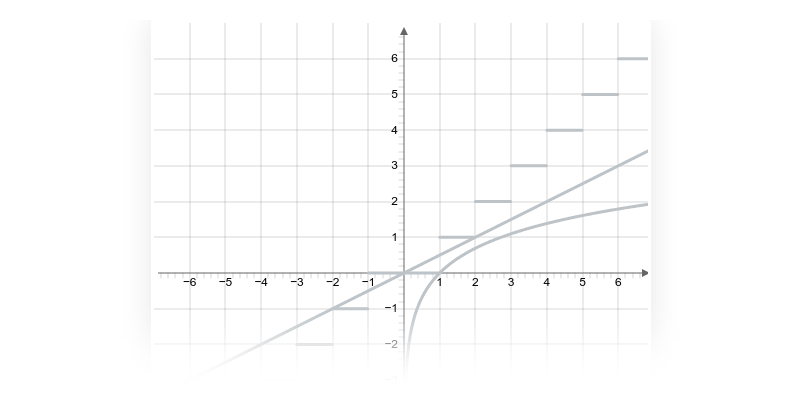
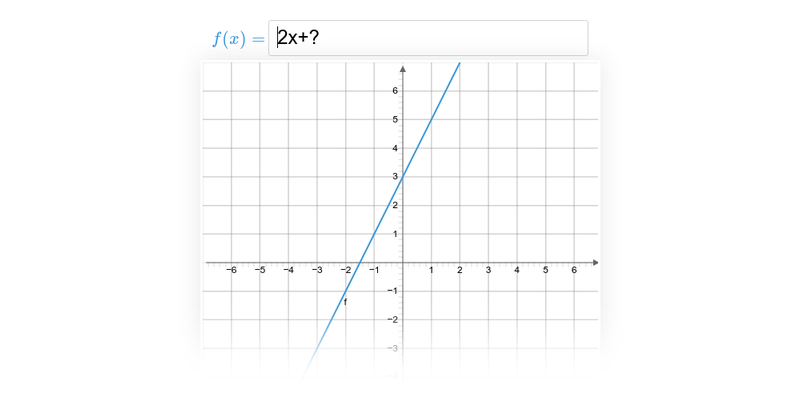
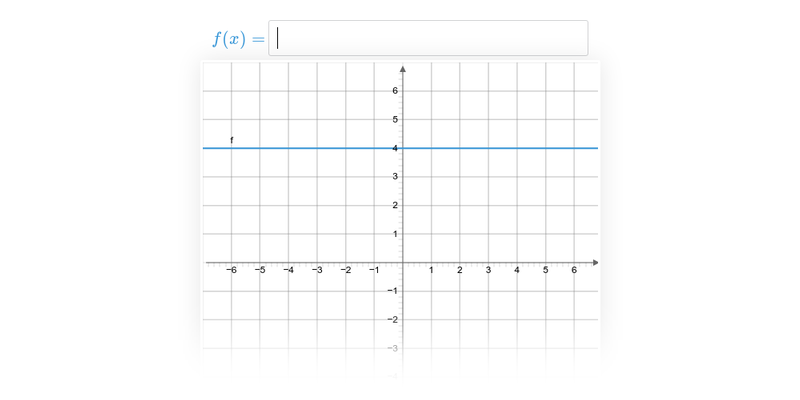
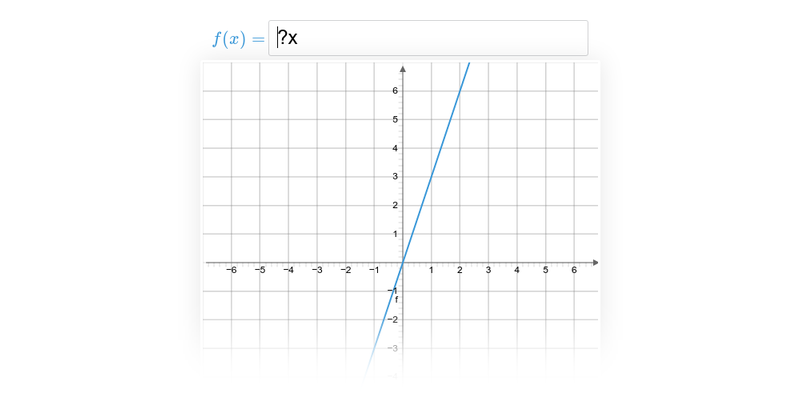
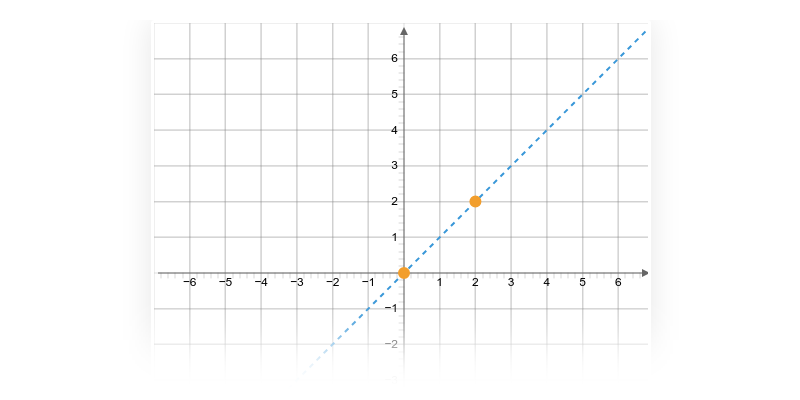
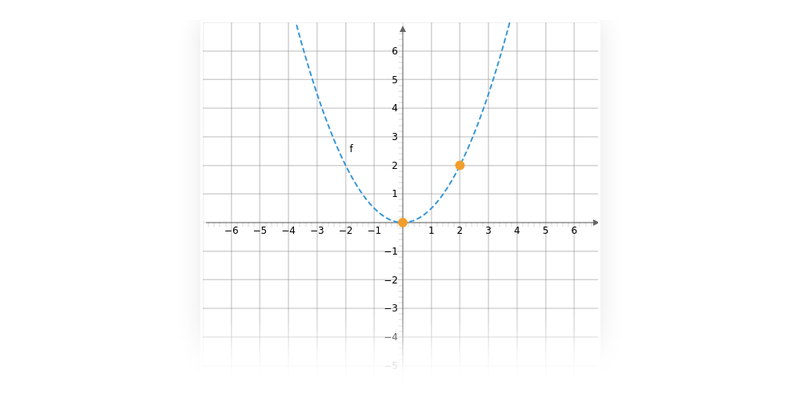
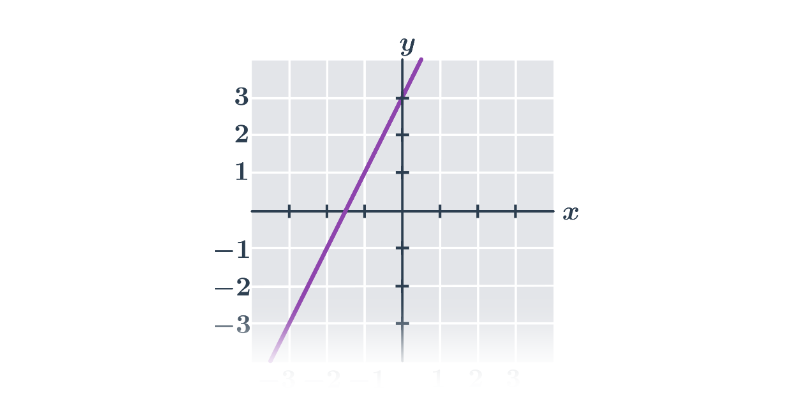
Příklad: graf funkce
Každému číslu x v definičním oboru funkce odpovídá právě jedna funkční hodnota y=f(x).
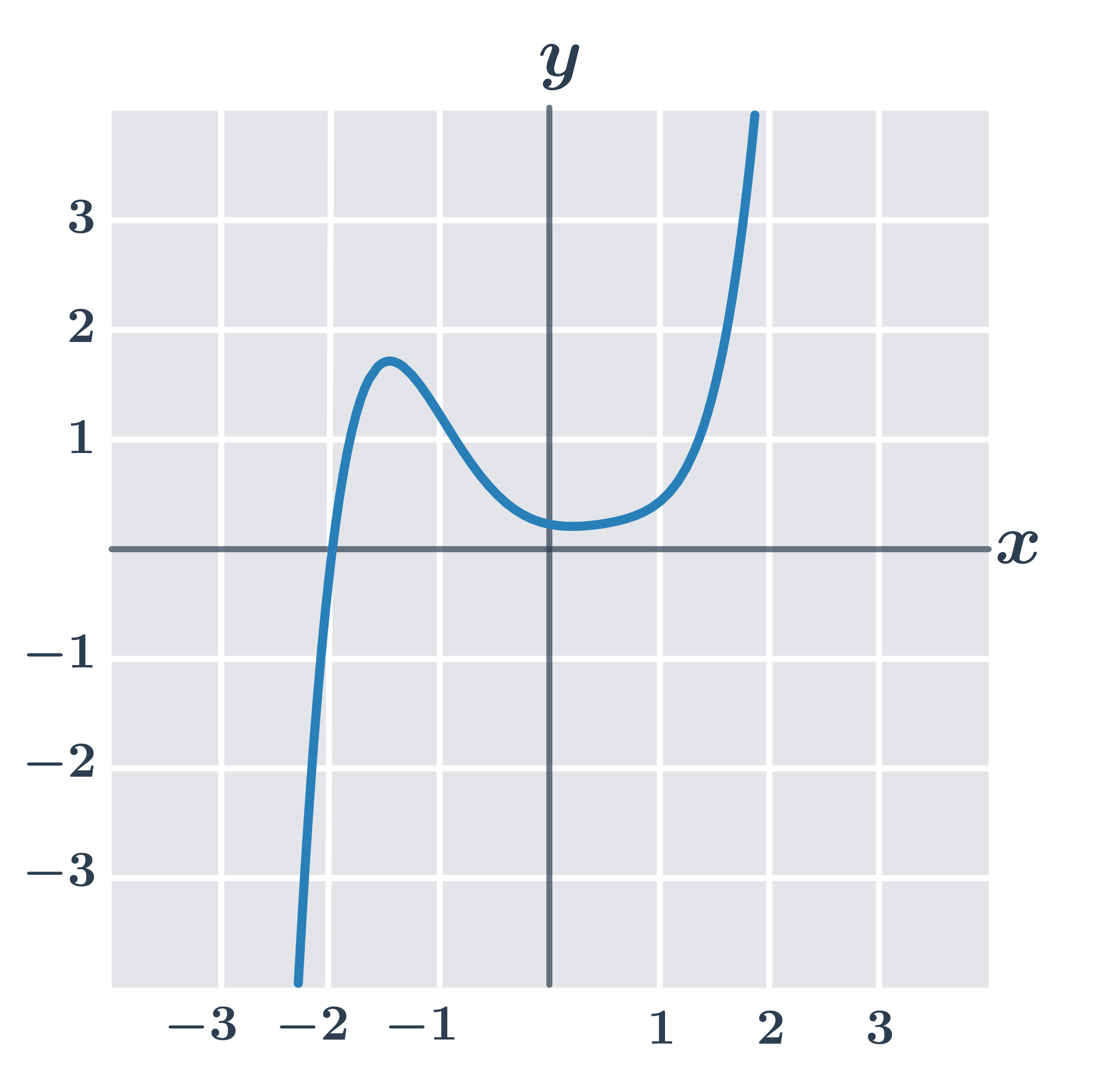
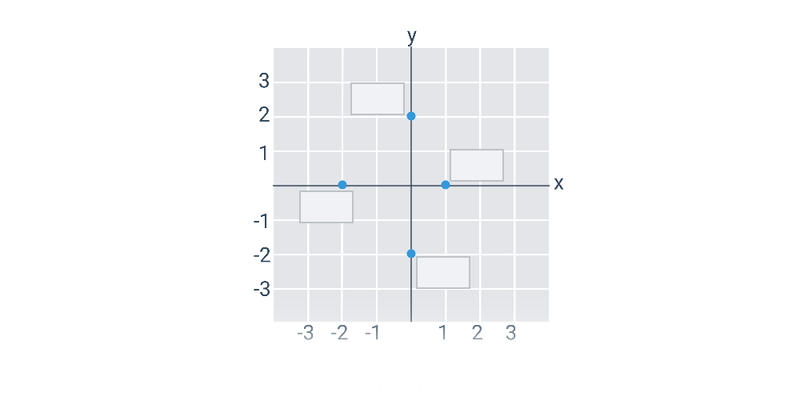
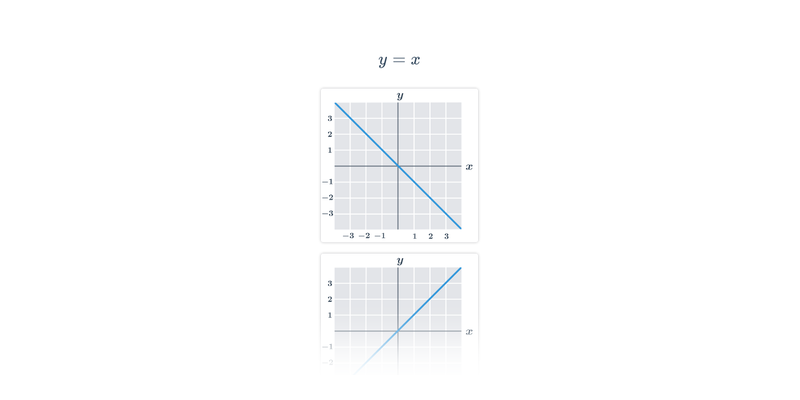
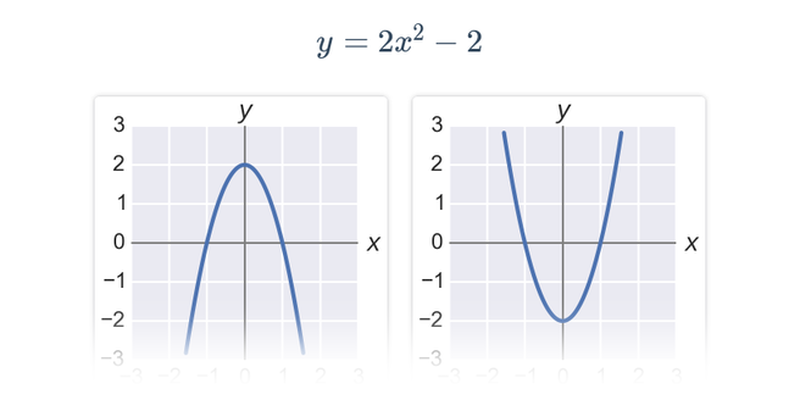
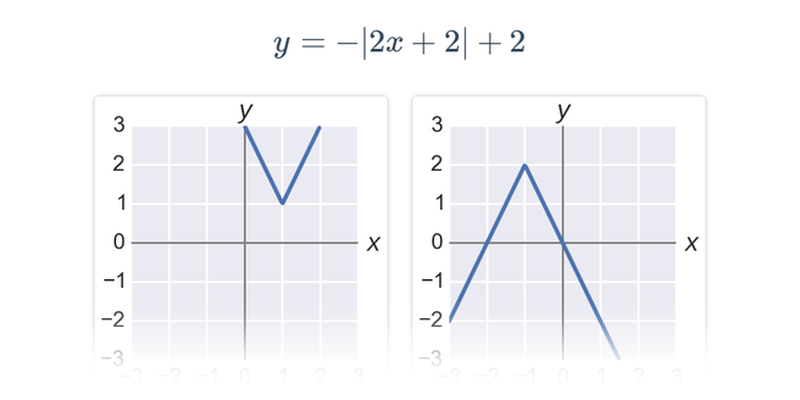
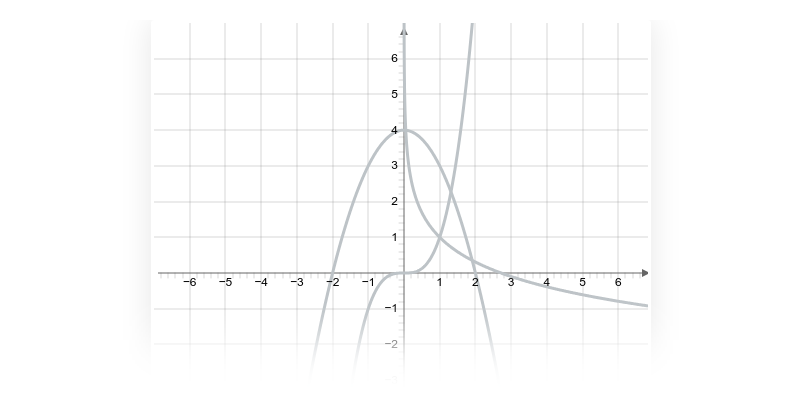
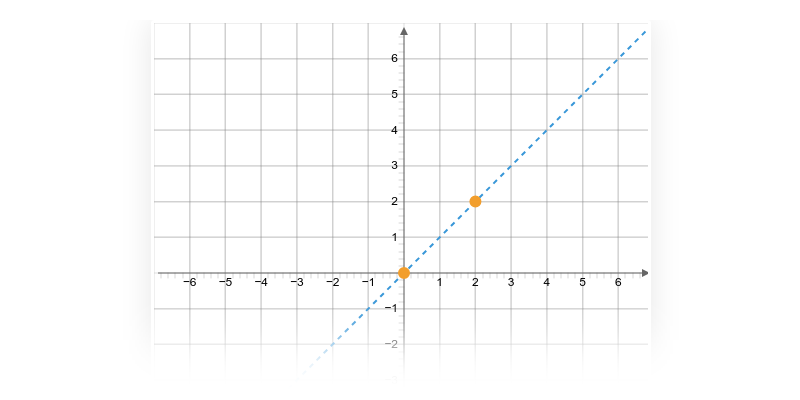
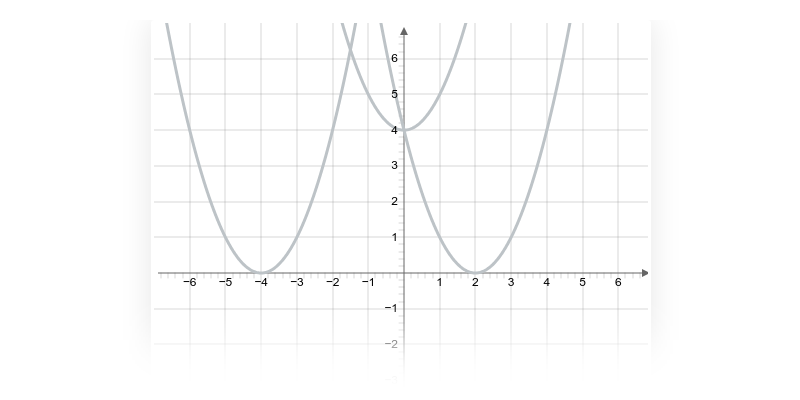
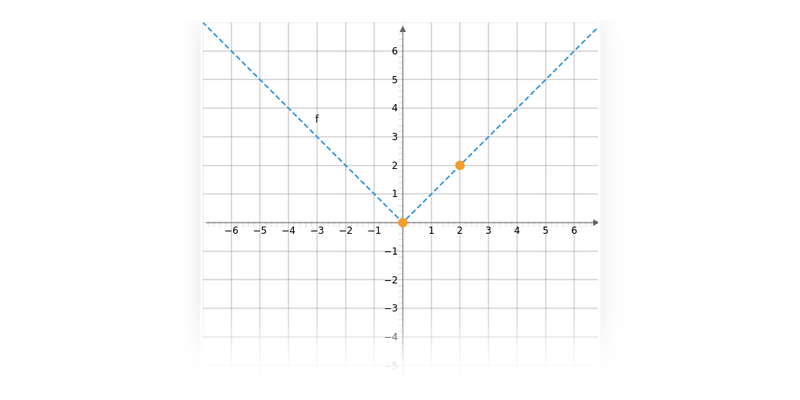
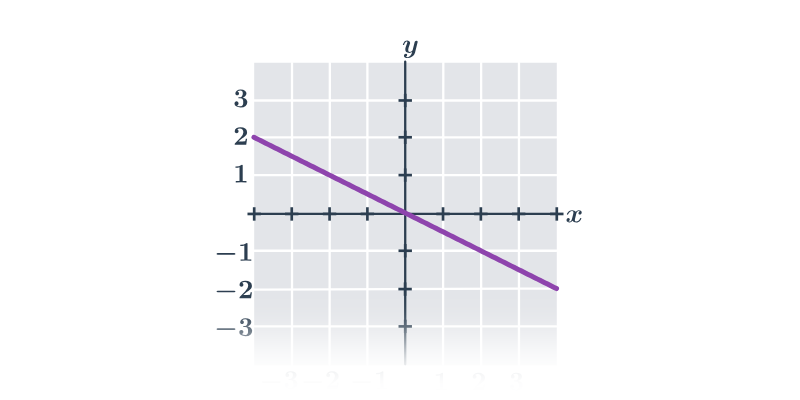
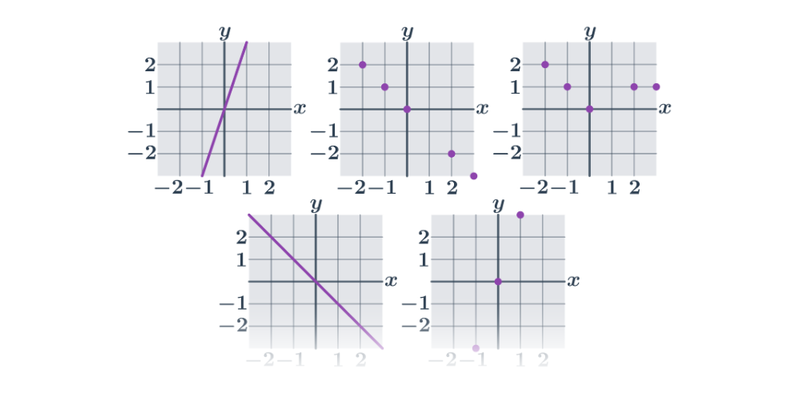
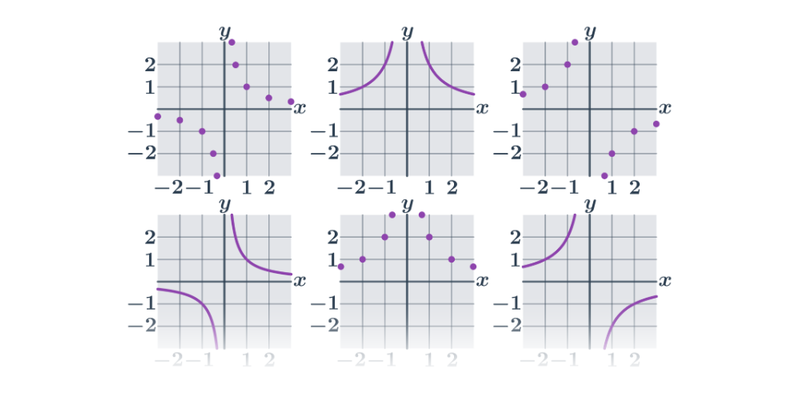
Příklad: toto není graf funkce
Na následujícím obrázku není graf funkce:
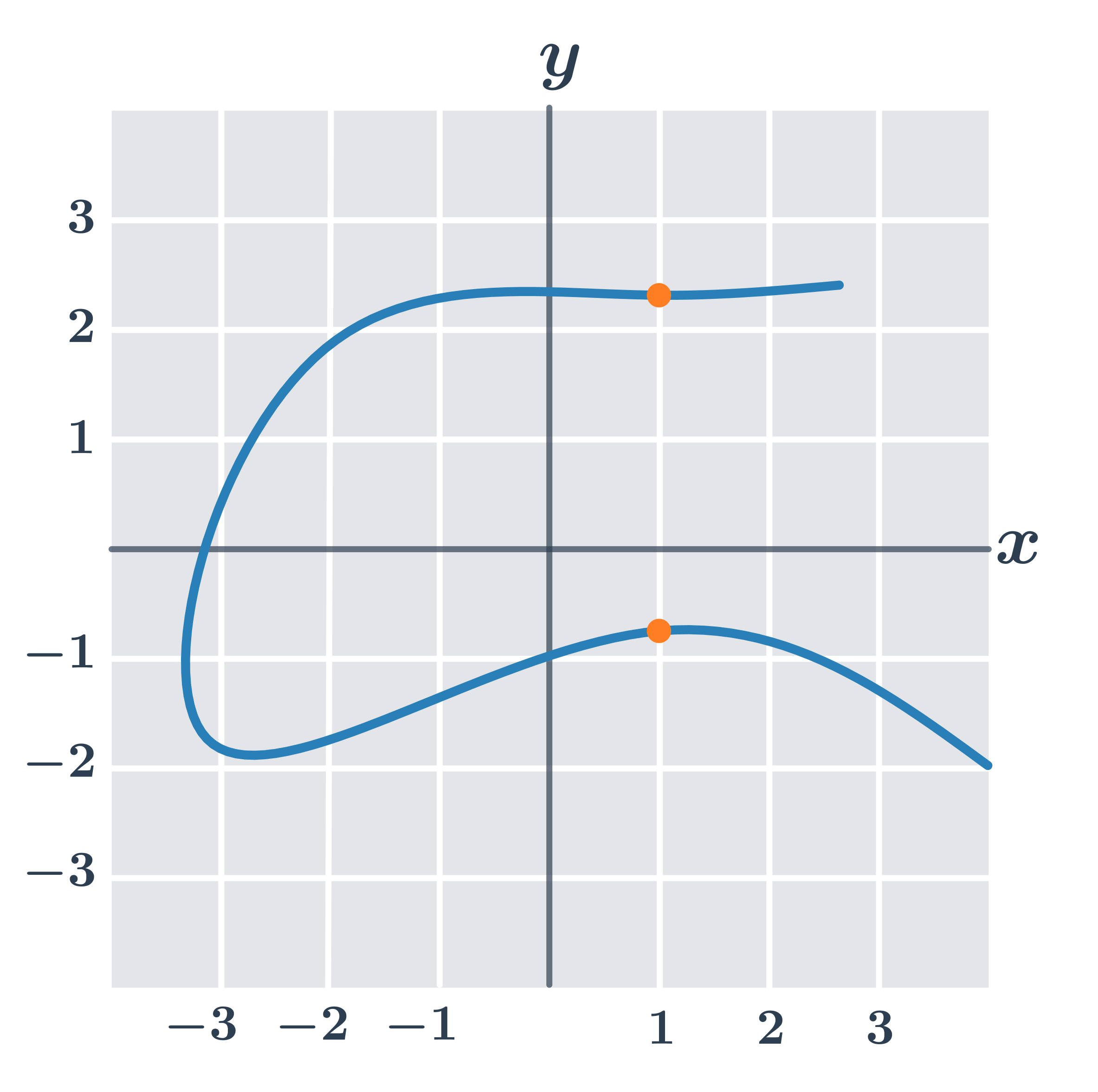
Například pro x=1 bychom neměli jednoznačně danou hodnotu y=f(x) (máme dva oranžově zvýrazněné body s x=1, ale dvěma různými souřadnicemi y).
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
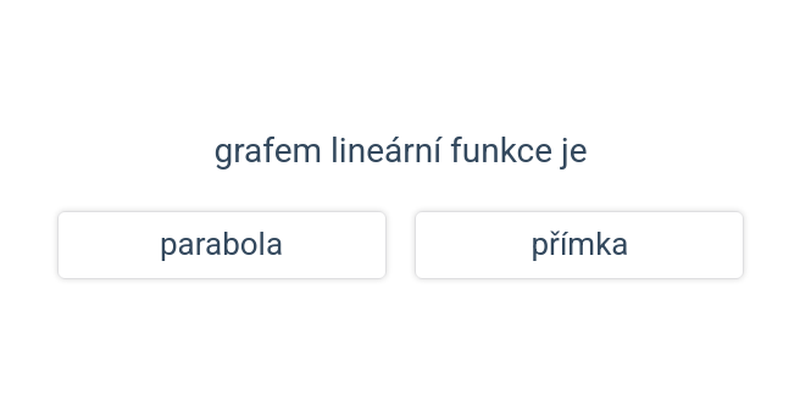
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Pexeso
Hledání dvojic, které k sobě patří.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Slovní úlohy
Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.
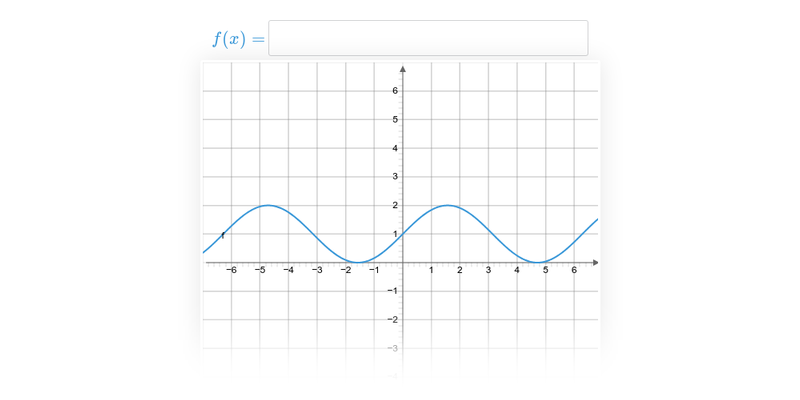
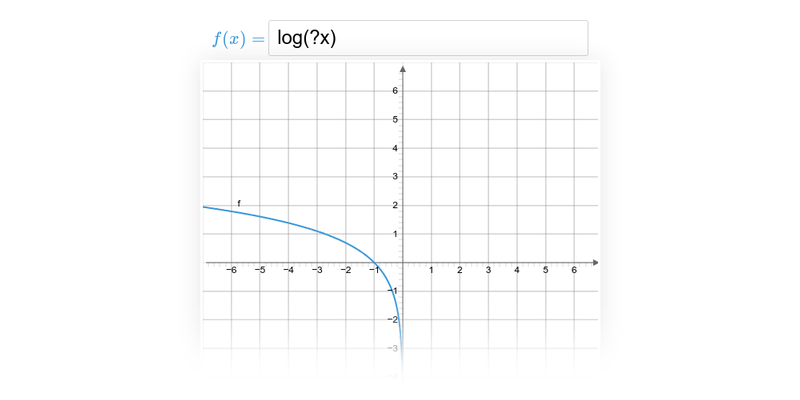
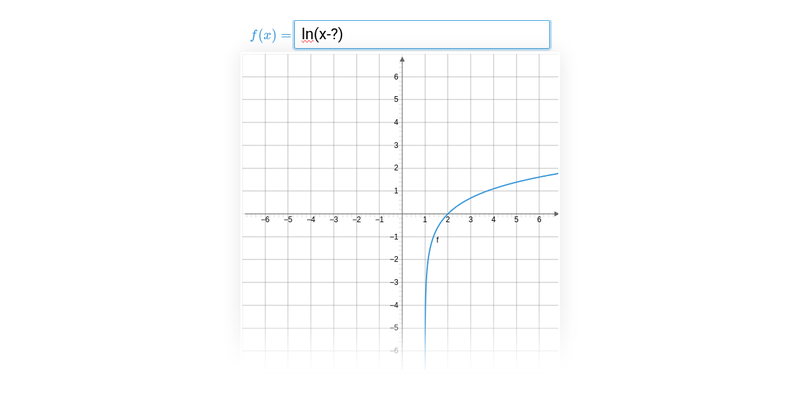
Grafař
Specializované cvičení na práci s grafem a funkcemi.
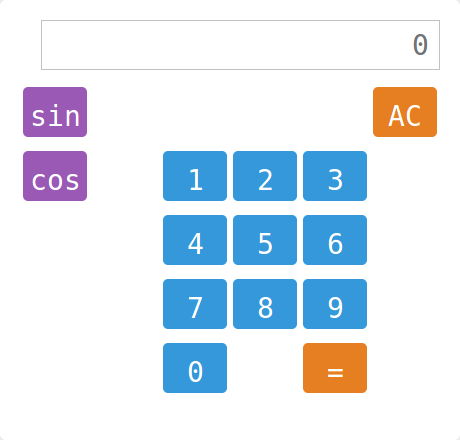
Kalkulačka
Úkolem je vyrobit na displeji kalkulačky zadaná čísla. Problém je, že jí chybí některá tlačítka…
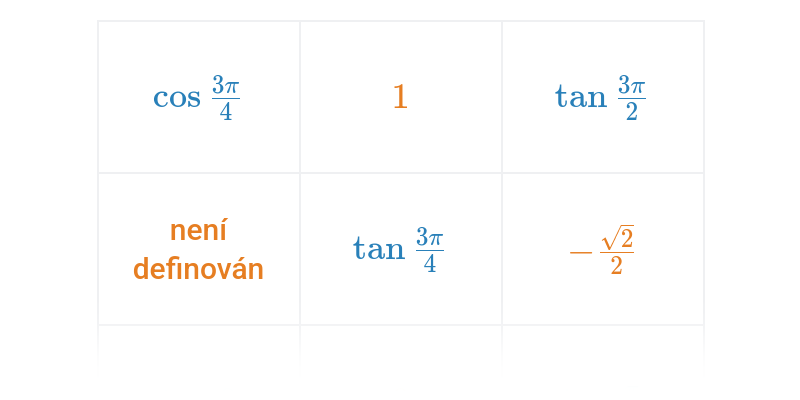
Goniometrické funkce
Bonus
Roboti
Závody na rychlost proti robotům. Jednoduché ovládání výběrem ze dvou možností.
| Funkce | ||
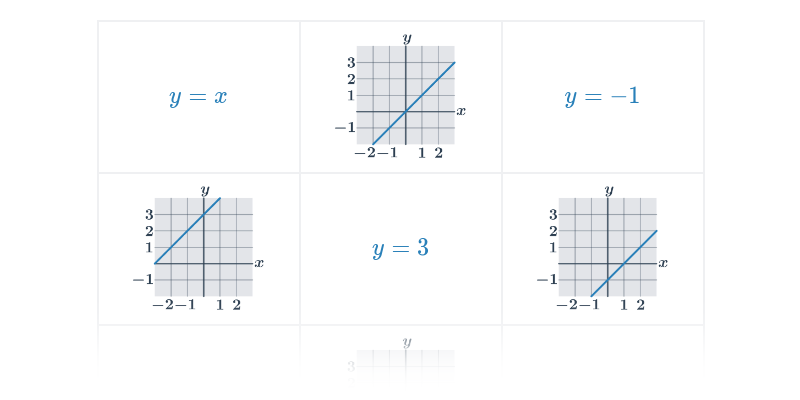
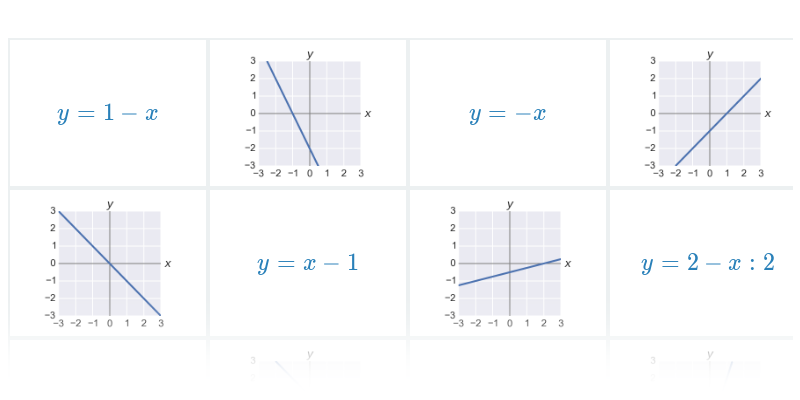
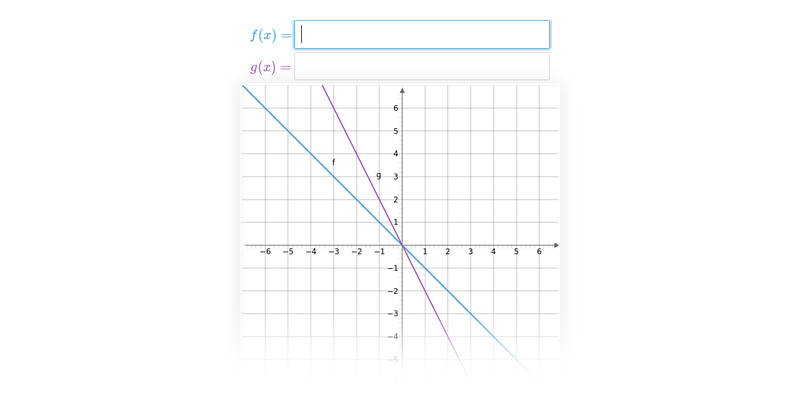
| Grafy funkcí | ||
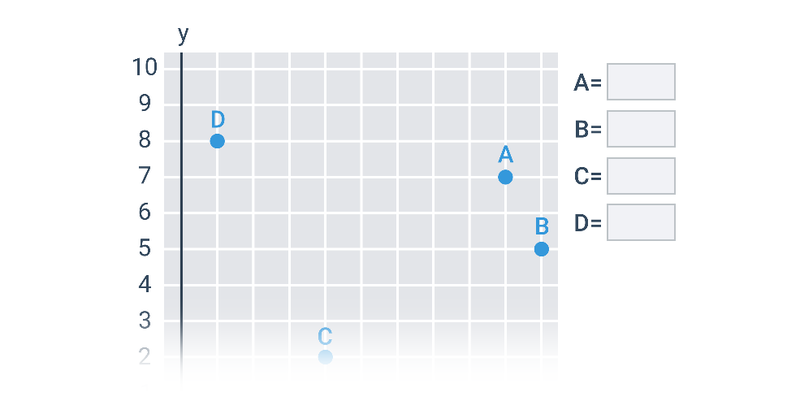
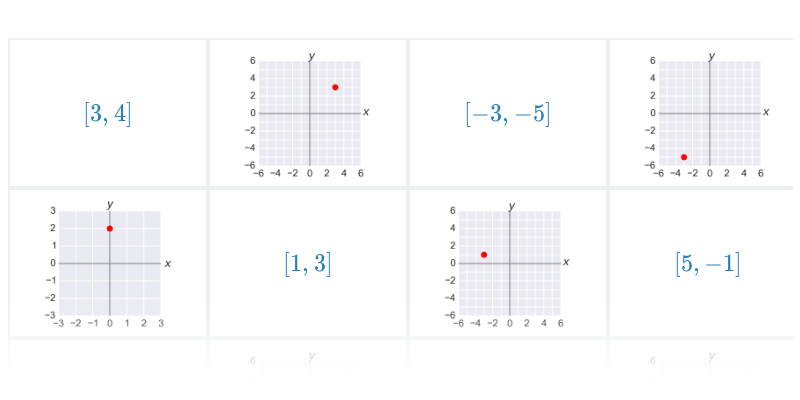
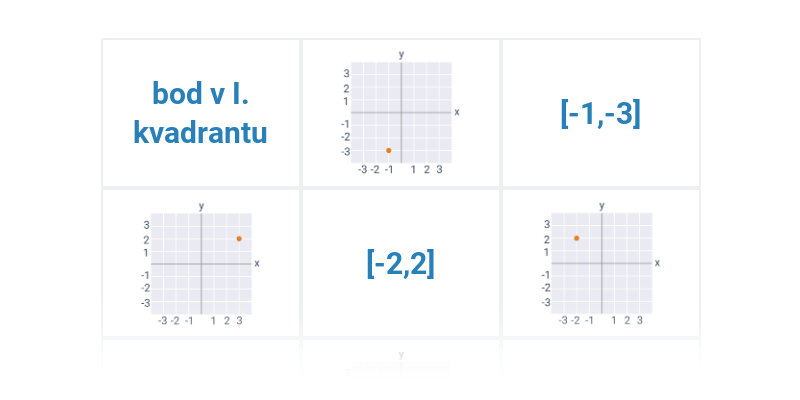
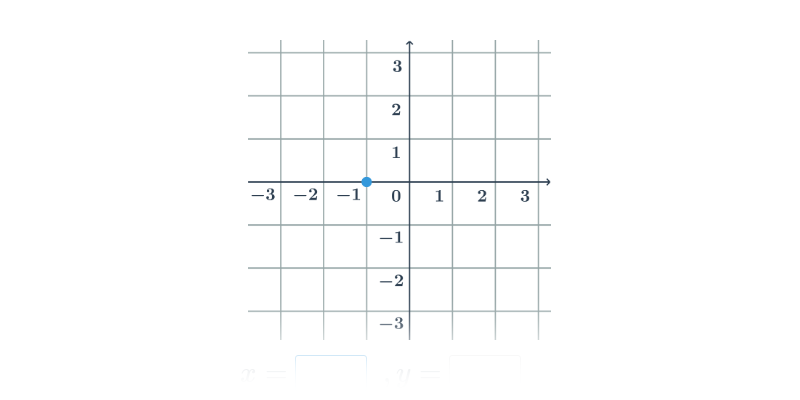
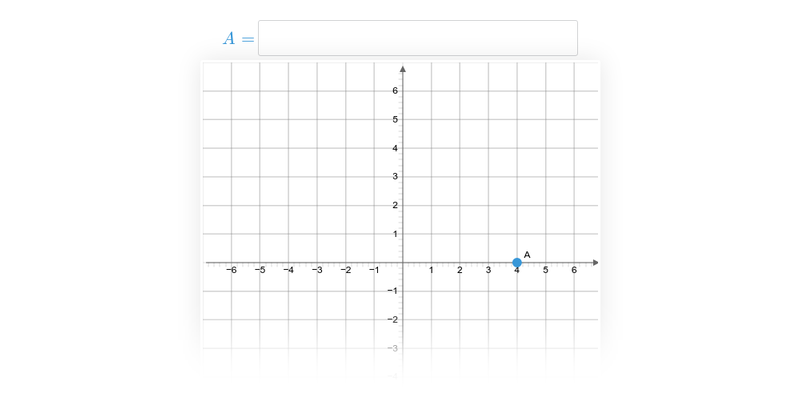
| Souřadnice bodů v rovině | Spustit | |
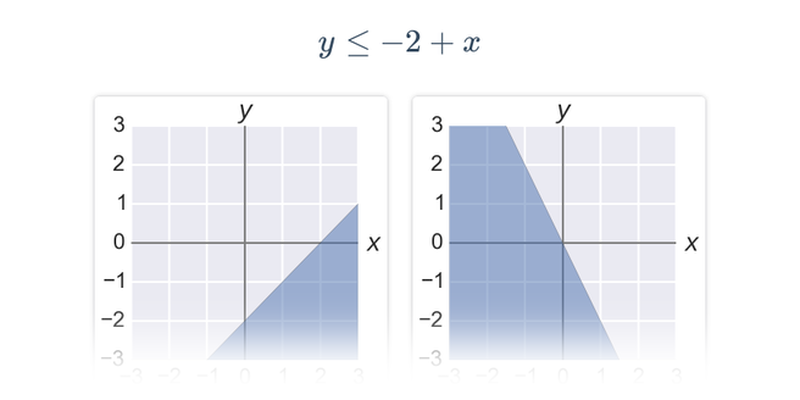
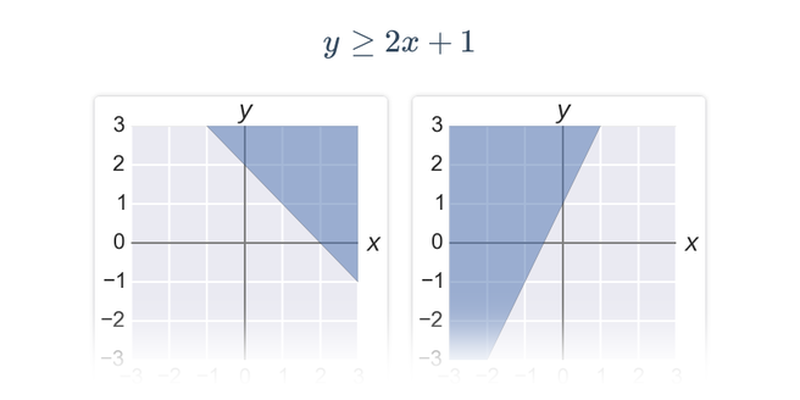
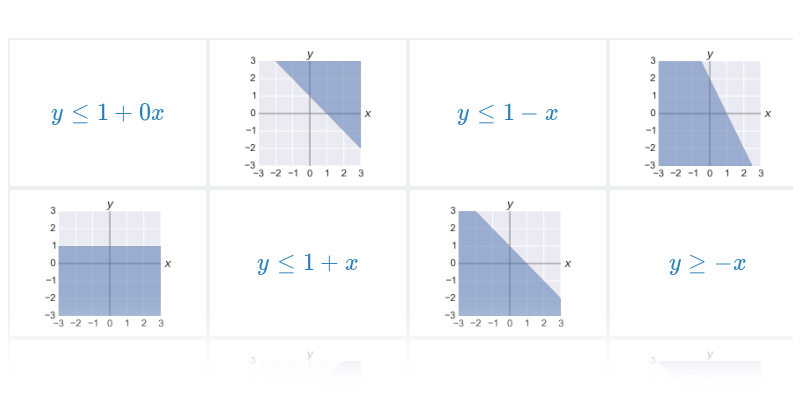
| Grafy lineárních nerovnic | Spustit | |
Označování
V zadaném obrázku či textu máte za úkol označit všechny oblasti, které splňují určitou vlastnost.