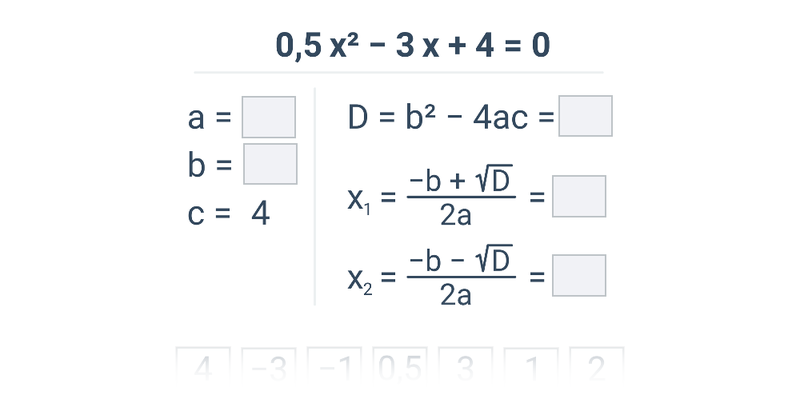Pojmy
Kvadratická rovnice je rovnice, ve které se vyskytuje jedna neznámá ve druhé mocnině. Základní tvar kvadratické rovnice je: ax^2+bx+c=0, kde a, b, c jsou reálná čísla a a\neq 0. Pro kvadratické rovnice používáme následující názvosloví:
- ax^2 je kvadratický člen,
- bx je lineární člen,
- c je absolutní člen.
Příklad: 2x^2+6x-20 = 0
| kvadratický člen | 2x^2 |
| lineární člen | 6x |
| absolutní člen | -20 |
| řešení rovnice | x=2 a x=-5 |
Speciální typy kvadratických rovnic:
- Pokud je b=0 nazýváme rovnici ryze kvadratickou: ax^2+c=0.
- Pokud je c=0 mluvíme o rovnici bez absolutního členu: ax^2+bx=0.
Řešení kvadratické rovnice
Každou kvadratickou rovnici lze řešit pomocí výpočtu diskriminantu D. Pro něj platí: D=b^2-4\cdot a\cdot c. Mohou nastat 3 situace:
- D \lt 0 – rovnice nemá v reálných číslech řešení.
- D = 0 – rovnice má jeden dvojnásobný kořen.
- D \gt 0 – rovnice má dva různé reálné kořeny.
Pro kořeny rovnice platí:
- x_1=\frac{-b+\sqrt{D}}{2a}
- x_2=\frac{-b-\sqrt{D}}{2a}
Řešený příklad: x^2+2x-3=0
- Pro tuto rovnici a=1, b=2, c=-3.
- Diskriminant D=b^2-4ac = 2^2-4\cdot 1\cdot(-3) = 4+12=16.
- D>0, rovnice má tedy dvě řešení.
- x_1 = \frac{-b+\sqrt{D}}{2a} = \frac{-2+\sqrt{16}}{2\cdot 1} = 1
- x_2 = \frac{-b-\sqrt{D}}{2a} = \frac{-2-\sqrt{16}}{2\cdot 1} = -3
- Řešení rovnice jsou tedy hodnoty 1 a -3.
Vietovy vzorce
Kvadratické rovnice můžeme řešit i bez počítání diskriminantu za využití Vietových vzorců. Pro kořeny rovnice platí: x_1+x_2=-\frac{b}{a}, x_1\cdot x_2=\frac{c}{a}. V případě a=1: x_1+x_2=-b, x_1\cdot x_2=c.
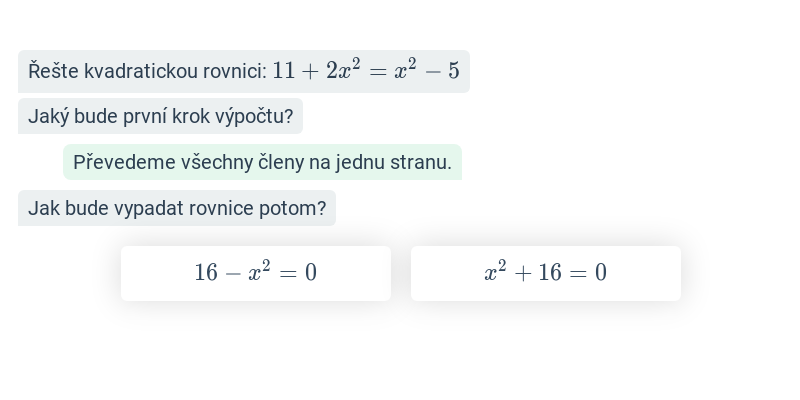
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
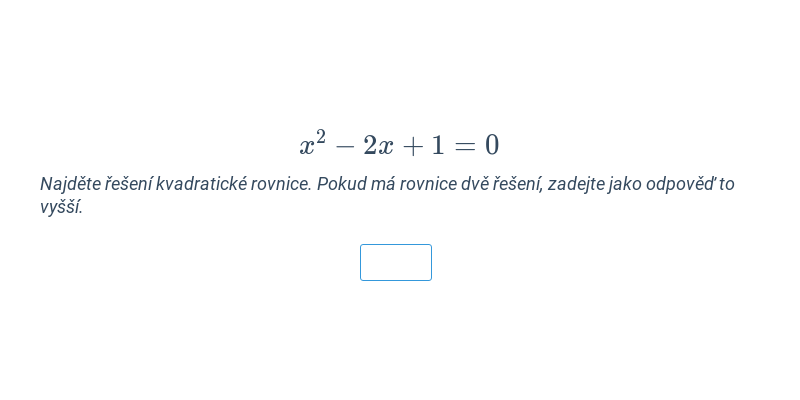
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Slovní úlohy
Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.