Logaritmické rovnice – 7. třída (7. ročník)

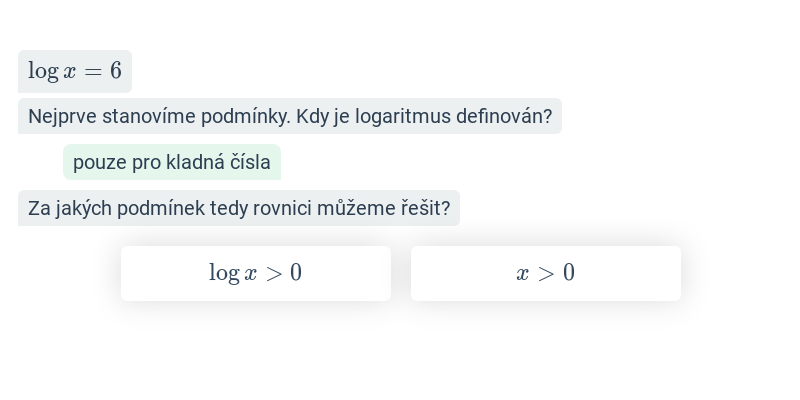
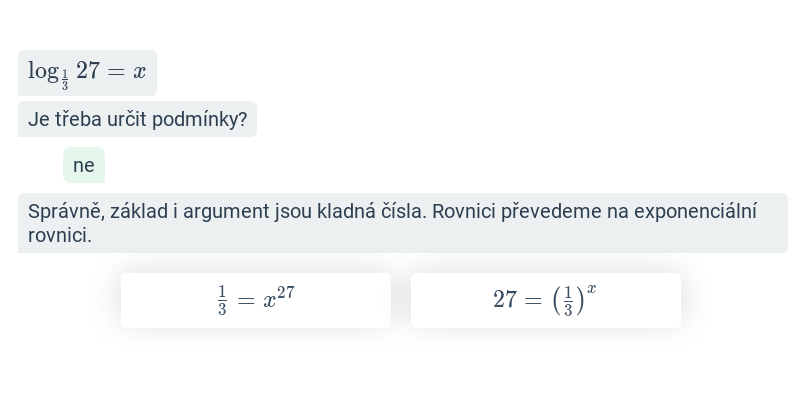
Logaritmická rovnice je taková, kde neznámá vystupuje jako argument logaritmické funkce, např. 2 \cdot \log_6(x-2) = \log_6(14-x).

U logaritmických rovnic musíme dávat pozor na podmínky řešení. Argument každého logaritmu totiž musí být vždy kladné číslo. V uvedeném příkladě tedy musí platit x-2>0 a současně 14-x > 0.

Logaritmické rovnice řešíme za využití vlastností logaritmické funkce a jejího vztahu k exponenciální funkci. Dílčí způsoby, jak řešit logaritmické rovnice:

• Převedeme rovnici na tvar \log_a f(x) = c. Pak musí platit f(x) = a^c.
• Převedeme rovnici na tvar \log_a f(x) = \log_a g(x). Pak musí platit f(x) = g(x).