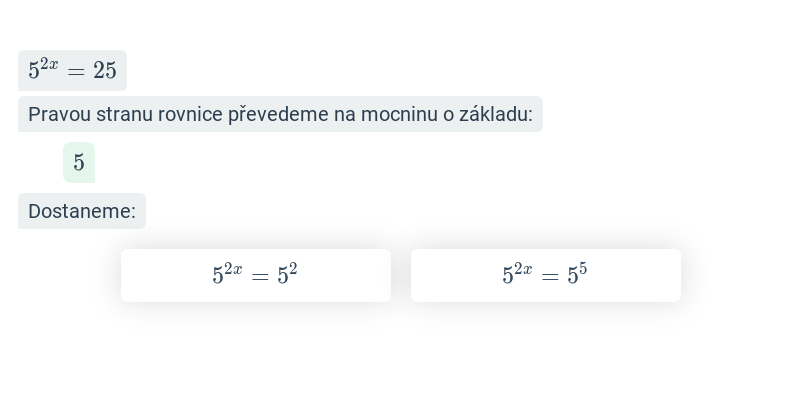
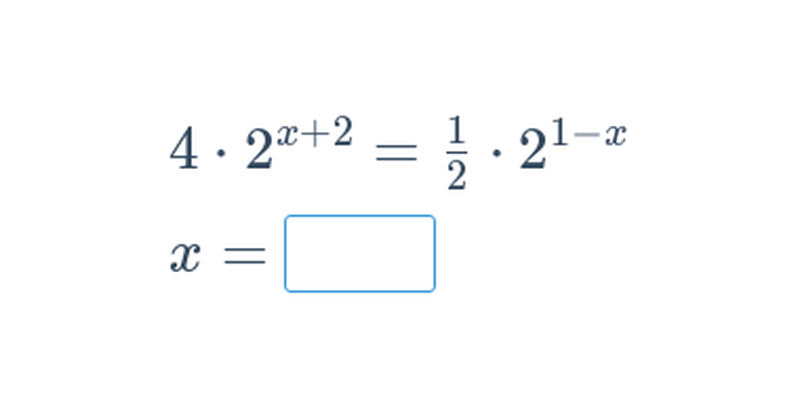Exponenciální rovnice

umime.to/F14

Exponenciální rovnice má neznámou v exponentu (mocniteli), např. 3^{2x}-3^x=6.

Exponenciální rovnice lze řešit různými způsoby. Nejjednodušší je řešení rovnice se stejnými základy. Pokud se nám podaří rovnici převést na tvar a^{f(x)} = a^{g(x)}, můžeme se zbavit exponenciální funkce a řešit f(x) = g(x). Složitější způsoby řešení exponenciálních rovnic jsou logaritmování a substituce.

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Exponenciální rovnice

Krok po kroku • střední

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Exponenciální rovnice

Psaná odpověď • těžké

Předcházející

Navazující

Cvičení

Exponenciální rovnice

umime.to/F14

Krok po kroku