Soustava dvou rovnic o dvou neznámých je podobná jako základní rovnice, jen máme místo jedné proměnné x navíc i proměnnou y a rovnice jsou dvě. Podobně jako rovnice o jedné proměnné může mít celou řadu různých typů, i dvě rovnice o dvou neznámých mohou být lineární, kvadratické, logaritmické a jiné. Většinou se však procvičují pouze základní lineární rovnice. Pokud totiž dobře zvládneme jejich řešení, můžeme naučené postupy použít i na složitější rovnice. Základní metody řešení soustavy dvou rovnic jsou dosazovací metoda a sčítací metoda.
| Příklad soustavy dvou rovnic o dvou neznámých: | x+y=8 |
| 2x-y=1 |
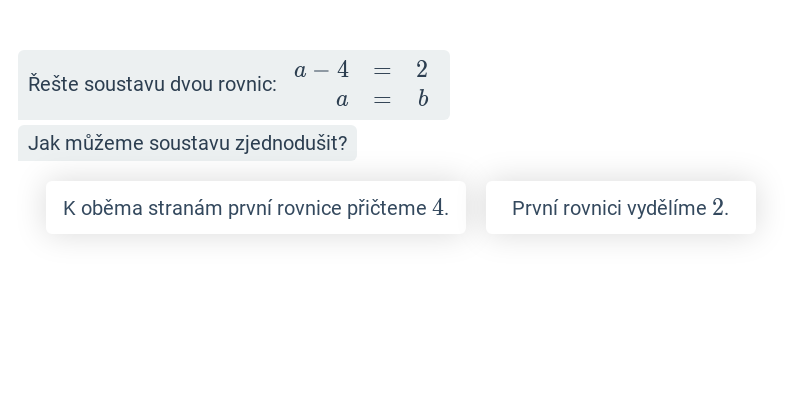
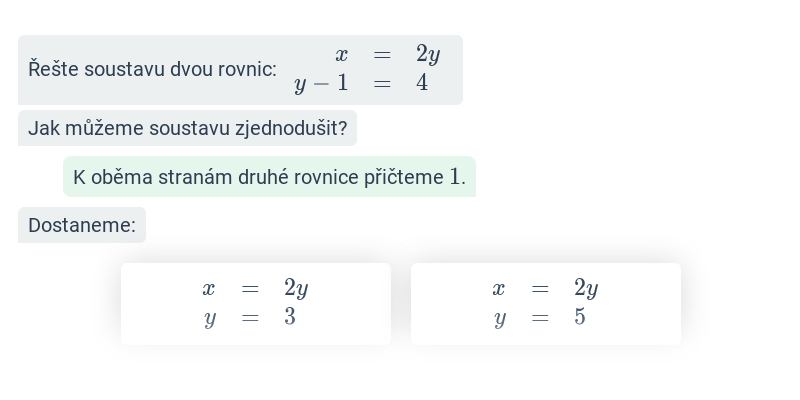
Dosazovací metoda
Při řešení dosazovací metodou vyjádříme z jedné rovnice jednu neznámou pomocí druhé. Toto vyjádření pak dosadíme do druhé rovnice, čímž dostaneme obyčejnou jednu rovnici o jedné neznámé. Ukázka postupu na uvedeném příkladě:
| Z první rovnice vyjádříme y: | y = 8 -x |
| Dosadíme do druhé rovnice: | 2x - y = 1 |
| 2x - (8-x) = 1 | |
| Řešíme jako obyčejnou rovnici: | 3x = 9 |
| x = 3 | |
| Nalezenou hodnotu dosadíme do výrazu pro y: | y = 8 - x = 8 - 3 = 5 |
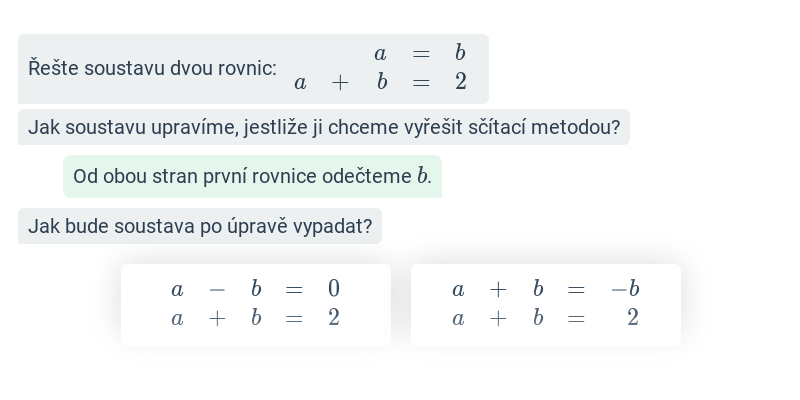
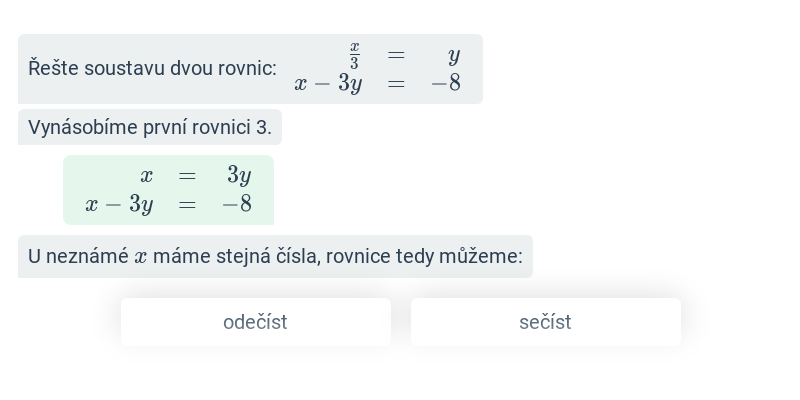
Sčítací metoda
Při řešení sčítací metodou sečteme (či odečteme) odděleně levé a pravé strany obou rovnic. Tato úprava vede k cíli, pokud nám při této operaci jedna z proměnných vypadne. V některých případech je proto nutné nejdříve jednu z rovnic vynásobit vhodným číslem. V případě naší ukázkové soustavy stačí rovnice prostě sečíst. Tím dostaneme 3x = 9, odtud x=3 a dosazením pak již dopočítáme y.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
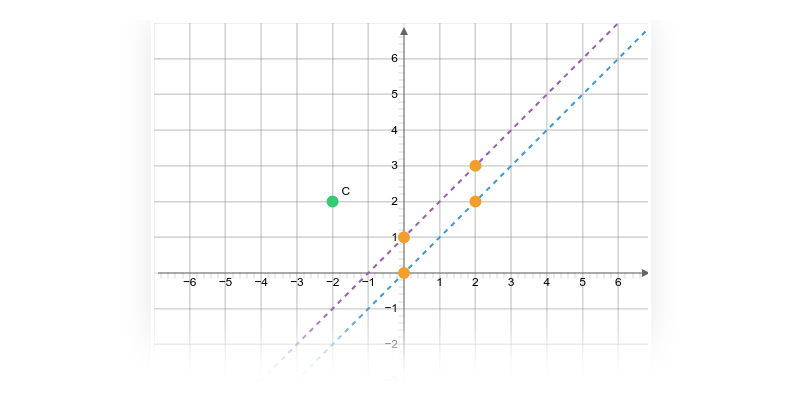
Grafař
Specializované cvičení na práci s grafem a funkcemi.