Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Tipovačka
Týmovka
Můj účet
Odhlásit sePorozumění
U každé úlohy máte k dispozici text či obrázek popisující matematický problém. Následuje pak několik otázek, které testují, jak jste textu či obrázku porozuměli.
Řazení podle
Výpis úloh
vybrané sadyjen přehled
Řady poskládaných útvarů
0/4
Řady poskládaných útvarů
Množinové operace
0/4
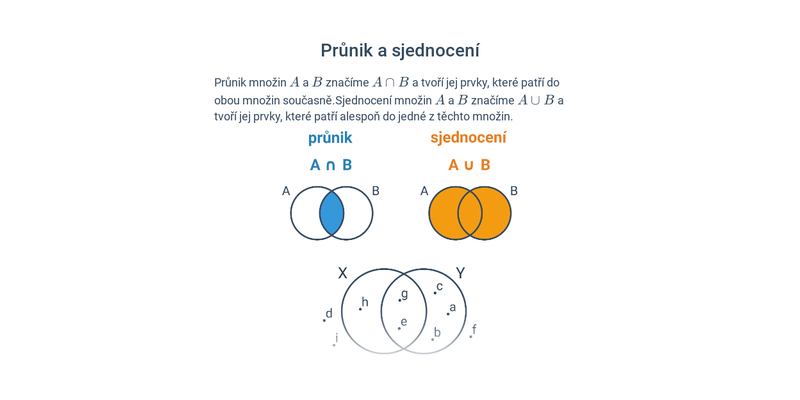
Množinové operace
Základní množinové operace a jejich vlastnosti můžeme názorně ilustrovat pomocí Vennových diagramů.
Pythagorova věta
0/4
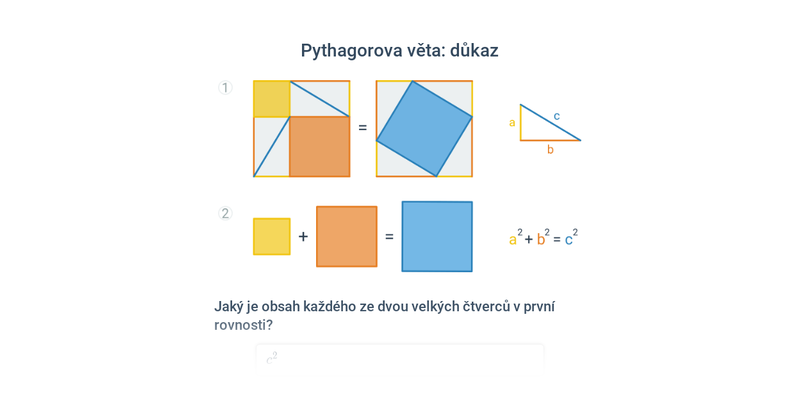
Pythagorova věta
Pythagorova věta je velmi užitečný nástroj, který využijeme v mnoha situacích.
Umění, vzory, geometrie
0/4
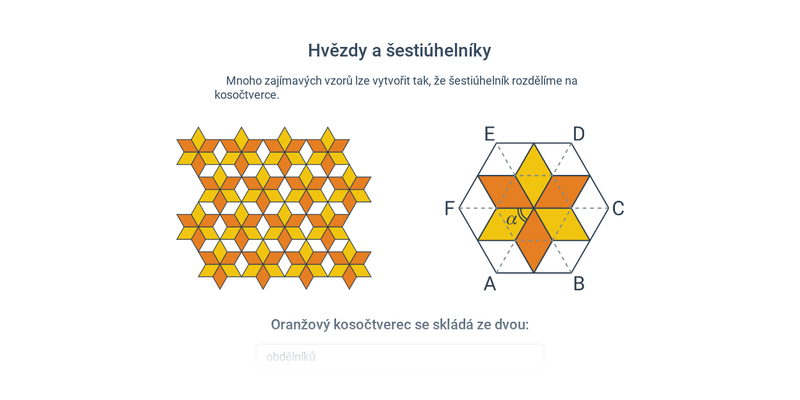
Umění, vzory, geometrie
Geometrie je základem mnoha vzorů vyskytujících se v umění. Pojďme některé prozkoumat.
Obrázkové důkazy
0/4
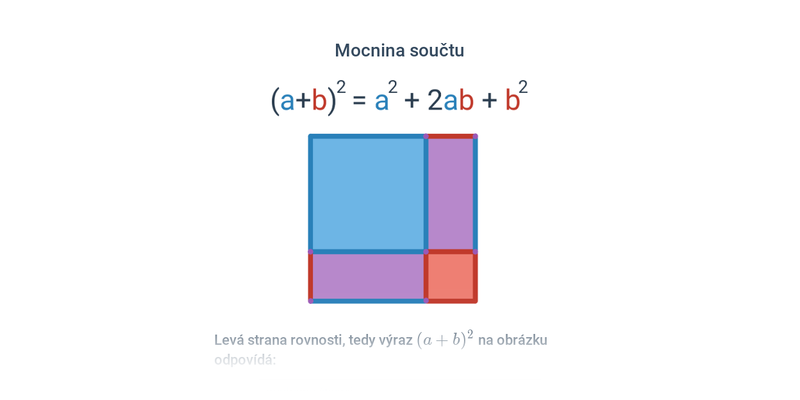
Obrázkové důkazy
Obrázek sice není plnohodnotným důkazem, ale často dokáže velmi výstižně ilustrovat základní myšlenku matematických tvrzení.
Matematická indukce
0/3
Matematická indukce
Zda nabízíme vypracované důkazy matematickou indukcí. Ke každému pak následuje několik otázek kontrolujících porozumění důkazu.
Celkem vyřešeno: 0 z 23
