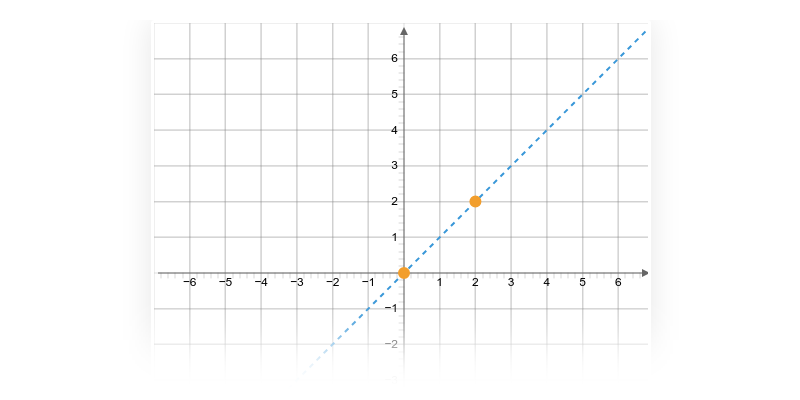
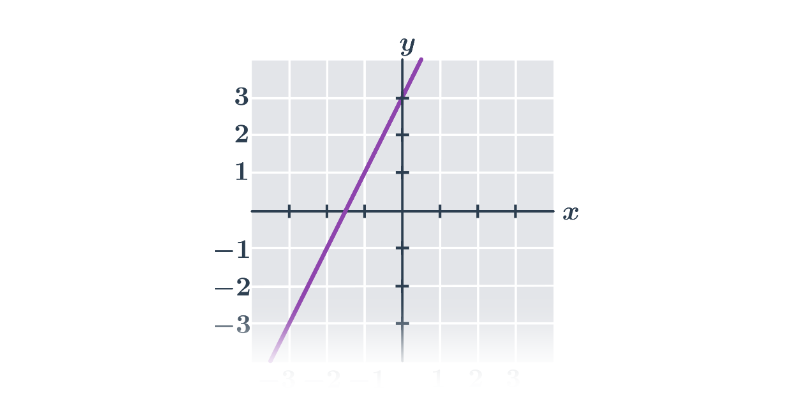
Lineární funkci můžeme vždy zapsat ve tvaru f(x)= a \cdot x + b, kde a a b jsou konstanty. Číslo a je směrnice (též nazývaná sklon), konstanta b je absolutní člen. Grafem lineární funkce je přímka, kterou snadno sestrojíme pomocí dvou bodů.
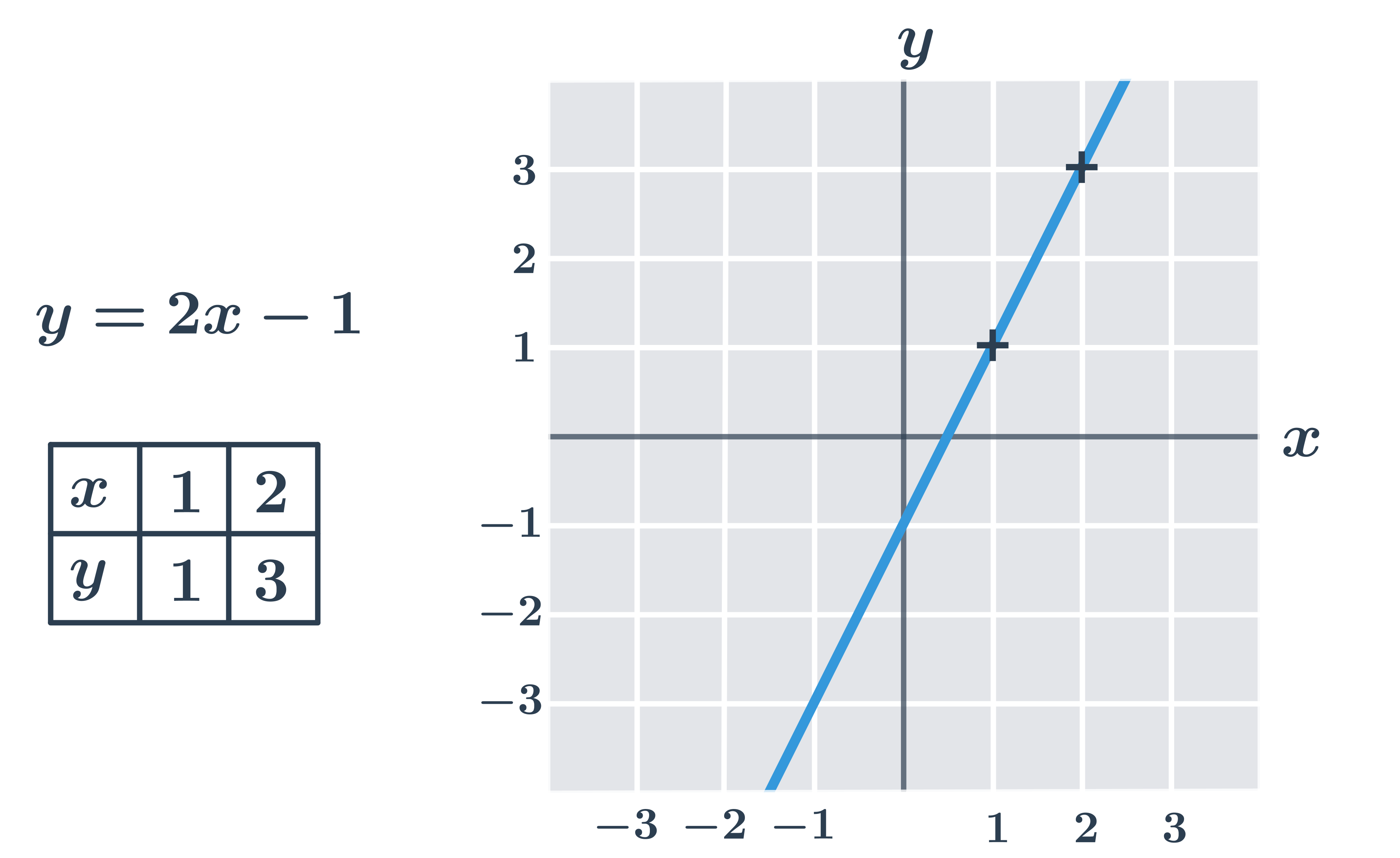
Příklad: graf funkce y=-0{,}5x+1.
- Zvolíme si dvě libovolné hodnoty proměnné x. Vhodnou volbou je x=0, tím zároveň určíme i průsečík s osou y.
- Pro x=0 dopočítáme hodnotu y, tedy: y=-0{,}5\cdot 0+2=0+1=1
- Dále zvolíme například x=2 a dosadíme: y=-0{,}5\cdot 2+1=-1+1=0
- Graf funkce y=-0{,}5x+1 pak prochází body [0;1] a [2;0].
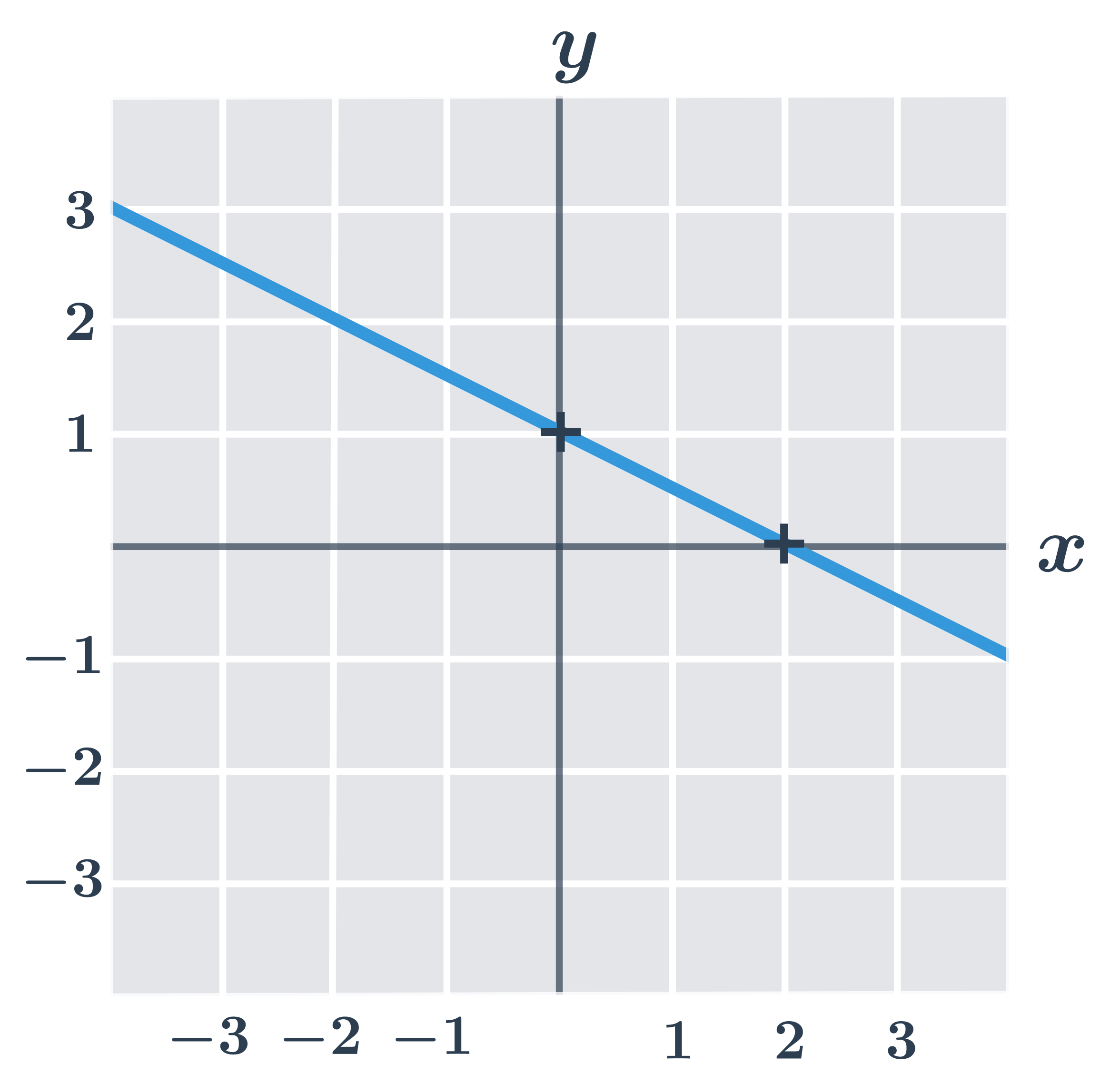
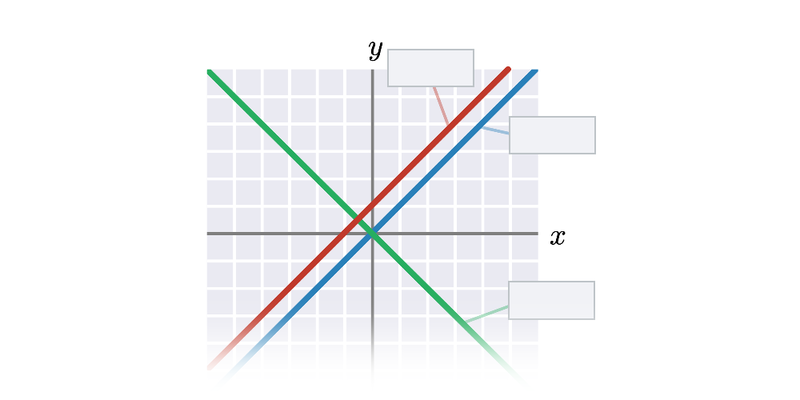
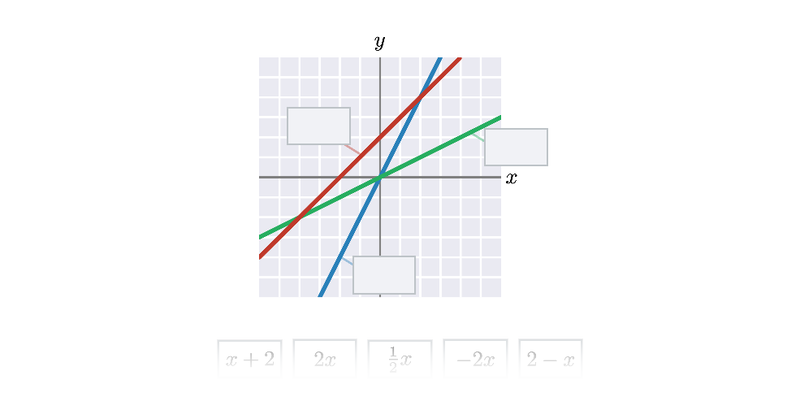
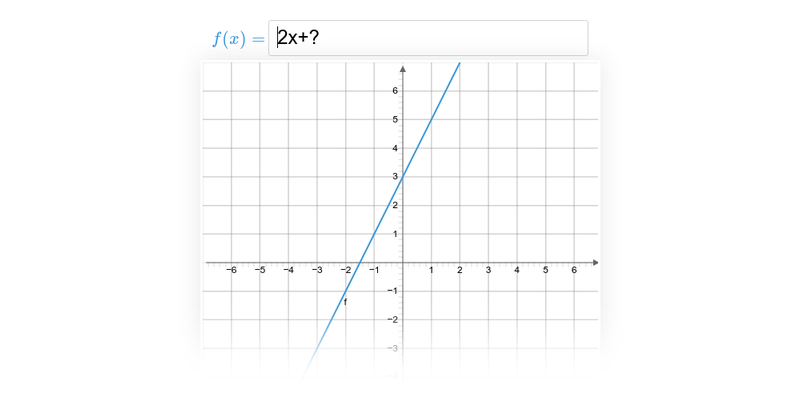
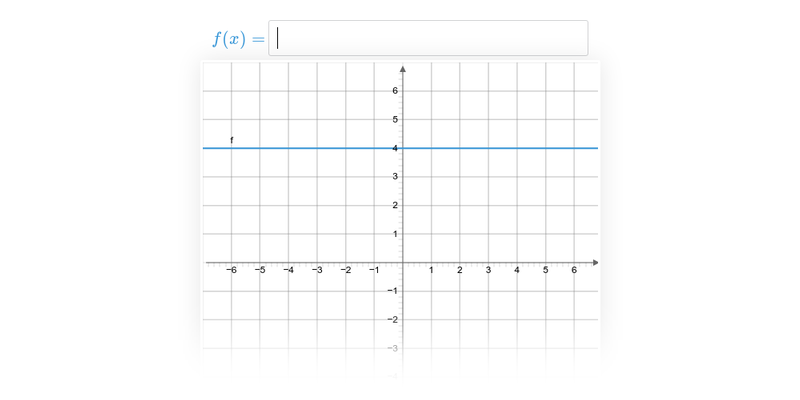
Přímku, která je grafem funkce f(x)=a\cdot x+b můžeme sestrojit také pomocí konstant a a b, přičemž platí:
- Absolutní člen b udává „svislý posun“. Je to průsečík přímky s osou y. V uvedených příkladech je vyznačen oranžovou barvou.
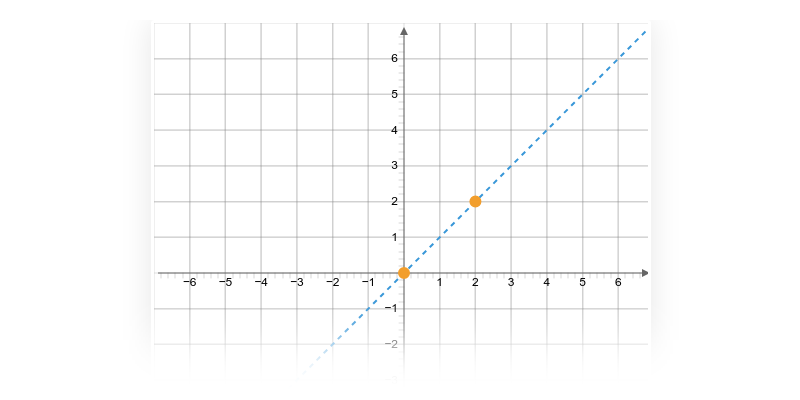
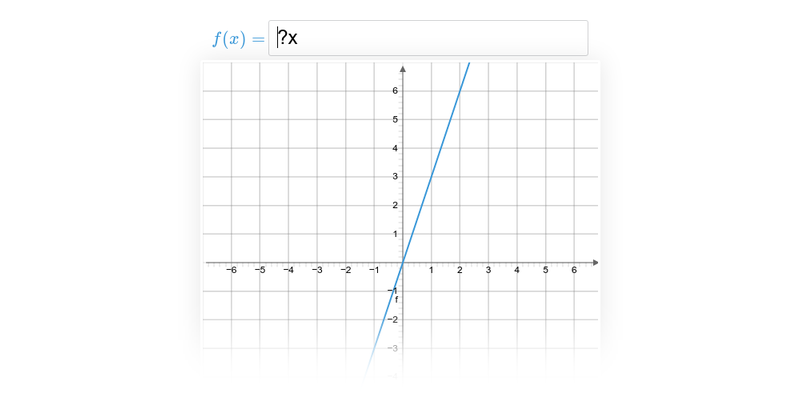
- Směrnice a udává sklon přímky, což můžeme vyjádřit jako „o kolik jednotek na ose y se po dané přímce posuneme, když se posuneme o jednu jednotku na ose x“. V uvedených příkladech je směrnice vyznačena žlutou barvou.
Důležitá jsou znamínka (naznačená v obrázcích šipkami). Kladný absolutní člen znamená posun nahoru, záporný absolutní člen znamená posun dolů. Kladná směrnice znamená stoupající přímku, záporná směrnice znamená klesající přímku.
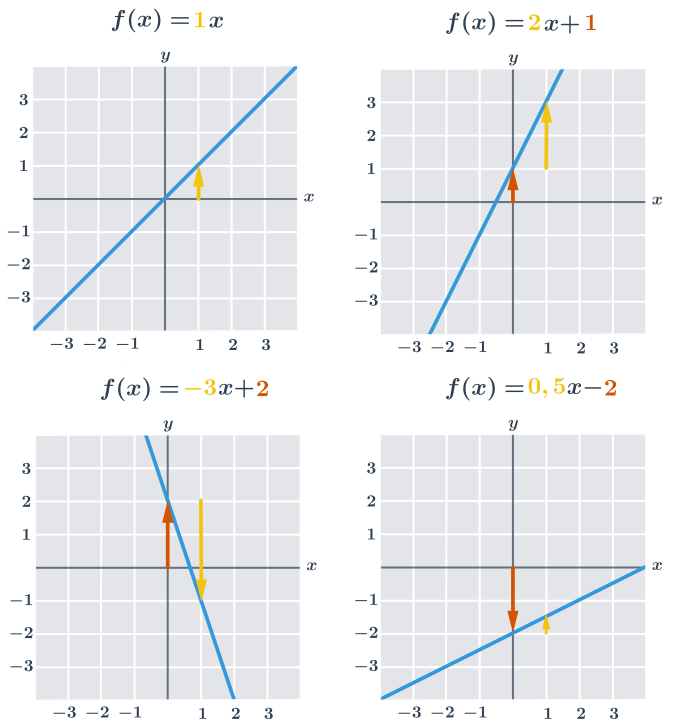
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Grafař
Specializované cvičení na práci s grafem a funkcemi.
Označování
V zadaném obrázku či textu máte za úkol označit všechny oblasti, které splňují určitou vlastnost.