Výpis souhrnů
Grafy funkcí
Podtémata
Grafy funkcí
Graf funkce f zadané předpisem y=f(x) pro všechna x z množiny D(f) je množina bodů v rovině, jejichž kartézské souřadnice x, y splňují následující podmínky:
- souřadnice x je v definičním oboru funkce f (neboli x \in D(f))
- závislost souřadnice y na x je popsaná funkčním předpisem y=f(x) (pro každé x z D(f) je v grafu právě jeden bod, jeho souřadnice jsou x a f(x))
Příklad: graf, definiční obor, obor hodnot funkce
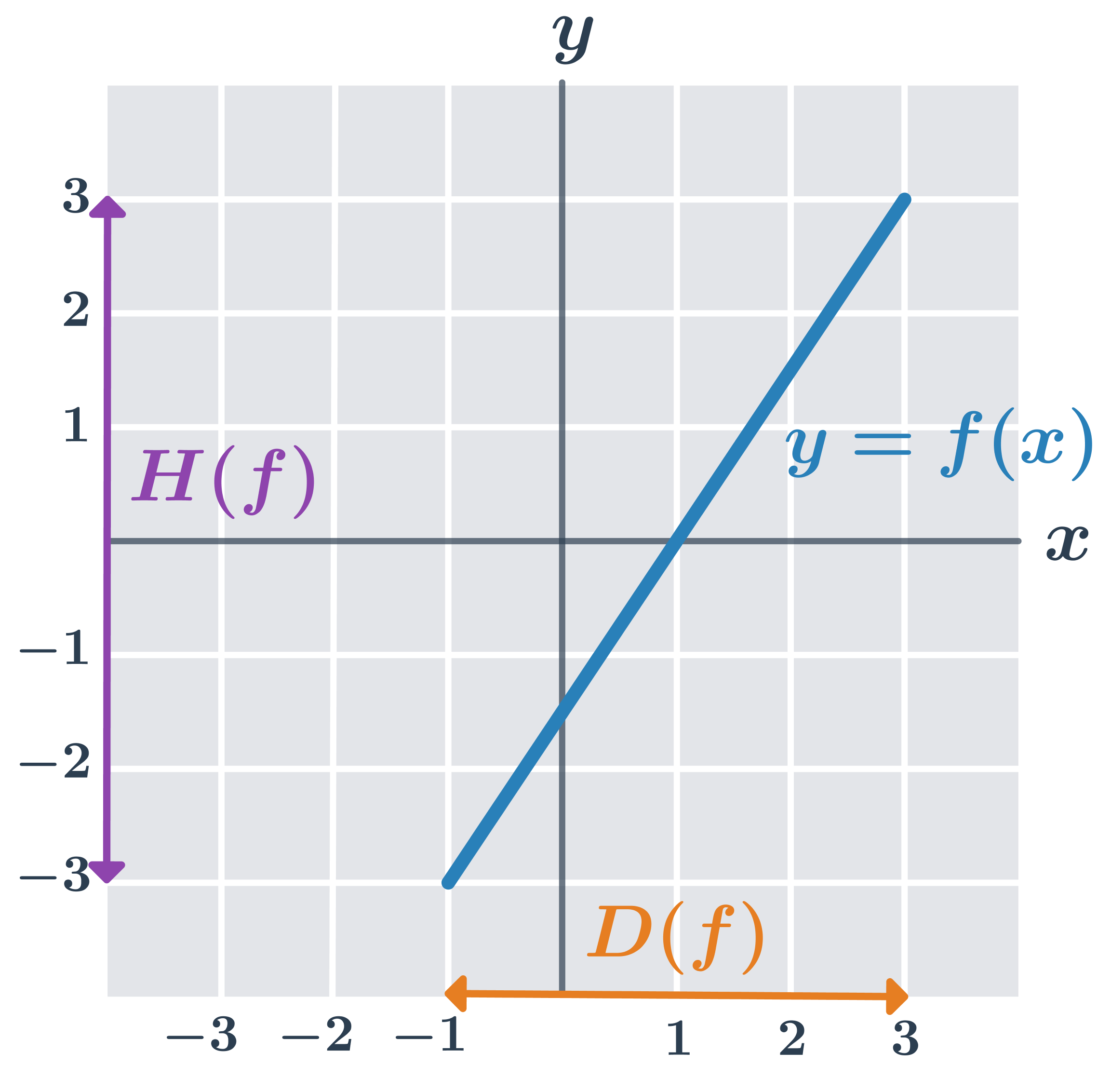
Na obrázku je graf funkce y=2x-1 pro x\in \langle -1;3\rangle. Definiční obor je vyznačen na ose x, obor hodnot na ose y.
Grafy lineárních funkcí
Lineární funkci můžeme vždy zapsat ve tvaru f(x)= a \cdot x + b, kde a a b jsou konstanty. Číslo a je směrnice (též nazývaná sklon), konstanta b je absolutní člen. Grafem lineární funkce je přímka, kterou snadno sestrojíme pomocí dvou bodů.
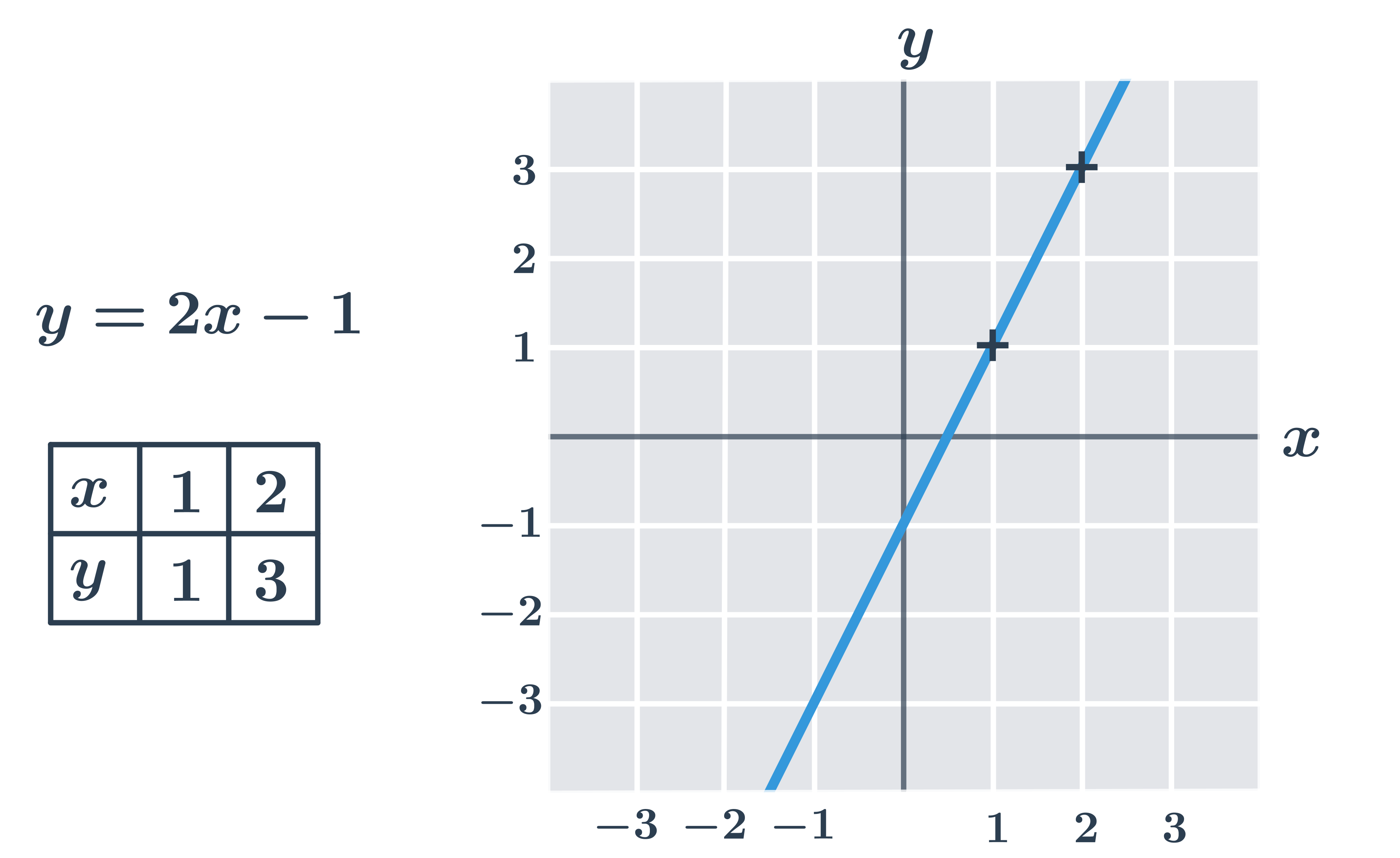
Příklad: graf funkce y=-0{,}5x+1.
- Zvolíme si dvě libovolné hodnoty proměnné x. Vhodnou volbou je x=0, tím zároveň určíme i průsečík s osou y.
- Pro x=0 dopočítáme hodnotu y, tedy: y=-0{,}5\cdot 0+2=0+1=1
- Dále zvolíme například x=2 a dosadíme: y=-0{,}5\cdot 2+1=-1+1=0
- Graf funkce y=-0{,}5x+1 pak prochází body [0;1] a [2;0].
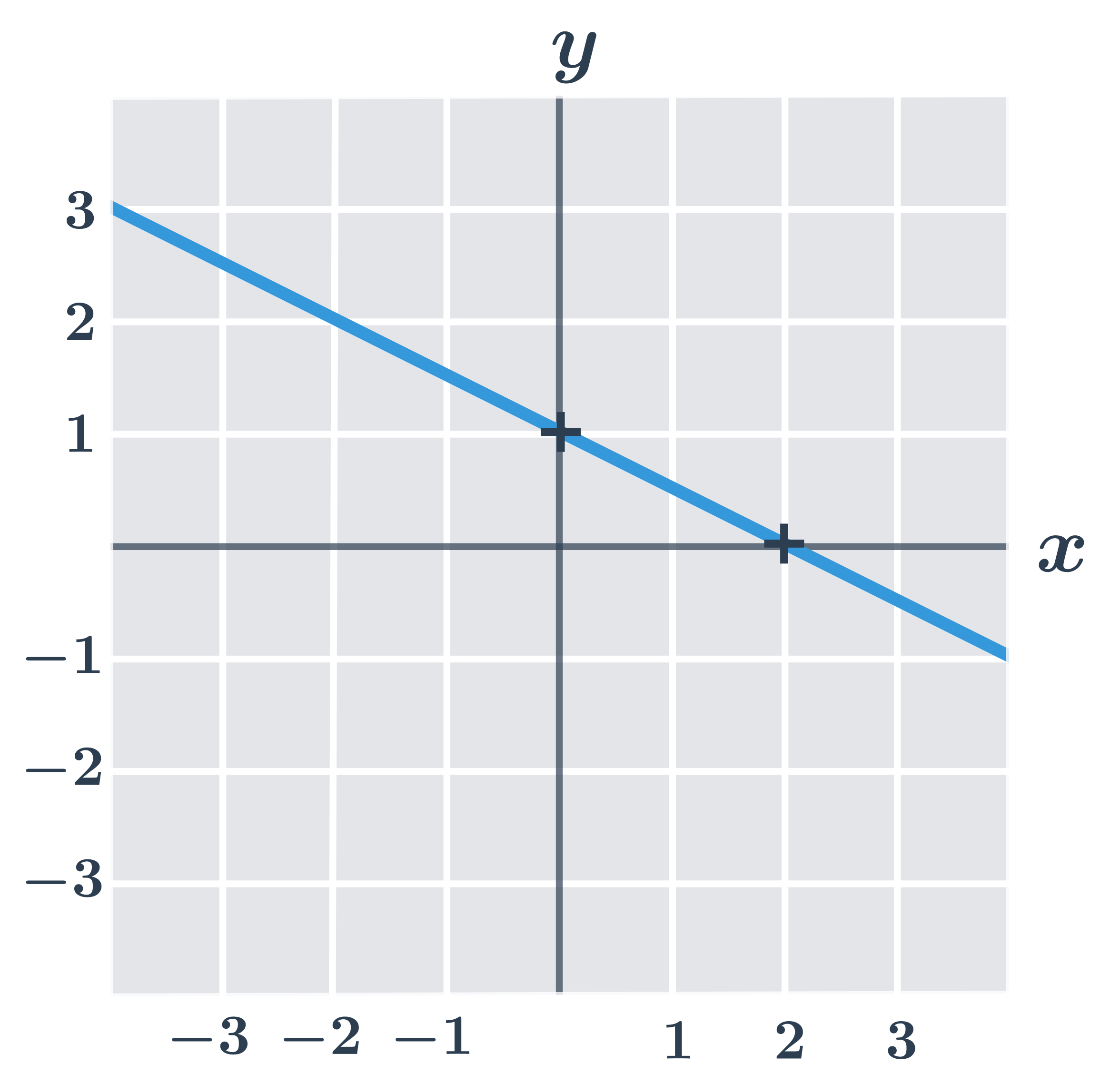
Přímku, která je grafem funkce f(x)=a\cdot x+b můžeme sestrojit také pomocí konstant a a b, přičemž platí:
- Absolutní člen b udává „svislý posun“. Je to průsečík přímky s osou y. V uvedených příkladech je vyznačen oranžovou barvou.
- Směrnice a udává sklon přímky, což můžeme vyjádřit jako „o kolik jednotek na ose y se po dané přímce posuneme, když se posuneme o jednu jednotku na ose x“. V uvedených příkladech je směrnice vyznačena žlutou barvou.
Důležitá jsou znamínka (naznačená v obrázcích šipkami). Kladný absolutní člen znamená posun nahoru, záporný absolutní člen znamená posun dolů. Kladná směrnice znamená stoupající přímku, záporná směrnice znamená klesající přímku.
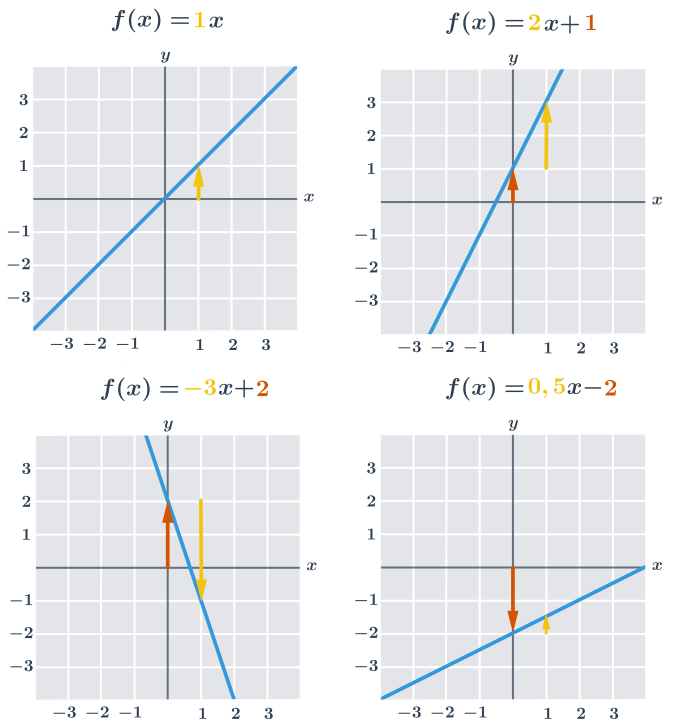
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruGrafy kvadratických funkcí
Kvadratickou funkci lze vyjádřit ve tvaru f(x) = ax^2 + bx + c, kde a\neq 0. Grafem kvadratické funkce je parabola. Tento graf zobrazuje funkci 0{,}5 x^2 + x - 4:
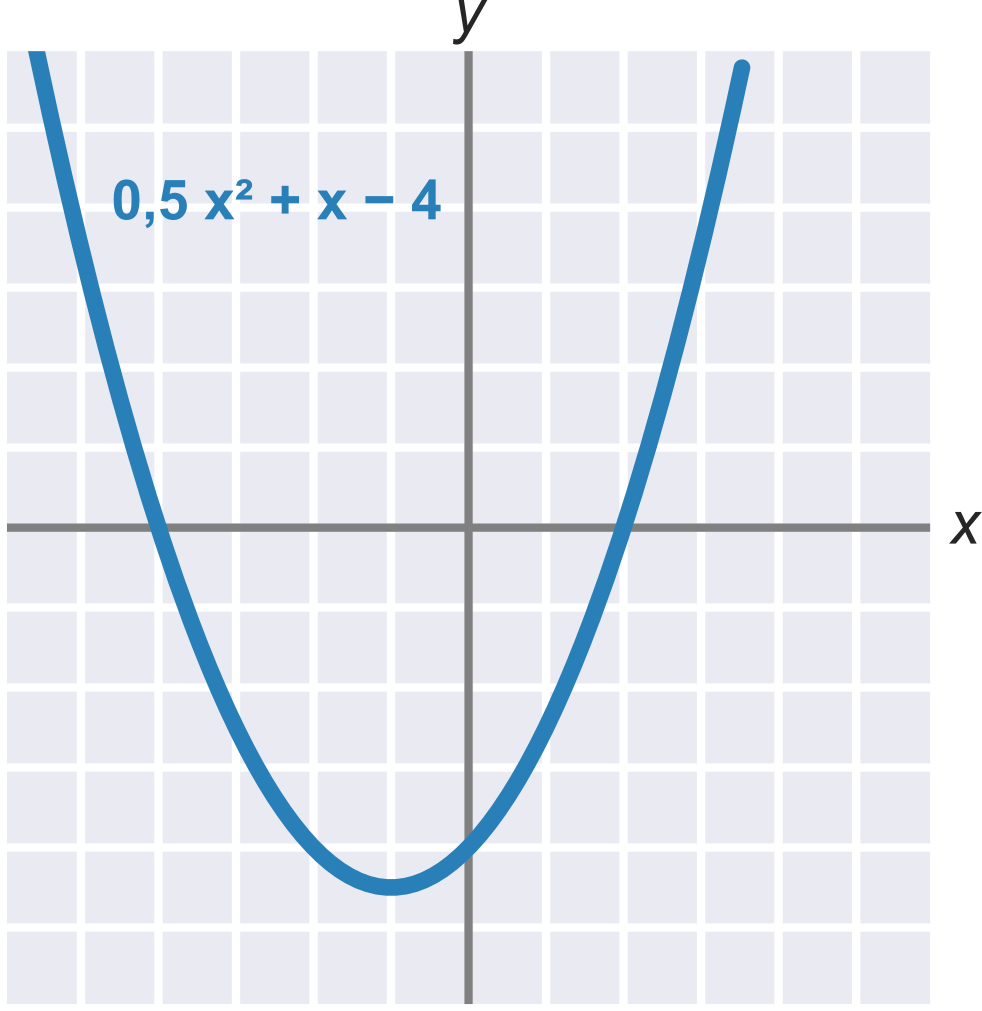
Průsečíky s osou x jsou řešení kvadratické rovnice ax^2 + bx + c = 0. Pro výše uvedený příklad 0{,}5 x^2 + x - 4 jsou těmito řešeními x_1 = -4 a x_2 = 2.
Vliv koeficientů a a c na tvar grafu kvadratické funkce
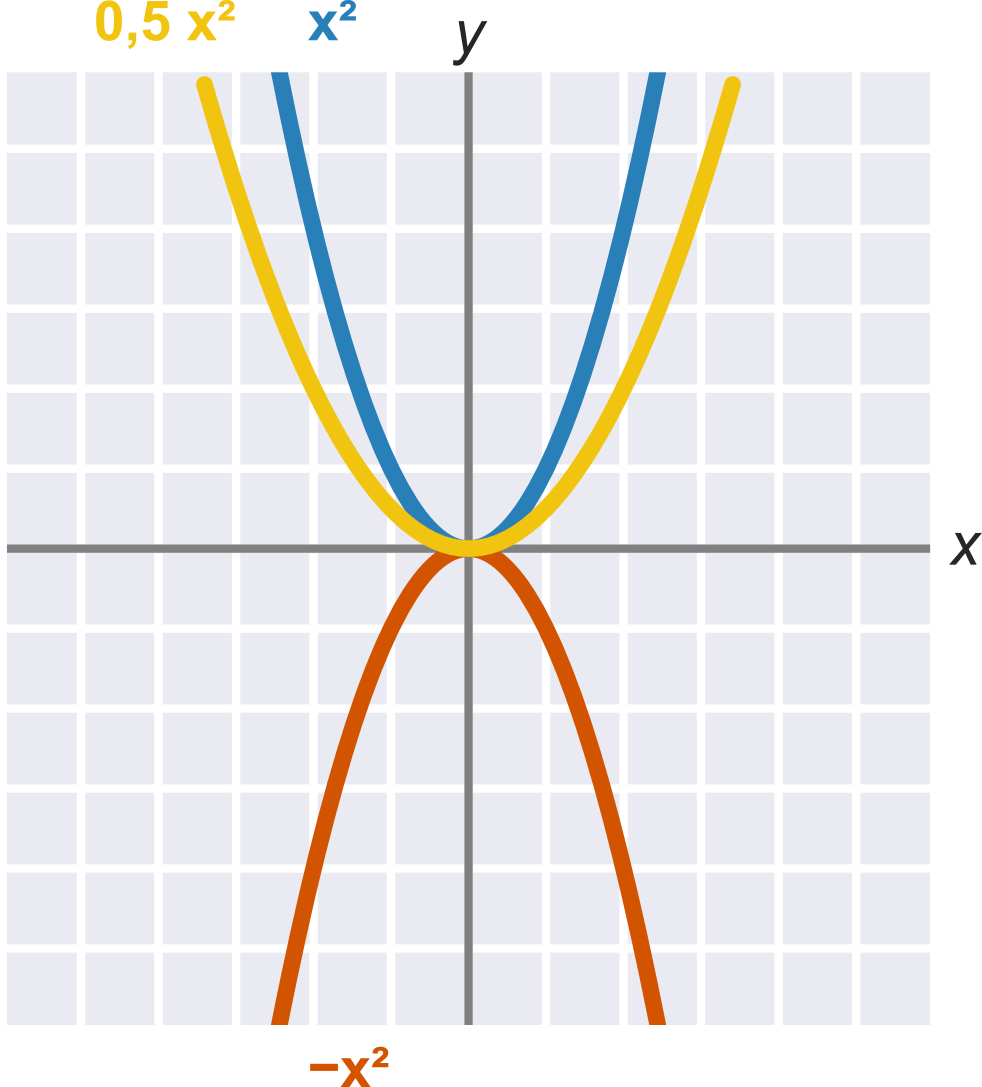
Kvadratický koeficient a ovlivňuje základní podobu paraboly:
- Pokud je a \gt 0, „směřuje parabola nahoru“ (přesněji: je to zdola omezená, konvexní funkce).
- Pokud je a \lt 0, „směřuje parabola dolů“ (přesněji: je to shora omezená, konkávní funkce).
- Velikost kvadratického koeficientu a ovlivňuje, jak je parabola „široká“.
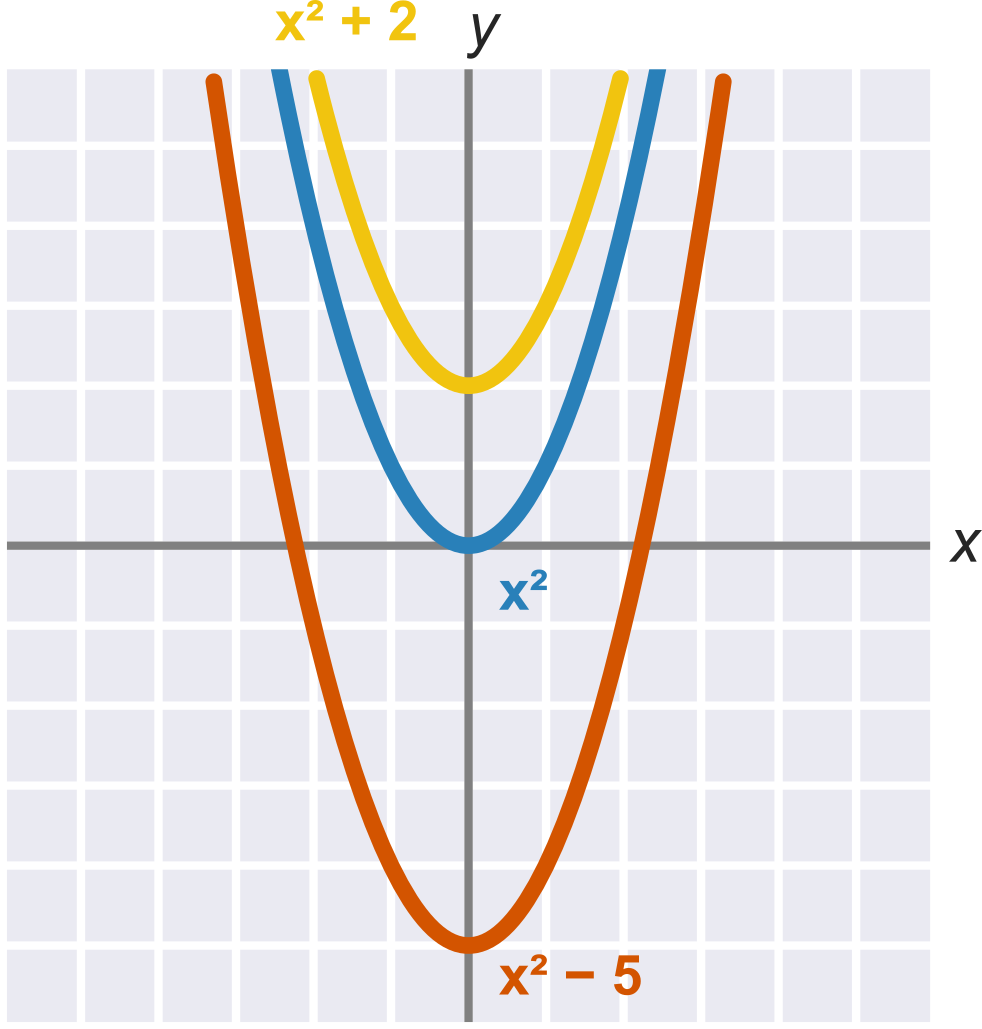
Konstantní člen c ovlivňuje posun paraboly – udává průsečík s osou y.
Určení vrcholu paraboly pomocí úpravy na čtverec
Funkční předpis upravíme tak, aby člen s proměnnou x byl ve tvaru (x-m)^2 (tzv. úprava na čtverec). Souřadnice x vrcholu paraboly je rovna číslu m, souřadnici y získáme jako funkční hodnotu zadané kvadratické funkce v bodě m.
Příklad: určení vrcholu paraboly úpravou na čtverec
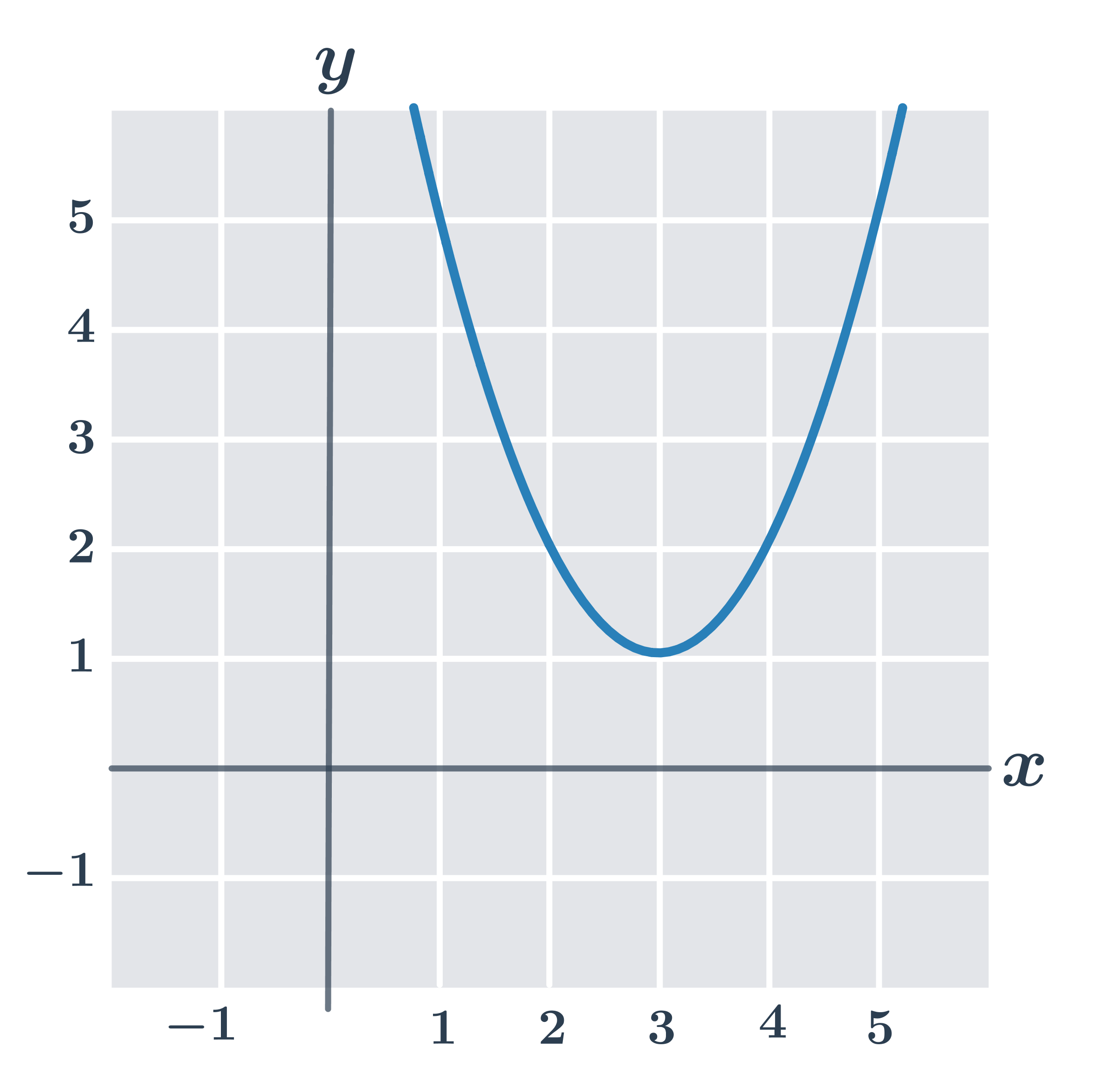
Určete vrchol paraboly, která je grafem kvadratické funkce dané předpisem: y=x^2-6x+10
\begin{array}{rrl}y&=&x^2-6x+10\\y&=&x^2-6x+9+1\\y&=&(x-3)^2+1\end{array}
Máme tedy souřadnice vrcholu paraboly x=3 a y=(3-3)^2+1=1.
Zajímavost z analytické geometrie: Převedením konstanty na levou stranu rovnice y=(x-3)^2+1 dostaneme vrcholovou rovnici paraboly y-1=(x-3)^2.
Parabola, která je grafem funkce, má vrchol v bodě [3,1].
Komiks pro zpestření
Grafy funkcí s absolutní hodnotou
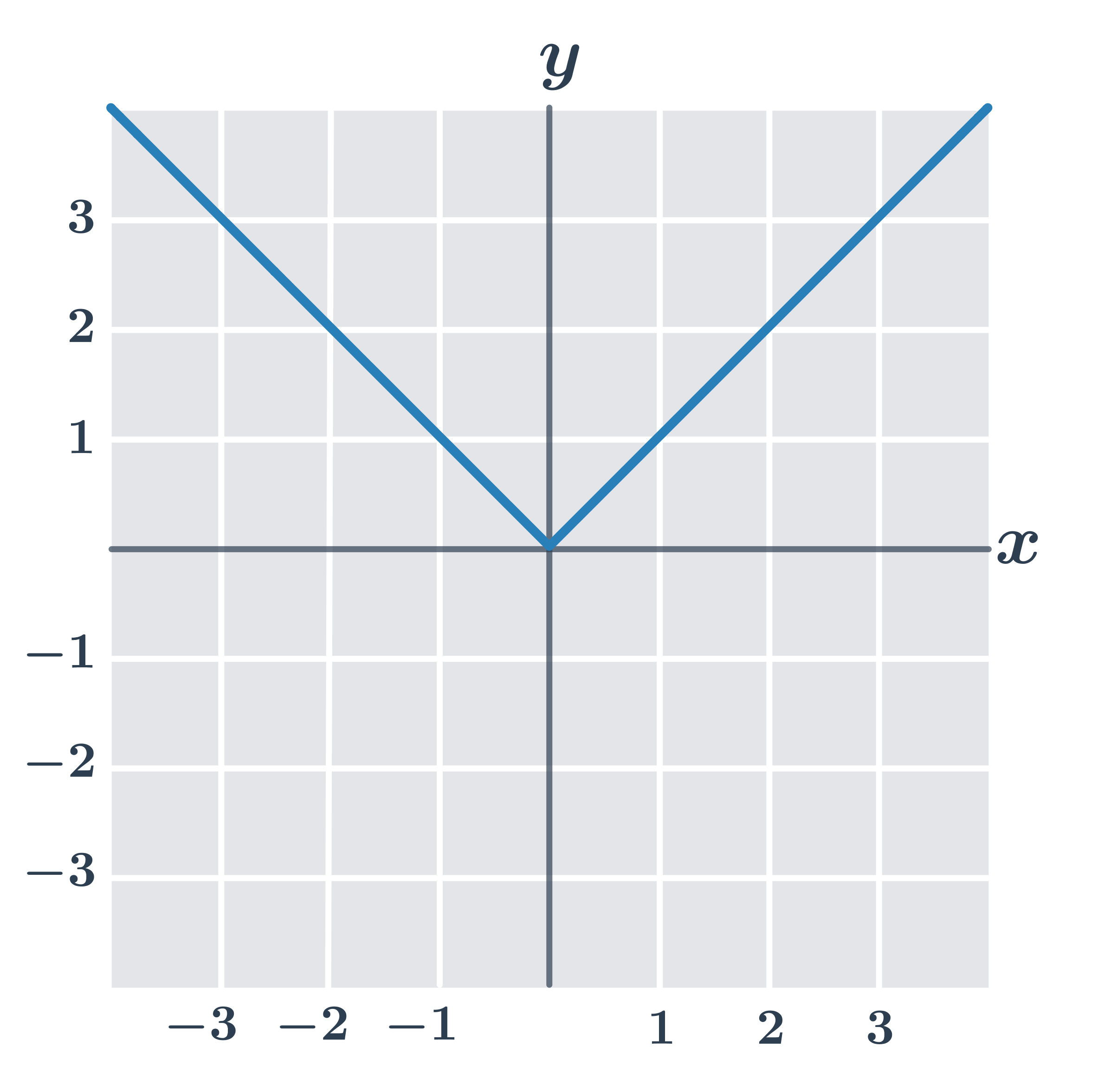
Na obrázku je graf funkce y=|x|. Tento graf tvoří dvě polopřímky s počátkem v bodě [0;0], protože pro absolutní hodnotu platí:
- absolutní hodnota kladného čísla je rovna tomuto číslu: |x|=x
- absolutní hodnota záporného čísla je rovna opačnému číslu: |x|=-x
- absolutní hodnota čísla nula je rovna nule: |0|=0
| x \gt 0 | Grafem funkce y=|x| je polopřímka s počátkem v bodě [0;0] daná rovnicí y=x. |
| x \lt 0 | Grafem funkce y=|x| je polopřímka s počátkem v bodě [0;0] s rovnicí y=-x. |
| x = 0 | Bod [0;0] je počátek polopřímek, které vytvoří graf funkce y=|x|. |
Pokud chceme nakreslit graf funkce y=|f(x)| postupujeme tak, že nakreslíme graf y=f(x) a potom záporné funkční hodnoty nahradíme opačnými. V oblasti, kde jsou funkční hodnoty záporné, se tedy graf překlopí kolem osy x.
Příklad 1: graf funkce y=|x-1|
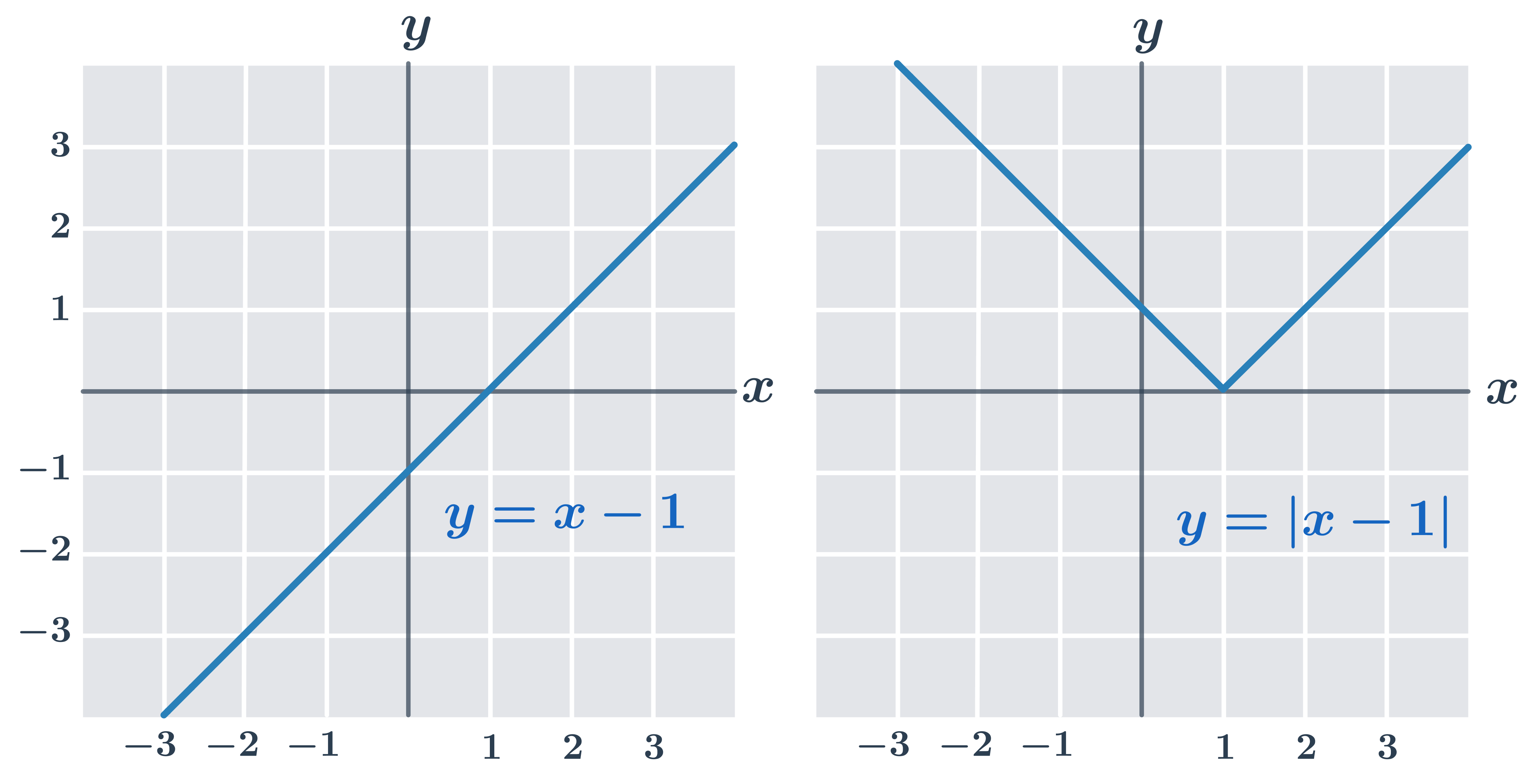
| Pro čísla x \lt 1 má funkce y=x-1 záporné funkční hodnoty. |
| Funkce y=|x-1| má v intervalu (-\infty;1) opačné hodnoty než funkce y=x-1 (graf y=|x-1| je vůči grafu y=x-1 v tomto intervalu překlopený podle osy x). |
| V intervalu (1;\infty) jsou grafy funkcí y=x-1 a y=|x-1| stejné. |
Příklad 2: graf funkce y=|x^2-4|
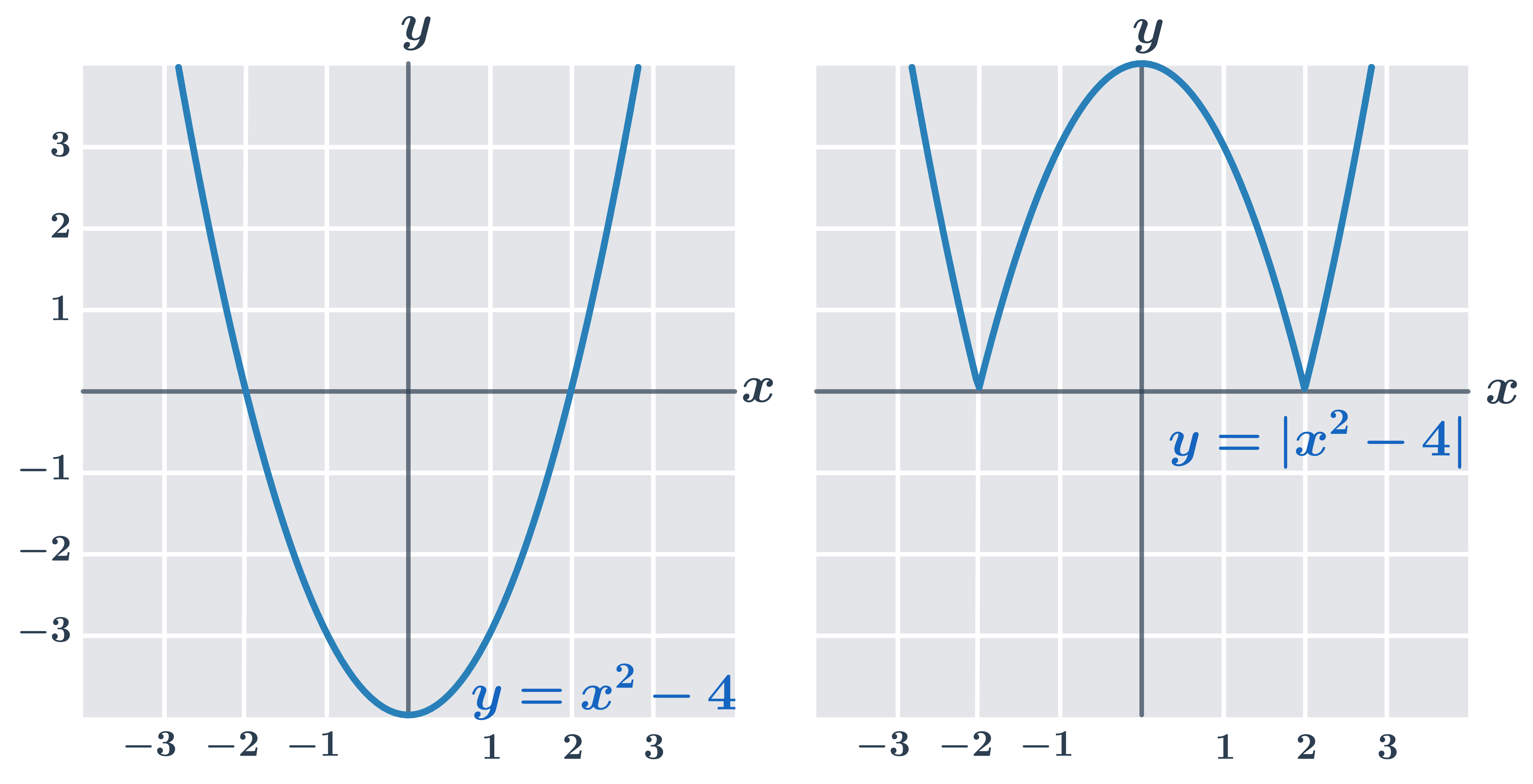
| V intervalu (-2;2) má funkce y=x^2-4 záporné funkční hodnoty. |
| Funkce y=|x^2-4| má v intervalu (-2;2) opačné hodnoty než funkce y=x^2-4 (graf je překlopený podle osy x). |
| V intervalech (-\infty;-2) a (2;\infty) jsou grafy funkcí y=x^2-4 a y=|x^2-4| stejné. |
Grafy lineárních lomených funkcí
Grafem lineární lomené funkce je hyperbola, která má asymptoty rovnoběžné se souřadnými osami x a y.
Asymptota rovnoběžná s osou y prochází bodem, který nepatří do definičního oboru a má tedy rovnici: x =-\frac{d}{c}.
Pro nalezení rovnice asymptoty rovnoběžné s osou x vydělíme čitatele a jmenovatele a funkční předpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnoběžná s osou x má rovnici: y =\frac{a}{c}.
Průsečík grafu s osou x je bod, pro který ax+b=0. V tomto bodě je hodnota funkce nulová, tedy čitatel zlomku \frac{ax+b}{cx+d} je nulový.
Průsečík grafu s osou y je bod, který dostaneme dosazením hodnoty x=0 do funkčního předpisu.
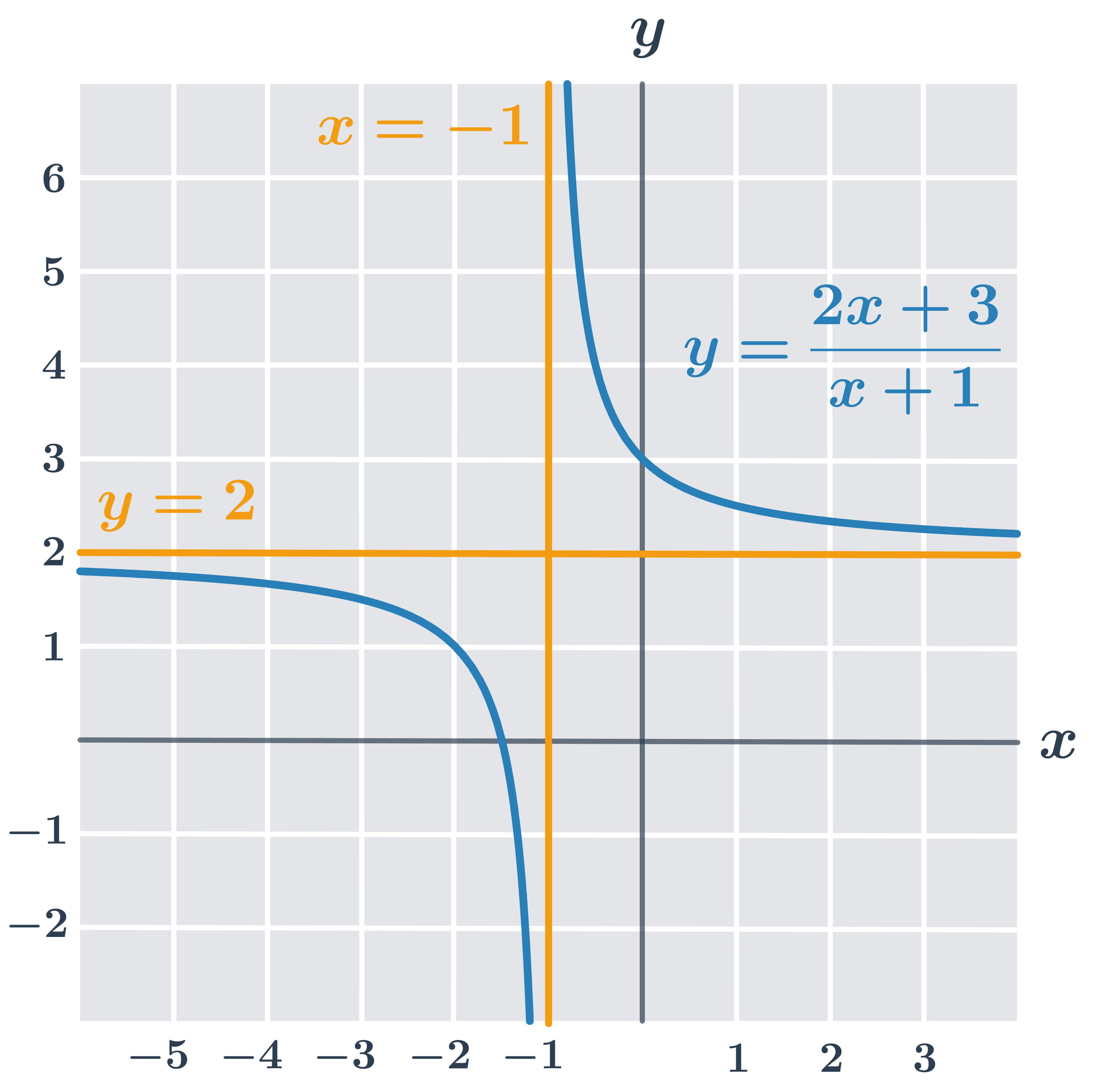
Příklad – funkce y =\frac{2x+3}{x+1}
Rozeberme si graf funkce z obrázku výše:
- definiční obor D(f)=\R - \{-1\}, protože x+1\neq0
- asymptota rovnoběžná s osou y má rovnici x =-1 (pro x=-1 není funkce definovaná, toto číslo neleží v jejím definičním oboru)
- asymptota rovnoběžná s osou x má rovnici y =2, což zjistíme úpravou funkčního předpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
- průsečík grafu s osou x je bod [0;-\frac{3}{2}] (řešení rovnice: 2x+3=0)
- průsečík grafu s osou y je bod [3;0], dosazením hodnoty x=0 do y =\frac{2x+3}{x+1}
Grafy mocninných funkcí
Grafy základních mocninných funkcí y= x^n
pro n sudé – graf je souměrný podle osy y, D(f)=\R, H(f)=\langle0, \infty)
pro n liché – graf je souměrný podle počátku, D(f)=\R, H(f)=\R
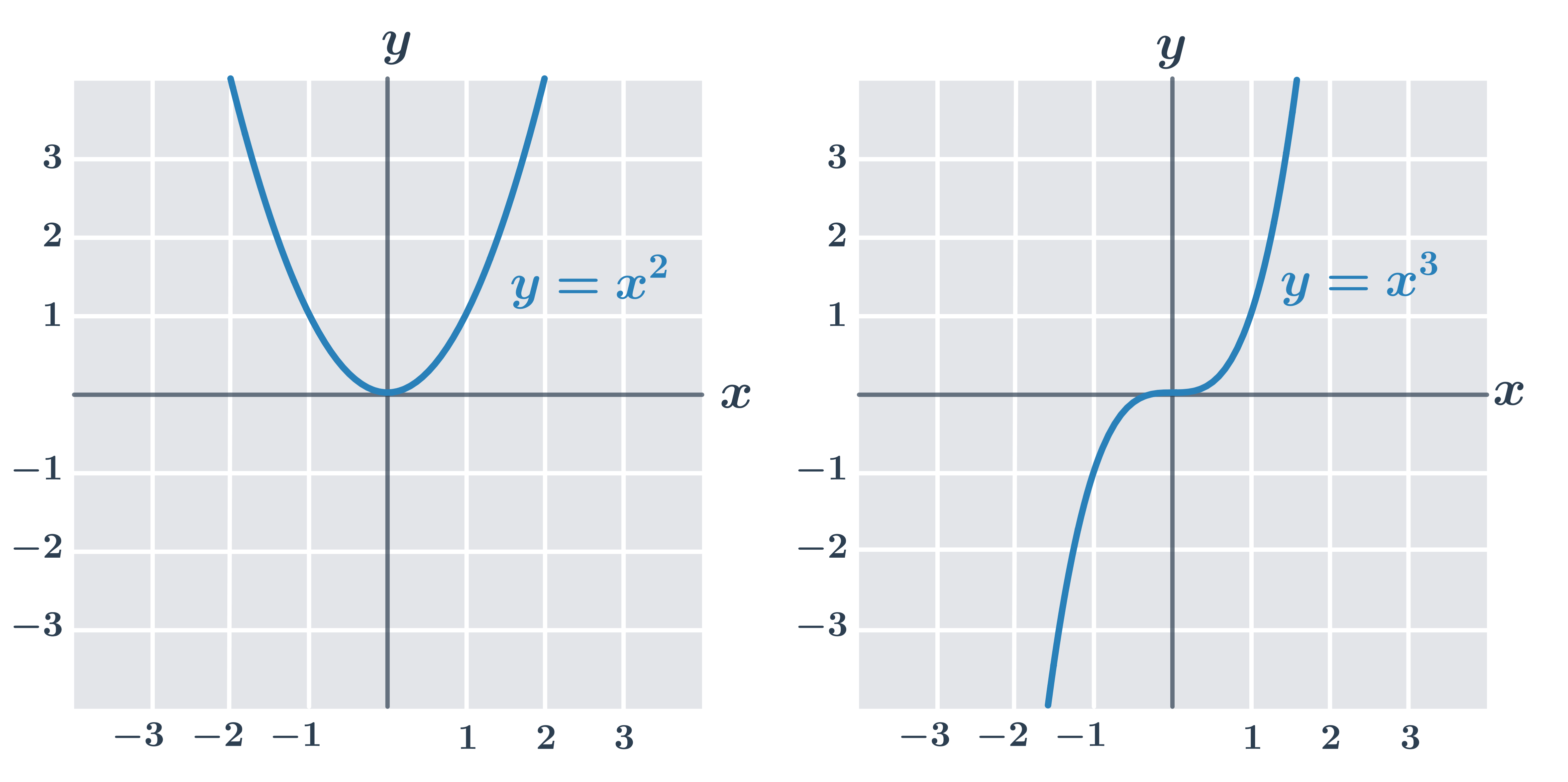
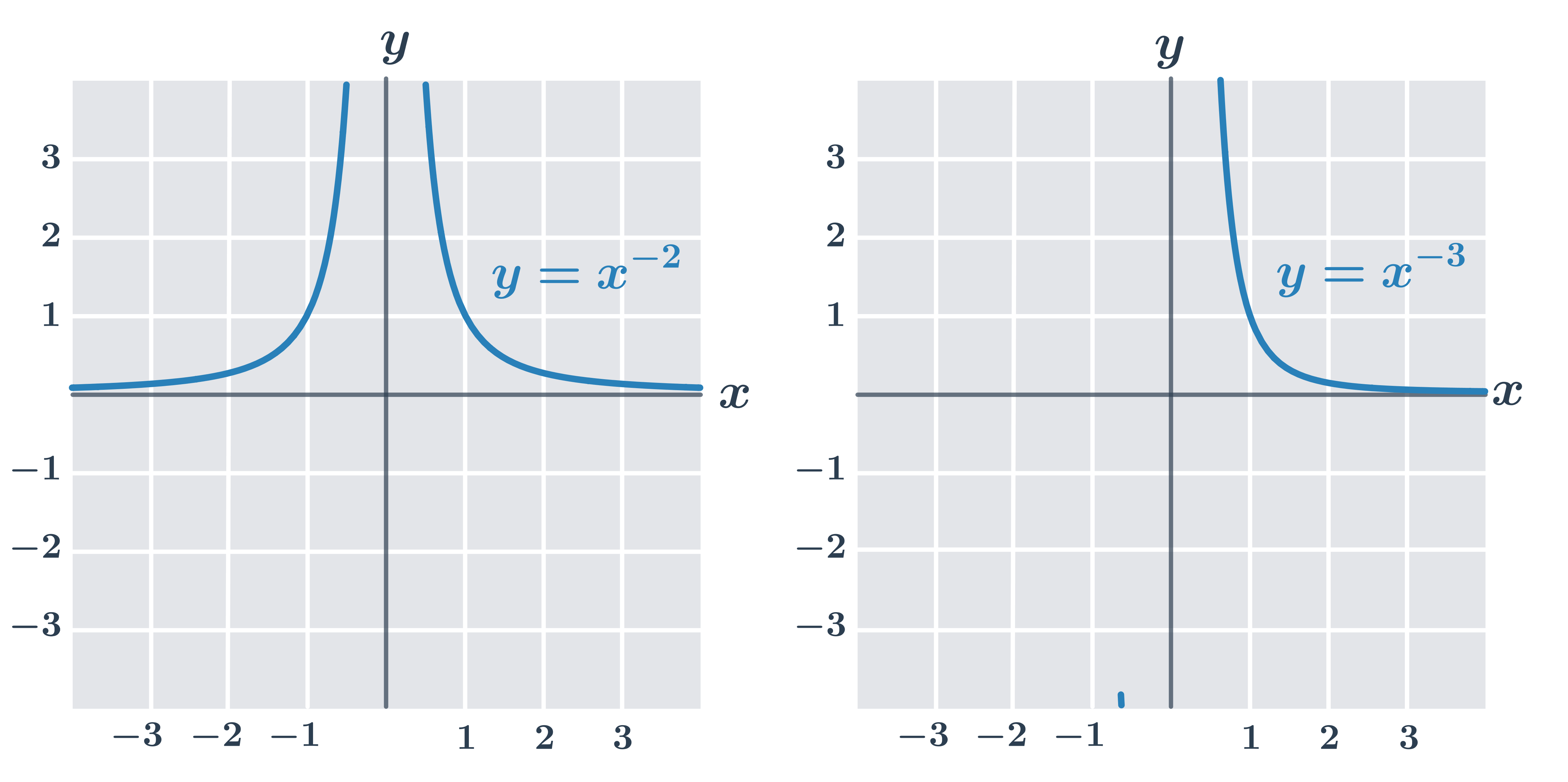
Grafy mocninných funkcí se záporným exponentem y= x^{-n}
pro n sudé – graf souměrný podle osy y, D(f)=\R- \{0\}, H(f)=\langle0, \infty)
pro n liché – graf souměrný podle počátku, D(f)=\R - \{0\}, H(f)=\R - \{0\}
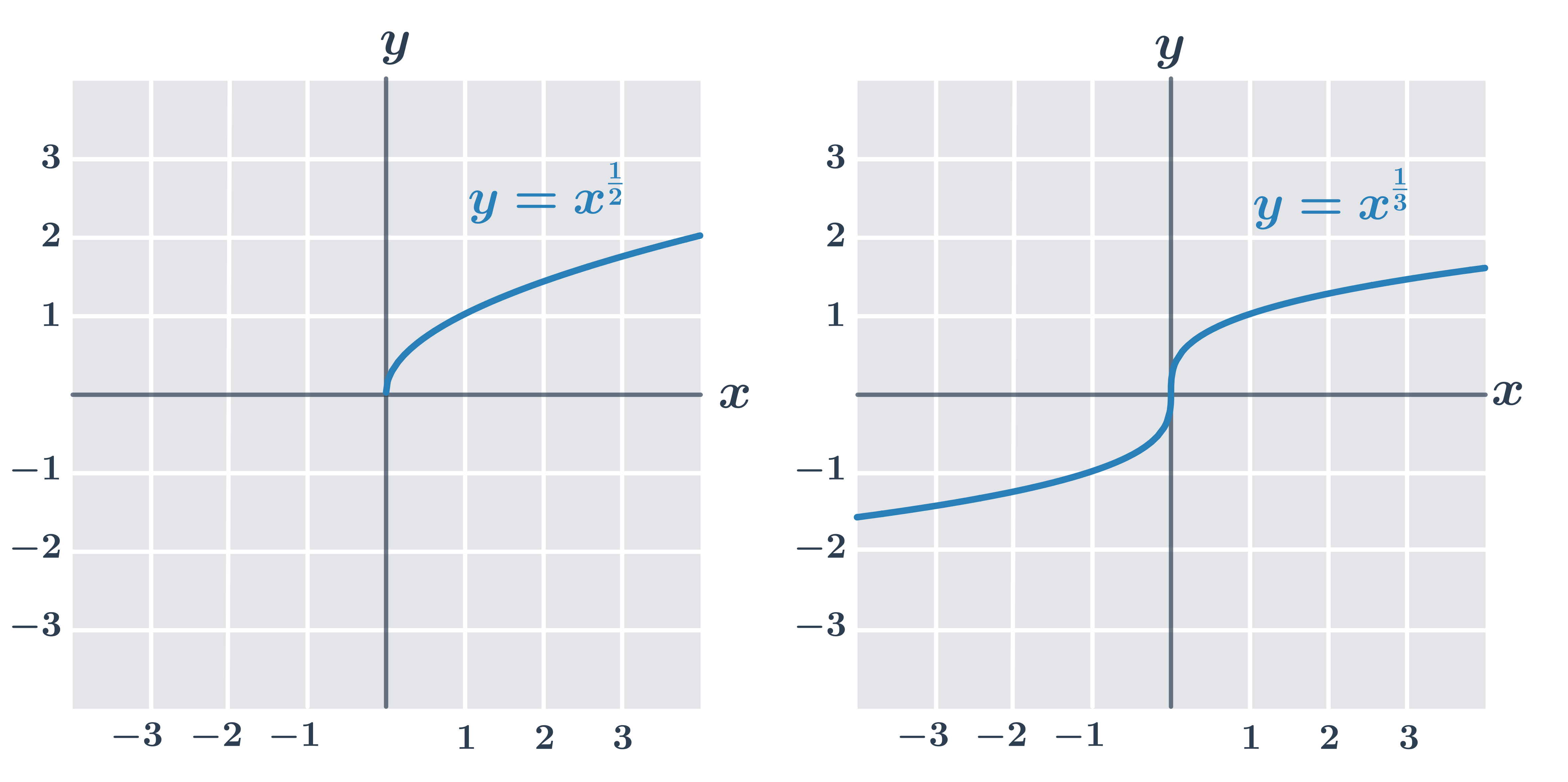
Grafy funkcí y= x^{\frac{1}{n}}:
pro sudé n – funkce y= x^{\frac{1}{n}} definována na kladných číslech, D(f)=\langle0, \infty), H(f)=\langle0, \infty)
pro liché n – funkce y=x^n je prostá, proto bychom mohli definovat n-tou odmocninu i pro záporná čísla, ale často se (např. jako příprava pro práci s mocninnými funkcemi s obecnějšími racionálními exponenty) všechny n-té odmocniny pro sudá i lichá n definují pro jednoduchost jen na intervalu [0,\infty).
Poznámka: výpočty s mocninami a odmocninami
Při výpočtech s mocninami a odmocninami musíme být obezřetní, hodně pravidel platí pro nezáporný základ (pokud počítáme s odmocninami), případně kladný základ (nulu můžeme odmocňovat, ale nesmíme dělit nulou). Příklady:
součin odmocnin je odmocnina součinu: pro nezáporná čísla jako základy odmocnin pravidlo platí, pokud bychom chtěli použít pro záporný základ, nemusí nám v oboru reálných čísel vycházet smysluplné věci: \sqrt{-2} není definovaná, ale \sqrt{(-2)\cdot(-2)} je \sqrt{4} = 2
racionální exponenty: mělo by x^{\frac{2}{6}} být totéž jako x^{\frac{1}{3}}? Exponent je „stejné racionální číslo“, ale pro záporná x by vycházely u těchto dvou předpisů jiné funkční hodnoty (6. odmocnina ze záporného x není definovaná, 6. odmocnina z druhé mocniny záporného čísla je kladná, a 3. odmocnina z x by pro záporná x byla záporná).
racionální exponenty konkrétněji: čemu by se mělo rovnat (-8)^{\frac{2}{6}}? Máme (-8)^{\frac{1}{3}}=-2, ale zároveň \sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2. Můžeme se dostat do potíží, když budeme pravidla, která platí pro mocniny a odmocniny kladných a nezáporných čísel, zkoušet používat i pro záporné základy.
Vliv úprav funkčního předpisu na graf mocninné funkce
Obrázek ukazuje několik úprav funkce y= x^3:
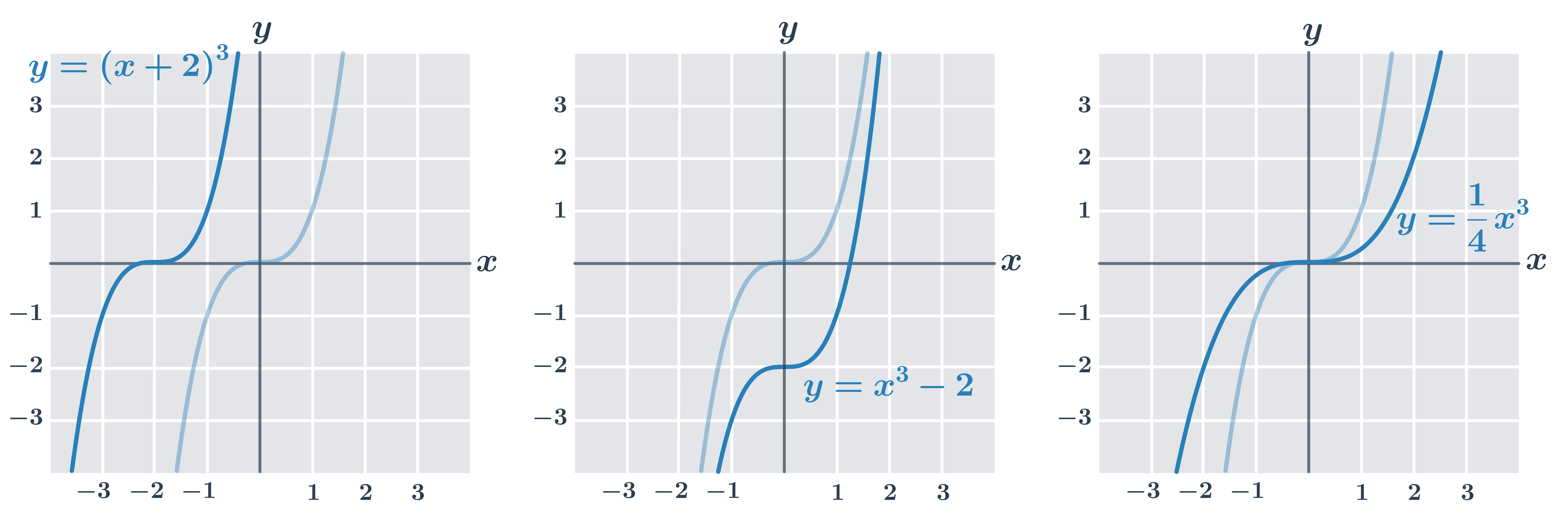
| y= (x+2)^3 | graf je posunutý ve směru osy x |
| y=x^3-2 | graf je posunutý ve směru osy y |
| y=\frac{1}{4} x^3 | graf bude natažený nebo smrštěný ve směru osy y (v uvedeném grafu se funkční hodnoty zmenší na čtvrtinu, například pro x=2 je hodnota funkce y=\frac{1}{4} \cdot 2^3=2) |
Grafy goniometrických funkcí
Grafy základních goniometrických funkcí intuitivně

Všimněte si
- graf které funkce protíná osu y v bodě x=0, y=0? (\sin, \tan)
- graf které funkce protíná osu y v bodě x=0, y=1? (\cos)
- která funkce je definovaná pro všechna x \in \mathbb{R}? (\sin, \cos)
Grafy goniometrických funkcí s popsanými osami
Funkce sinus y=\sin x:
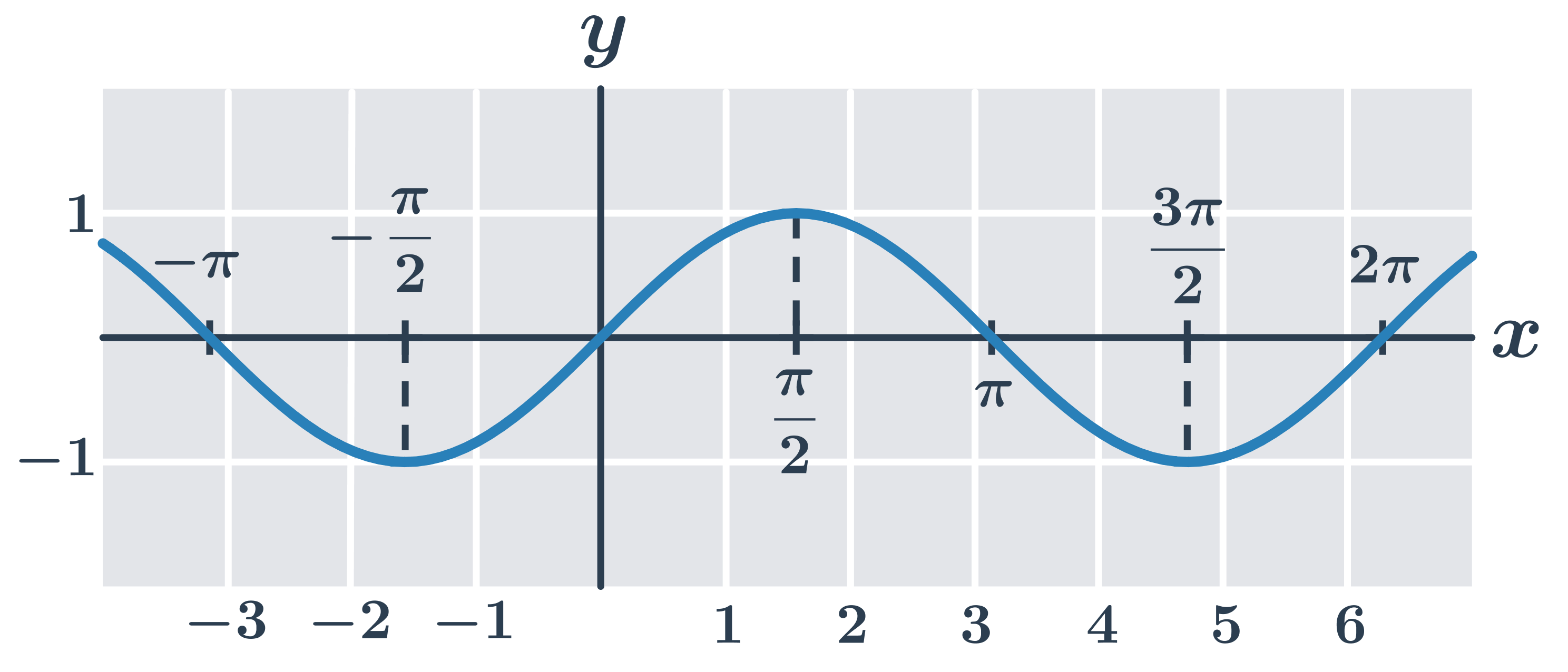
Funkce cosinus y=\cos x:
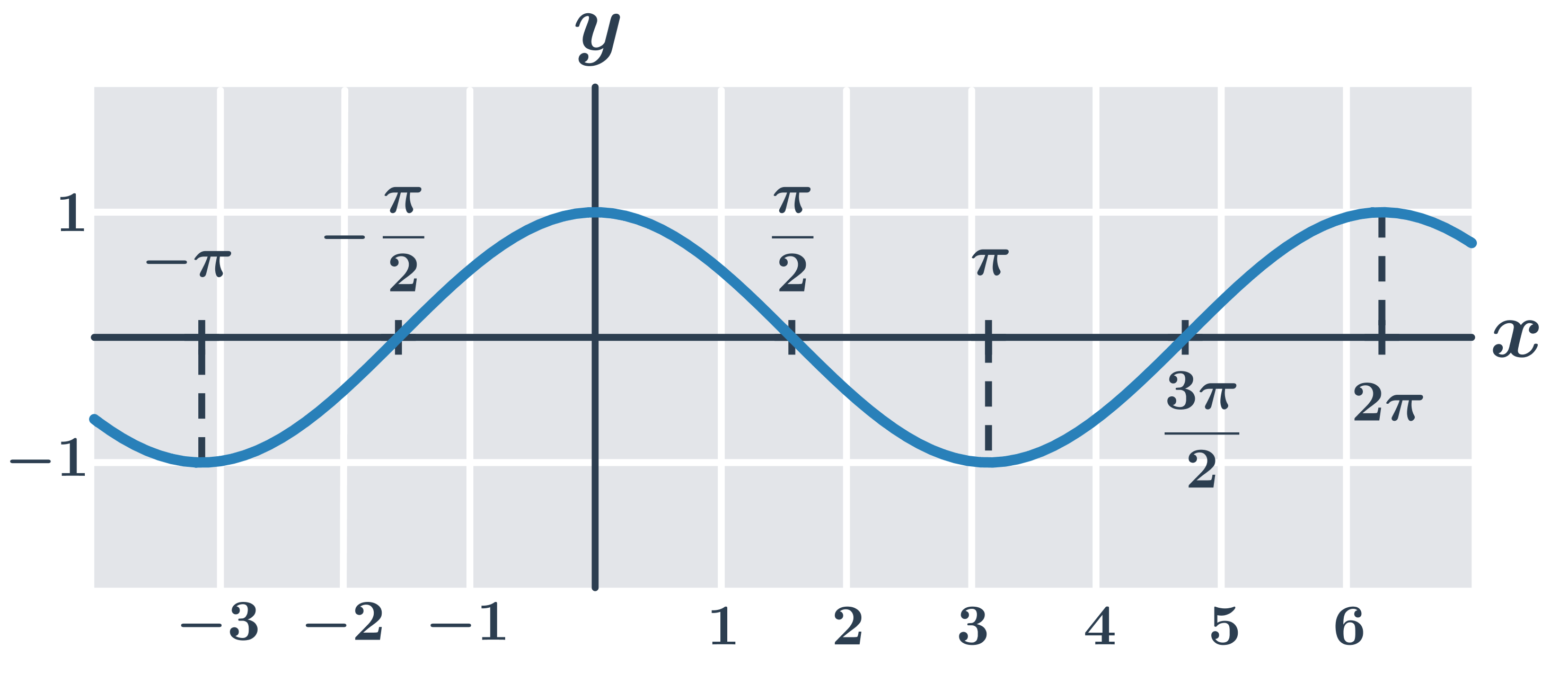
Funkce tangens y=\tan x:
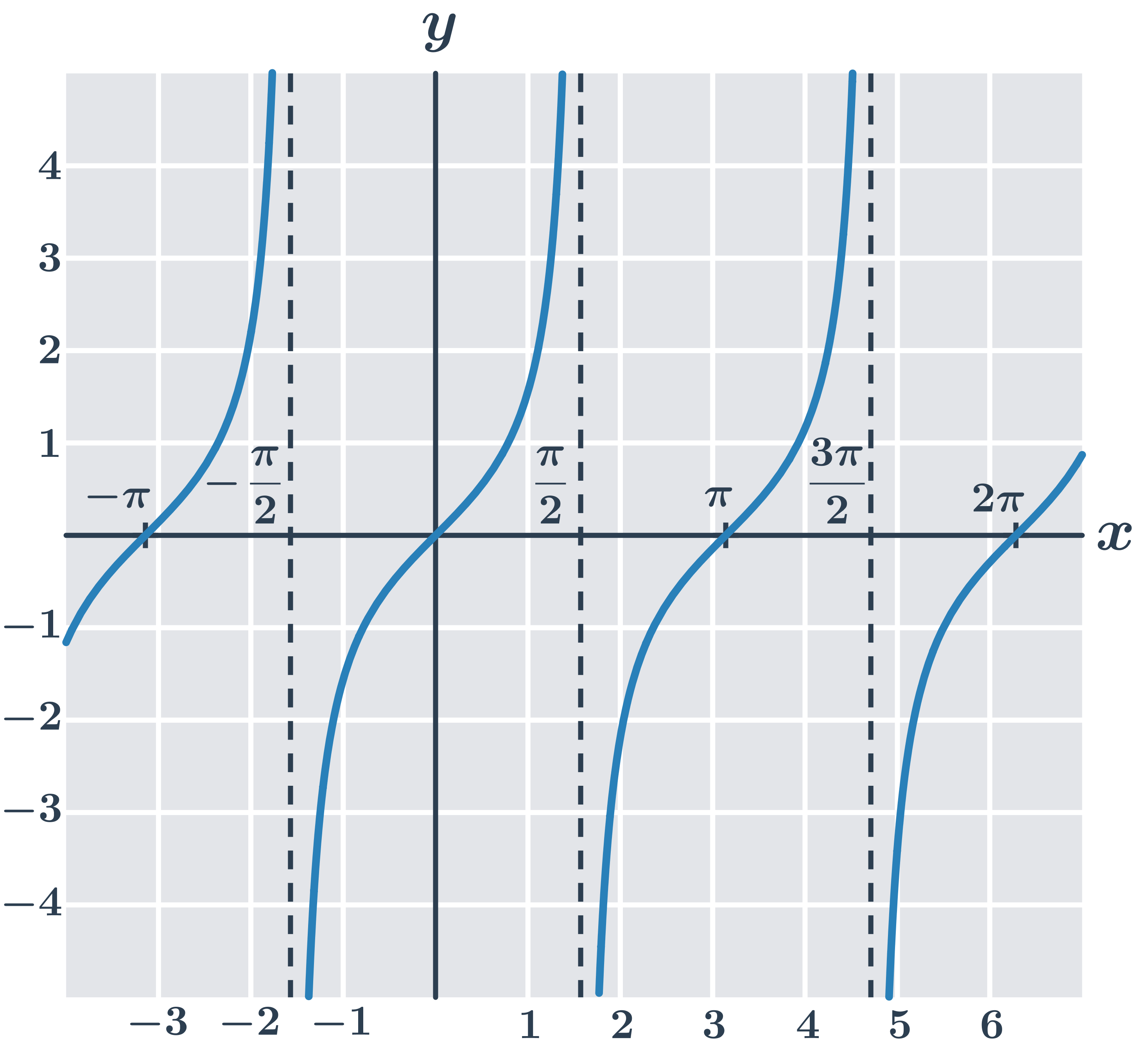
Funkce kotangens y=\cot x:
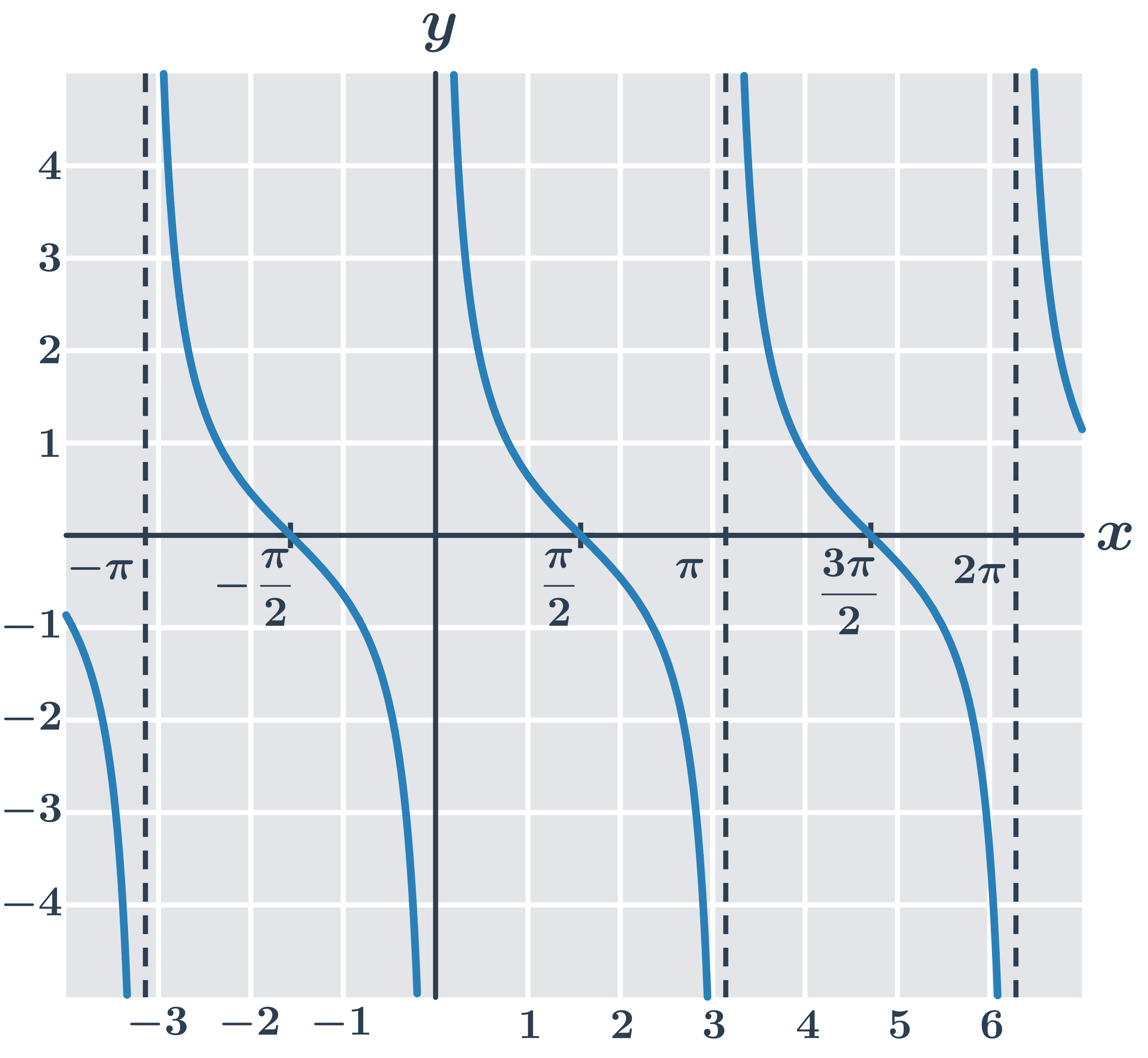
Dopad úprav funkce na graf

Obrázek ukazuje grafy několika úprav funkce \sin x.
| \sin(x+1) | posun grafu ve směru osy x |
| \sin(x)+1 | graf je posunutý ve směru osy y |
| \sin 2x | funkce má změněnou délku periody (v uvedeném příkladu je graf „zmáčknutý“ ve směru osy x, funkce má poloviční délku periody oproti \sin x) |
| 2\sin x | změní se maximální a minimální funkční hodnota (v uvedeném příkladu je graf „roztažený“ ve směru osy y na dvojnásobnou výšku) |
Zajímavost: fyzikální popis některých úprav
| \sin(x+1) | graf má posunutou fázi |
| 2\sin x | změnila se velikost amplitudy |
Grafy exponenciálních funkcí
Grafem exponenciální funkce je křivka jménem exponenciála. Na obrázku jsou grafy exponenciálních funkcí se základy 2 a e = 2{,}7 182 818 284\ldots. Vidíme také, že grafy funkcí e^x a e^{-x} jsou spolu souměrné podle osy y.
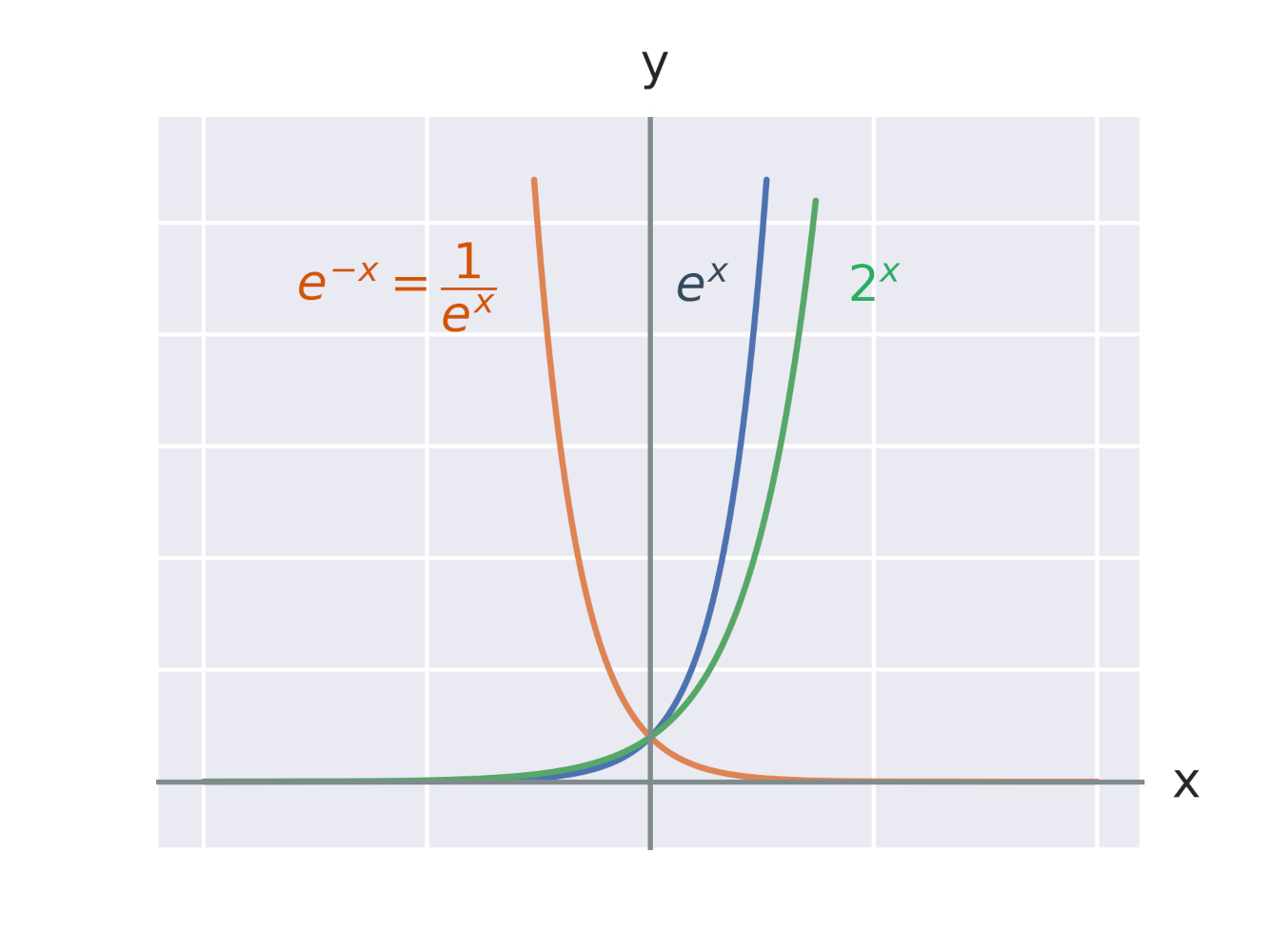
Graf každé exponenciální funkce tvaru f:y =a^x prochází bodem [0,1], protože pro libovolnou konstantu a platí: a^0=1.
Efekt přičtení konstanty k exponenciální funkci
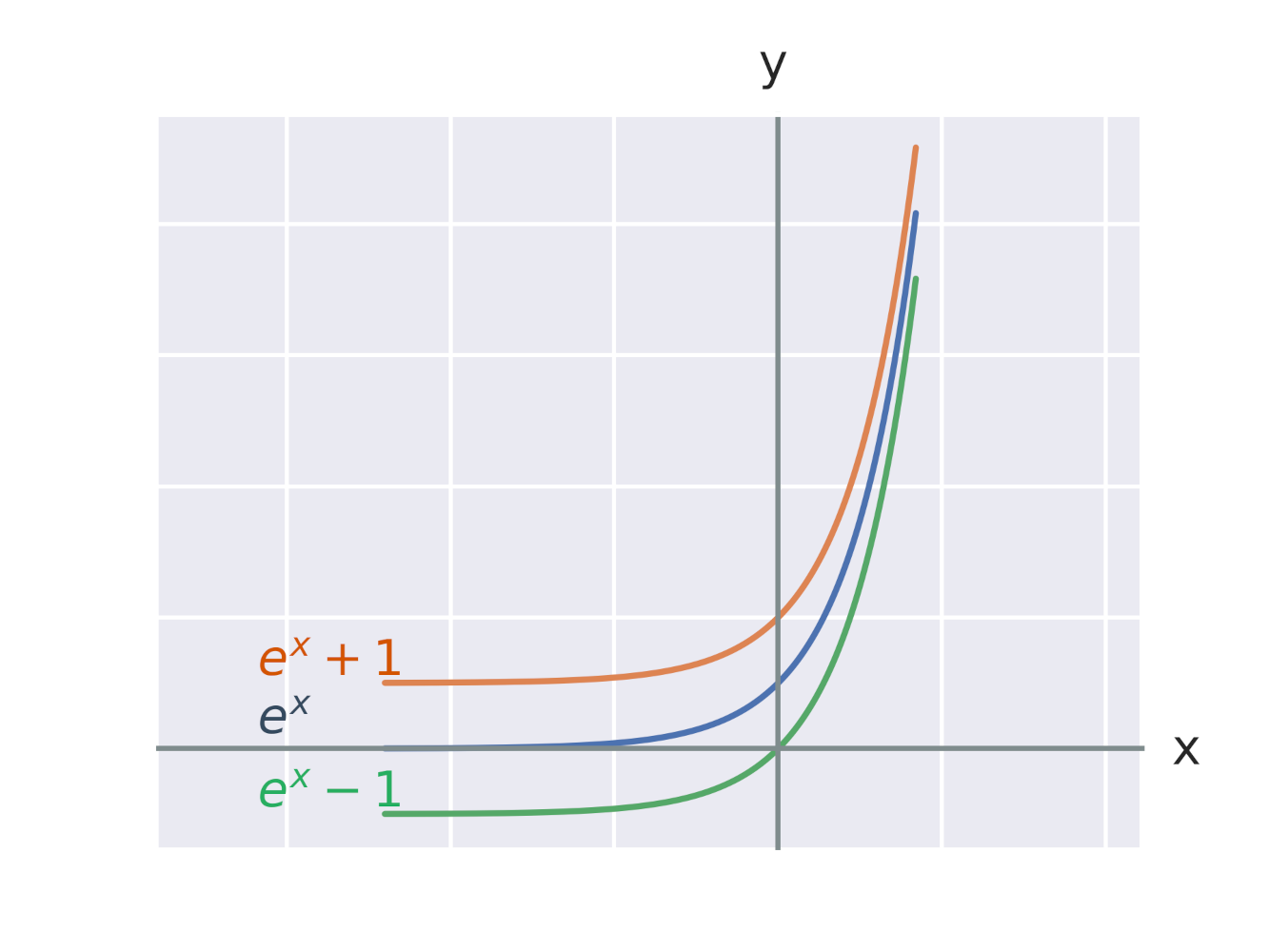
Efekt přičtení konstanty k exponentu
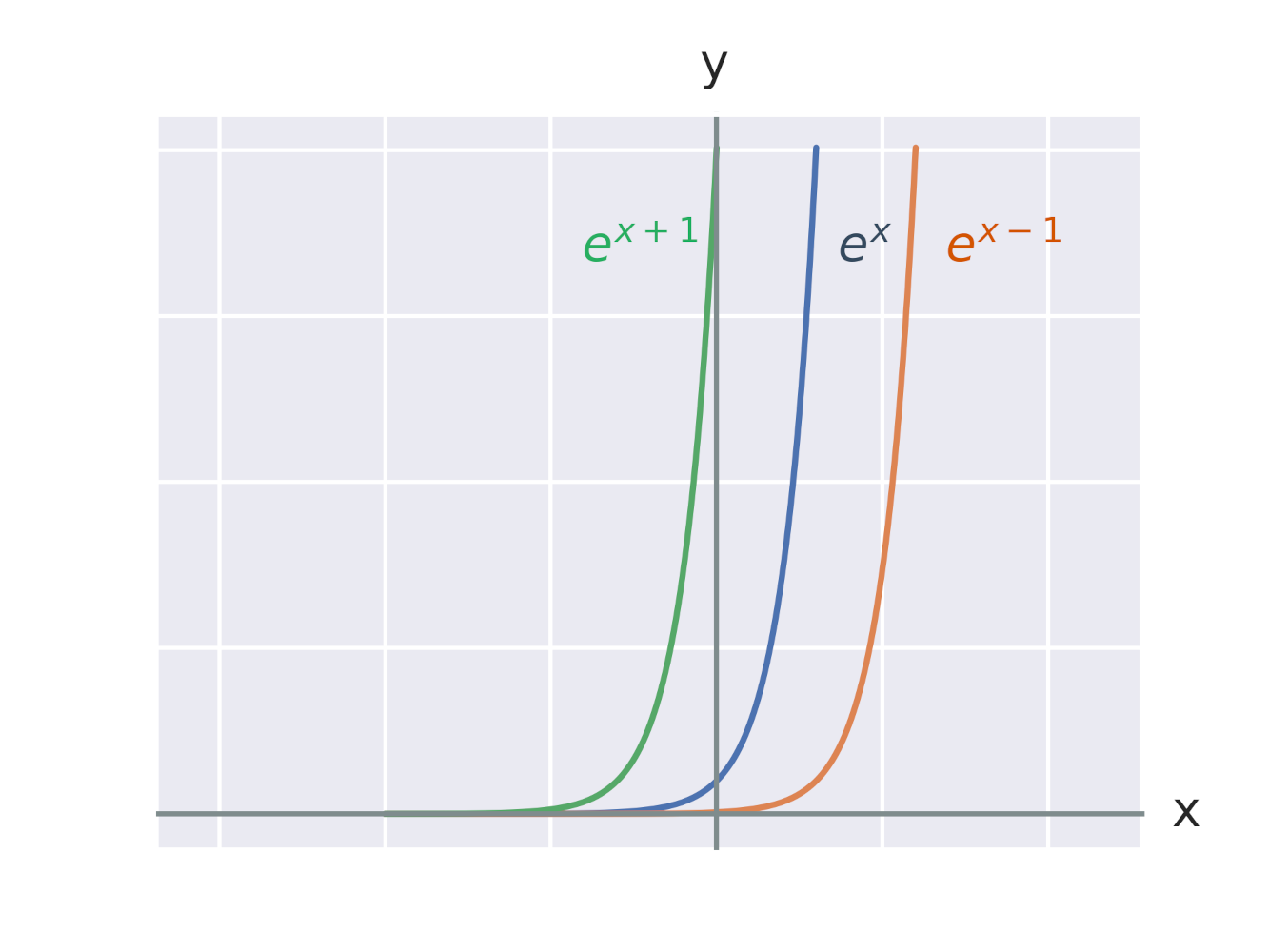
Efekt vynásobení exponenciální funkce konstantou
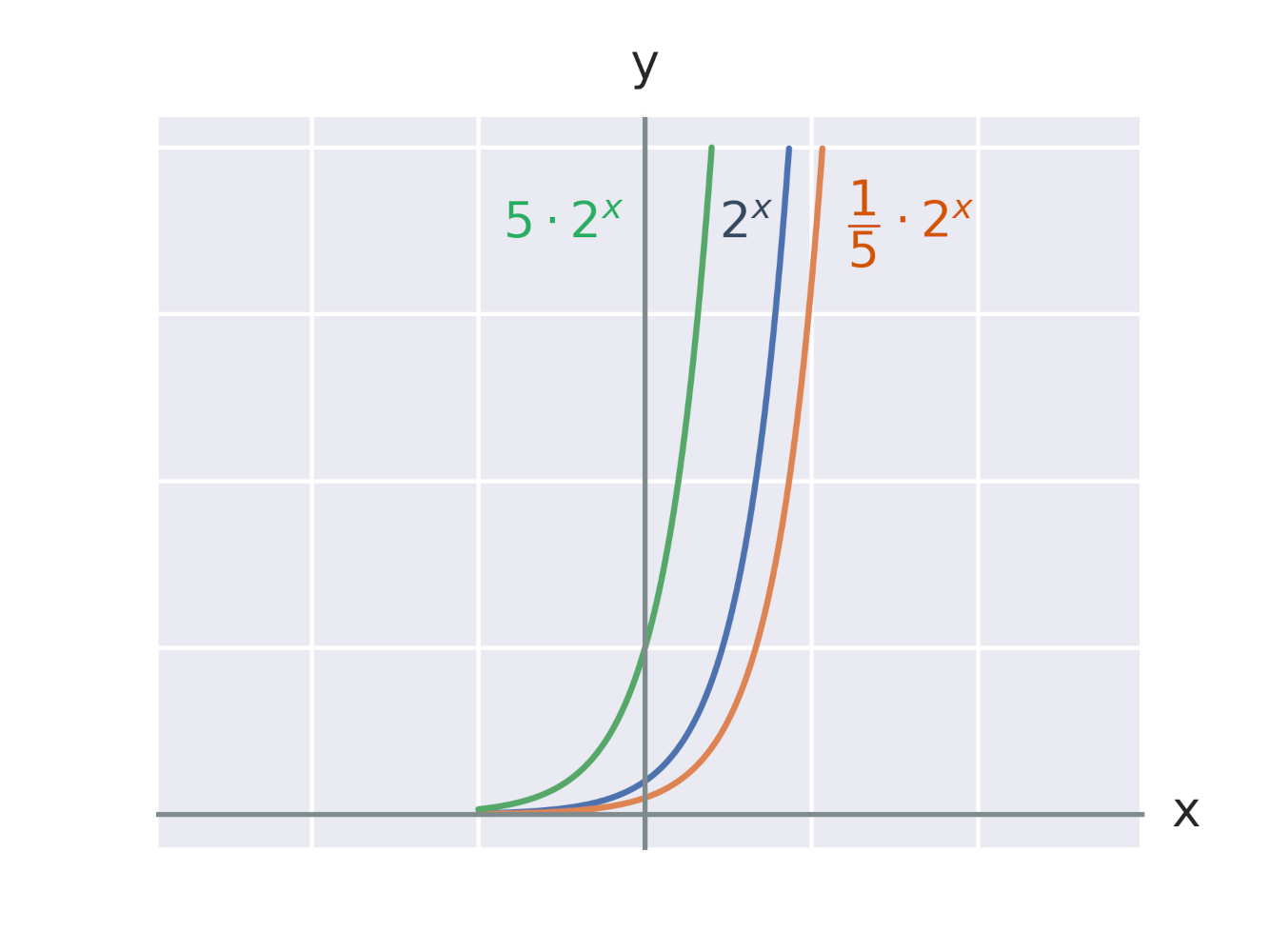
Efekt vynásobení exponentu konstantou
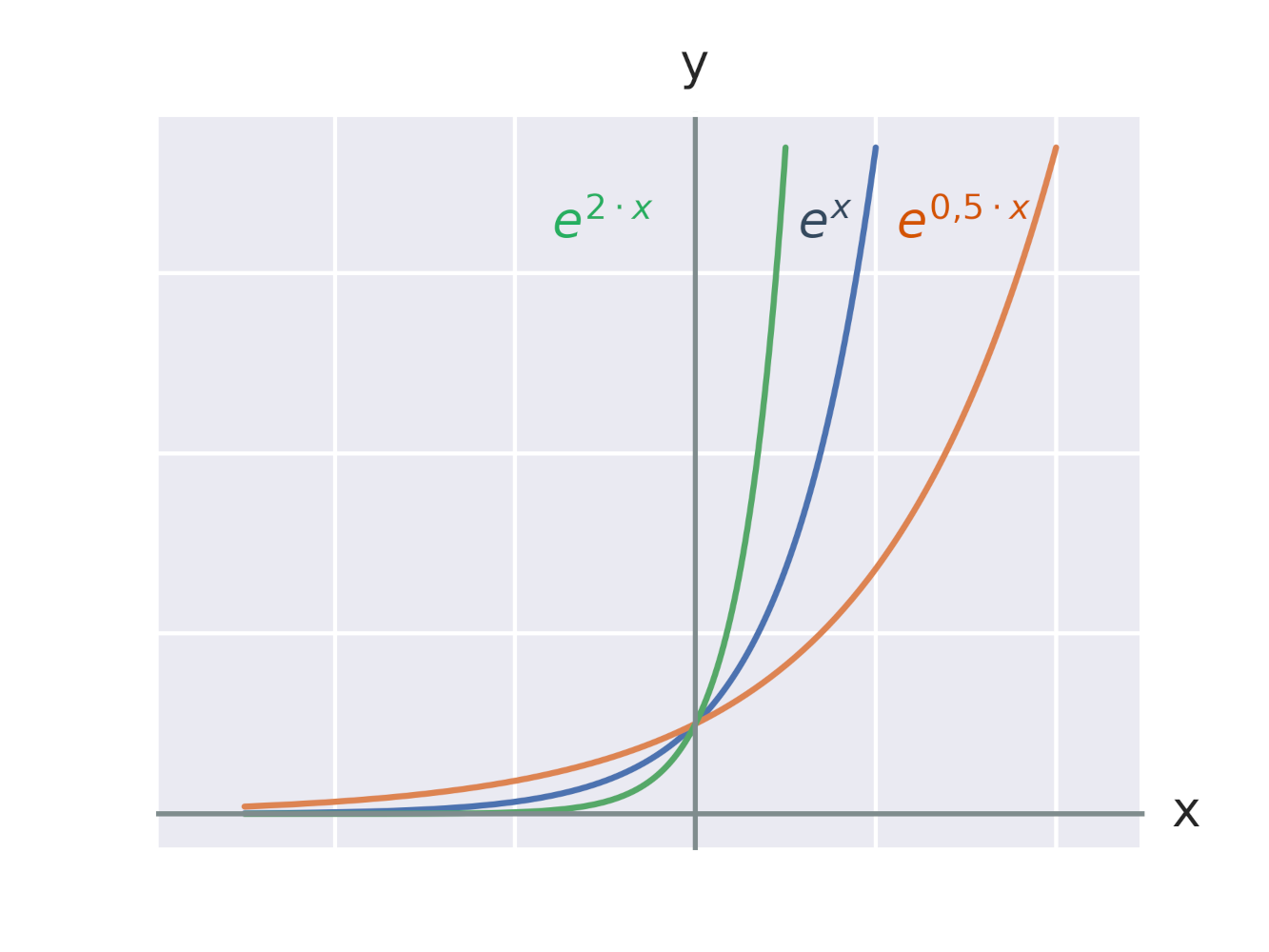
Grafy logaritmických funkcí
Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).
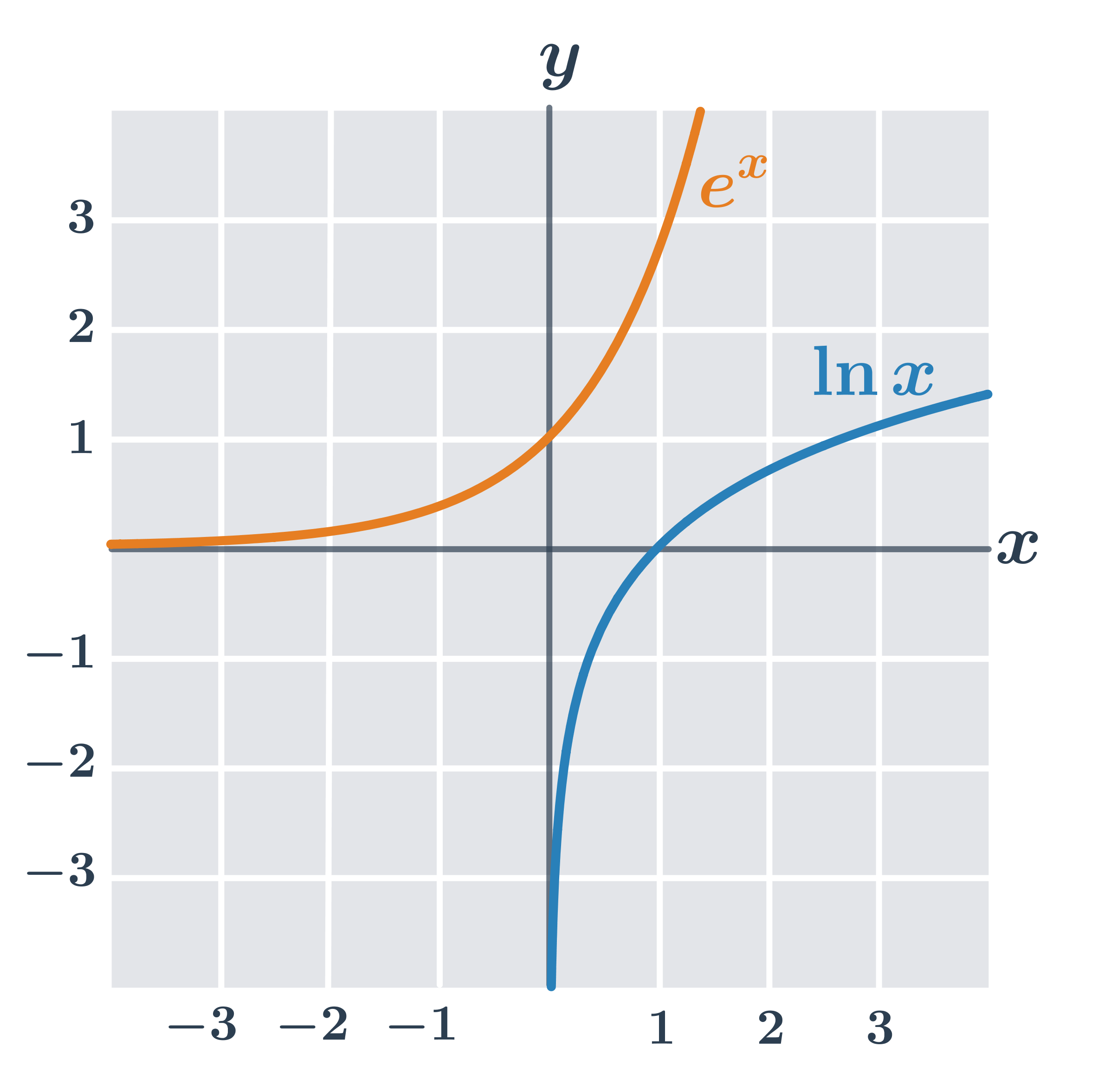
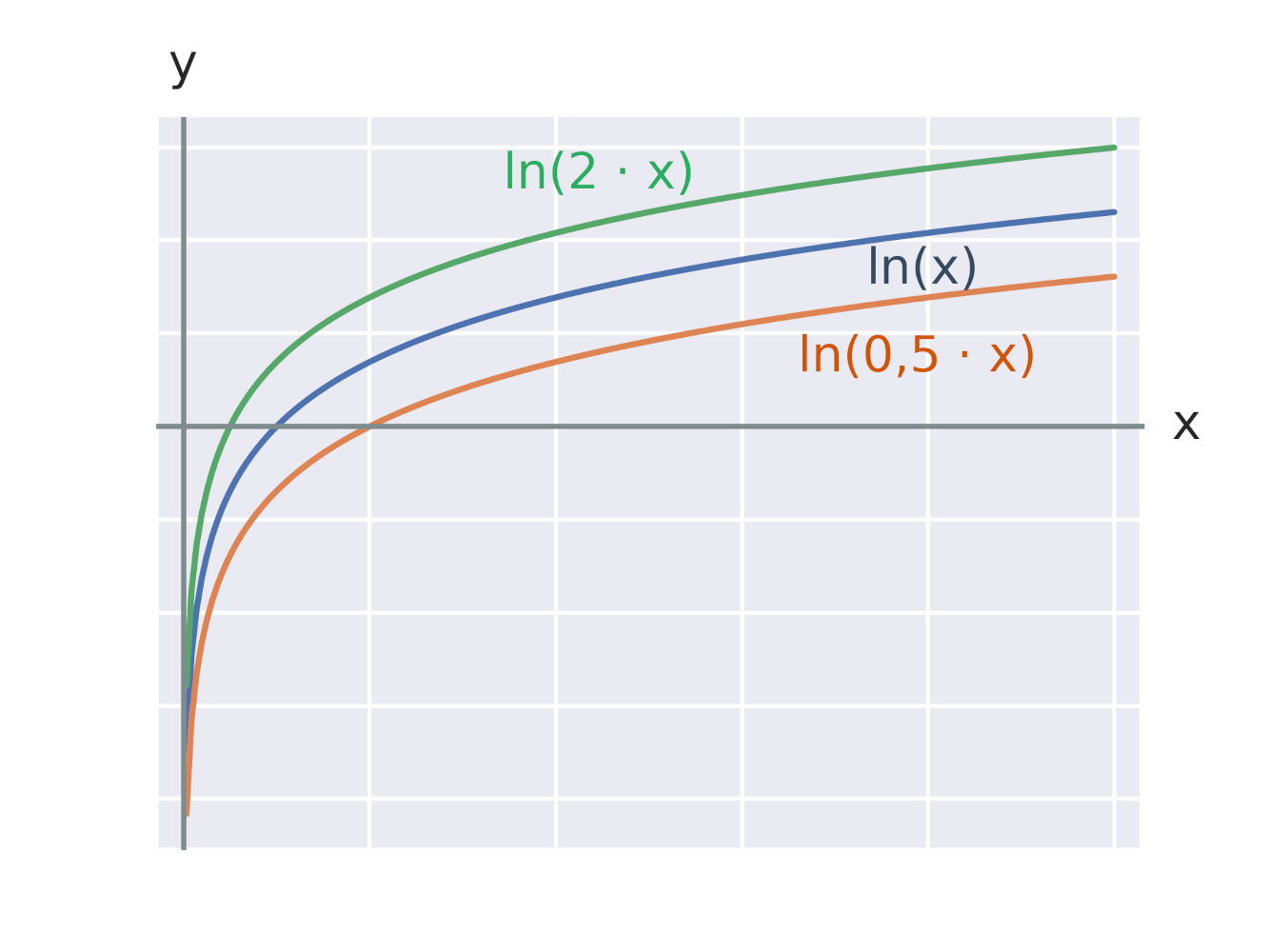
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.
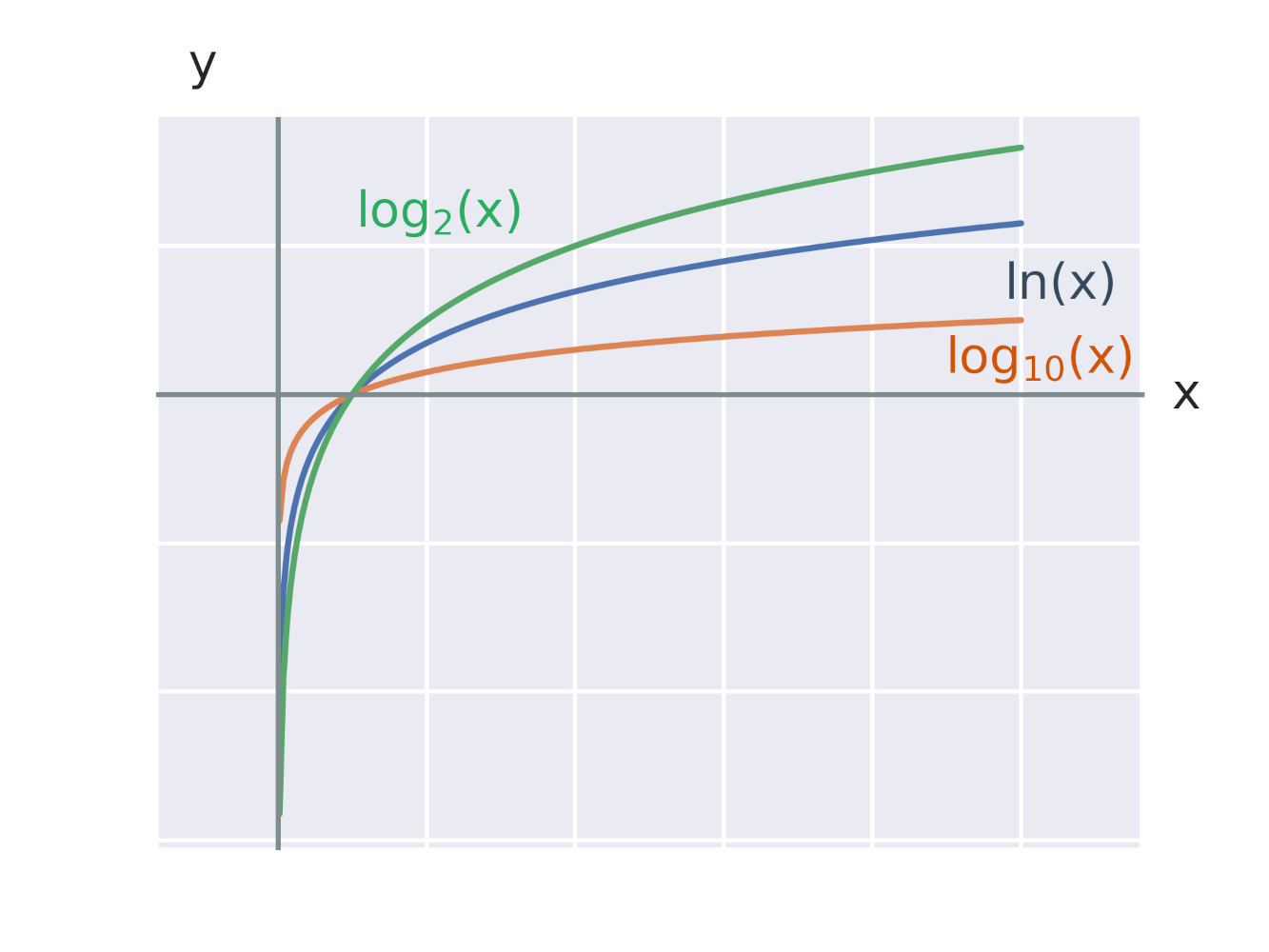
Značení některých význačných logaritmických funkcí:
| funkce | popis | další možná značení |
|---|---|---|
| \log_a x | obecně logaritmus x o základu a pro nějaké a >0, a\neq 1 | |
| \ln x | přirozený logaritmus x, tj. logaritmus x o základu e | v angl. textech někdy \log x |
| \log x | dekadický logaritmus x, tj. logaritmus x o základu 10 | \log_{10}x |
| \log_2 x | binární logaritmus x, tj. logaritmus x o základu 2 | někdy se objevuje \mathrm{lb}\;x |
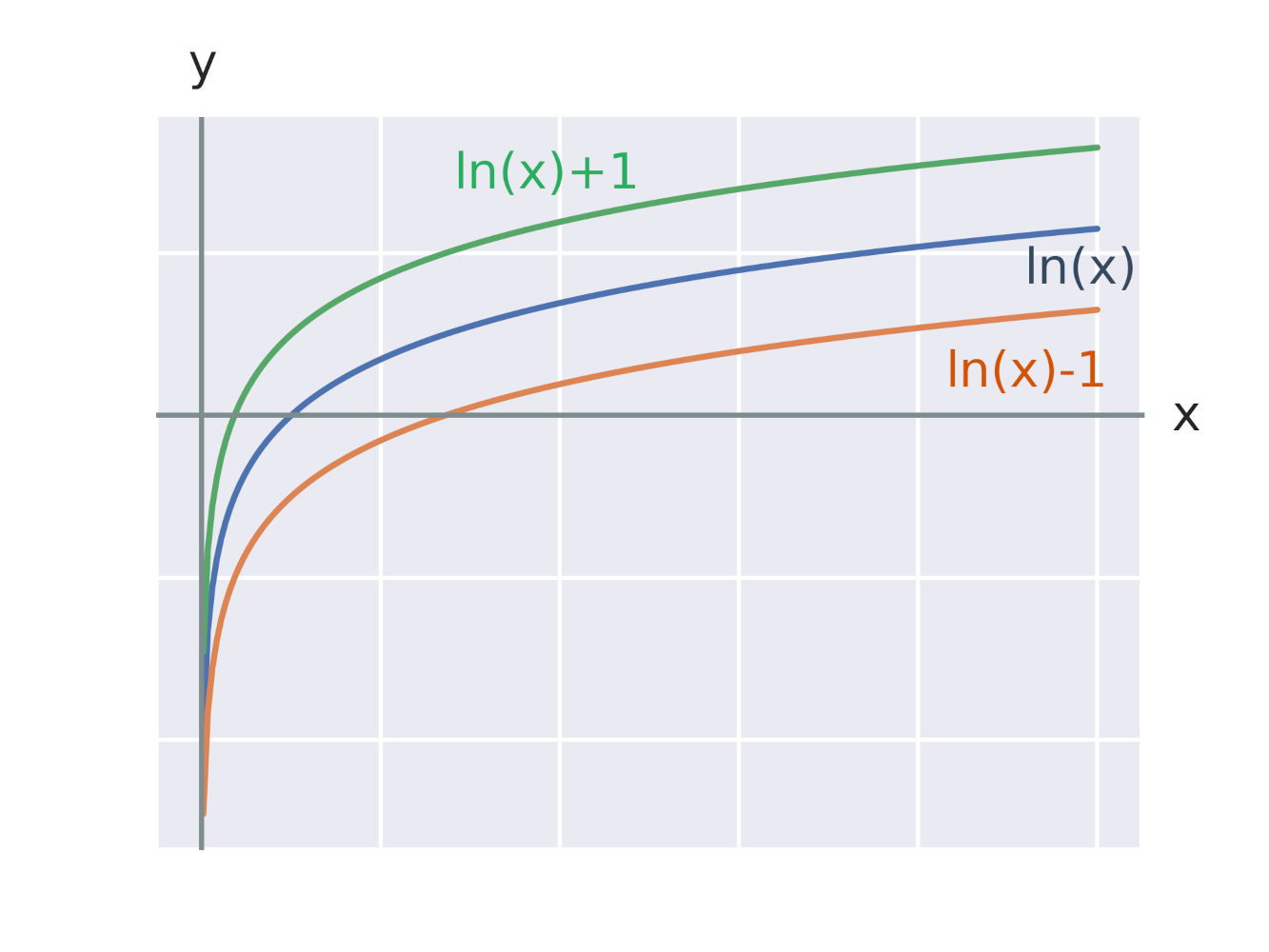
Efekt přičtení konstanty k logaritmické funkci
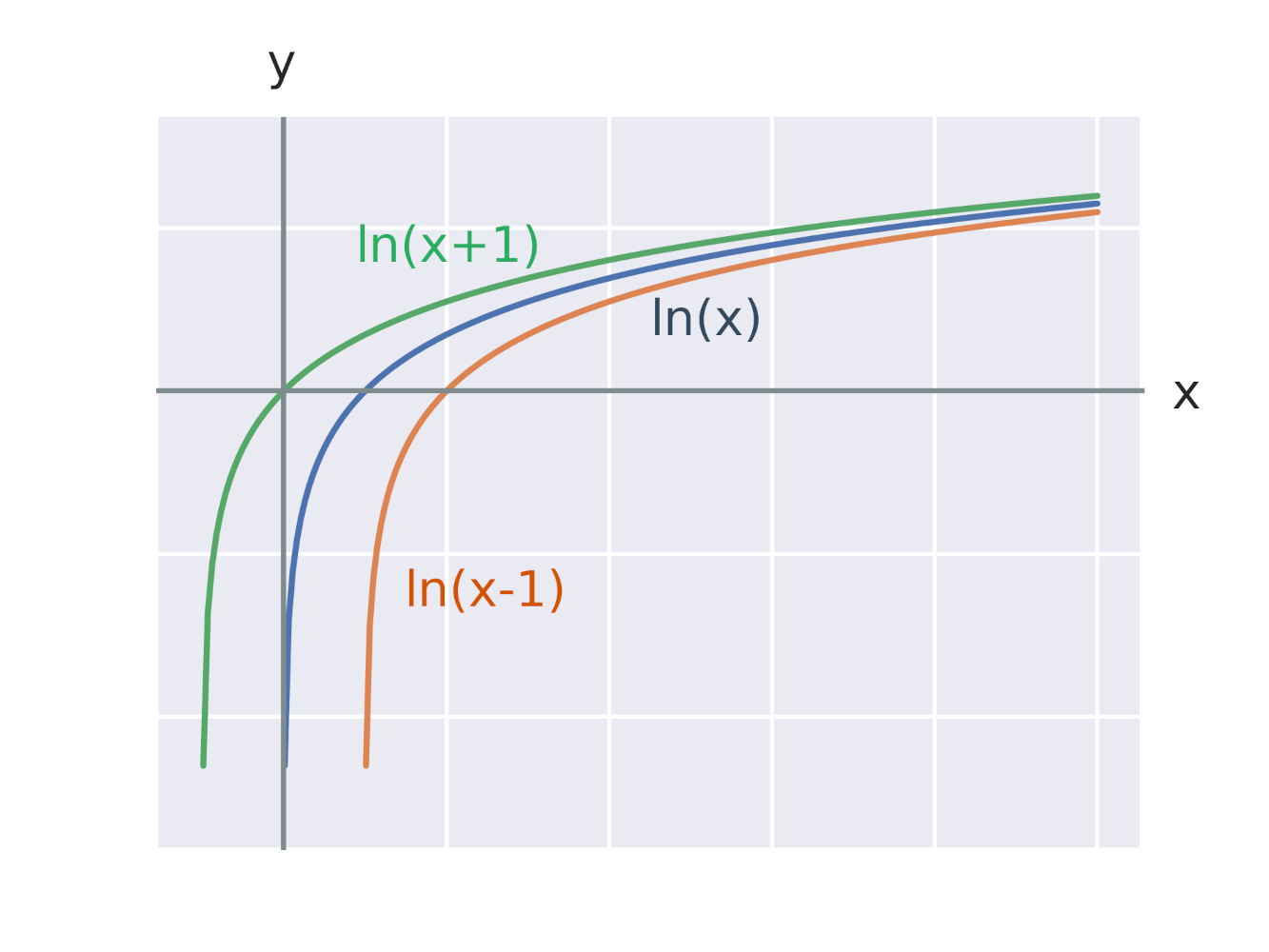
Efekt přičtení konstanty k argumentu logaritmické funkce
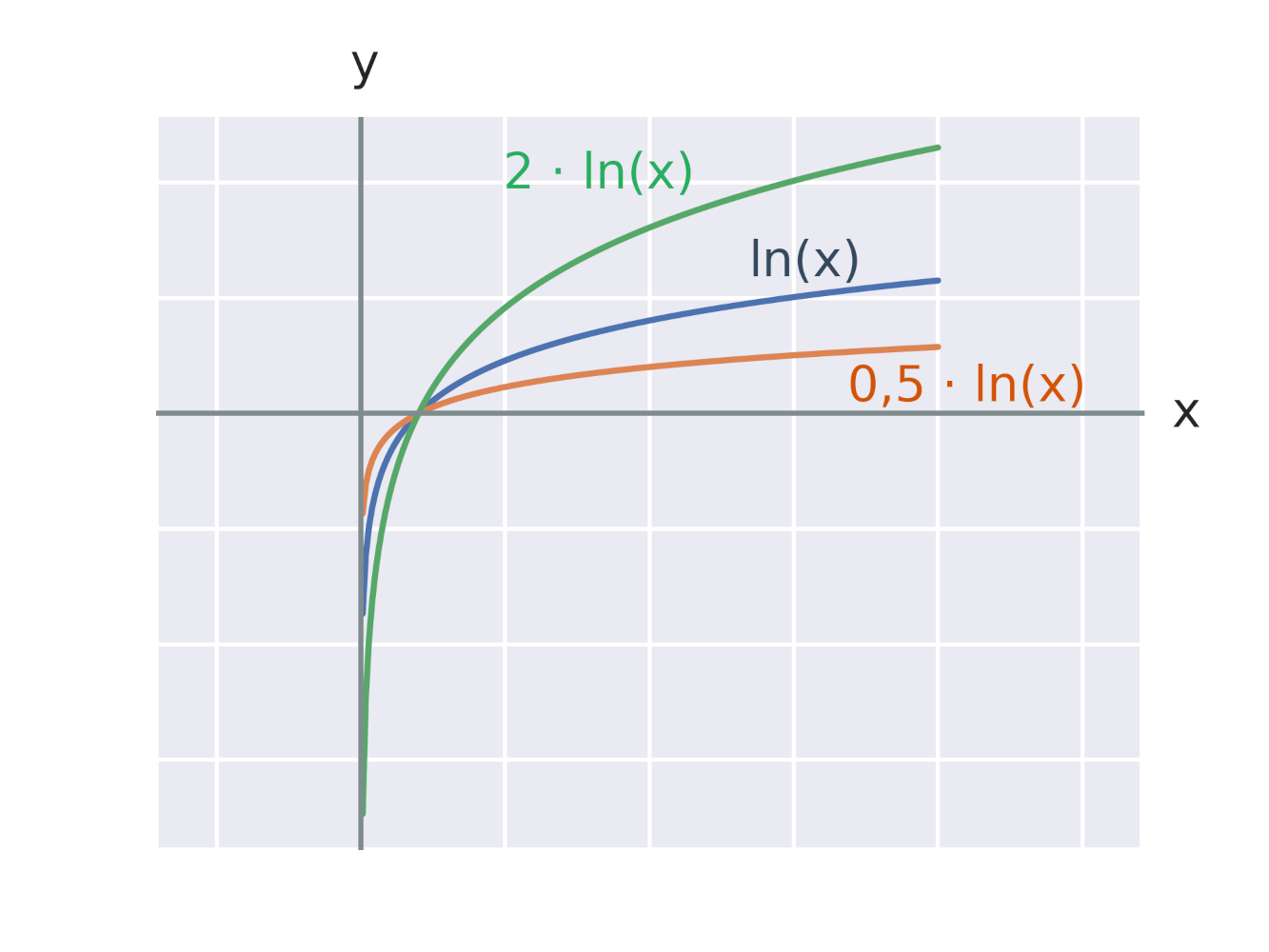
Efekt vynásobení logaritmické funkce konstantou
Efekt vynásobení argumentu logaritmické funkce konstantou
Grafy lineárních nerovnic
Grafem funkce dané předpisem y= ax+b je přímka. Množinou řešení lineární nerovnice budou všechny body [x,y] ležící v polorovině s hraniční přímkou y= ax+b. Může nastat jedna ze čtyř možností:
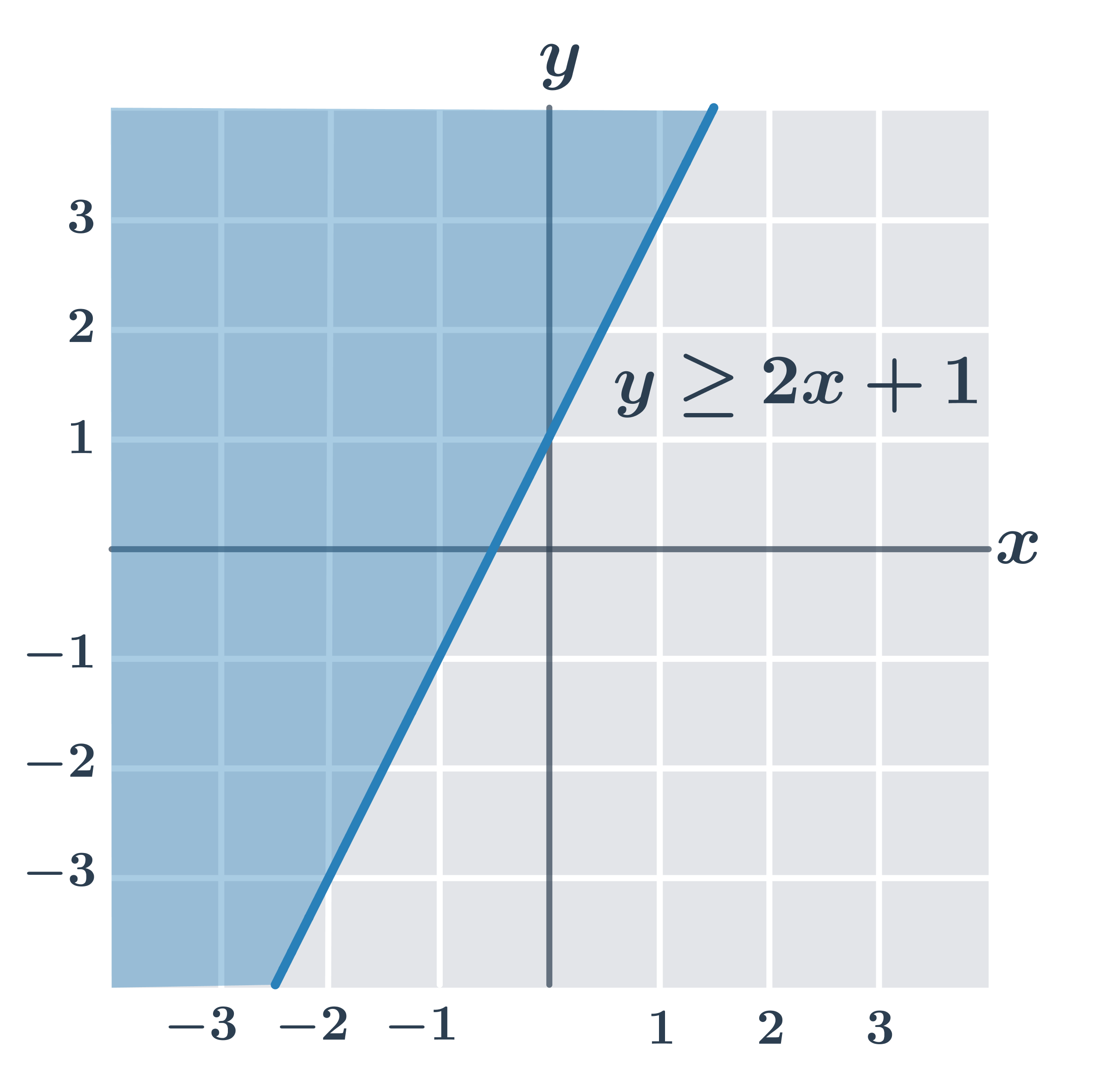
| y\geq ax+b | Nerovnost splňují všechny body v rovině, které leží přímo na přímce dané rovnicí y=ax+b nebo “nad” touto přímkou (se souřadnicí y větší než ax+b). |
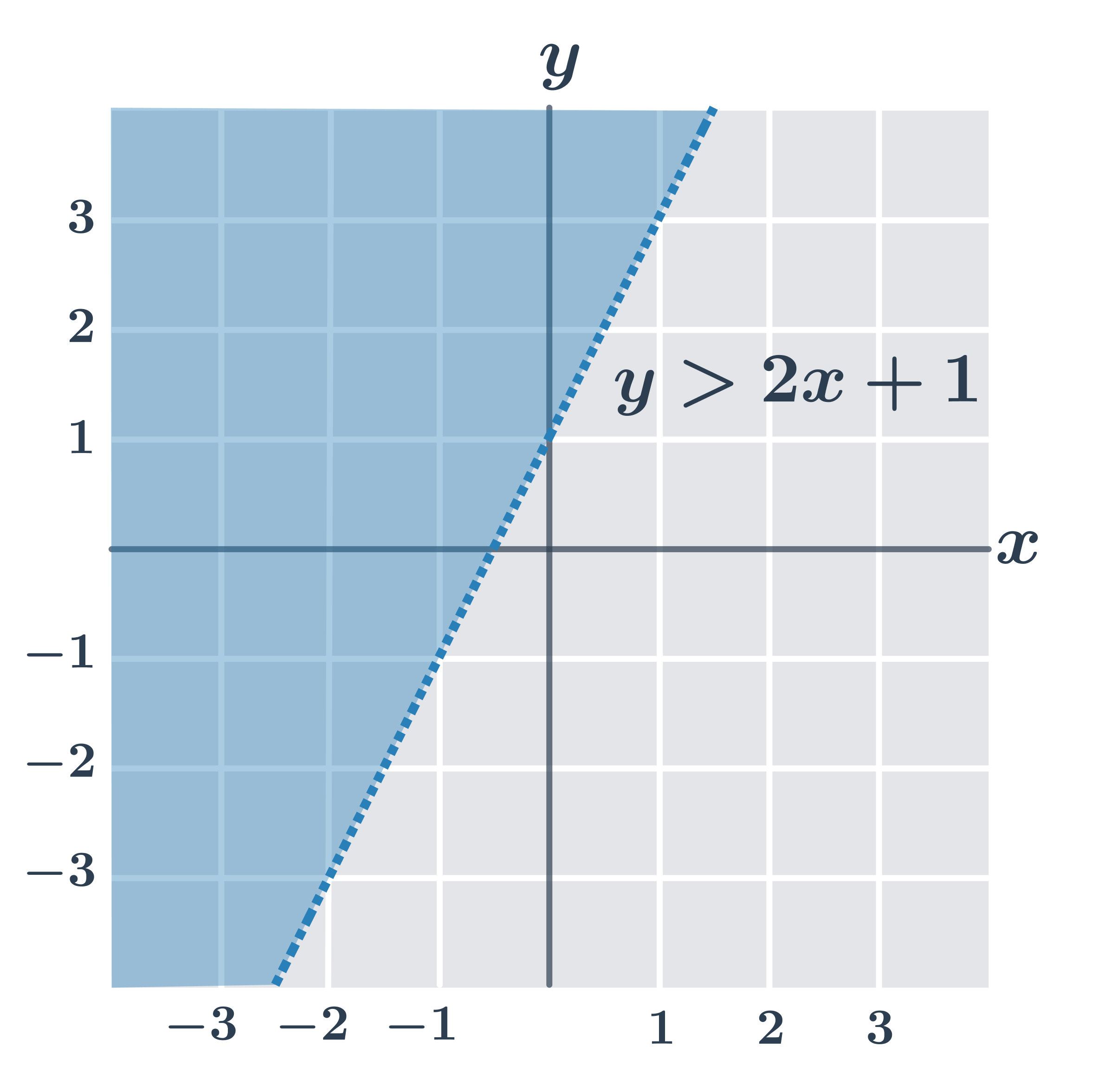
| y \gt ax+b | Nerovnost splňují všechny body v rovině, které leží “nad” přímkou o rovnici y=ax+b. |
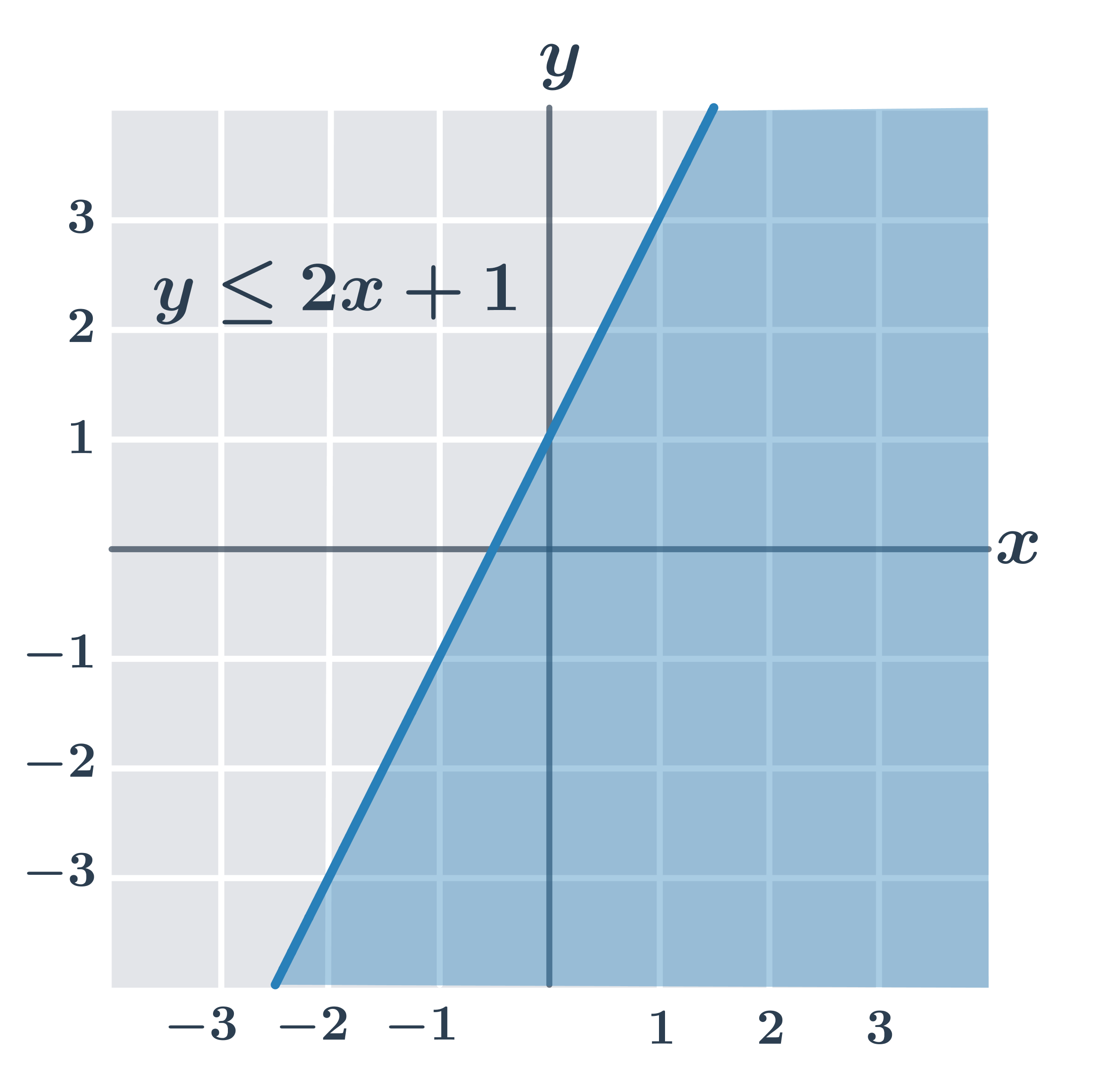
| y\leq ax+b | Nerovnost splňují všechny body v rovině, které leží na přímce o rovnici y=ax+b nebo “pod” touto přímkou (se souřadnicí y menší než ax+b). |
| y \lt ax+b | Nerovnost splňují všechny body v rovině, které leží “pod” přímkou o rovnici y=ax+b. |
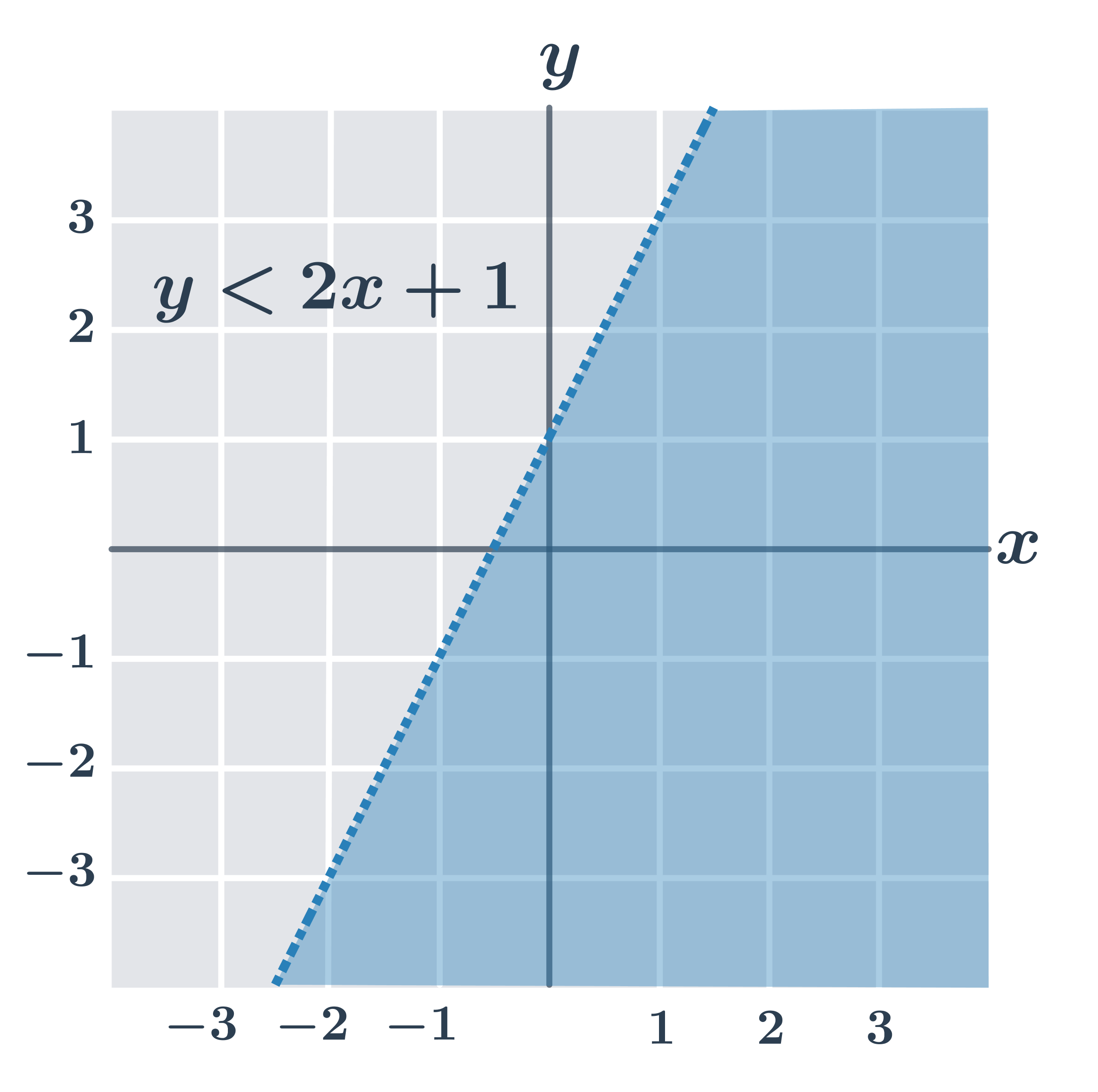
Na obrázcích jsou řešení všech typů lineárních nerovnic (všimněte si, že pokud je v nerovnici jen znaménko \gt nebo \lt, body přímo na hraniční přímce lineární nerovnici nesplňují).
- y\geq 2x+1
- y \gt 2x+1
- y\leq 2x+1
- y \lt 2x+1
Souřadnice bodů v rovině
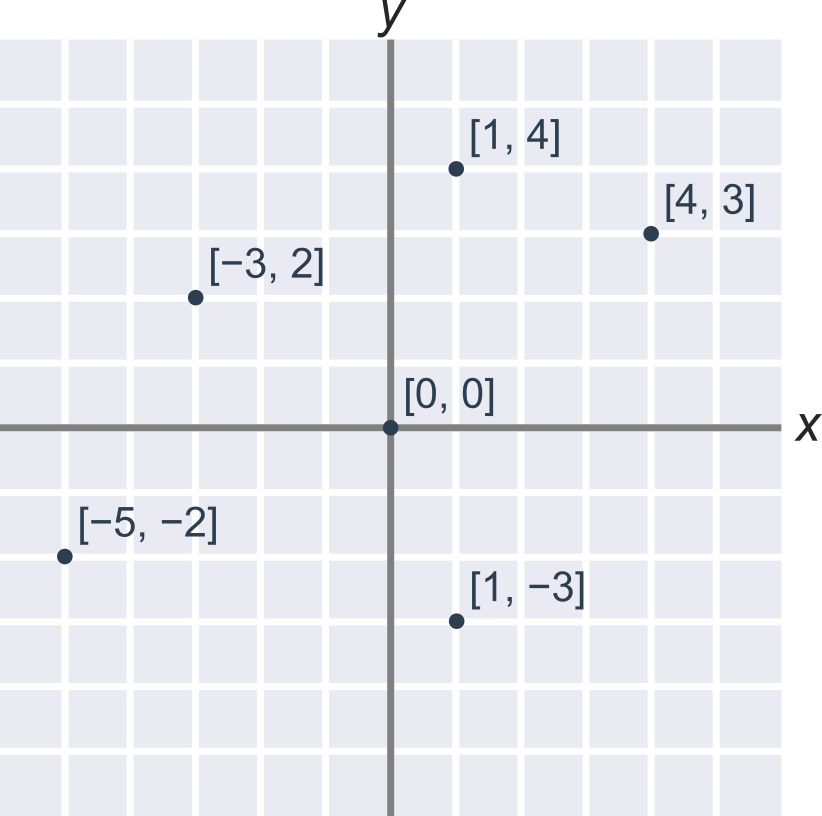
Souřadnice bodů většinou zapisujeme pomocí kartézské soustavy souřadnic v rovině, která má jako osy dvě kolmé přímky. Vodorovná přímka se tradičně označuje x a souřadnice podél této osy se zapisuje první. Svislá přímka se tradičně označuje y a souřadnice podle této osy se zapisuje druhá. Přímky x, y se protínají v bodě [0;0].
Přímky x a y jsou souřadné osy, bod [0;0] je počátek soustavy souřadnic.
Příklad: Souřadnice bodu A
Bod A na obrázku je v dané soustavě souřadnic určen jako x=1, y=2, což můžeme zapsat jako A[1;2].
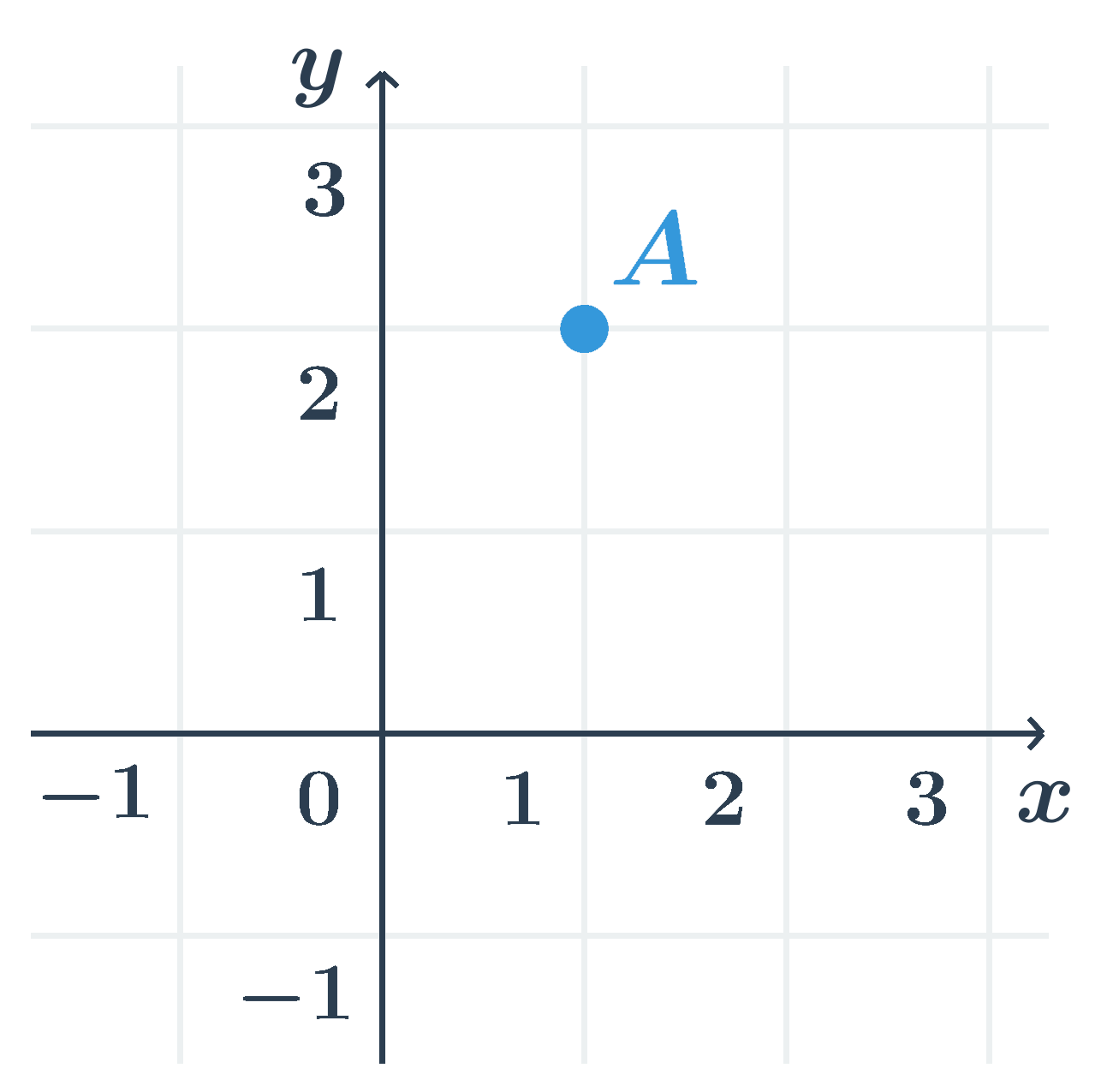
Další příklady souřadnic bodů