Poměry: změna a rozdělení čísla

F69

umime.to/F69

Stáhnout QR kód

Změna čísla

Změna čísla v zadaném poměru a:b je vynásobení čísla odpovídajícím zlomkem \frac{a}{b}.

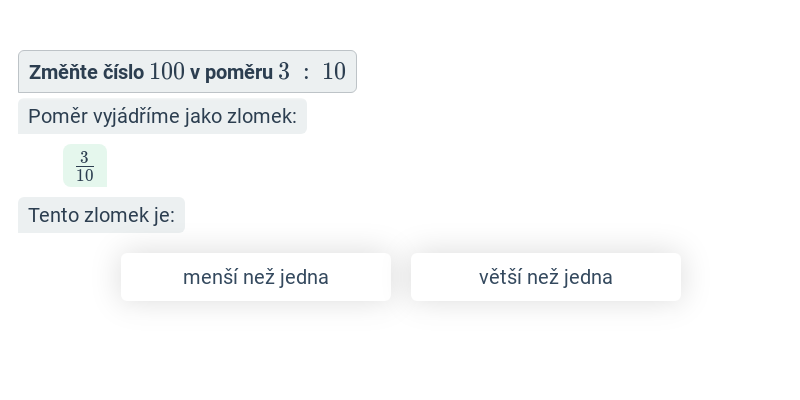
Pokud je a < b a tedy \frac{a}{b}<1, budeme číslo zmenšovat.
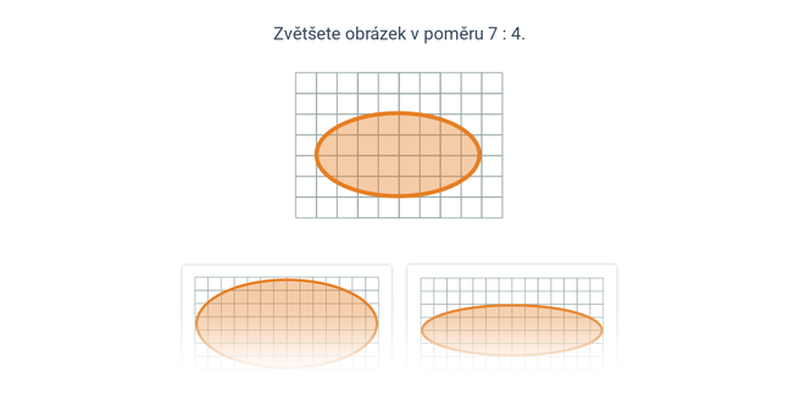
Pokud je a > b a tedy \frac{a}{b}>1, budeme číslo zvětšovat.

Příklad: změna čísla v zadaném poměru

Změna čísla 10 v poměru 2:5 znamená vynásobení čísla 10 zlomkem \frac{2}{5}. Vyjde nám číslo 4.

Rozdělení čísla

Rozdělení čísla v zadaném poměru a:b znamená rozdělení čísla na dvě části, které jsou v poměru a:b.

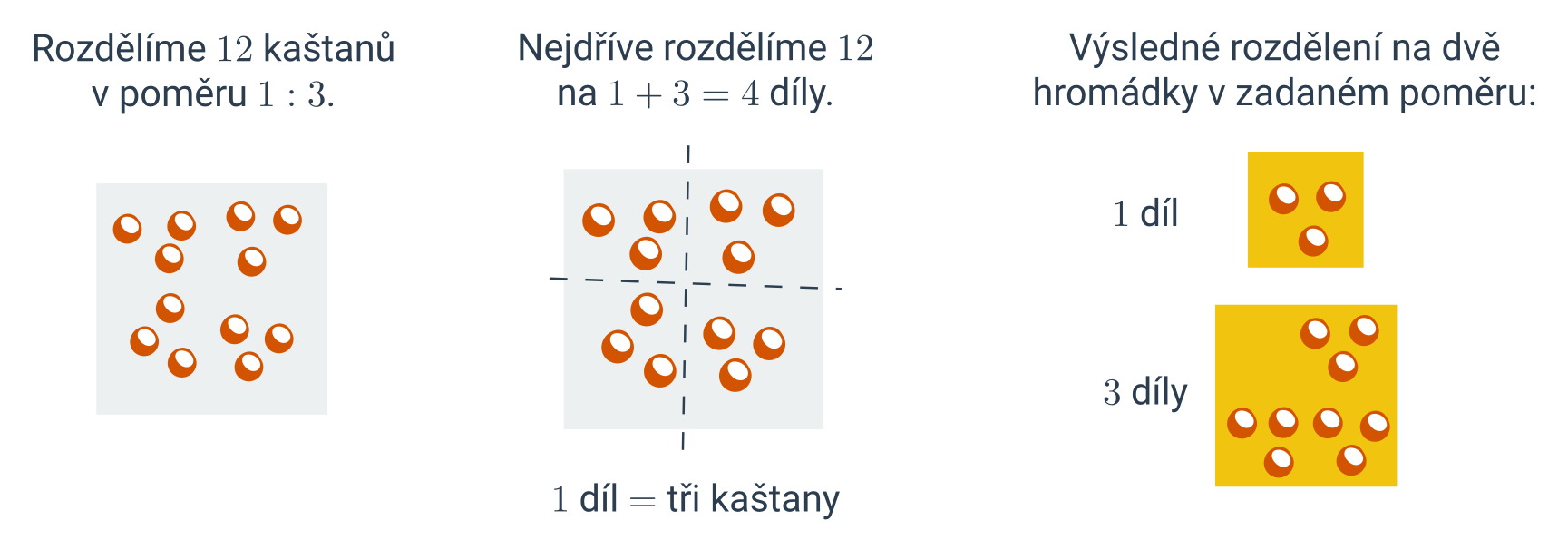
Příklad: rozdělení čísla v zadaném poměru

Rozdělte číslo 30 v poměru 2:3. Celkem budeme rozdělovat na 2+3=5 dílů. Jeden díl je tedy roven \frac{30}{5}=6.

Výsledná čísla jsou rovna 2 dílům, tj. 2\cdot 6= 12, a 3 dílům, tj. 3\cdot 6=18. Rozdělili jsme číslo 30 v poměru 2:3 na 12 a 18.

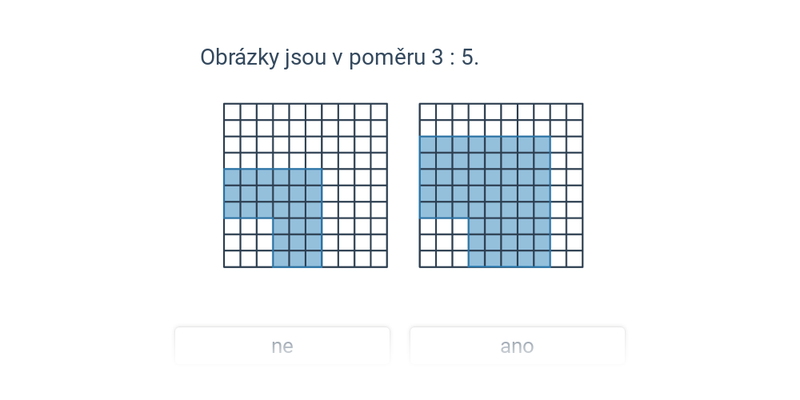
Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Poměry: změna a rozdělení čísla

Rozhodovačka • střední

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Poměry: změna a rozdělení čísla

Krok po kroku • střední

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Poměry: změna a rozdělení čísla

Psaná odpověď • střední

Předcházející

Navazující

Cvičení

Poměry: změna a rozdělení čísla

umime.to/F69

Změna čísla

Rozdělení čísla

Rozhodovačka