Výpis souhrnů
Poměry
Podtémata
Poměr dvou nebo více čísel vyjadřuje vztah jejich velikostí – tedy kolikrát je jedno číslo větší (nebo menší) než druhé. S poměry se setkáváme v běžném životě i v matematice: určují například poměr stran obrazovky (16 : 9), měřítko mapy (1 : 50 000) nebo směs dvou látek v určitém poměru. Poměry úzce souvisejí se zlomky nebo pojmem podobnost v geometrii.
- Základy poměrů – zápis poměru, základní tvar, postupný a převrácený poměr, vztah ke zlomkům
- Změna a rozdělení čísla – zvětšení nebo zmenšení čísla v daném poměru, rozdělení čísla v poměru (např. rozdělit 12 v poměru 1 : 3 na 3 a 9)
- Výpočty s poměry – výpočty při znalosti součtu nebo rozdílu částí, příklady s poměry a rovnicemi
- Měřítko mapy – použití poměrů při práci s mapami, plány nebo modely, převody skutečných a zmenšených vzdáleností
Poměry: základy
Poměr dvou kladných hodnot, např. 2:4, vyjadřuje vztah jejich velikostí.
Dědeček našel 10 hřibů a 1 bedlu. Poměr počtu hřibů ku počtu bedel v dědečkově košíku je 10:1.
Podobně jako u zlomků můžeme poměry krátit a rozšiřovat kladnými čísly.
Poměr počtu hřibů ku počtu bedel 10:1 může být zrovna tak vyjádřen jako 20:2 nebo 1:0{,}1.
Poměr, který je vyjádřen dvěma celými čísly a nejde už víc zkrátit, je v základním tvaru.
Základní tvar poměru 2:4 je 1:2.
Lze zapsat i poměr více než dvou hodnot, pak jde o postupný poměr.
Kedlubny, ředkvičky a mrkve nám na zahrádce vyrostly v poměru 2 : 10 : 11.
Převráceným poměrem k poměru a:b myslíme poměr b:a.
Poměr objemů sirupu a vody v nápoji je 1:10, převrácený poměr 10:1 značí poměr objemů vody ku sirupu.
Jaký je rozdíl mezi poměrem a zlomkem? Poměr popisuje vztah dvou částí. Zlomek je část z celku.

Poměry: změna a rozdělení čísla
Změna čísla
Změna čísla v zadaném poměru a:b je vynásobení čísla odpovídajícím zlomkem \frac{a}{b}.
- Pokud je a \lt b a tedy \frac{a}{b} \lt 1, budeme číslo zmenšovat.
- Pokud je a > b a tedy \frac{a}{b}>1, budeme číslo zvětšovat.

Příklad: změna čísla v zadaném poměru
Změna čísla 10 v poměru 2:5 znamená vynásobení čísla 10 zlomkem \frac{2}{5}. Vyjde nám číslo 4.
Rozdělení čísla
Rozdělení čísla v zadaném poměru a:b znamená rozdělení čísla na dvě části, které jsou v poměru a:b.
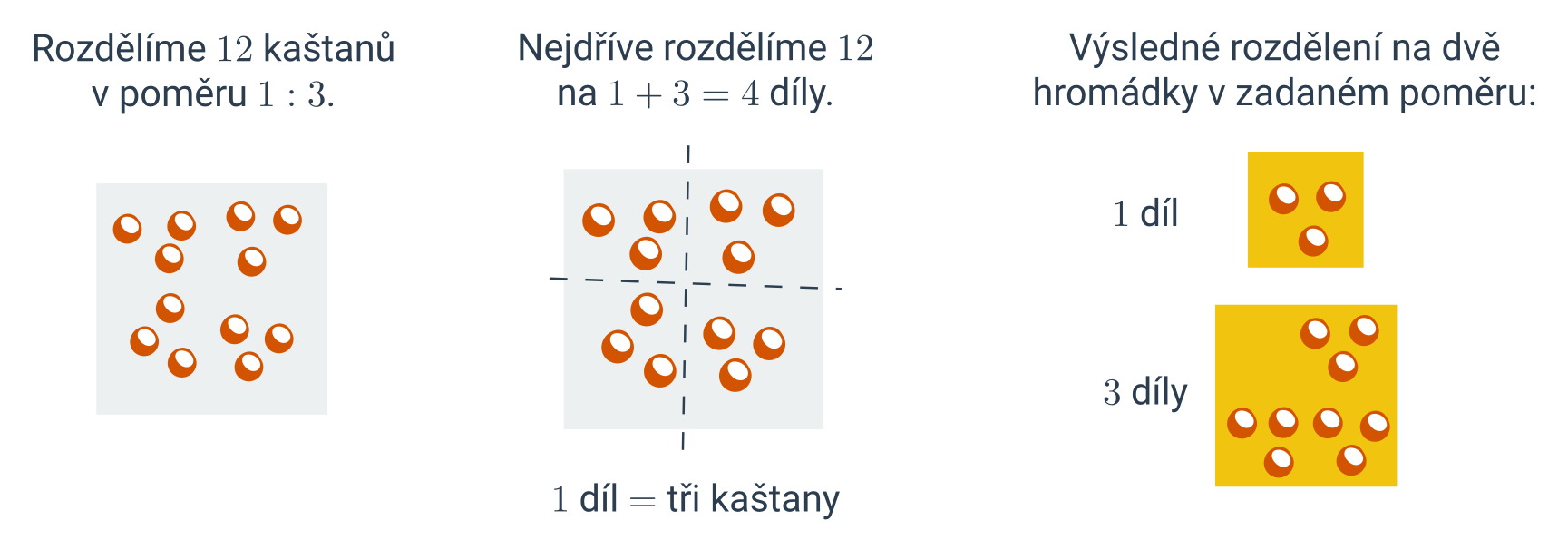
Příklad: rozdělení čísla v zadaném poměru
Rozdělte číslo 30 v poměru 2:3. Celkem budeme rozdělovat na 2+3=5 dílů. Jeden díl je tedy roven \frac{30}{5}=6.
Výsledná čísla jsou rovna 2 dílům, tj. 2\cdot 6= 12, a 3 dílům, tj. 3\cdot 6=18. Rozdělili jsme číslo 30 v poměru 2:3 na 12 a 18.
Poměry: výpočty
Výpočty při znalosti součtu (rozdílu)
Hledáme dvě čísla, když známe jejich poměr a známe jejich součet (případně rozdíl, součin, nebo nějaký jiný výraz). V takovém případě nám většinou pomůže spočítat si nejdříve čemu odpovídá jeden díl v poměru. Pokračujeme obvykle výpočtem hledaných čísel podle toho, kolika dílům v poměru odpovídá první a druhé číslo.
Příklad: výpočet čísel, když známe jejich poměr
Poměr nabitých a vybitých baterií v Gargamelově detektoru šmoulů je 1:4. Vybitých baterií je přitom o 6 více než nabitých. Jaké jsou počty nabitých a vybitých baterií?
Nejdříve si spočítáme, kolika bateriím odpovídá jeden díl. Víme, že vybitých baterií je o 6 více než nabitých. Vybitých baterií jsou přitom 4 díly a nabitých 1 díl, takže vybitých je o 4-1=3 díly více než nabitých. Takže 3 díly odpovídají 6 bateriím. Jeden díl odpovídá \frac{6}{3}=2 bateriím. Gargamel tedy má 2 nabité baterie a 4 \cdot 2 = 8 vybitých baterií.
Výsledek: Gargamel má dvě nabité a osm vybitých baterií.
Výpočty pomocí rovnic
Pokud už se vyznáme v řešení rovnic, můžeme při řešení využít zápisu pomocí dvou rovnic pro dvě neznámé.
- První rovnici zapíšeme ze známého poměru.
- Druhou rovnici zapíšeme z informace o hodnotě součtu (nebo rozdílu, součinu, atd.).
Těžší příklad pro ty, kteří už znají rovnice a obvod kruhu
Víme, že poloměry dvou kruhů jsou v poměru 2 : 5 a že součet jejich obvodů je 70 \pi. O jaké poloměry jde?
Označíme si poloměry a a b a zapíšeme si rovnice. Známe poměr a : b = 2 : 5, takže máme první rovnici \frac{a}{b}=\frac{2}{5}. Součet obvodů kruhů o poloměrech a,b je roven 2a\cdot \pi + 2b\cdot \pi. Tento součet známe, takže druhá rovnice zní 2(a+b)\cdot\pi = 70 \pi.
Řešíme soustavu rovnic. První rovnici vynásobíme 5b (má smysl pro b\neq 0) a dostaneme 5a=2b. Vydělíme druhou rovnici kladným číslem 2\pi a dostaneme a+b=35. Vyjádříme a z druhé rovnice a dosadíme do první. 5\cdot(35-b)=2b. Zjednodušíme a vypočítáme b. 175= 7b, tedy b=25. Spočítáme druhý poloměr a=35-b=10.
Výsledné poloměry kruhů jsou a=10,b=25.
Poměry: měřítko mapy
Měřítko mapy, plánku, zmenšeného modelu
Měřítko mapy je speciální případ poměru. Jde o poměr, ve kterém je obraz krajiny na mapě ku krajině ve skutečnosti.
Příklady
- Mapa s měřítkem 1 : 10\,000. Centimetr na této mapě odpovídá 10\,000\ \text{cm} = 100\ \text{m} ve skutečnosti.
- Nákres, na kterém je délka pětimetrové sochy 2\ \text{cm}, má měřítko 2 : (100\cdot 5) = 2 : 500 = 1 : 250.
Měřítko zvětšeného modelu
Podobně u zvětšeného modelu hodně malé věci nebo tvora použijeme opět poměr velikosti obrazu ku velikosti ve skutečnosti.
Příklady
- Model lidského neuronu v kabinetu biologie má šířku 20 \ \text{cm}. Skutečný motoneuron, který byl inspirací pro tento model, má velikost 80\ \mu \text{m} = 0{,}000\,08 \ \text{m}= 0{,}008 \ \text{cm}. Měřítko modelu je 20 : 0{,}008 = 20\,000 : 8 = 2\,500 : 1.
- Pojďme si ještě určit, čemu odpovídá 1\ \text{cm} na tomto modelu neuronu. Centimetr na modelu odpovídá \frac{1}{2\,500}\ \text{cm} ve skutečnosti, tedy 1\ \text{cm} na modelu neuronu odpovídá 0{,}000\,4\ \text{cm} = 0{,}000\,004\ \text{m} = 4\ \mu \text{m} ve skutečnosti.

