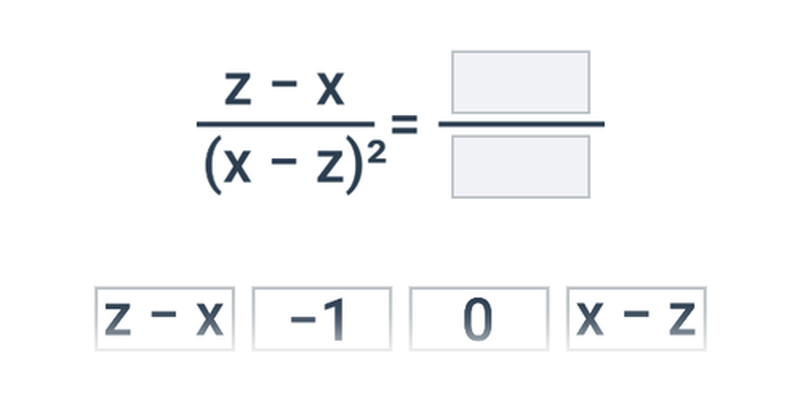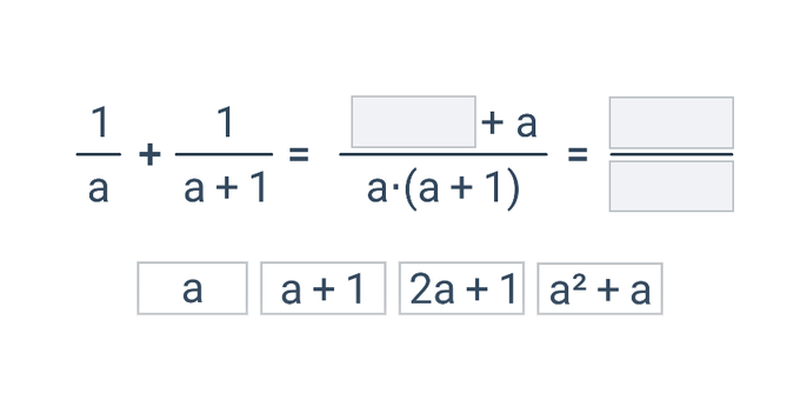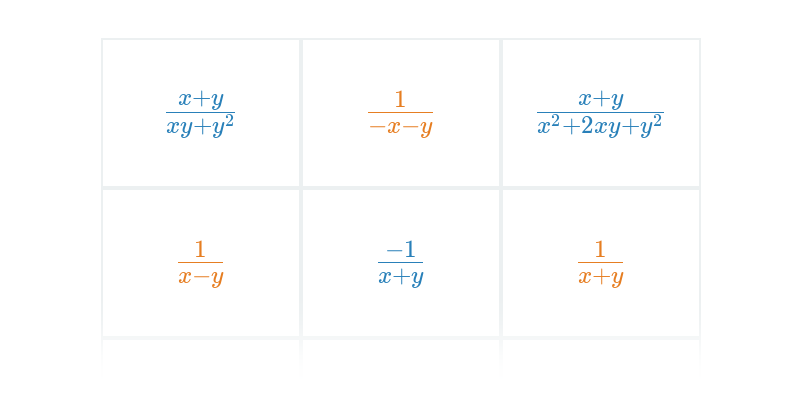Lomené výrazy
FZBZkopírovat kód tématu
Zkopírovat krátkou adresu (umime.to/FZB)
Ukázat QR kód
Všechny souhrnyLomený výraz je podíl dvou mnohočlenů. Zapisujeme většinou jako zlomek, například \frac{x+2}{x^2-1}. Toto téma dělíme na dvě podtémata:
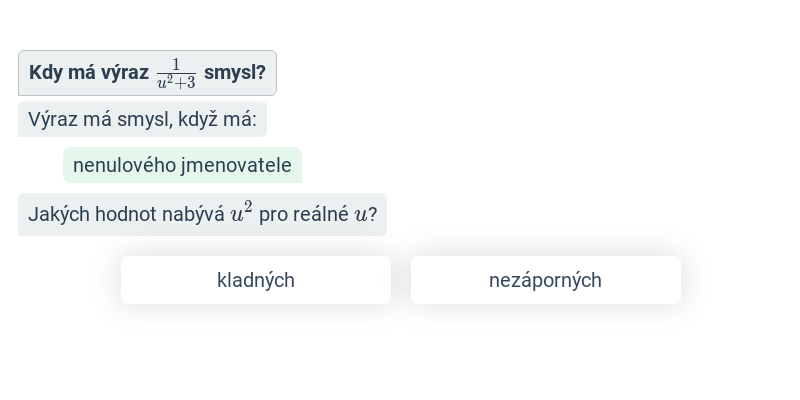
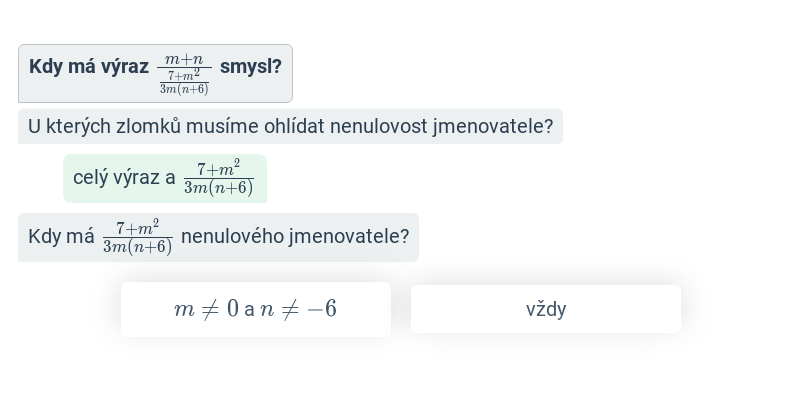
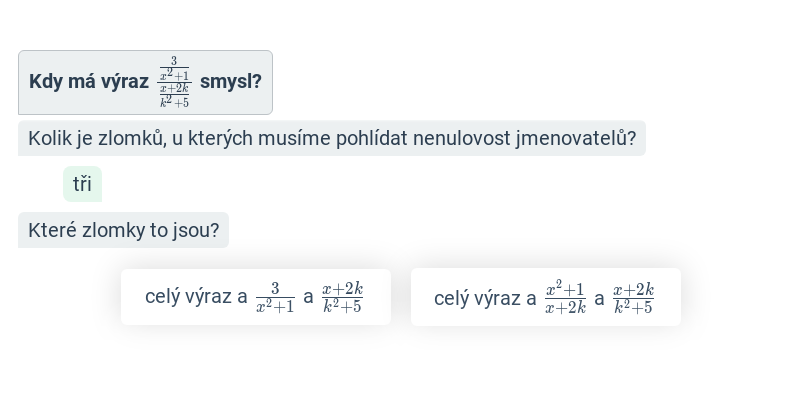
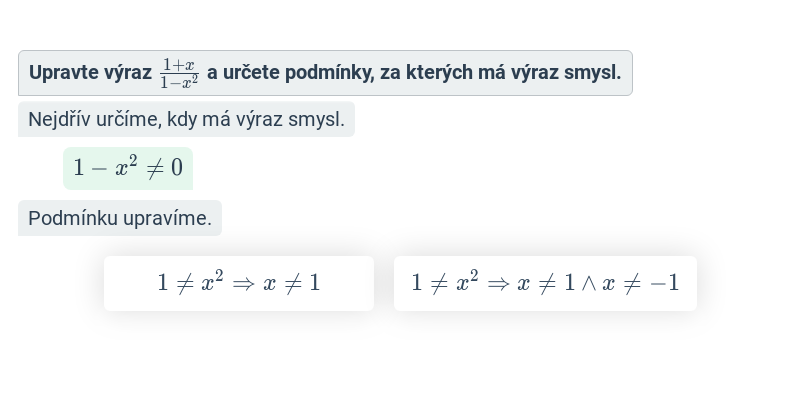
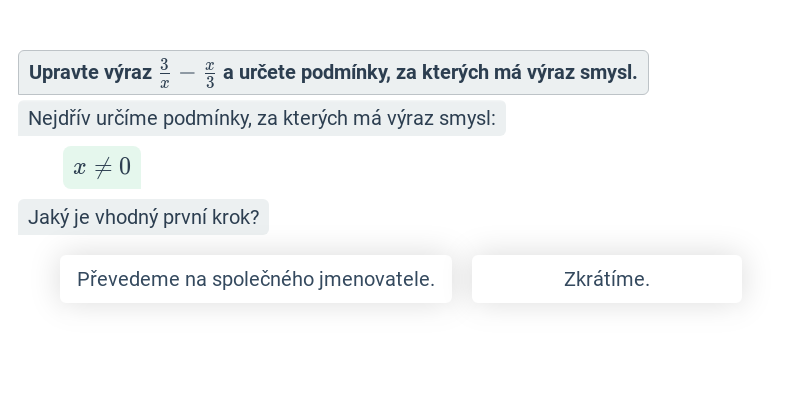
- Podmínky lomených výrazů – Přesněji řečeno jde o „podmínky, za kterých má daný lomený výraz smysl“. Musíme se jimi zabývat, protože pro takové hodnoty proměnných, pro které výraz ve jmenovateli lomeného výrazu nabývá hodnoty nula, nemá celý lomený výraz smysl.
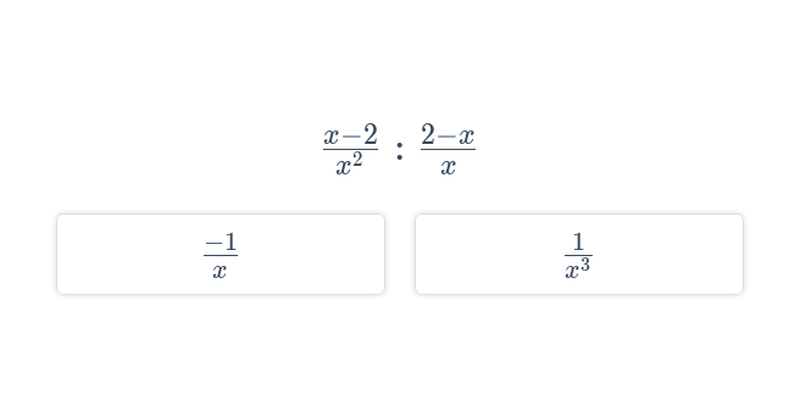
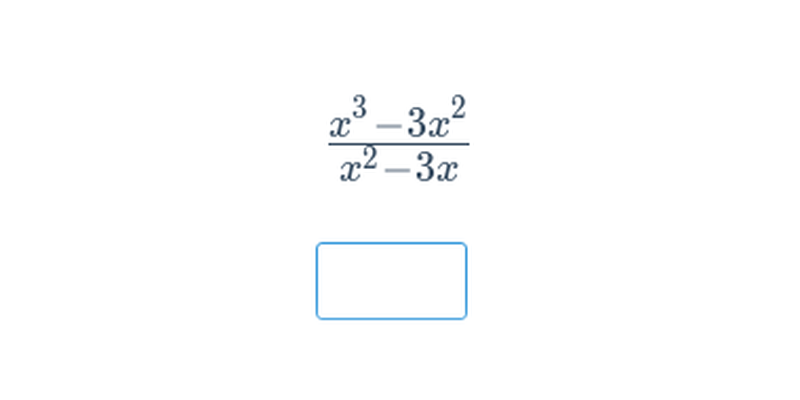
- Výpočty s lomenými výrazy a jejich úpravy – Ty provádíme podobně, jako když pracujeme se zlomky, jenom musíme mít na paměti, že čitatelé a jmenovatelé jsou u lomených výrazů mnohočleny.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Lomené výrazy
Lomené výrazy: mix
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Lomené výrazy
Úpravy lomených výrazů
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Lomené výrazy
Početní operace s lomenými výrazy
Lomené výrazy: mix
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.