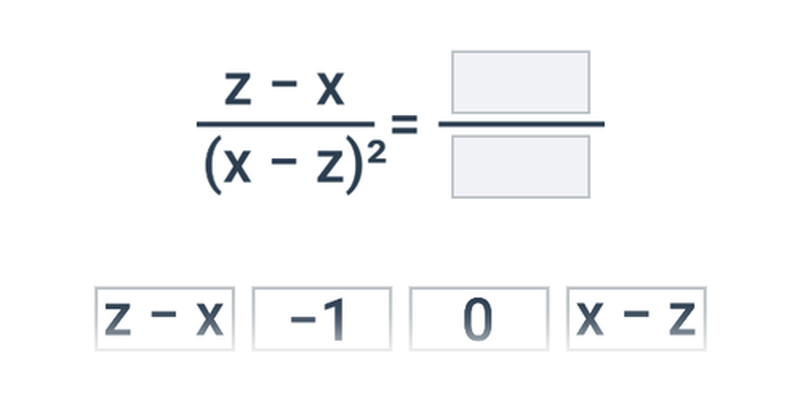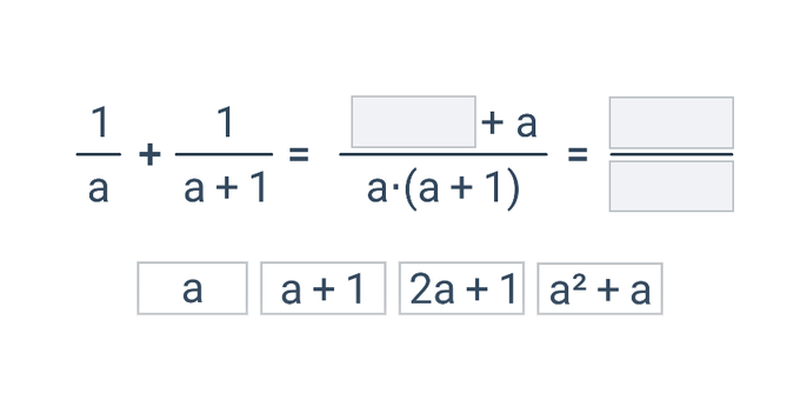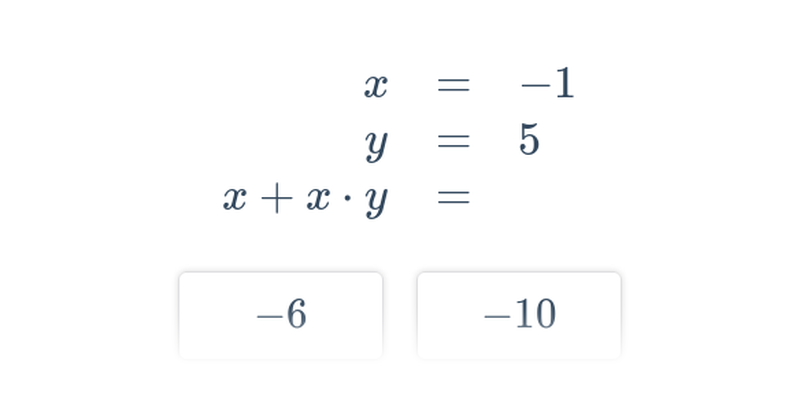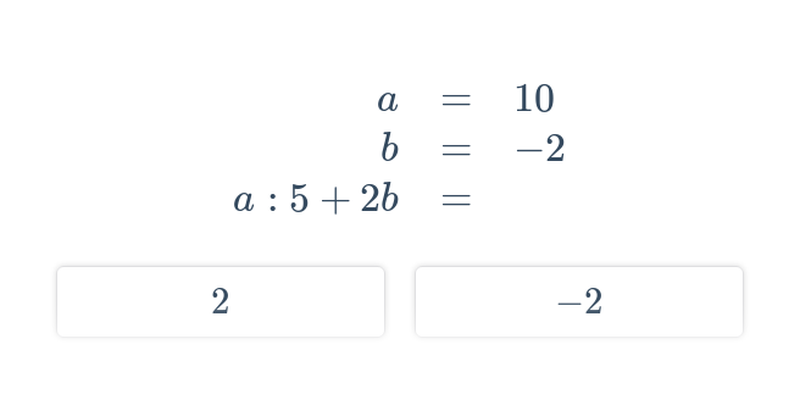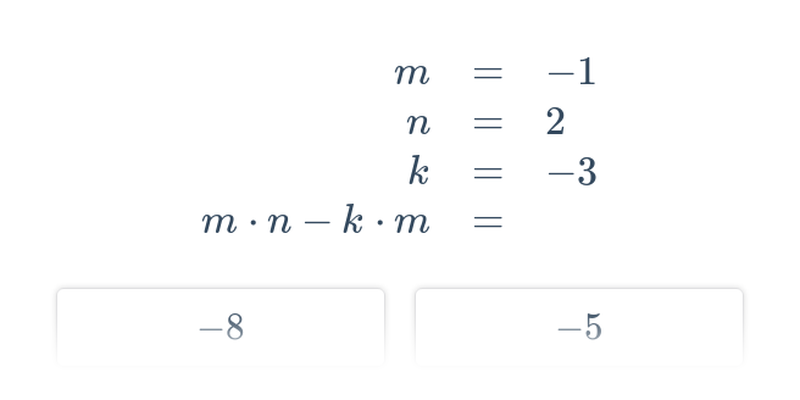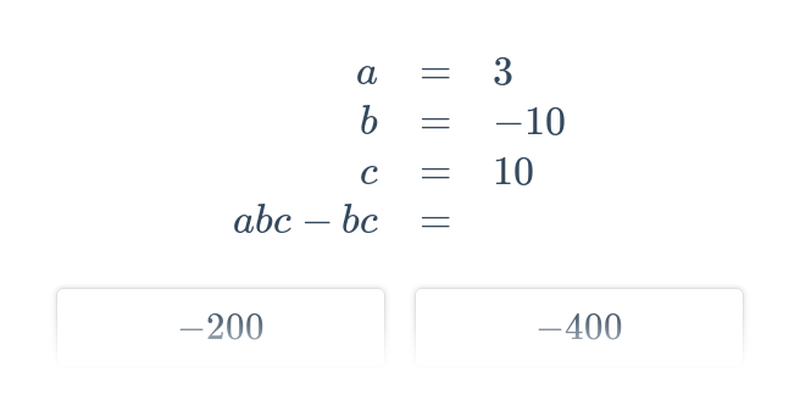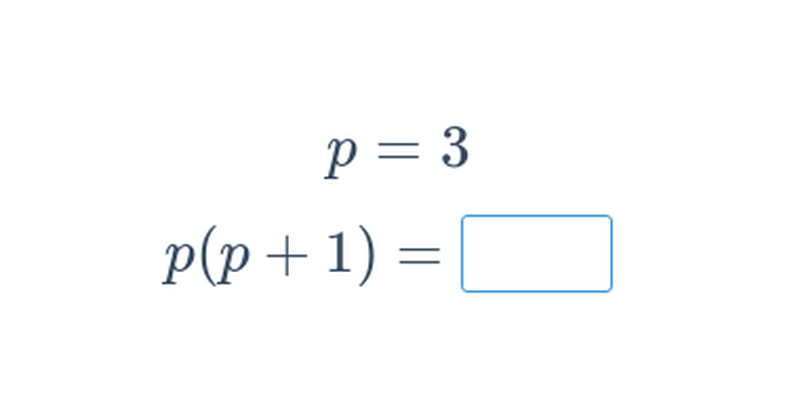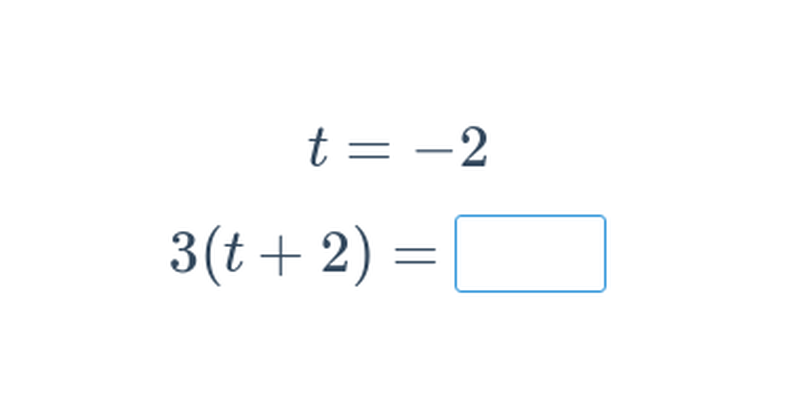Filtr podle ročníku
Algebraické výrazy a jejich úpravy
FX9Algebraický výraz je tvořen z konstant („čísla“) a proměnných („písmenka“), které jsou dohromady spojeny pomocí algebraických operací (např. sčítání, násobení) a závorek. Proměnná zastupuje čísla z určitého oboru hodnot. Pomocí algebraických výrazů můžeme provádět obecné výpočty.
Příklad: počet noh zvířat
- Sedlák Sedloň má na dvorku p prasat a s slepic.
- Výraz 4\cdot p + 2 \cdot s vyjadřuje celkový počet nohou, která zvířata na dvorku mají.
- V tomto výrazu jsou čísla 4 a 2 konstanty, písmena p a s jsou proměnné, jejichž oborem jsou přirozená čísla.
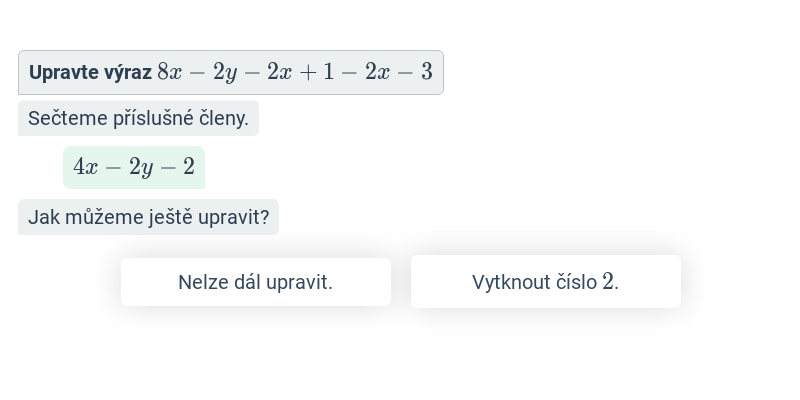
- Výraz můžeme upravit do tvaru 2(2p+s). Tato úprava zachovává hodnotu výrazu pro všechna možná přiřazení hodnot proměnných.
| téma | příklad (zadání) | příklad (výsledek) |
|---|---|---|
| Dosazování do výrazů | dosadit x = 3 do výrazu 2x + 5 | 11 |
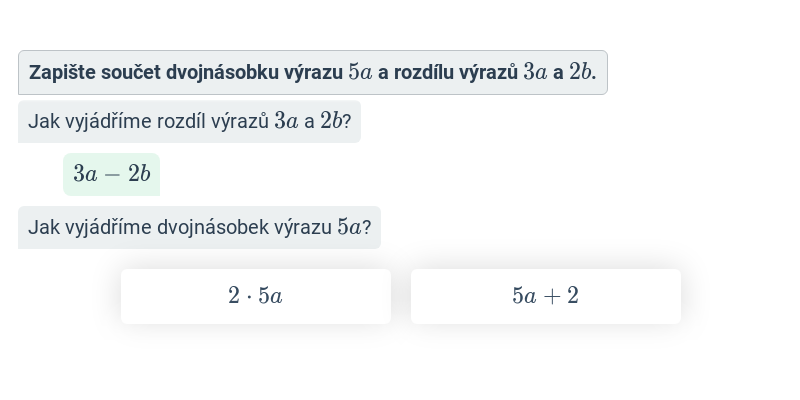
| Zápis pomocí výrazů | „O 5 větší než dvojnásobek čísla x“ | 2x + 5 |
| Úpravy výrazů s jednou proměnnou | 3x - 2 \cdot(3+x) | x - 6 |
| Úpravy výrazů s více proměnnými | 2a + 3b - a + 4b | a + 7b |
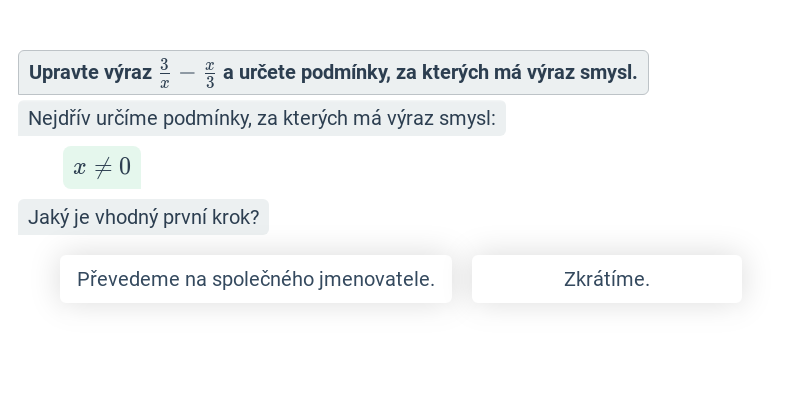
| Úpravy výrazů se zlomky | \frac{x}{2} + \frac{x}{3} | \frac{5x}{6} |
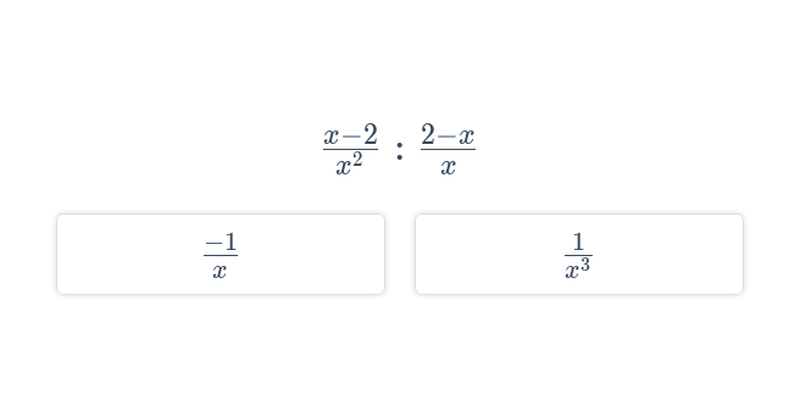
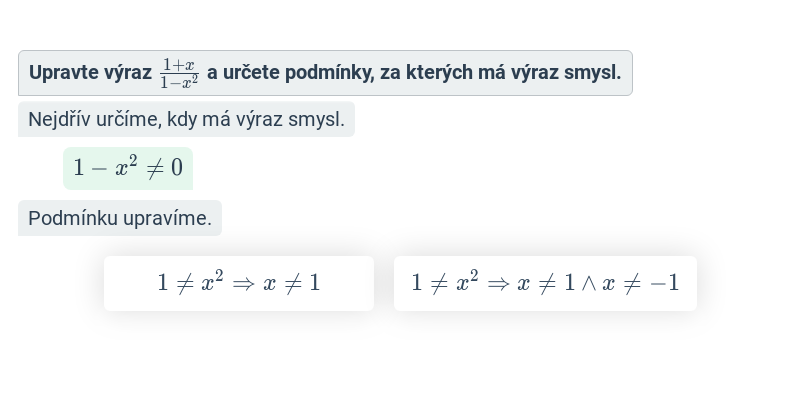
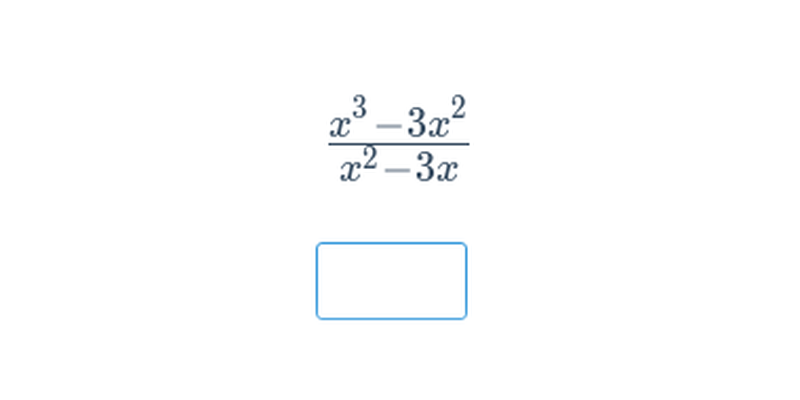
| Lomené výrazy | \frac{x^2 - 9}{x - 3} | x + 3 pro x \ne 3 |
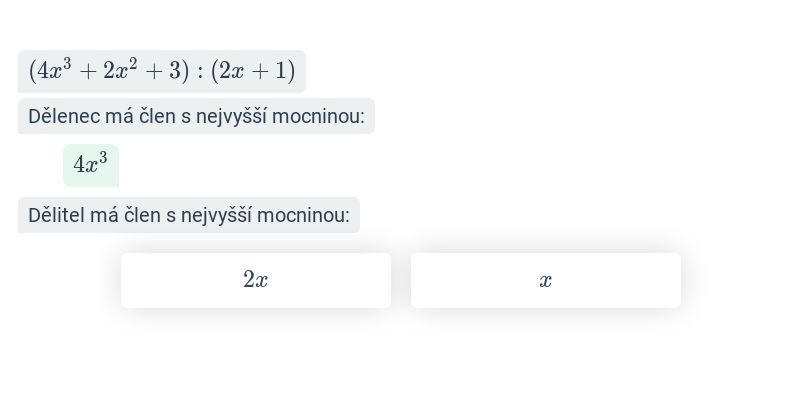
| Dělení mnohočlenu mnohočlenem | \frac{2x^4 + x + 4}{x^2 + 2} | 2x^2 - 4, zbytek x+12 |
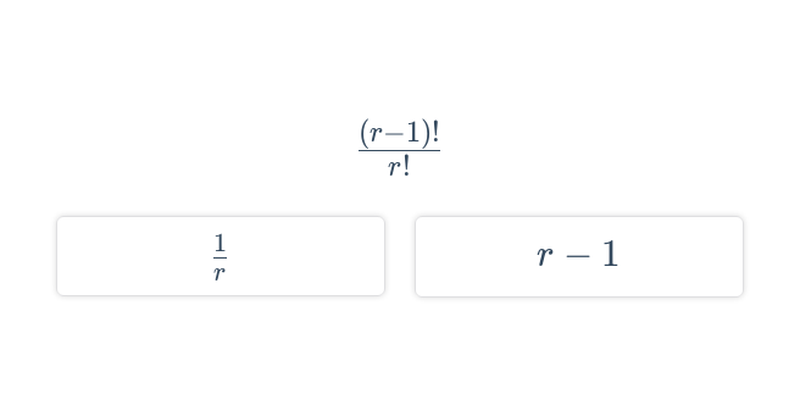
| Výrazy s faktoriálem a kombinačními čísly | \frac{n!}{(n+1)!} | \frac{1}{n+1} |
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Úpravy výrazů s jednou proměnnou (střední) • FG6
Typicky zabere: 5 min.
Lomené výrazy: mix (střední) • GX9
Typicky zabere: 7 min.
Lomené výrazy: mix (těžké) • FGK
Typicky zabere: 6 min.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Dosazování do výrazů (lehké) • GVW
Typicky zabere: 5 min.
Dosazování do výrazů (střední) • EL6
Typicky zabere: 9 min.
Dosazování do výrazů (těžké) • GG3
Typicky zabere: 8 min.
Zápis výrazů s proměnnými (střední) • FOH
Typicky zabere: 7 min.
Zápis výrazů s proměnnými (těžké) • FTA
Typicky zabere: 9 min.
Zápis zadání pomocí výrazu (střední) • FOJ
Typicky zabere: 8 min.
Zápis zadání pomocí výrazu (těžké) • FTB
Typicky zabere: 11 min.
Úpravy výrazů s jednou proměnnou (lehké) • FBJ
Typicky zabere: 5 min.
Úpravy výrazů s jednou proměnnou (střední) • EJT
Typicky zabere: 7 min.
Úpravy výrazů s jednou proměnnou (těžké) • ELX
Typicky zabere: 9 min.
Úpravy výrazů s více proměnnými (střední) • FHB
Typicky zabere: 6 min.
Úpravy výrazů s více proměnnými (těžké) • EFM
Typicky zabere: 8 min.
Úpravy výrazů: vnořené mocniny (těžké) • E2K
Typicky zabere: 7 min.
Rozklad na součin (těžké) • ENC
Typicky zabere: 7 min.
Úpravy výrazů se zlomky (střední) • EJS
Typicky zabere: 7 min.
Podmínky lomených výrazů (lehké) • GTZ
Typicky zabere: 4 min.
Podmínky lomených výrazů (střední) • GT1
Typicky zabere: 5 min.
Podmínky lomených výrazů (těžké) • EJV
Typicky zabere: 8 min.
Úpravy lomených výrazů (střední) • FHO
Typicky zabere: 7 min.
Úpravy lomených výrazů (těžké) • EJU
Typicky zabere: 9 min.
Úpravy výrazů s faktoriálem (těžké) • EJW
Typicky zabere: 8 min.
Úpravy výrazů s kombinačním číslem (těžké) • EJX
Typicky zabere: 6 min.
Výrazy a jejich úpravy: mix (střední) • ERE
Typicky zabere: 8 min.
Výrazy a jejich úpravy: mix (těžké) • ERF
Typicky zabere: 9 min.
Pexeso
Hledání dvojic, které k sobě patří.
Úpravy výrazů s jednou proměnnou (lehké) • FPV
Typicky zabere: 6 min.
Úpravy výrazů s jednou proměnnou (střední) • E9W
Typicky zabere: 5 min.
Úpravy výrazů s více proměnnými (lehké) • FPW
Typicky zabere: 6 min.
Úpravy výrazů s více proměnnými (střední) • EBZ
Typicky zabere: 6 min.
Lomené výrazy: mix (těžké) • E9X
Typicky zabere: 5 min.
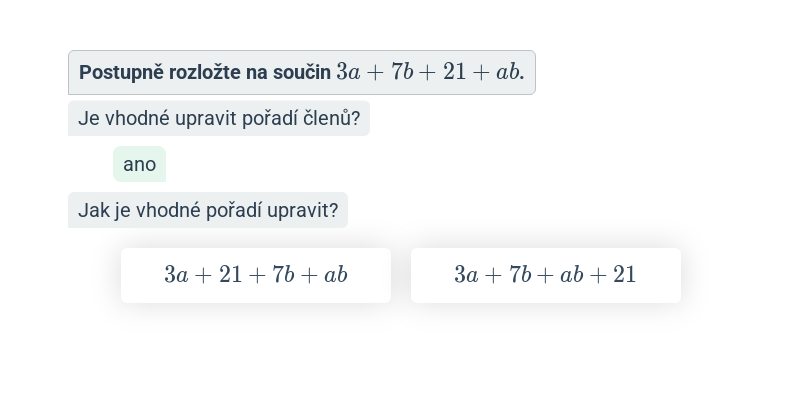
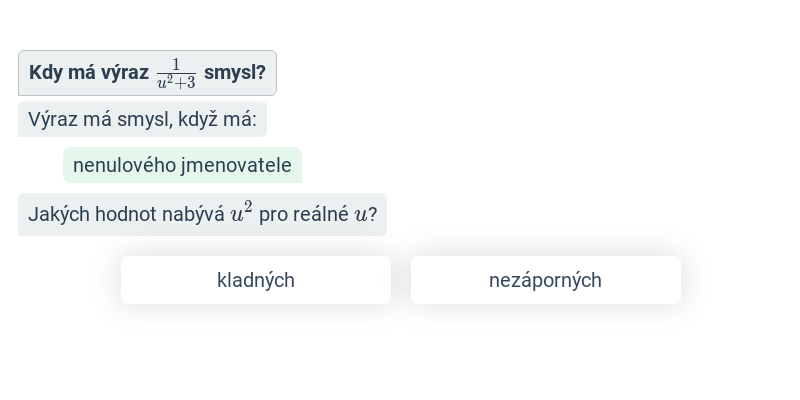
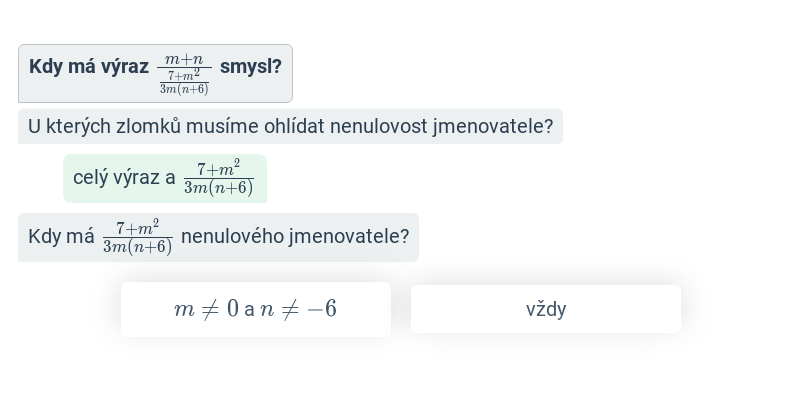
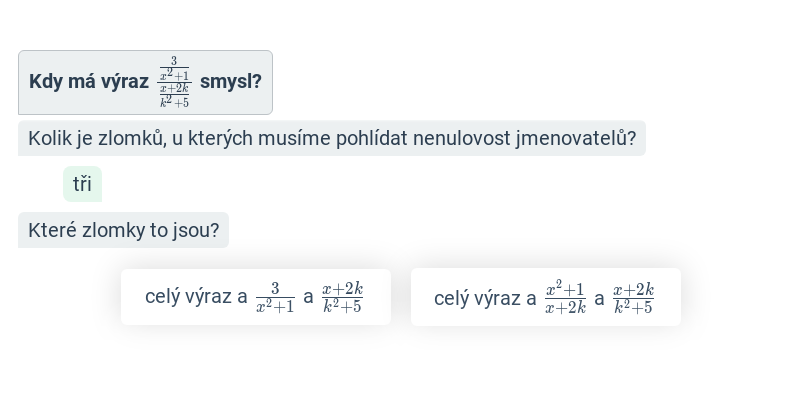
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Dosazování do výrazů (lehké) • FMD
Typicky zabere: 7 min.
Dosazování do výrazů (střední) • FME
Typicky zabere: 9 min.
Zápis výrazů s proměnnými (střední) • GHM
Typicky zabere: 9 min.
Zápis zadání pomocí výrazu (střední) • GHN
Typicky zabere: 9 min.
Úpravy výrazů s jednou proměnnou (lehké) • FL1
Typicky zabere: 8 min.
Úpravy výrazů s jednou proměnnou (střední) • EM1
Typicky zabere: 8 min.
Úpravy výrazů s jednou proměnnou (těžké) • FJU
Typicky zabere: 8 min.
Úpravy výrazů s více proměnnými (střední) • FL4
Typicky zabere: 9 min.
Úpravy výrazů s více proměnnými (těžké) • FJV
Typicky zabere: 8 min.
Rozklad na součin (postupné vytýkání) (střední) • E2R
Typicky zabere: 7 min.
Rozklad na součin (postupné vytýkání) (těžké) • G2W
Typicky zabere: 6 min.
Podmínky lomených výrazů (lehké) • FTD
Typicky zabere: 8 min.
Podmínky lomených výrazů (střední) • FTE
Typicky zabere: 9 min.
Podmínky lomených výrazů (těžké) • E3H
Typicky zabere: 8 min.
Početní operace s lomenými výrazy (lehké) • F7K
Typicky zabere: 7 min.
Početní operace s lomenými výrazy (střední) • FT6
Typicky zabere: 9 min.
Početní operace s lomenými výrazy (těžké) • F7L
Typicky zabere: 11 min.
Lomené výrazy: mix (lehké) • F7P
Typicky zabere: 9 min.
Lomené výrazy: mix (střední) • FTC
Typicky zabere: 10 min.
Lomené výrazy: mix (těžké) • ENE
Typicky zabere: 10 min.
Dělení mnohočlenu mnohočlenem (lehké) • FTZ
Typicky zabere: 7 min.
Dělení mnohočlenu mnohočlenem (střední) • FTS
Typicky zabere: 9 min.
Dělení mnohočlenu mnohočlenem (těžké) • FT2
Typicky zabere: 11 min.
Dělení mnohočlenu jednočlenem (střední) • F7M
Typicky zabere: 8 min.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Dosazování do výrazů (lehké) • GUT
Typicky zabere: 4 min.
Dosazování do výrazů (střední) • EBH
Typicky zabere: 5 min.
Dosazování do výrazů (těžké) • EPJ
Typicky zabere: 7 min.
Úpravy výrazů s jednou proměnnou (střední) • EPF
Typicky zabere: 5 min.
Úpravy výrazů s jednou proměnnou (těžké) • FBK
Typicky zabere: 6 min.
Úpravy výrazů s více proměnnými (střední) • EWU
Typicky zabere: 6 min.
Úpravy výrazů s více proměnnými (těžké) • FBL
Typicky zabere: 6 min.
Lomené výrazy: úpravy a výpočty (střední) • EPG
Typicky zabere: 7 min.
Výrazy a jejich úpravy: mix (střední) • E4C
Typicky zabere: 6 min.
Výrazy a jejich úpravy: mix (těžké) • FBR
Typicky zabere: 6 min.
