Úpravy výrazů s více proměnnými

FWV

umime.to/FWV

Stáhnout QR kód

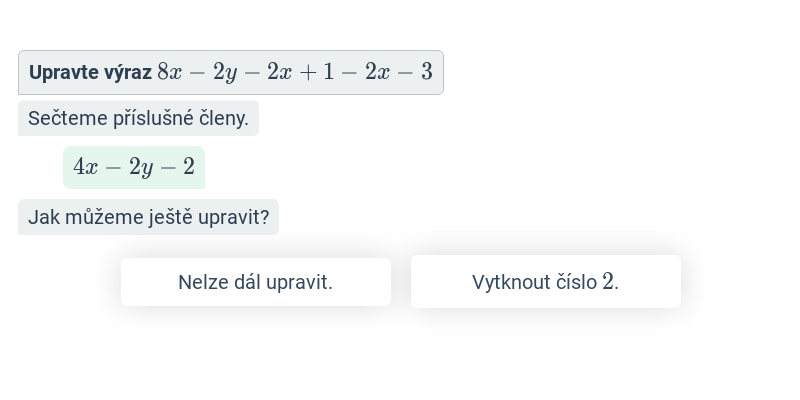
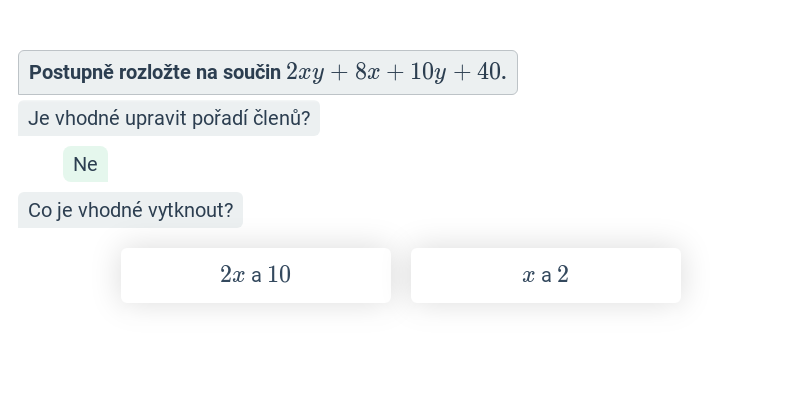
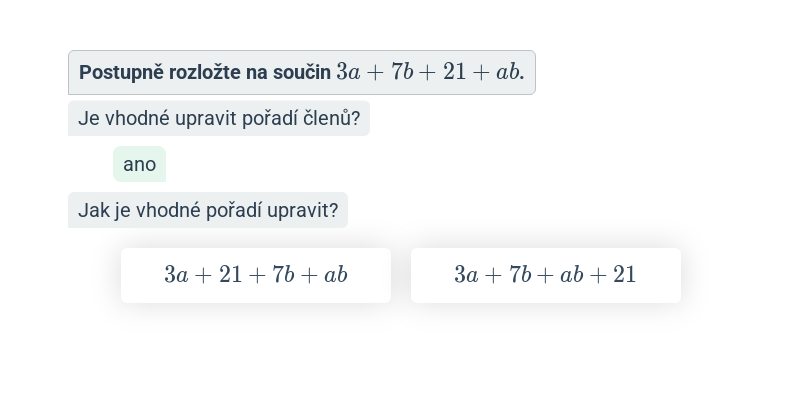
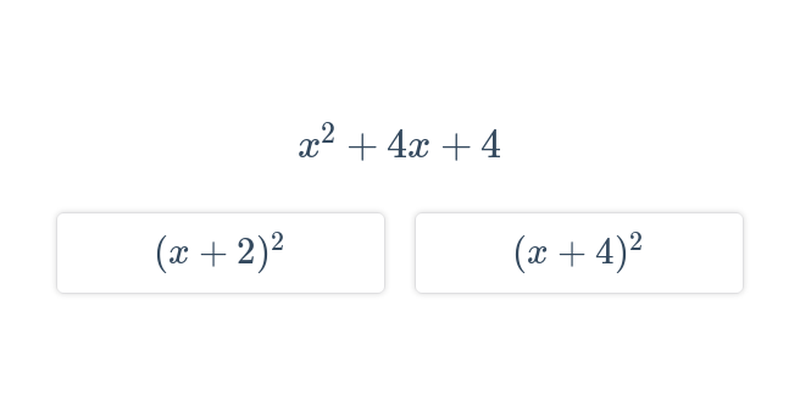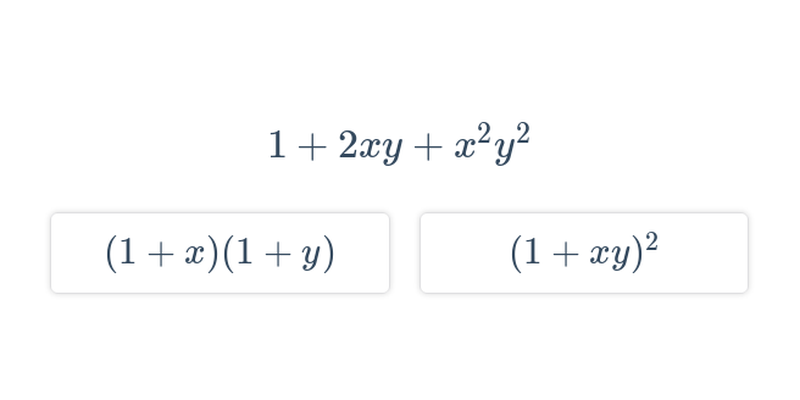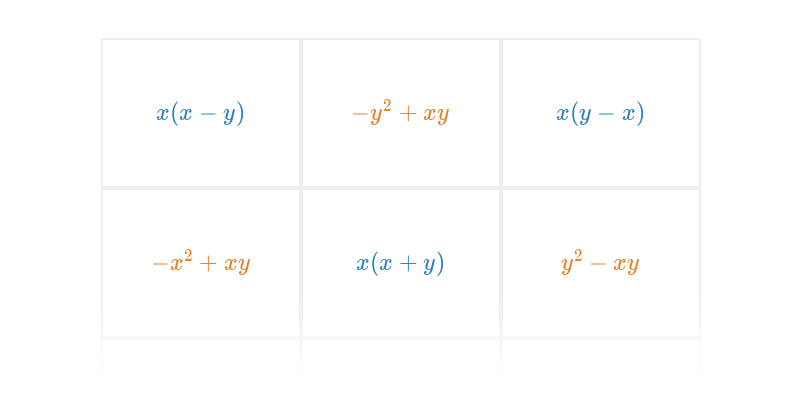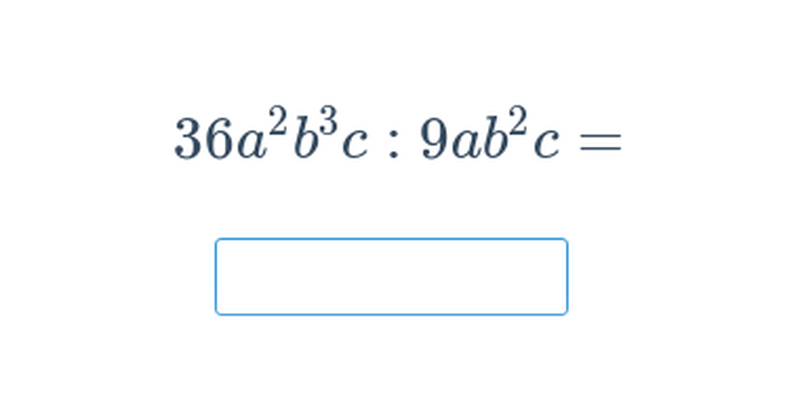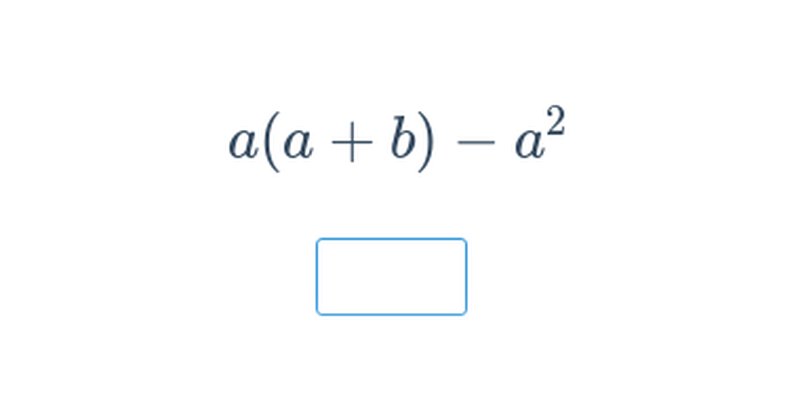Provádíme takové úpravy výrazů, které zachovávají hodnotu výrazu pro všechna možná dosazení za proměnné. Příklady úprav:

Popis	Výraz	Upravený výraz
Sečtení členů se stejnou proměnnou	3x+2y+4x	=7x+2y
Roznásobení závorky	x(y-2)	=xy-2x
Vytknutí	4x-x^2y+3	=x(4-xy)+3
Umocnění	(a+b)^2	=(a+b)(a+b)=a^2+2ab+b^2
Roznásobení dvou závorek	(a+b)(a-b)	=(a+b)(a-b)=a^2+ab-ab-b^2 = a^2-b^2

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Úpravy výrazů s více proměnnými

Úpravy výrazů: vnořené mocniny

Rozklad na součin

Úpravy výrazů s více proměnnými

Rozhodovačka • těžké

Úpravy výrazů s více proměnnými

Pexeso

Hledání dvojic, které k sobě patří.

Úpravy výrazů s více proměnnými

Úpravy výrazů s více proměnnými

Pexeso • lehké

Úpravy výrazů s více proměnnými

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Úpravy výrazů s více proměnnými

Rozklad na součin (postupné vytýkání)

Úpravy výrazů s více proměnnými

Krok po kroku • těžké

Úpravy výrazů s více proměnnými

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Úpravy výrazů s více proměnnými

Úpravy výrazů s více proměnnými

Psaná odpověď • střední

Úpravy výrazů s více proměnnými

NAPIŠTE NÁM

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Nejprve se prosím podívejte na časté dotazy:

Časté dotazy Návody pro učitele

Čeho se zpráva týká?

Vzkaz Obsah Ovládání Přihlášení Licence