Nejmenší společný násobek (NSN) dvou celých čísel je nejmenší číslo, které je beze zbytku dělitelné oběma čísly. Příklady: NSN(12, 15) = 60, NSN(6, 8) = 24, NSN(3, 15) = 15. Pojem nejmenšího společného násobku lze zobecnit i na větší počet vstupních čísel. Například NSN(2, 3, 4) = 12. Typické využití nejmenšího společného násobku je při převodu zlomků na společného jmenovatele při sčítání zlomků.
Pro malá čísla můžeme nejmenší společný násobek najít tak, že si vypíšeme několik prvních násobků od obou čísel.
Příklad: NSN(12, 15) řešený výčtem násobků
- Násobky čísla 12 jsou 12, 24, 36, 48, 60, 72, 84, …
- Násobky čísla 15 jsou 15, 30, 45, 60, 75, 90, …
- Nejmenší společný násobek je první číslo, které se vyskytuje v obou seznamech. V tomto případě tedy 60.
Pro větší čísla můžeme nejmenší společný násobek nalézt pomocí prvočíselného rozkladu. NSN je roven součinu všech prvočísel, které se vyskytují alespoň v jednom rozkladu (v nejvyšší mocnině, v jaké se vyskytují).
Příklad: NSN(24, 45) řešený pomocí rozkladu
- 24 = 2^3\cdot 3
- 45 = 3^2 \cdot 5
- \mathit{NSN}(24, 45) = 2^3 \cdot 3^2 \cdot 5 = 360
Nejmenší společný násobek lze vypočítat také pomocí největšího společného dělitele (NSD): \mathit{NSN}(a, b) = \frac{a\cdot b}{\mathit{NSD}(a, b)}
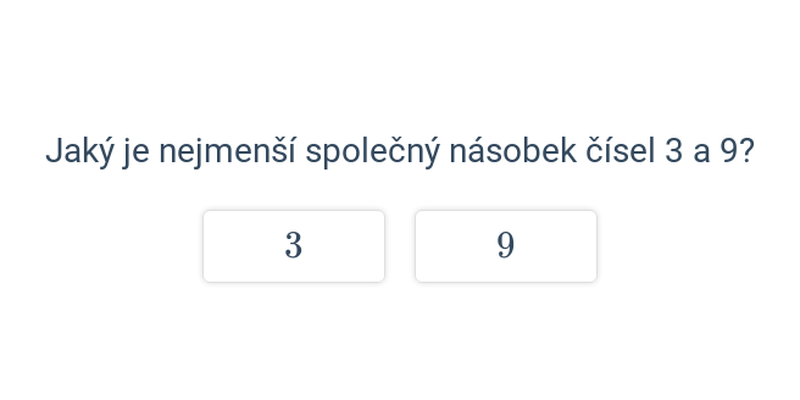
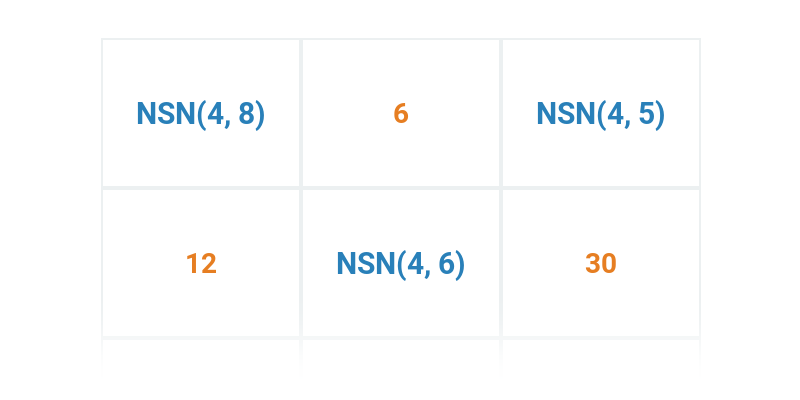
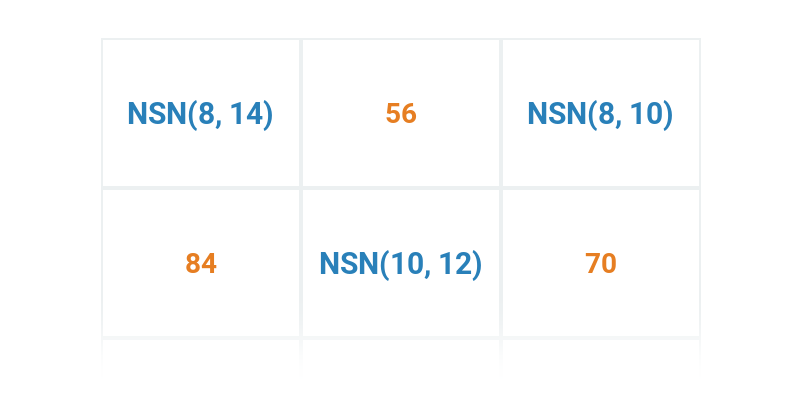
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.