Pexeso
Krok po kroku
Psaná odpověď
Slovní úlohy
Grafař
Porozumění
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Podmínky dělitelnosti
Nadřazené: Dělitelnost
Předcházející: Dělení se zbytkem, Sudé, liché
Navazující: Prvočísla, Největší společný dělitel, Nejmenší společný násobek
Cvičení
Přesouvání
Rozhodovačka
Roboti
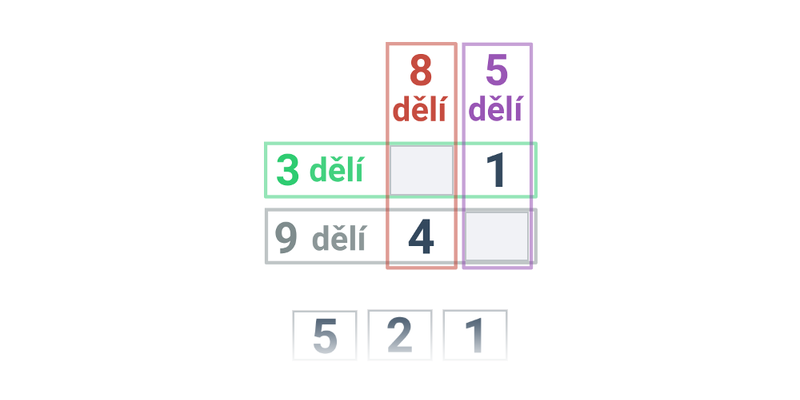
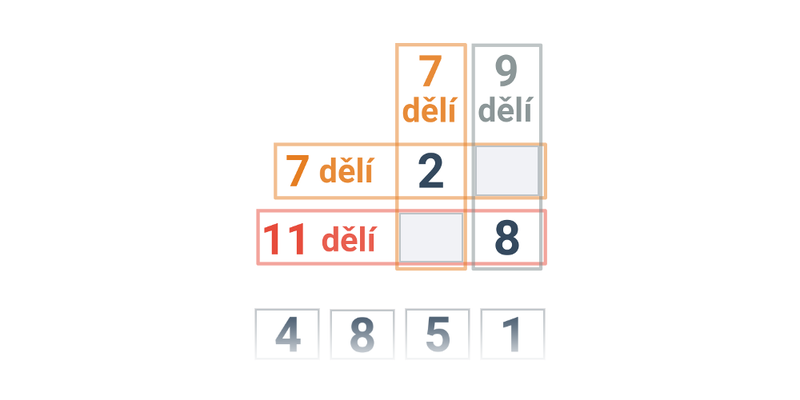
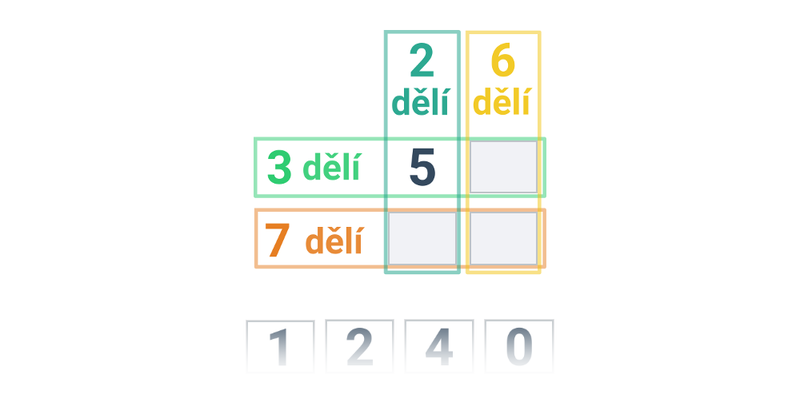
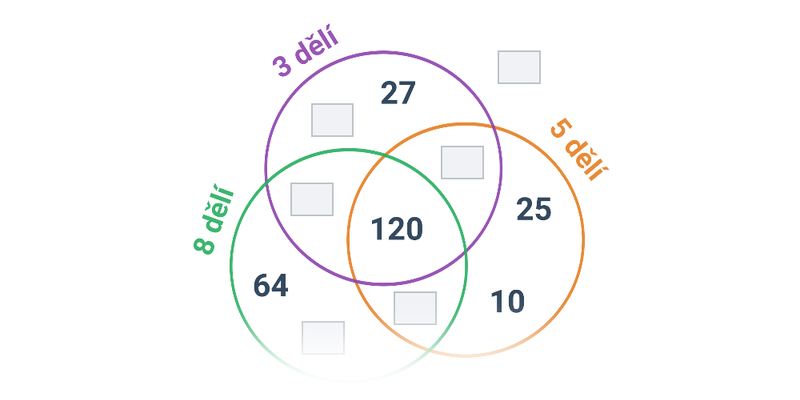
Číslo a je dělitelné nenulovým celým číslem b právě tehdy, když a je celočíselným násobkem b, tj. a = k\cdot b. Jinými slovy: číslo a dává po dělení číslem b zbytek 0. Příklady:
- Číslo 15 je dělitelné číslem 5, protože 15 = 3\cdot 5.
- Číslo 25 není dělitelné číslem 4, protože 25 = 6\cdot 4 + 1 (zbytek není nulový).
Pro některé dělitele můžeme dělitelnost rozpoznat poměrně snadno:
| Dělitel | Kritérium | Příklady |
|---|---|---|
| 2 | Sudé číslo na místě jednotek. | 18, 2546, 27781452 |
| 3 | Ciferný součet dělitelný číslem 3. | 252867 (2+5+2+8+6+7=30) |
| 4 | Poslední dvojčíslí je dělitelné číslem 4. | 180, 73524 |
| 5 | Na místě jednotek je 0 nebo 5. | 90, 1265 |
| 9 | Ciferný součet dělitelný číslem 9. | 252864 (2+5+2+8+6+4=27) |
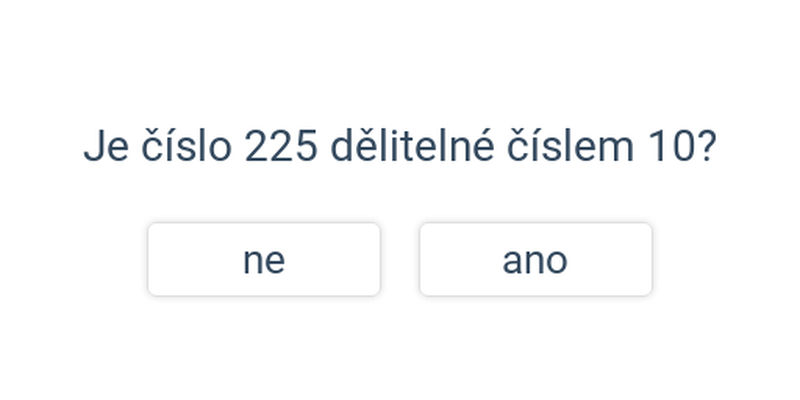
| 10 | Na místě jednotek je 0. | 250, 18763520 |
Vysvětlení mi pomohlo Vysvětlení mi nepomohlo
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Podmínky dělitelnosti 
Křížovka dělitelnosti
lehkéKřížovka dělitelnosti (lehké)
18 Zadání
Typicky zabere: 8 min
středníKřížovka dělitelnosti (střední)
19 Zadání
Typicky zabere: 8 min
těžkéKřížovka dělitelnosti (těžké)
18 Zadání
Typicky zabere: 9 min
Dělitelnost a Vennův diagram
středníDělitelnost a Vennův diagram (střední)
10 Zadání
Typicky zabere: 7 min
těžkéDělitelnost a Vennův diagram (těžké)
8 Zadání
Typicky zabere: 6 min
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Podmínky dělitelnosti
lehkéPodmínky dělitelnosti (lehké)
70 Zadání
Typicky zabere: 4 min
Ukázka
Je číslo 9 dělitelné číslem 3?Je číslo 2 dělitelné číslem 5?Je číslo 13 dělitelné číslem 2?
Roboti
Závody na rychlost proti robotům. Jednoduché ovládání výběrem ze dvou možností.
| Podmínky dělitelnosti | 1 2 3 |  Spustit |
