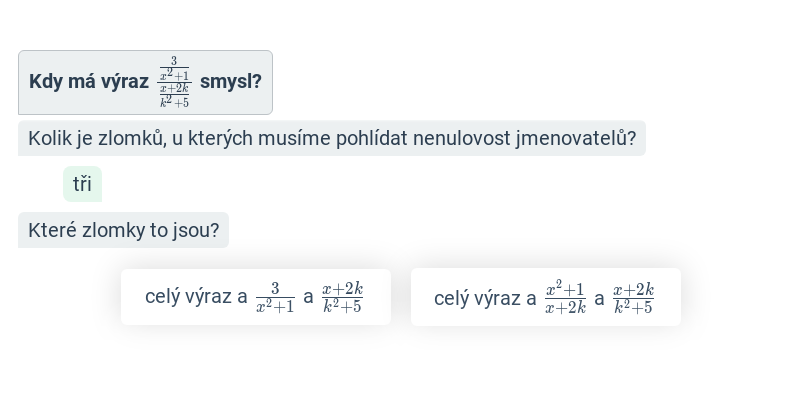
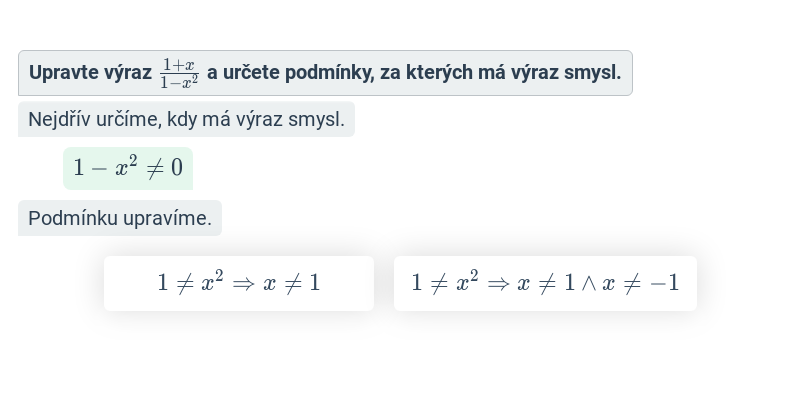
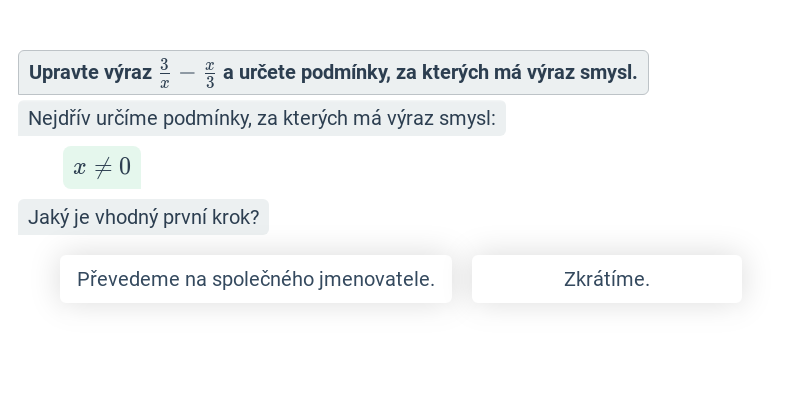
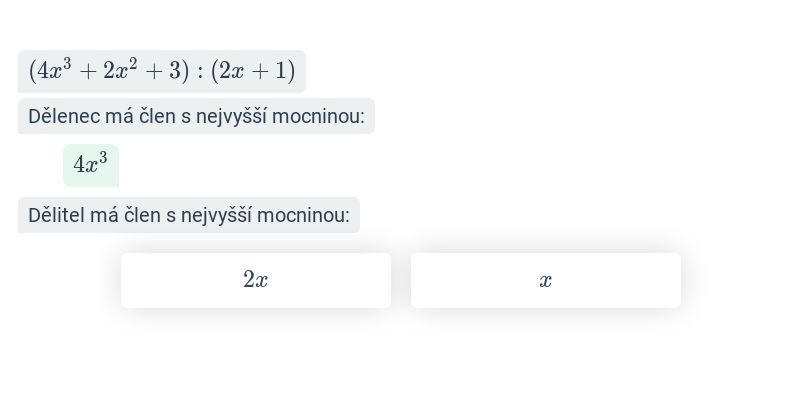
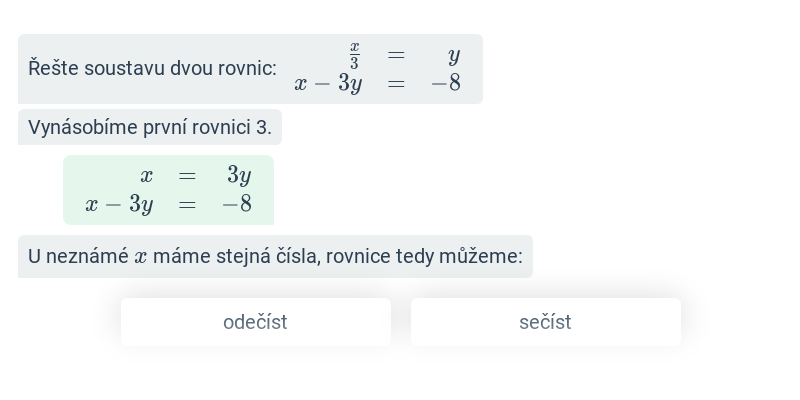
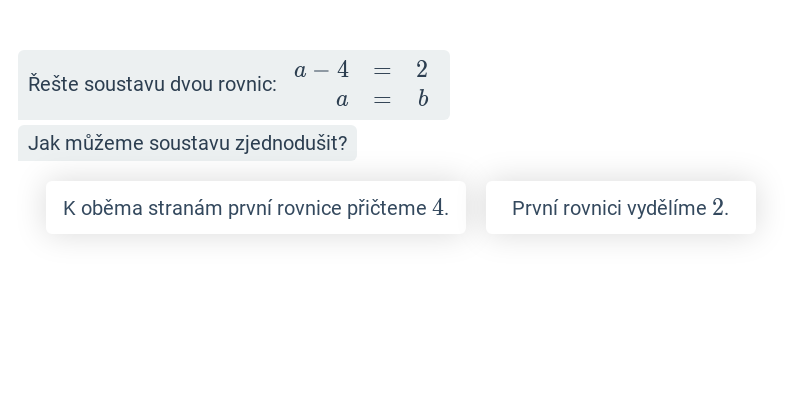
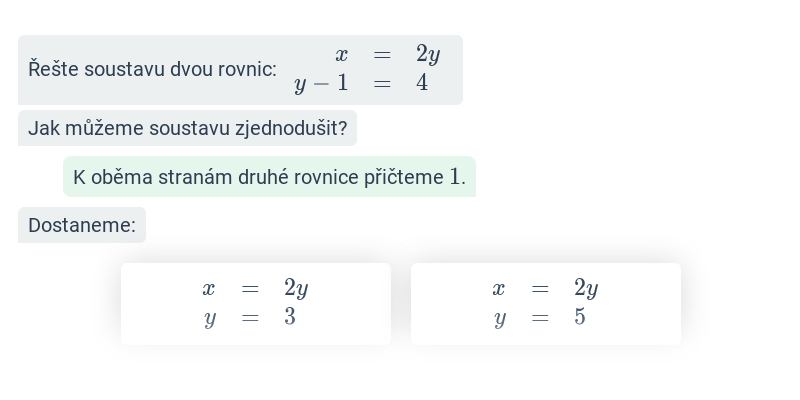
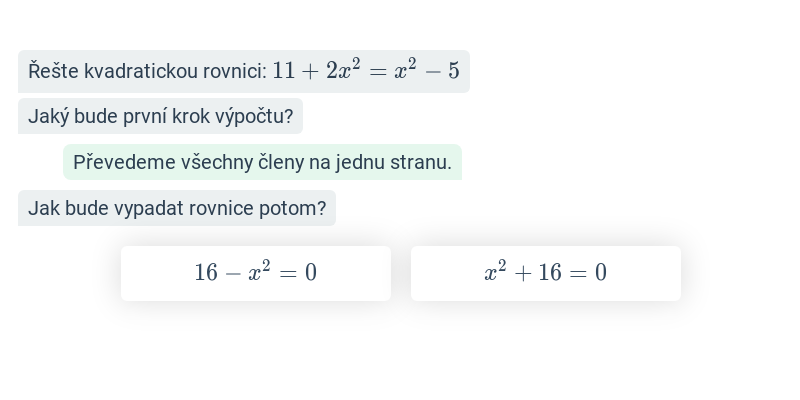
Krok po kroku – 9. třída
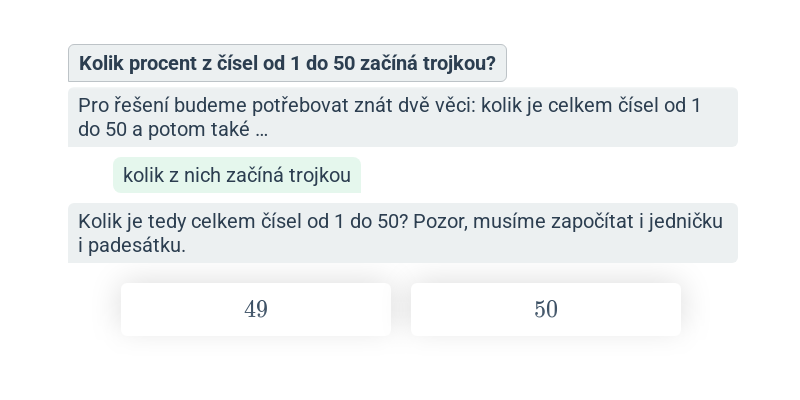
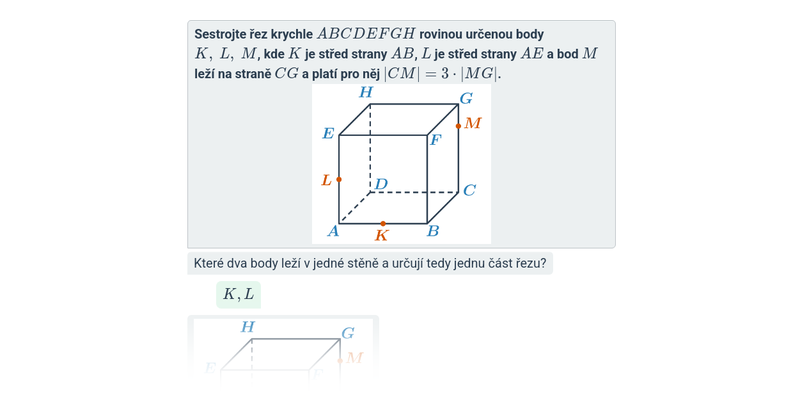
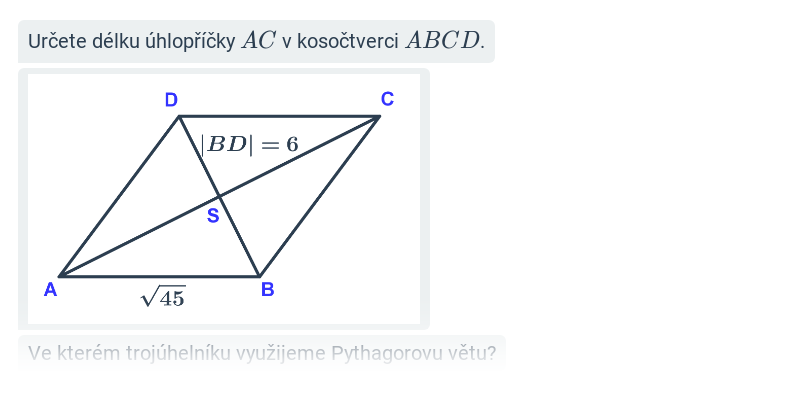
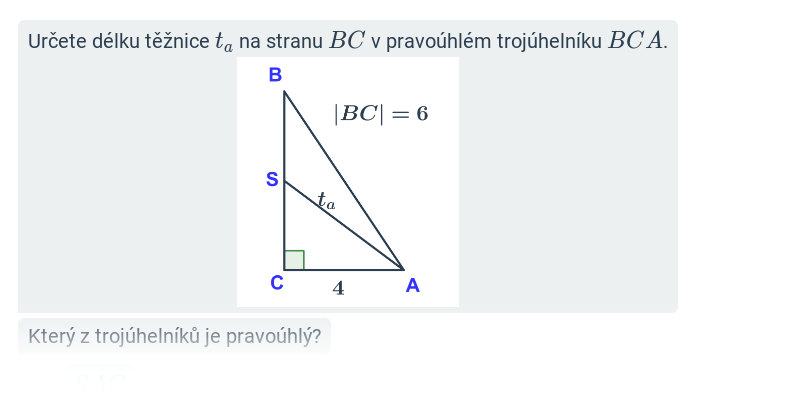
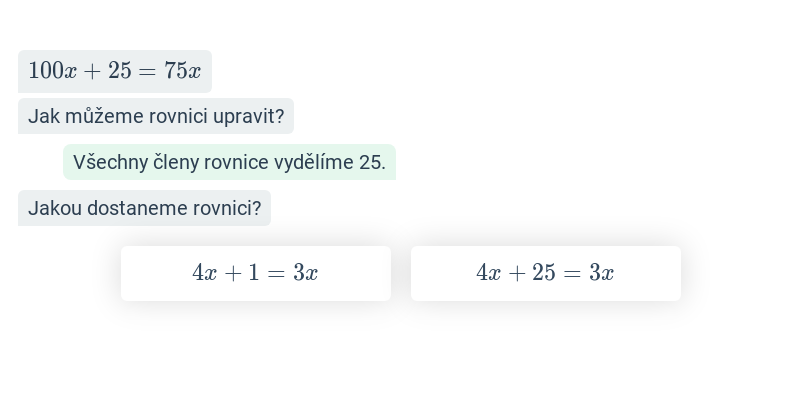
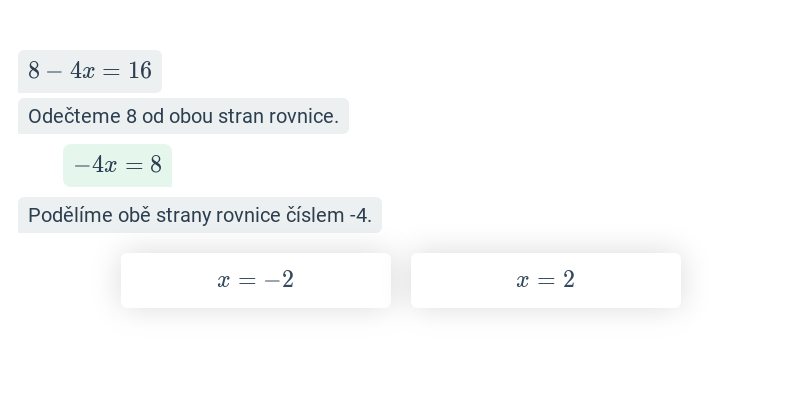
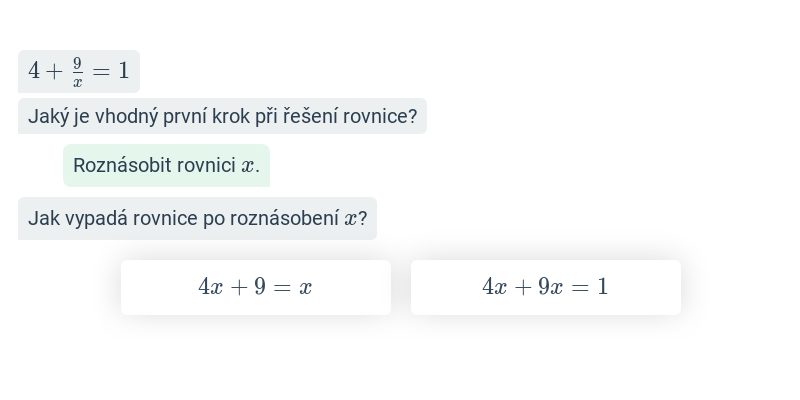
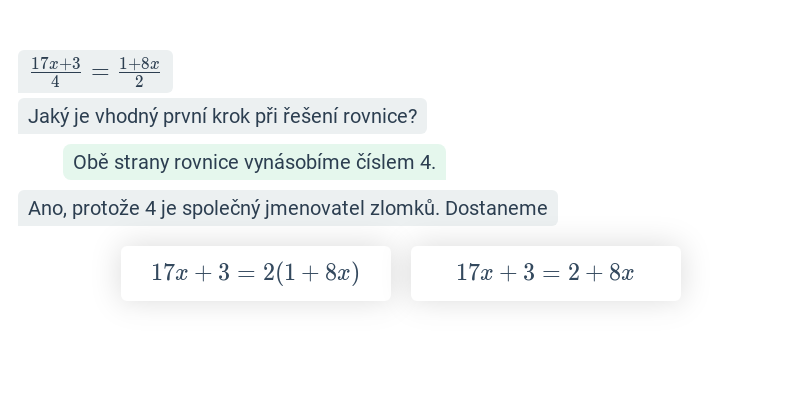
V tomto cvičení doplňujete jednotlivé kroky v rozsáhlejším postupu – například jednotlivé kroky v úpravě výrazů nebo při řešení rovnic. Cvičení je dobrou rozcvičkou na samostatné řešení kompletních příkladů.
Filtr podle ročníku
Aritmetika
Dělitelnost
Největší společný dělitel
NSD s použitím mocnin
Nejmenší společný násobek
NSN bez použití mocnin
NSN s použitím mocnin
Mocniny a odmocniny
Výrazy s mocninami a odmocninami
Zlomky, procenta, desetinná čísla
Zlomky
Výpočty se zlomky
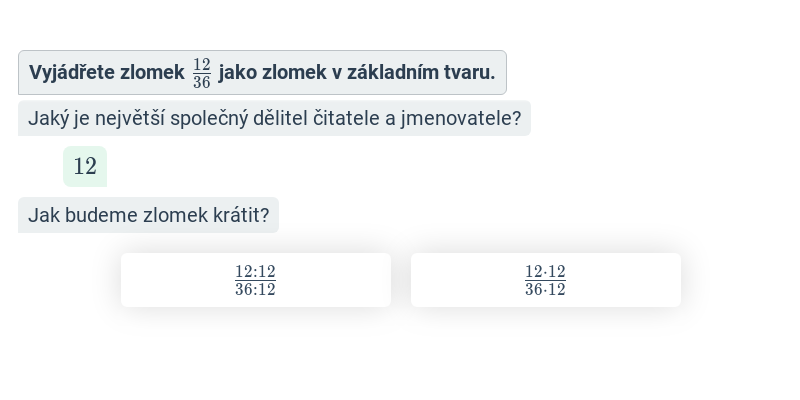
Krácení zlomků
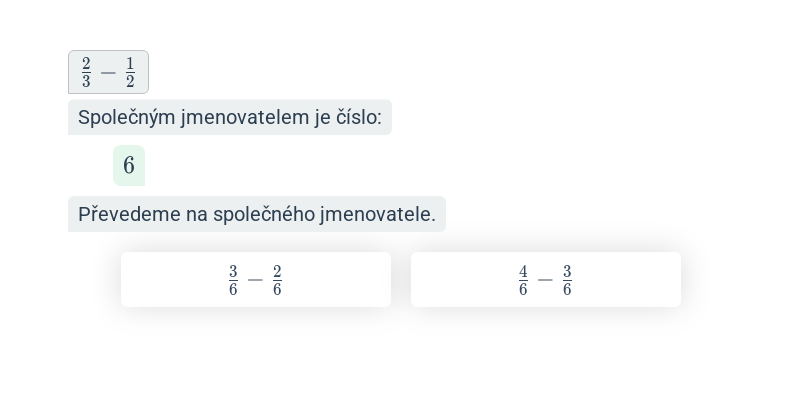
Sčítání a odčítání zlomků
Sčítání a odčítání zlomků s obrázky
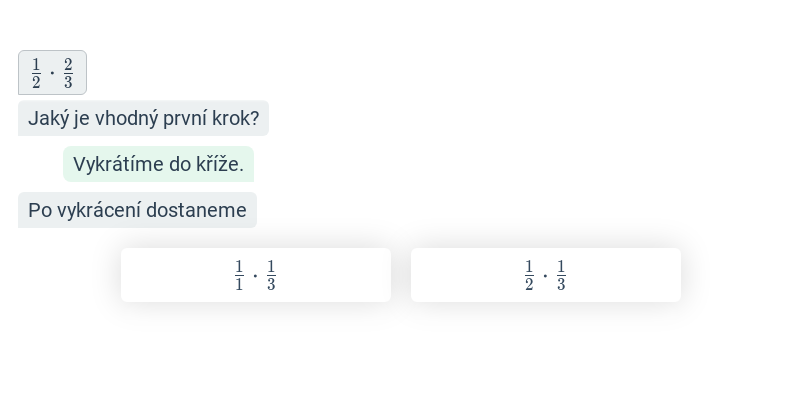
Násobení a dělení zlomků
Kombinace operací se zlomky
Procenta
Počítání s procenty
Desetinná čísla
Pokročilé počítání s desetinnými čísly
Desetinná čísla, mocniny, odmocniny
Geometrie
Prostorová představivost
Řezy krychle
Rovinné útvary
Trojúhelník
Pythagorova věta
Pythagorova věta: aplikace
Pythagorova věta: slovní úlohy po krocích
Obsah a obvod
Obsah
Obsah: kombinace útvarů
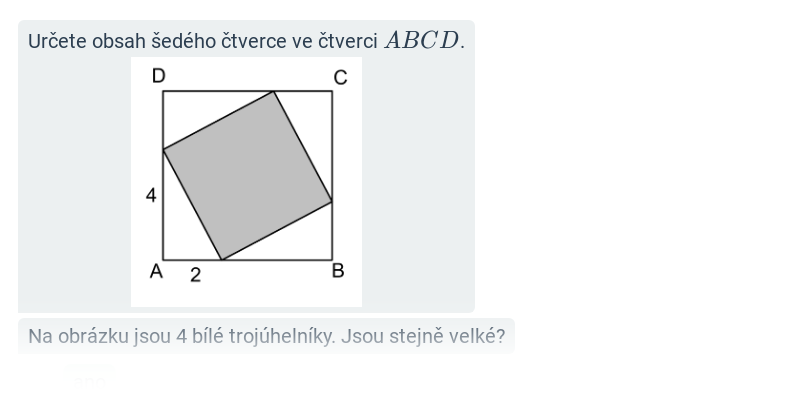
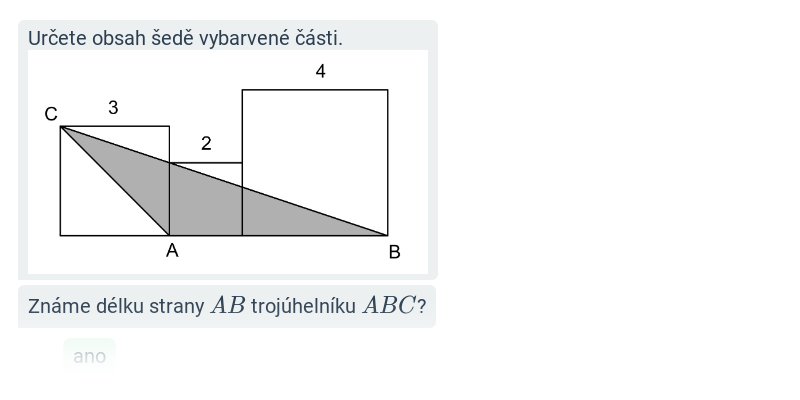
Obsah šedé oblasti
Objem a povrch
Objem, povrch: mix
Objem a povrch: koule, válec, kužel
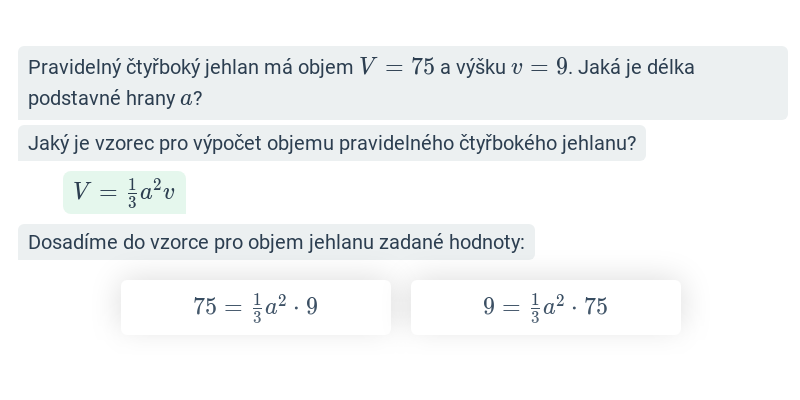
Objem a povrch: kvádr, jehlan, hranol
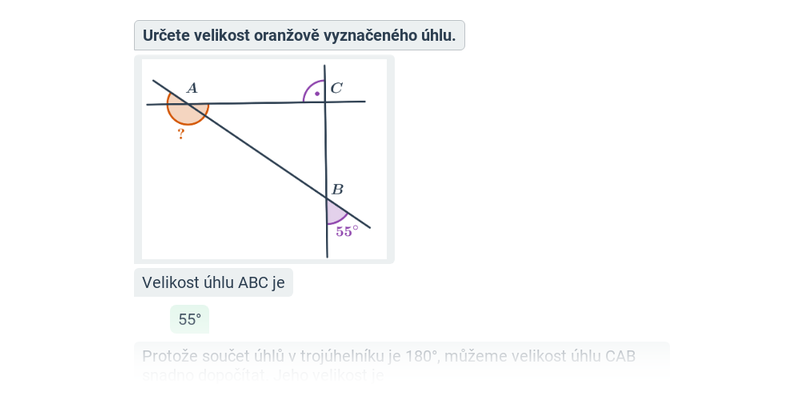
Úhly
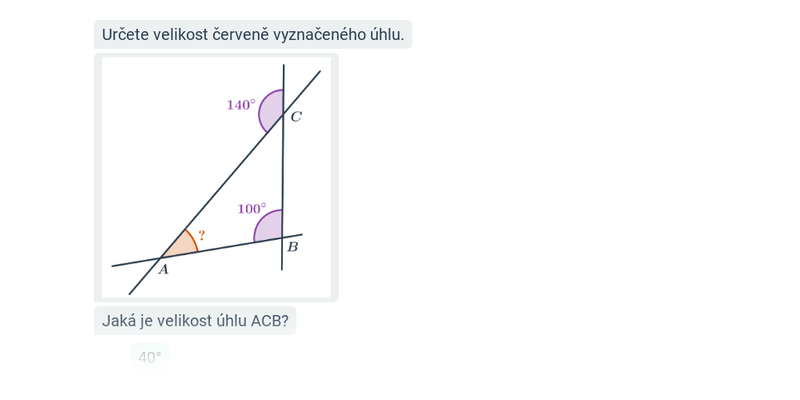
Úhly v trojúhelníku
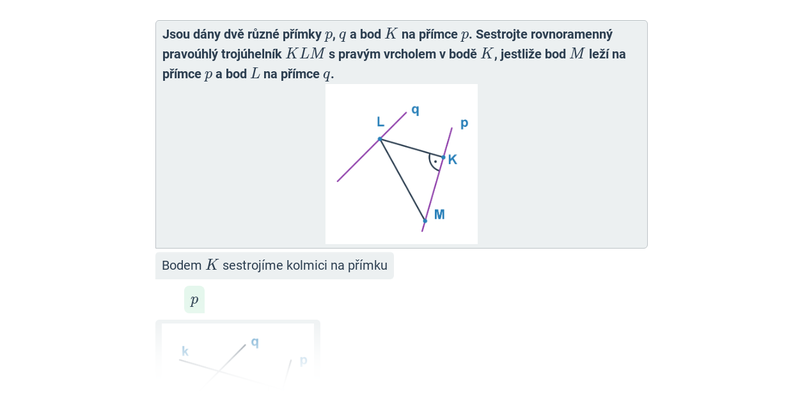
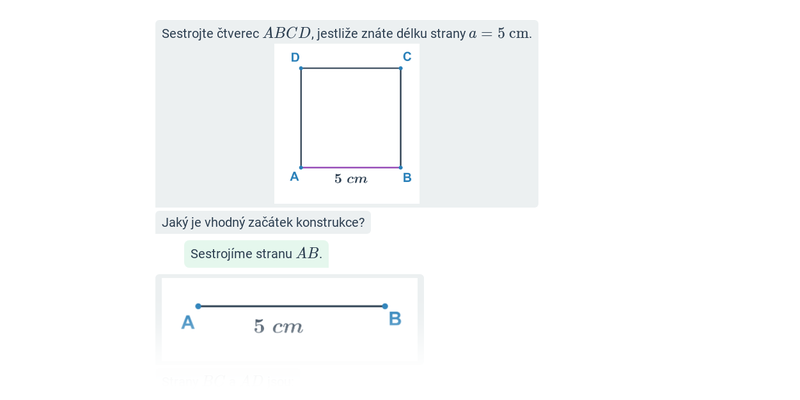
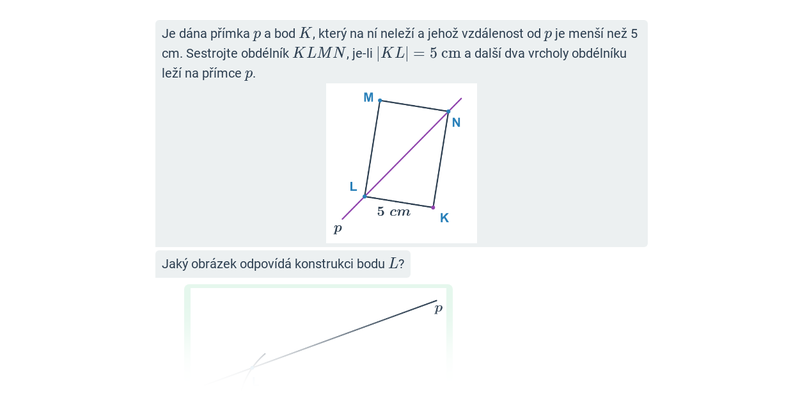
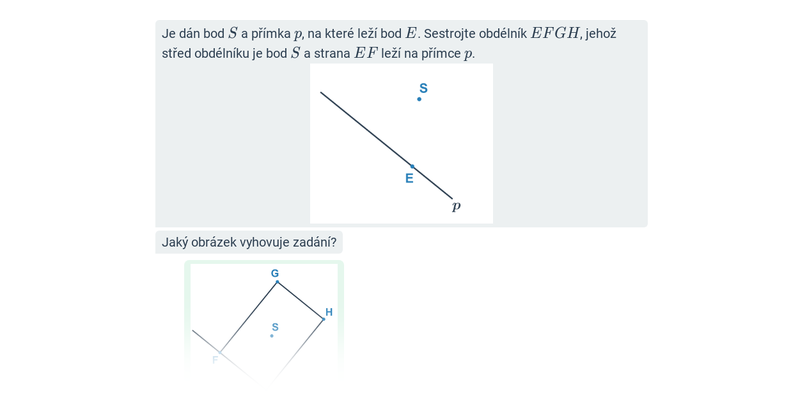
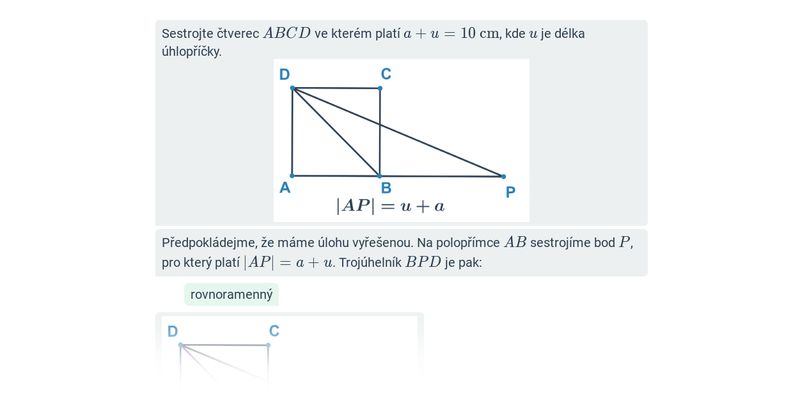
Geometrické konstrukce
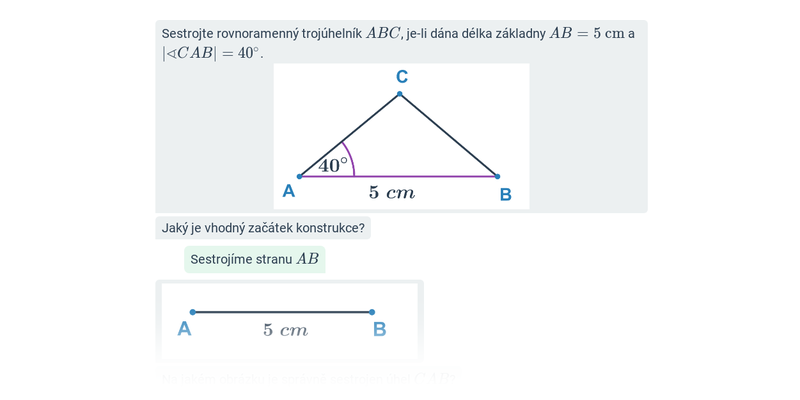
Konstrukční úlohy: trojúhelníky
Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
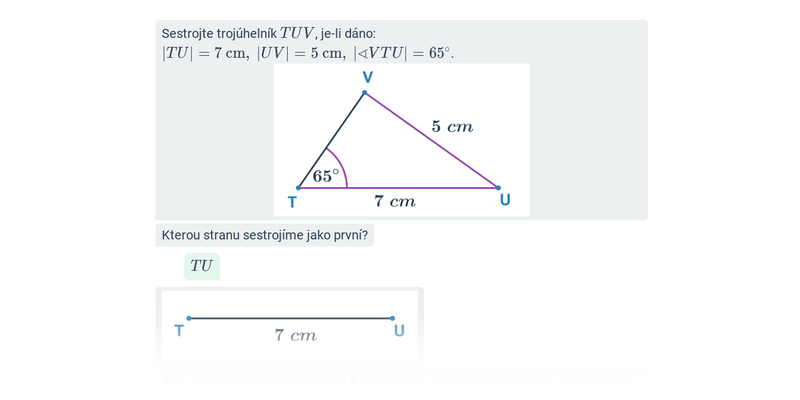
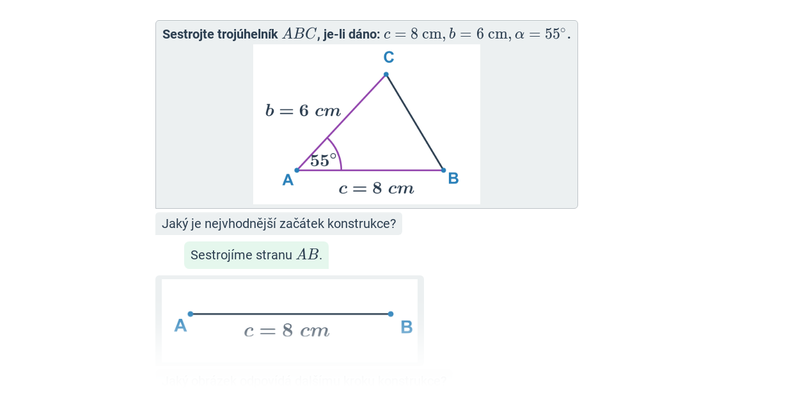
Konstrukce trojúhelníků: věty sss, sus, usu, Ssu
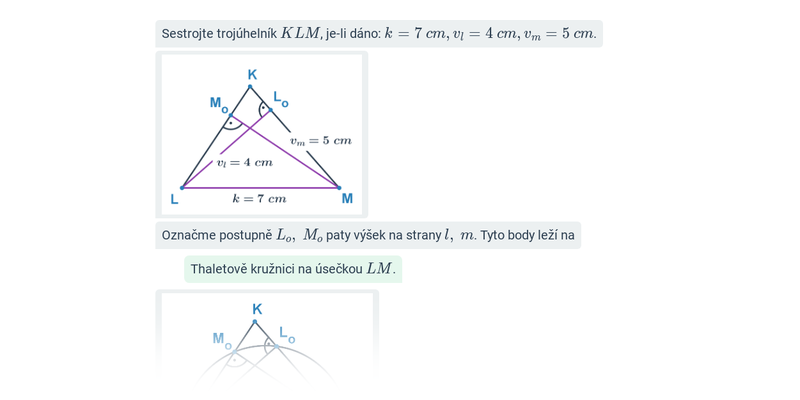
Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
Konstrukce trojúhelníků: mix
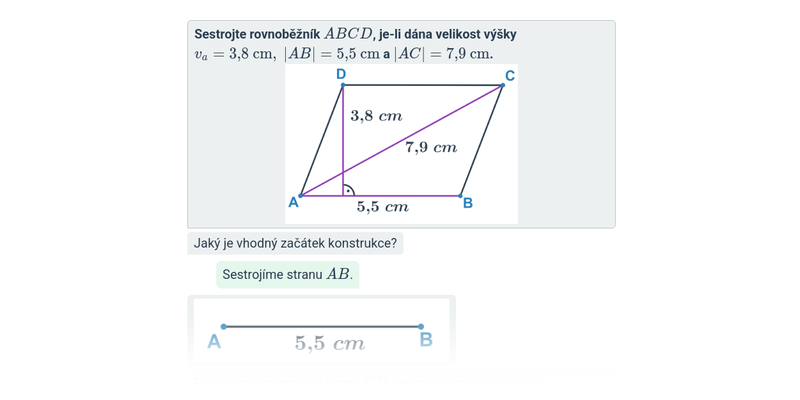
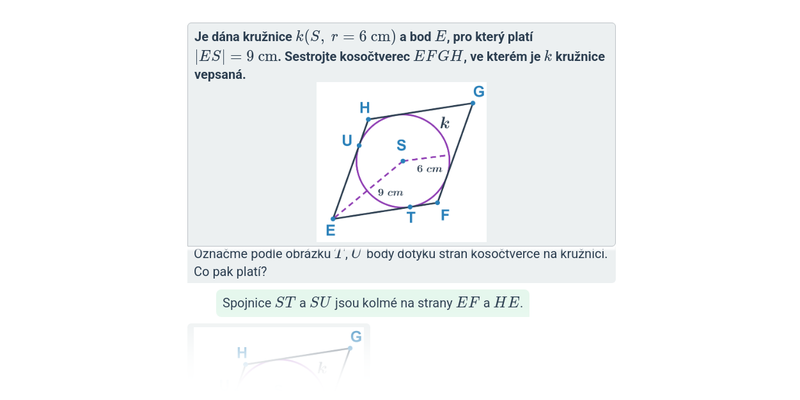
Konstrukční úlohy: čtyřúhelníky
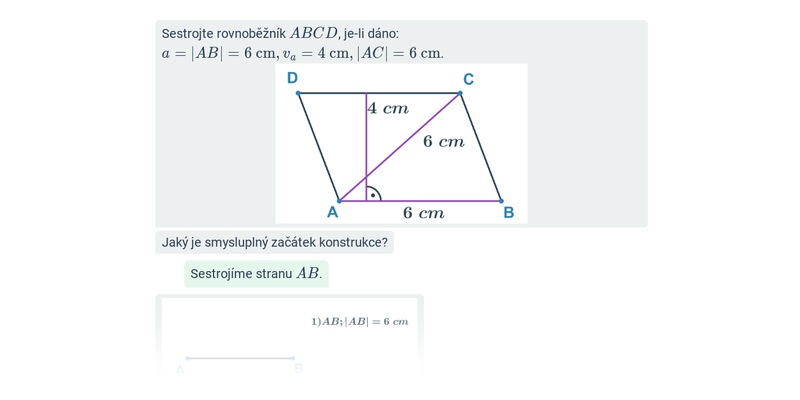
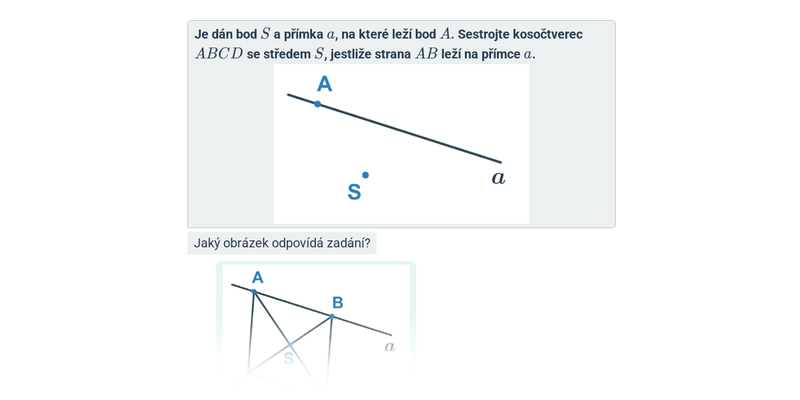
Konstrukce čtyřúhelníků: rovnoběžníky
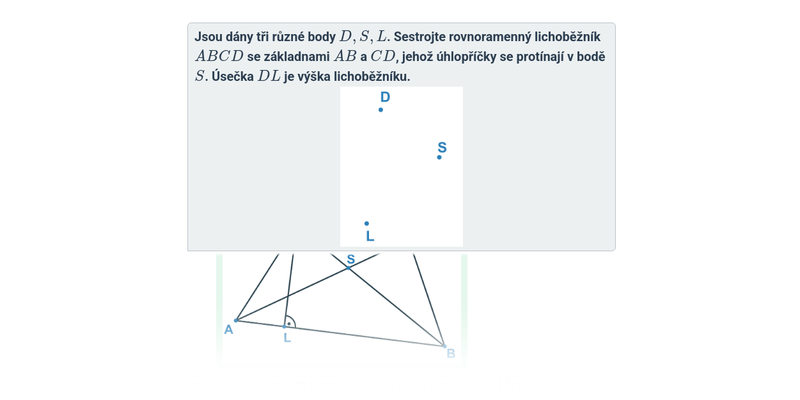
Konstrukce čtyřúhelníků: lichoběžníky
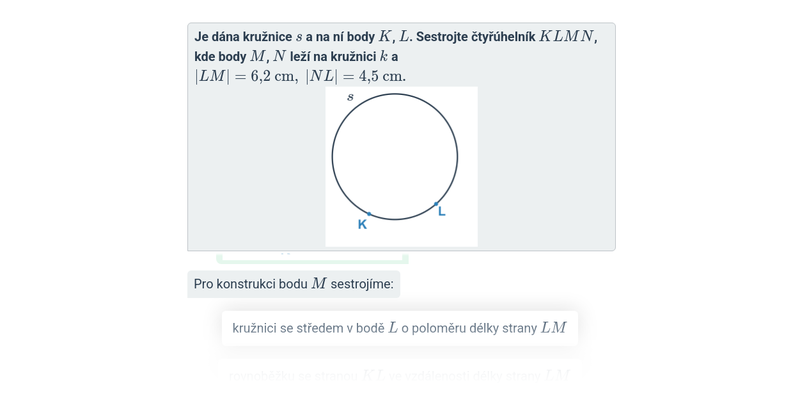
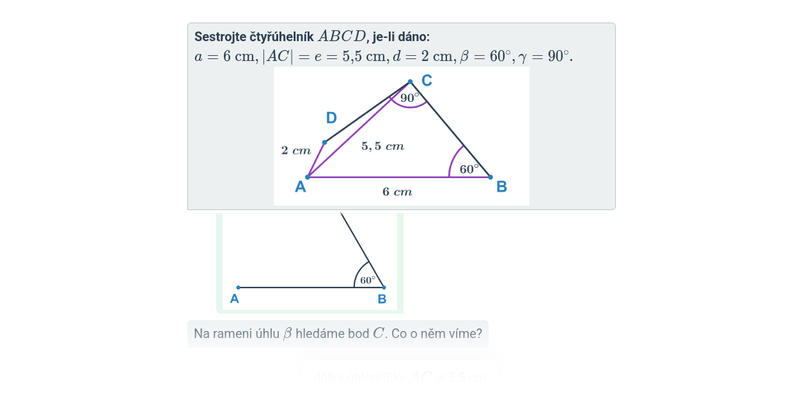
Konstrukce obecných čtyřúhelníků
Konstrukce čtyřúhelníků: mix
Konstrukční úlohy průřezově
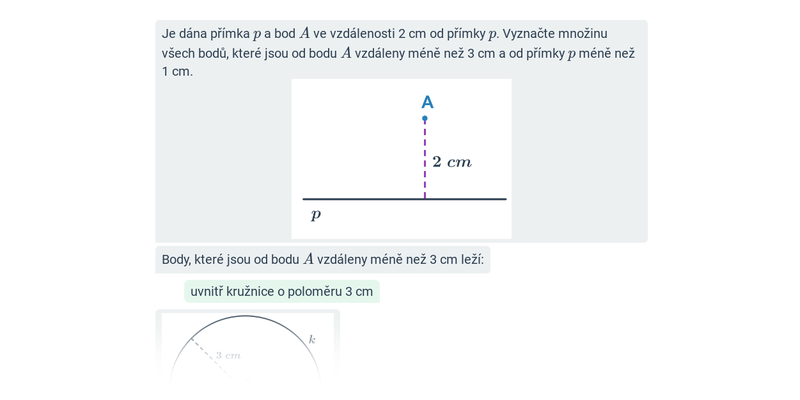
Konstrukce: osová a středová souměrnost
Analytická geometrie
Úsečky
Střed úsečky v rovině
Přímky
Přímky: mix
Elementární algebra
Úměrnosti
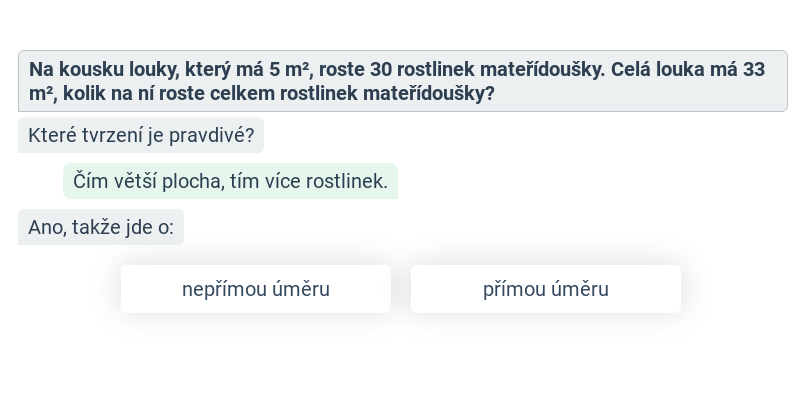
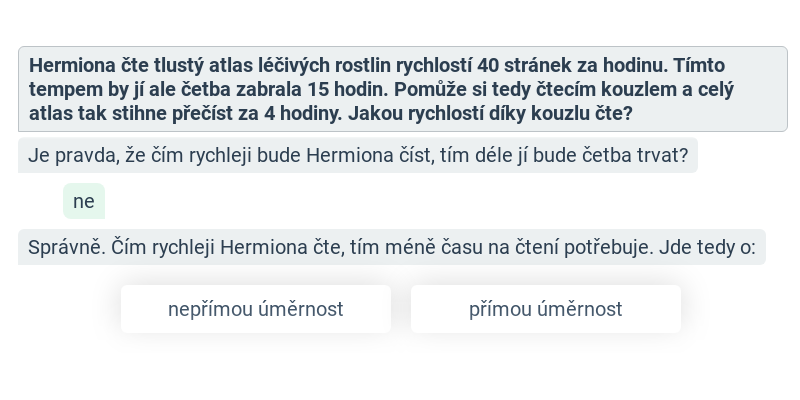
Přímá a nepřímá úměrnost
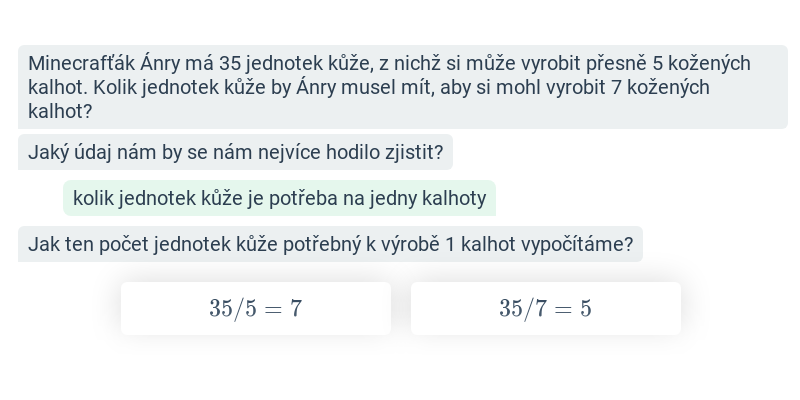
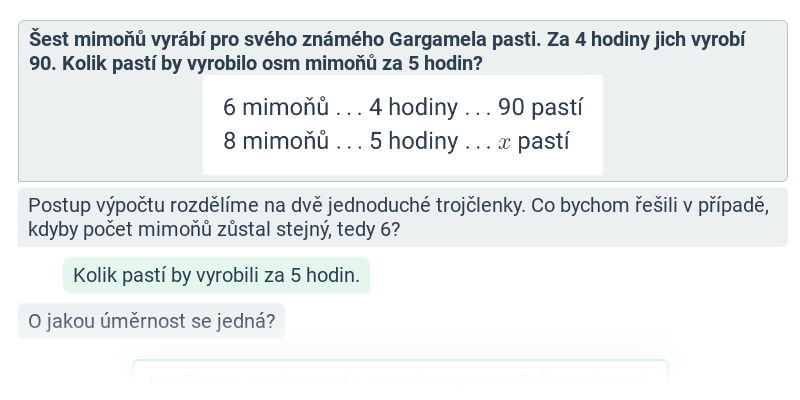
Trojčlenka
Úměrnosti: mix
Úměrnosti a trojčlenka: aplikace
Poměry
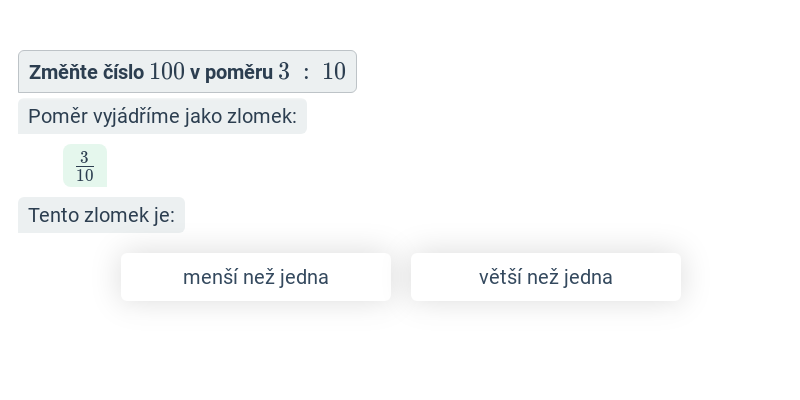
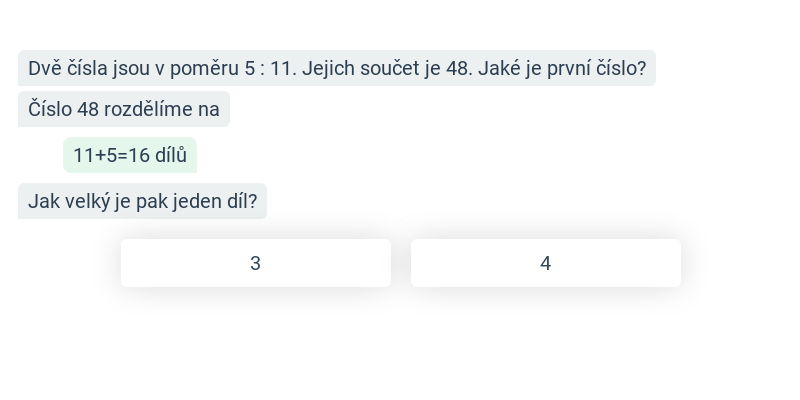
Poměry: změna a rozdělení čísla
Poměry: výpočty
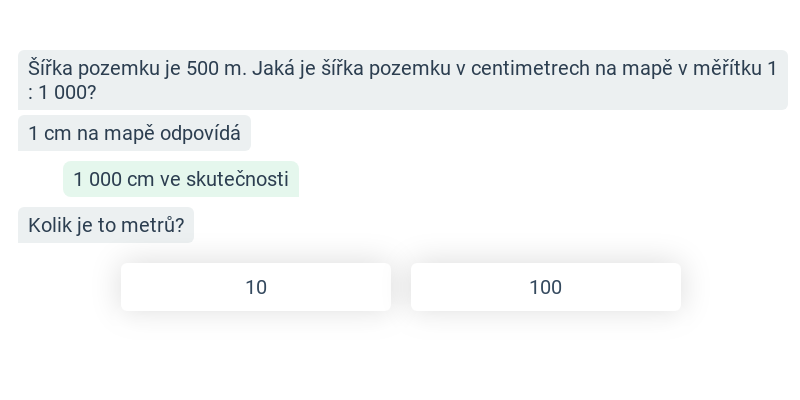
Poměry: měřítko mapy
Algebraické výrazy a jejich úpravy
Dosazování do výrazů
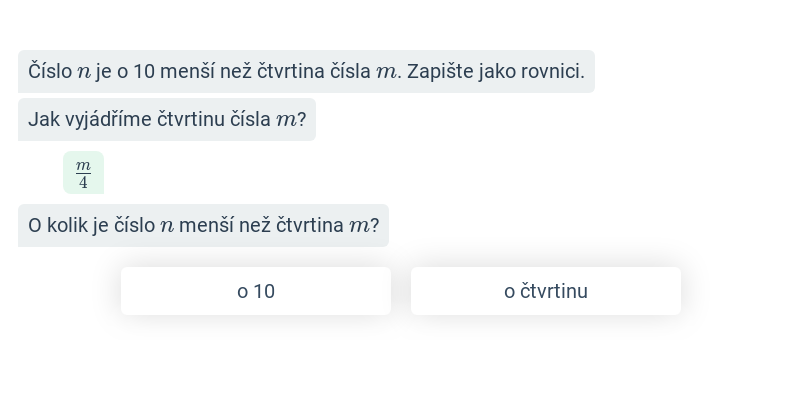
Zápis pomocí výrazů
Zápis výrazů s proměnnými
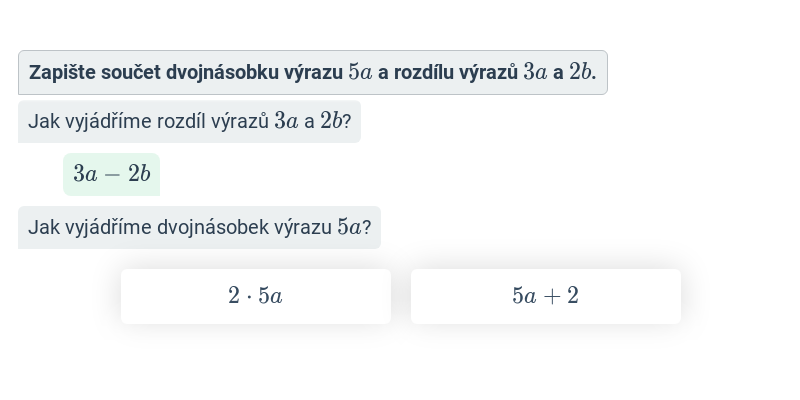
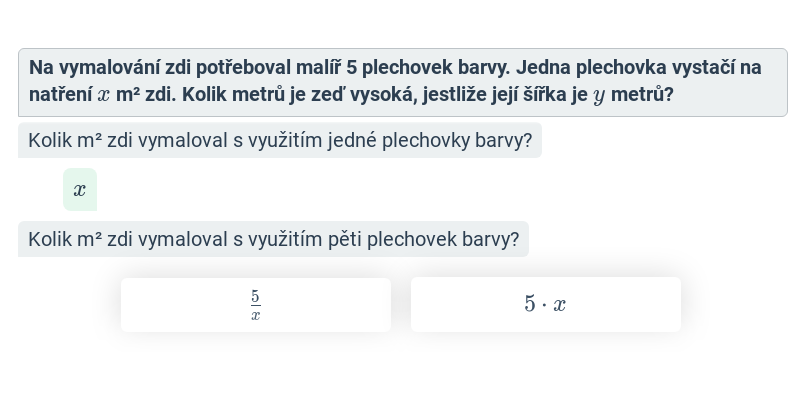
Zápis zadání pomocí výrazu
Úpravy výrazů s jednou proměnnou
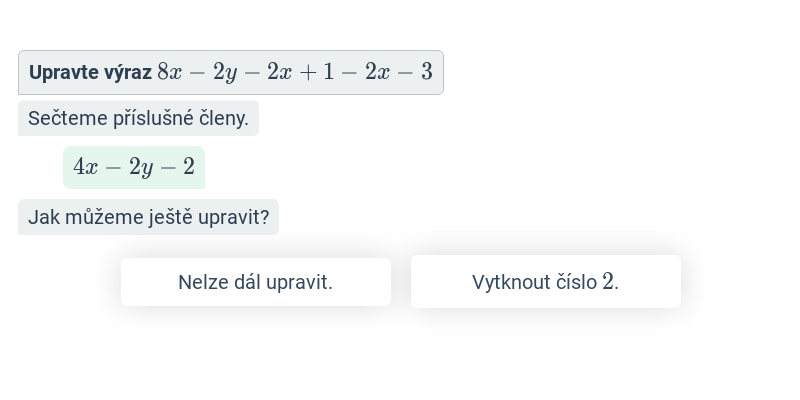
Úpravy výrazů s více proměnnými
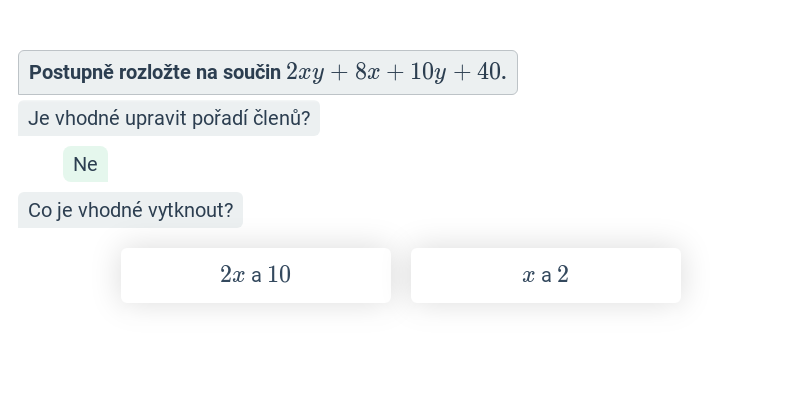
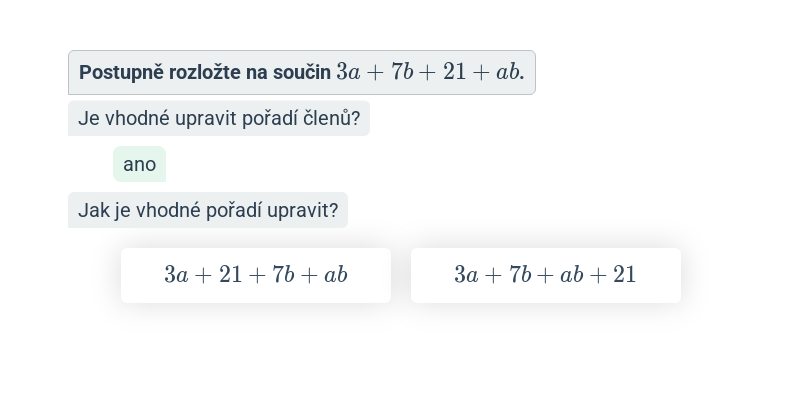
Rozklad na součin (postupné vytýkání)
Lomené výrazy
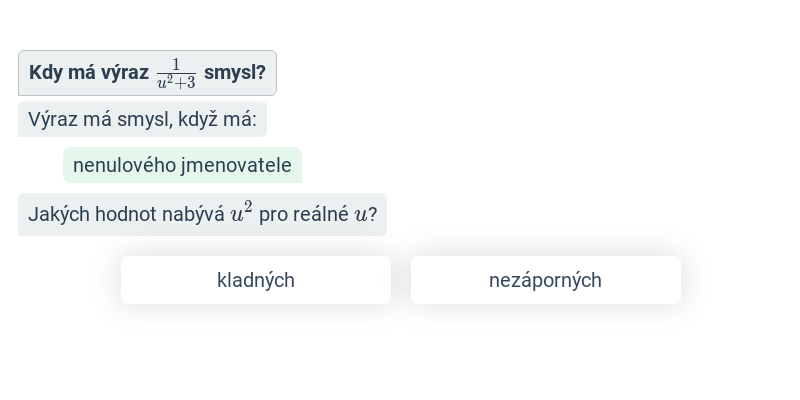
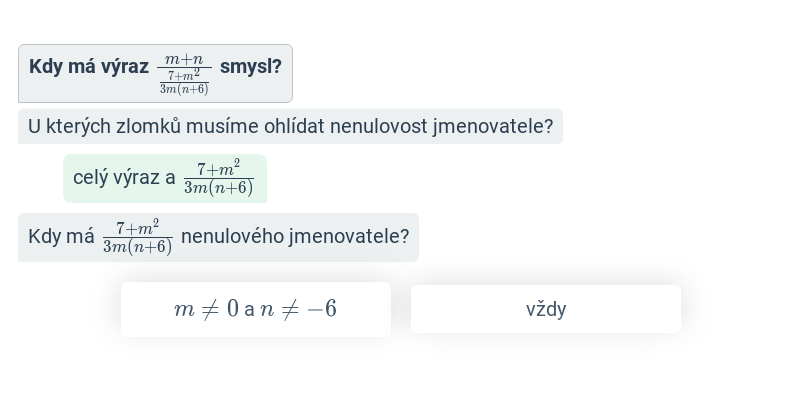
Podmínky lomených výrazů
Lomené výrazy: úpravy a výpočty
Početní operace s lomenými výrazy
Lomené výrazy: mix
Dělení mnohočlenu mnohočlenem
Dělení mnohočlenu jednočlenem
Rovnice
Základní rovnice s jednou neznámou
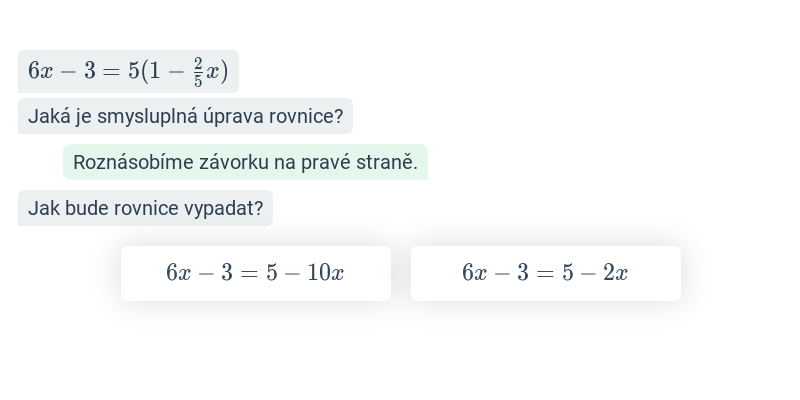
Rovnice se závorkami
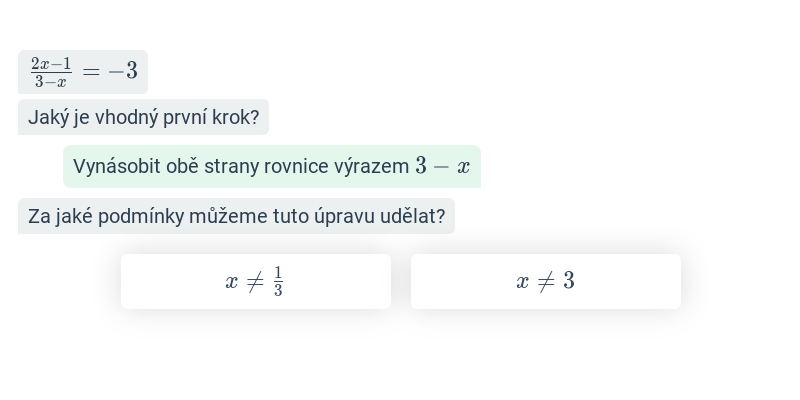
Rovnice s neznámou ve jmenovateli
Rovnice se zlomky
Pokročilé rovnice
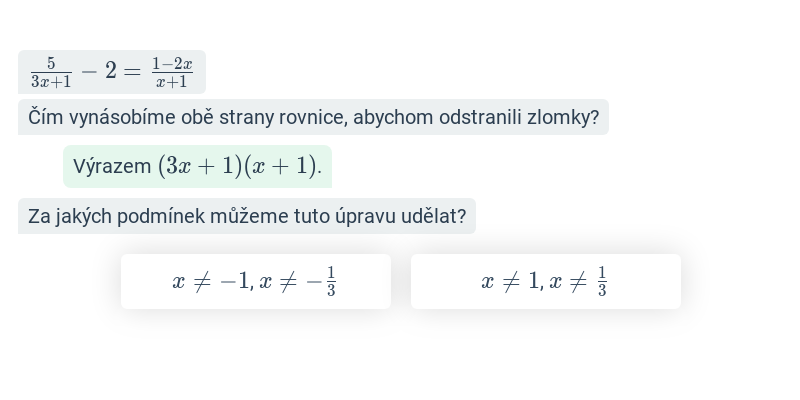
Rovnice s lomenými výrazy
Dvě rovnice o dvou neznámých
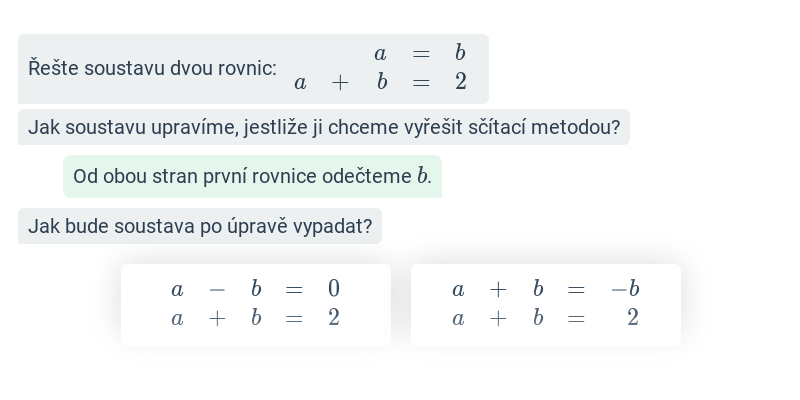
Soustava dvou rovnic: sčítací metoda řešení
Soustava dvou rovnic: dosazovací metoda řešení
Kvadratické rovnice
Ryze kvadratické rovnice
Kvadratické rovnice bez absolutního členu
Kvadratické rovnice: diskriminant
Kvadratické rovnice: Vietovy vzorce
Úlohy s rovnicemi
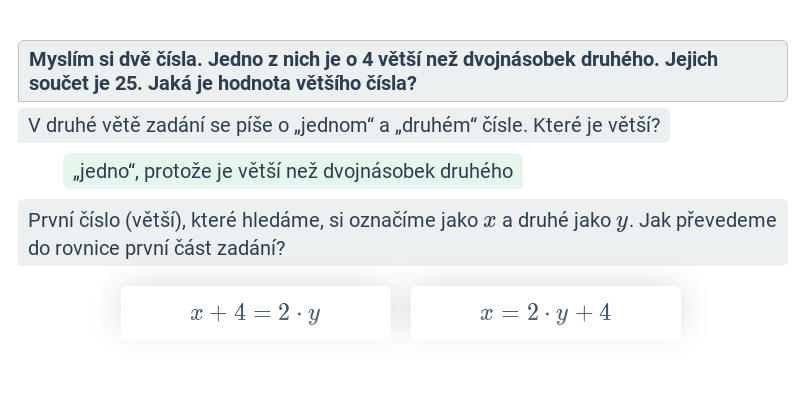
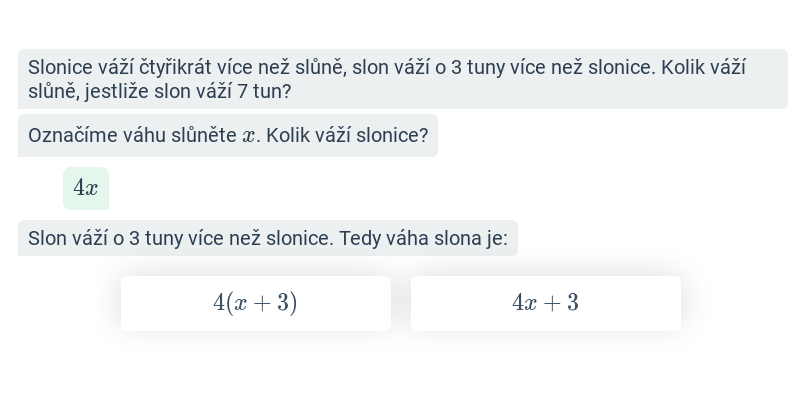
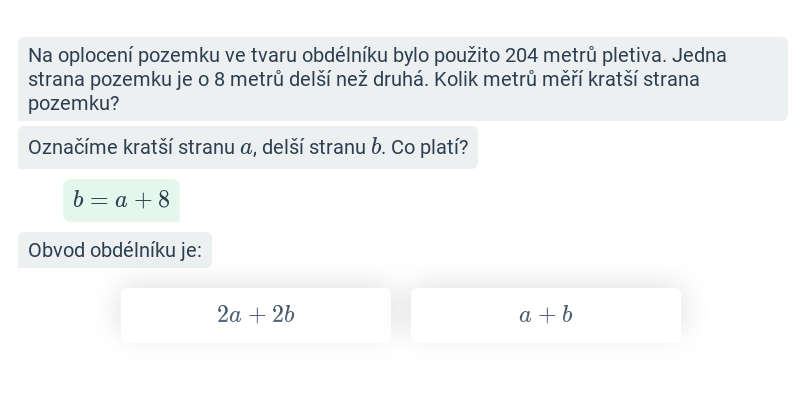
Zápis zadání pomocí rovnice
Myslím si číslo
Úlohy o směsích
Úlohy s rovnicemi: mix
Obecné slovní úlohy s rovnicemi
Nerovnice
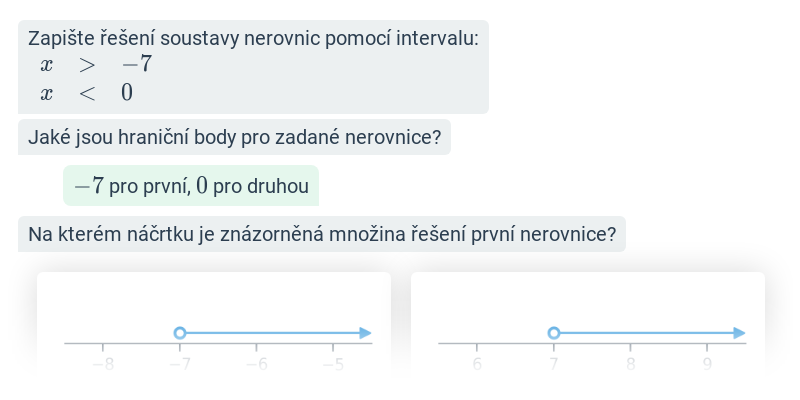
Nerovnice: zápis řešení
Nerovnice: ekvivalentní úpravy
Funkce
Grafy funkcí
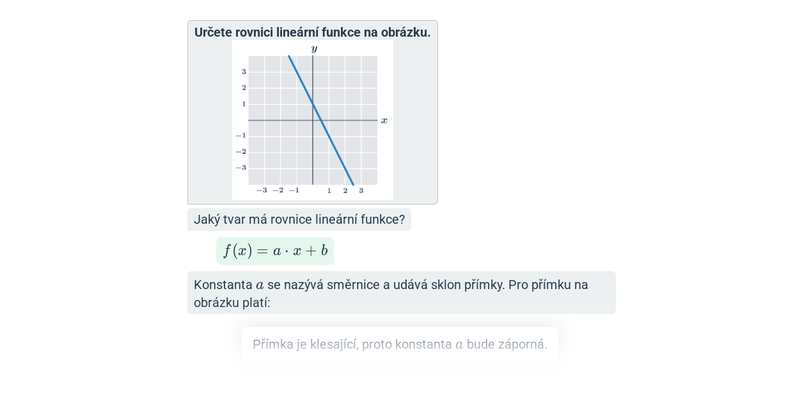
Grafy lineárních funkcí
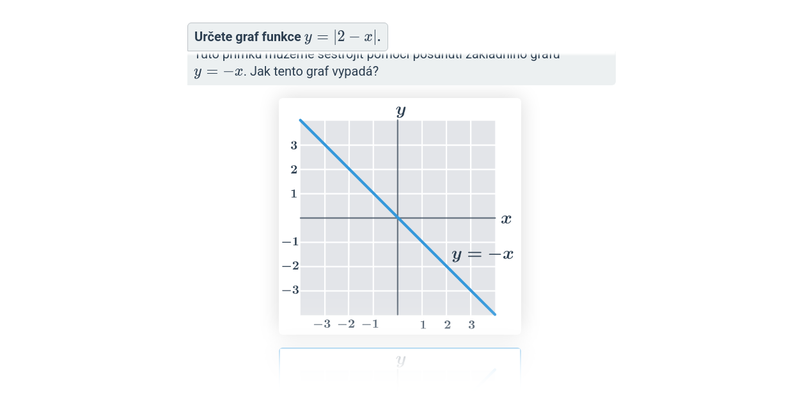
Grafy funkcí s absolutní hodnotou
Grafy funkcí s absolutními hodnotami výrazů
Goniometrické funkce
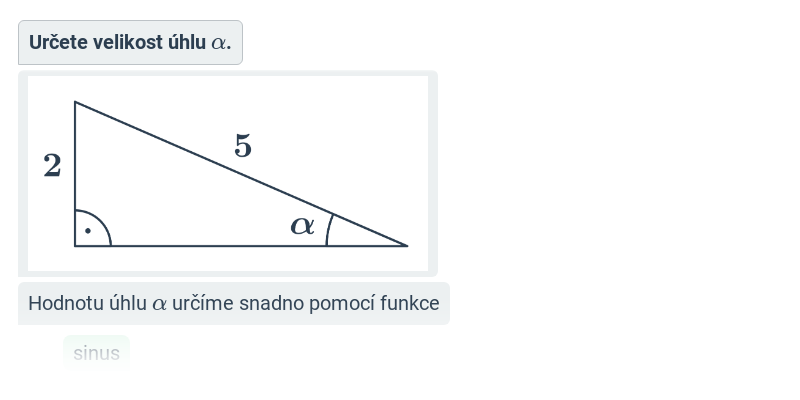
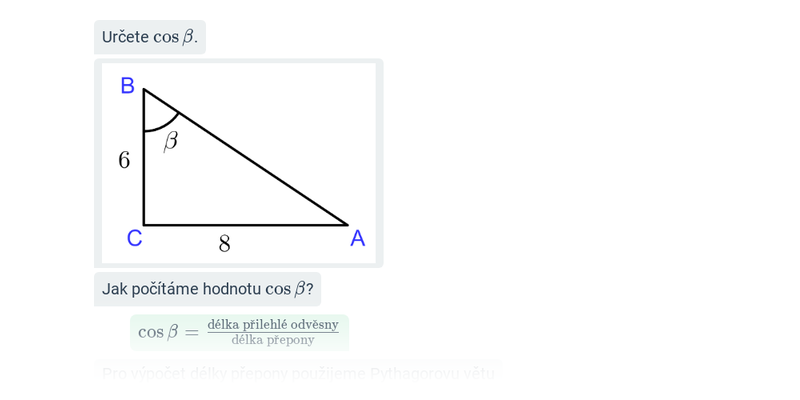
Goniometrické funkce a pravoúhlý trojúhelník
Jednotky, míry
Čas
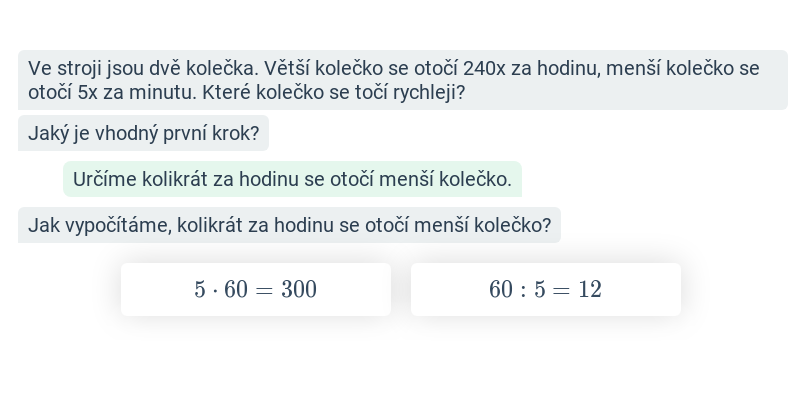
Jednotky času
Jednotky
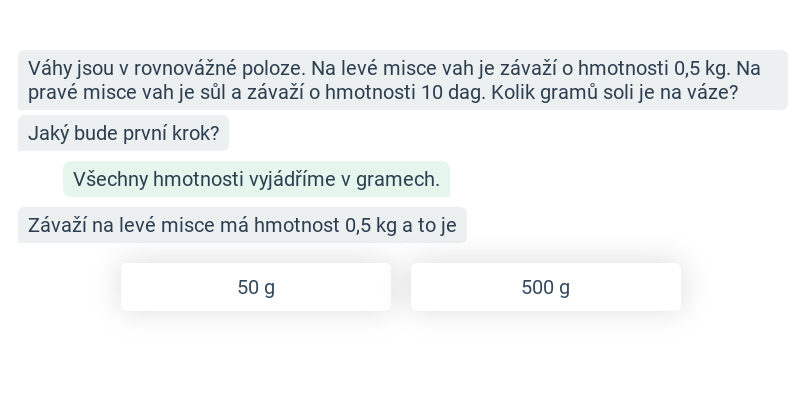
Jednotky hmotnosti
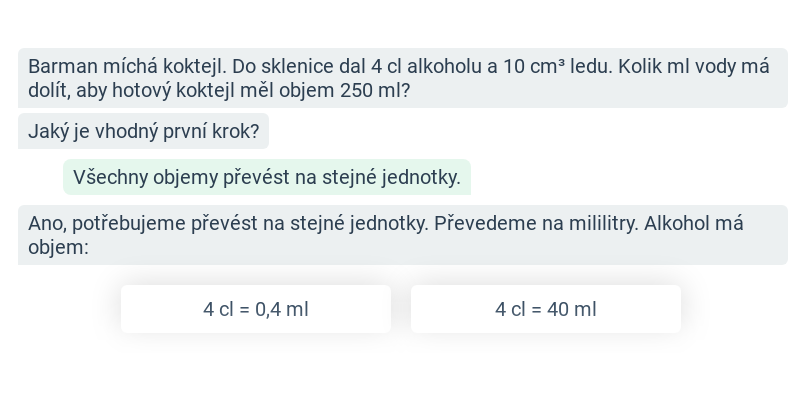
Jednotky objemu
Finanční gramotnost
Počítání s penězi
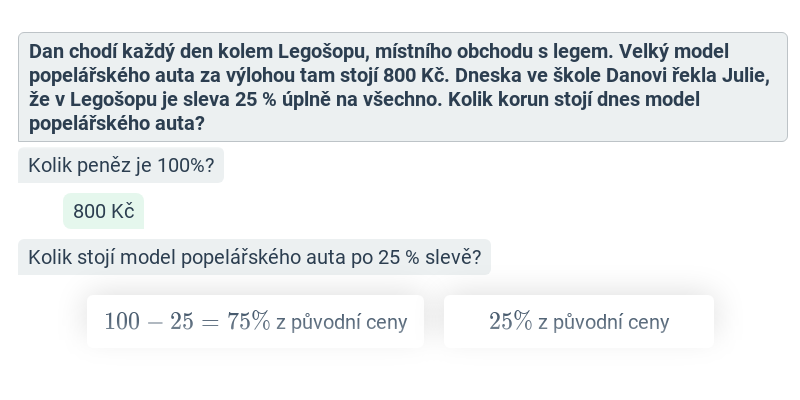
Peníze a procenta
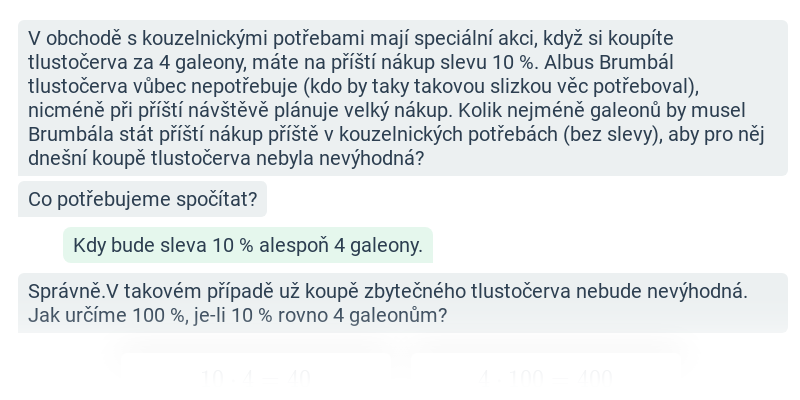
Sleva, daň, přirážka, jednoduchý úrok
Finanční pojmy a principy
Jednoduché úročení
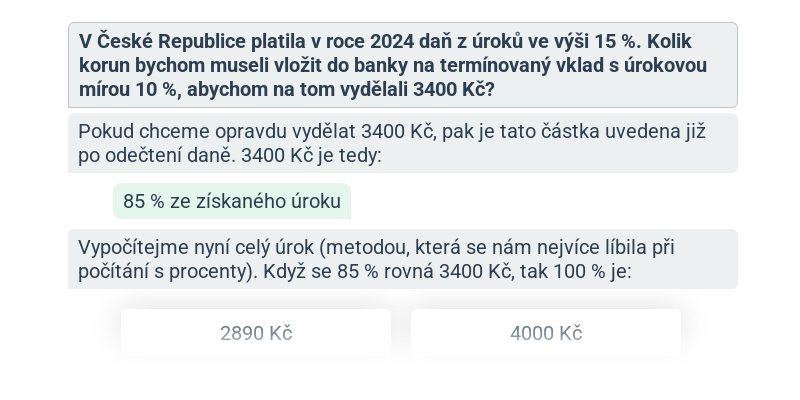
Jednoduché úročení: výpočty s daní
Složené úročení