Konstrukční úlohy: trojúhelníky
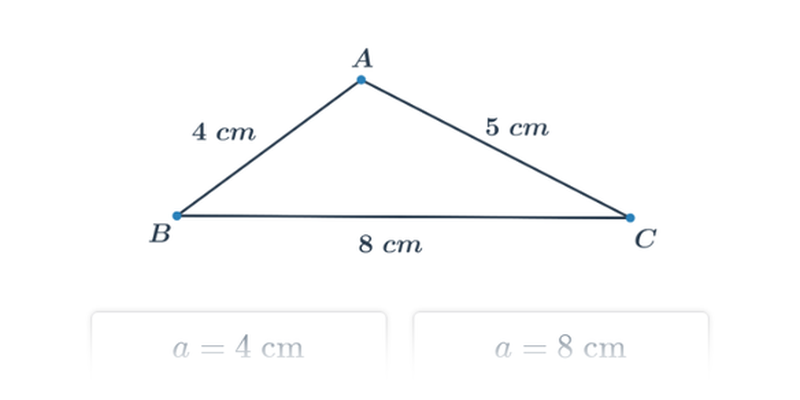
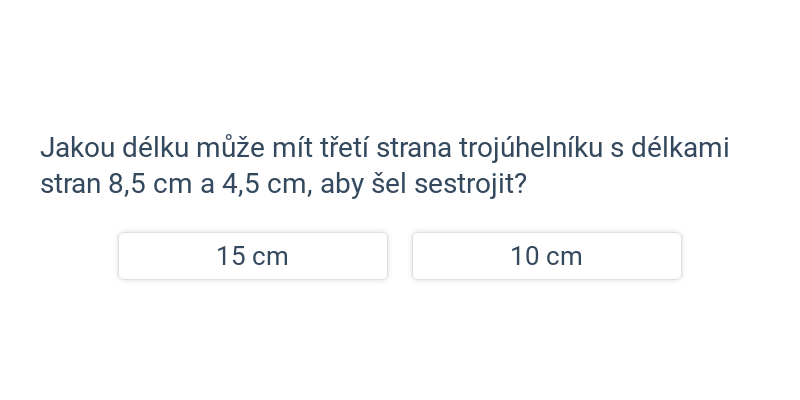
F2GPři řešení jednodušších úloh provádíme konstrukce trojúhelníků se známými délkami stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, jedině pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
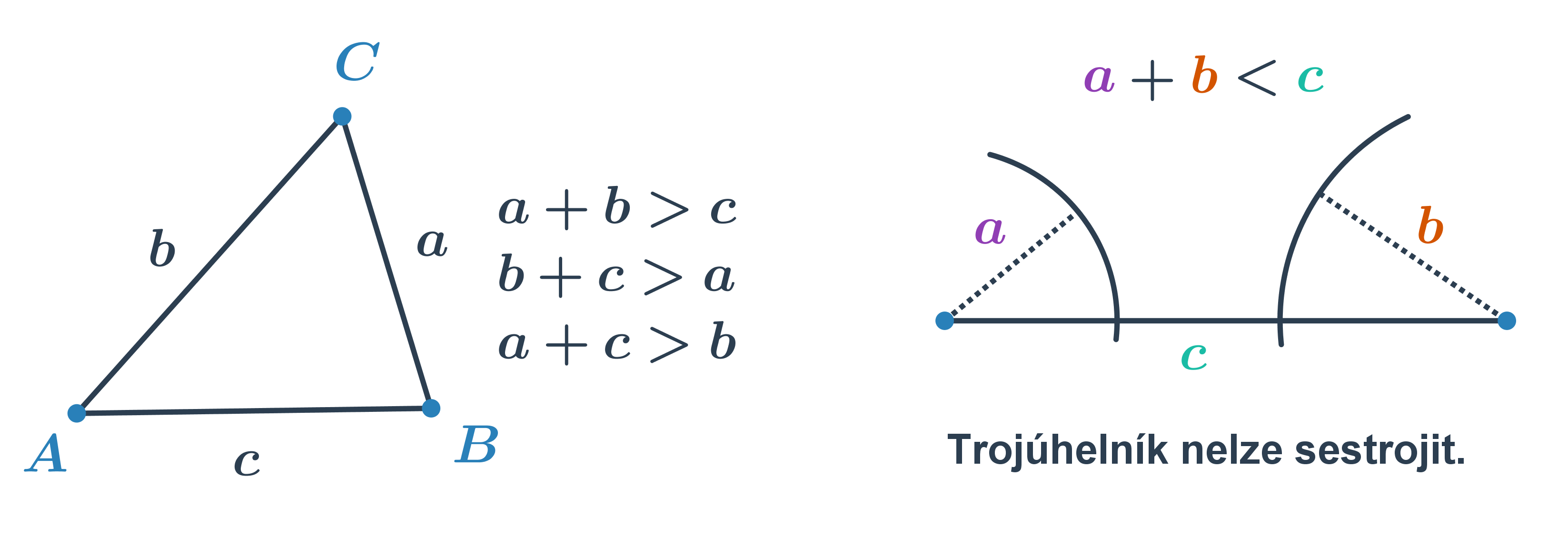
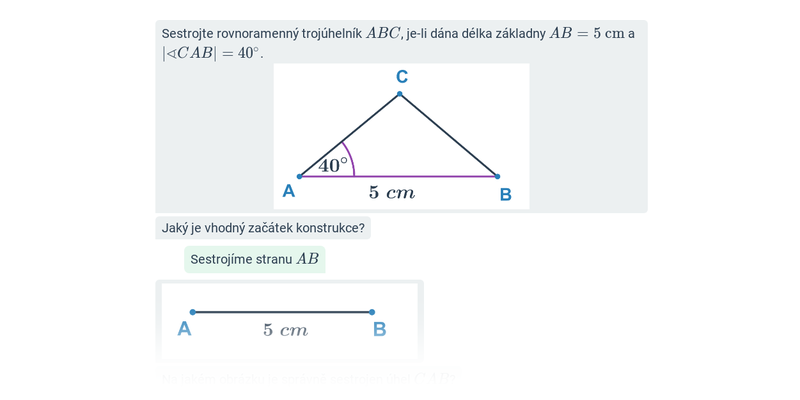
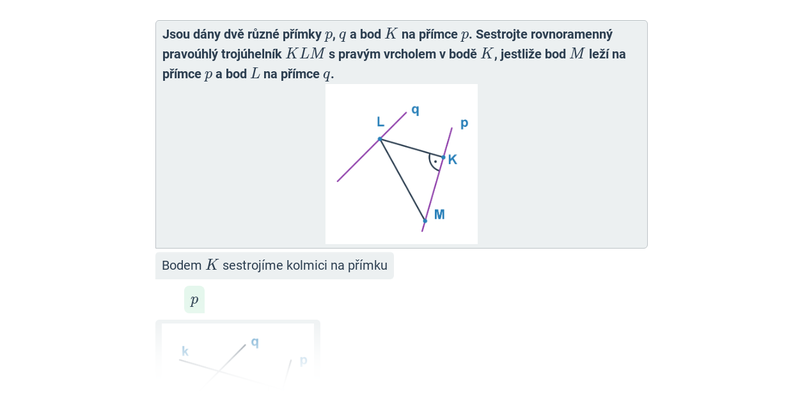
Občas má některý trojúhelník zajímavou vlastnost, která nám pomůže odvodit si potřebné informace k jeho sestrojení — může jít např. o konstrukci rovnoramenného nebo rovnostranného trojúhelníku.
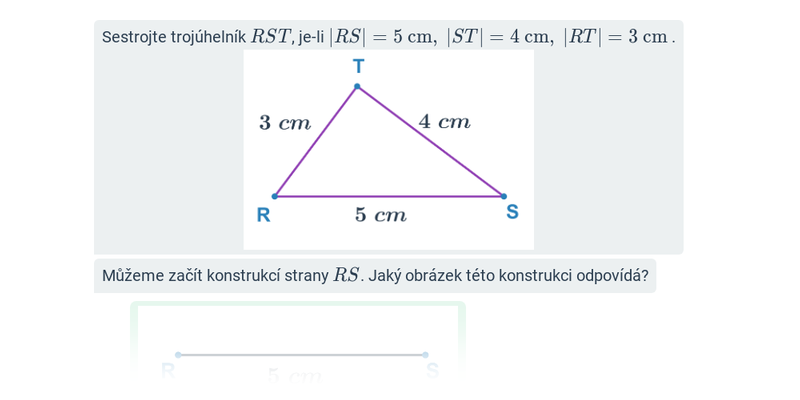
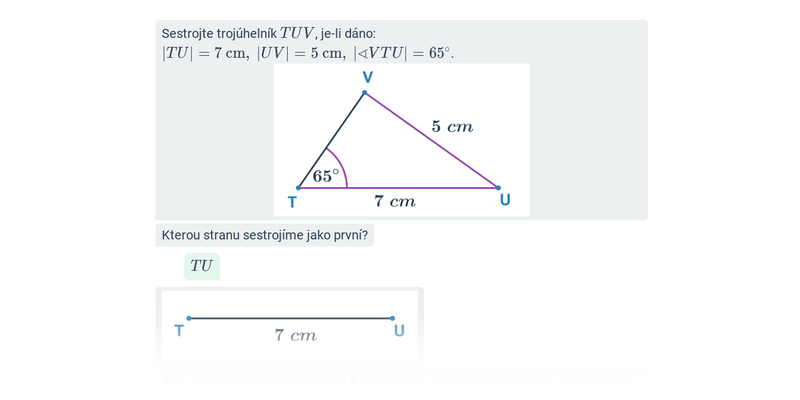
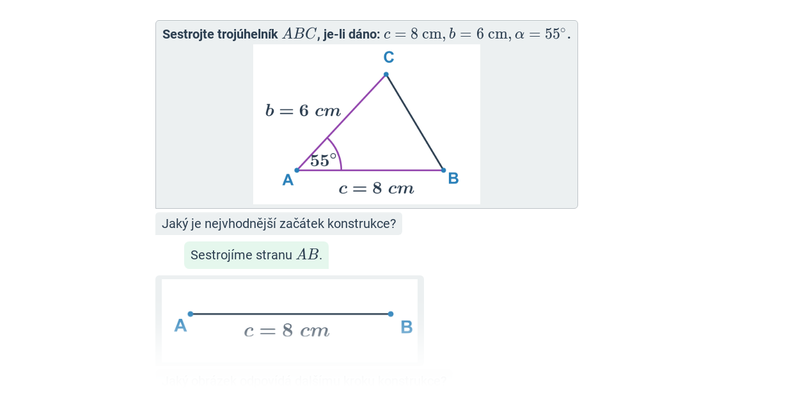
Při řešení složitějších příkladů provádíme konstrukci trojúhelníků podle vět sss, sus, usu, Ssu, využíváme přitom známé věty o sestrojitelnosti trojúhelníků.
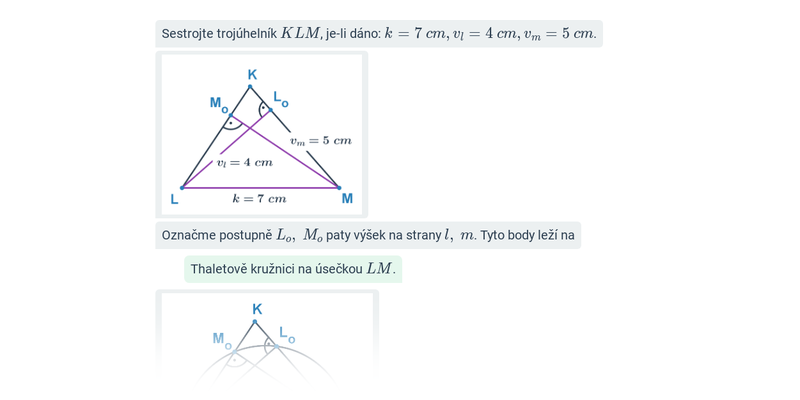
U nejtěžších příkladů, jako je konstrukce trojúhelníků, kdy známé údaje zahrnují těžnice, výšky, opsanou nebo vepsanou kružnici trojúhelníka využíváme při konstrukci další pojmy související s trojúhelníkem, či množiny bodů daných vlastností.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Mřížkovaná
Úloha na procvičení geometrie s jednoduchým ovládáním a zajímavými úlohami.