Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Porozumění
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Můj účet
Odhlásit se- Elementární algebra
Všechny souhrny
Filtr podle ročníku
Elementární algebra
FUBElementární algebra rozšiřuje aritmetiku („počítání s čísly“, např. 3+5\cdot8) o práci s neznámými veličinami (např. x-4\cdot y). Tato oblast má uplatnění nejen v mnoha dalších částech matematiky, ale je klíčová třeba i pro porozumění fyzice.
| téma | ukázky pojmů a příkladů |
|---|---|
| Úměrnosti | přímá a nepřímá úměrnost, trojčlenka |
| Poměry | měřítko mapy, poměry surovin v jídle |
| Algebraické výrazy a jejich úpravy | 3x - (x+2), (a+b)^2 |
| Rovnice | 4x + 3 = 27 |
| Pokročilé rovnice | 2x^2+6x=20 |
| Úlohy s rovnicemi | úlohy o směsích, společná práce |
| Nerovnice | 2x + 5 \leq 8 |
| Posloupnosti a řady | aritmetická a geometrická posloupnost |
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Trojčlenka (střední) • GUW
zadání: 10
Typicky zabere: 6 min
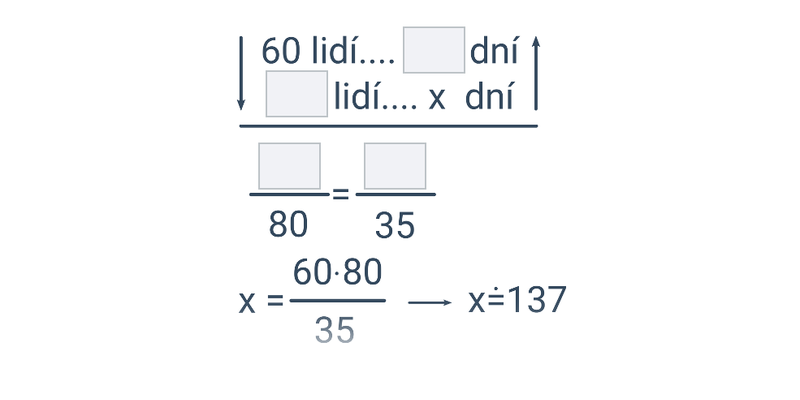
Poměry: základy (lehké) • FR7
zadání: 15
Typicky zabere: 5 min
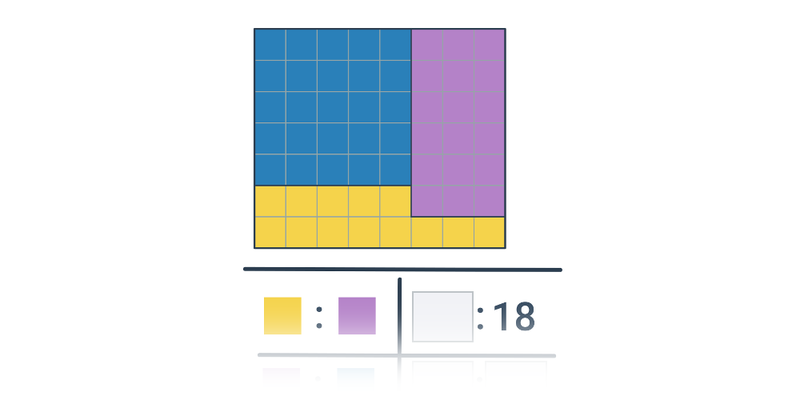
Poměry: základy (střední) • FPM
zadání: 33
Typicky zabere: 6 min
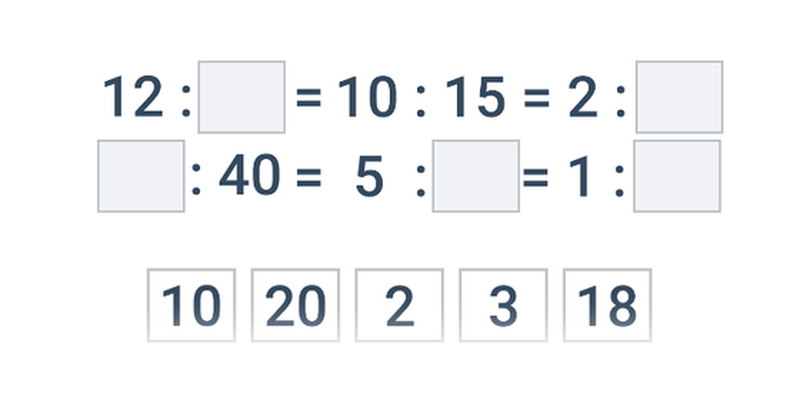
Úpravy výrazů s jednou proměnnou (střední) • FG6
zadání: 12
Typicky zabere: 5 min
Lomené výrazy: mix (střední) • GX9
zadání: 16
Typicky zabere: 5 min
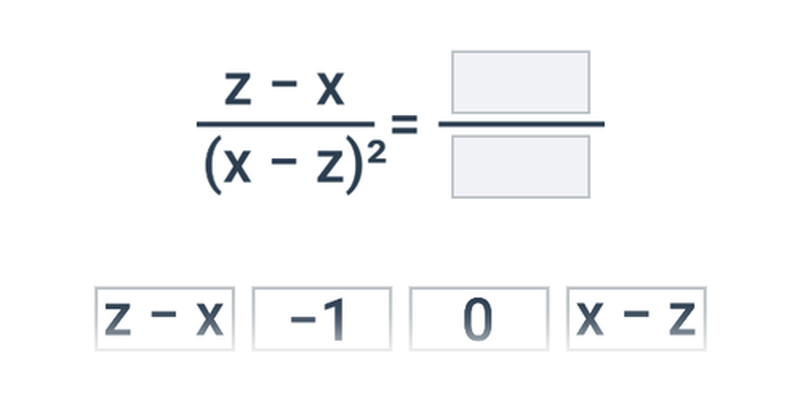
Lomené výrazy: mix (těžké) • FGK
zadání: 16
Typicky zabere: 6 min
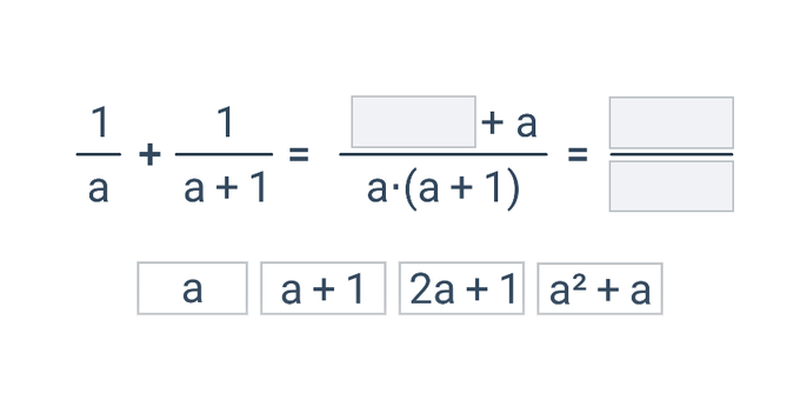
Základní rovnice s jednou neznámou (lehké) • GWF
zadání: 10
Typicky zabere: 4 min
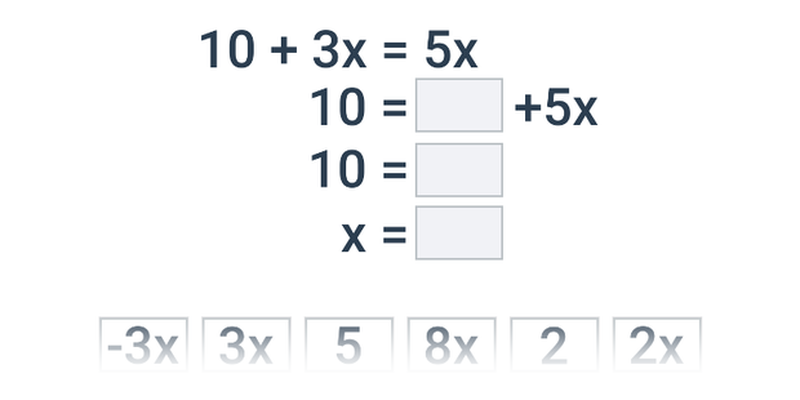
Kvadratické rovnice (těžké) • FKD
zadání: 7
Typicky zabere: 7 min
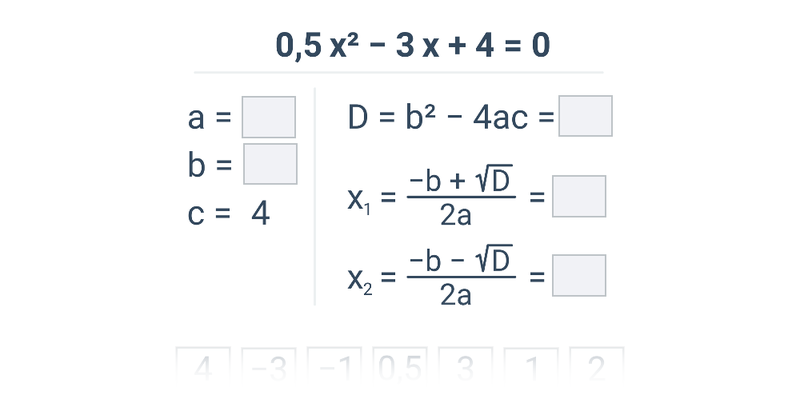
Nerovnice s absolutní hodnotou (střední) • F7N
zadání: 10
Typicky zabere: 6 min
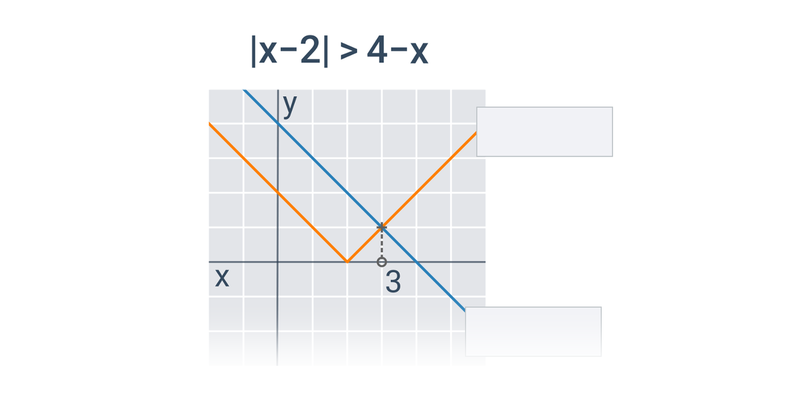
Kvadratické nerovnice (těžké) • FT4
zadání: 10
Typicky zabere: 6 min
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Přímá a nepřímá úměrnost (střední) • FOS
zadání: 30
Typicky zabere: 8 min
Přímá a nepřímá úměrnost (těžké) • GX6
zadání: 44
Typicky zabere: 8 min
Trojčlenka (střední) • FTJ
zadání: 60
Typicky zabere: 8 min
Poměry: základy (lehké) • FOV
zadání: 50
Typicky zabere: 5 min
Poměry: základy (střední) • FNU
zadání: 51
Typicky zabere: 7 min
Poměry: základy (těžké) • FOL
zadání: 44
Typicky zabere: 11 min
Poměry: změna a rozdělení čísla (střední) • FTT
zadání: 30
Typicky zabere: 8 min
Poměry: změna a rozdělení čísla (těžké) • FTU
zadání: 30
Typicky zabere: 9 min
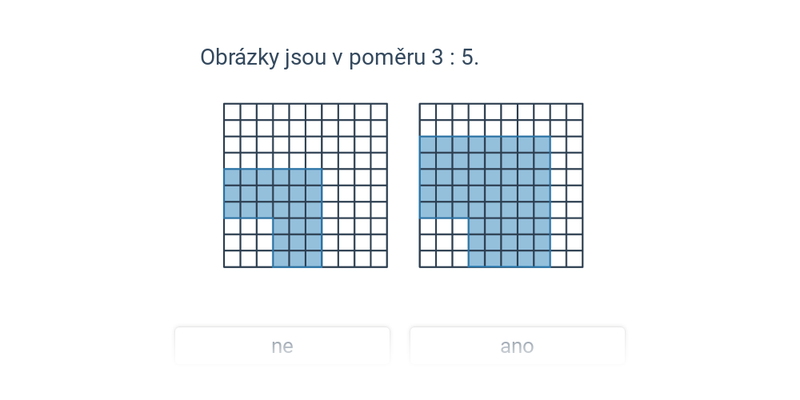
Poměry: výpočty (střední) • FTM
zadání: 58
Typicky zabere: 9 min
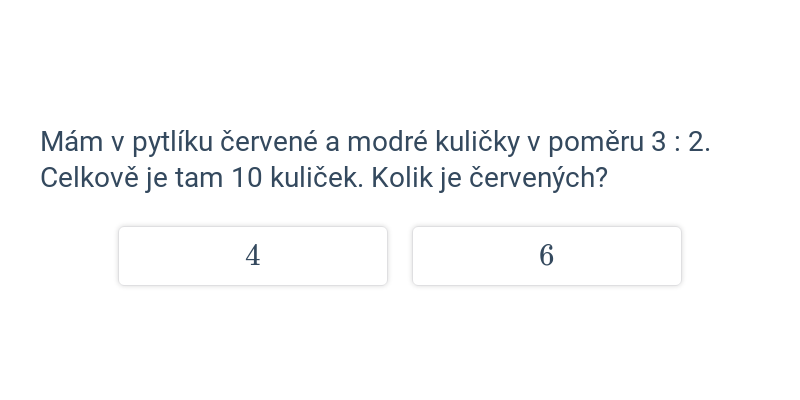
Poměry: výpočty (těžké) • FTN
zadání: 56
Typicky zabere: 10 min
Dosazování do výrazů (lehké) • GVW
zadání: 32
Typicky zabere: 6 min
Dosazování do výrazů (střední) • EL6
zadání: 36
Typicky zabere: 9 min
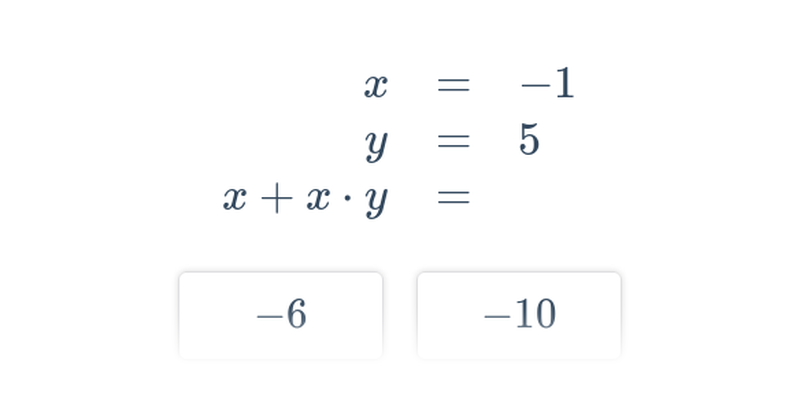
Dosazování do výrazů (těžké) • GG3
zadání: 51
Typicky zabere: 9 min
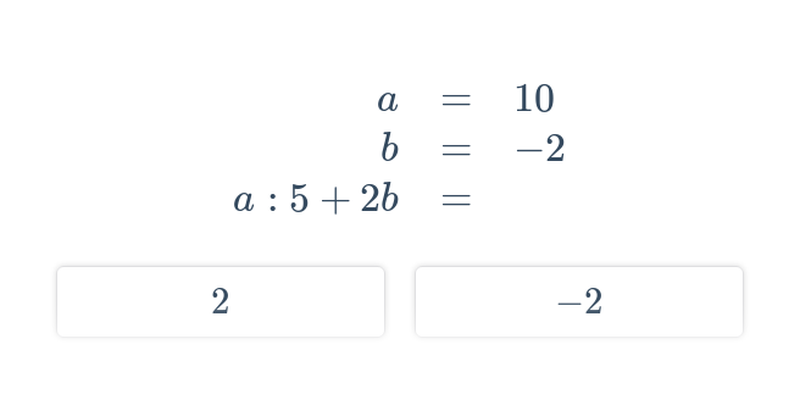
Zápis výrazů s proměnnými (střední) • FOH
zadání: 69
Typicky zabere: 7 min
Zápis výrazů s proměnnými (těžké) • FTA
zadání: 51
Typicky zabere: 9 min
Zápis zadání pomocí výrazu (střední) • FOJ
zadání: 61
Typicky zabere: 9 min
Zápis zadání pomocí výrazu (těžké) • FTB
zadání: 76
Typicky zabere: 12 min
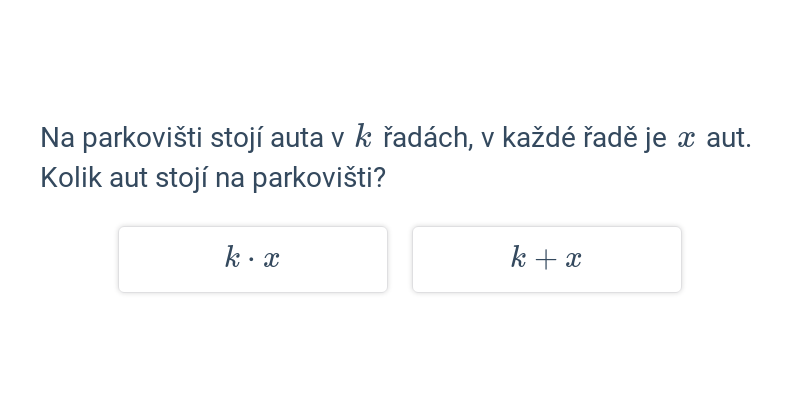
Úpravy výrazů s jednou proměnnou (lehké) • FBJ
zadání: 68
Typicky zabere: 5 min
Úpravy výrazů s jednou proměnnou (střední) • EJT
zadání: 74
Typicky zabere: 7 min
Úpravy výrazů s jednou proměnnou (těžké) • ELX
zadání: 114
Typicky zabere: 9 min
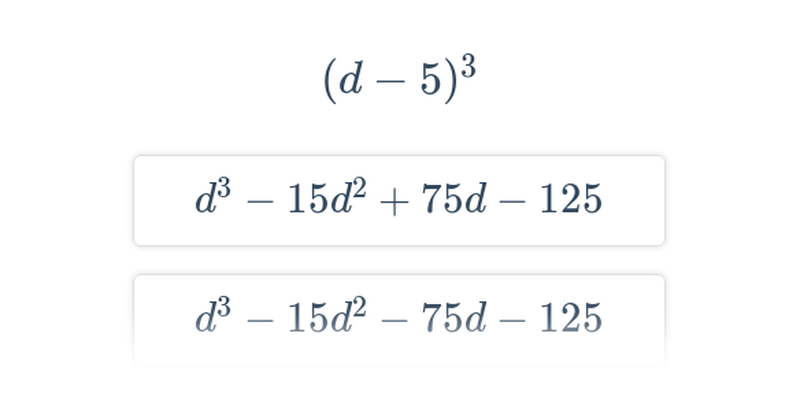
Úpravy výrazů s více proměnnými (střední) • FHB
zadání: 44
Typicky zabere: 7 min
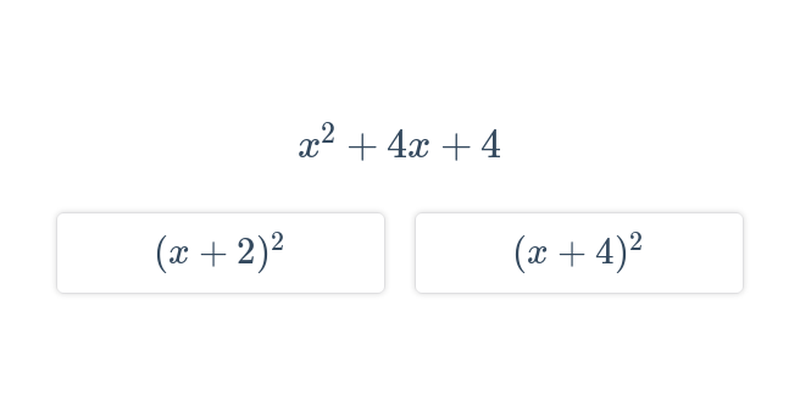
Úpravy výrazů s více proměnnými (těžké) • EFM
zadání: 46
Typicky zabere: 8 min
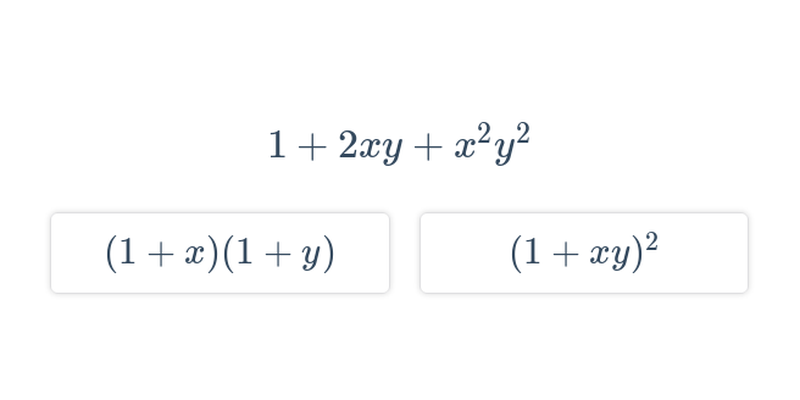
Úpravy výrazů: vnořené mocniny (těžké) • E2K
zadání: 50
Typicky zabere: 7 min
Rozklad na součin (těžké) • ENC
zadání: 30
Typicky zabere: 8 min
Úpravy výrazů se zlomky (střední) • EJS
zadání: 60
Typicky zabere: 7 min
Podmínky lomených výrazů (lehké) • GTZ
zadání: 24
Typicky zabere: 4 min
Podmínky lomených výrazů (střední) • GT1
zadání: 27
Typicky zabere: 5 min
Podmínky lomených výrazů (těžké) • EJV
zadání: 37
Typicky zabere: 8 min
Úpravy lomených výrazů (střední) • FHO
zadání: 45
Typicky zabere: 7 min
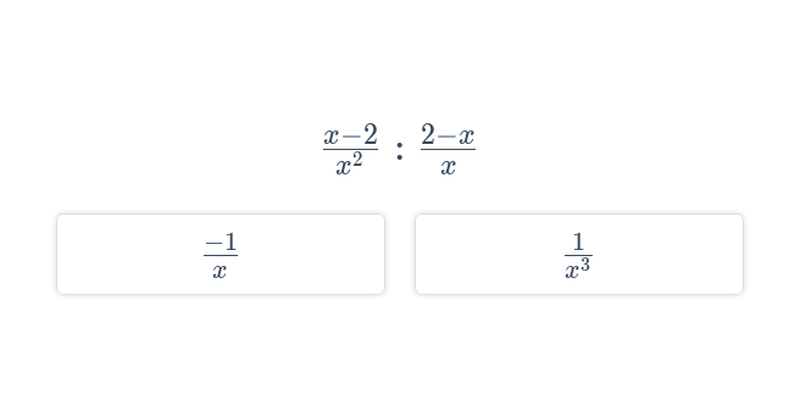
Úpravy lomených výrazů (těžké) • EJU
zadání: 63
Typicky zabere: 10 min
Úpravy výrazů s faktoriálem (těžké) • EJW
zadání: 24
Typicky zabere: 8 min
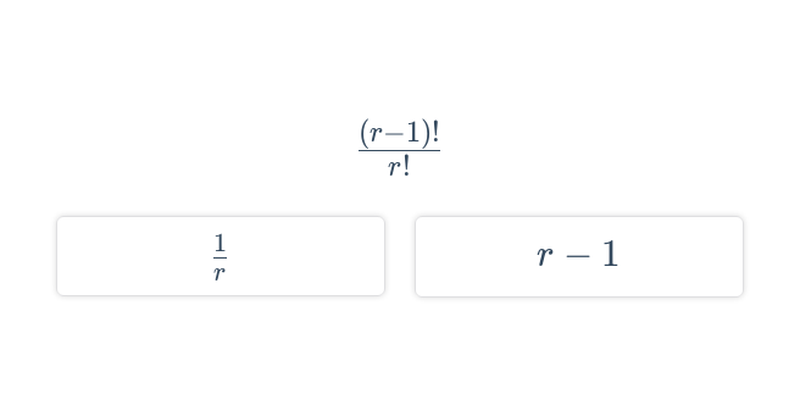
Úpravy výrazů s kombinačním číslem (těžké) • EJX
zadání: 30
Typicky zabere: 6 min
Výrazy a jejich úpravy: mix (střední) • ERE
zadání: 237
Typicky zabere: 8 min
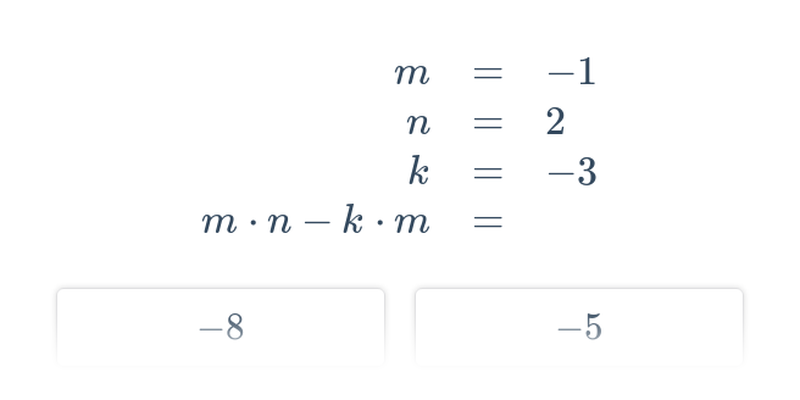
Výrazy a jejich úpravy: mix (těžké) • ERF
zadání: 272
Typicky zabere: 10 min
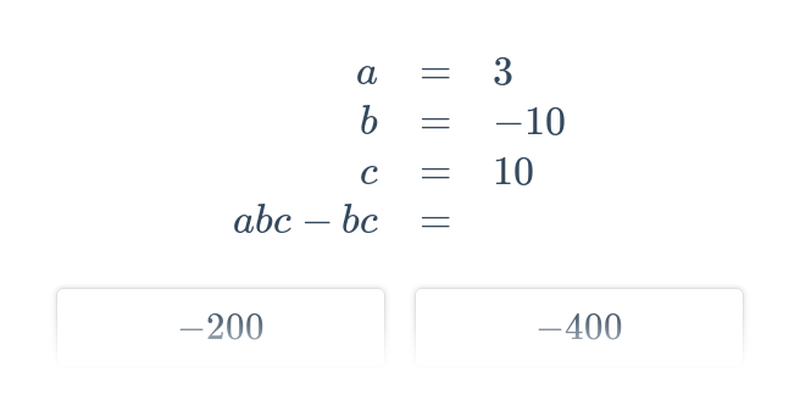
Sčítací a dosazovací metoda řešení (střední) • GJH
zadání: 53
Typicky zabere: 7 min
Zápis zadání pomocí rovnice (lehké) • GOH
zadání: 30
Typicky zabere: 7 min
Zápis zadání pomocí rovnice (střední) • FOG
zadání: 130
Typicky zabere: 12 min
Nerovnice: zápis řešení (střední) • FTH
zadání: 30
Typicky zabere: 6 min
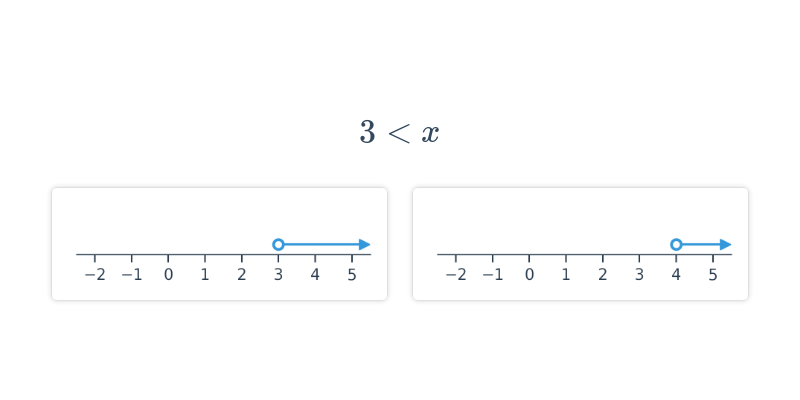
Nerovnice: ekvivalentní úpravy (střední) • FT1
zadání: 40
Typicky zabere: 6 min
Aritmetická a geometrická posloupnost (těžké) • E2H
zadání: 31
Typicky zabere: 5 min
Zápis posloupností (těžké) • E19
zadání: 46
Typicky zabere: 10 min
Pexeso
Hledání dvojic, které k sobě patří.
Úpravy výrazů s jednou proměnnou (lehké) • FPV
zadání: 12
Typicky zabere: 6 min
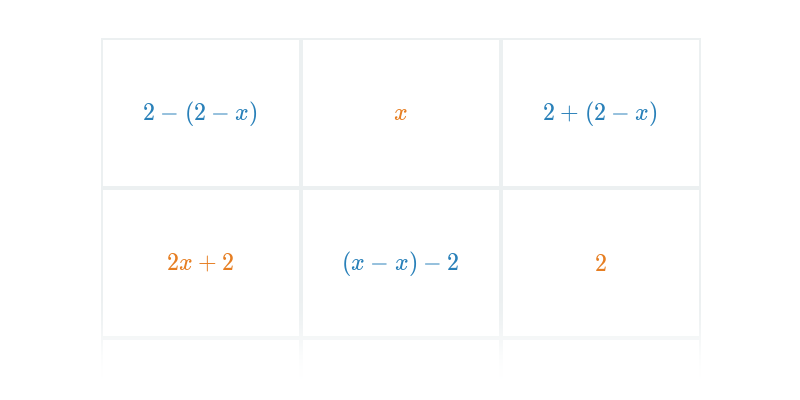
Úpravy výrazů s jednou proměnnou (střední) • E9W
zadání: 11
Typicky zabere: 5 min
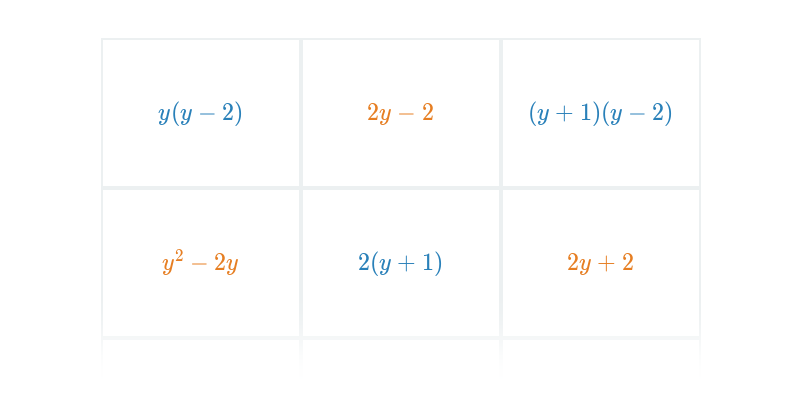
Úpravy výrazů s více proměnnými (lehké) • FPW
zadání: 10
Typicky zabere: 6 min
Úpravy výrazů s více proměnnými (střední) • EBZ
zadání: 12
Typicky zabere: 6 min
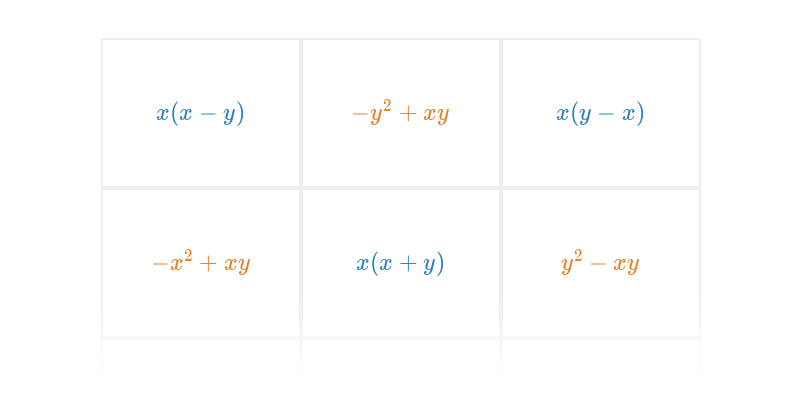
Lomené výrazy: mix (těžké) • E9X
zadání: 11
Typicky zabere: 5 min
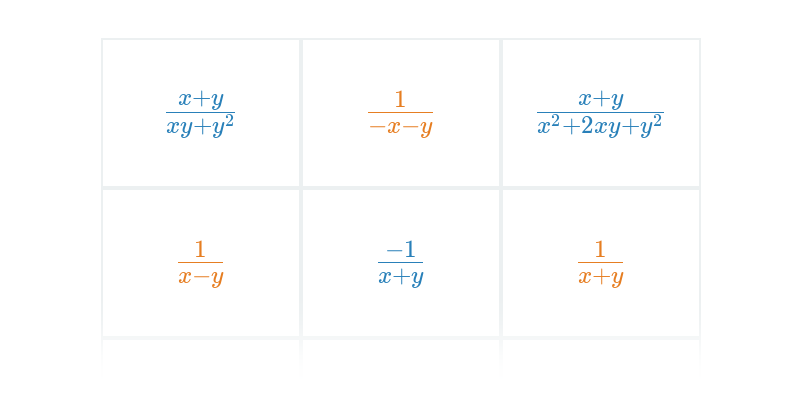
Základní rovnice s jednou neznámou (lehké) • FJ4
zadání: 13
Typicky zabere: 3 min
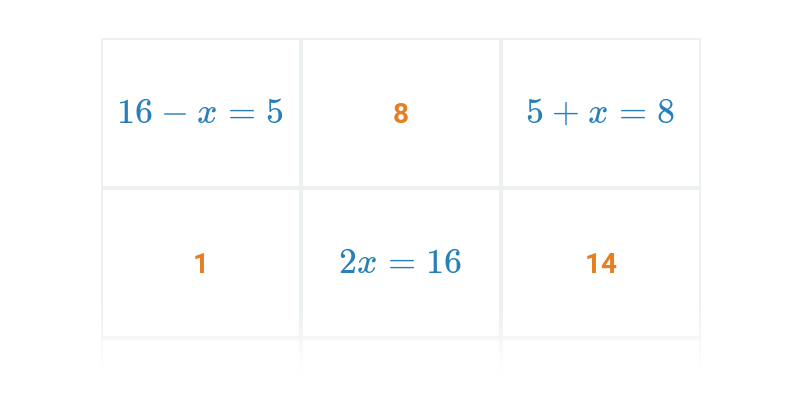
Základní rovnice s jednou neznámou (střední) • FAJ
zadání: 8
Typicky zabere: 5 min
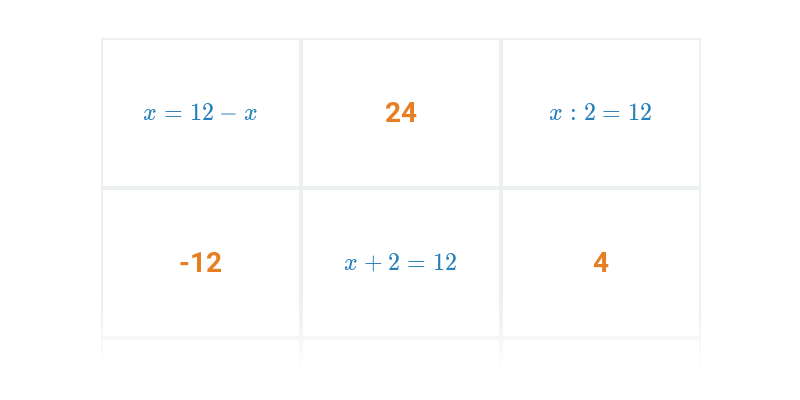
Základní rovnice s jednou neznámou (těžké) • FPU
zadání: 10
Typicky zabere: 5 min
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Přímá a nepřímá úměrnost (střední) • FBE
zadání: 20
Typicky zabere: 11 min
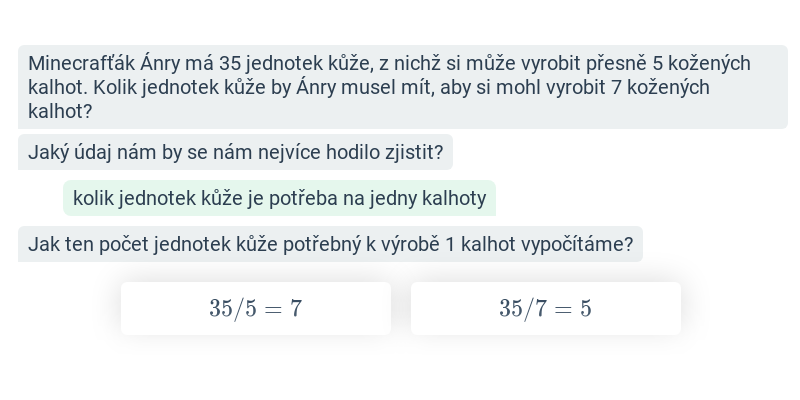
Přímá a nepřímá úměrnost (těžké) • GT9
zadání: 20
Typicky zabere: 10 min
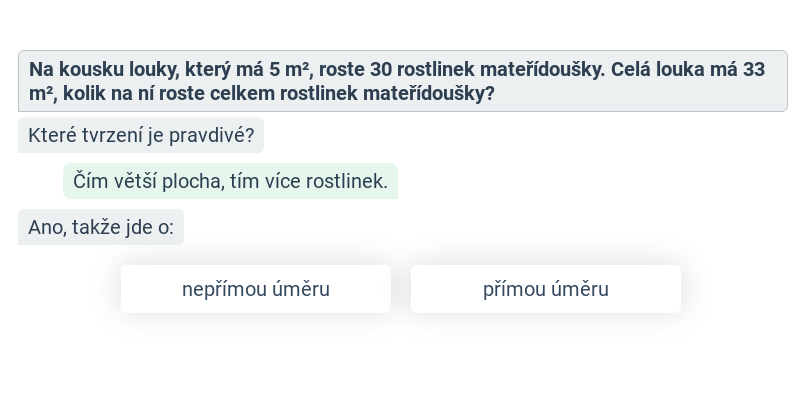
Trojčlenka (střední) • GUE
zadání: 20
Typicky zabere: 9 min
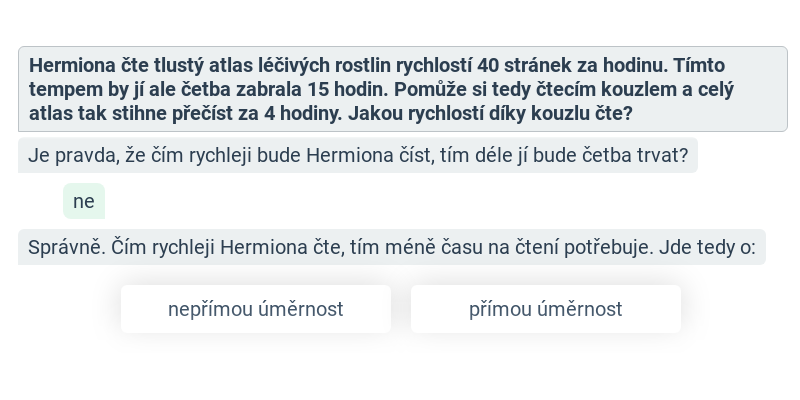
Úměrnosti a trojčlenka: aplikace (střední) • GUF
zadání: 10
Typicky zabere: 10 min
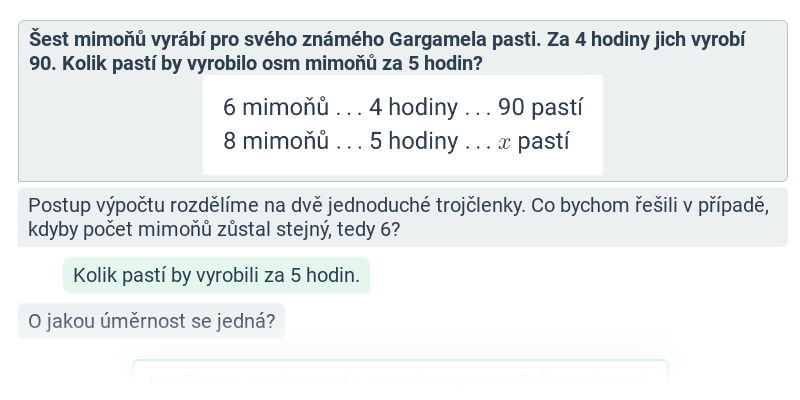
Poměry: změna a rozdělení čísla (střední) • F9B
zadání: 15
Typicky zabere: 6 min
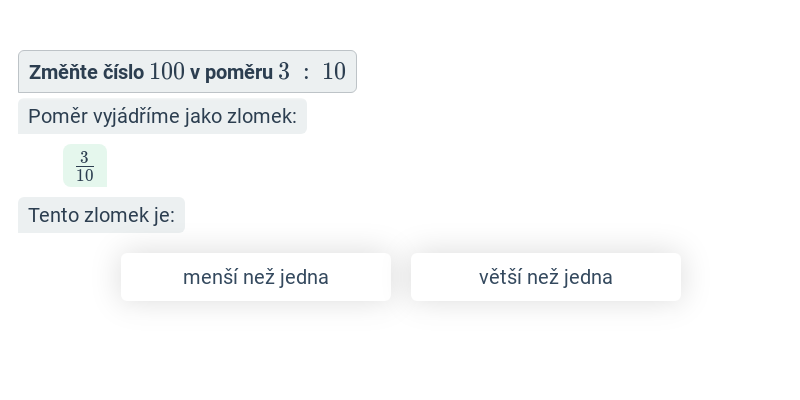
Poměry: výpočty (střední) • FN6
zadání: 25
Typicky zabere: 11 min
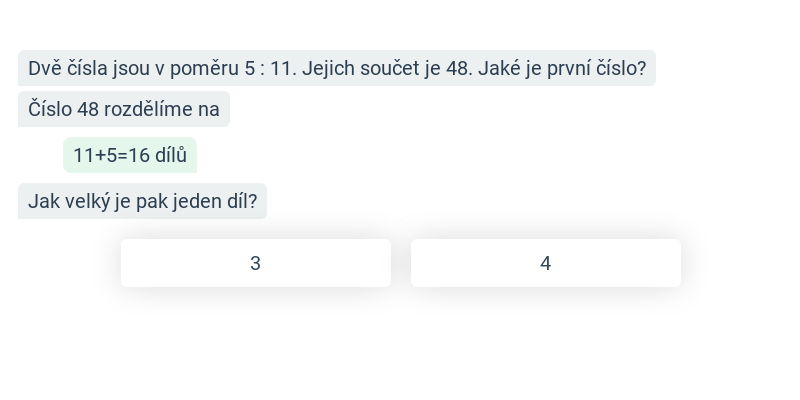
Poměry: měřítko mapy (střední) • FN7
zadání: 17
Typicky zabere: 11 min
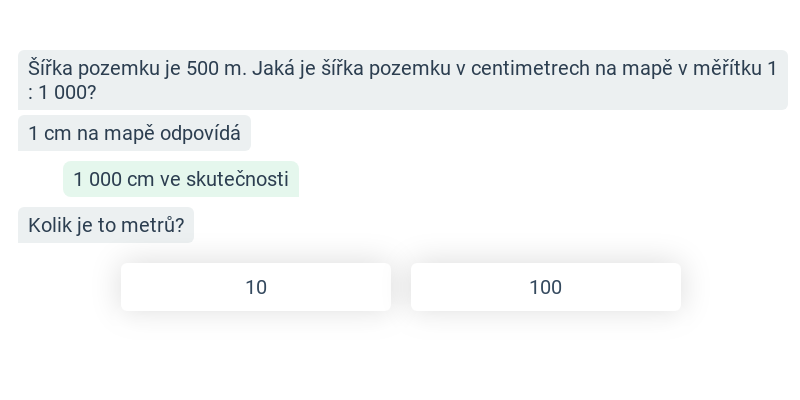
Poměry: měřítko mapy (těžké) • G2Z
zadání: 17
Typicky zabere: 11 min
Dosazování do výrazů (lehké) • FMD
zadání: 52
Typicky zabere: 7 min
Dosazování do výrazů (střední) • FME
zadání: 28
Typicky zabere: 9 min
Zápis výrazů s proměnnými (střední) • GHM
zadání: 15
Typicky zabere: 9 min
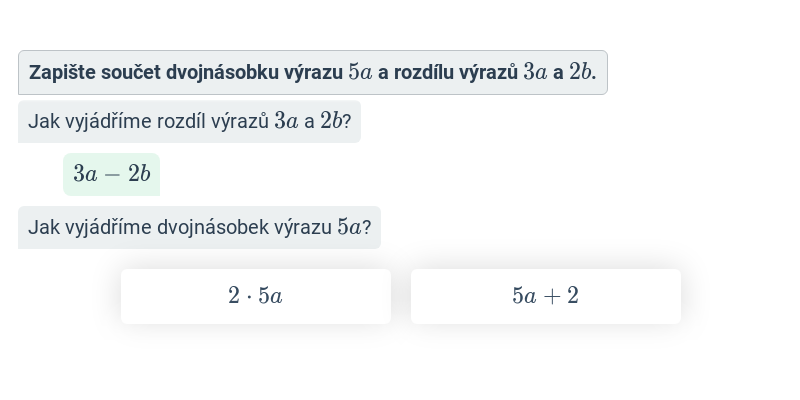
Zápis zadání pomocí výrazu (střední) • GHN
zadání: 19
Typicky zabere: 9 min
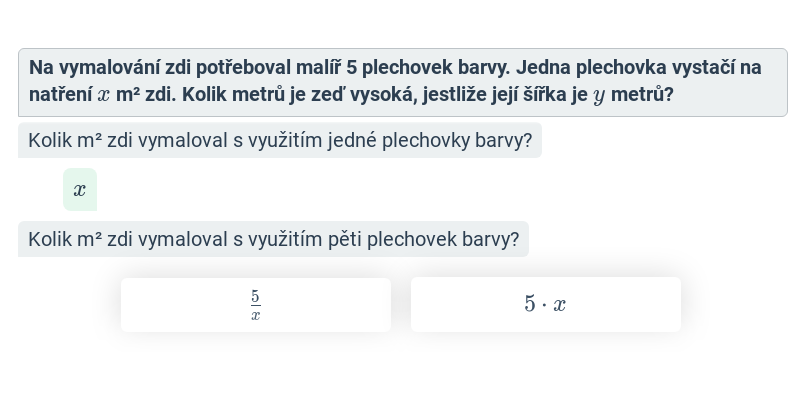
Úpravy výrazů s jednou proměnnou (lehké) • FL1
zadání: 61
Typicky zabere: 8 min
Úpravy výrazů s jednou proměnnou (střední) • EM1
zadání: 19
Typicky zabere: 8 min
Úpravy výrazů s jednou proměnnou (těžké) • FJU
zadání: 23
Typicky zabere: 8 min
Úpravy výrazů s více proměnnými (střední) • FL4
zadání: 22
Typicky zabere: 9 min
Úpravy výrazů s více proměnnými (těžké) • FJV
zadání: 22
Typicky zabere: 9 min
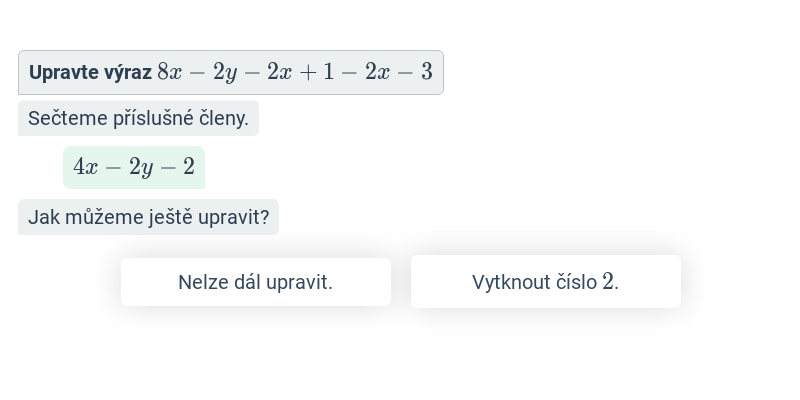
Rozklad na součin (postupné vytýkání) (střední) • E2R
zadání: 14
Typicky zabere: 8 min
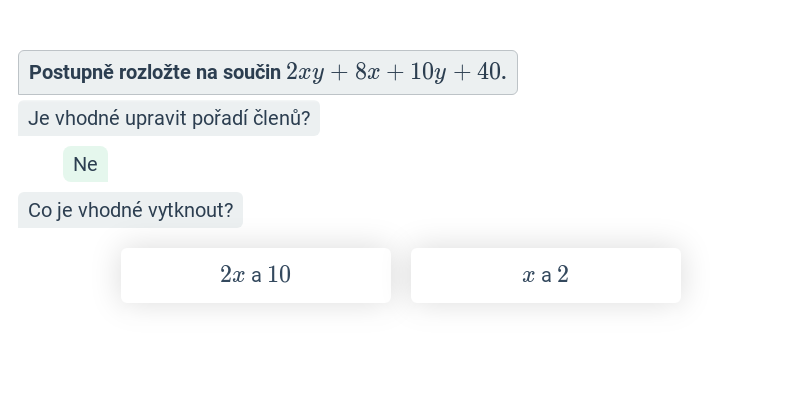
Rozklad na součin (postupné vytýkání) (těžké) • G2W
zadání: 14
Typicky zabere: 7 min
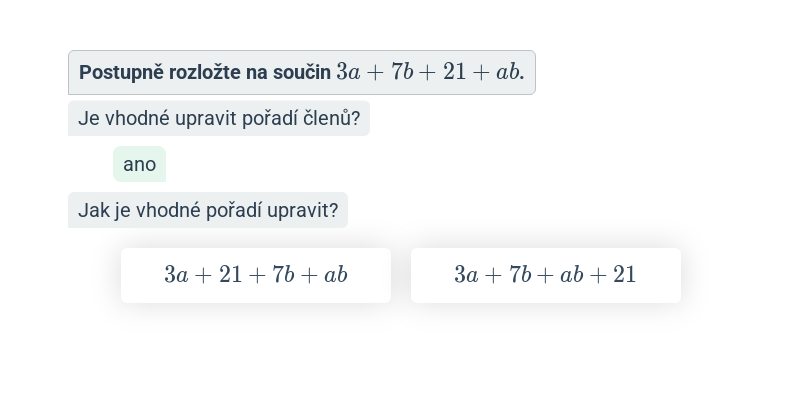
Podmínky lomených výrazů (lehké) • FTD
zadání: 23
Typicky zabere: 8 min
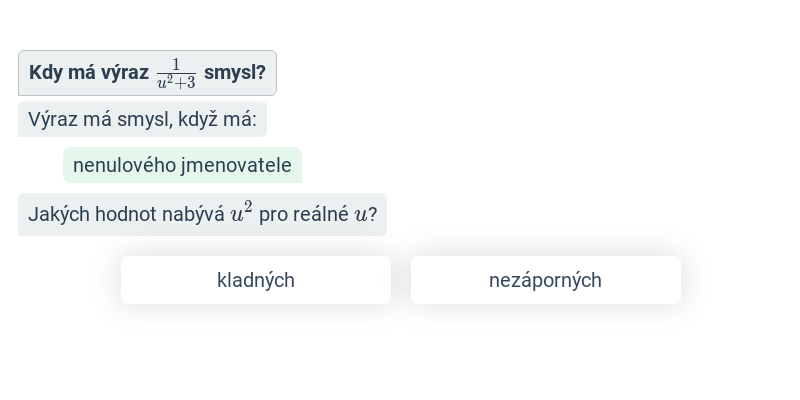
Podmínky lomených výrazů (střední) • FTE
zadání: 20
Typicky zabere: 9 min
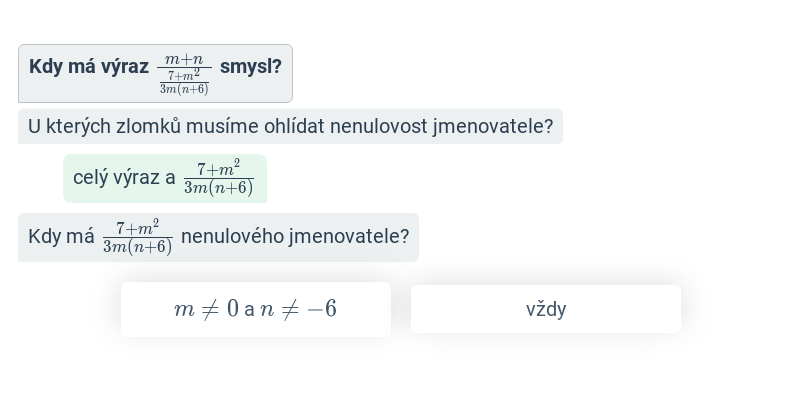
Podmínky lomených výrazů (těžké) • E3H
zadání: 22
Typicky zabere: 8 min
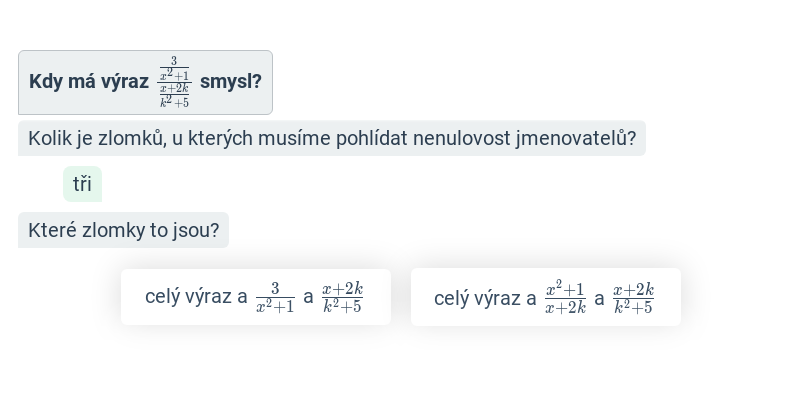
Početní operace s lomenými výrazy (lehké) • F7K
zadání: 10
Typicky zabere: 8 min
Početní operace s lomenými výrazy (střední) • FT6
zadání: 10
Typicky zabere: 9 min
Početní operace s lomenými výrazy (těžké) • F7L
zadání: 10
Typicky zabere: 11 min
Lomené výrazy: mix (lehké) • F7P
zadání: 30
Typicky zabere: 9 min
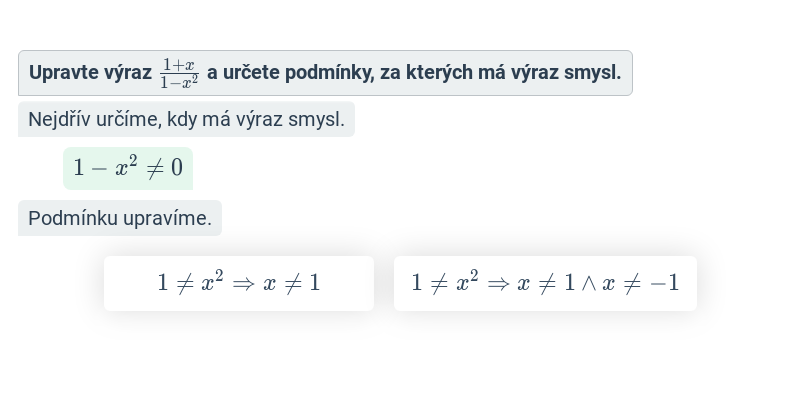
Lomené výrazy: mix (střední) • FTC
zadání: 15
Typicky zabere: 10 min
Lomené výrazy: mix (těžké) • ENE
zadání: 20
Typicky zabere: 10 min
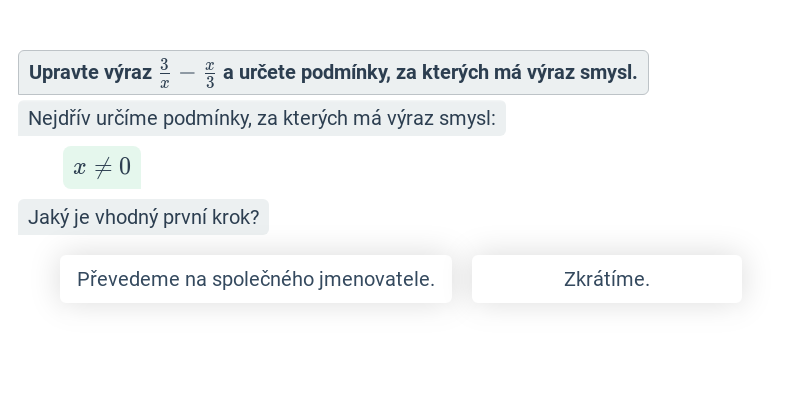
Dělení mnohočlenu mnohočlenem (lehké) • FTZ
zadání: 10
Typicky zabere: 7 min
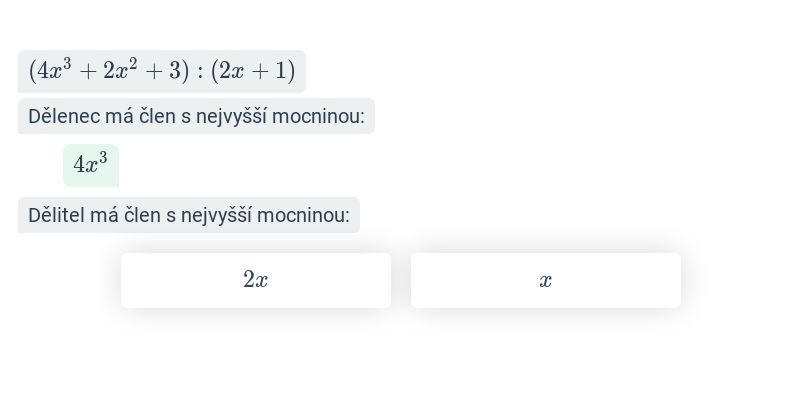
Dělení mnohočlenu mnohočlenem (střední) • FTS
zadání: 10
Typicky zabere: 9 min
Dělení mnohočlenu mnohočlenem (těžké) • FT2
zadání: 10
Typicky zabere: 11 min
Dělení mnohočlenu jednočlenem (střední) • F7M
zadání: 10
Typicky zabere: 8 min
Základní rovnice s jednou neznámou (lehké) • FHS
zadání: 34
Typicky zabere: 7 min
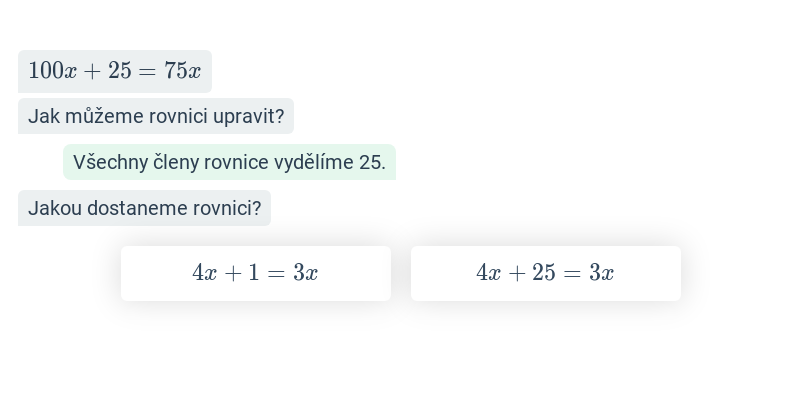
Základní rovnice s jednou neznámou (střední) • EMZ
zadání: 21
Typicky zabere: 7 min
Základní rovnice s jednou neznámou (těžké) • FMJ
zadání: 22
Typicky zabere: 7 min
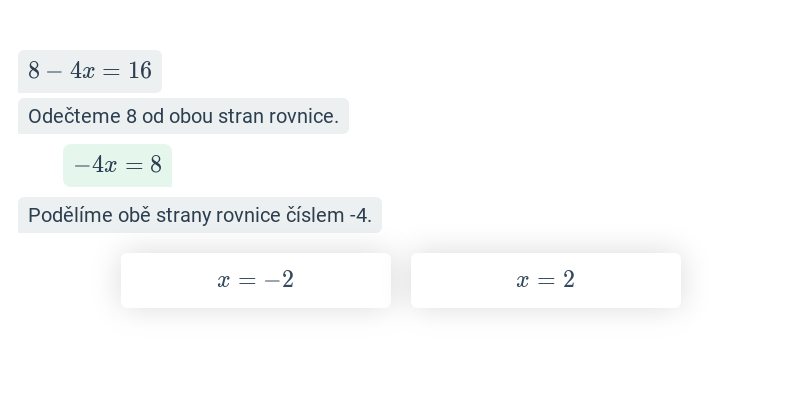
Rovnice se závorkami (střední) • E41
zadání: 37
Typicky zabere: 8 min
Rovnice se závorkami (těžké) • FH7
zadání: 52
Typicky zabere: 7 min
Rovnice s neznámou ve jmenovateli (střední) • E42
zadání: 15
Typicky zabere: 6 min
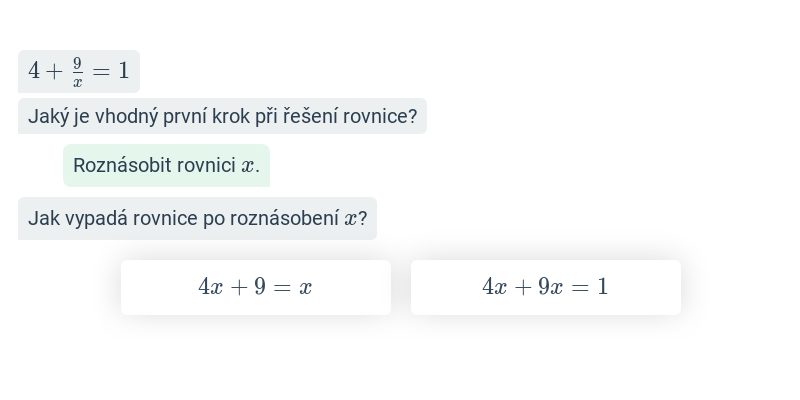
Rovnice se zlomky (lehké) • FS7
zadání: 36
Typicky zabere: 7 min
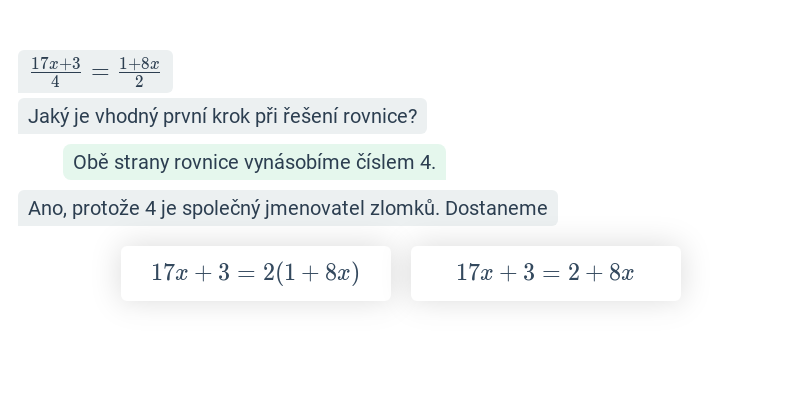
Rovnice se zlomky (střední) • FAO
zadání: 22
Typicky zabere: 8 min
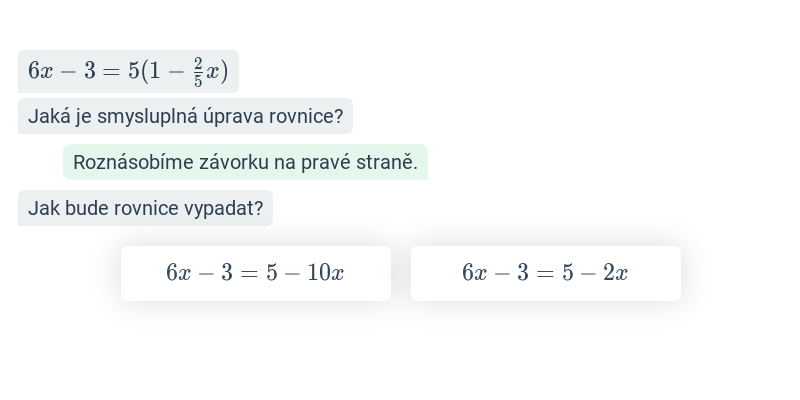
Rovnice se zlomky (těžké) • FHM
zadání: 21
Typicky zabere: 10 min
Rovnice s lomenými výrazy (lehké) • F9F
zadání: 15
Typicky zabere: 7 min
Rovnice s lomenými výrazy (střední) • F9G
zadání: 15
Typicky zabere: 7 min
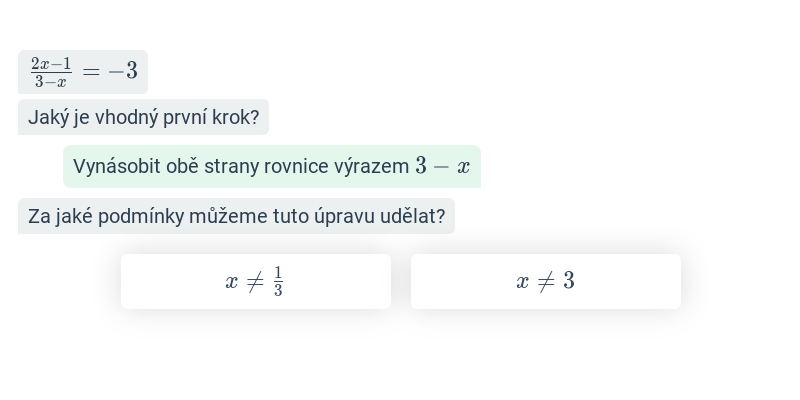
Rovnice s lomenými výrazy (těžké) • FGX
zadání: 15
Typicky zabere: 8 min
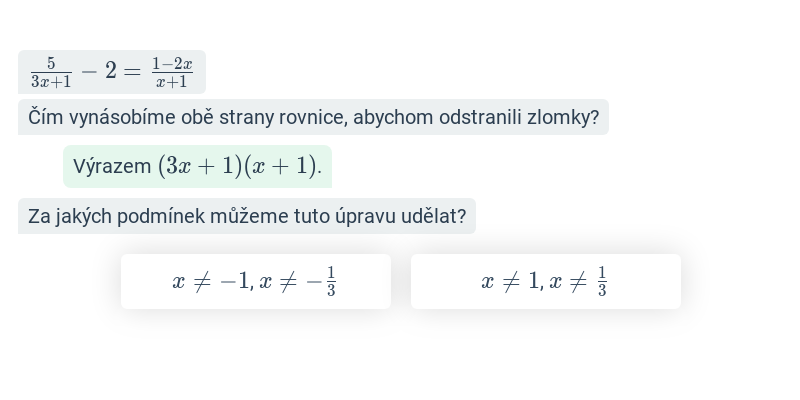
Soustava dvou rovnic: sčítací metoda řešení (lehké) • GHR
zadání: 20
Typicky zabere: 8 min
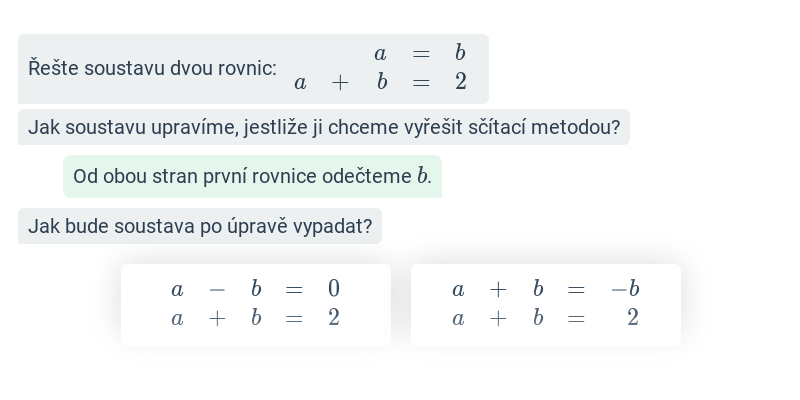
Soustava dvou rovnic: sčítací metoda řešení (střední) • FAL
zadání: 44
Typicky zabere: 8 min
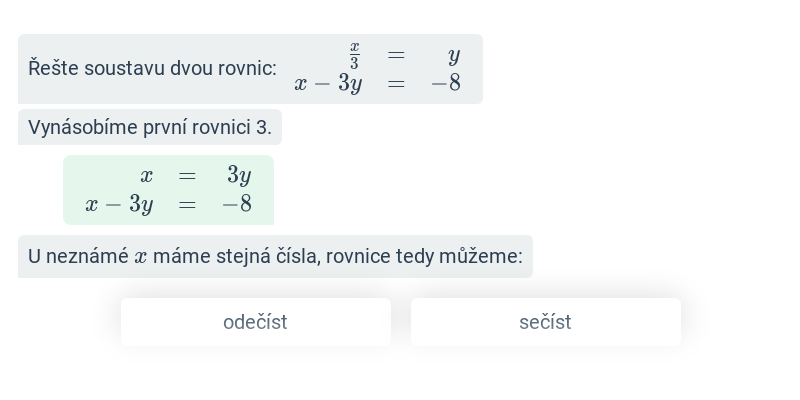
Soustava dvou rovnic: sčítací metoda řešení (těžké) • FJE
zadání: 37
Typicky zabere: 8 min
Soustava dvou rovnic: dosazovací metoda řešení (lehké) • GJF
zadání: 25
Typicky zabere: 6 min
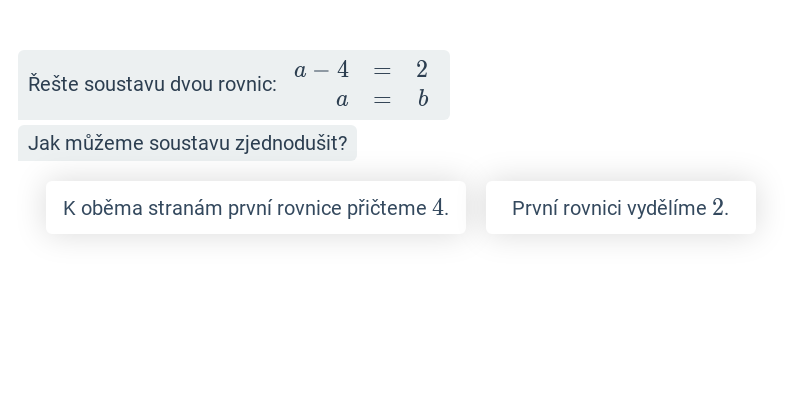
Soustava dvou rovnic: dosazovací metoda řešení (střední) • FAM
zadání: 59
Typicky zabere: 10 min
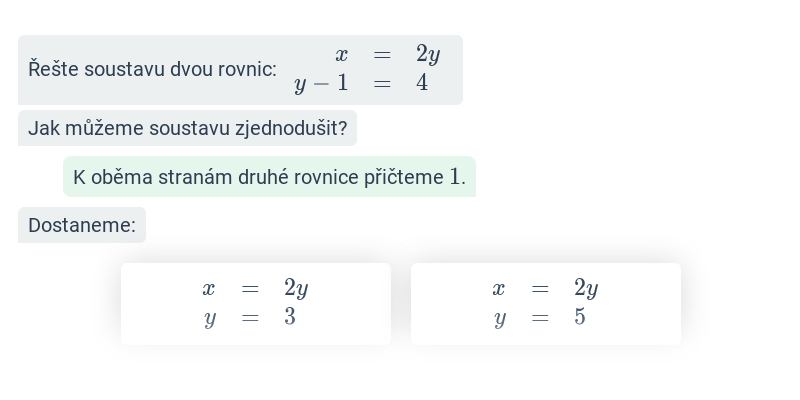
Soustava dvou rovnic: dosazovací metoda řešení (těžké) • FJD
zadání: 20
Typicky zabere: 9 min
Kvadratické rovnice (těžké) • E3D
zadání: 58
Typicky zabere: 8 min
Ryze kvadratické rovnice (střední) • E2V
zadání: 14
Typicky zabere: 5 min
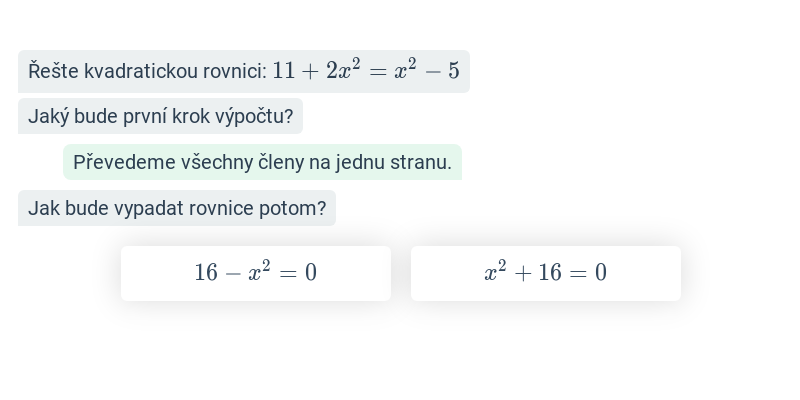
Kvadratické rovnice bez absolutního členu (střední) • E3A
zadání: 14
Typicky zabere: 6 min
Kvadratické rovnice: diskriminant (těžké) • E3B
zadání: 15
Typicky zabere: 7 min
Kvadratické rovnice: Vietovy vzorce (těžké) • E3C
zadání: 15
Typicky zabere: 8 min
Exponenciální rovnice (lehké) • FTP
zadání: 12
Typicky zabere: 6 min
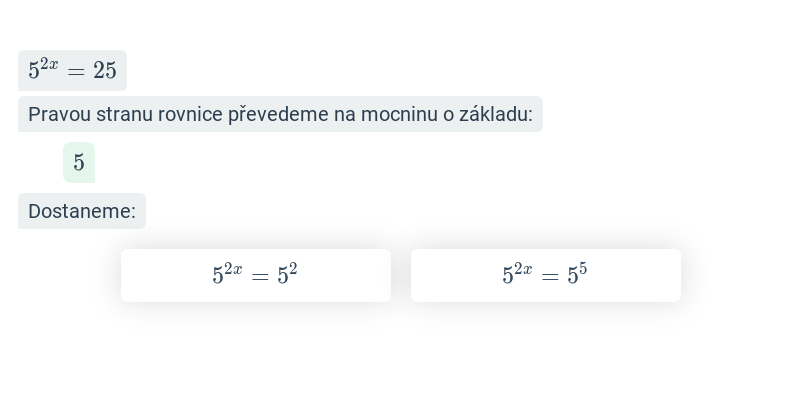
Exponenciální rovnice (střední) • FBF
zadání: 15
Typicky zabere: 8 min
Exponenciální rovnice (těžké) • FBG
zadání: 20
Typicky zabere: 11 min
Logaritmické rovnice (lehké) • FTK
zadání: 12
Typicky zabere: 8 min
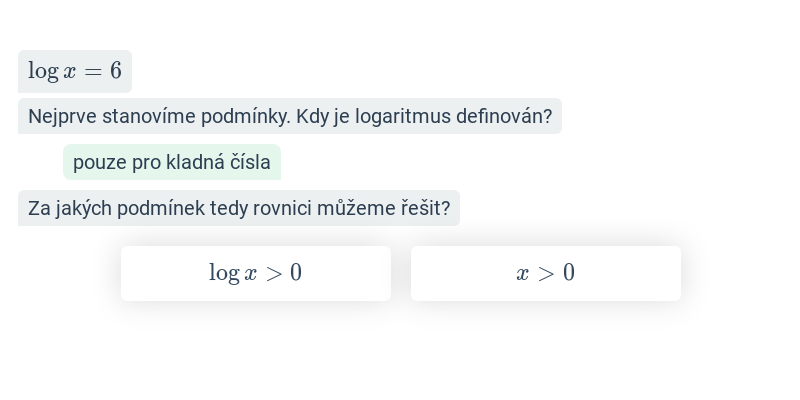
Logaritmické rovnice (střední) • FTL
zadání: 12
Typicky zabere: 8 min
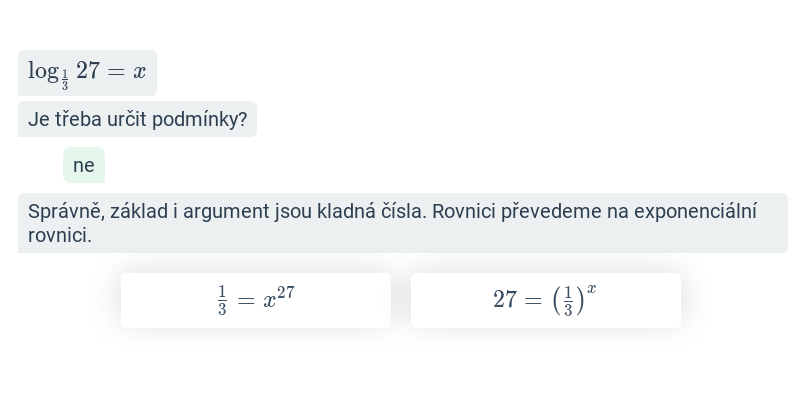
Logaritmické rovnice (těžké) • FBH
zadání: 18
Typicky zabere: 9 min
Goniometrické rovnice (střední) • GUU
zadání: 15
Typicky zabere: 12 min
Zápis zadání pomocí rovnice (střední) • GHS
zadání: 18
Typicky zabere: 9 min
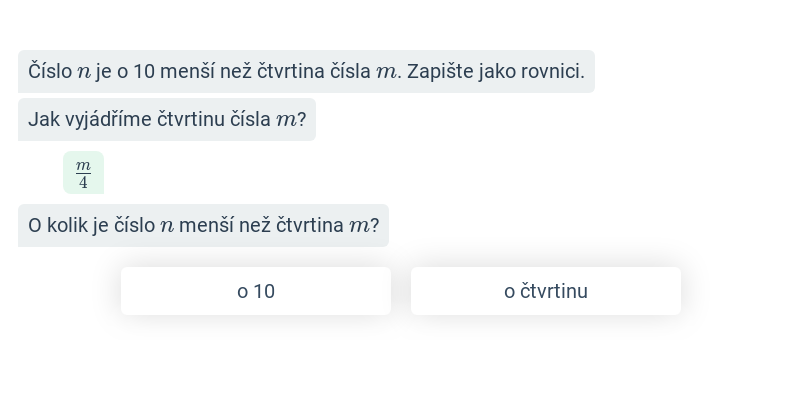
Myslím si číslo (střední) • E3K
zadání: 20
Typicky zabere: 12 min
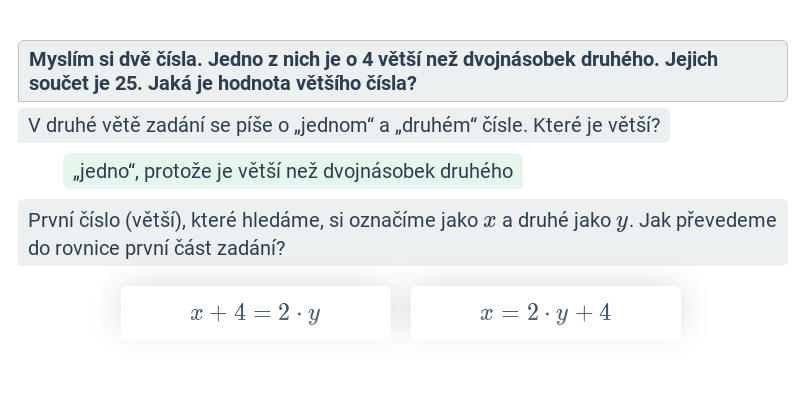
Úlohy o směsích (střední) • E2T
zadání: 12
Typicky zabere: 13 min
Obecné slovní úlohy s rovnicemi (lehké) • FTV
zadání: 10
Typicky zabere: 10 min
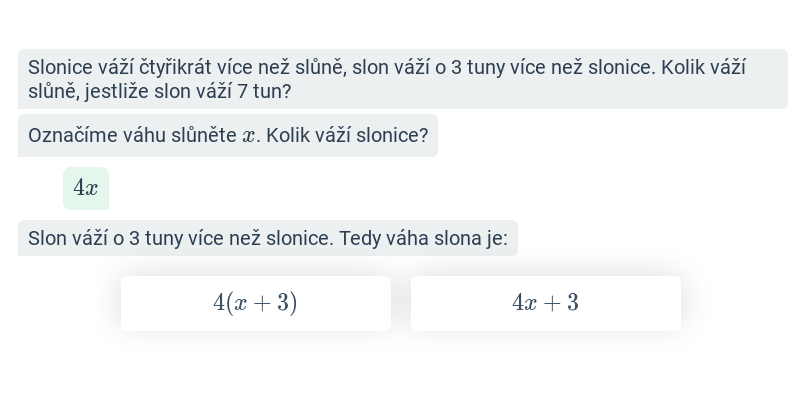
Obecné slovní úlohy s rovnicemi (střední) • E3J
zadání: 6
Typicky zabere: 11 min
Obecné slovní úlohy s rovnicemi (těžké) • FTW
zadání: 8
Typicky zabere: 9 min
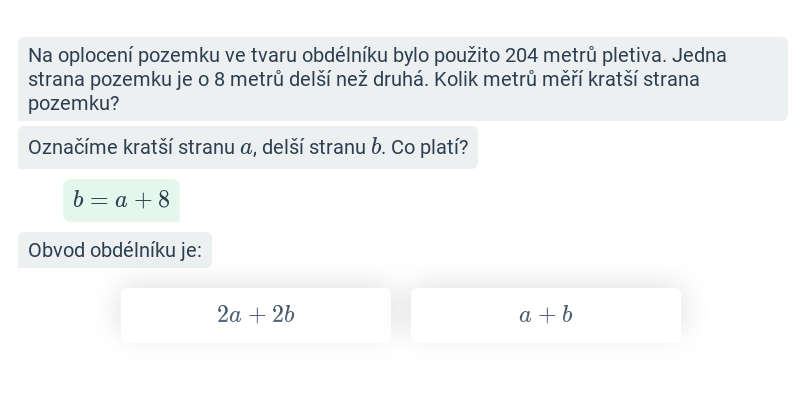
Nerovnice: zápis řešení (střední) • F93
zadání: 15
Typicky zabere: 5 min
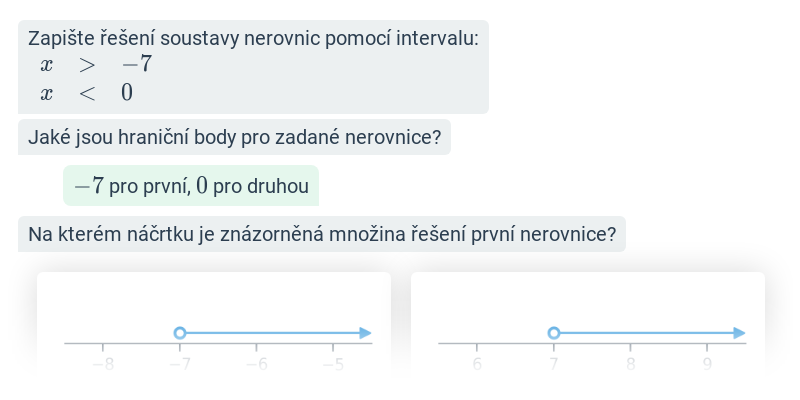
Nerovnice: ekvivalentní úpravy (střední) • F9A
zadání: 16
Typicky zabere: 6 min
Nerovnice s absolutní hodnotou (střední) • F7J
zadání: 15
Typicky zabere: 11 min
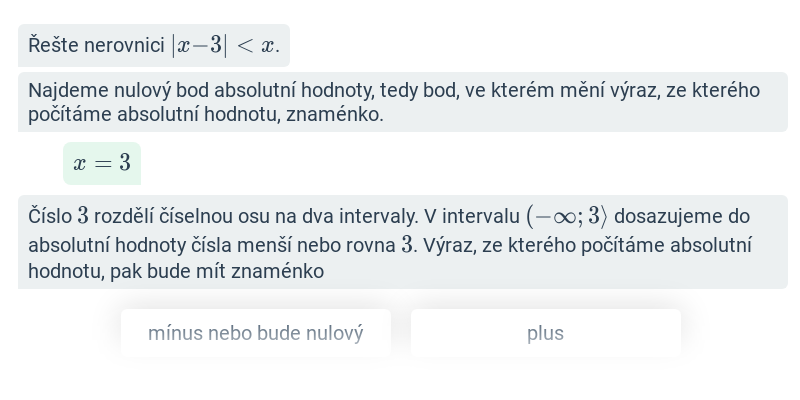
Kvadratické nerovnice (střední) • FT3
zadání: 15
Typicky zabere: 9 min
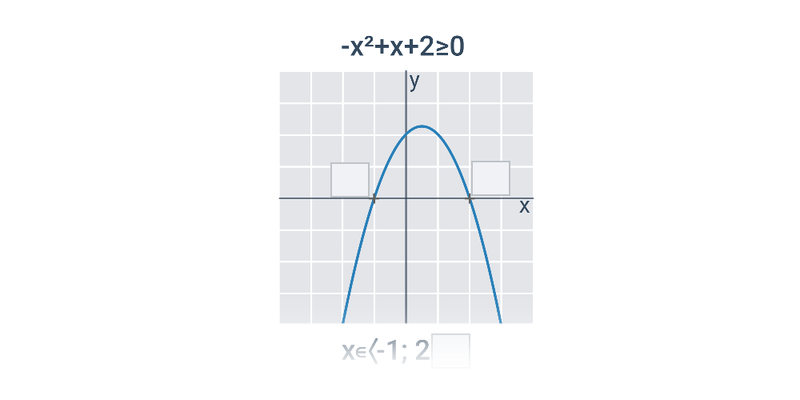
Kvadratické nerovnice: řešení pomocí grafu (střední) • F7W
zadání: 15
Typicky zabere: 8 min
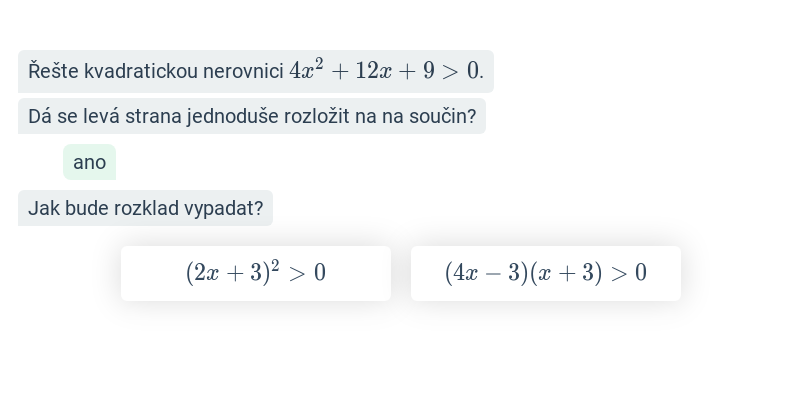
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Poměry: změna a rozdělení čísla (střední) • FTO
zadání: 30
Typicky zabere: 7 min
Poměry: výpočty (střední) • FNV
zadání: 34
Typicky zabere: 7 min
Poměry: měřítko mapy (střední) • FNW
zadání: 28
Typicky zabere: 9 min
Poměry: měřítko mapy (těžké) • FPH
zadání: 36
Typicky zabere: 9 min
Dosazování do výrazů (lehké) • GUT
zadání: 30
Typicky zabere: 4 min
Dosazování do výrazů (střední) • EBH
zadání: 33
Typicky zabere: 5 min
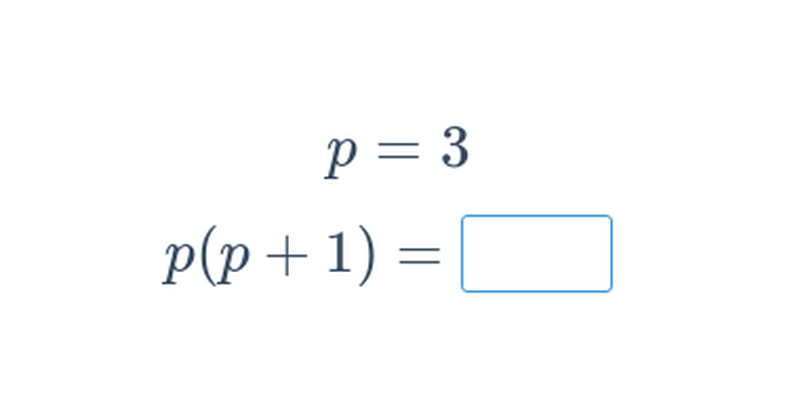
Dosazování do výrazů (těžké) • EPJ
zadání: 40
Typicky zabere: 7 min
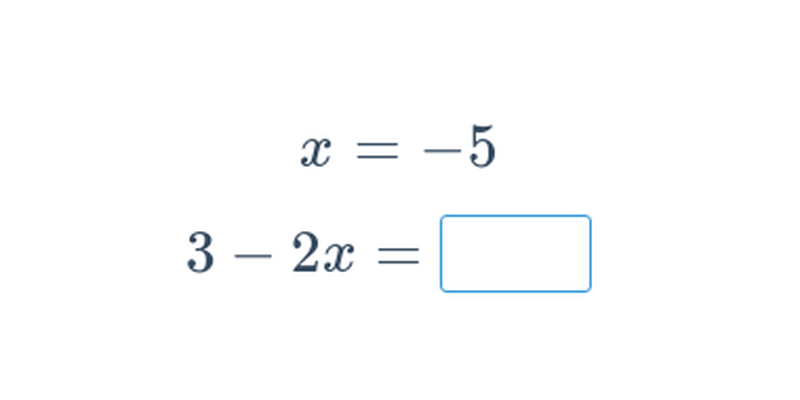
Úpravy výrazů s jednou proměnnou (střední) • EPF
zadání: 35
Typicky zabere: 5 min
Úpravy výrazů s jednou proměnnou (těžké) • FBK
zadání: 51
Typicky zabere: 6 min
Úpravy výrazů s více proměnnými (střední) • EWU
zadání: 30
Typicky zabere: 6 min
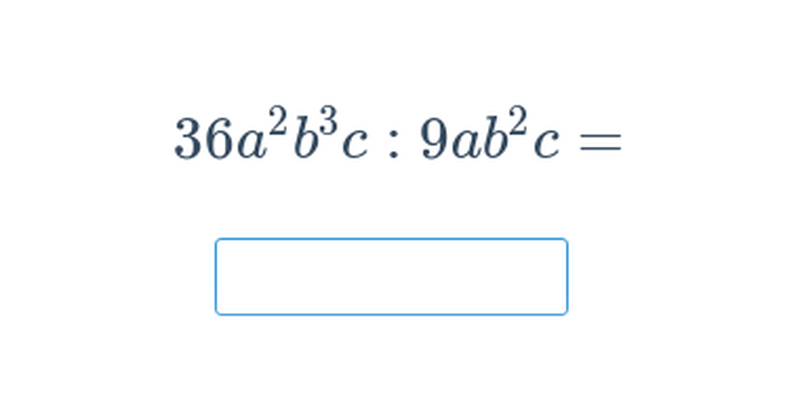
Úpravy výrazů s více proměnnými (těžké) • FBL
zadání: 44
Typicky zabere: 6 min
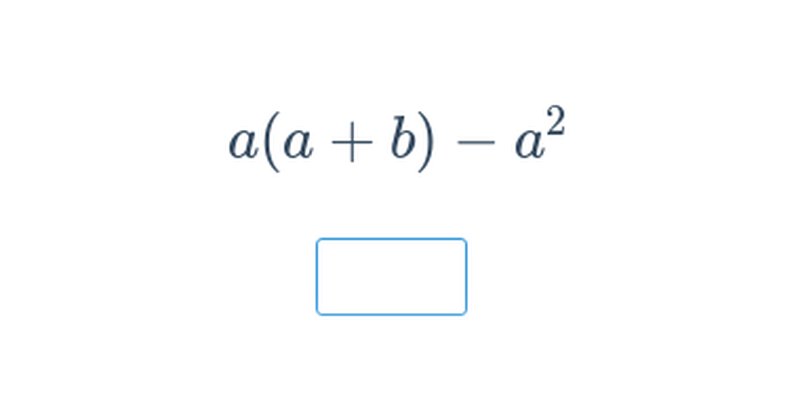
Lomené výrazy: úpravy a výpočty (střední) • EPG
zadání: 30
Typicky zabere: 7 min
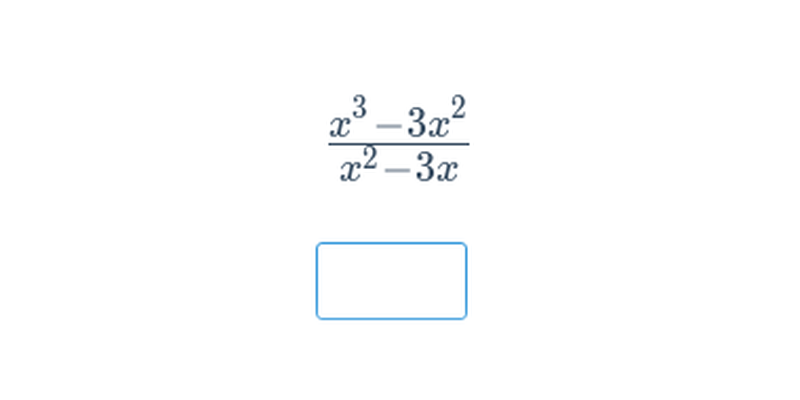
Výrazy a jejich úpravy: mix (střední) • E4C
zadání: 128
Typicky zabere: 6 min
Výrazy a jejich úpravy: mix (těžké) • FBR
zadání: 135
Typicky zabere: 6 min
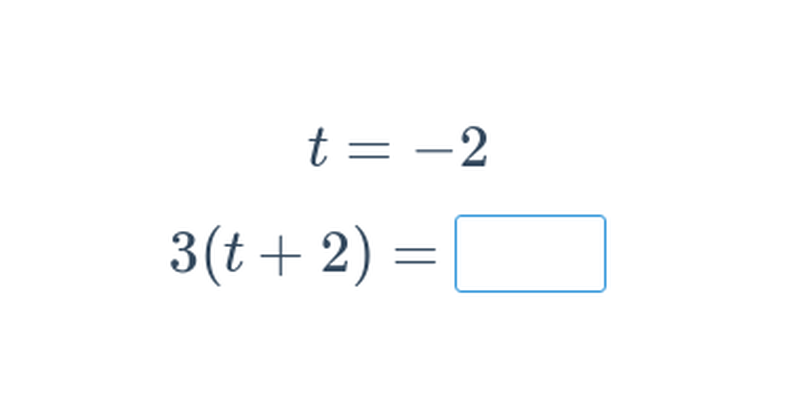
Jednokrokové rovnice (lehké) • FAD
zadání: 42
Typicky zabere: 3 min
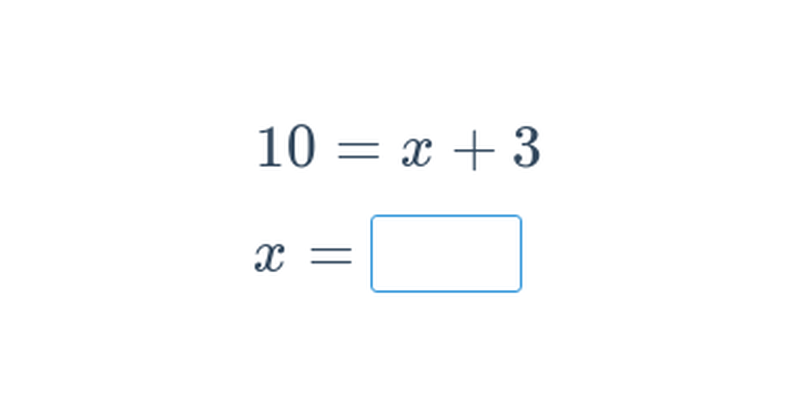
Základní rovnice s jednou neznámou (lehké) • E1R
zadání: 43
Typicky zabere: 4 min
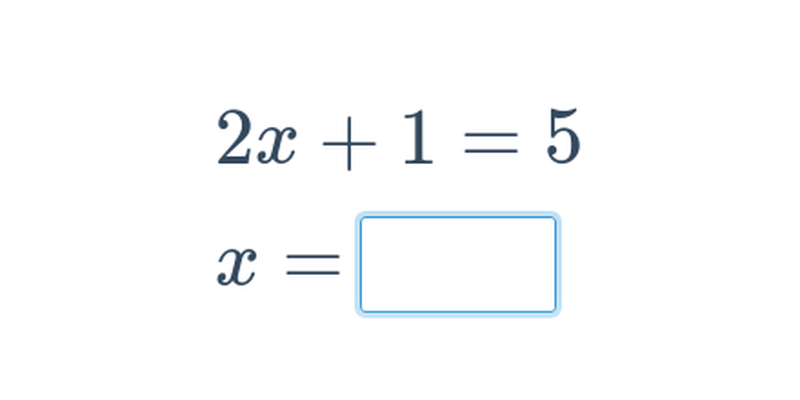
Základní rovnice s jednou neznámou (střední) • EA9
zadání: 44
Typicky zabere: 5 min
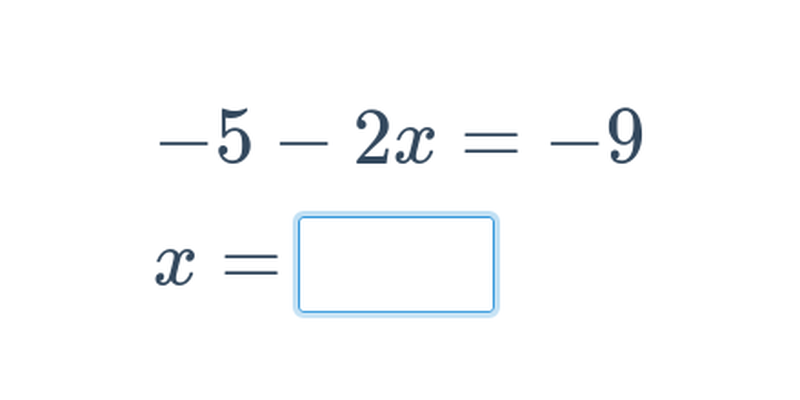
Základní rovnice s jednou neznámou (těžké) • EGP
zadání: 51
Typicky zabere: 6 min
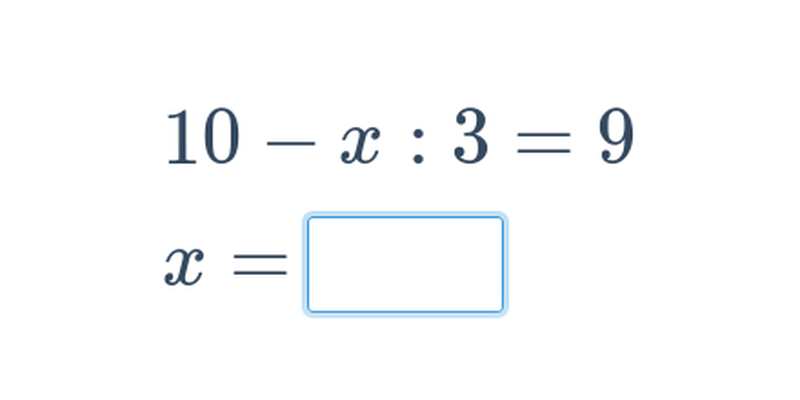
Rovnice se závorkami (střední) • E1S
zadání: 22
Typicky zabere: 6 min
Rovnice se závorkami (těžké) • EKE
zadání: 32
Typicky zabere: 6 min
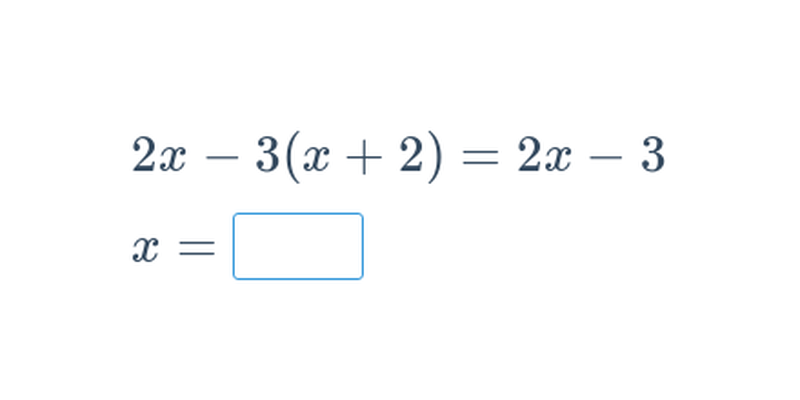
Rovnice s neznámou ve jmenovateli (střední) • E1T
zadání: 19
Typicky zabere: 6 min
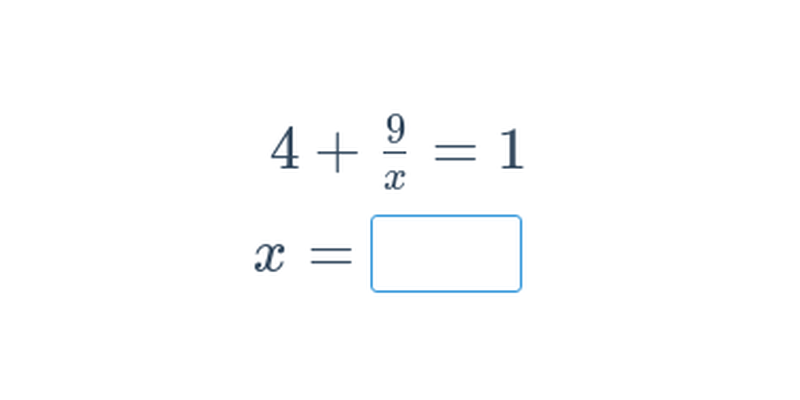
Rovnice se zlomky (střední) • FAF
zadání: 22
Typicky zabere: 6 min
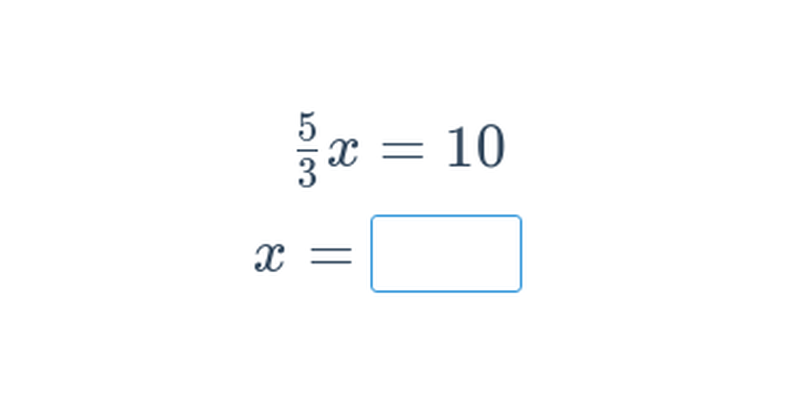
Rovnice se zlomky (těžké) • EKF
zadání: 24
Typicky zabere: 7 min
Rovnice s desetinnými čísly (těžké) • FAE
zadání: 22
Typicky zabere: 5 min
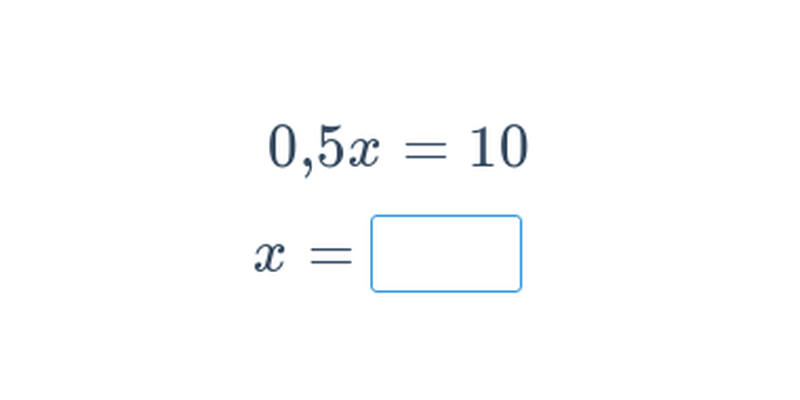
Základní rovnice: mix (střední) • E1W
zadání: 88
Typicky zabere: 6 min
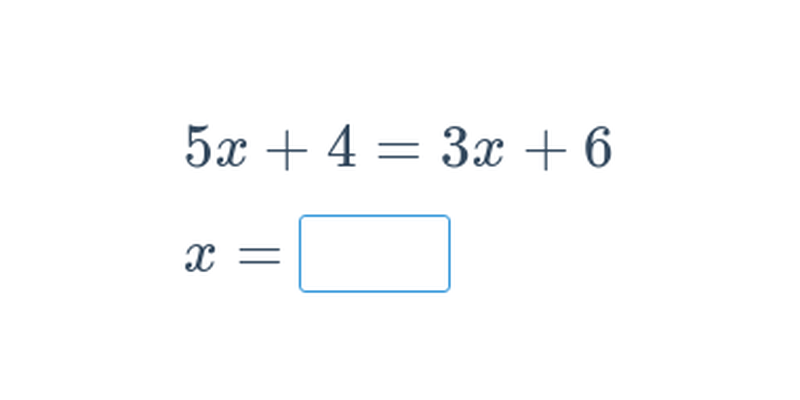
Základní rovnice: mix (těžké) • EMN
zadání: 129
Typicky zabere: 8 min
Rovnice s lomenými výrazy (těžké) • EKG
zadání: 31
Typicky zabere: 6 min
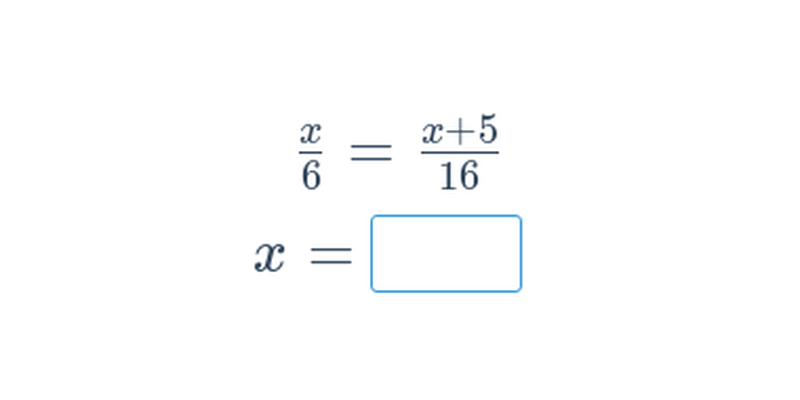
Dvě rovnice o dvou neznámých (střední) • ED2
zadání: 21
Typicky zabere: 8 min
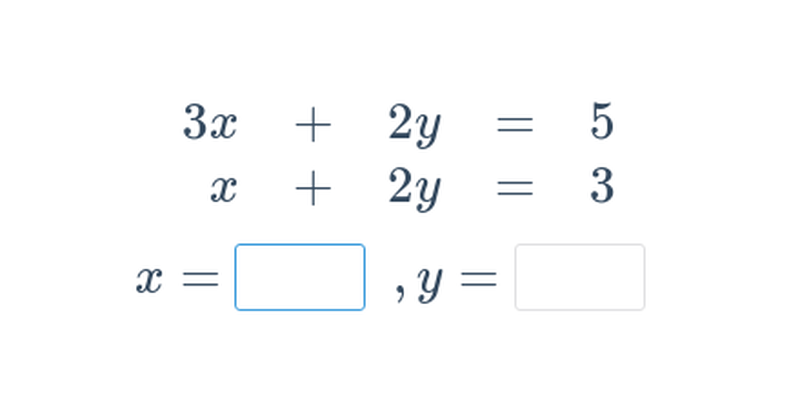
Dvě rovnice o dvou neznámých (těžké) • EPP
zadání: 22
Typicky zabere: 8 min
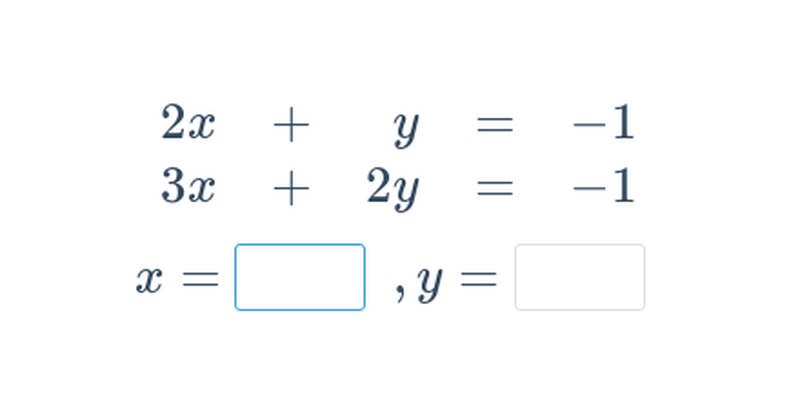
Dosazovací metoda řešení (lehké) • GJG
zadání: 30
Typicky zabere: 7 min
Dosazovací metoda řešení (střední) • GJJ
zadání: 22
Typicky zabere: 7 min
Soustava dvou rovnic: sčítací metoda řešení (lehké) • GN2
zadání: 30
Typicky zabere: 6 min
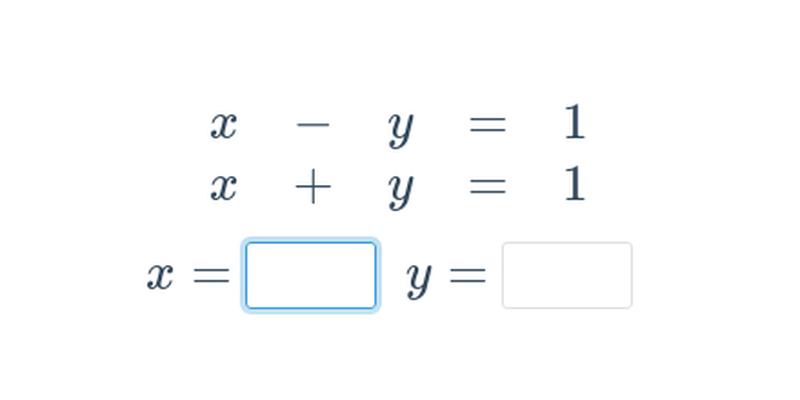
Soustava dvou rovnic: sčítací metoda řešení (střední) • GN3
zadání: 33
Typicky zabere: 7 min
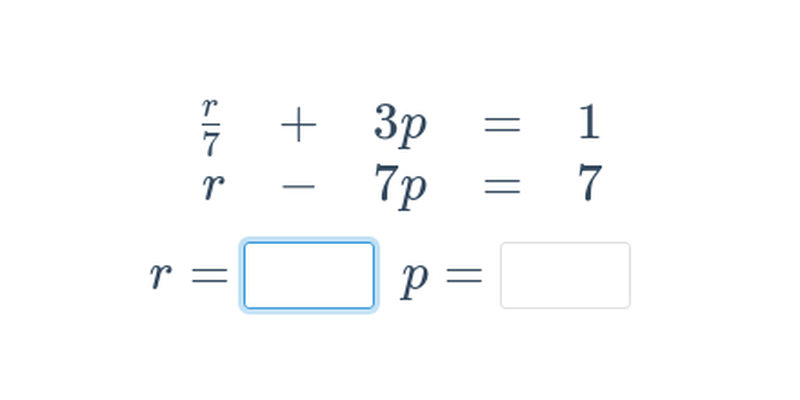
Kvadratické rovnice (střední) • FAH
zadání: 20
Typicky zabere: 5 min
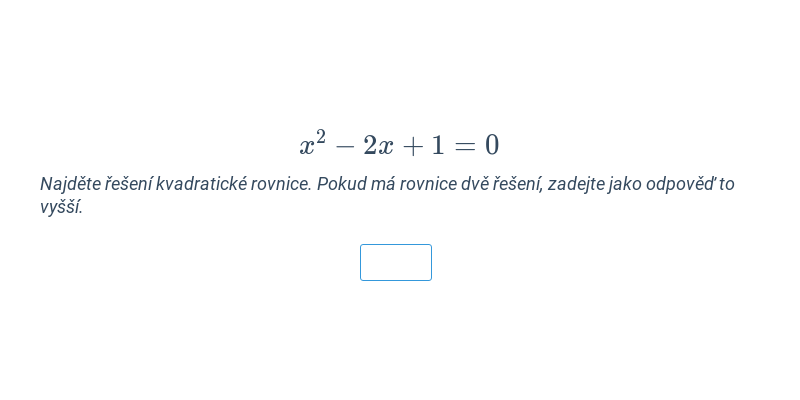
Kvadratické rovnice (těžké) • ED1
zadání: 22
Typicky zabere: 6 min
Exponenciální rovnice (těžké) • E17
zadání: 28
Typicky zabere: 8 min
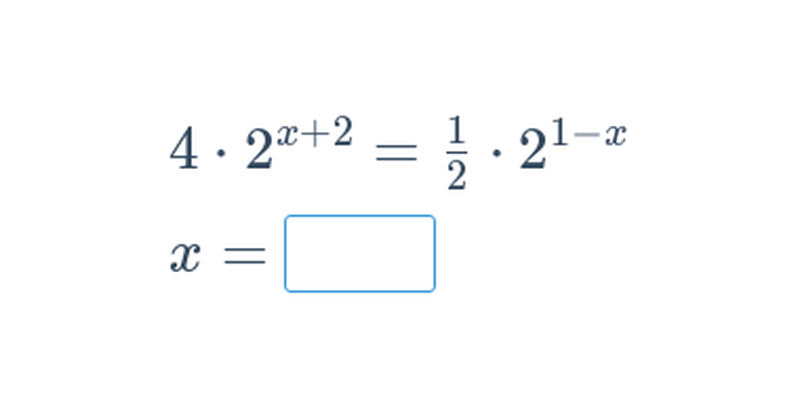
Logaritmické rovnice (těžké) • E6N
zadání: 13
Typicky zabere: 9 min
Pokročilé rovnice: mix (lehké) • GSB
zadání: 60
Typicky zabere: 5 min
Pokročilé rovnice: mix (střední) • GSC
zadání: 96
Typicky zabere: 5 min
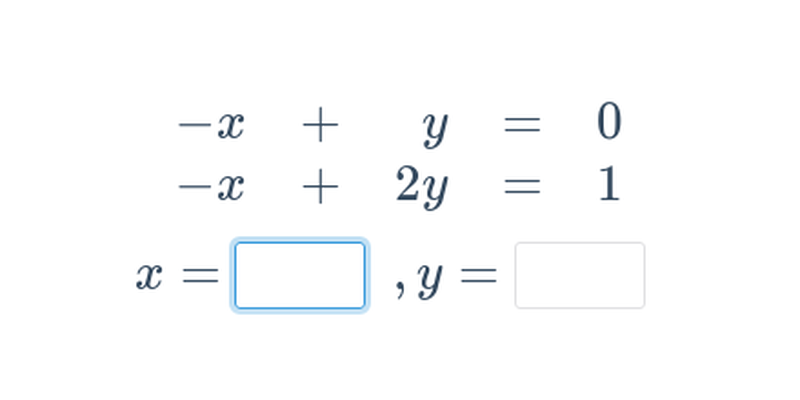
Pokročilé rovnice: mix (těžké) • GSD
zadání: 116
Typicky zabere: 6 min
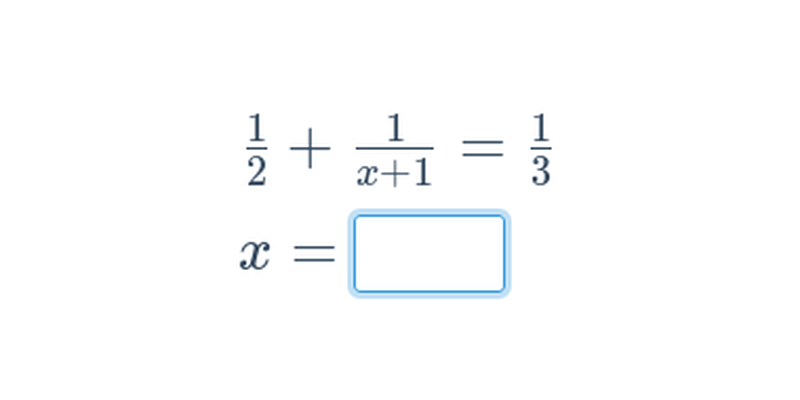
Vyjádření neznámé z rovnice (střední) • FNF
zadání: 30
Typicky zabere: 7 min
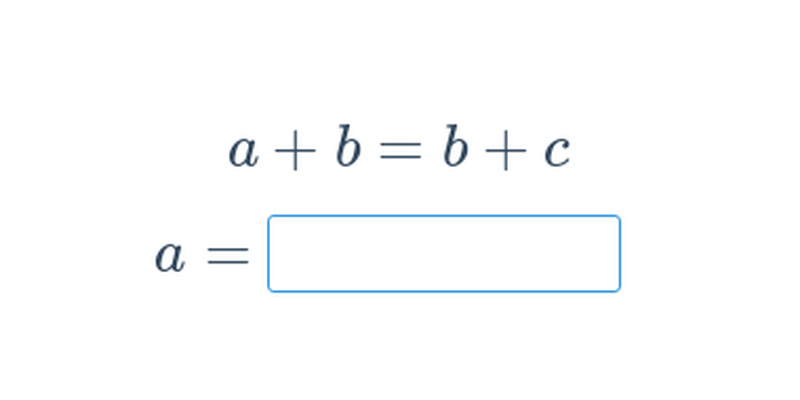
Vyjádření neznámé z rovnice (těžké) • E1U
zadání: 33
Typicky zabere: 7 min
Slovní úlohy
Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.
Přímá a nepřímá úměrnost (střední) • EGL
zadání: 26
Typicky zabere: 8 min
Přímá a nepřímá úměrnost (těžké) • EPD
zadání: 30
Typicky zabere: 9 min
Poměry: výpočty (střední) • FPJ
zadání: 30
Typicky zabere: 8 min
Kvadratické rovnice (těžké) • E3N
zadání: 19
Typicky zabere: 7 min
Myslím si číslo (střední) • EET
zadání: 17
Typicky zabere: 6 min
Myslím si číslo (těžké) • EEL
zadání: 24
Typicky zabere: 8 min
Úlohy o směsích (těžké) • EO2
zadání: 14
Typicky zabere: 9 min
Společná práce (střední) • EO1
zadání: 15
Typicky zabere: 10 min
Úlohy s pohybem (střední) • EEO
zadání: 14
Typicky zabere: 8 min
Úlohy s rovnicemi: mix (těžké) • E2W
zadání: 52
Typicky zabere: 11 min
Obecné slovní úlohy s rovnicemi (střední) • EEM
zadání: 25
Typicky zabere: 10 min
Grafař
Specializované cvičení na práci s grafem a funkcemi.
Grafické řešení soustavy lineárních rovnic (těžké) • E6H
zadání: 9
Typicky zabere: 11 min
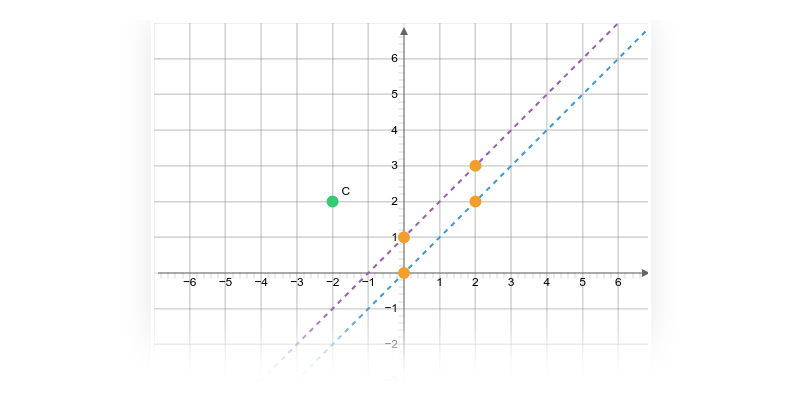
Označování
V zadaném obrázku či textu máte za úkol označit všechny oblasti, které splňují určitou vlastnost.
Lineární nerovnice (střední) • G1L
zadání: 16
Typicky zabere: 8 min
Aritmetická a geometrická posloupnost (střední) • G1M
zadání: 16
Typicky zabere: 5 min
