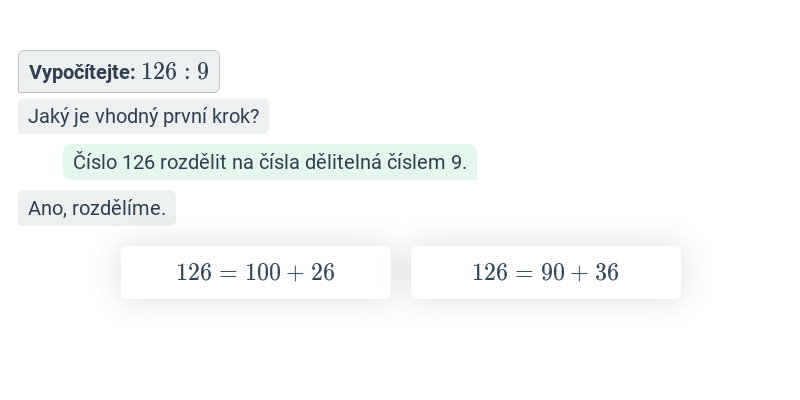
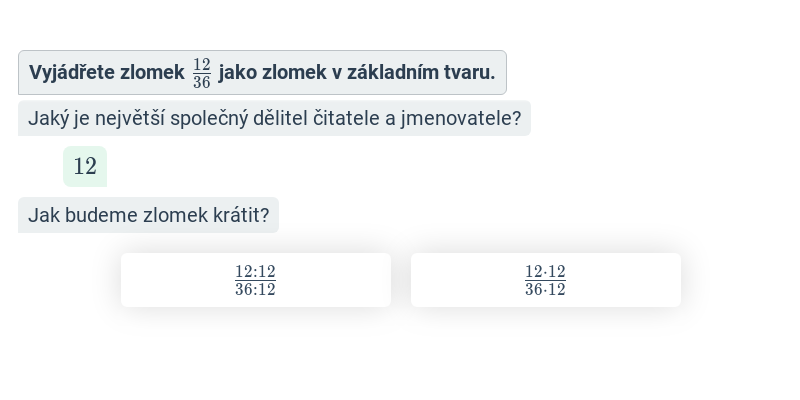
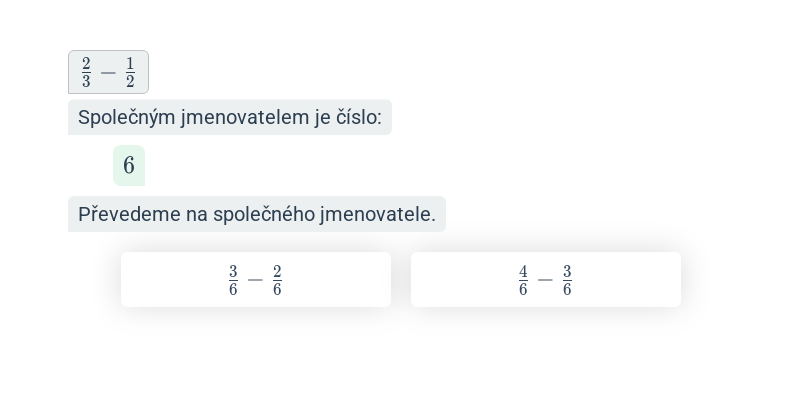
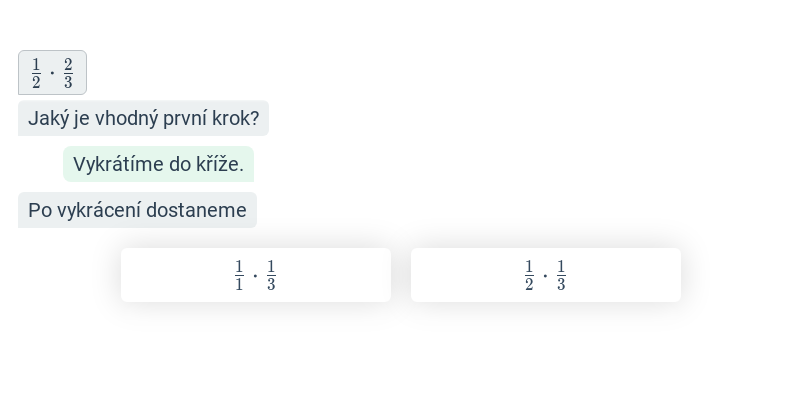
Krok po kroku – 6. třída (6. ročník)

V tomto cvičení doplňujete jednotlivé kroky v rozsáhlejším postupu – například jednotlivé kroky v úpravě výrazů nebo při řešení rovnic. Cvičení je dobrou rozcvičkou na samostatné řešení kompletních příkladů.

Filtr podle ročníku

Úzký výběr

Tipy pro vás

Konstrukce trojúhelníků: známé délky stran

Krok po kroku • lehké

Aritmetika

Násobení a dělení

Násobení víceciferné

Dělení víceciferné

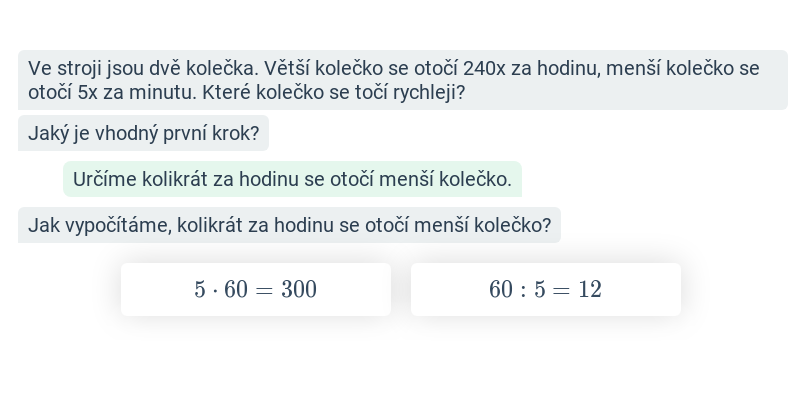
Počítání: kombinace operací

Pořadí operací, závorky

Kladná a záporná čísla

Počítání se zápornými čísly

Dělitelnost

Největší společný dělitel

NSD bez použití mocnin

Nejmenší společný násobek

NSN bez použití mocnin

Zlomky, procenta, desetinná čísla

Zlomky

Výpočty se zlomky

Krácení zlomků

Sčítání a odčítání zlomků

Sčítání a odčítání zlomků s obrázky

Násobení a dělení zlomků

Kombinace operací se zlomky

Desetinná čísla

Výpočty s desetinnými čísly

Zlomky a desetinná čísla

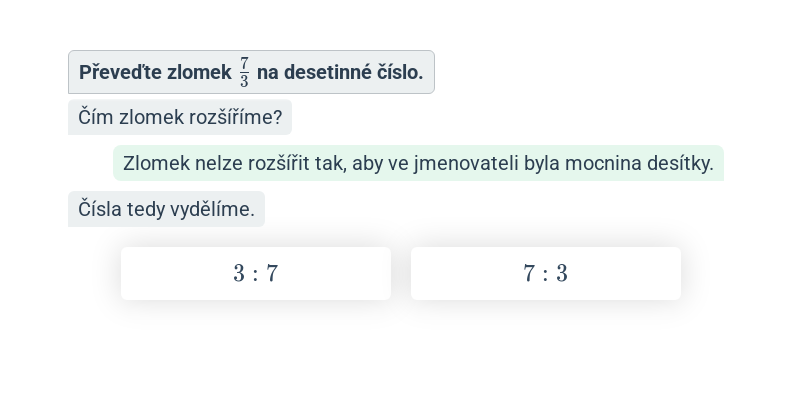
Převod zlomku na desetinné číslo

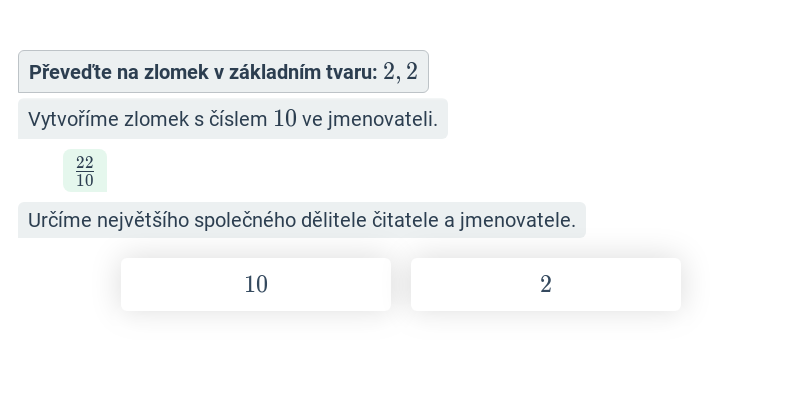
Převod desetinného čísla na zlomek

Geometrie

Úhly

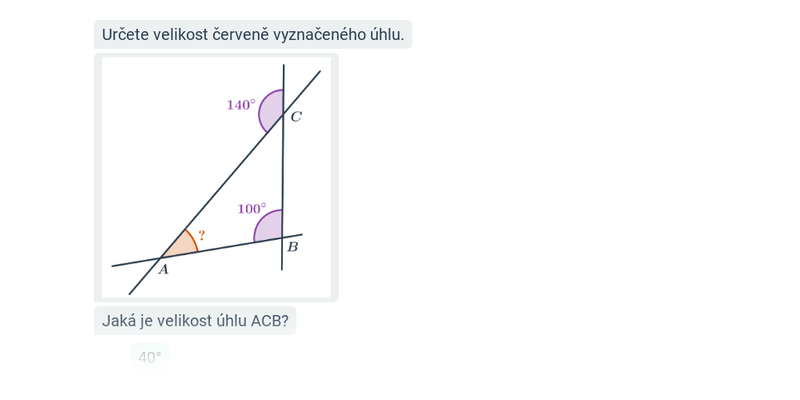
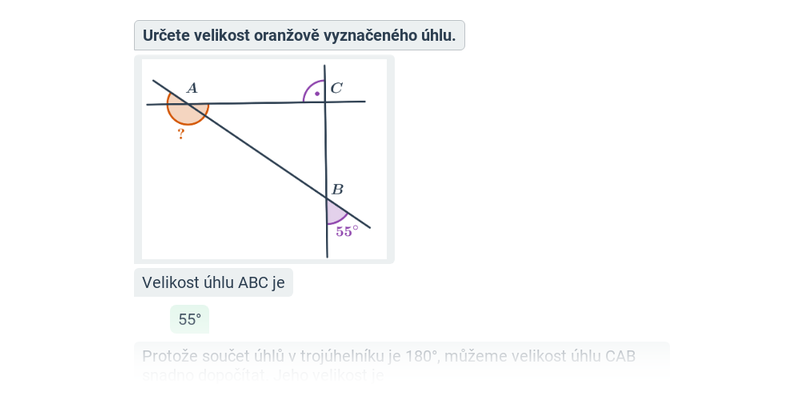
Úhly v trojúhelníku

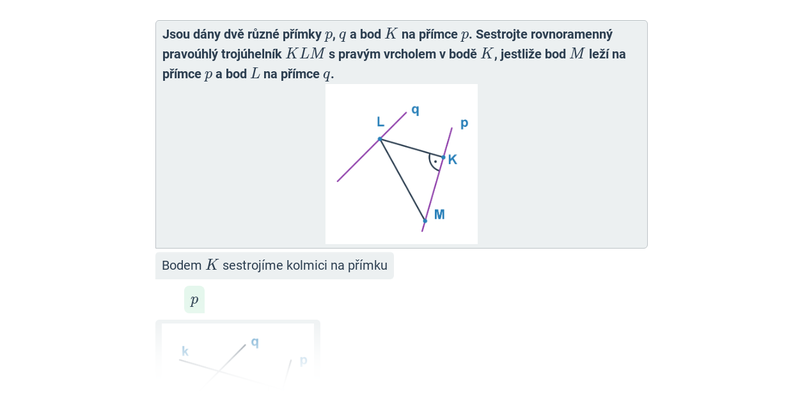
Geometrické konstrukce

Konstrukční úlohy: trojúhelníky

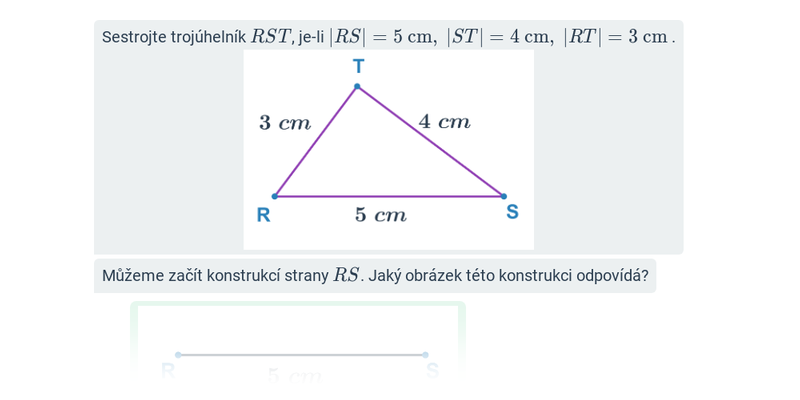
Konstrukce trojúhelníků: známé délky stran

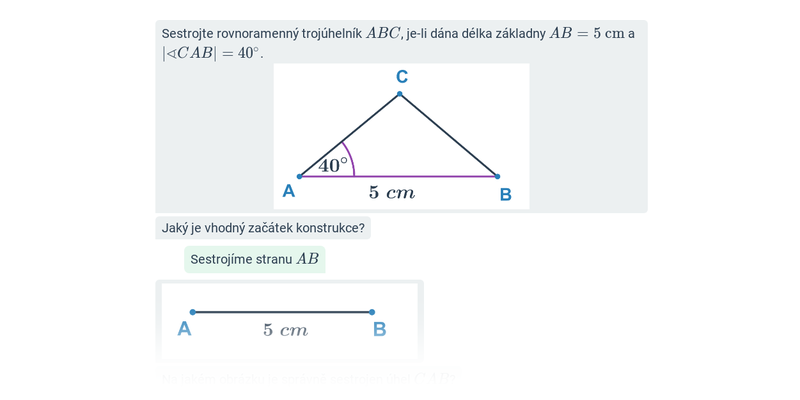
Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky

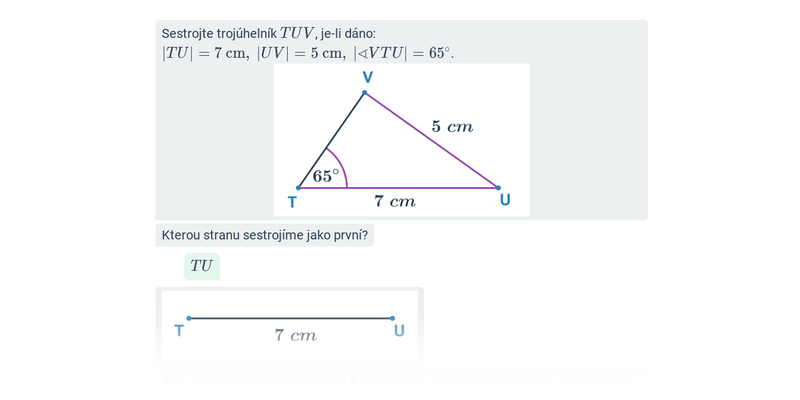
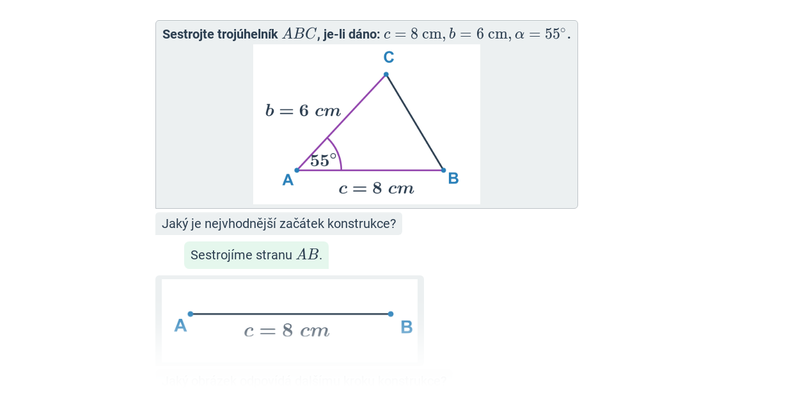
Konstrukce trojúhelníků: věty sss, sus, usu, Ssu

Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice

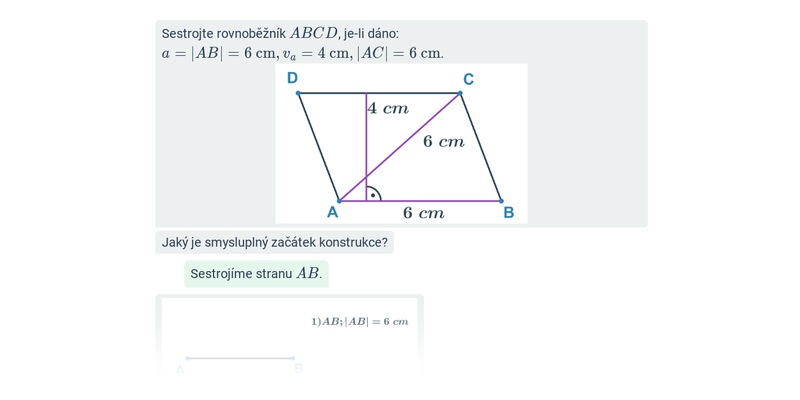
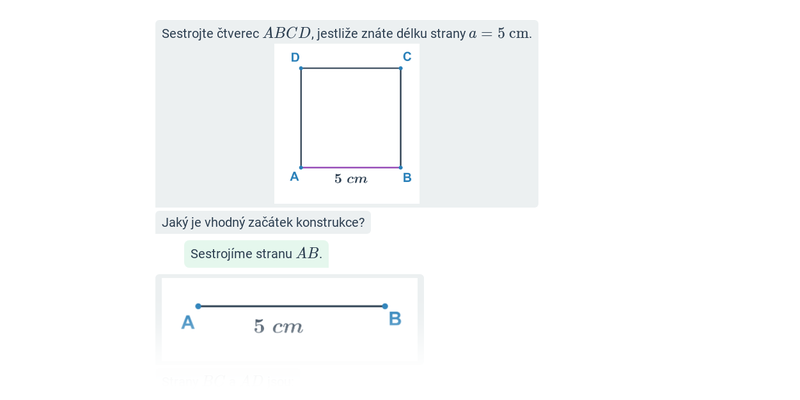
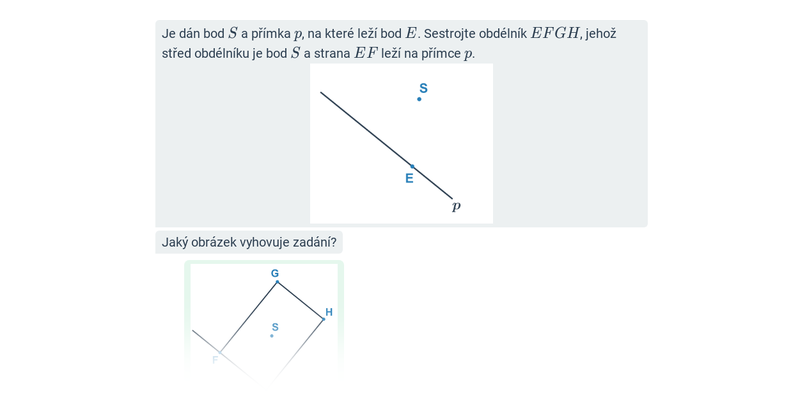
Konstrukční úlohy: čtyřúhelníky

Konstrukční úlohy průřezově

Elementární algebra

Úměrnosti

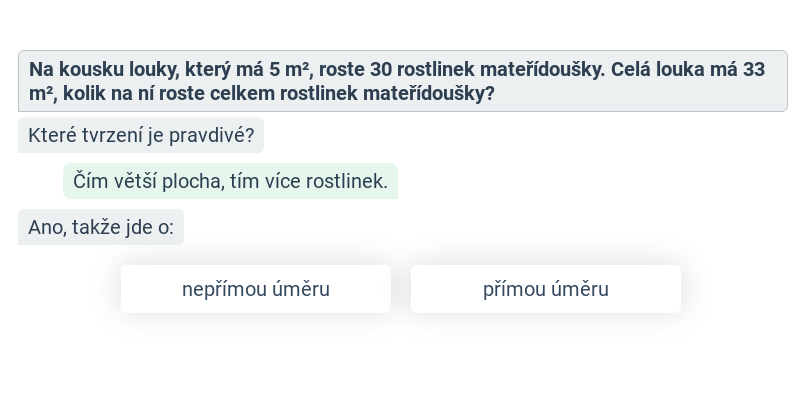
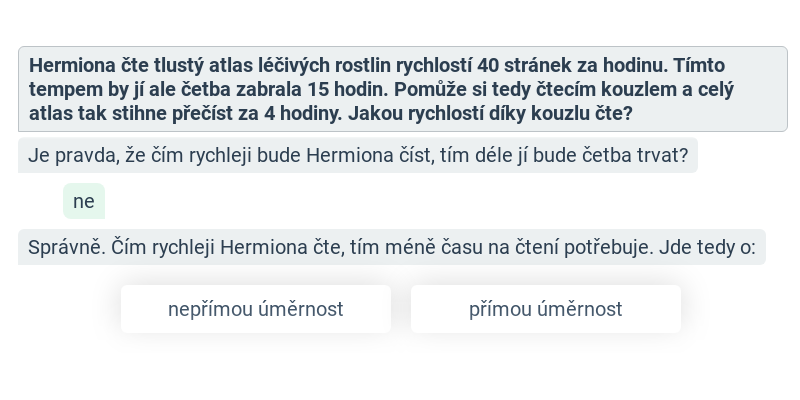
Přímá a nepřímá úměrnost

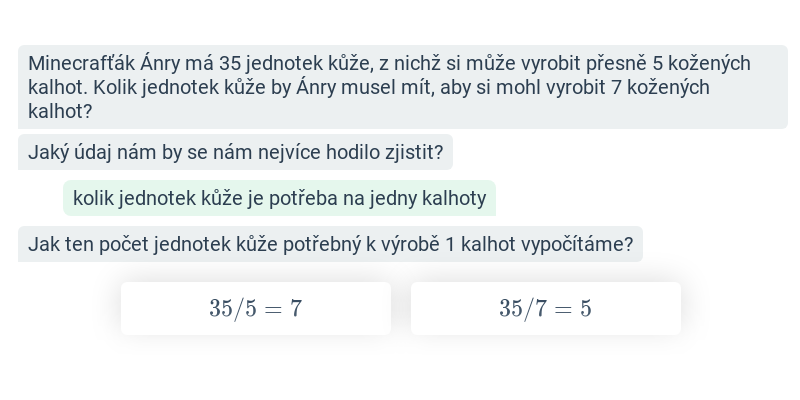
Trojčlenka

Poměry

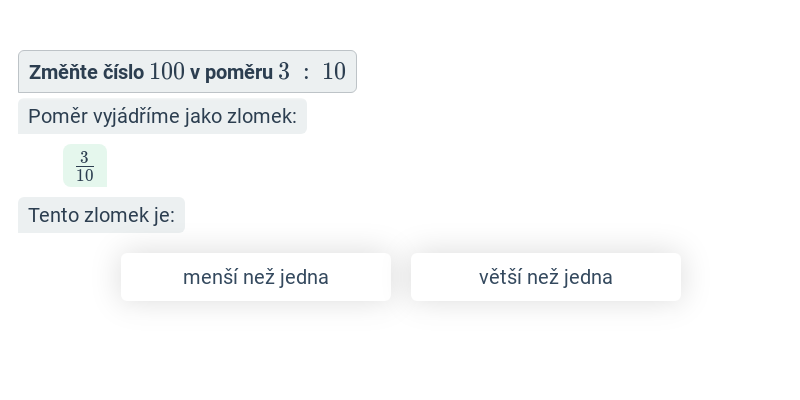
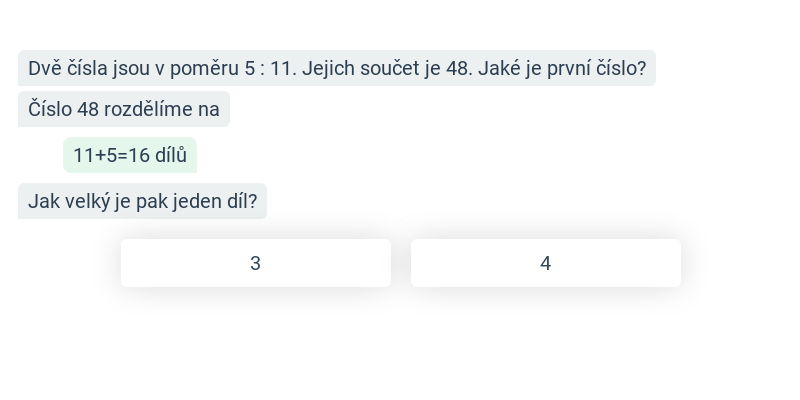
Poměry: změna a rozdělení čísla

Poměry: výpočty

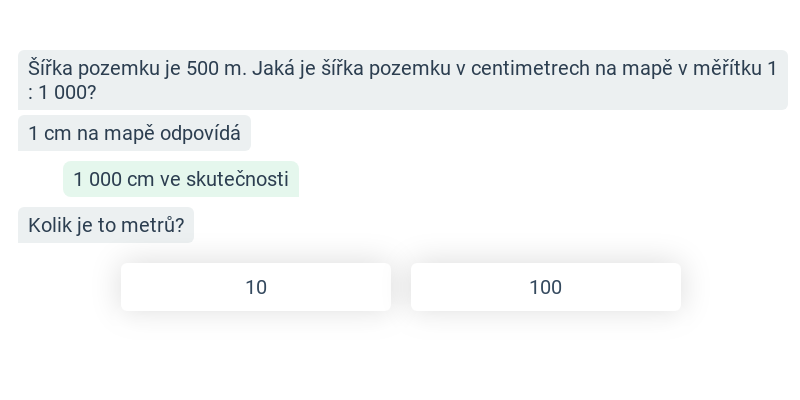
Poměry: měřítko mapy

Algebraické výrazy a jejich úpravy

Dosazování do výrazů

Rovnice

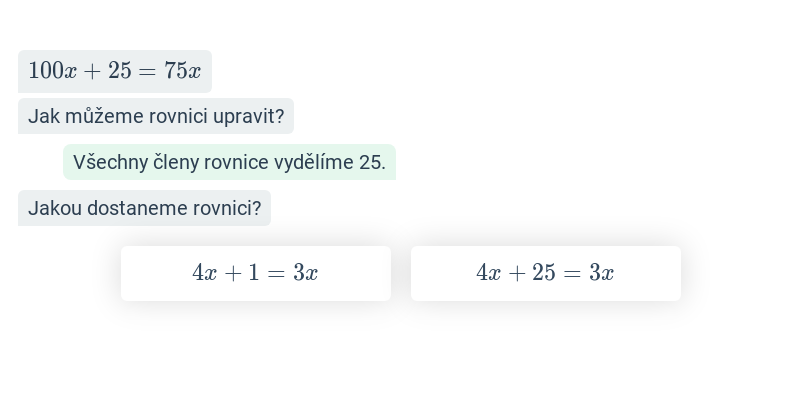
Základní rovnice s jednou neznámou

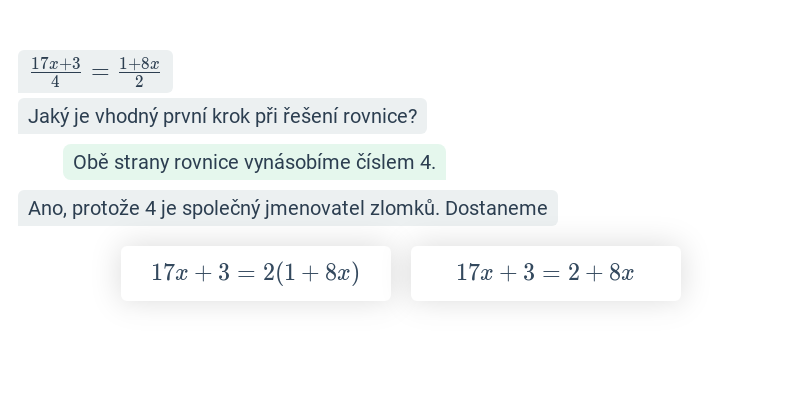
Rovnice se zlomky

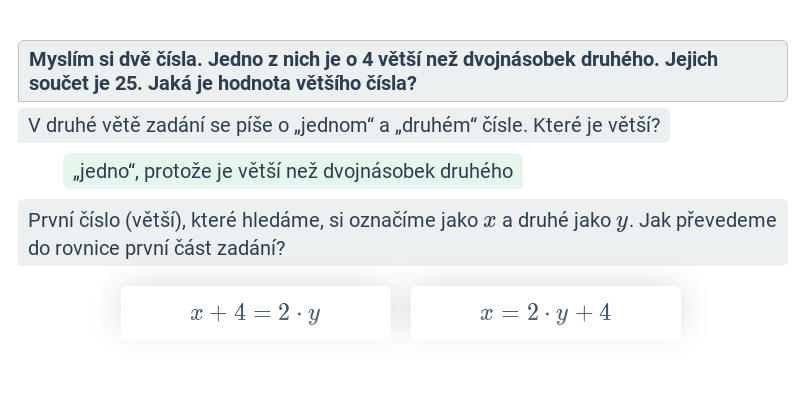
Úlohy s rovnicemi

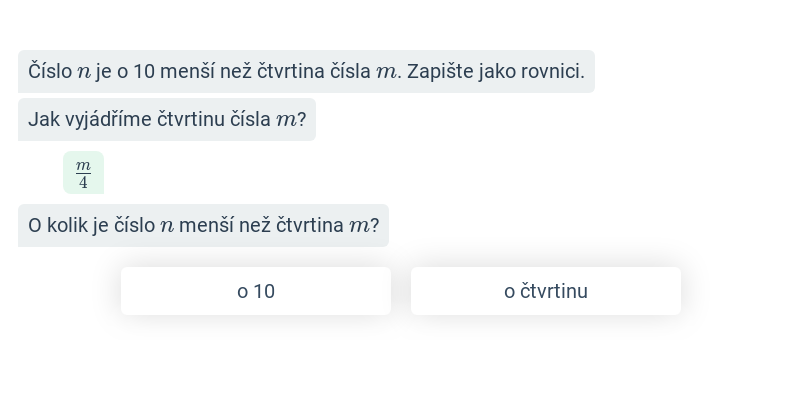
Zápis zadání pomocí rovnice

Myslím si číslo

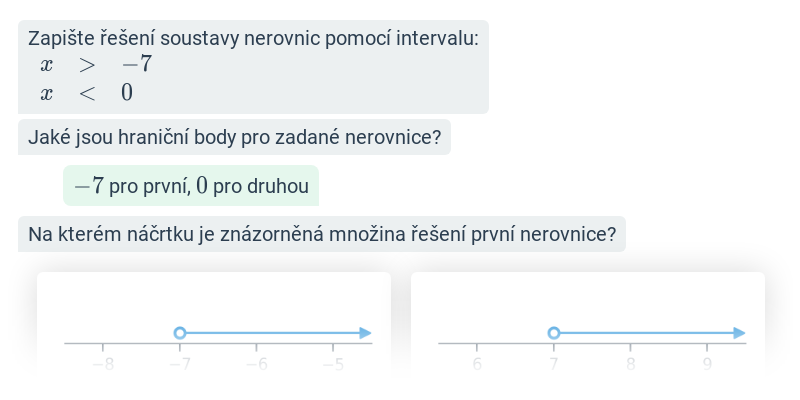
Nerovnice

Nerovnice: zápis řešení

Nerovnice: ekvivalentní úpravy

Jednotky, míry

Čas

Jednotky času

Jednotky

Jednotky délky

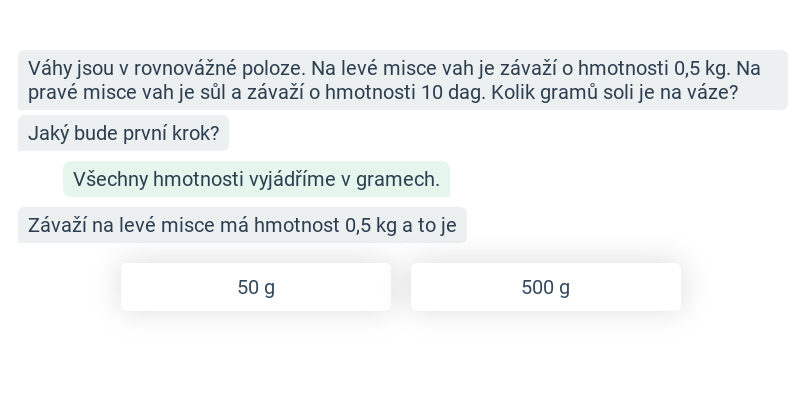
Jednotky hmotnosti

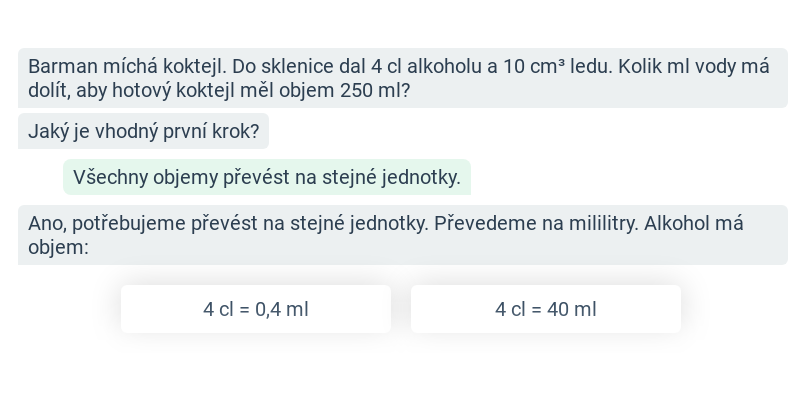
Jednotky objemu

Ukázky

Konstrukční úlohy průřezově

Krok po kroku • lehké

Konstrukční úlohy průřezově

Přímá a nepřímá úměrnost

Krok po kroku • těžké

Přímá a nepřímá úměrnost

Jednotky délky

Krok po kroku • lehké

Jednotky délky

Zápis zadání pomocí rovnice

Krok po kroku • střední

Zápis zadání pomocí rovnice

Násobení a dělení zlomků

Krok po kroku • střední

Násobení a dělení zlomků

Dělení víceciferné

Krok po kroku • lehké

Dělení víceciferné

Převod zlomku na desetinné číslo

Krok po kroku • střední

Převod zlomku na desetinné číslo

Jednotky objemu

Krok po kroku • střední

Jednotky objemu

NAPIŠTE NÁM

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Nejprve se prosím podívejte na časté dotazy:

Časté dotazy Návody pro učitele

Čeho se zpráva týká?

Vzkaz Obsah Ovládání Přihlášení Licence