Zlomky a desetinná čísla

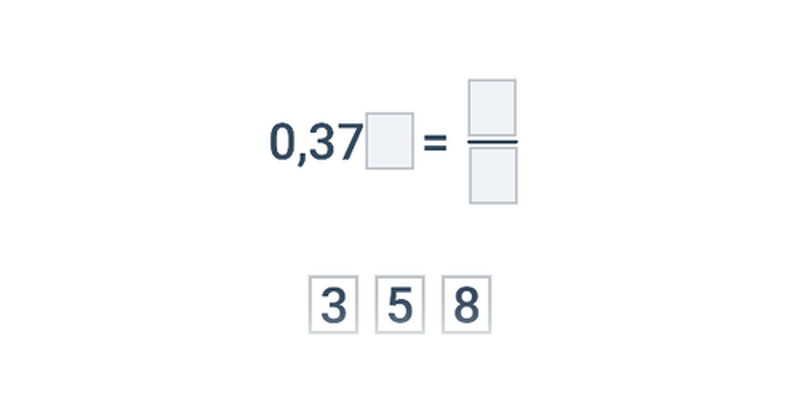
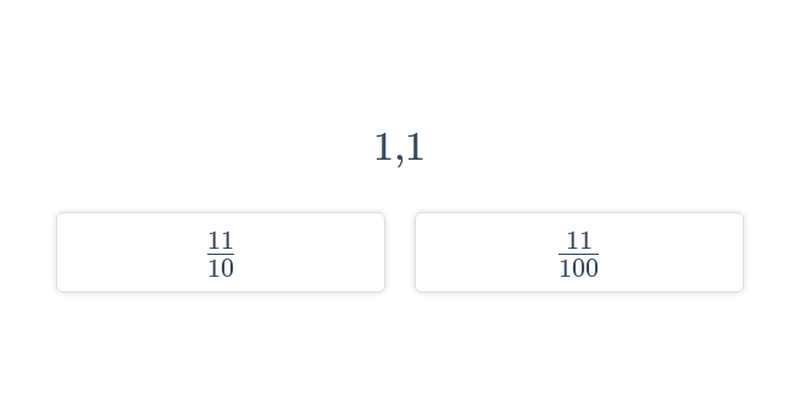
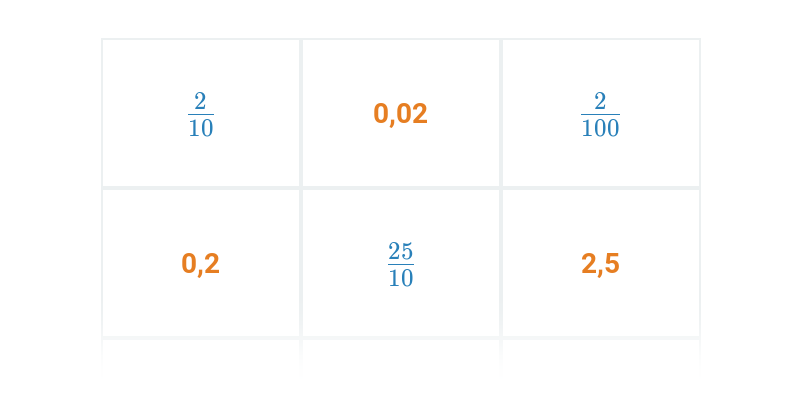
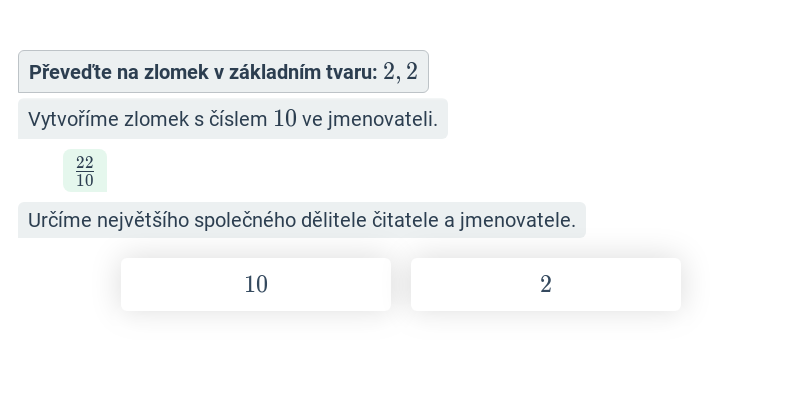
Převod desetinného čísla na zlomek: Desetinné číslo roznásobíme pomocí mocniny desítky tak, abychom se „zbavili“ desetinné čárky. Následně zlomek vykrátíme (největším společným dělitelem), abychom dostali zlomek v základním tvaru. Příklady:

• 1{,}5 = 1{,}5\cdot \frac{10}{10} = \frac{1{,}5\cdot 10}{10} = \frac{15}{10} = \frac{3}{2}

• 1{,}25 = 1{,}25 \cdot \frac{100}{100} = \frac{1{,}25\cdot 100}{100} = \frac{125}{100} = \frac{5}{4}

Počítání nám může usnadnit, když si zapamatujeme některé užitečné převody, s jejichž pomocí vhodné úvahy vyřešit i další příklady:

• 0{,}01 = \frac{1}{100}

• 0{,}1 = \frac{1}{10}

• 0{,}2 = \frac{1}{5}

• 0{,}25 = \frac{1}{4}

• 0{,}333\ldots = \frac{1}{3}

• 0{,}5 = \frac{1}{2}

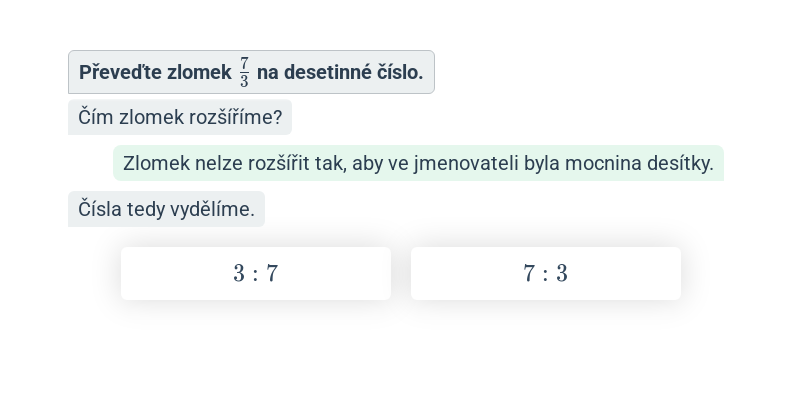
Převod zlomku na desetinné číslo: Význam zlomku je prostě podíl čitatele a jmenovatele. Zlomek tedy vyjádříme jako desetinné číslo prostě tak, že podělíme čitatele jmenovatelem (může se hodit postup pro „dělení pod sebou“). Příklady:

• \frac{3}{4} = 3:4 = 0{,}75

• \frac{6}{5} = 6:5 = 1{,}2

• \frac{3}{20} = 3:20 = 0{,}15