Výpis souhrnů
Aritmetika
Podtémata
- Aritmetika
- Čísla
- Číselná osa do 20
- Římské číslice
- Porovnávání a zaokrouhlování
- Zaokrouhlování na desítky a stovky
- Zaokrouhlování velkých čísel
- Sčítání a odčítání
- Sčítání a odčítání od 20 do 100
- Sčítání pod sebou
- Odčítání pod sebou
- Sčítání, odčítání a logické myšlení
- Násobení a dělení
- Malá násobilka
- Písemné násobení pod sebou
- Dělení jednociferné
- Dělení se zbytkem
- Násobení, dělení a logické myšlení
- Počítání: kombinace operací
- Pořadí operací, závorky
- Počítání a logické myšlení
- Kladná a záporná čísla
- Číselná osa: kladná a záporná čísla
- Počítání se zápornými čísly
- Výrazy s absolutní hodnotou
- Dělitelnost
- Sudé, liché
- Podmínky dělitelnosti
- Prvočísla
- Největší společný dělitel
- Nejmenší společný násobek
- Mocniny a odmocniny
- Mocniny
- Odmocniny
- Výrazy s mocninami a odmocninami
- Záporné mocniny
- Vědecký zápis čísel
- Zlomky, mocniny, odmocniny
- Logaritmus
- Logaritmus: výpočet
- Výrazy s logaritmy
- Logaritmické rovnice
- Grafy exponenciálních funkcí
- Grafy logaritmických funkcí
- Číselná osa
- Zlomky na číselné ose
- Desetinná čísla na číselné ose
Aritmetika
Aritmetika je základní oblast matematiky, která se zabývá čísly a početními operacemi s nimi. Učíme se zde sčítat, odčítat, násobit a dělit, porovnávat čísla, pracovat s mocninami či odmocninami. Aritmetika tvoří základ pro další matematické disciplíny, ale i pro běžné situace každodenního života – od nakupování až po výpočty v přírodních vědách či technice.
Procvičování aritmetiky pokrývá širokou škálu témat a obtížnosti – od 1+1 až po výpočty logaritmů.
| téma | ukázky příkladů a pojmů |
|---|---|
| Čísla | čísla a číslice, slovní vyjádření, římská čísla |
| Porovnávání a zaokrouhlování | 98 < 135, \ 2784 zaokrouhleno na stovky |
| Sčítání a odčítání | 5+8,\ 37-20,\ 356 + 487 |
| Násobení a dělení | 4 \cdot 8, \ 56 : 7, \ 254 \cdot 3 |
| Počítání: kombinace operací | 58 - 3 \cdot (6 + 4) |
| Kladná a záporná čísla | -3 + 7,\ (-4)\cdot(-2), \ 8\cdot |-5| |
| Dělitelnost | největší společný dělitel, prvočísla |
| Mocniny a odmocniny | 4^2, \ \sqrt{49}, \ 5^3 - \sqrt{25} |
| Logaritmus | \log_{10} 1000, \ \log_2 32 |
| Číselná osa | znázornění čísel na ose |
Čísla jsou základním stavebním kamenem matematiky. Pro dobré základní pochopení čísel nabízíme procvičování v těchto tématech:
- Počítání do 20 – základní přiřazení čísel k obrázkově vyjádřeným počtům, posloupnost čísel
- Číselná osa do 20 – umístění čísel na číselnou osu, což pomáhá lépe porozumět pořadí a hodnotám čísel
- Počítání do 100 – přiřazení čísel k obrázkově vyjádřeným počtům do 100
- Čísla a číslice – pochopení rozdílu mezi čísly a číslicemi, například jak se číslo 25 skládá z číslic 2 a 5
- Římské číslice – práce s římskými číslicemi (I, V, X, L, C, D, M)
- Čísla do 1 000 slovně – vztah mezi čísly a jejich slovním vyjádřením, např. 456 a „čtyři sta padesát šest“
- Velká čísla slovně – práce s velkými čísly ve slovní podobě
Číselná osa do 20
Číselná osa znázorňuje čísla. Čísla jsou na ní vyznačena značkami. Popsány jsou většinou jen některé značky, jinak by se popisky překrývaly a bylo by to nepřehledné. Zbylá čísla si dopočítáme. Číselnou osu si můžeme představit jako procházku. Začínáme na startu, kterým je číslo nula, a každý krok vede na novou značku s novým číslem.
Jednoduchý příklad číselné osy, na které hledáme číslo 7:

Římské číslice
Římské číslice představují způsob zápisu čísel pomocí písmen latinské abecedy. Na rozdíl od běžně používaného zápisu čísel (arabské číslice, desítková soustava) jde o nepoziční číselnou soustavu. Římské číslice nejsou vhodné pro matematické výpočty, například násobení v tomto zápisu je výrazně náročnější než v desítkové soustavě. Římské číslice se však stále používají, například pro uvádění letopočtů na památnících, na hodinách, pro číslování kapitol v knihách, …
Základní římské číslice jsou I, V, X, L, C, D, M. Jejich hodnoty jsou následující:
| I | V | X | L | C | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Další čísla vytváříme spojováním a opakováním symbolů. Symboly řadíme za sebe podle velikosti. Pro zkrácení zápisu se využívá odčítání v případě, že menší symbol předchází větší. Příklady:
| Římské | Desítkové | Vysvětlení |
|---|---|---|
| XXVII | 27 | prosté sčítání příslušných symbolů: 10 + 10 + 5 + 1 + 1 |
| MDCCXIII | 1713 | opět prosté sčítání příslušných symbolů: 1000 + 500 + 100 + 100 + 10 + 1 + 1 + 1 |
| IV | 4 | I je před V, odčítáme tedy: -1 + 5 |
| XIX | 19 | I je před X, opět odčítáme: 10 - 1 + 10 |
| DCCXC | 790 | X je před C, odčítáme tedy 10: 500 + 100 + 100 - 10 + 100 |
Komiks pro zpestření

Porovnávání a zaokrouhlování
Ještě než začneme s čísly počítat, potřebujeme mít dobrou představu o tom, co představují a v jakém jsou vztahu – které číslo vyjadřuje větší či menší hodnotu. K tomu slouží procvičování porovnávání.
Zaokrouhlování nám pak pomáhá soustředit se na „důležitou“ část čísla, což se hodí pro dobrou základní představu o významu čísel. Také nám to pomáhá rychle odhadovat a kontrolovat výsledky výpočtů – jak už při práci v matematice, tak v běžném životě (např. při práci s penězi či měření).
| téma | příklady |
|---|---|
| Porovnávání čísel do 20 | 8 < 12, \ 19 > 9 |
| Porovnávání čísel do 100 | 60 < 90,\ 84 > 48 |
| Porovnávání čísel do 1000 | 578 > 99, \ 895 < 958 |
| Porovnávání čísel do 1 000 000 | 125\,340 < 213\,405 |
| Zaokrouhlování na desítky a stovky | 276 zaokrouhleno na desítky |
| Zaokrouhlování velkých čísel | 3\,746\,260 zaokrouhleno na statisíce |
Zaokrouhlování na desítky a stovky
Zaokrouhlování znamená, že vezmeme číslo a nahradíme jej jiným, které má přibližně stejnou velikost, ale je „jednodušší“. Například číslo 96 můžeme zaokrouhlit na číslo 100. Zaokrouhlování nám umožňuje například provádět přibližné výpočty nebo snadněji komunikovat.
Zaokrouhlování na desítky znamená, že číslo nahradíme nejbližším násobkem desítky. Například k číslu 37 je nejbližší násobek desítky číslo 40 (má vzdálenost 3). U čísel, která končí cifrou 5, není takto definované zaokrouhlování jednoznačné, například číslo 35 má stejnou vzdálenost od čísel 30 a 40. Pro tyto případy je zavedeno pravidlo, které říká, že zaokrouhlujeme nahoru, tj. číslo 35 zaokrouhlujeme na 40. Zaokrouhlování na stovky funguje stejně, jen nahrazujeme číslo nejbližším násobkem stovky.
Příklady zaokrouhlování na desítky
- 44 zaokrouhleno na desítky je 40.
- 47 zaokrouhleno na desítky je 50.
- 165 zaokrouhleno na desítky je 170.
- 30 zaokrouhleno na desítky je 30 (číslo 30 už je násobek desítky, tak jej prostě necháme být).
- 3 zaokrouhleno na desítky je 0 (číslo 3 je blíže žádným desítkám než jedné desítce).
Příklady zaokrouhlování na stovky
- 98 zaokrouhleno na stovky je 100.
- 44 zaokrouhleno na stovky je 0 (nejbližší násobek stovky je 0).
- 487 zaokrouhleno na stovky je 500.
- 1842 zaokrouhleno na stovky je 1800.
- 850 zaokrouhleno na stovky je 900.
- 1111 zaokrouhleno na stovky je 1100.
- 2070 zaokrouhleno na stovky je 2100.
Komiks pro zpestření

Zaokrouhlování velkých čísel
Zaokrouhlování velkých čísel i na vyšší řády než desítky a stovky probíhá podobně jako u zaokrouhlování menších čísel. Zaokrouhlujeme‑li na určitý řád, řídíme se podle číslice, která je na místě nejbližšího menšího řádu.
Při zaokrouhlování na tisíce nás zajímá, zda je číslice na místě stovek menší než 5 (zaokrouhlujeme dolů), a nebo větší nebo rovna 5 (zaokrouhlujeme nahoru). Při zaokrouhlování na desetitisíce se rozhodujeme podle hodnoty na místě tisíců, atd.
Můžeme zaokrouhlovat i menší čísla na vyšší řády, např. zaokrouhlit číslo 64 na desetitisíce, na místě tisíců má nulu, což je menší než 5, takže 64 zaokrouhleno na desetitisíce je 0.
Další příklady zaokrouhlování velkých čísel
- 12 345 zaokrouhleno na tisíce je 12 000.
- 47 000 zaokrouhleno na desetitisíce je 50 000.
- 91 875 zaokrouhleno na statisíce je 100 000.
- 10 222 189 zaokrouhleno na miliony je 10 000 000.
- 10 522 189 zaokrouhleno na miliony je 11 000 000.
- 9 zaokrouhleno na tisíce je 0 (řídíme se podle 0 na místě stovek, takže 0 na místě tisíců nebudeme zaokrouhlovat nahoru na 1, ale zůstává 0; odpovídá to faktu, že číslo 9 je blíže žádným tisícům než jednomu tisíci).
- 1000 zaokrouhleno na statisíce je také 0.
Sčítání a odčítání
Sčítání a odčítání jsou základní matematické operace, které tvoří základ pro další početní dovednosti. Procvičování tohoto tématu začíná prací s malými čísly, kde získáváme základní představu o těchto operacích (například pomocí grafických rozkladů) a učíme se počítat zpaměti. Následně pokračuje k písemnému počítání a provázání počítání a logického myšlení.
- Sčítání a odčítání do 10 – úplné základy, zadání doplněné o znázornění čísel obrázkem
- Sčítání a odčítání do 20 – důkladné pamětné zvládnutí základů, rozklad desítky
- Sčítání a odčítání od 20 do 100 – počítání po desítkách, operace bez přechodu i s přechodem přes desítku
- Sčítání a odčítání nad 100 – práce s většími čísly, počítání z hlavy i písemné sčítání a odčítání („pod sebou“)
- Sčítání, odčítání a logické myšlení – různé zajímavé logické úlohy, u kterých je potřeba nejen dobře sčítat a odčítat, ale také promyslet správný postup řešení
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 1.–2. ročník | úplné základy, obrázková zadání | |
| 1.–2. ročník | přechod přes desítku, plynulé zvládnutí sčítání a odčítání do 20 | |
| 1.–3. ročník | zvládnutí různých strategií, rozklady, netradiční úlohy | |
| 3.–5. ročník | počítání zpaměti i písemné postupy, slovní a problémové úlohy |
Sčítání a odčítání od 20 do 100
Pro snadnější zvládnutí lze procvičovat samostatně sčítání a odčítání:
Kromě interaktivních cvičení je k dispozici také pracovní list na vytištění, který může posloužit například pro souhrnné opakování:
NahoruSčítání pod sebou
Při písemném sčítání postupujeme následovně:
- Čísla si napíšeme pod sebe, zarovnaná doprava.
- Postupujeme z pravé strany.
- Vždy sečteme dvě čísla pod sebou a výsledek zapíšeme pod ně.
- Pokud je výsledek větší než 10, zapisujeme pouze číslo na pozici jednotek. Číslo na pozici desítek přenášíme dál doleva – přičteme jej v dalším sloupci.
Řešený příklad 3728+436
- Postupujeme zprava, tedy nejprve sečteme 8+6=14. Zapisujeme 4, 1 přenášíme dál.
- Dále sčítáme 2+3 a navíc přičteme 1 z předchozího sloupce. Zapisujeme 6.
- Dále sčítáme 7+4=11 (z předchozího sloupce nic nepřenášíme), zapisujeme 1 a 1 přenášíme.
- Dále už máme jen 3, z druhého čísla nám nic nezbylo. Přidáme ovšem ještě 1 z předchozího sloupce. Zapisujeme 4.
- Dostáváme výsledek 4164.
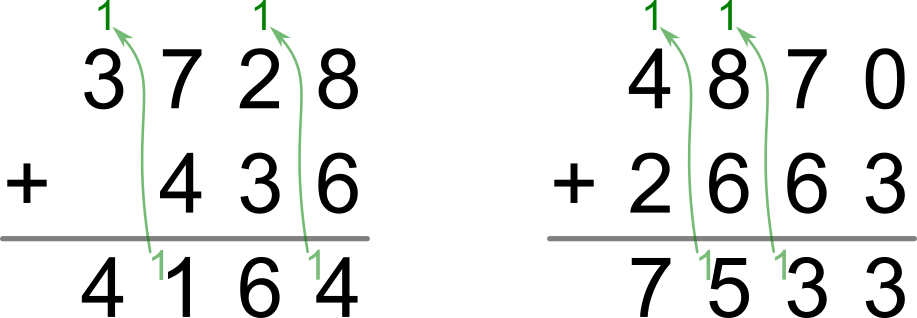
Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list na vytištění:
NahoruOdčítání pod sebou
Při písemném odčítání postupujeme následovně:
- Čísla si napíšeme pod sebe, zarovnaná doprava.
- Postupujeme z pravé strany.
- Vždy odečteme dvě čísla pod sebou a výsledek zapíšeme pod ně.
- Pokud je horní číslo menší než spodní, tak si „půjčíme“ desítku a místo ní v dalším sloupci odečteme o 1 víc.
Řešený příklad 3728−436
- Postupujeme zprava, tedy nejprve odečteme 8−6=2.
- V dalším sloupci odečítáme 2−3. Zde je 2 menší než 3, „půjčíme“ si desítku a počítáme 12−3=9.
- Dále odečítáme 7−4, musíme ale ještě odečíst 1 za půjčenou desítku z předchozího sloupce, tedy 7−4−1=2.
- V dalším sloupci již máme jen 3, od ní nemáme co odečíst.
- Výsledek je tedy 3292.
Řešený příklad 4830−2663
- Postupujeme zprava. Nejprve chceme odečíst 0−3. Jenže 0 je menší než 3, tak si „půjčíme“ desítku a počítáme 10−3=7. Do dalšího sloupečku si pamatujeme 1.
- V dalším sloupci musíme navíc odečíst zapamatovanou jedničku. Odečítáme 3−6−1, neboli 3−7. Máme 3 menší než 7, takže si „půjčíme“ desítku: počítáme 13−7=6 a do dalšího sloupečku si pamatujeme 1.
- V dalším sloupci opět odečítáme navíc zapamatovanou jedničku, počítáme 8−6−1, tedy 8−7=1.
- V posledním sloupci počítáme 4−2=2.
- Výsledek je tedy 2167.
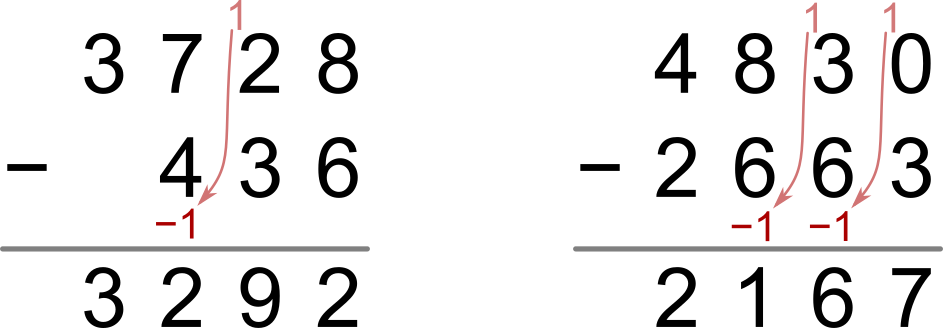
Sčítání, odčítání a logické myšlení
Zde najdete zajímavé úlohy, na kterých můžete zábavnou formou potrénovat nejen operace sčítání a odčítání, ale také svou schopnost logicky přemýšlet a plánovat postup řešení.
NahoruNásobení a dělení
Násobení a dělení jsou základní početní operace, které navazují na sčítání a odčítání.
Násobení a dělení malými čísly se vyplatí umět důkladně zpaměti. Je to něco jako znalost základních slovíček v cizím jazyce. Bez hladkého zvládnutí základních výpočtů se v matematice „nedomluvíme“.
Na tyto základy navazuje násobení a dělení vícecifernými čísly. Na tom si dobře procvičíme základní násobilku a důkladné pochopení principu násobení a dělení:
Pro větší čísla pak používáme písemný zápis:
Téma násobení, dělení a logické myšlení pak představuje různé zajímavé logické úlohy, u kterých je potřeba nejen dobře počítat, ale také promyslet správný postup řešení.
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 2.–4. ročník | násobení a dělení v rozsahu malé násobilky (jednociferní činitelé), důraz na pamětné počítání | |
| 4.–6. ročník | počítání s vícecifernými čísly, písemné postupy, slovní úlohy |
Malá násobilka
Násobení nám říká, kolik čtverečků má čokoláda, když víme, kolik má řádků a sloupců:
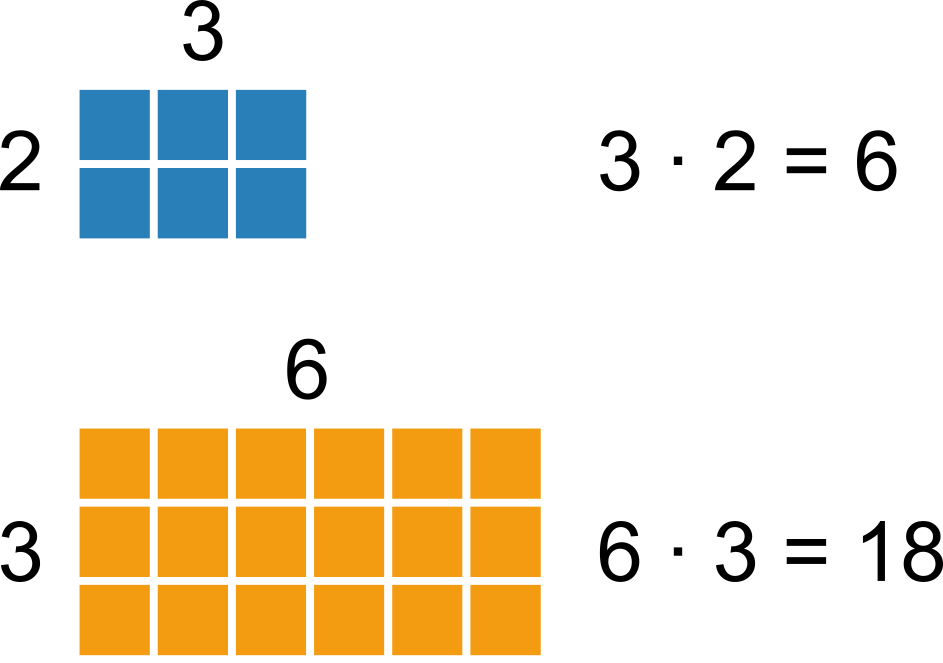
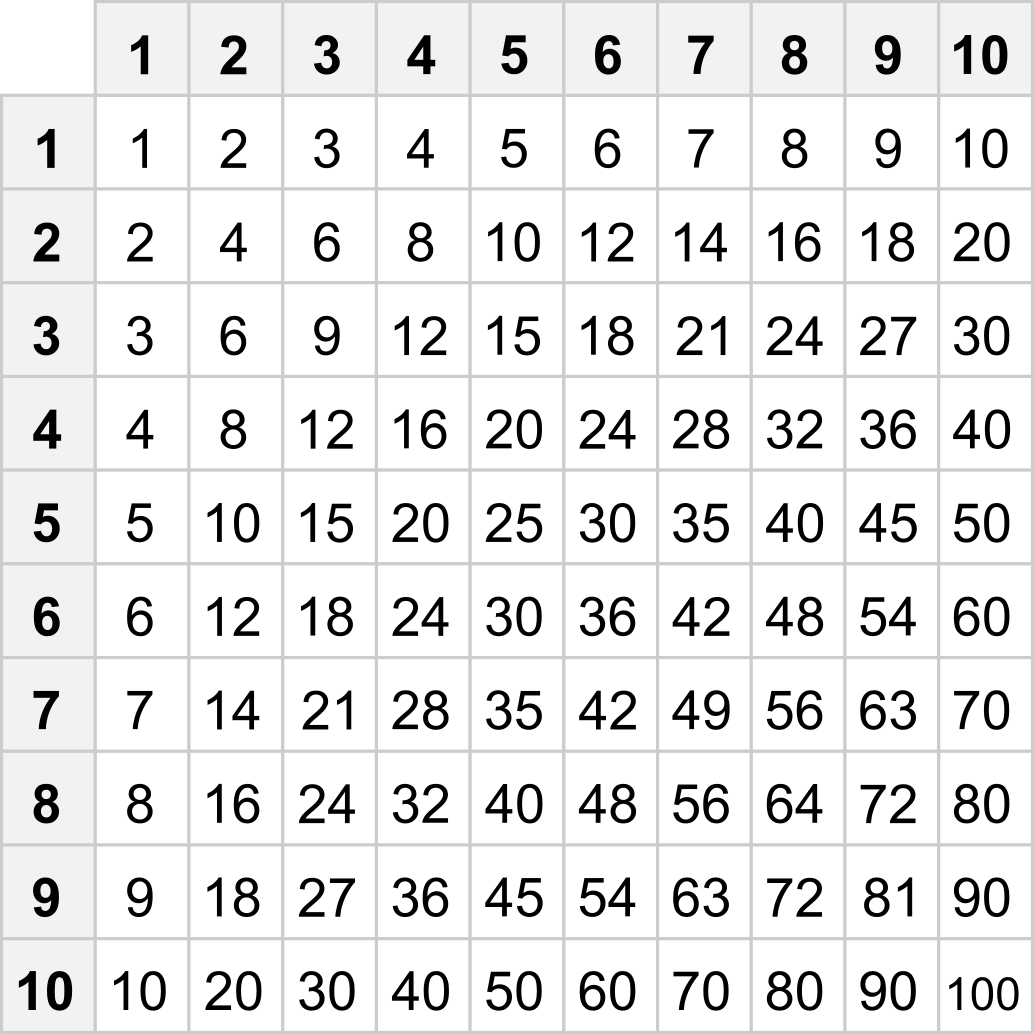
Násobení využíváme v matematice i v běžném životě velice často. Proto se velmi vyplatí naučit se základní násobky zpaměti. Malá násobilka zahrnuje vzájemné součiny čísel od 1 do 10. Ty můžeme přehledně vyjádřit tabulkou malé násobilky:
Pracovní list: slovní úlohy
Kromě interaktivních cvičení je k dispozici také pracovní list na vytištění:
Komiks pro zpestření
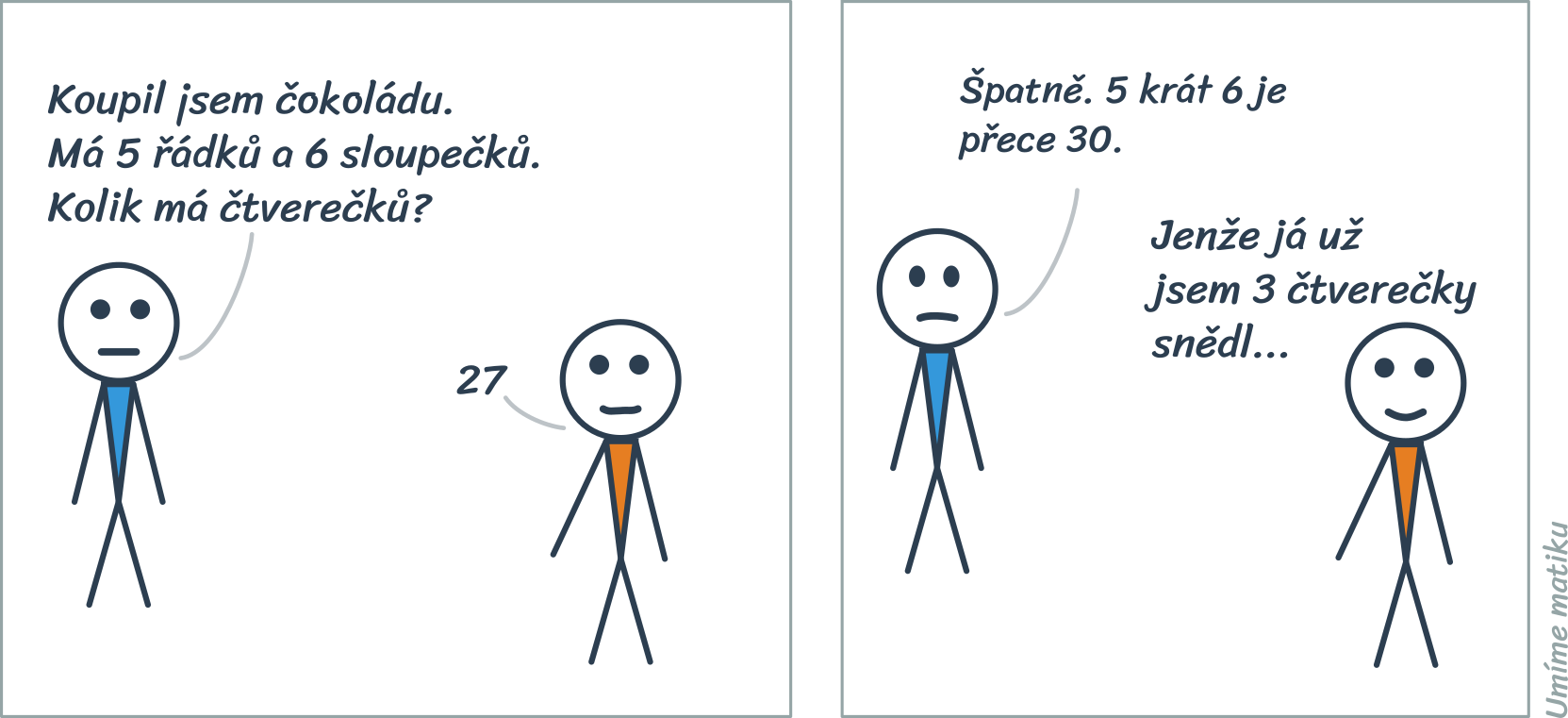
Písemné násobení pod sebou
Při písemném násobení postupujeme následovně:
- Čísla si napíšeme pod sebe, zarovnaná doprava.
- Postupně jednotlivými ciframi spodního čísla pronásobíme celé horní číslo.
- Výsledky dílčích násobení zapisujeme na řádky pod sebe. Výsledky odsazujeme podle pozice cifry, kterou jsme násobili.
- Nakonec všechny dílčí výsledky sečteme (viz postup pro sčítání pod sebou).
Obrázek ukazuje příklad násobení čísel 79 a 68.

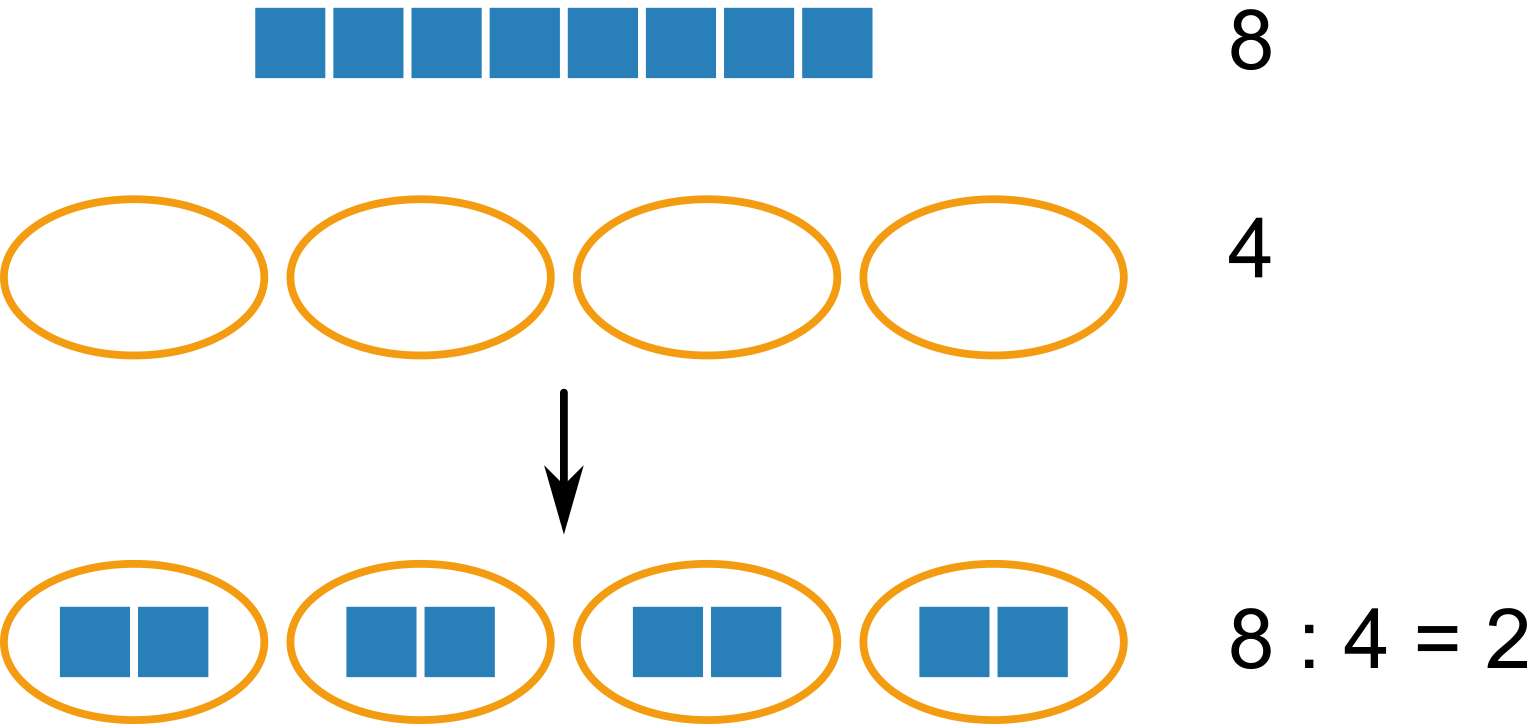
Dělení jednociferné
Když mám 8 jablíček a chci je rozdělit rovnoměrně do 4 košíků, kolik jablíček bude v každém košíku? Této otázce v matematice odpovídá dělení:
Dělení se zbytkem
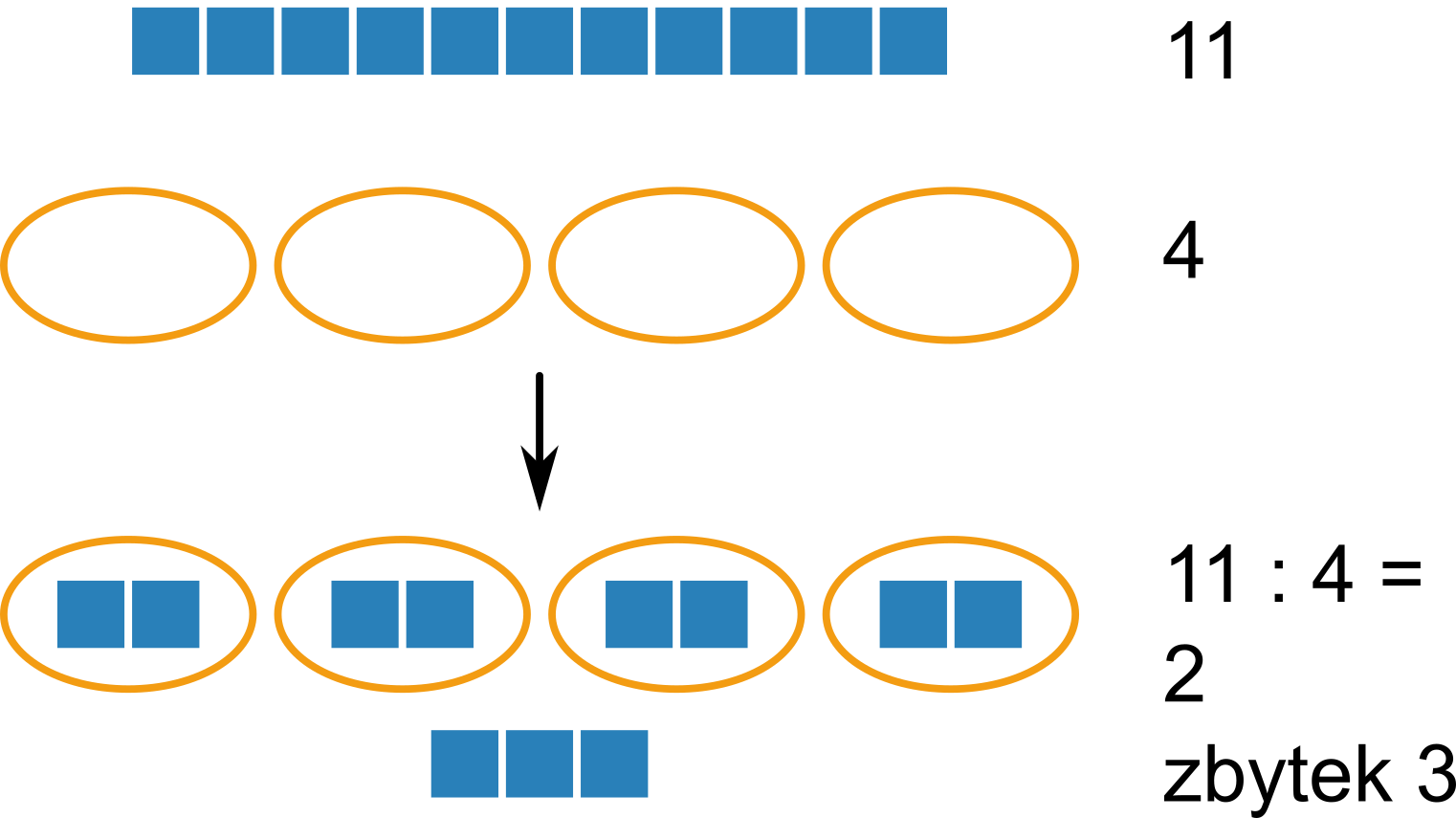
Zbytek po dělení je početní operace související s celočíselným dělením. Pokud dělíme a:b, pak můžeme psát a = k\cdot b + z, přičemž 0 \leq z \lt b. Číslo k nazýváme podíl, číslo z zbytek. Operace dělení se zbytkem se v matematice nazývá též modulo.
Příklad: 11:4 dává podíl 2 a zbytek 3, protože 11 = 2\cdot 4 + 3. Pokud mám 11 jablek a rozdělím je rovnoměrně do 4 košíků, v každém košíku budou 2 jablka a ještě mi 3 zbydou.
Další příklady:
- 17:5 dává zbytek 2, protože 17 = 3\cdot 5 + 2.
- 21:6 dává zbytek 3, protože 21 = 3\cdot 6 + 3.
- 12:7 dává zbytek 5, protože 12 = 1\cdot 7 + 5.
- 4:6 dává zbytek 4, protože 4 = 0\cdot 6 + 4.
Komiks pro zpestření
Násobení, dělení a logické myšlení
Zde jsou zajímavé úlohy, na kterých si můžete zábavnou formou procvičit operace násobení a dělení a také svou schopnost logicky přemýšlet a naplánovat si správný postup.
NahoruPočítání: kombinace operací
Předcházející témata v rámci aritmetiky se zabývají jednotlivými početními operacemi samostatně. Zde jsou zahrnuty příklady, ve kterých se kombinuje více operací.
| téma | příklady |
|---|---|
| Porovnávání výsledků: sčítání a odčítání do 20 | 8 + 5 < 7 + 9 |
| Sčítání a odčítání se závorkami | (12 + 40) - (17 + 5) |
| Pořadí operací, závorky | (1+2)\cdot 3 - 4:2 |
| Porovnávání výsledků výpočtů | 29 + 13 > 8\cdot 5 |
| Zápis číselných výrazů | součet čísel 2 a 7 zvětšený třikrát |
| Přibližné počítání | přibližná hodnota 7264 \cdot 8 |
| Počítání a logické myšlení | číselné křížovky, magické čtverce, obrázkové rovnice… |
Pořadí operací, závorky
Výrazy vyhodnocujeme v tomto pořadí:
- závorky,
- násobení a dělení,
- sčítání a odčítání.
Pokud se ve výrazu vyskytují operace na stejné úrovni, provádějí se zleva doprava. Pokud jsou ve výrazu závorky v několika úrovních, postupujte vždy od vnitřních po vnější závorky.
Příklady
| 1+ 2\cdot 3 + 4 | = 1+ 6+4=11 | Nejdříve násobení, potom sčítání. |
| (1+2)\cdot 3 +4 | = 3\cdot 3 +4 = 9 + 4 = 13 | Nejdříve závorka, potom násobení, nakonec sčítání. |
| (1+2)\cdot(3 +4) | = 3\cdot 7 = 21 | Nejdříve obě závorky, potom násobení. |
| 9 - 5 + 2 | = 4 + 2 = 6 | Sčítání a odčítání jsou na stejné úrovni, vyhodnocujeme zleva doprava. |
| (9 - (2 + 3))\cdot 2 | =(9-5)\cdot 2 = 4\cdot 2 = 8 | Nejdříve vnitřní závorka, potom vnější závorka. |
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruPočítání a logické myšlení
Pod tímto tématem najdete zábavné úlohy a hříčky na procvičení základních operací (sčítání, odčítání, násobení a dělení). Řešení následujících úkolů potrénuje také vaši schopnost logicky myslet a plánovat si správný postup.
NahoruKladná a záporná čísla
Kladná čísla představují množství nebo růst (například počet jablek nebo příjmy), zatímco záporná čísla vyjadřují nedostatek nebo pokles (například snědená jablka nebo výdaje).
Procvičování práce s kladnými a zápornými čísly je rozděleno na několik podtémat:
- Porovnávání kladných a záporných čísel – například -2 \lt 3 nebo 5 > -1
- Číselná osa: kladná a záporná čísla – umístění kladných a záporných čísel na číselnou osu, což nám pomáhá řešit ostatní úkoly
- Počítání se zápornými čísly – například -3 + 5 = 2 nebo 4 - (-6) = 10
- Výrazy s absolutní hodnotou – příklady pracující s absolutní hodnotou, která udává vzdálenost čísla od nuly, například |-4| = 4
Číselná osa: kladná a záporná čísla
Číselná osa je přímka znázorňující čísla. Značkami jsou na ní vyznačená vybraná čísla – většinou celá čísla. Popsány jsou většinou jen některé značky, jinak by se popisky překrývaly a bylo by to nepřehledné. Zbylá čísla si dopočítáme.
Tradičně se na číselné ose píší menší čísla vlevo, větší čísla vpravo. Záporná čísla jsou tedy vlevo od nuly. Příklad číselné osy s vyznačenými hodnotami 7 a -7:

Počítání se zápornými čísly
Při počítání se zápornými čísly často používáme princip „mínus a mínus dává plus“. Konkrétní příklady:
| Přičítání záporného čísla je to stejné jako odčítání: | 6 + (-2) = 6-2=4 |
| Odčítání záporného čísla se upraví na přičítání: | 6 - (-2) = 6+2=8 |
| Násobení kladného a záporného čísla dá záporný výsledek: | 6\cdot(-2) = -12 |
| Násobení dvou záporných čísel dá kladný výsledek: | (-6)\cdot(-2) = 12 |
| Dělení kladného čísla záporným dá záporný výsledek: | 6:(-2) = -3 |
| Dělení záporného čísla záporným dá kladný výsledek: | (-6):(-2) = 3 |
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruVýrazy s absolutní hodnotou
Absolutní hodnota čísla je jeho vzdálenost od nuly. Absolutní hodnotu čísla x značíme pomocí svislých čar: |x|.
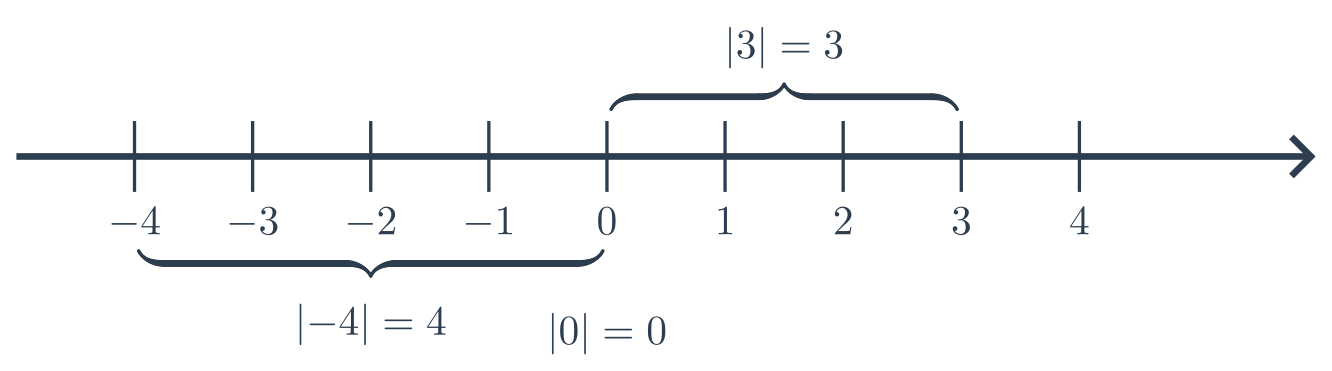
Příklady:
- |5| = 5
- \left|-5\right| = 5
- \left|-13\right| = 13
- |2{,}45| = 2{,}45
Pro kladné x je |x|=x, pro záporné x je |x| = -x.
Při vyhodnocování výrazů, ve kterých se vyskytuje absolutní hodnota, nejdříve vyhodnotíme výraz uvnitř svislých čar (podobně jako u závorek) a pak aplikujeme samotnou absolutní hodnotu:
- 3 + |4-6| = 3 + \left|-2\right| = 3+2=5
- 5-3 \cdot |4-2| = 5 -3\cdot|2| = 5 -3\cdot2 = 5 - 6 = -1
Dáváme pozor na rozdíl mezi kulatou závorkou (která pouze vyznačuje přednost operací) a svislými čárami (které značí absolutní hodnotu):
- 3+(-2) = 3 - 2 = 1
- 3+\left|-2\right| = 3 + 2 = 5
Také dáváme dobrý pozor, kde se vyskytují znamínka mínus (před versus za svislou čárou):
- \left|-4\right| = 4
- -|4| = -4
- \left|-3-2\right| = \left|-5\right| = 5
- -|3-2| = -|1| = -1
Dělitelnost
Dělitelnost se zabývá určováním, zda jedno číslo je dělitelné druhým bez zbytku. Například číslo 24 je dělitelné číslem 6, ale není dělitelné číslem 7.
Sudost a lichost odpovídají dělitelnosti číslem 2, jde o nejjednodušší případ dělitelnosti.
Podmínky dělitelnosti nám pomáhají určit, zda je jedno číslo dělitelné jiným číslem bez toho, abychom prováděli samotné dělení. Například číslo je dělitelné číslem 3, pokud je jeho ciferný součet dělitelný číslem 3. Abychom tedy poznali, že číslo 513 je dělitelné číslem 3, stačí si všimnout, že ciferný součet (5+1+3=9) je dělitelný číslem 3 a nemusíme provádět dělení 513:3.
Prvočísla jsou čísla větší než 1, která mají pouze dva dělitele: jedničku a sama sebe. Prvočísla jsou základními stavebními kameny ostatních čísel ve smyslu jejich dělitelnosti.
Největší společný dělitel je největší číslo, kterým jsou dvě nebo více čísel beze zbytku dělitelná. Společný dělitel hraje klíčovou roli při zjednodušování zlomků a řešení rovnic.
Nejmenší společný násobek je nejmenší číslo, které je násobkem dvou nebo více čísel. Společný násobek se často používá při práci se zlomky.
Dělitelnost je základem pro mnoho konceptů v matematice a má bohaté využití například v moderní kryptologii (šifrování).
NahoruSudé, liché
Sudá čísla jsou celá čísla, která jsou beze zbytku dělitelná dvěma. Sudá čísla končí cifrou 0, 2, 4, 6 nebo 8. Příklady sudých čísel jsou 138, 12, 0, 9356, -34, 6.
Lichá čísla jsou celá čísla, která po dělení dvěma dávají zbytek jedna. Lichá čísla končí cifrou 1, 3, 5, 7 nebo 9. Příklady lichých čísel jsou 15, 891, -7, 1, 95.
NahoruPodmínky dělitelnosti
Číslo a je dělitelné nenulovým celým číslem b právě tehdy, když a je celočíselným násobkem b, tj. a = k\cdot b. Jinými slovy: číslo a dává po dělení číslem b zbytek 0. Příklady:
- Číslo 15 je dělitelné číslem 5, protože 15 = 3\cdot 5.
- Číslo 25 není dělitelné číslem 4, protože 25 = 6\cdot 4 + 1 (zbytek není nulový).
Pro některé dělitele můžeme dělitelnost rozpoznat poměrně snadno:
| Dělitel | Kritérium | Příklady |
|---|---|---|
| 2 | Sudé číslo na místě jednotek. | 18, 2546, 2 778 1452 |
| 3 | Ciferný součet dělitelný číslem 3. | 252 867 (2+5+2+8+6+7=30) |
| 4 | Poslední dvojčíslí je dělitelné číslem 4. | 180, 73524 |
| 5 | Na místě jednotek je 0 nebo 5. | 90, 1265 |
| 9 | Ciferný součet dělitelný číslem 9. | 252 864 (2+5+2+8+6+4=27) |
| 10 | Na místě jednotek je 0. | 250, 1 876 3520 |
Prvočísla
Prvočíslo je přirozené číslo větší než 1, které je dělitelné pouze jedničkou a sebou samým.
Složené číslo je přirozené číslo větší než 1, které není prvočíslem, tj. má i jiného dělitele než jedničku a samo sebe.
Příklady složených čísel a prvočísel
- 6 je složené číslo, protože je dělitelné například číslem 2.
- 7 je prvočíslo, protože je dělitelné pouze čísly 1 a 7.
- 13 je prvočíslo, protože je dělitelné pouze čísly 1 a 13.
- 15 je složené číslo, protože je dělitelné například číslem 3.
Podle výše uvedené definice není číslo 1 prvočíslo ani složené číslo. To je běžná matematická konvence, protože to vede k elegantnější formulaci různých matematických výsledků. Existují ale i jiné přístupy k pojetí prvočíselnosti jedničky (vesměs historické).
Prvočísel je nekonečně mnoho. Prvočísla menší než 100 jsou: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Každé číslo lze rozložit jednoznačně na prvočíselný rozklad.
Příklad: prvočíselné rozklady čísel
- 12 = 2 \cdot 2 \cdot 3
- 30 = 2 \cdot 3\cdot 5
- 1638 = 2 \cdot 3^2\cdot 7\cdot 13
Největší společný dělitel
Největší společný dělitel (NSD) dvou celých čísel je největší číslo, které beze zbytku dělí obě čísla. Příklady: NSD(18, 24) = 6, NSD(12, 21) = 3, NSD(24, 35) = 1. Pojem největšího společného dělitele lze zobecnit i na větší počet vstupních čísel. Například NSD(30, 85, 90) = 5. Typickým využitím největšího společného dělitele je krácení zlomků.
- Pokud největší společný dělitel dvou čísel je 1, nazýváme je nesoudělná. Například čísla 15 a 32 jsou nesoudělná.
- Pokud je největší společný dělitel větší než 1, jde o čísla soudělná. Například čísla 20 a 24 mají největší společný dělitel 4, tedy jsou soudělná.
Pro malá čísla můžeme největšího společného dělitele určit tak, že si prostě vypíšeme všechny dělitele.
Příklad: NSD(18, 24) řešený výčtem dělitelů
- Dělitelé čísla 18 jsou 1, 2, 3, 6, 9, 18.
- Dělitelé čísla 24 jsou 1, 2, 3, 4, 6, 8, 12, 24.
- Společní dělitelé čísel 18 a 24 jsou 1, 2, 3, 6.
- Největší společný dělitel je 6.
Pro větší čísla můžeme největšího společného dělitele určit pomocí prvočíselného rozkladu. Obě čísla rozepíšeme jako součin prvočísel, výsledný NSD je součin prvočísel vyskytujících se v obou rozkladech umocněných na příslušné nejmenší exponenty.
Příklad NSD(18, 24) řešený pomocí rozkladu
- 18 = 2\cdot 3 \cdot 3 = 2\cdot3^2
- 24 = 2 \cdot 2 \cdot 2\cdot 3 = 2^3\cdot 3
- Společná část prvočíselného rozkladu: 2, 3.
- \mathit{NSD}(18, 24) = 2\cdot 3 = 6
Příklad NSD(540, 315) řešený pomocí rozkladu
- 540 = 2\cdot 2\cdot3\cdot 3\cdot 3\cdot 5 = 2^2\cdot3^3\cdot 5
- 315 = 3\cdot 3 \cdot 5\cdot 7 = 3^2 \cdot 5\cdot 7
- Společná část prvočíselného rozkladu: 3, 3, 5
- \mathit{NSD}(540, 315) = 3\cdot 3\cdot 5 = 3^2\cdot 5 = 45
Pro praktické výpočty se používají jiné algoritmy, především Euklidův algoritmus.
NahoruNejmenší společný násobek
Nejmenší společný násobek (NSN) dvou celých čísel je nejmenší číslo, které je beze zbytku dělitelné oběma čísly. Příklady: NSN(12, 15) = 60, NSN(6, 8) = 24, NSN(3, 15) = 15. Pojem nejmenšího společného násobku lze zobecnit i na větší počet vstupních čísel. Například NSN(2, 3, 4) = 12. Typické využití nejmenšího společného násobku je při převodu zlomků na společného jmenovatele při sčítání zlomků.
Pro malá čísla můžeme nejmenší společný násobek najít tak, že si vypíšeme několik prvních násobků od obou čísel.
Příklad: NSN(12, 15) řešený výčtem násobků
- Násobky čísla 12 jsou 12, 24, 36, 48, 60, 72, 84, …
- Násobky čísla 15 jsou 15, 30, 45, 60, 75, 90, …
- Nejmenší společný násobek je první číslo, které se vyskytuje v obou seznamech. V tomto případě tedy 60.
Pro větší čísla můžeme nejmenší společný násobek nalézt pomocí prvočíselného rozkladu. NSN je roven součinu všech prvočísel, které se vyskytují alespoň v jednom rozkladu (v nejvyšší mocnině, v jaké se vyskytují).
Příklad: NSN(24, 45) řešený pomocí rozkladu
- 24 = 2^3\cdot 3
- 45 = 3^2 \cdot 5
- \mathit{NSN}(24, 45) = 2^3 \cdot 3^2 \cdot 5 = 360
Nejmenší společný násobek lze vypočítat také pomocí největšího společného dělitele (NSD): \mathit{NSN}(a, b) = \frac{a\cdot b}{\mathit{NSD}(a, b)}
NahoruMocniny a odmocniny
Umocňování je opakované násobení. Například 3^5 = 3\cdot 3\cdot 3\cdot 3\cdot 3 = 243. Odmocňování je opačnou operací k umocňování. Například druhá odmocnina z 36 je 6 (\sqrt{36}=6), protože 6^2 = 6\cdot 6 = 36. Mocniny a odmocniny využíváme v mnoha oblastech matematiky, například při práci s mnohočleny, řešení kvadratických rovnic, výpočtu obsahu a objemu nebo při určování délek stran v trojúhelníku.
Téma mocnin a odmocnin pokrývá širokou škálu obtížnosti principů a příkladů. Proto toto téma dělíme na více dílčích podtémat, která jsou snáz zvládnutelná:
| téma | příklady |
|---|---|
| Druhé mocniny a odmocniny malých čísel | 5^2,\ 7^2,\ 2^3 |
| Mocniny deseti a 0,1 | 10^4,\ 0{,}1^3 |
| Mocniny | 9^2,\ 5^3,\ (-3)^2,\ 11^2,\ 5^0 |
| Odmocniny | \sqrt{36},\ \sqrt{81},\sqrt[4]{10 000} |
| Výrazy s mocninami a odmocninami | 3^4\cdot 3^5,\ \sqrt{\frac{4}{9}},\ \sqrt[3]{5^6} |
| Záporné mocniny | 2^{-3},\ 0{,}5^{-2},\ 10^{-5} |
| Vědecký zápis čísel | 5{,}97 \cdot 10^{24} |
| Zlomky, mocniny, odmocniny | (\frac{2}{5})^2,\ \sqrt{\frac{2}{3}},\ 81^\frac{3}{4} |
| Desetinná čísla, mocniny, odmocniny | \sqrt{0{,}25},\ 4^{0{,}5} |
Tip k procvičování
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytuje výukový modul určený pro 7.–9. ročník.
Mocniny jsou zkráceným zápisem opakujícího se násobení. Příklady:
- 3^2 = 3\cdot 3 = 9
- 2^3 = 2\cdot 2 \cdot 2= 8
- 5^4 = 5\cdot 5\cdot 5\cdot 5 = 625
Tabulka druhých mocnin čísel 1 až 20
| 1^2 | = | 1 |
| 2^2 | = | 4 |
| 3^2 | = | 9 |
| 4^2 | = | 16 |
| 5^2 | = | 25 |
| 6^2 | = | 36 |
| 7^2 | = | 49 |
| 8^2 | = | 64 |
| 9^2 | = | 81 |
| 10^2 | = | 100 |
| 11^2 | = | 121 |
| 12^2 | = | 144 |
| 13^2 | = | 169 |
| 14^2 | = | 196 |
| 15^2 | = | 225 |
| 16^2 | = | 256 |
| 17^2 | = | 289 |
| 18^2 | = | 324 |
| 19^2 | = | 361 |
| 20^2 | = | 400 |
Při umocňování záporných čísel je výsledek kladný pro sudé mocniny, záporný pro liché mocniny.
- (-3)^2 = (-3)\cdot (-3) = 9
- (-3)^3 = (-3)\cdot (-3)\cdot (-3) = -27
- (-3)^4 = (-3)\cdot (-3)\cdot (-3)\cdot (-3) = 81
Nultá mocnina jakéhokoliv čísla je 1 (např. 5^0=1, 564^0=1). Nula umocněna na libovolné číslo je 0 (např. 0^3 = 0\cdot 0\cdot 0 = 0). Což vede na zajímavou otázku: Čemu se rovná 0^0?
NahoruOdmocniny
Odmocňování v matematice je částečně inverzní (opačnou) operací k umocňování. Druhá odmocnina z čísla x je takové nezáporné číslo a, pro které platí a^2 = x. Druhou odmocninu značíme \sqrt{x}.
Příklady druhých odmocnin
- \sqrt{9} = 3, protože 3^2 = 9
- \sqrt{25} = 5, protože 5^2 = 25
- \sqrt{100} = 10, protože 10^2 = 100
Obecně pak n-tá odmocnina z x je takové číslo a, pro které platí a^n = x, n-tou odmocninu značíme \sqrt[n]{x}.
Příklady obecných odmocnin
- \sqrt[3]{125} = 5, protože 5^3 = 125
- \sqrt[5]{32} = 2, protože 2^5 = 32
- \sqrt[4]{10 000} = 10, protože 10^4 = 10 000
Odmocňování má i geometrický význam. Pokud máme čtverec o obsahu S, pak tento čtverec má délku strany rovnou druhé odmocnině \sqrt{S}. Pokud máme krychli o objemu V, pak tato krychle má délku hranu rovnou třetí odmocnině \sqrt[3]{V}. Odmocniny hojně využijeme například při aplikaci Pythagorovy věty.
Graf funkce odmocnina
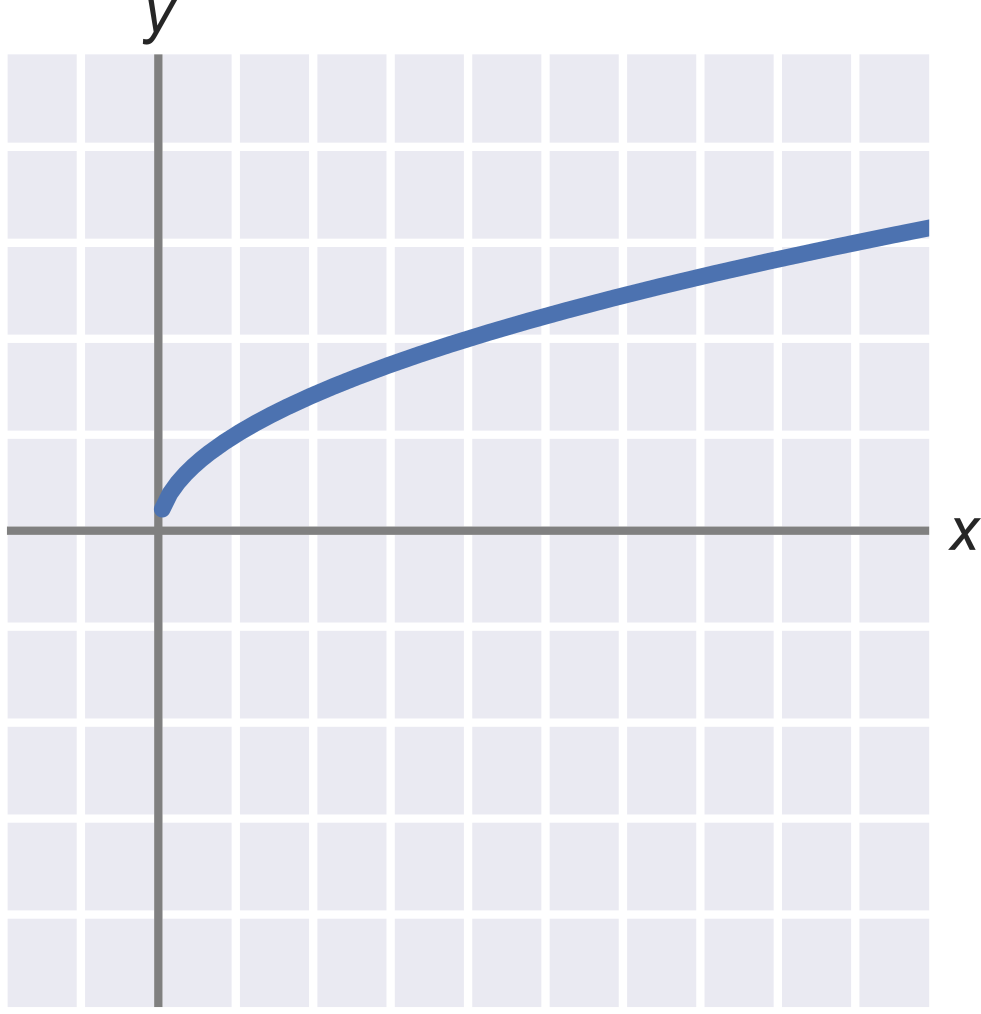
Odmocnina a záporná čísla
Když hledáme odmocninu třeba z 25, tak hledáme číslo, které po umocnění dá 25. To splňuje 5\cdot 5, ale také (-5)\cdot (-5). Odmocnina je však definována jako nezáporné číslo, takže \sqrt{25} = 5.
Druhou odmocninu můžeme počítat pouze z kladných čísel, protože jakékoliv číslo umocněné na druhou je kladné. Odmocnina ze záporných čísel není definována. Nebo vlastně je, ale to musíme zavést komplexní čísla (což je velice zajímavý a užitečný nástroj, ale trochu pokročilý a ten tu nebudeme rozebírat).
Pro běžná reálná čísla můžeme počítat odmocniny ze záporných čísel pro liché stupně n.
Příklady odmocnin ze záporných čísel
- \sqrt[3]{-8} = -2, protože (-2)^3 = -8
- \sqrt[5]{-100 000} = -10, protože (-10)^5 = -100 000
Výrazy s mocninami a odmocninami
Pro mocniny platí následující vztahy:
- x^0 = 1
- x^a \cdot x^b = x^{a+b}
- x^a : x^b = x^{a-b}
- (x^a)^b = x^{a\cdot b}
- (x\cdot y)^a = x^a\cdot y^a
Konkrétní příklady, která názorně ilustrují, proč uvedené vztahy platí:
- 7^3\cdot 7^2 = (7\cdot 7\cdot7) \cdot (7\cdot 7) = 7^{3+2} = 7^5
- 6^4: 6^2 = (6\cdot 6\cdot 6\cdot 6) : (6\cdot 6) = 6^{4-2} = 6^2
- (5^3)^2 = (5\cdot 5\cdot 5)^2 = (5\cdot 5\cdot 5) \cdot (5\cdot 5\cdot 5) = 5^{3\cdot 2} = 5^6
- (7\cdot 8)^3 = (7\cdot 8) \cdot (7\cdot 8) \cdot (7\cdot 8) = (7\cdot 7\cdot 7) \cdot (8\cdot 8\cdot 8) = 7^3 \cdot 8^3
Pro odmocniny platí následující vztahy (předpokládáme x, y > 0):
- \sqrt{0} = 0
- \sqrt{1} = 1
- \sqrt{x}\cdot \sqrt{x} = x
- \sqrt{xy} = \sqrt{x} \cdot \sqrt{y}
- \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}
- \sqrt[n]{x^k} = x^{\frac{k}{n}}
- \sqrt[n]{\sqrt[m]{x}} = \sqrt[n\cdot m]{x}
Příklady:
- \sqrt{24} = \sqrt{4\cdot 6} = \sqrt{4} \cdot \sqrt{6} = 2\sqrt{6}
- \sqrt{3} \cdot \sqrt{3} = (\sqrt{3})^2 = 3
- \sqrt[3]{5^6} = 5^\frac63 = 5^2 = 25
Záporné mocniny
Mocnina se záporným exponentem odpovídá převrácené hodnotě příslušné mocniny s kladným exponentem. Tedy x^{-n} = \frac{1}{x^n}. Toto pravidlo je důsledkem vlastnosti násobení x^n\cdot x^m = x^{n+m}. Musí tedy platit x^{-n} \cdot x^n = x^{-n+n} = x^0 = 1.
Příklady:
- 2^{-1} = \frac{1}{2} = 0,5
- 2^{-2} = \frac{1}{2^2} = \frac{1}{4} = 0,25
- 10^{-2} = \frac{1}{10^2} = 0,01
- 0,5^{-1} = 2^1 = 2
Vědecký zápis čísel
Vědecký zápis čísel je zápis čísel pomocí součinu m\cdot 10^n, kde m je reálné číslo (mantisa) a 10^n je mocnina desítky. Tento zápis čísel je užitečný zejména při práci s velmi velkými nebo velmi malými čísly. Například hmotnost Země je přibližně 5 970 000 000 000 000 000 000 000 kg, což je daleko přehlednější v zápisu 5{,}97\cdot 10^{24} kg. Příklady:
| 5 | 5\cdot 10^0 |
| 0,4 | 4\cdot 10^{-1} |
| 8100 | 8{,}1\cdot 10^{3} |
| 0,032 | 3{,}2\cdot 10^{-2} |
| 8 713 000 000 | 8{,}713\cdot 10^{9} |
| 0,000 000 009 52 | 9{,}52\cdot 10^{-9} |
Zlomky, mocniny, odmocniny
Umocňování a odmocňování zlomku
Při umocňování (odmocňování) zlomku prostě umocníme (odmocníme) čitatele i jmenovatele:
\large(\frac{2}{3}\large)^2 = \frac{2^2}{3^2} = \frac{4}{9}
\sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}}
\large(\frac{4}{5}\large)^{-1} = \frac{4^{-1}}{5^{-1}} = \frac{5}{4} (umocňování na -1 odpovídá prohození čitatele a jmenovatele)
Umocňování na zlomek
Umocňování na zlomek odpovídá tomu, že vezmeme mocninu podle čitatele a odmocninu podle jmenovatele, tj. x^\frac{a}{b} = \sqrt[b]{x^a}. Příklady:
2^\frac{2}{3} = \sqrt[3]{2^2} = \sqrt[3]{4} = 1{,}587\ldots
4^\frac{1}{2} = \sqrt{4^1} = 2
81^\frac{3}{4} = \sqrt[4]{81^3} = \sqrt[4]{81}^3 = 3^3 = 27
Logaritmus
Definice a využití logaritmu
Logaritmus je inverzní operace k umocňování. Logaritmus kladného čísla x při základu a je takové reálné číslo y = \log_a(x), pro které platí a^y = x. Číslo a se nazývá základ logaritmu (báze). Procvičením této základní definice se zabývá téma Logaritmus: výpočet.
Logaritmus o základu e=2{,}71 828 182... (Eulerovo číslo) se nazývá přirozený logaritmus a značí se většinou \ln. Logaritmus o základu 10 se nazývá dekadický logaritmus (značíme \log, v cizojazyčných textech se vyskytuje také zápis \lg).
Logaritmy mají velmi široké využití v mnoha oblastech matematiky. Historicky se využívaly jako užitečná početní pomůcka („logaritmické pravítko“), která využívala faktu, že logaritmus součinu je součet logaritmů. Dnes na logaritmy často narazíme například v informatice při návrhu a analýze algoritmů.
Vlastnosti logaritmů
Při práci s logaritmy, například při práci na tématu Výrazy s logaritmy, často využijeme následující vlastnosti logaritmů:
- Logaritmus je definován pouze pro kladná čísla.
- Logaritmus o základu 1 není definován.
- Logaritmus jedničky je nula, \log_a(1)=0.
- Logaritmus o stejném základu a argumentu je 1, \log_a{a}=1.
- Logaritmus součinu je součet logaritmů, \log_a(x\cdot y)=\log_a{x}+\log_a{y}.
- Logaritmus podílu je rozdíl logaritmů, \log_a\left(\frac{x}{y}\right)=\log_a{x}-\log_a{y}.
- Logaritmus je inverzní funkcí k exponenciální funkci o stejném základu, \log_a{x}=y \Leftrightarrow a^y=x.
- Logaritmus mocniny je součin exponentu a logaritmu základu mocniny, \log_a(x^n)=n\log_a{x}.
Graf logaritmu
Graf zobrazuje logaritmus o základu 2:
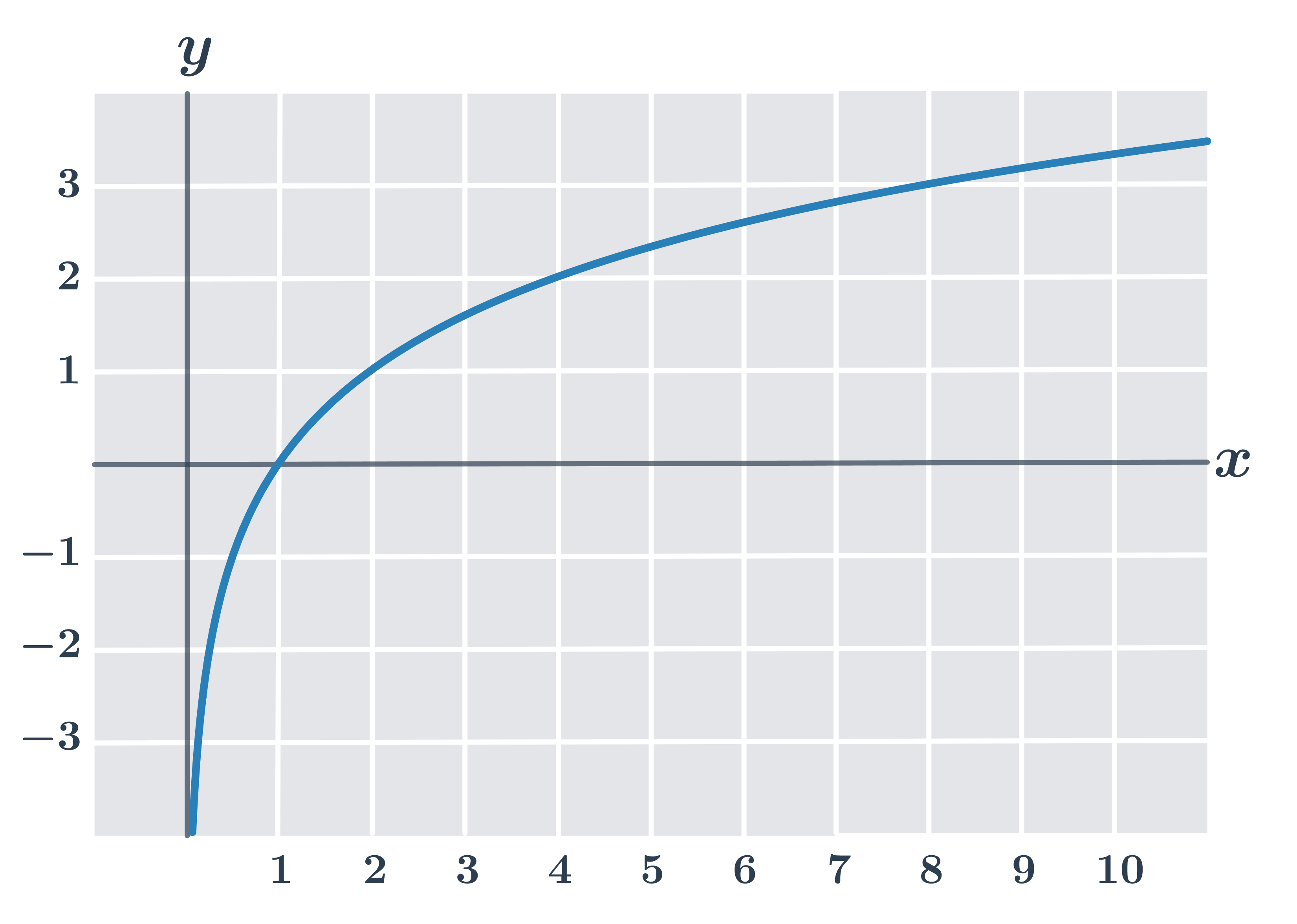
Podrobněji se grafy logaritmu zabývá téma Grafy logaritmických funkcí.
Komiks pro zpestření

Logaritmus: výpočet
Logaritmus kladného čísla x při základu a je takové reálné číslo y = \log_a(x), pro které platí a^y = x. Příklady:
| \log_{10}(100) = 2 | protože 10^2 = 100 |
| \log_2(32) = 5 | protože 2^5 = 32 |
| \log_5(125) = 3 | protože 5^3 = 125 |
| \log_7(1) = 0 | protože 7^0 = 1 |
| \log_2(0{,}5) = -1 | protože 2^{-1} = \frac{1}{2} = 0{,}5 |
Výrazy s logaritmy
Některé základní vlastnosti logaritmů vyjádřené pomocí vzorců:
- \log_a(a)=1
- \log_a(1)=0
- \log_a(x\cdot y) = \log_a(x) + \log_a(y) (logaritmus součinu je součet logaritmů)
- \log_a(\frac{x}{y}) = \log_a(x) - \log_a(y) (logaritmus podílu je rozdíl logaritmů)
- \log_a(x^k)=k\log_a(x)
- \log_a(x)=\frac{\log_b(x)}{\log_b(a)}
Logaritmické rovnice
Logaritmická rovnice je taková, kde neznámá vystupuje jako argument logaritmické funkce, např. 2 \cdot \log_6(x-2) = \log_6(14-x).
U logaritmických rovnic musíme dávat pozor na podmínky řešení. Argument každého logaritmu totiž musí být vždy kladné číslo. V uvedeném příkladě tedy musí platit x-2>0 a současně 14-x > 0.
Logaritmické rovnice řešíme za využití vlastností logaritmické funkce a jejího vztahu k exponenciální funkci. Dílčí způsoby, jak řešit logaritmické rovnice:
- Převedeme rovnici na tvar \log_a f(x) = c. Pak musí platit f(x) = a^c.
- Převedeme rovnici na tvar \log_a f(x) = \log_a g(x). Pak musí platit f(x) = g(x).
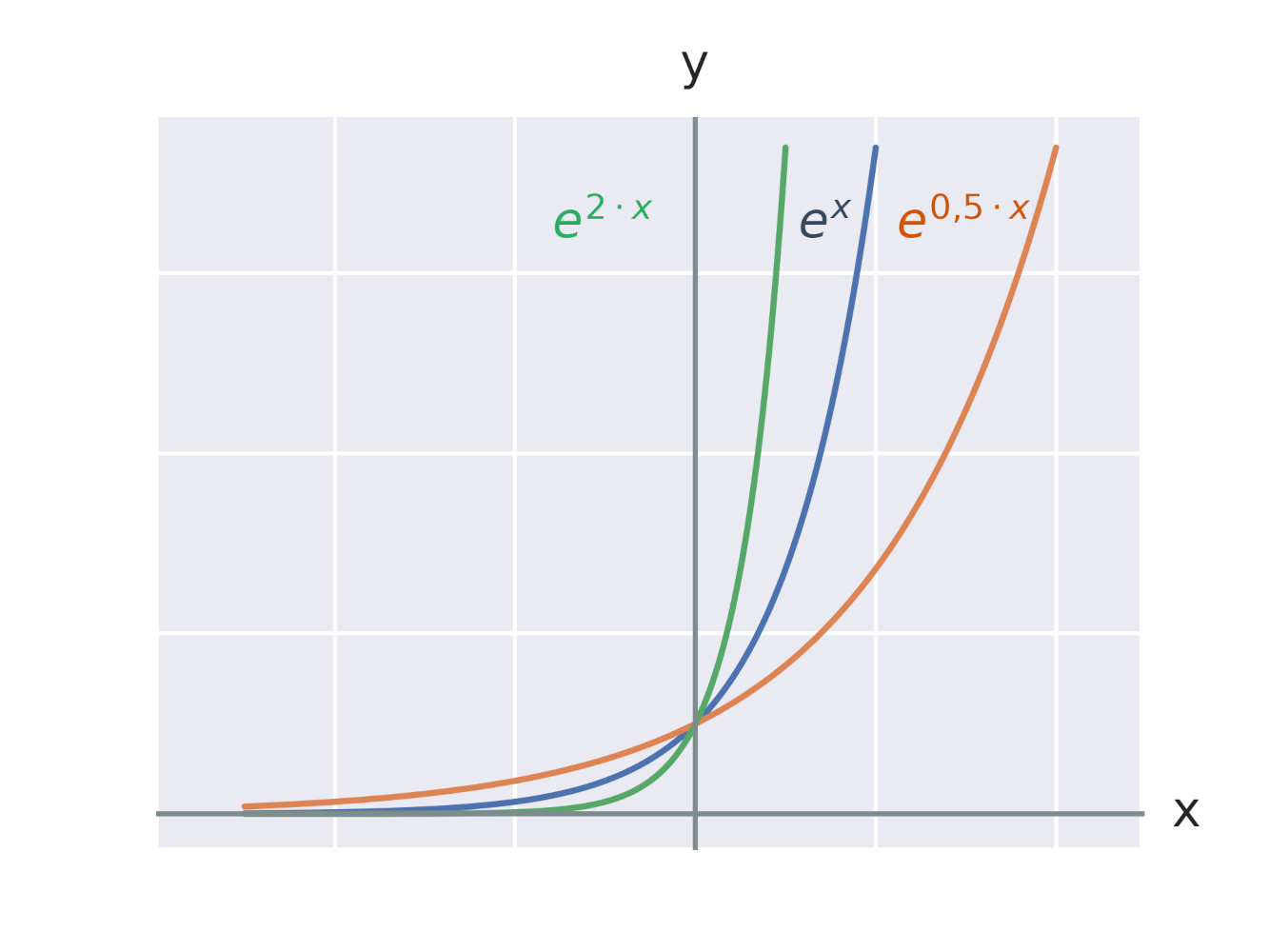
Grafy exponenciálních funkcí
Grafem exponenciální funkce je křivka jménem exponenciála. Na obrázku jsou grafy exponenciálních funkcí se základy 2 a e = 2{,}7 182 818 284\ldots. Vidíme také, že grafy funkcí e^x a e^{-x} jsou spolu souměrné podle osy y.
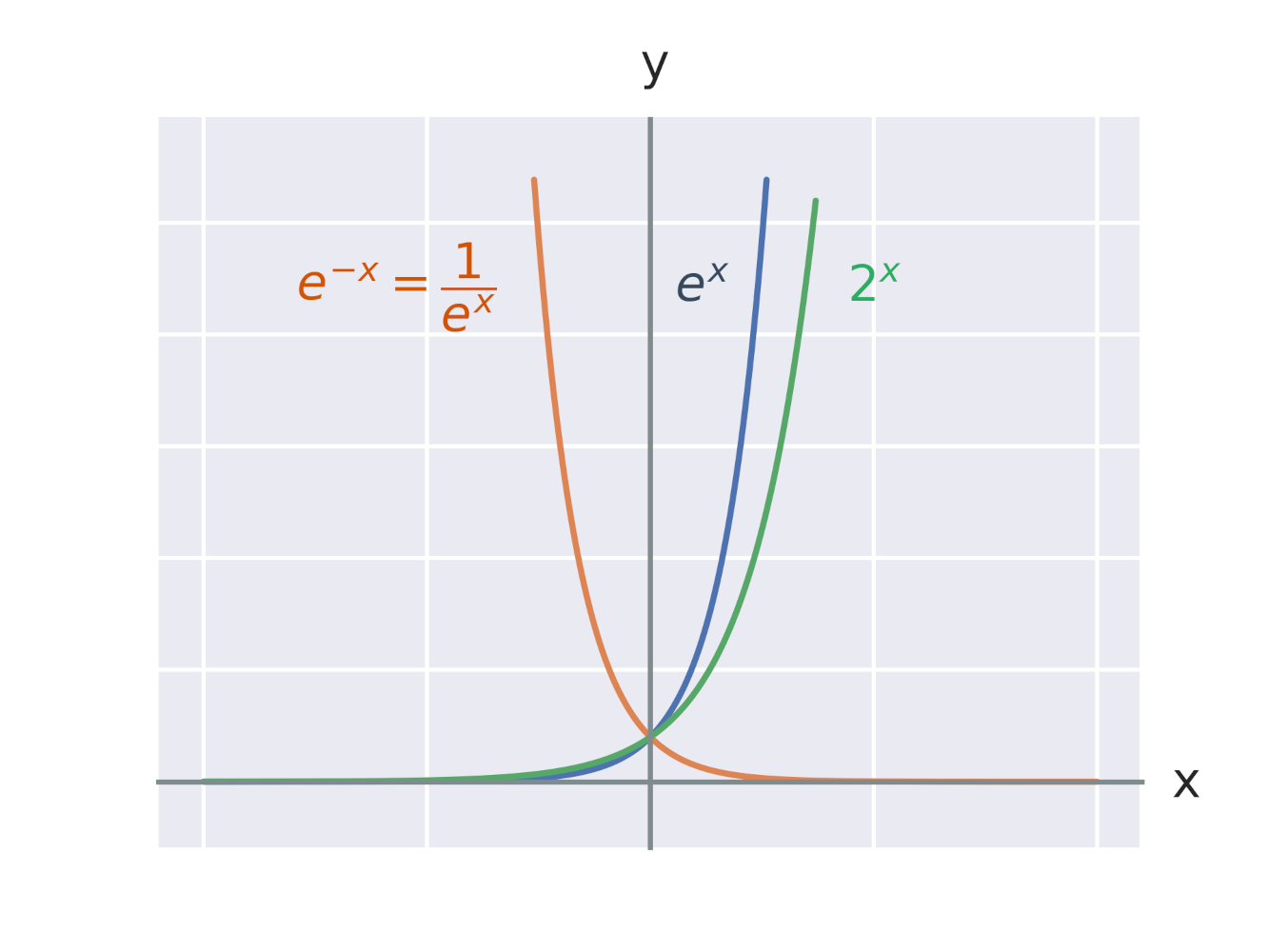
Graf každé exponenciální funkce tvaru f:y =a^x prochází bodem [0,1], protože pro libovolnou konstantu a platí: a^0=1.
Efekt přičtení konstanty k exponenciální funkci
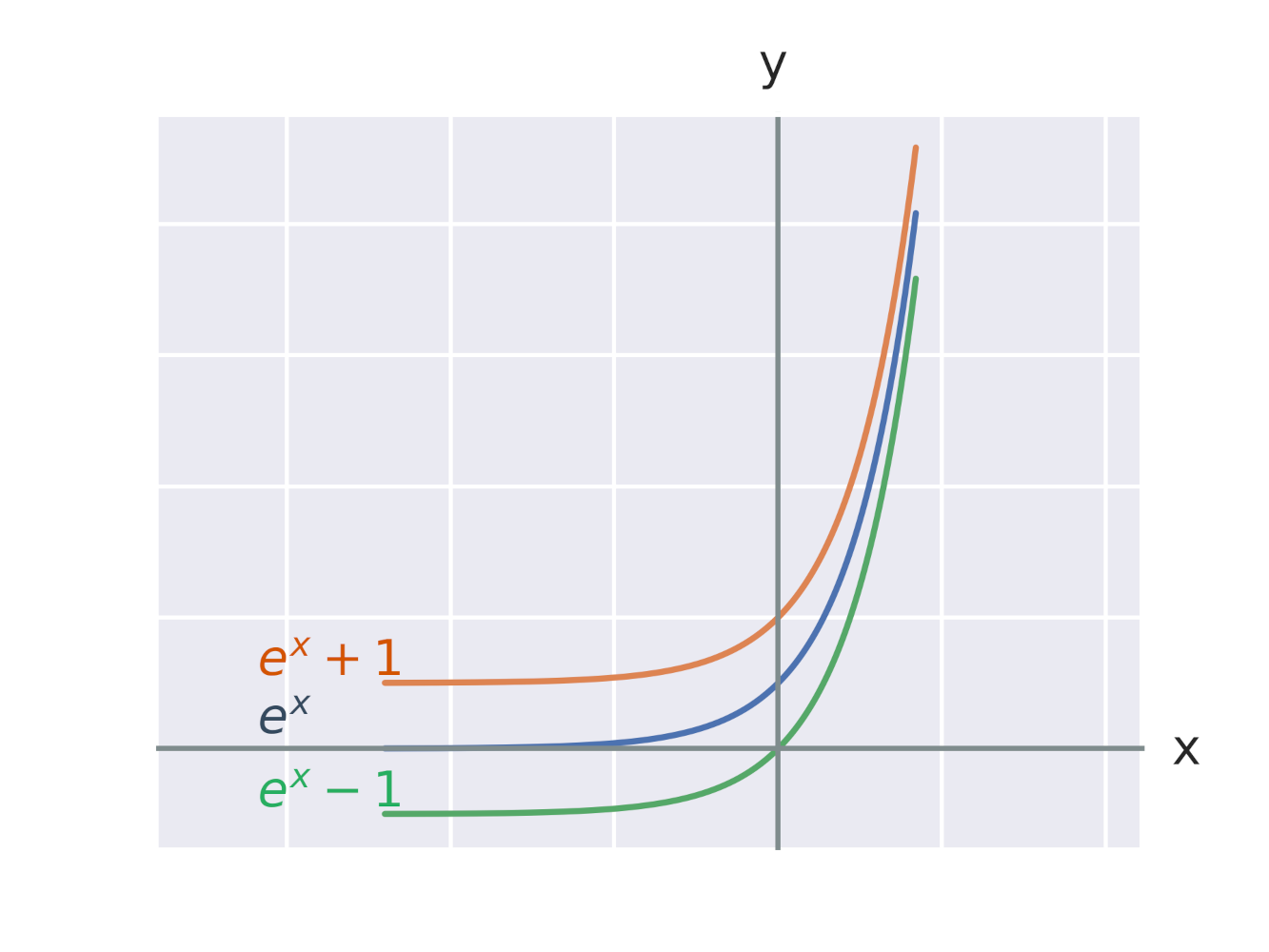
Efekt přičtení konstanty k exponentu
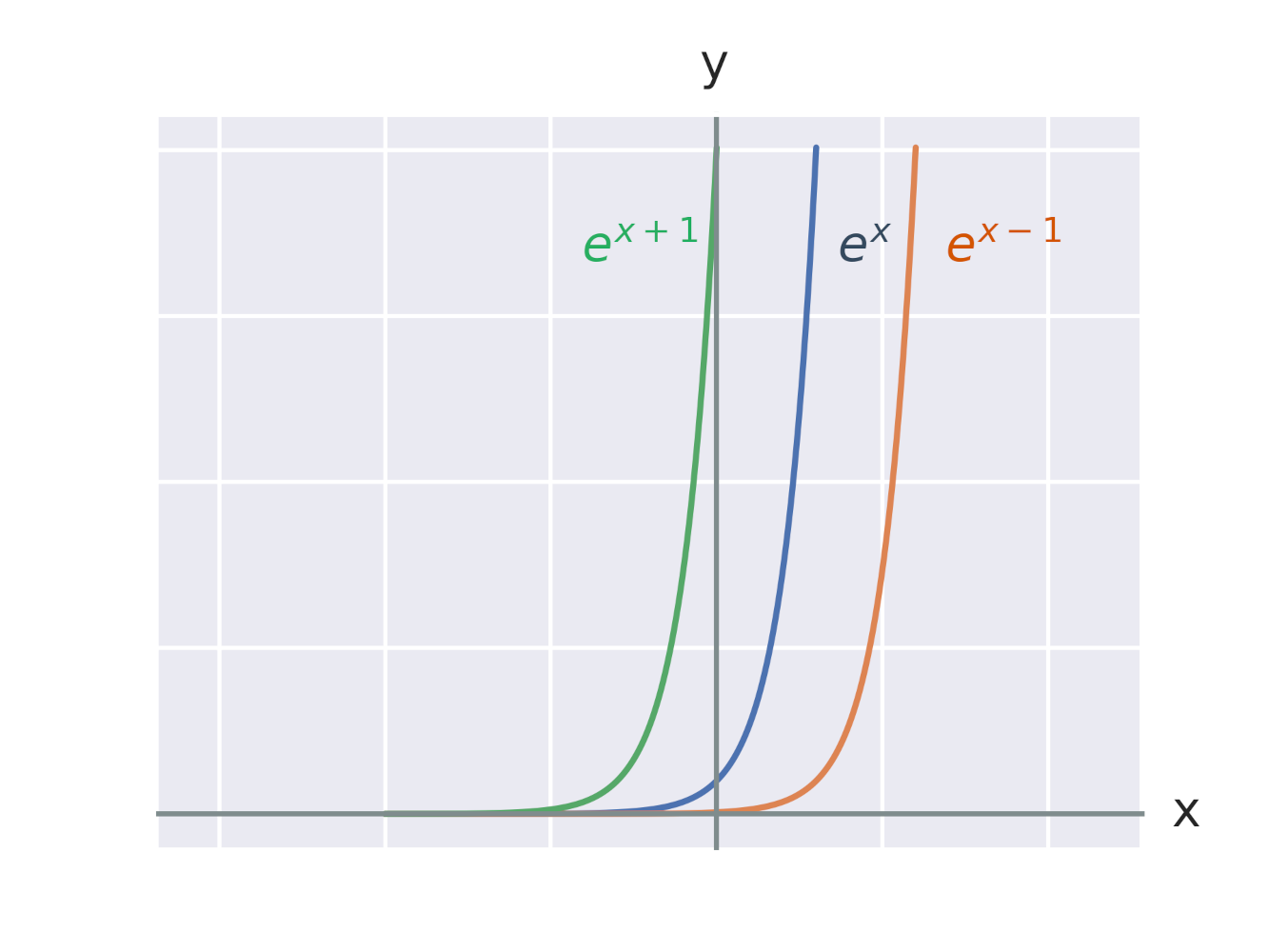
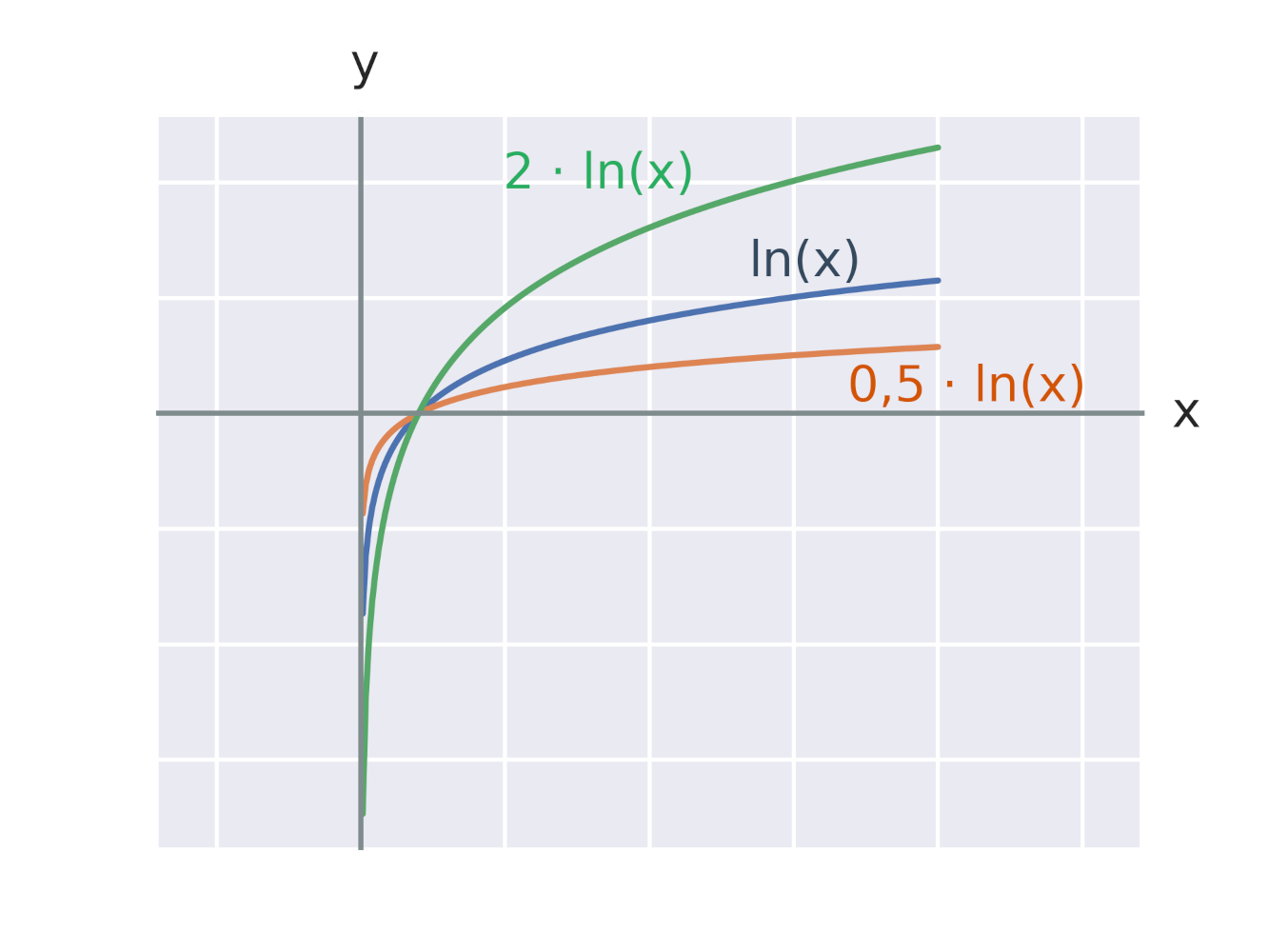
Efekt vynásobení exponenciální funkce konstantou
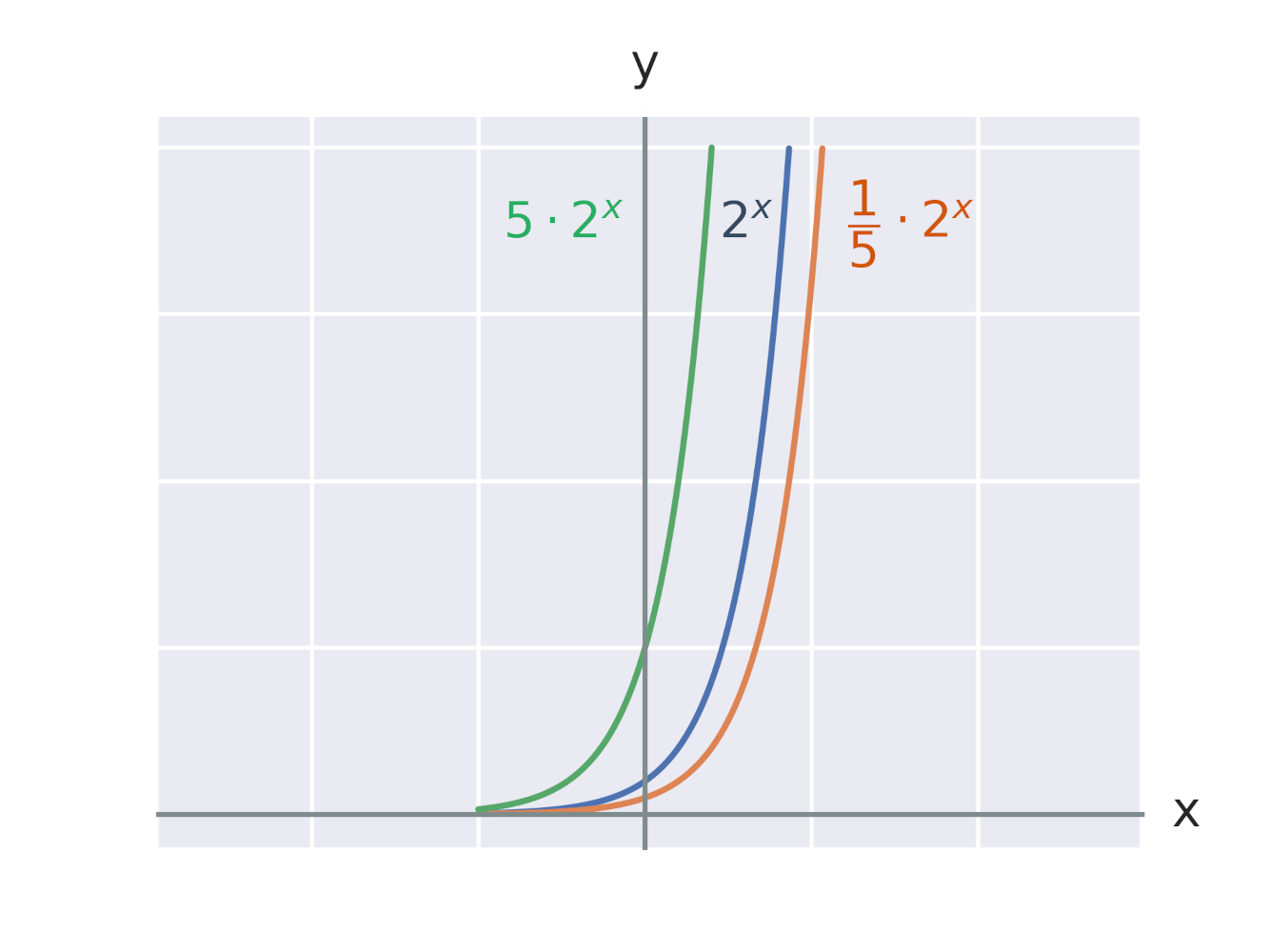
Efekt vynásobení exponentu konstantou
Grafy logaritmických funkcí
Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).
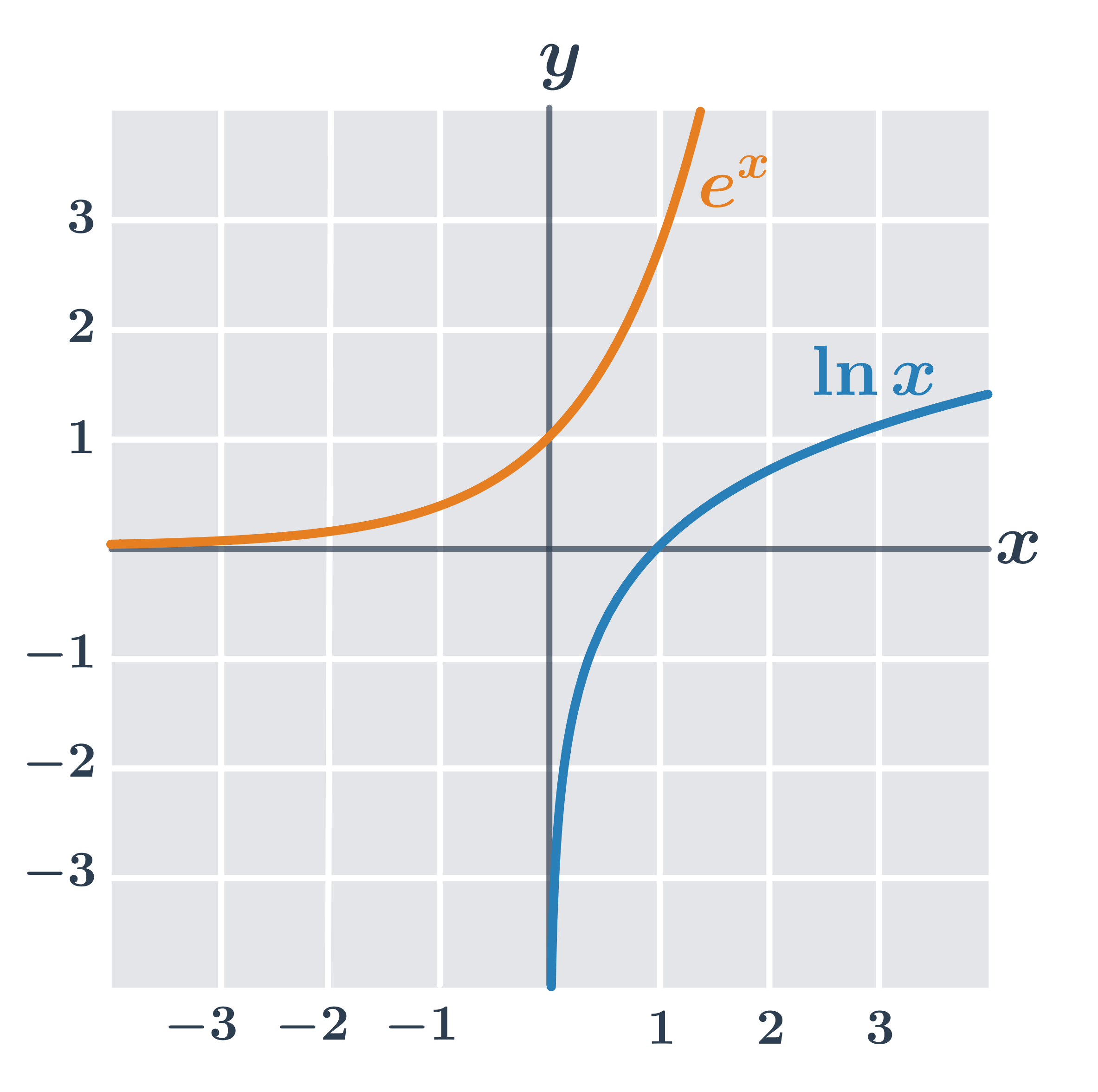
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.
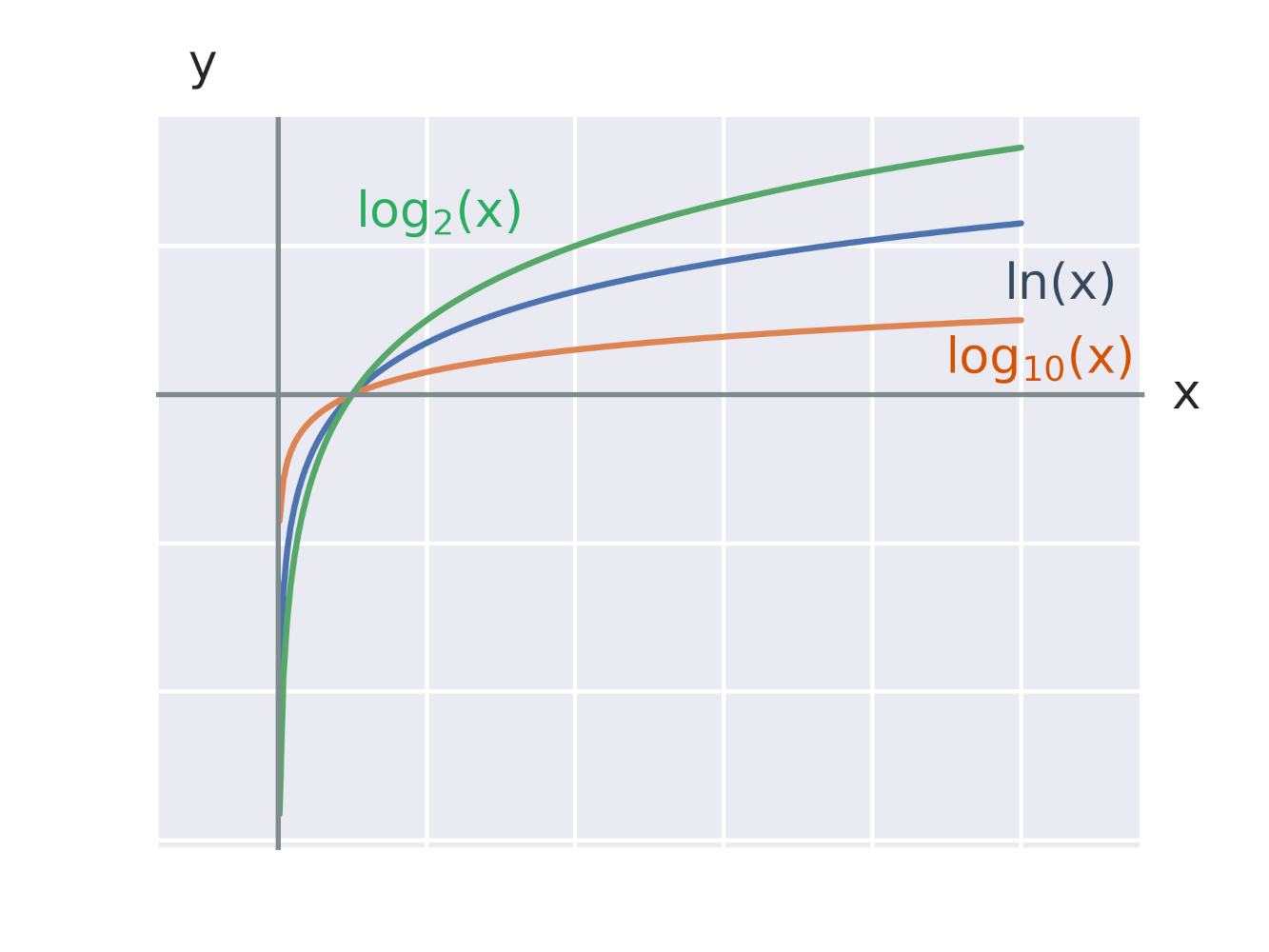
Značení některých význačných logaritmických funkcí:
| funkce | popis | další možná značení |
|---|---|---|
| \log_a x | obecně logaritmus x o základu a pro nějaké a >0, a\neq 1 | |
| \ln x | přirozený logaritmus x, tj. logaritmus x o základu e | v angl. textech někdy \log x |
| \log x | dekadický logaritmus x, tj. logaritmus x o základu 10 | \log_{10}x |
| \log_2 x | binární logaritmus x, tj. logaritmus x o základu 2 | někdy se objevuje \mathrm{lb}\;x |
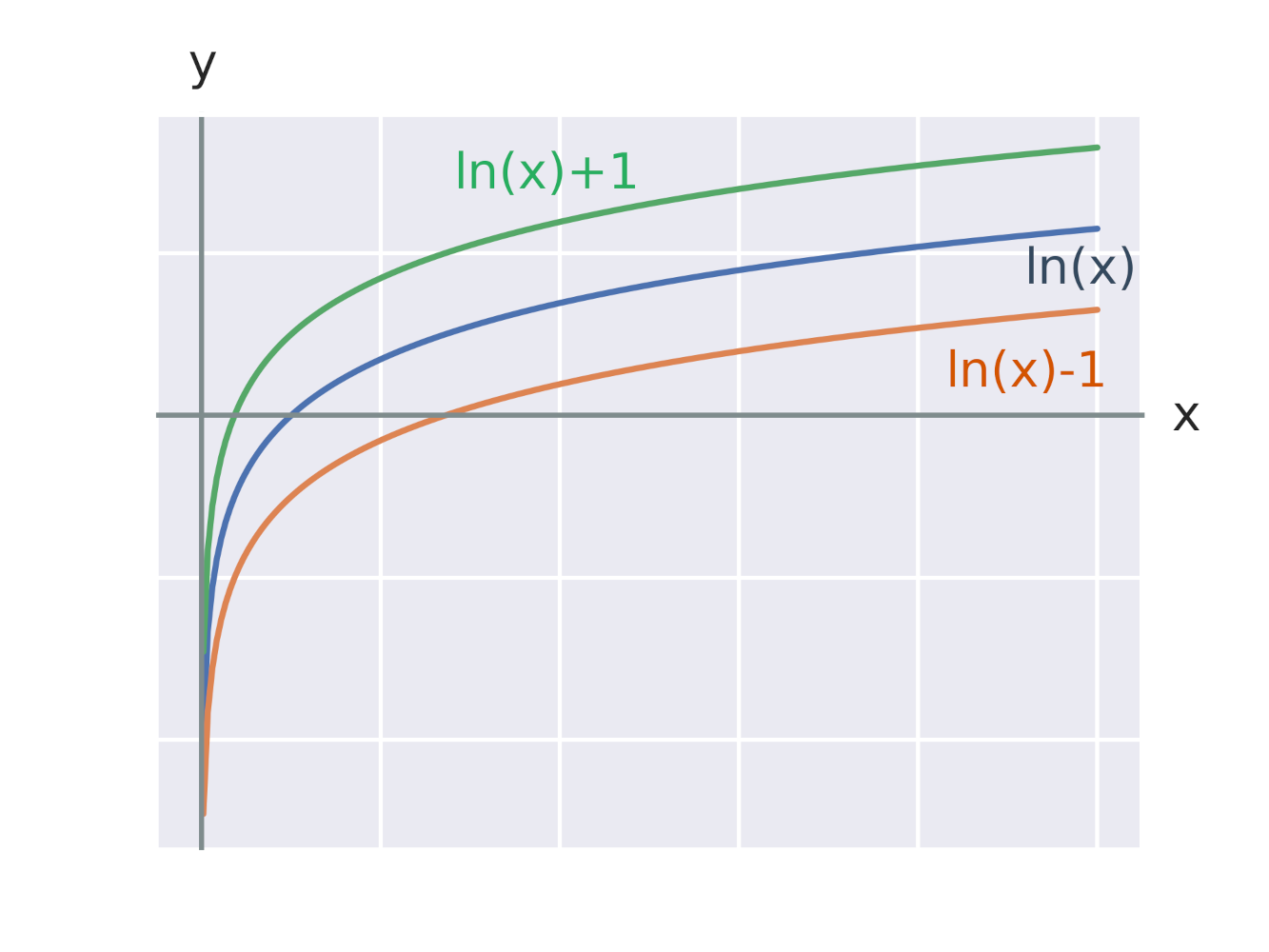
Efekt přičtení konstanty k logaritmické funkci
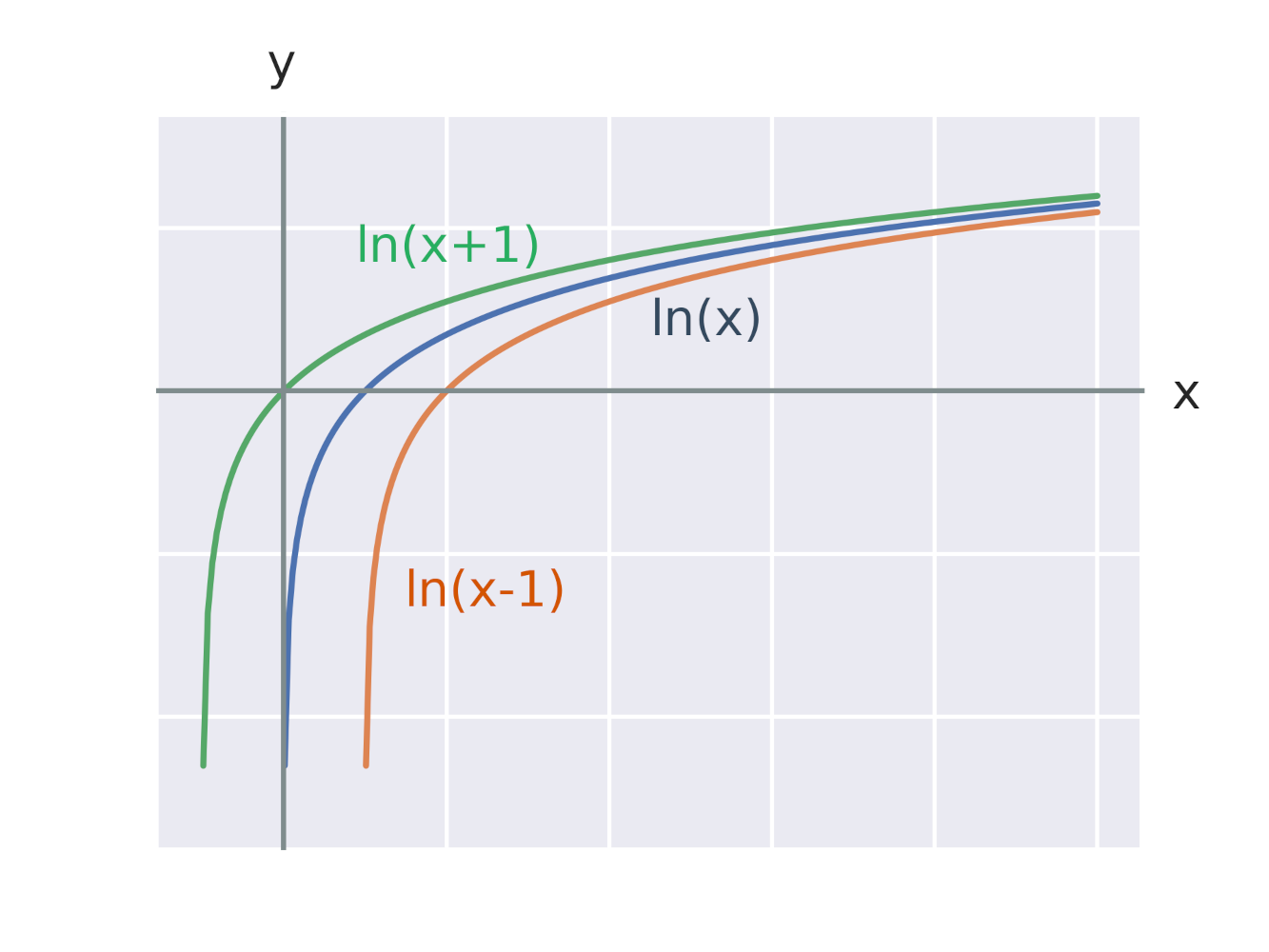
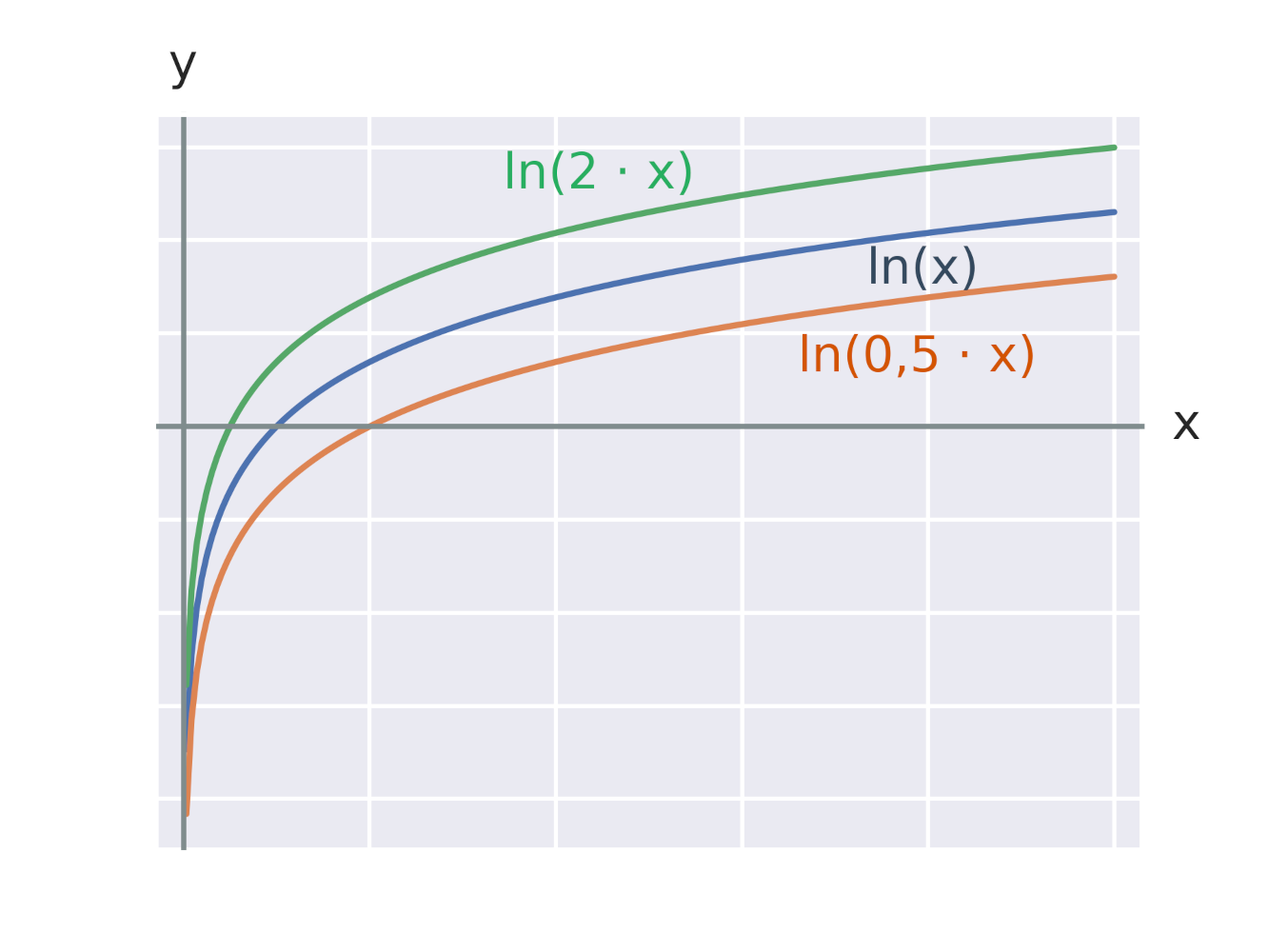
Efekt přičtení konstanty k argumentu logaritmické funkce
Efekt vynásobení logaritmické funkce konstantou
Efekt vynásobení argumentu logaritmické funkce konstantou
Číselná osa
Číselná osa je přímka znázorňující čísla. Značkami jsou na ní vyznačená vybraná čísla – většinou celá čísla. Popsány jsou většinou jen některé značky, jinak by se popisky překrývaly a bylo by to nepřehledné. Zbylá čísla si dopočítáme. Jednoduchý příklad číselné osy, na které hledáme číslo 7:

Na základní číselné ose mají značky rozestup jedna. To však zdaleka neplatí vždy. Kdykoliv pracujeme s číselnou osou, musíme si nejdříve ujasnit, jaký je rozestup mezi značkami. To určíme na základě popisků. V následujícím příkladě je rozestup 10:

Zlomky na číselné ose
Zlomek můžeme na číselnou osu umístit tak, že ho převedeme na desetinné číslo (vydělíme prostě čitatele jmenovatelem) a pak postupujeme stejně jako u desetinných čísel. Například \frac{6}{5} = 1{,}2, tj. zlomek \frac{6}{5} leží dvě desetiny za jedničkou. Další příklady:
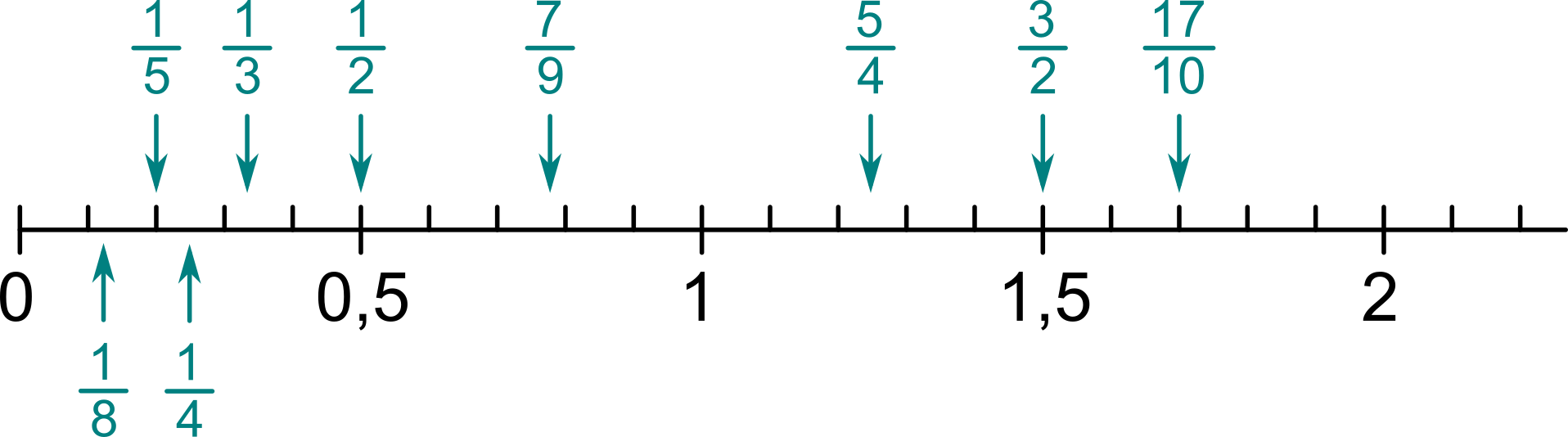
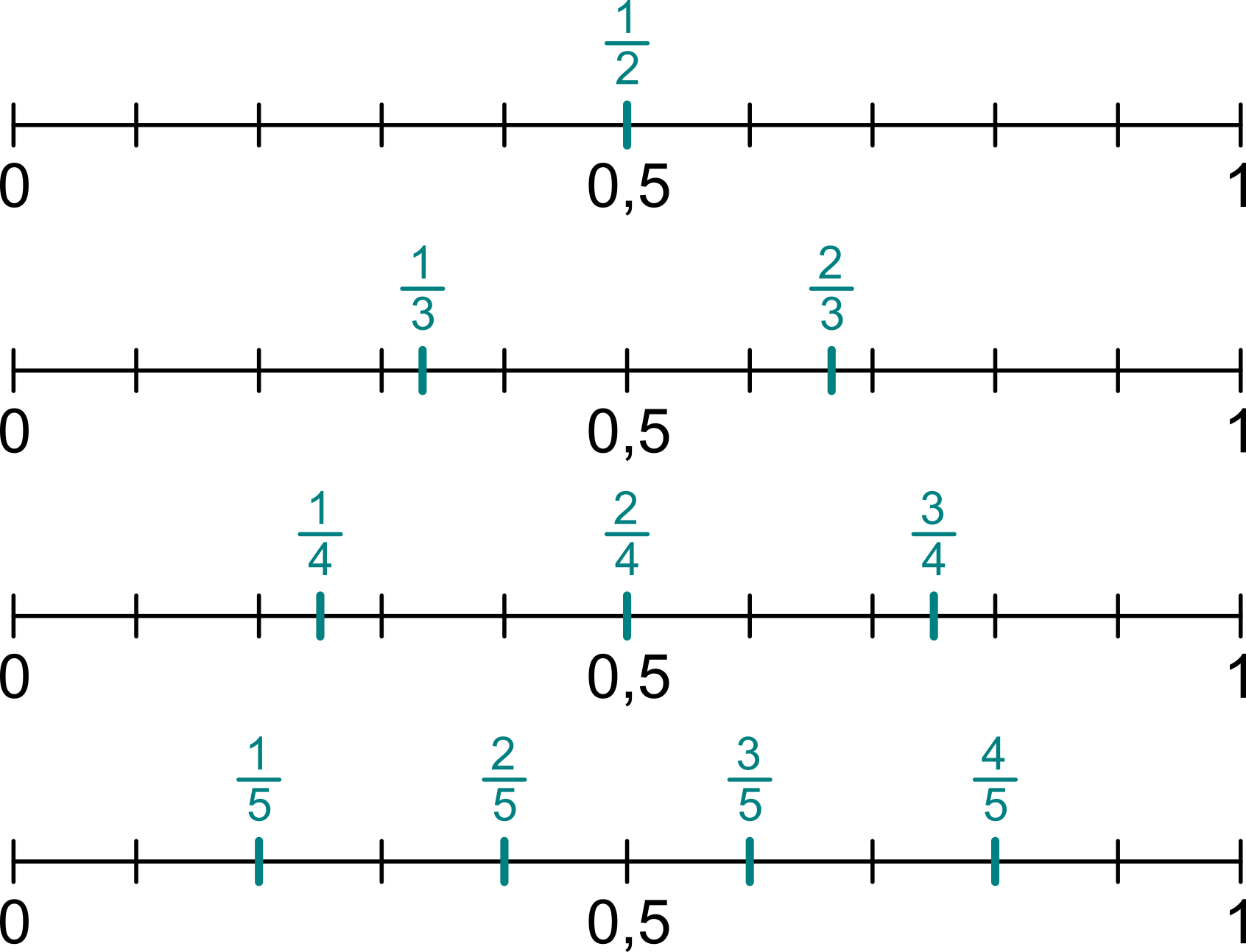
Zlomky menší než 1 můžeme umisťovat na číselnou osu také přímo (bez převodu na desetinné číslo) díky představě „část z celku“. Pokud máme umístit zlomek \frac{3}{7}, představíme si, jak bychom rozdělili úsečku od 0 po 1 na sedm stejných dílků. Zlomek \frac{3}{7} pak umístíme na třetí pozici.
Hodí se vybudovat si dobrou představu zejména pro zlomky s malým jmenovatelem:
Desetinná čísla na číselné ose
Podobně jako na jiných číselných osách, první krok je určit, jaké jsou rozestupy mezi značkami na číselné ose. Při práci s desetinnými čísly bývá často rozestup 0,1 (jedna desetina), ale nemusí to tak být nutně.
Příklad:


