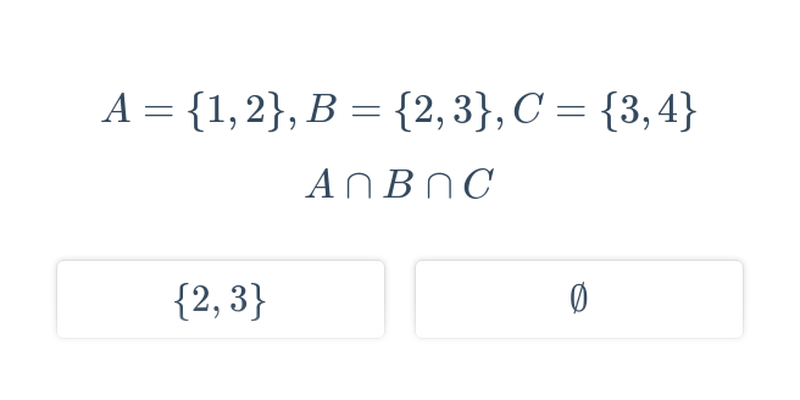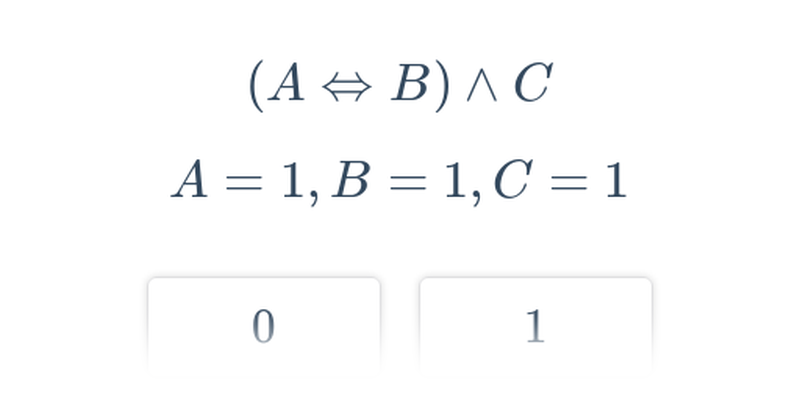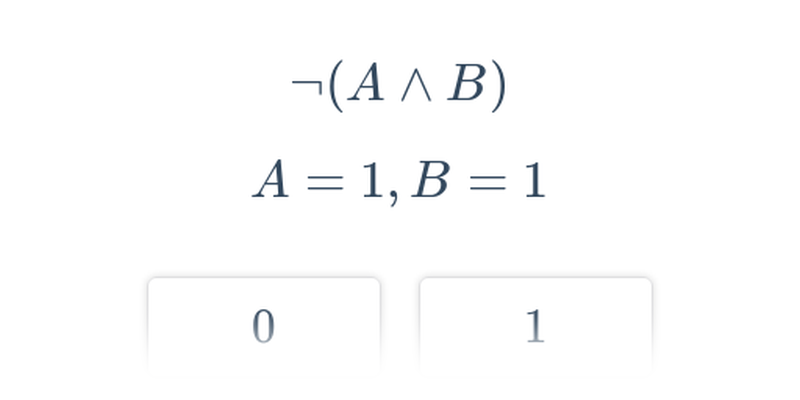Diskrétní matematika
F1NDiskrétní matematika je zastřešující oblast matematiky, která se zabývá studiem diskrétních objektů – jasně oddělitelných částí. Například Lego kostky nebo karty jsou diskrétní. Můžeme je různě kombinovat či řadit, ale pracujeme s nimi vždy po jedné, nemá smysl je dělit. Naopak taková přímka je spojitá, můžeme ji dělit na stále jemnější části.
Pojem diskrétní matematika i názvy jednotlivých oblastí mohou znít abstraktně a složitě. Dají se však použít i v snadno představitelných případech, jako jsou třeba různé hry.
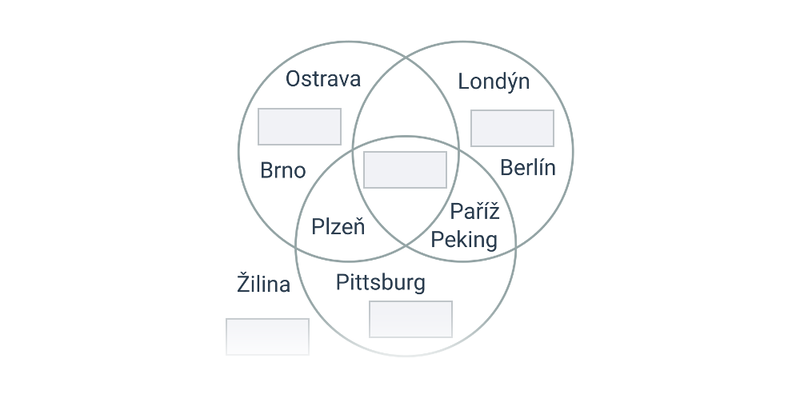
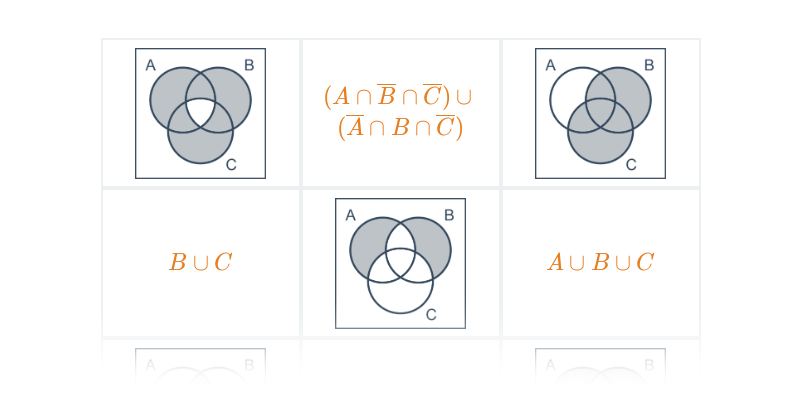
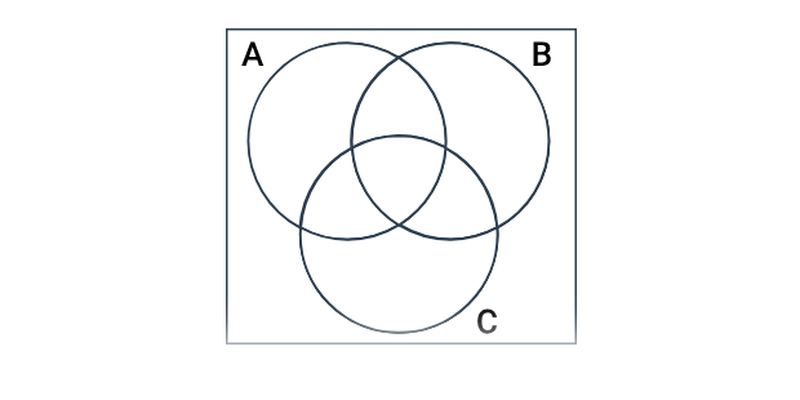
Množiny jsou soubory prvků. Můžeme například uvážit množinu černých šachových figurek nebo množinu fotbalových útočníků. Práce s množinami představuje základ mnoha oblastí matematiky.
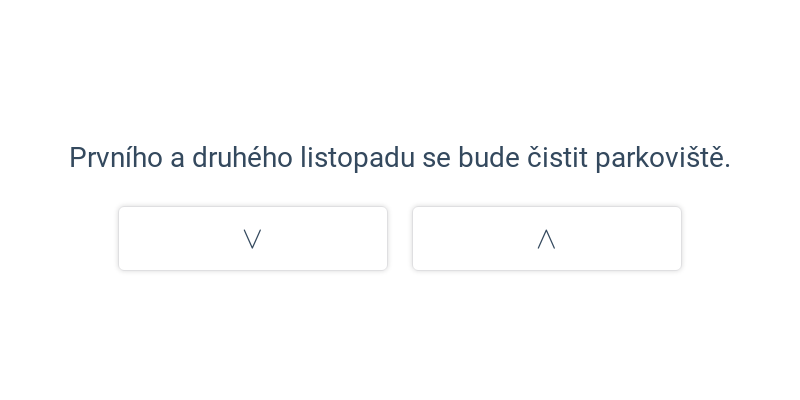
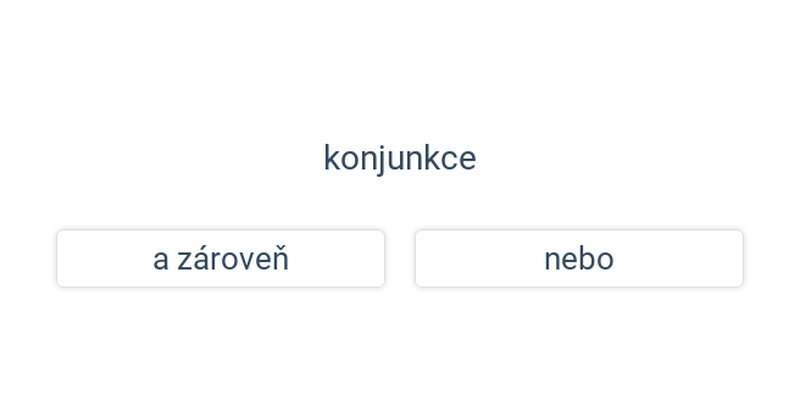
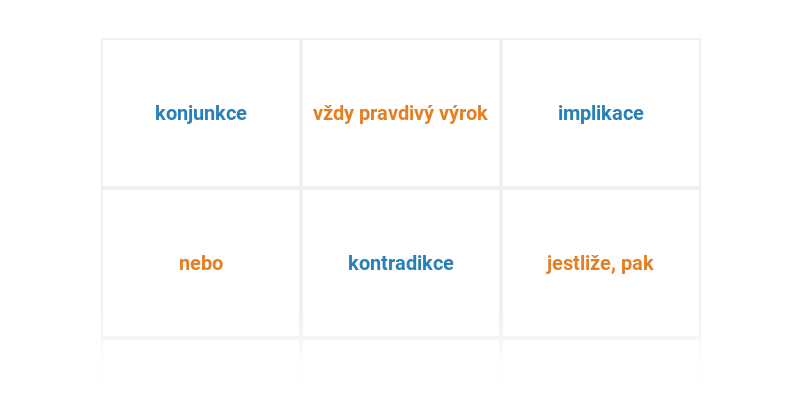
Logika zkoumá způsoby, jak vyvozujeme závěry z předpokladů. Pomocí logiky můžeme dokázat, že určitá pozice v šachu je vítězná pro jednoho z hráčů.
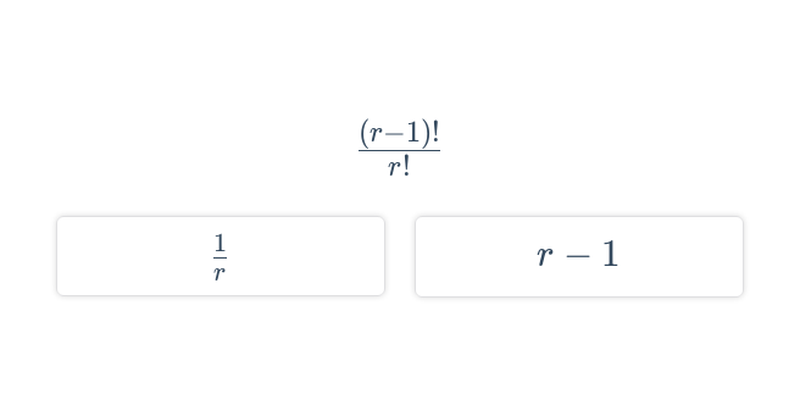
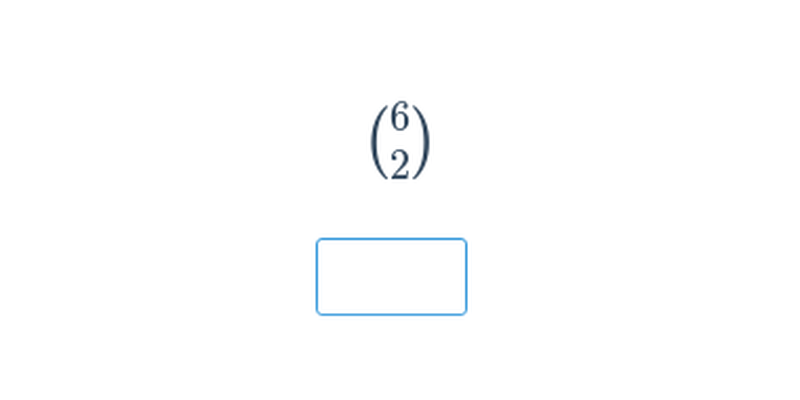
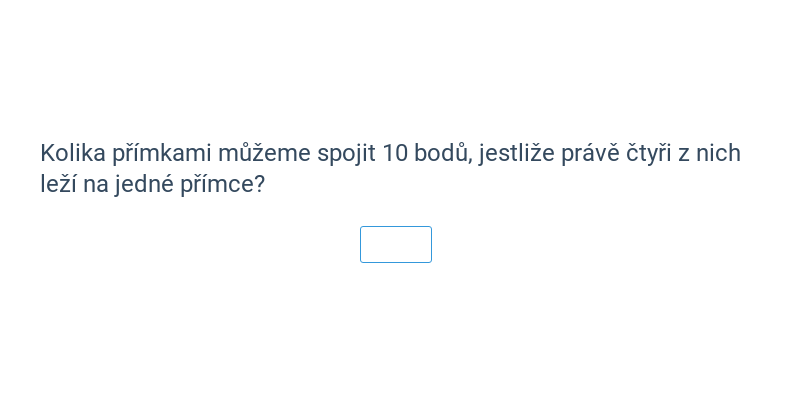
Kombinatorika se zabývá počítáním možností, jak můžeme objekty vzájemně kombinovat. Pomocí kombinatoriky můžeme určit počet způsobů, jak rozdělit skupinu hráčů do dvou fotbalových týmů.
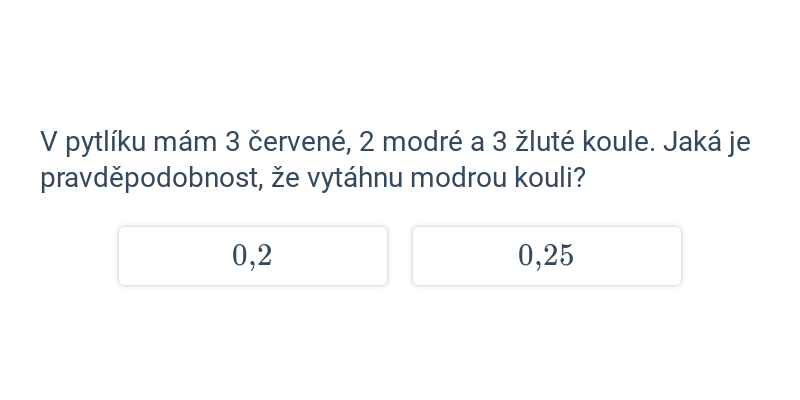
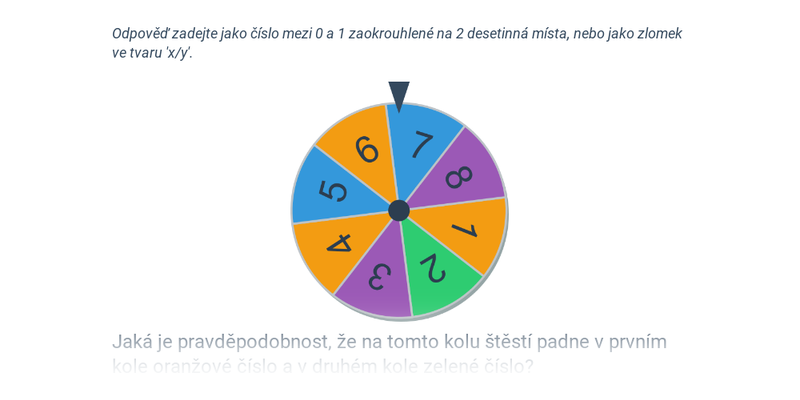
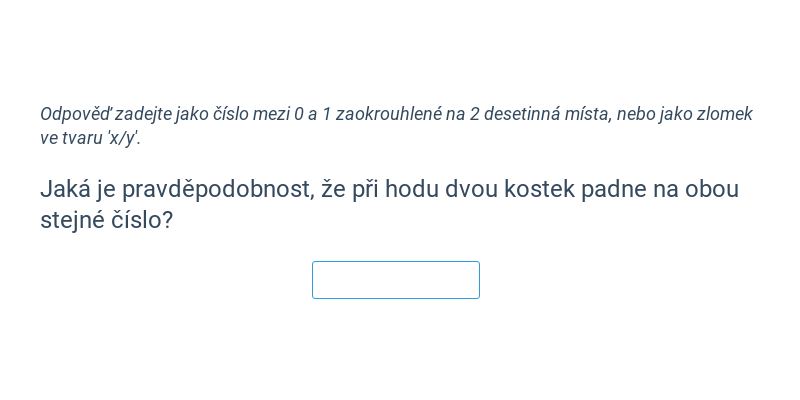
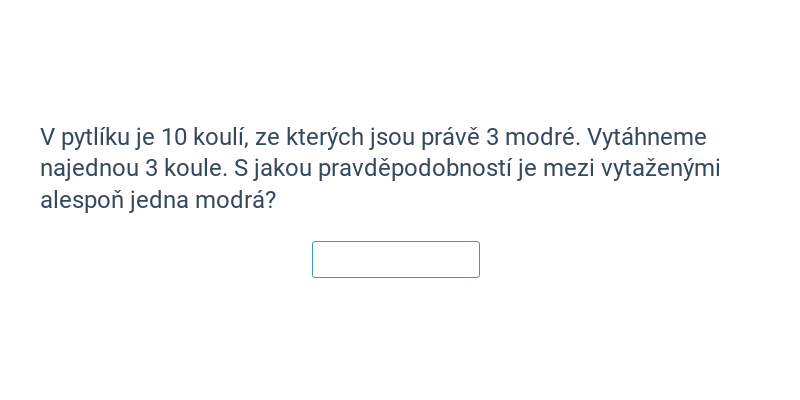
Pravděpodobnost zkoumá pravidla, kterými se řídí náhodné události. Za využití pravděpodobnosti můžeme vypočítat, jak moc (ne)výhodné jsou sázky v hazardní hře s kostkami.
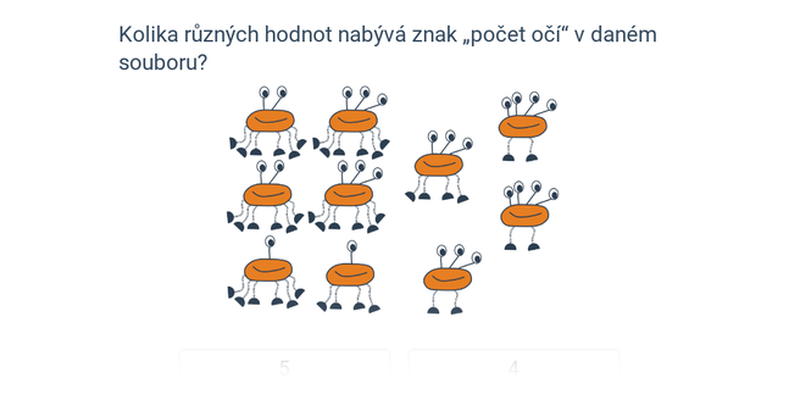
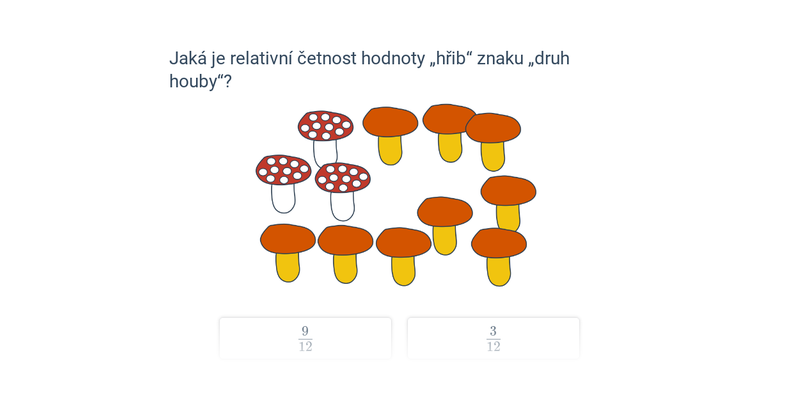
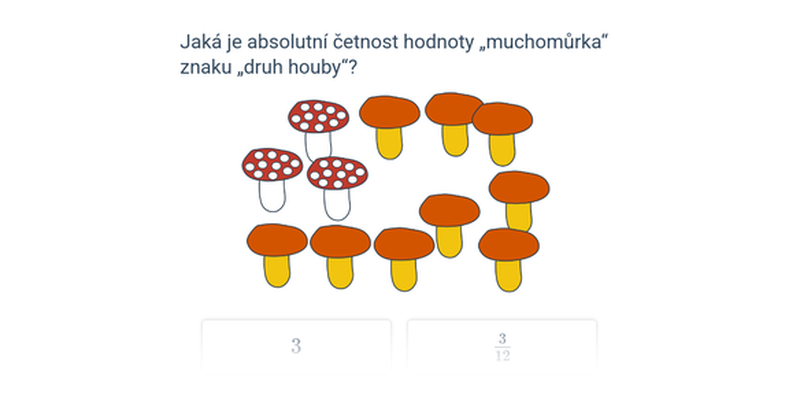
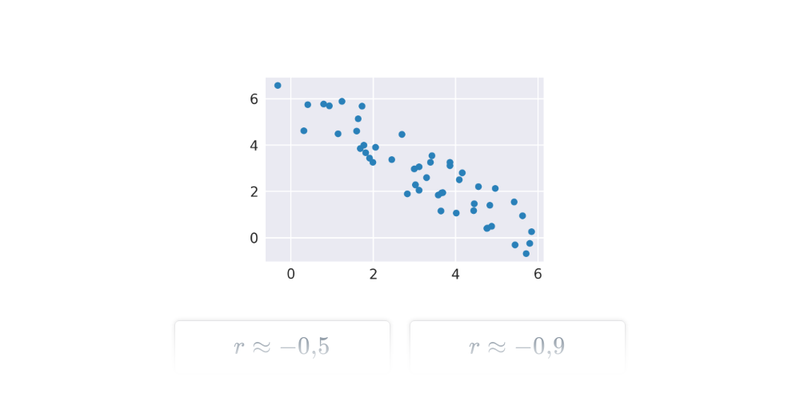
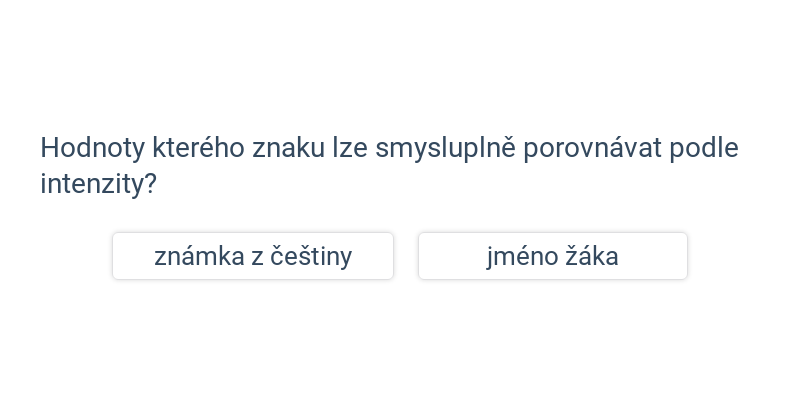
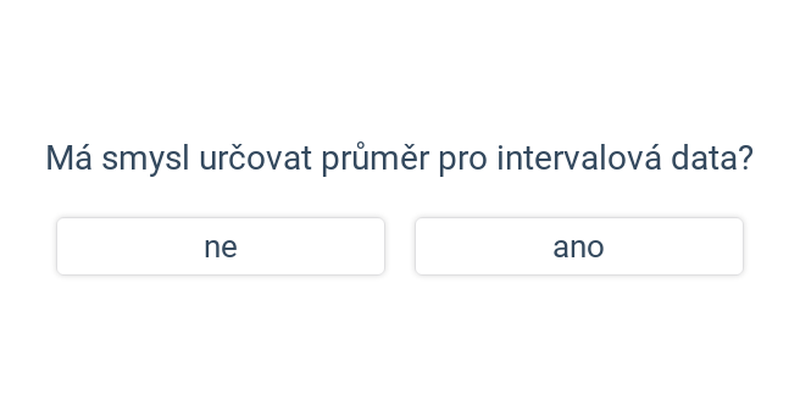
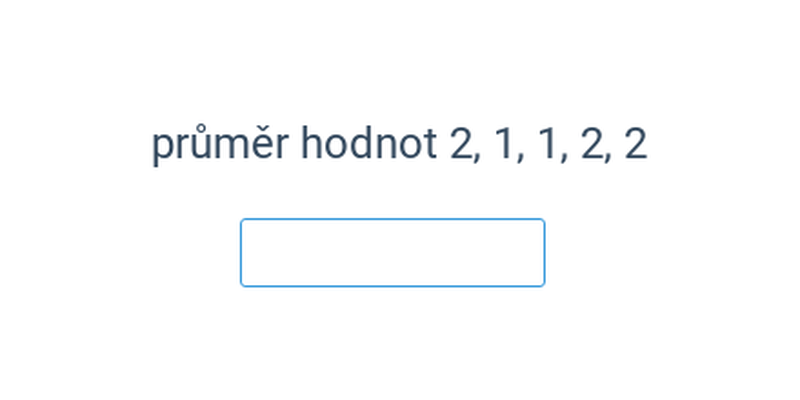
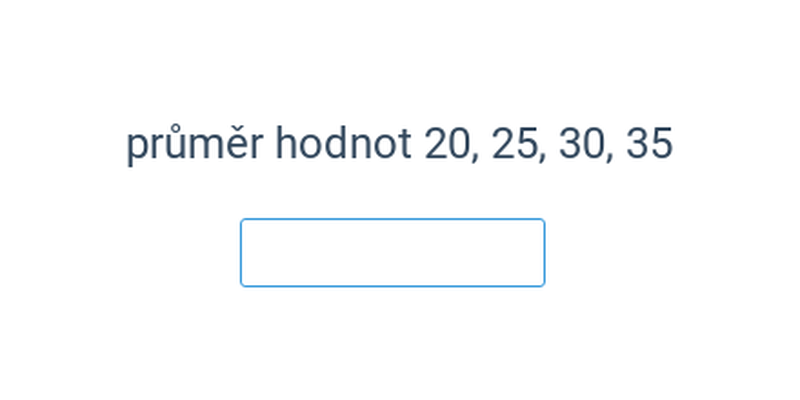
Popisná statistika se zabývá popisem jevů, které vykazují vliv náhody. Pomocí popisné statistiky můžeme srovnávat úspěšnost fotbalových útočníků v průběhu sezóny.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
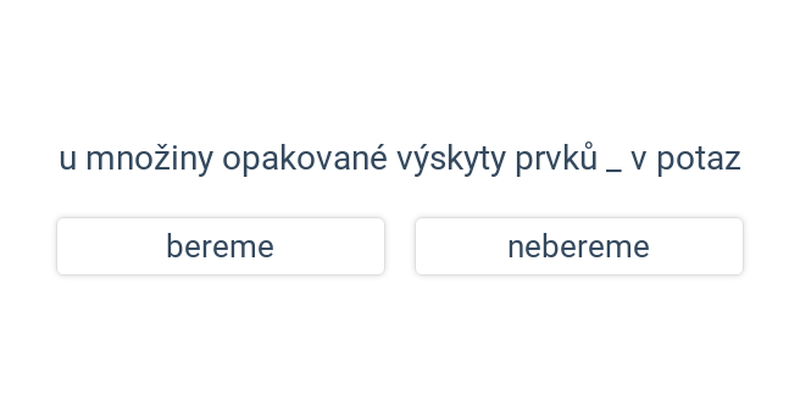
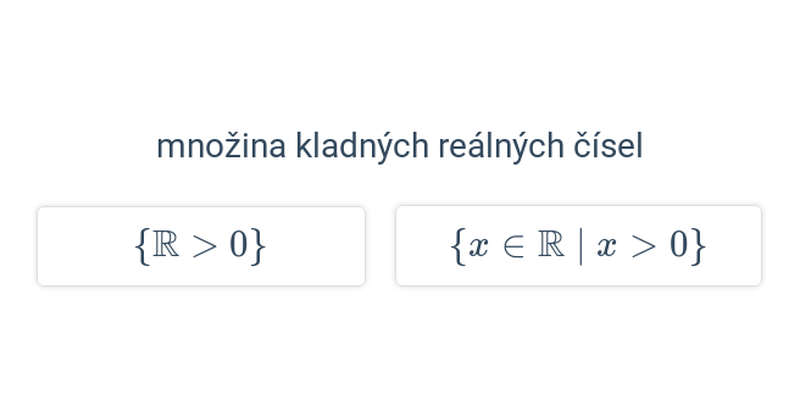
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Pexeso
Hledání dvojic, které k sobě patří.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Slovní úlohy
Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.
Porozumění
Čtení textů, odpovídání na otázky testující porozumění textu.
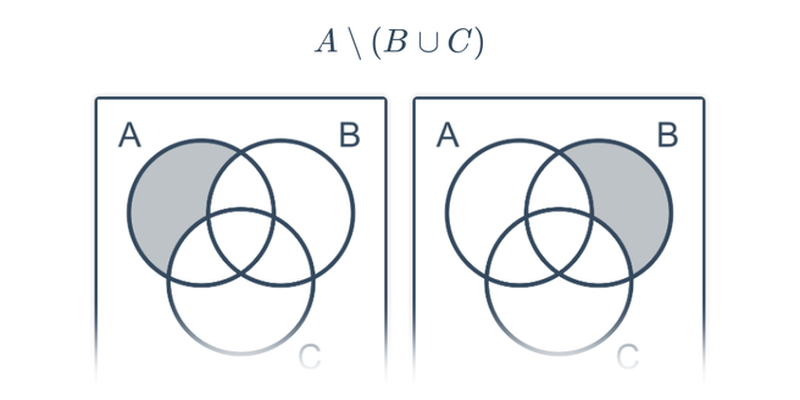
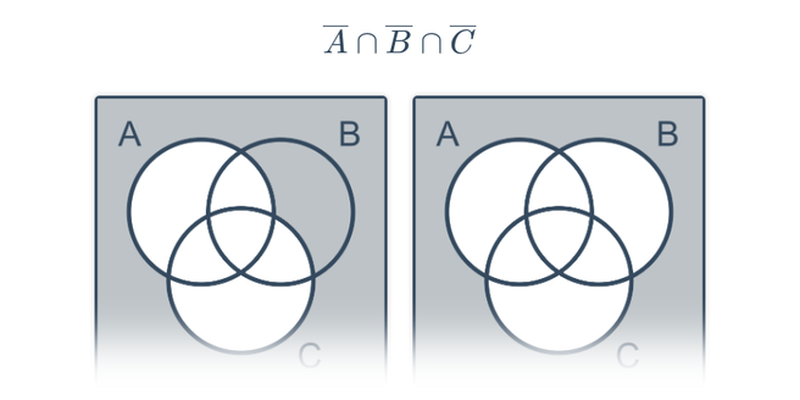
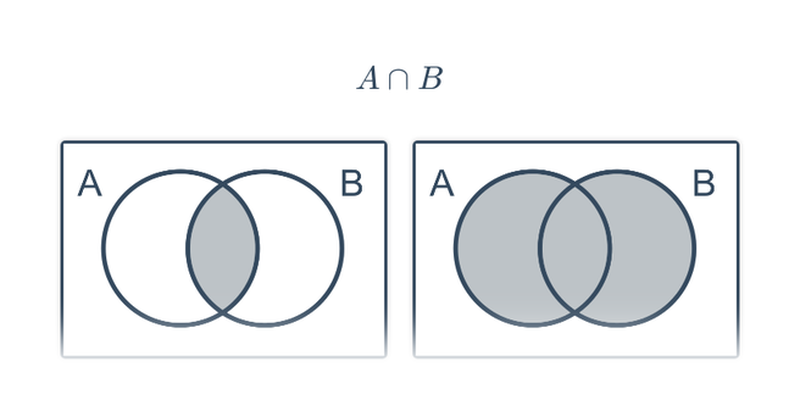
Množinové operace
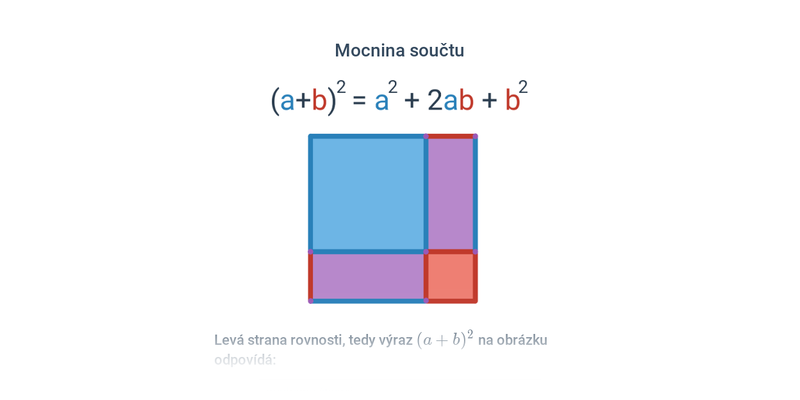
Obrázkové důkazy
Matematická indukce
Označování
V zadaném obrázku či textu máte za úkol označit všechny oblasti, které splňují určitou vlastnost.