Výpis souhrnů
Diskrétní matematika
Podtémata
- Diskrétní matematika
- Množiny
- Množiny: pojmy a značení
- Zápis množin
- Množinové operace
- Vlastnosti množin a množinových operací
- Vennovy diagramy
- Množiny množin, potenční množina
- Logika
- Logika: pojmy a značení
- Vyhodnocování logických výrazů
- Úpravy logických výrazů
- Kvantifikátory
- Kombinatorika
- Permutace, kombinace, variace
- Kombinační čísla
- Pravděpodobnost: pojmy a značení
- Průměr a medián
- Kvantily a kvartily
- Absolutní a relativní četnost
- Korelační koeficient
- Typy statistických dat
- Průměr, medián a modus (použití)
Diskrétní matematika
Diskrétní matematika je zastřešující oblast matematiky, která se zabývá studiem diskrétních objektů – jasně oddělitelných částí. Například Lego kostky nebo karty jsou diskrétní. Můžeme je různě kombinovat či řadit, ale pracujeme s nimi vždy po jedné, nemá smysl je dělit. Naopak taková přímka je spojitá, můžeme ji dělit na stále jemnější části.
Pojem diskrétní matematika i názvy jednotlivých oblastí mohou znít abstraktně a složitě. Dají se však použít i v snadno představitelných případech, jako jsou třeba různé hry.
Množiny jsou soubory prvků. Můžeme například uvážit množinu černých šachových figurek nebo množinu fotbalových útočníků. Práce s množinami představuje základ mnoha oblastí matematiky.
Logika zkoumá způsoby, jak vyvozujeme závěry z předpokladů. Pomocí logiky můžeme dokázat, že určitá pozice v šachu je vítězná pro jednoho z hráčů.
Kombinatorika se zabývá počítáním možností, jak můžeme objekty vzájemně kombinovat. Pomocí kombinatoriky můžeme určit počet způsobů, jak rozdělit skupinu hráčů do dvou fotbalových týmů.
Pravděpodobnost zkoumá pravidla, kterými se řídí náhodné události. Za využití pravděpodobnosti můžeme vypočítat, jak moc (ne)výhodné jsou sázky v hazardní hře s kostkami.
Popisná statistika se zabývá popisem jevů, které vykazují vliv náhody. Pomocí popisné statistiky můžeme srovnávat úspěšnost fotbalových útočníků v průběhu sezóny.
NahoruMnožina je soubor prvků. Množiny využíváme jako dílčí prvek v mnoha oblastech matematiky. Příklad z geometrie: kružnice je množina bodů, které mají stejnou vzdálenost od středu. Množiny mají i mnoho praktických využití. Například při vývoji internetového obchodu program pracuje s množinou dostupných výrobků. Množiny jsou také důležité pro studium základů matematiky. Pomáhají nám například ujasnit si, co je to nekonečno.
K procvičování množin máme následující podtémata:
- Pojmy a značení – prázdná množina (\emptyset), průnik (A \cap B), podmnožina (A \subseteq B)…
- Zápis množin – zápis výčtem, zápis charakteristickou vlastností, standardní značky (\mathbb{N}, \mathbb{R})
- Množinové operace – průnik, sjednocení, rozdíl, symetrický rozdíl, aplikace na konkrétní příklady množin
- Vlastnosti množin a množinových operací – podmnožiny, množinové operace, jejich vzájemné vztahy, zápis obecných vlastností pomocí matematické notace
- Vennovy diagramy – grafické znázornění množin, jejich vztahů a operací s nimi
- Množiny množin, potenční množina – pokročilejší téma, kdy uvažujeme množiny, které mohou obsahovat jako svoje prvky jiné množiny
Množiny: pojmy a značení
Množina je soubor prvků. U množiny není důležité pořadí prvků a nezohledňuje opakované výskyty prvků. Následující množiny jsou tady všechny stejné:
- \{\square, \bigcirc, \triangle\}
- \{\bigcirc, \triangle, \square\}
- \{\square, \square, \square, \bigcirc, \bigcirc, \triangle\}
| Značení | Pojem | Komentář |
|---|---|---|
| \emptyset | prázdná množina | |
| \overline{A} | doplněk | prvky, které nepatří do množiny A |
| x \in A | patří do množiny | prvky x patří do množiny A |
| A \cap B | průnik | prvky, které patří do obou množin A, B |
| A \cup B | sjednocení | prvky, které patří alespoň do jedné z množin A, B |
| A \setminus B | rozdíl | prvky, které patří do množiny A, ale nepatří do B |
| A = B | rovnost | rovnost množin A, B |
| A \subseteq B | podmnožina | všechny prvky množiny A patří i do množiny B |
| A \subset B | vlastní podmnožina | A je podmnožina B a současně A \neq B |
| |A| | velikost množiny | počet prvků množiny |
| A \cap B = \emptyset | disjunktní množiny | množiny A, B nemají žádný společný prvek |
Zápis množin
Důležité číselné množiny mají v matematice svoje standardní označení:
| \mathbb{N} | množina přirozených čísel |
| \mathbb{Z} | množina celých čísel |
| \mathbb{Q} | množina racionálních čísel |
| \mathbb{R} | množina reálných čísel |
Ostatní množiny zapisujeme dvěma hlavními způsoby:
Zápis výčtem. Prostě vyjmenujeme prvky množiny a zapíšeme je pomocí složené závorky. Například M = \{3, 7, 9\} je tříprvková množina obsahující čísla 3, 7 a 9.
Zápis pomocí charakteristické vlastnosti. Určíme, ze které množiny prvky vybíráme a jakou musí splňovat vlastnost. Například M = \{x \in \mathbb{N} \mid x \lt 10\} je množina přirozených čísel menších než 10.
NahoruMnožinové operace
| Značení | Pojem | Komentář |
|---|---|---|
| A \cap B | průnik | prvky, které patří do obou množin A, B |
| A \cup B | sjednocení | prvky, které patří alespoň do jedné z množin A, B |
| A \setminus B | rozdíl | prvky, které patří do množiny A, ale nepatří do B |
| A \ominus B | symetrický rozdíl | prvky, které patří právě do jedné z množinA a B |
Znázornění množinových operací pomocí Vennových diagramů:
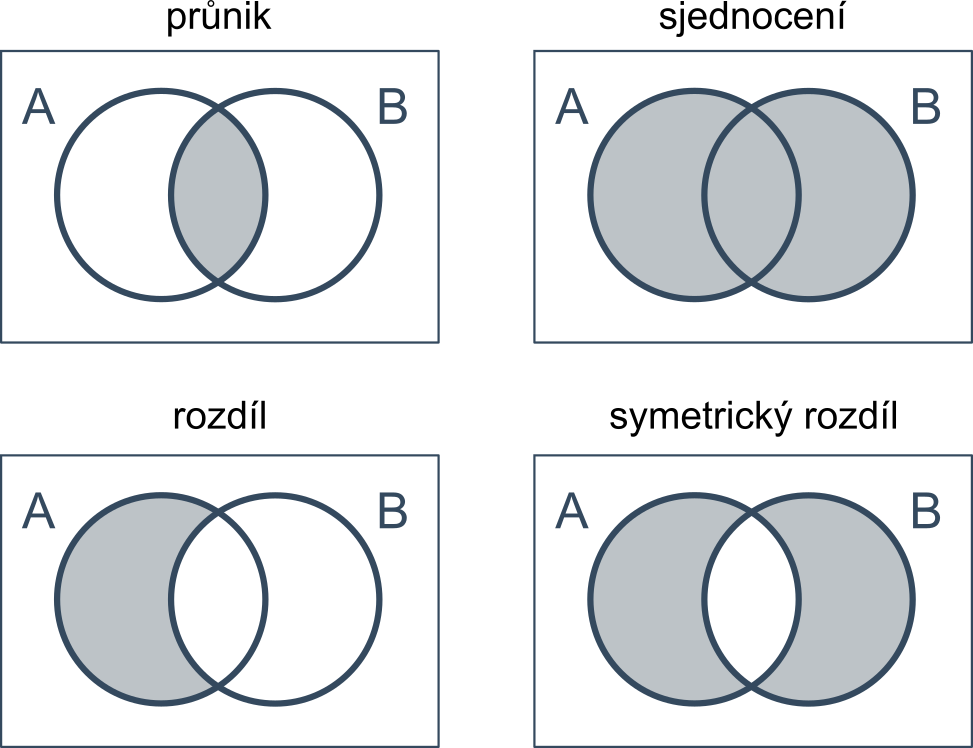
Vlastnosti množin a množinových operací
- Každá množina je svou podmnožinou: A\subseteq A
Příklady A\subseteq B
Příklady množin A, B splňující A \subseteq B:
- A = \{11, 50, 415\}, B = \{11, 50, 333, 415\}
- A = \{1,4,8\}, B = \{1,4,8\}
- A = množina všech přirozených čísel, B = množina všech celých čísel
- Množina nemůže být svou vlastní podmnožinou: A\not\subset A
Příklady A\subset B a A \not\subset B
Příklady množin A, B splňující A \subset B:
- A = \{11, 50, 415\}, B = \{11, 50, 333, 415\} (kvůli přítomnosti čísla 333 v množině B)
- A = množina všech přirozených čísel, B = množina všech celých čísel (záporná čísla jsou v množině všech celých čísel, ale nejsou v množině všech přirozených čísel)
Příklady množin, pro které A \not\subset B:
- A = \{1, 4, 8\}, B = \{1,4,8\} (protože v B není žádný prvek, který by nebyl v A)
- Prázdná množina je podmnožina jakékoliv množiny: \emptyset \subseteq A
- Prázdná množina nemá žádnou vlastní podmnožinu.
- A \subseteq A \cup B
- A \cap B \subseteq A
- A \subseteq B \wedge B \subseteq A \Leftrightarrow A=B
Vennovy diagramy
Vennův diagram znázorňuje všechny možné vztahy několika množin. Vennův diagram znázorňuje prvky množin jako body v rovině a množiny jako plochy uvnitř křivek. Nejčastěji používané jsou Vennovy diagramy pro dvě a tři množiny, ve kterých jsou množiny znázorněny pomocí kruhů. Je možné ztvárnit Vennovy diagramy i pro více množin, ale k tomu již nevystačíme s kruhy (tyto diagramy nejsou přehledné a tudíž se příliš nevyužívají).
Typický Vennův diagram pro tři množiny:
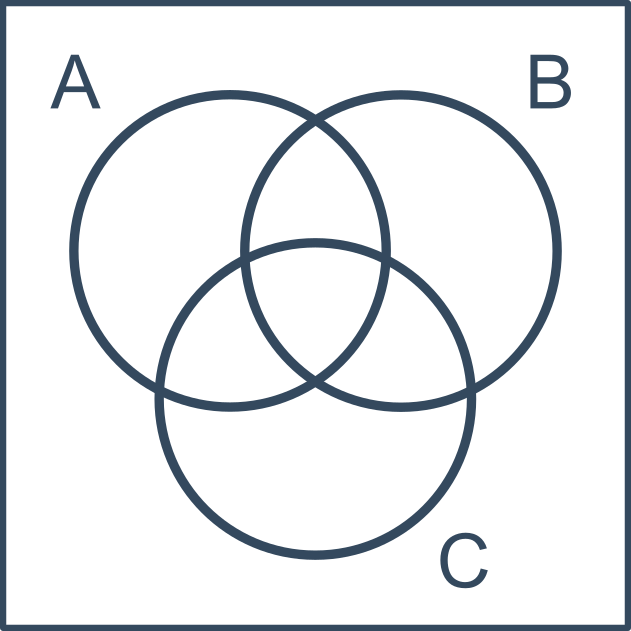
Příklad s konkrétními prvky (množina A obsahuje červené útvary, množina B obsahuje kolečka, množina C obsahuje vyplněné útvary):
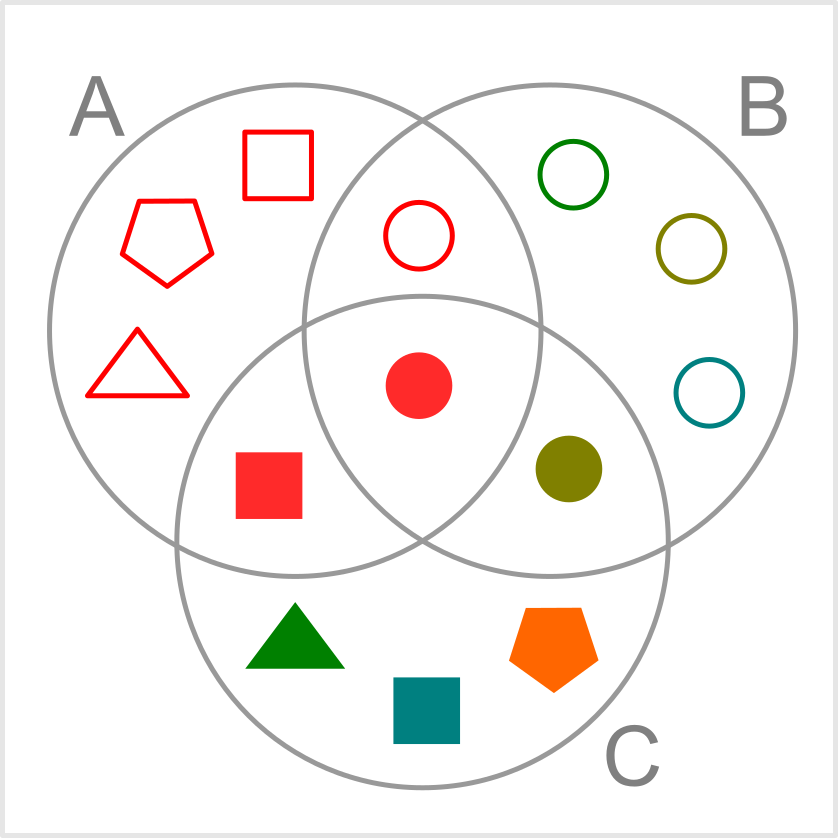
Vennovy diagramy využíváme například pro názornou ilustraci množinových operací. Následující obrázek ilustruje B \cap (A \cup C):
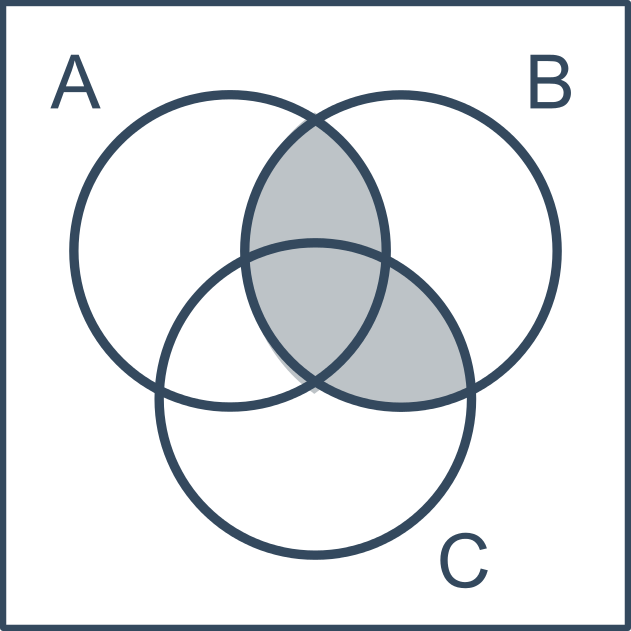
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření
Množiny množin, potenční množina
Množina prvkem množiny
Prvkem množiny může být i jiná množina. S takovým prvkem pracujeme stejně jako s jinými prvky, jen se nesmíme nechat zmást.
Příklad: Množina M = \{a, \{b, c, d, e\}, \emptyset\} obsahuje tři prvky:
- „obyčejný“ prvek a
- čtyřprvkovou množinu \{b, c, d, e\}
- prázdnou množinu \emptyset
Pozor na rozdíl mezi prázdnou množinou a množinou obsahující prázdnou množinu:
- \emptyset (též můžeme psát \{\}) je prázdná množina, její velikost je 0,
- \{\emptyset\} je množina obsahující prázdnou množinu, její velikost je 1.
Potenční množina
Potenční množina množiny M obsahuje všechny podmnožiny množiny M. Potenční množinu značíme \mathcal{P}(M) (existují i další značení, například 2^M).
Příklad: Pro množinu M = \{a, b, c\} jsou všechny její podmnožiny:
- \{\}
- \{a\}
- \{b\}
- \{c\}
- \{a, b\}
- \{a, c\}
- \{b, c\}
- \{a, b, c\}
Potenční množina je množina všech těchto množin, tj. \mathcal{P}(M)=\{\{\}, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.
Potenční množina množiny M vždy obsahuje jako svůj prvek samotnou množinu M. Každá potenční množina také obsahuje jako svůj prvek prázdnou množinu.
NahoruLogika zkoumá způsoby, jak vyvozujeme závěry z předpokladů. Logika původně vznikla jako součást filosofie, později se výrazně rozvinula v matematice. Dnes má důležité uplatnění i v informatice.
Základ matematického pojetí logiky je výroková logika, ve které pracujeme s výroky (tvrzení, která jsou buď pravdivá, nebo nepravdivá) a logickými spojkami (a zároveň, nebo, negace). Rozšířením výrokové logiky je predikátová logika, ve které navíc používáme kvantifikátory (existuje, pro každý).
Přehled témat o logice dostupných v rámci předmětu matematika:
| téma | obsah |
|---|---|
| Logické výroky | slovní zápis logických výroků |
| Logika: pojmy a značení | zápis výroků pomocí logických spojek \wedge, \vee, \neg, \Rightarrow, \Leftrightarrow |
| Vyhodnocování logických výrazů | vyhodnocování pravdivosti logických výrazů zapsaných pomocí logických operací |
| Úpravy logických výrazů | úprava a zjednodušení logického výrazu podle pravidel práce s logickými operacemi |
| Kvantifikátory | obohacení logických výrazů o existenční a obecný kvantifikátor \exists, \forall |
| Důkazy | exaktní matematické postupy, jak ověřit platnost logických výroků |
V rámci najdete logiku také na informatice. Tam je důraz kladen na logické spojky používané při programování a na řešení logických úloh.
NahoruLogika: pojmy a značení
Výroky
Výrok je sdělení, u kterého má smysl otázka, zda je pravdivý nebo nepravdivý, přičemž může nastat jen jedna z těchto možností.
Příklady výroků:
Město Brno leží v České republice. (pravdivý výrok)
Brno je hlavní město České republiky. (nepravdivý výrok)
Na Marsu je zakopán poklad. (výrok, jehož pravdivost neznáme)
Příklady vět, které nejsou výroky: Máš hlad? Běž do obchodu pro vajíčka.
Logické spojky
| Zápis | Název | Význam |
|---|---|---|
| \neg A | negace | neplatí A |
| A \wedge B | konjunkce, a zároveň | A a B platí současně |
| A \vee B | disjunkce, nebo | platí alespoň jedno z A a B |
| A \Rightarrow B | implikace, jestliže-pak | pokud platí A, pak platí i B |
| A \Leftrightarrow B | ekvivalence, právě když | A platí právě tehdy, když platí B |
Tautologie a kontradikce
Tautologie je výroková formule, která je vždy pravdivá. Příklady:
- A \vee \neg A (zákon vyloučení třetího)
- (A \Rightarrow B) \Leftrightarrow (\neg B \Rightarrow \neg A)
Kontradikce je výroková formule, která je vždy nepravdivá. Příkladem je formule A \wedge \neg A (zákon sporu).
Formule je splnitelná, pokud není kontradikcí.
NahoruVyhodnocování logických výrazů
Pravdivostní tabulka logických operací
| A | B | A \vee B | A \wedge B | A \Rightarrow B | A \Leftrightarrow B |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Úpravy logických výrazů
Přepis implikace a ekvivalence
| Výrok | Ekvivalentní výrok | |
|---|---|---|
| A\Rightarrow B | \neg A\vee B | |
| A\Rightarrow B | \neg B\Rightarrow \neg A | |
| A\Leftrightarrow B | (A\wedge B)\vee (\neg A \wedge \neg B) |
Negování složených výroků
| Výrok | Ekvivalentní výrok | |
|---|---|---|
| \neg (\neg A) | A | |
| \neg (A\vee B) | \neg A\wedge \neg B | |
| \neg (A\wedge B) | \neg A\vee \neg B | |
| \neg (A\Rightarrow B) | A\wedge \neg B | |
| \neg (A\Leftrightarrow B) | (\neg A\wedge B)\vee(A \wedge \neg B) |
Pravidla pro negaci disjunkce a konjunkce (2. a 3. řádek tabulky) se nazývají De Morganovy zákony.
Analogické zákony jako při počítání s čísly
Pro logické operace \wedge, \vee také platí komutativní (1. a 2. řádek následující tabulky), asociativní (3. a 4. řádek) a distributivní zákony (5. a 6. řádek):
| Výrok | Ekvivalentní výrok | |
|---|---|---|
| A \wedge B | B \wedge A | |
| A \vee B | B \vee A | |
| (A \wedge B) \wedge C | A \wedge (B \wedge C) | |
| (A \vee B) \vee C | A \vee (B \vee C) | |
| A \wedge (B \vee C) | (A \wedge B) \vee (A \wedge C) | |
| A \vee (B \wedge C) | (A \vee B) \wedge (A \vee C) |
Kvantifikátory
Kvantifikátory
| Značení | Pojem | Význam |
|---|---|---|
| \exists x | existenční kvantifikátor | existuje x, takové že… |
| \forall x | obecný (univerzální) kvantifikátor | pro každé x platí… |
Příklady výroků s kvantifikátory
Vlastnost Číslo x je sudé. můžeme vyjádřit jako Existuje celé číslo k takové, že x = 2\cdot k. To můžeme zapsat jako \exists k \in \mathbb{Z}: x = 2\cdot k.
Výrok Ponorky (P) nemohou létat (L). můžeme zapsat jako \forall x: P(x) \Rightarrow \neg L(x).
U složitějších výroků s více kvantifikátory musíme dávat na pořadí kvantifikátorů:
- \exists x\in M\ \forall y \in M: y \leq x – existuje prvek v množině M, který je větší roven všem ostatním prvkům v M, tj. výrok říká, že množina má největší prvek.
- \forall x\in M\ \exists y \in M: y \leq x – pro každý prvek v množině M existuje prvek y, který je menší nebo roven X. Protože klidně můžeme vybrat y=x, je to splněno pro každou množinu (pro pokročilé: za předpokladu, že uvažujeme množiny čísel a \leq jako běžné uspořádání na číslech).
Negace výroků s kvantifikátory
Při negování výroků s kvantifikátory měníme existenční kvantifikátor na obecný (a naopak) a posouváme negaci „dovnitř“.
Příklad: negace výroku Všechny kočky (K) jsou černé (C).
| Není pravda, že všechny kočky (K) jsou černé (C). |
| \neg (\forall x: K(x) \Rightarrow C(x)) |
| Změníme obecný kvantifikátor na existenční a znegujeme výrok: |
| \exists x: \neg(K(x) \Rightarrow C(x)) |
| Nyní znegujeme implikaci pomocí pravidla \neg(A \Rightarrow B) \Leftrightarrow (A \wedge \neg B): |
| \exists x: K(x) \wedge \neg C(x) |
| Existuje kočka, která není černá. |
Kombinatorika
Kombinatorika je obor matematiky, který se zabývá počítáním možností a uspořádáním prvků v různých situacích. Využívá se například k určení počtu různých kombinací při losování, sestavování týmů nebo určování pořadí.
- Kombinatorika: pojmy – základní pojmy a principy
- Základní kombinatorická pravidla – pravidlo součinu a součtu
- Permutace, kombinace, variace – různé způsoby uspořádání a výběru prvků, včetně jejich vzorců a příkladů
- Kombinační čísla – důkladnější procvičení klíčového pojmu v kombinatorice
- Výrazy s faktoriálem a kombinačními čísly – cílené procvičení výpočtů s faktoriály a kombinačními čísly, což je častý dílčí krok v kombinatorických výpočtech
Permutace, kombinace, variace
Pojmy
- Permutace je uspořádání prvků do fixního pořadí.
- Kombinace (k prvková) je výběr k prvků ze zadané množiny.
- Kombinace s opakováním (k prvková) je výběr k prvků ze zadané množiny, přičemž prvky se mohou opakovat.
- Variace (k prvková) je uspořádaný výběr k prvků ze zadané množiny.
- Variace s opakováním (k prvková) je uspořádaný výběr k prvků ze zadané množiny, přičemž prvky se mohou opakovat.
Příklady
| permutace | \{A, B, C\} | ABC, ACB, BAC, BCA, CAB, CBA |
| kombinace | \{A, B, C, D\}; k=2 | AB, AC, AD, BC, BD, CD |
| kombinace s opakováním | \{A, B, C, D\}; k=2 | AA, AB, AC, AD, BB, BC, BD, CC, CD, DD |
| variace | \{A, B, C, D\}; k=2 | AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC |
| variace s opakováním | \{A, B, C\}; k=2 | AA, AB, AC, BA, BB, BC, CA, CB, CC |
Vzorce
Počty permutací, kombinací a variací udává následující tabulka:
| počet všech permutací n prvků | n! |
| počet všech k prvkových kombinací z n prvků | \binom{n}{k} = \frac{n!}{(n-k)!k!} |
| počet všech k prvkových kombinací s opakováním z n prvků | \binom{n + k - 1}{k} |
| počet všech k prvkových variací z n prvků | \frac{n!}{(n-k)!} |
| počet všech k prvkových variací s opakováním z n prvků | n^k |
Komiks pro zpestření

Kombinační čísla
Kombinační číslo udává počet kombinací, tj. způsobů, jak vybrat k prvků z n prvkové množiny. Kombinační čísla se vyskytují velmi často v kombinatorických výpočtech, a proto mají speciální značení \binom{n}{k} (čteme „n nad k“).
Pro n \geq k \geq 0 platí: \binom{n}{k} = \frac{n!}{k!(n-k)!}
Pro kombinační čísla platí řada dalších vztahů, například:
- \binom{n}{k} = \binom{n}{n-k}
- \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}
- \sum_{k=0}^n \binom{n}{k} = 2^n
Příklady:
| \binom{3}{1} | = 3 |
| \binom{4}{2} | = 6 |
| \binom{5}{3} | = 10 |
| \binom{6}{2} | = 15 |
| \binom{15}{15} | = 1 |
Pravděpodobnost: pojmy a značení
Náhodný jev je výsledek náhodného pokusu, o kterém lze po provedení pokusu rozhodnout, zda nastal nebo nenastal. Jeho typickým rysem je, že může, ale nemusí nastat. Pravděpodobnost jevu je míra očekávání, že jev nastane. Pravděpodobnost je číslo mezi 0 a 1. V běžném jazyce vyjadřujeme často pravděpodobnost v procentech, což je stonásobek pravděpodobnosti používané v matematice.
Pojmy a značení
| jev elementární | 0 \leq P(A) \leq 1 | základní výsledek pokusu, který nelze dále rozložit |
| jev jistý | P(A) = 1 | nastane vždy |
| jev nemožný | P(A) = 0 | nenastane nikdy |
| B je jev opačný k jevu A | P(B) = 1-P(A) | B nastane právě, když nenastane A |
| jevy A a B jsou neslučitelné | A\cap B=\emptyset | jevy A a B nemohou nastat současně |
Příklad
- V pytlíku mám pět koulí, z toho dvě jsou červené, dvě modré a jedna žlutá. Koule jsou stejné až na barvu. Pokus spočívá v tom, že z pytlíku poslepu vytáhnu kouli.
- „Vytáhnu červenou kouli.“ je náhodný jev. Jde o jev elementární. Jeho pravděpodobnost je 0,4 (v běžné řeči bychom mohli říct 40 %).
- „Vytáhnu červenou nebo žlutou kouli.“ je složený jev. Jeho pravděpodobnost je 0,6.
- „Vytáhnu kouli.“ je jev jistý.
- „Vytáhnu zelenou kouli.“ je jev nemožný.
Průměr a medián
Průměr a medián vyjadřují „typickou“ hodnotu proměnných z určitého vzorku, jsou to míry centrální (střední) tendence.
Průměr je součet hodnot vydělený jejich počtem. Přesněji řečeno jde o aritmetický průměr (existují i jiné druhy průměrů, např. harmonický či geometrický).
Medián je prostřední hodnota ze seřazené posloupnosti hodnot. Je definován jako hodnota větší nebo rovna polovině hodnot v souboru a menší nebo rovna polovině hodnot v souboru.
Příklad: průměr a medián souboru 10, 3, 8, 4, 5
Uvažme soubor hodnot 10, 3, 8, 4, 5.
- Průměr je součet dělený počtem, tj. 30:5=6.
- Pro určení mediánu hodnoty nejdříve seřadíme: 3, 4, 5, 8, 10.
- Medián je prostřední hodnota, tedy 5.
Pokud má soubor sudý počet prvků, většinou se za medián označuje průměr dvou prostředních hodnot.
Příklad: medián souboru 10, 2, 9, 4, 14, 5
Uvažme soubor se sudým počtem hodnot 10, 2, 9, 4, 14, 5.
- Seřazená posloupnost je 2, 4, 5, 9, 10, 14.
- Hodnoty uprostřed posloupnosti jsou 5 a 9, medián je tedy 7.
Někdy máme soubor hodnot, které lze uspořádat podle velikosti, ale není možné vypočítat aritmetický průměr dvou hodnot.
Příklad: medián souboru S, M, XL, XXL
Uvažme soubor čtyř hodnot S, M, XL, XXL velikostí oblečení.
- Pro něj splňuje definici mediánu jakákoliv hodnota od M do XL, tedy M, L, i XL.
Kvantily a kvartily
Kvantily jsou charakteristiky polohy statistického znaku podobně jako např. aritmetický průměr a medián. Kvantily lze určit pro ordinální, intervalové a poměrové typy dat.
Soubor n hodnot uspořádáme podle velikosti: x_1 \le x_2 \le \ldots \le x_{n-1} \le x_n
Mějme číslo \theta mezi nulou a jedničkou. Kvantil Q_{\theta} je hodnota, která dělí uspořádanou posloupnost hodnot v souboru na dolní a horní část tak, že dolní část obsahuje alespoň \theta \cdot n hodnot a horní část alespoň (1-\theta)\cdot n hodnot.
x_1 \le \ldots \le x_c \le Q_{\theta} \le x_{c+1} \le \ldots \le x_n
- Je-li \theta \cdot n necelé číslo, a nejbližší větší celé číslo je k, volíme obvykle Q_{\theta}=x_k.
- Je-li \theta \cdot n=m celé číslo, volíme Q_{\theta} = \frac{x_{m}+x_{m+1}}{2} (pokud je možné tento aritmetický průměr spočítat – tedy pro intervalové a poměrové znaky).
Příklad: určení kvantilů Q_{0{,}1} a Q_{0{,}75} souboru 0,0,0,0,1,2,3,4
Vezmeme soubor osmi čísel 0,0,0,0,1,2,3,4.
- Kvantil Q_{0{,}1} určíme takto: 0{,}1 \cdot 8 = 0{,}8, nejbližší větší celé číslo je 1, takže Q_{0{,}1}=x_1=0.
- Kvantil Q_{0{,}75} určíme takto: 0{,}75 \cdot 8 = 6, takže Q_{0{,}75}=\frac{x_6+x_7}{2}=\frac{2+3}{2}=2{,}5.
Pro ordinální znaky nemusí být možné spočítat aritmetický průměr. Jako kvantil Q_{\theta} pak zvolíme některou hodnotu, která vhodně dělí uspořádanou posloupnost hodnot souboru.
Příklad: určení kvantilu Q_{0{,}8} souboru S, S, M, L, XXL
Spočítejme kvantil Q_{0{,}8} pro hodnoty S, S, M, L, XXL znaku „velikost oblečení“.
- 5 \cdot 0{,}8=4, takže Q_{0{,}8} je jakákoliv hodnota mezi x_4 a x_5, tedy L,XL, nebo XXL.
p% kvantil Q_{\frac{p}{100}} se nazývá p. percentil.
Některé významné kvantily:
| kvantil | název | |
|---|---|---|
| Q_{0{,}5} | medián | |
| Q_{0{,}25} | dolní kvartil | |
| Q_{0{,}75} | horní kvartil | |
| Q_{0{,}01},Q_{0{,}02},\ldots, Q_{0{,}99} | 1. percentil, 2. percentil, … , 99.percentil |
Mezikvartilové rozpětí je rozdíl horního a dolního kvartilu: Q_{0{,}75}-Q_{0{,}25} Mezikvartilové rozpětí (někdy označované jako IQR) lze spočítat pro intervalové a poměrové znaky.
Příklad: mezikvartilové rozpětí pro soubor 0,0,0,0,1,2,3,4
Určeme mezikvartilové rozpětí pro soubor osmi hodnot 0,0,0,0,1,2,3,4.
- Horní kvartil Q_{0{,}75} jsme už v předchozích příkladech spočítali, je to 2{,}5.
- Dolní kvartil Q_{0{,}25} je \frac{x_2+x_3}{2}=\frac{0+0}{2}=0.
- Mezikvartilové rozpětí je 2{,}5-0=2{,}5.
Absolutní a relativní četnost
Statistický soubor má rozsah n, pokud obsahuje právě n jednotek. Například statistickým souborem s rozsahem 10 může být skupinka 10 dětí ze třetí třídy. Jednotliví žáci a žákyně jsou pak jednotky statistického souboru.
Příklady statistických znaků, které nás mohou zajímat: jméno, výška, známka z prvouky. Předpokládejme, že jména dětí z naší skupinky deseti žáků a žákyň jsou: Anna, Eva, Jan, Jan, Jan, Vanesa, Vanesa, Mirka, Tobiáš, Tomáš.
Znak jméno tedy v našem statistickém souboru nabývá sedmi různých hodnot – Anna, Eva, Jan, Vanesa, Mirka, Tobiáš, Tomáš. Některé děti se mohou jmenovat stejně.
Absolutní četnost hodnoty znaku v daném statistickém souboru je počet jednotek ze statistického souboru, které mají danou hodnotu znaku.
Například absolutní četnost hodnoty „Jan“ znaku jméno je 3, protože ve skupince jsou tři žáci jménem Jan. Absolutní četnost hodnoty „Eva“ znaku jméno je 1.
Relativní četnost hodnoty znaku v daném statistickém souboru vypočítáme jako podíl počtu jednotek s danou hodnotou znaku počtem všech jednotek statistického souboru. Také se dá říci, že relativní četnost hodnoty znaku je podíl absolutní četnosti této hodnoty znaku a rozsahu n statistického souboru. Relativní četnost se zadává jako číslo v intervalu [0,1] nebo v procentech.
Například relativní četnost hodnoty „Vanesa“ znaku jméno je \frac{2}{10}=0{,}2, protože ve skupince celkem deseti dětí jsou dvě žákyně jménem Vanesa. Relativní četnost hodnoty „Vanesa“ znaku jméno můžeme zapsat také jako 20\ \%.
Součet absolutních četností všech hodnot jednoho znaku je roven rozsahu n daného statistického souboru.
Součet relativních četností všech hodnot jednoho znaku je 1 neboli 100\ \%.
NahoruKorelační koeficient
Korelace je vztah mezi dvěma veličinami. Korelační koeficient je číslo, které vyjadřuje sílu tohoto vztahu.
Existuje více způsobů, jak korelaci měřit. Nejčastěji používaný je Pearsonův korelační koeficient. Ten se značí r a má následující vlastnosti:
- Nabývá hodnot z intervalu [-1, 1].
- Měří pouze lineární závislost mezi veličinami.
- Pokud je hodnota kladná, odpovídá zvětšení jedné veličiny zvětšení druhé.
- Pokud je hodnota záporná, odpovídá zvětšení jedné veličiny zmenšení druhé.
- Pokud je hodnota nulová, není mezi veličinami lineární závislost.
- Pokud je hodnota přesně 1 nebo -1, je mezi veličinami přesná lineární závislost.
Typy statistických dat
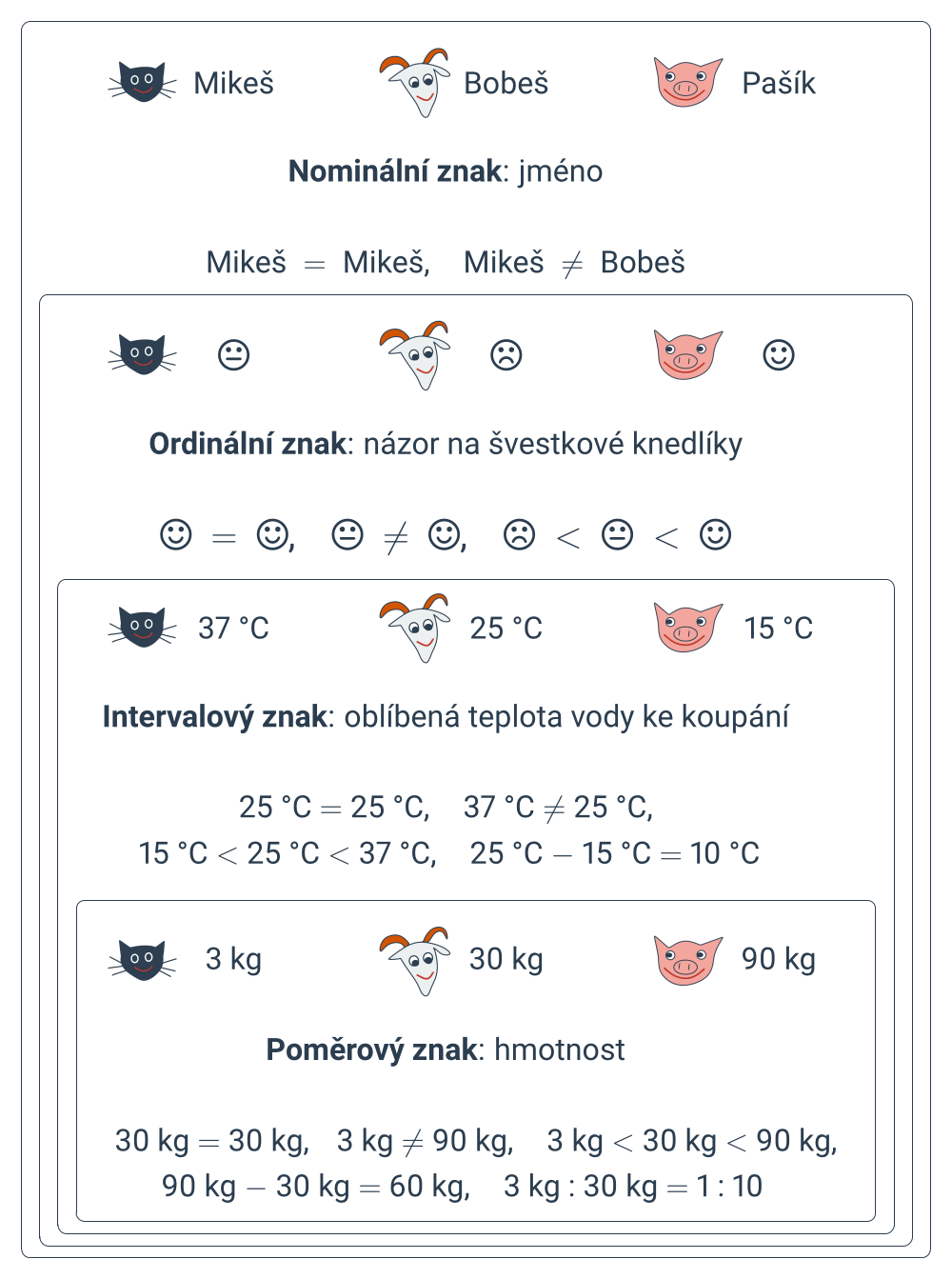
Uvažujme statistický soubor zvířátek z Hrusic. Vezměme z něj tři jednotky na ukázku: kocourka Mikeše, kozla Bobeše a prasátko Pašíka. Budeme si u nich všímat různých typů znaků.
Nominální znak nabývá hodnot, u kterých můžeme testovat rovnost, tj. určit, jestli jsou stejné nebo různé. Například jméno, barva.
Ordinální znak nabývá hodnot, u kterých můžeme testovat rovnost a které navíc umíme porovnávat, tj. určit, která ze dvou různých hodnot je menší a která větší. Například známka z počtů, velikost oblečení (XS, S, M, L, XL), obliba brokolicové polívky („fuj“,„nic moc“,„mňam“).
Intervalový znak nabývá hodnot, u kterých můžeme testovat rovnost, porovnávat je a určit rozdíl dvou hodnot, tj. stejný interval mezi jednou a druhou dvojicí hodnot vyjadřuje i stejný rozdíl v intenzitě zkoumané vlastnosti. Například teplota ve stupních Celsia, rok narození.
Poměrový znak nabývá hodnot, u kterých můžeme testovat rovnost, porovnávat je, určit rozdíl dvou hodnot a určit poměr dvou hodnot, tj. spočítat jejich podíl, který smysluplně vyjadřuje kolikrát je jedna hodnota větší než druhá. Například teplota ve stupních Kelvina, hmotnost. Teplota ve stupních Celsia může jít i do záporných čísel a těleso o teplotě 10 °C nemá dvakrát větší kinetickou energii částic než těleso o teplotě 5 °C, takže teplota ve stupních Celsia není poměrový znak.
Alternativní znak je pojem mimo tuto hierarchii, znamená to, že znak nabývá pouze dvou hodnot. Například zdravý – nemocný, má boty – nemá boty.
Průměr, medián a modus (použití)
Aritmetický průměr, medián a modus jsou charakteristiky polohy znaku. Používáme je k popisu typické hodnoty znaku.
Aritmetický průměr pro daný soubor se počítá jako podíl součtu hodnot znaku a rozsahu souboru.
- Aritmetický průměr lze spočítat pro intervalové a poměrové znaky.
- Nejlépe se hodí k popisu typické hodnoty znaku, který nabývá v daném souboru podobných hodnot bez příliš odlišných extrémů, které by aritmetický průměr vychýlily mimo typické hodnoty.
Příklad použití aritmetického průměru – soubor hodnot 122, 116, 120, 118 znaku „výška dítěte v cm“ má aritmetický průměr 119.
Medián dělí řadu vzestupně seřazených hodnot na dvě stejně početné poloviny.
- Pro lichý počet hodnot je medián prostřední prvek.
- Pro sudý počet hodnot může definici mediánu odpovídat více hodnot, někdy se v takovém případě bere jako medián aritmetický průměr dvou prostředních hodnot (samozřejmě jen pokud lze pro daný znak aritmetický průměr spočítat).
- Medián lze určit pro ordinální, intervalové a poměrové znaky.
- Na rozdíl od aritmetického průměru není ovlivněn extrémními hodnotami.
Příklad použití mediánu – soubor hodnot 1, 1000, 1002, 1003 znaku „hmotnost krokodýla v kg“ má medián 1001 (nebo jakékoli číslo od 1000 do 1002). Extrémní malá hodnota 1 způsobí, že aritmetický průměr je 751{,}5, což neodpovídá typické hodnotě „něco málo přes 1000 kg“.
Modus je hodnota znaku, která má v daném souboru největší relativní (i absolutní) četnost.
- Takových hodnot může být víc než jedna.
- Modus můžeme spočítat pro nominální, ordinální, intervalové a poměrové znaky.
Příklad použití – modus souboru hodnot 1, 1, 1, 1, 2, 2 znaku „počet hrbů velblouda“ je 1.
Nahoru
