Permutace, kombinace, variace

umime.to/F1W

Stáhnout QR kód

Nadřazené	Diskrétní matematika » Kombinatorika » Permutace, kombinace, variace
Předcházející	Kombinatorika: pojmy

Cvičení

Pojmy

Permutace je uspořádání prvků do fixního pořadí.
Kombinace (k prvková) je výběr k prvků ze zadané množiny.
Kombinace s opakováním (k prvková) je výběr k prvků ze zadané množiny, přičemž prvky se mohou opakovat.
Variace (k prvková) je uspořádaný výběr k prvků ze zadané množiny.
Variace s opakováním (k prvková) je uspořádaný výběr k prvků ze zadané množiny, přičemž prvky se mohou opakovat.

Příklady

permutace	\{A, B, C\}	ABC, ACB, BAC, BCA, CAB, CBA
kombinace	\{A, B, C, D\}; k=2	AB, AC, AD, BC, BD, CD
kombinace s opakováním	\{A, B, C, D\}; k=2	AA, AB, AC, AD, BB, BC, BD, CC, CD, DD
variace	\{A, B, C, D\}; k=2	AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB, DC
variace s opakováním	\{A, B, C\}; k=2	AA, AB, AC, BA, BB, BC, CA, CB, CC

Vzorce

Počty permutací, kombinací a variací udává následující tabulka:

počet všech permutací n prvků	n!
počet všech k prvkových kombinací z n prvků	\binom{n}{k} = \frac{n!}{(n-k)!k!}
počet všech k prvkových kombinací s opakováním z n prvků	\binom{n + k - 1}{k}
počet všech k prvkových variací z n prvků	\frac{n!}{(n-k)!}
počet všech k prvkových variací s opakováním z n prvků	n^k

Komiks pro zpestření

Slovní úlohy

Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.

Permutace, kombinace, variace

Kombinace bez opakování

Kombinace s opakováním

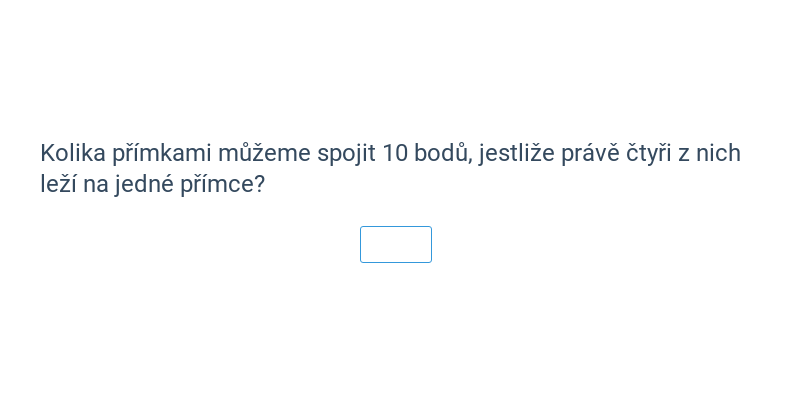
Permutace a variace bez opakování

Permutace a variace s opakováním

Permutace a variace s opakováním

Slovní úlohy • střední

NAPIŠTE NÁM

Nevíte si rady?

Nejprve se prosím podívejte na časté dotazy:

Časté dotazy Návody pro učitele

Čeho se zpráva týká?

Vzkaz Obsah Ovládání Přihlášení Licence