Kombinační číslo udává počet kombinací, tj. způsobů, jak vybrat k prvků z n prvkové množiny. Kombinační čísla se vyskytují velmi často v kombinatorických výpočtech, a proto mají speciální značení \binom{n}{k} (čteme „n nad k“).
Pro n \geq k \geq 0 platí: \binom{n}{k} = \frac{n!}{k!(n-k)!}
Pro kombinační čísla platí řada dalších vztahů, například:
- \binom{n}{k} = \binom{n}{n-k}
- \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}
- \sum_{k=0}^n \binom{n}{k} = 2^n
Příklady:
| \binom{3}{1} | = 3 |
| \binom{4}{2} | = 6 |
| \binom{5}{3} | = 10 |
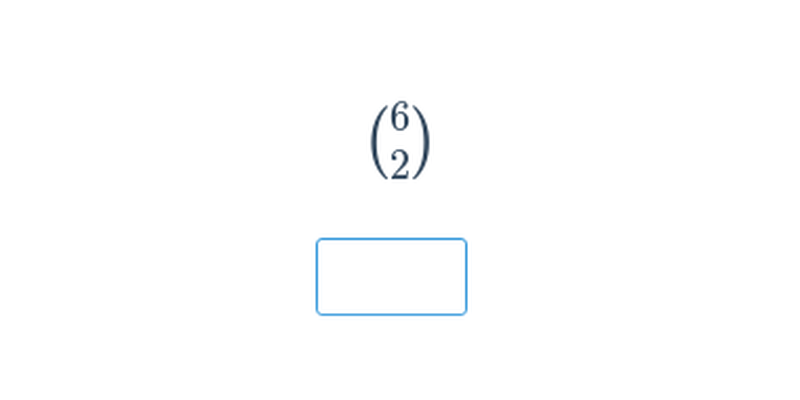
| \binom{6}{2} | = 15 |
| \binom{15}{15} | = 1 |