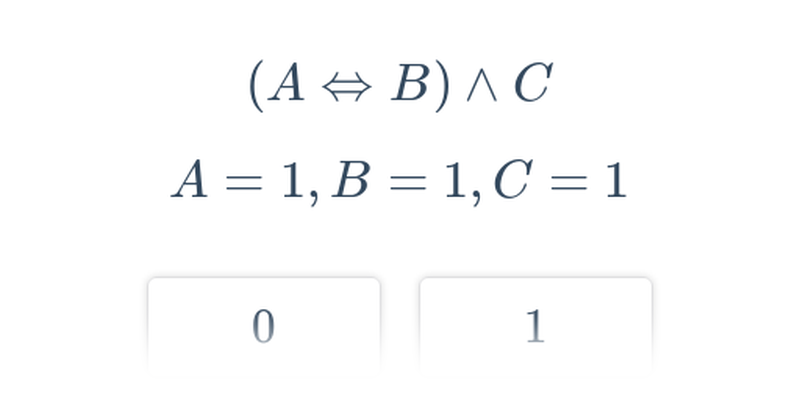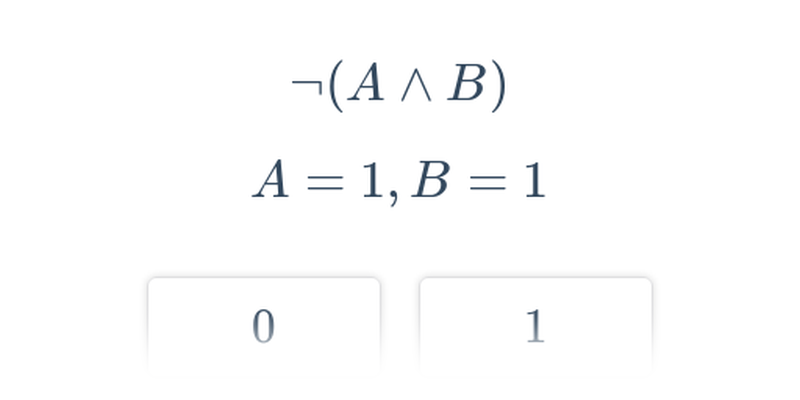Čeština
Angličtina
Informatika
Biologie
Umíme to
Němčina
Zeměpis
Chemie
Dějepis
Fyzika
Aritmetika
Zlomky, procenta
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Psaná odpověď
Grafař
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Logika
Krátká adresa: umime.to/F1O
| Nadřazené | Diskrétní matematika » Logika |
Logika zkoumá způsoby, jak vyvozujeme závěry z předpokladů. Logika původně vznikla jako součást filosofie, později se výrazně rozvinula v matematice. Dnes má důležité uplatnění i v informatice.
Základ matematického pojetí logiky je výroková logika, ve které pracujeme s výroky (tvrzení, která jsou buď pravdivá, nebo nepravdivá) a logickými spojkami (a zároveň, nebo, negace). Rozšířením výrokové logiky je predikátová logika, ve které navíc používáme kvantifikátory (existuje, pro každý).
Přehled témat o logice dostupných na Umíme matiku:
| téma | obsah |
|---|---|
| Logické výroky | slovní zápis logických výroků |
| Logika: pojmy a značení | zápis výroků pomocí logických spojek \wedge, \vee, \neg, \Rightarrow, \Leftrightarrow |
| Vyhodnocování logických výrazů | vyhodnocování pravdivosti logických výrazů zapsaných pomocí logických operací |
| Úpravy logických výrazů | úprava a zjednodušení logického výrazu podle pravidel práce s logickými operacemi |
| Kvantifikátory | obohacení logických výrazů o existenční a obecný kvantifikátor \exists, \forall |
| Důkazy | exaktní matematické postupy, jak ověřit platnost logických výroků |
V rámci systémů Umíme najdete logiku také na informatice: logika na Umíme informatiku. Tam je důraz kladen na logické spojky používané při programování a na řešení logických úloh.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Logické výroky (střední)
30 zadání
Typicky zabere: 7 min
Mořská logika (lehké)
30 zadání
Typicky zabere: 4 min
Mořská logika (střední)
33 zadání
Typicky zabere: 5 min
Logika: pojmy a značení (střední)
30 zadání
Typicky zabere: 4 min
Vyhodnocování logických výrazů (střední)
41 zadání
Typicky zabere: 5 min
Vyhodnocování logických výrazů (těžké)
52 zadání
Typicky zabere: 7 min
Úpravy logických výrazů (těžké)
35 zadání
Typicky zabere: 11 min
Kvantifikátory (střední)
30 zadání
Typicky zabere: 4 min
Kvantifikátory (těžké)
34 zadání
Typicky zabere: 9 min
Logika: mix (střední)
101 zadání
Typicky zabere: 5 min
Logika: mix (těžké)
121 zadání
Typicky zabere: 10 min
Pexeso
Hledání dvojic, které k sobě patří.
Krok po kroku
V tomto cvičení doplňujete jednotlivé kroky v rozsáhlejším postupu – například jednotlivé kroky v úpravě výrazů nebo při řešení rovnic. Cvičení je dobrou rozcvičkou na samostatné řešení kompletních příkladů.
Porozumění
U každé úlohy máte k dispozici text či obrázek popisující matematický problém. Následuje pak několik otázek, které testují, jak jste textu či obrázku porozuměli.
Obrázkové důkazy
Obrázek sice není plnohodnotným důkazem, ale často dokáže velmi výstižně ilustrovat základní myšlenku matematických tvrzení.
Matematická indukce
Zda nabízíme vypracované důkazy matematickou indukcí. Ke každému pak následuje několik otázek kontrolujících porozumění důkazu.
