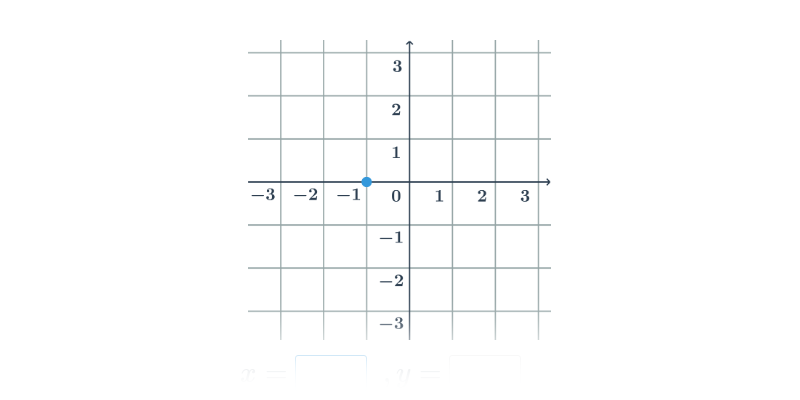
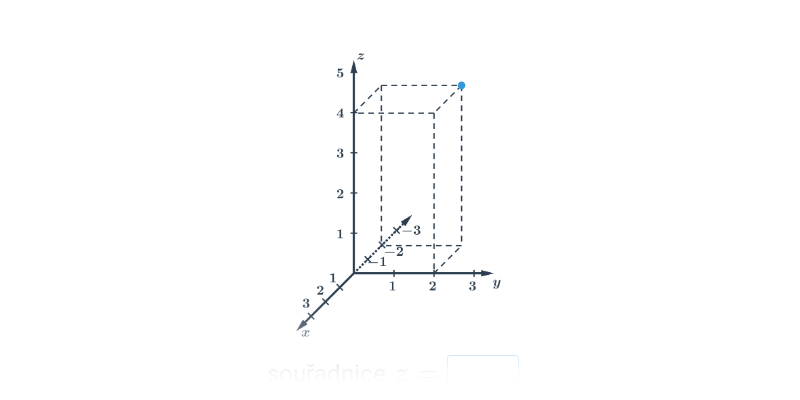
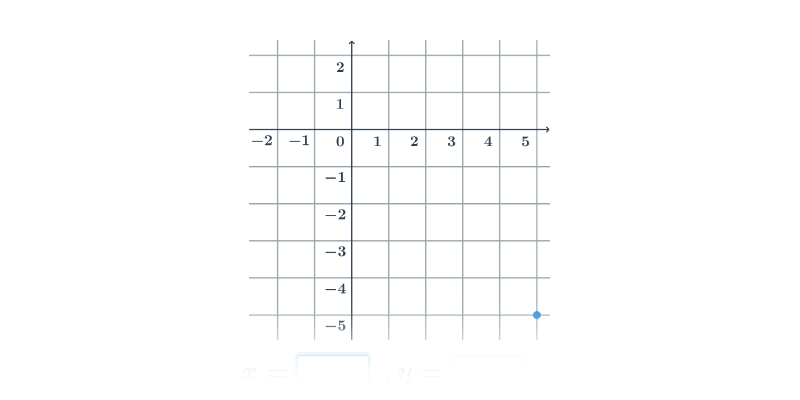
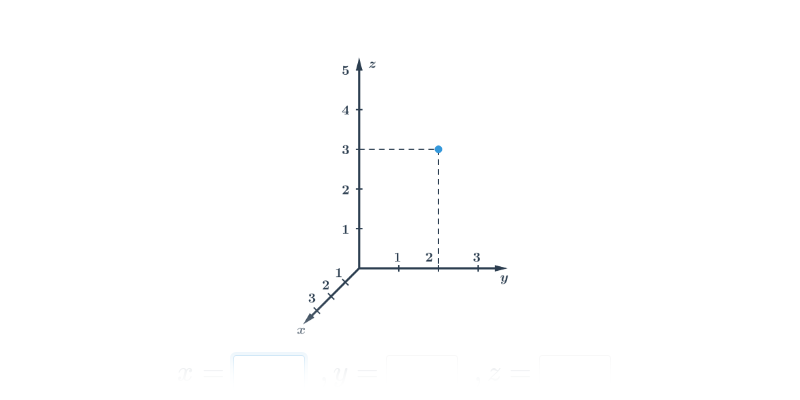
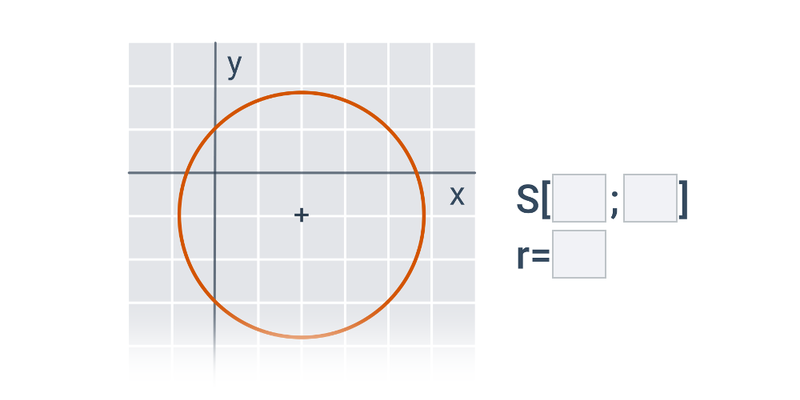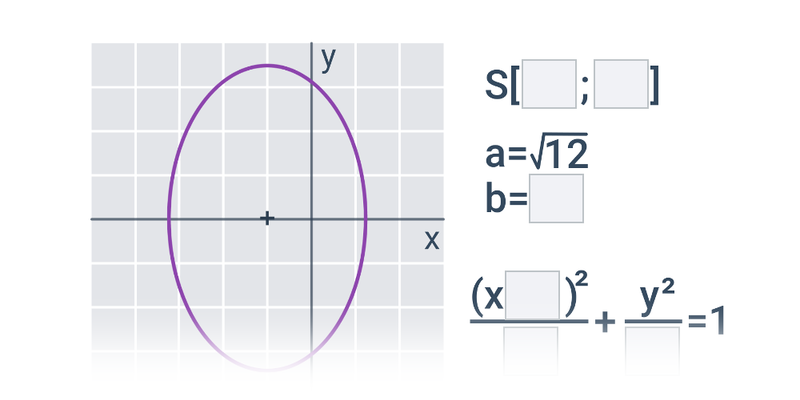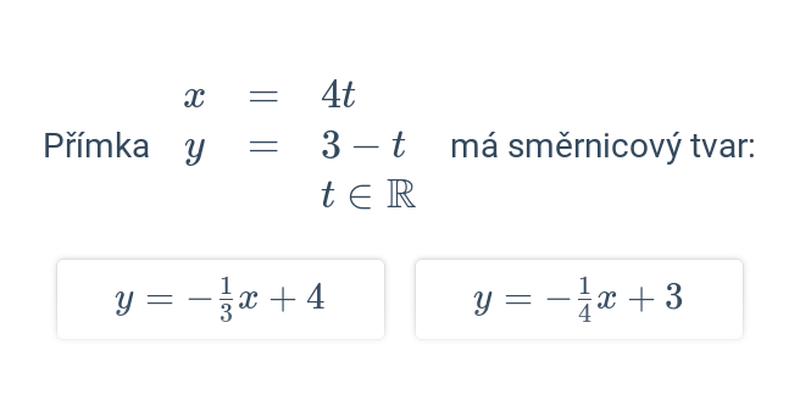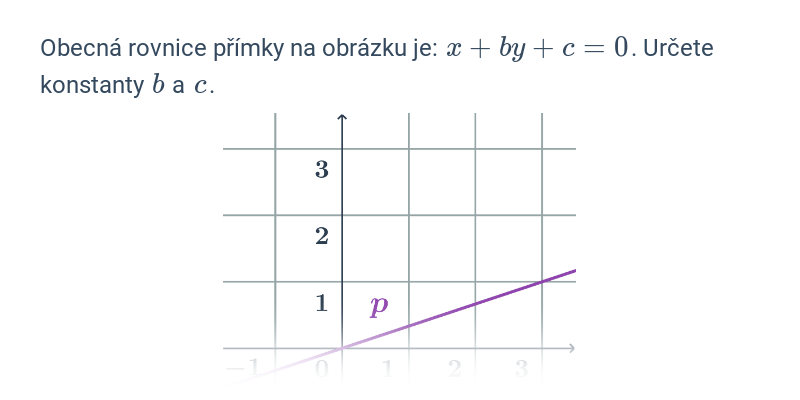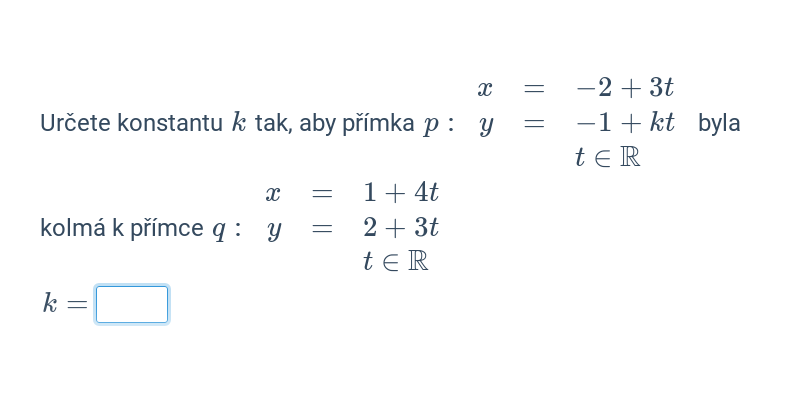Analytická geometrie

F4Z

umime.to/F4Z

Analytická geometrie nám dovoluje zapsat geometrické problémy algebraicky a vyřešit je pomocí rovnic.

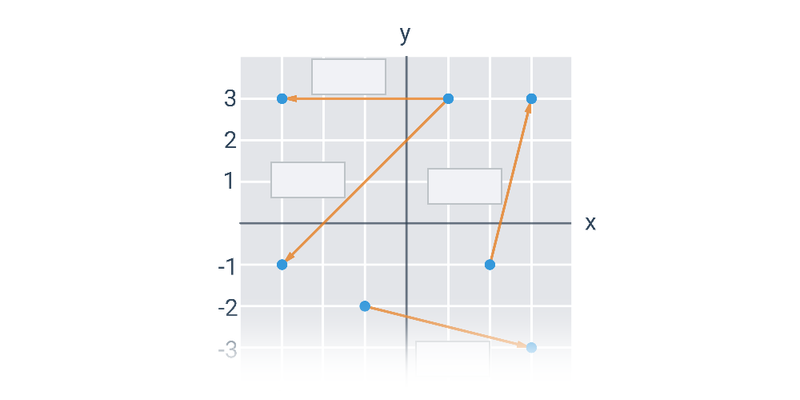
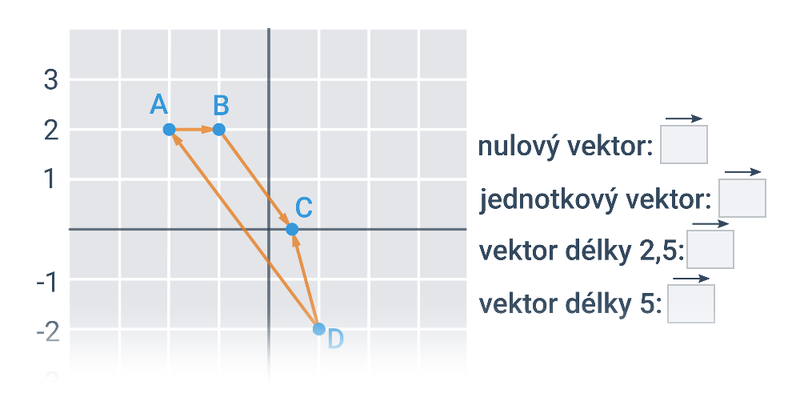
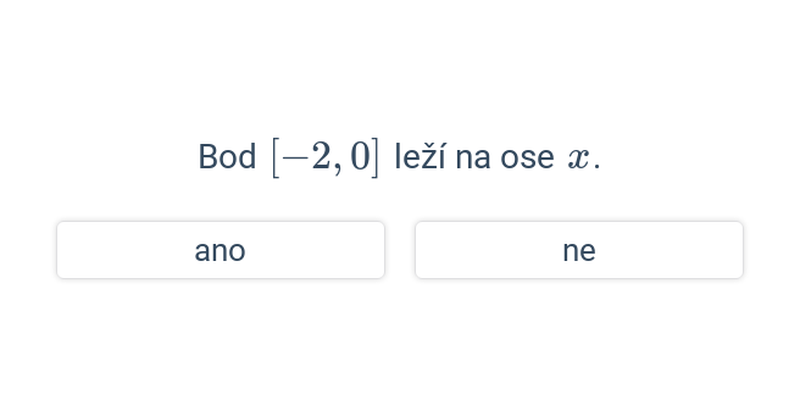
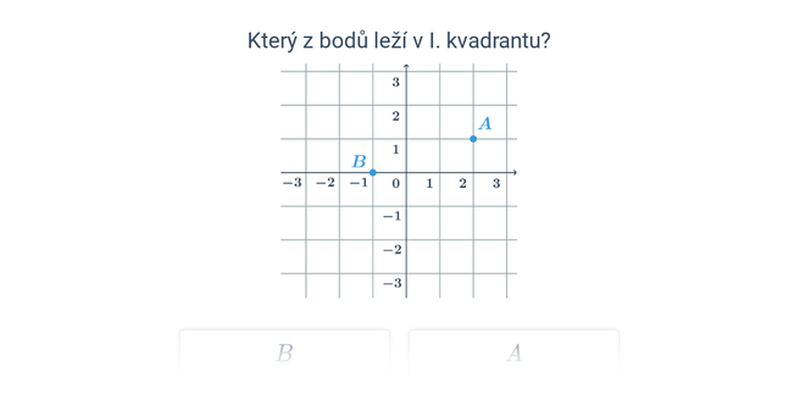
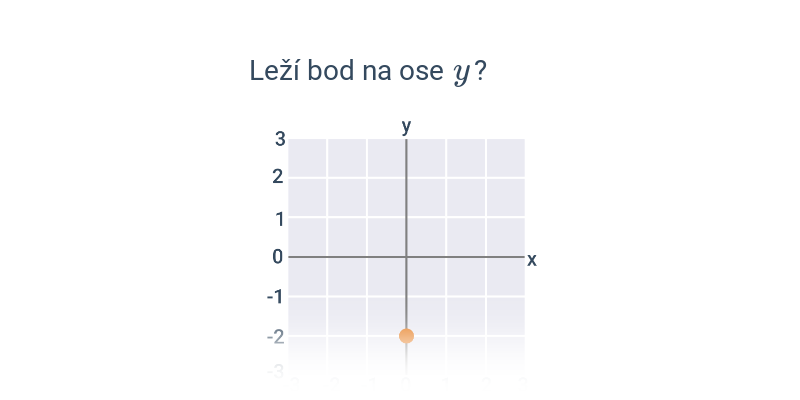
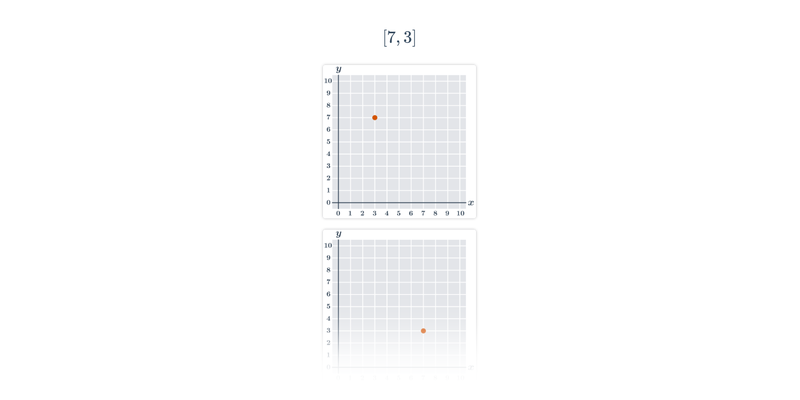
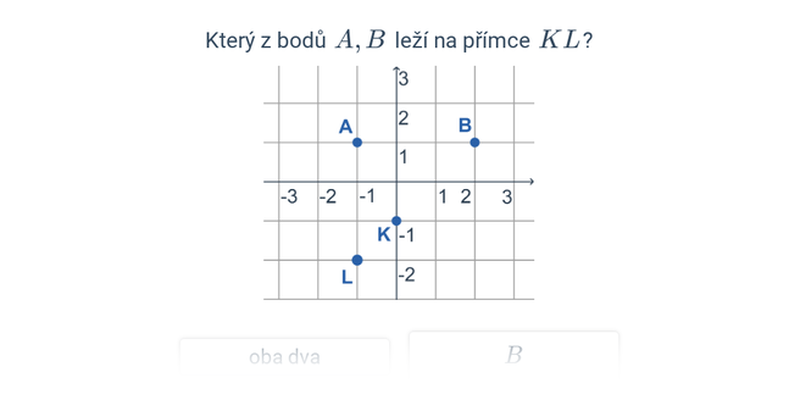
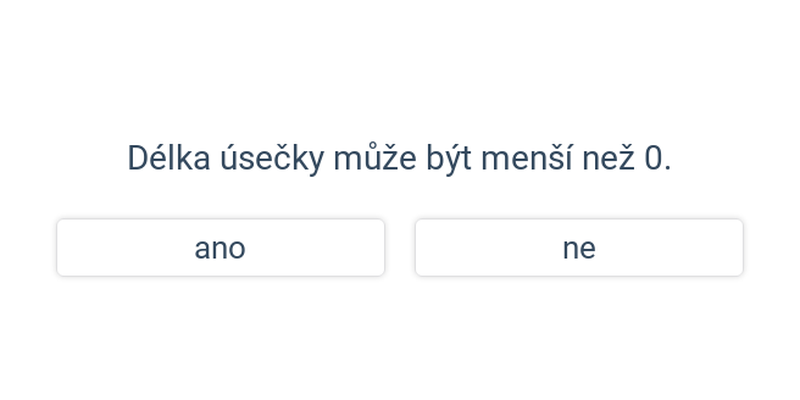
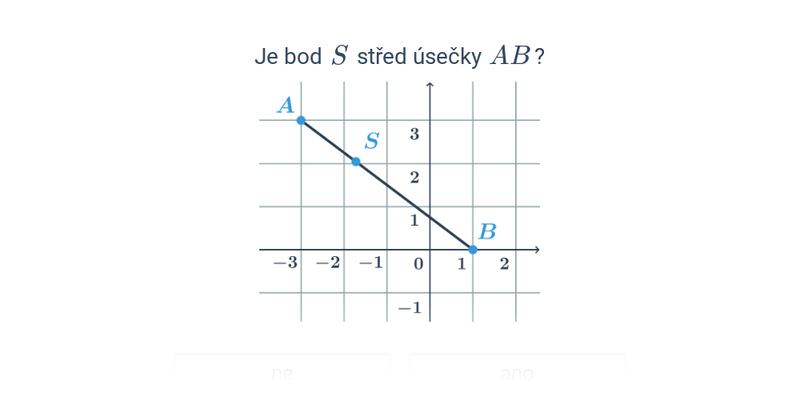
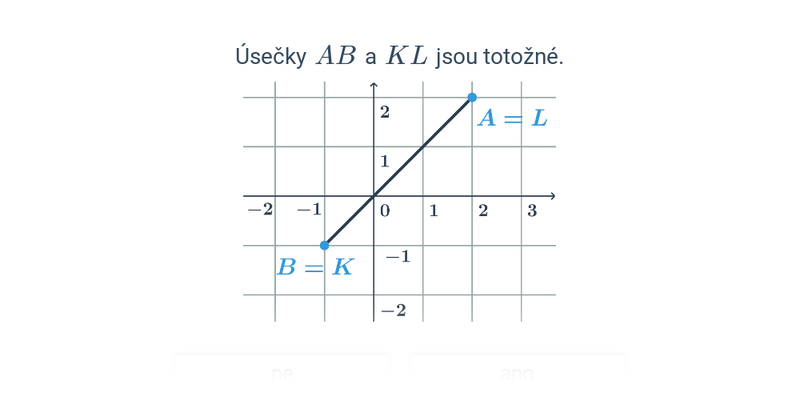
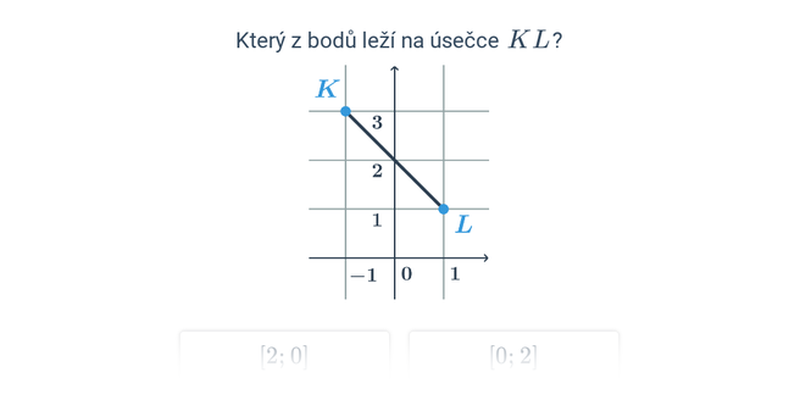
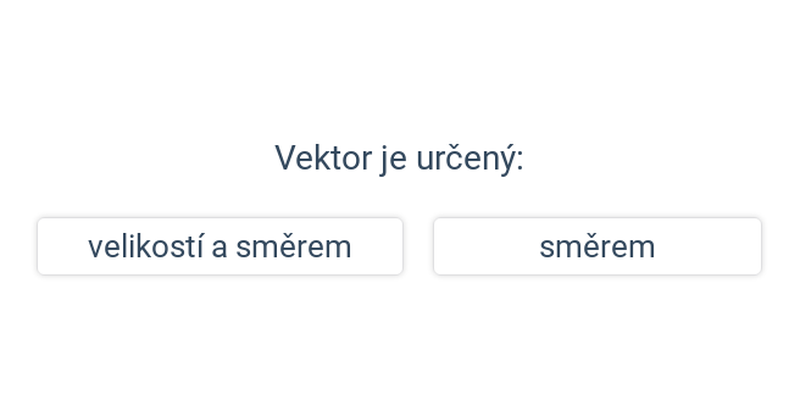
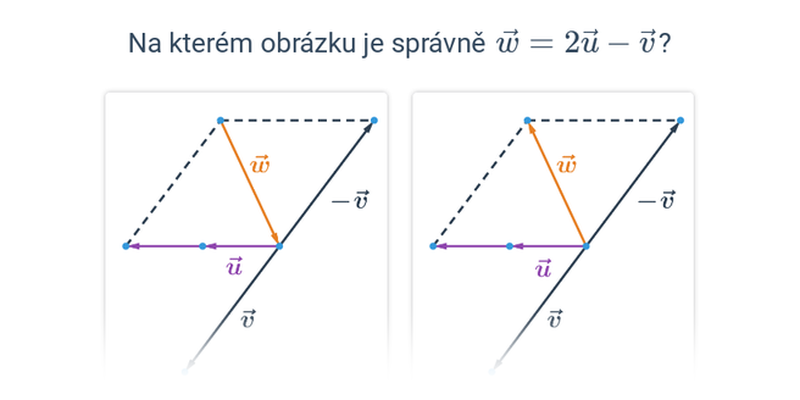
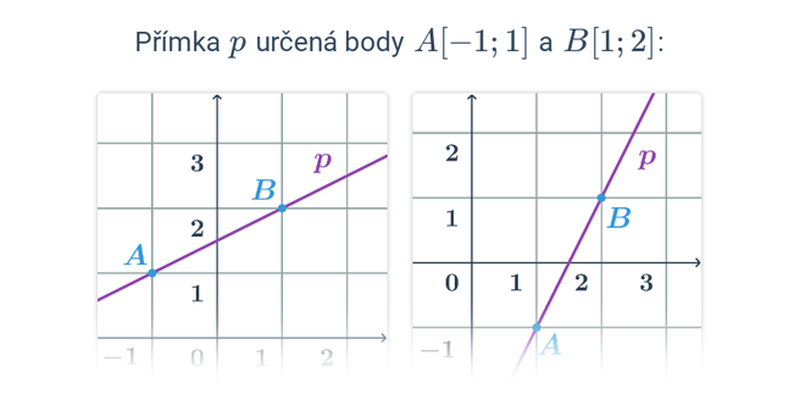
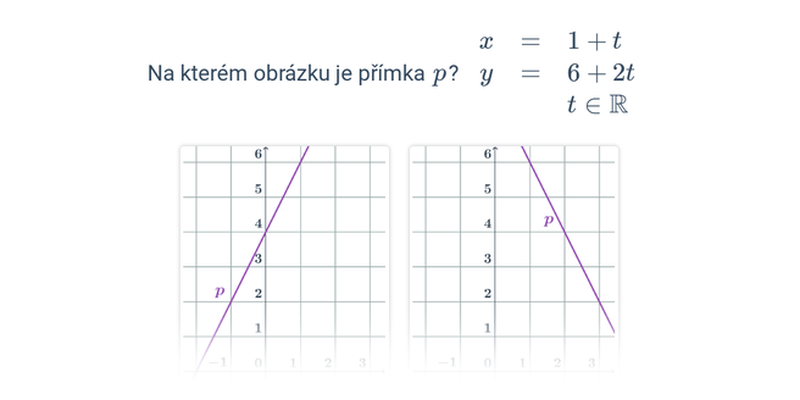
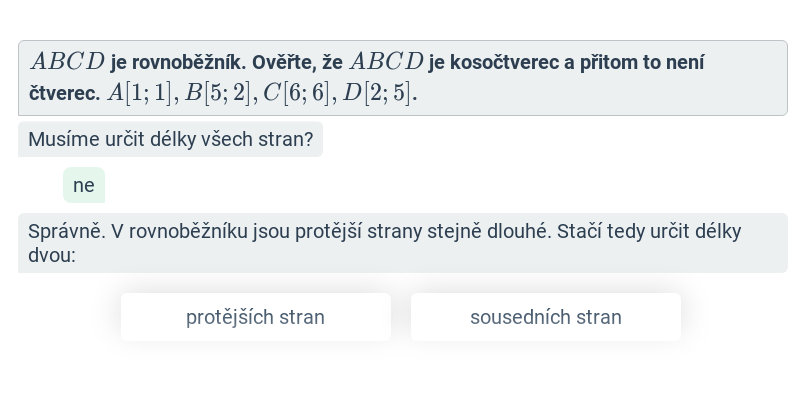
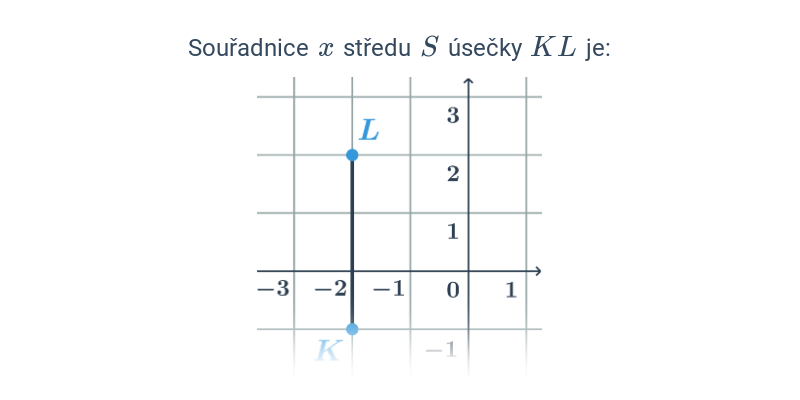
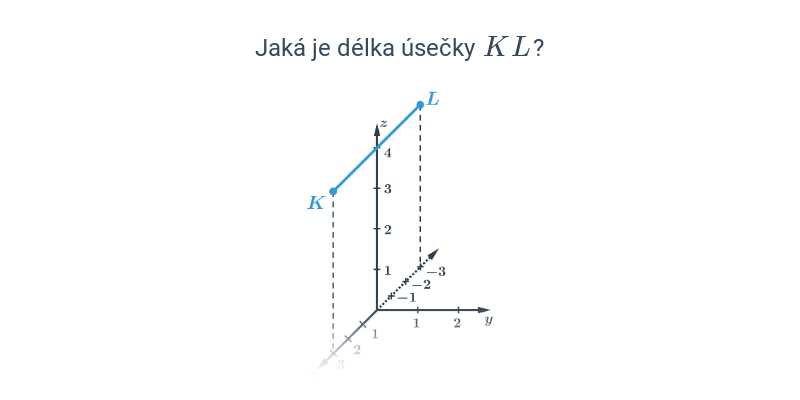
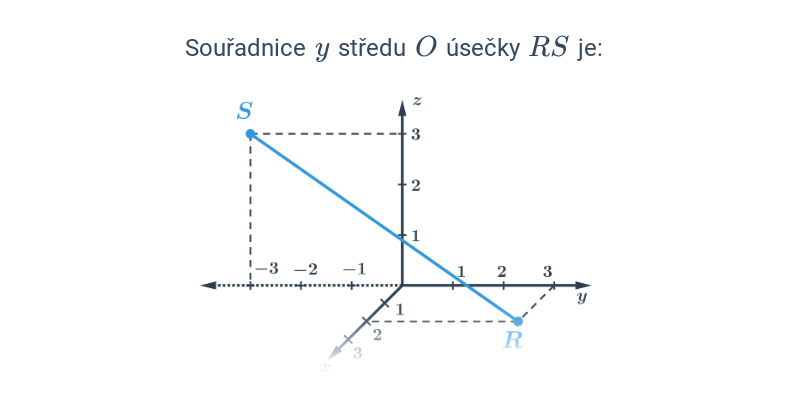
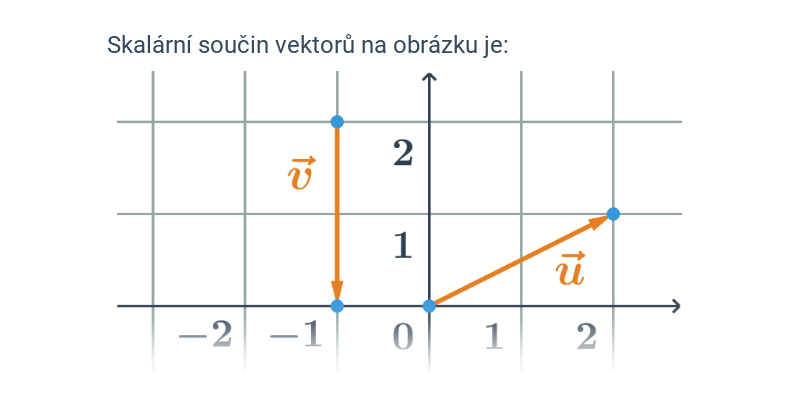
Nejjednodušší objekty popsatelné analyticky jsou body, úsečky a vektory v rovině nebo v prostoru. Když už umíme manipulovat s vektory, můžeme je použít například k popisu přímky nebo roviny.

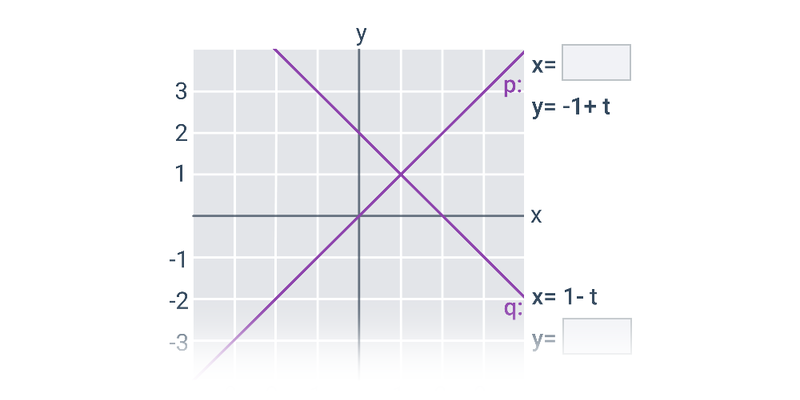
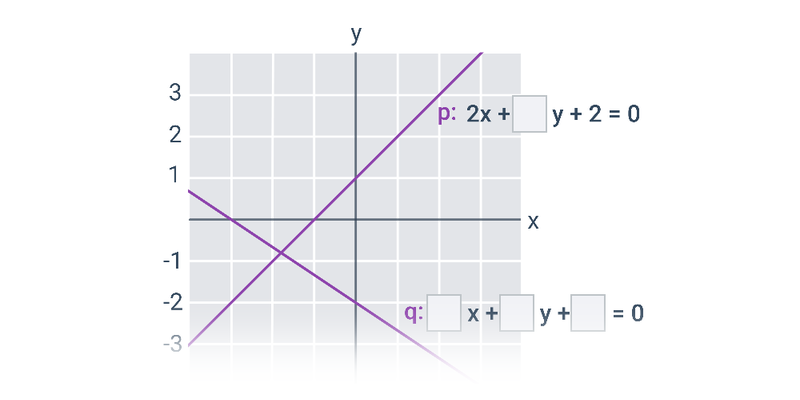
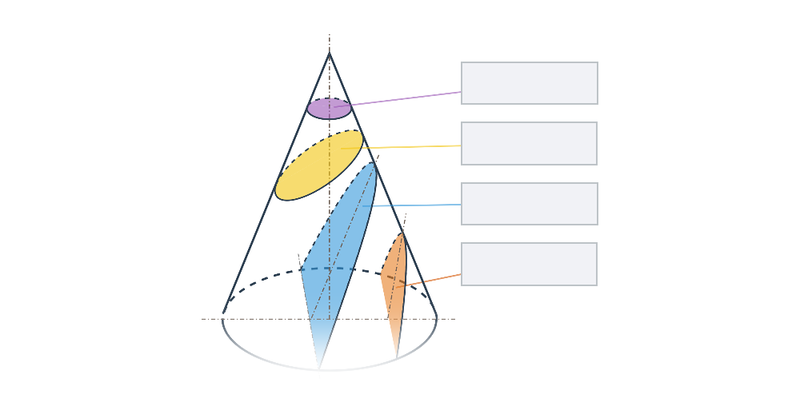
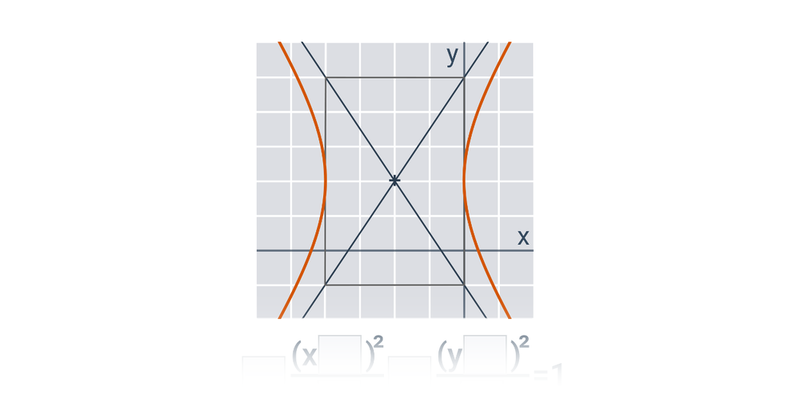
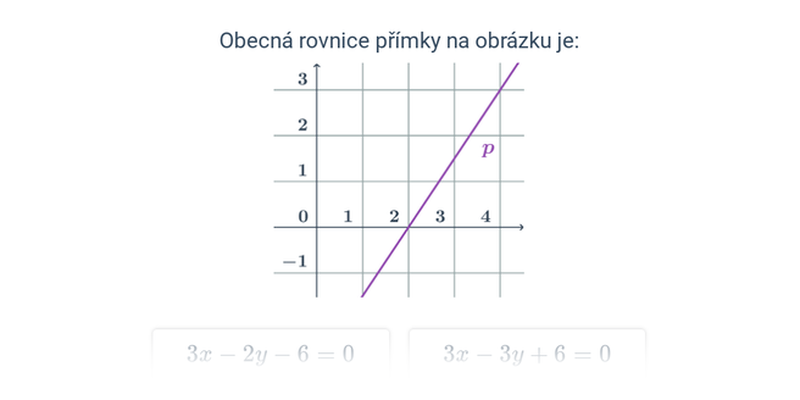
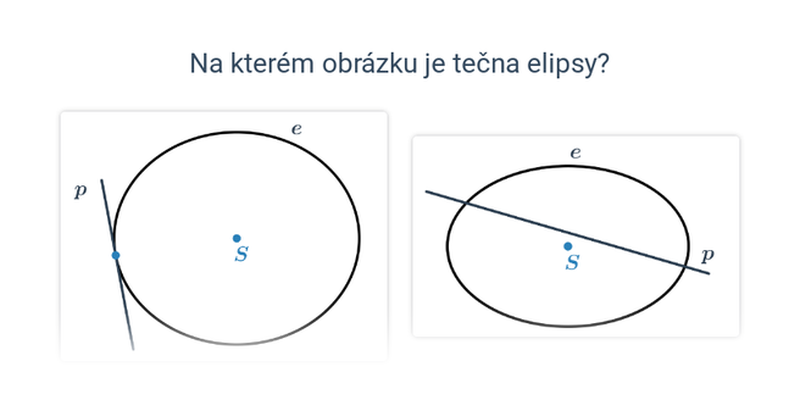
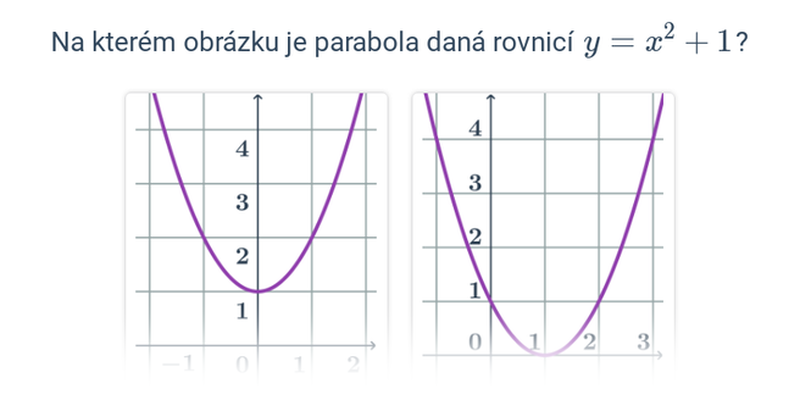
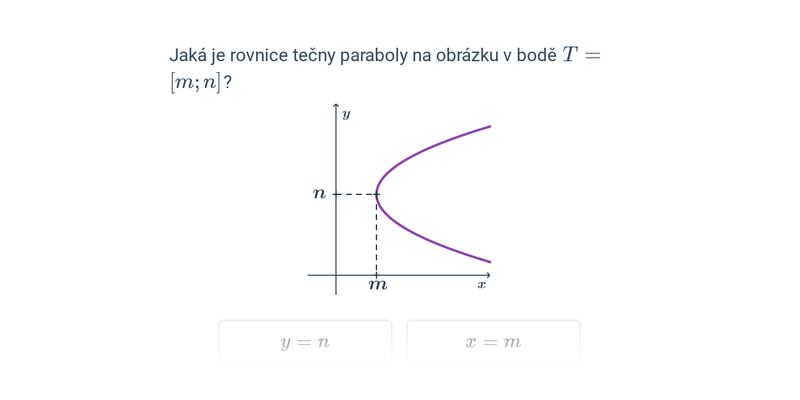
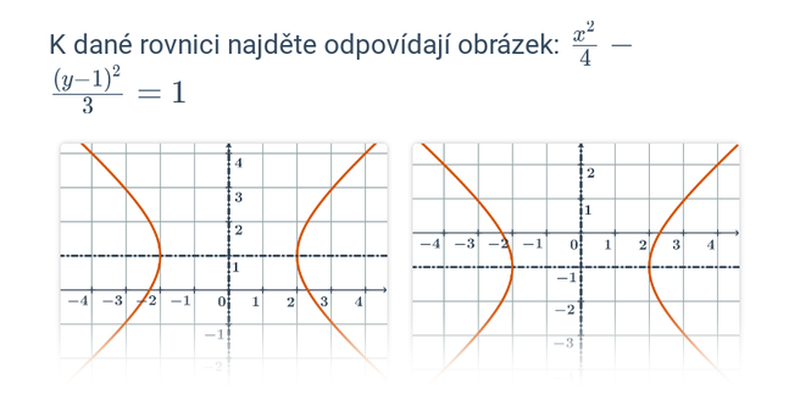
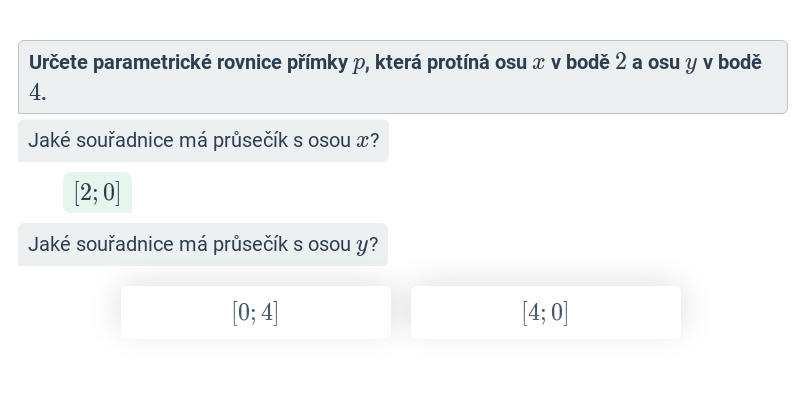
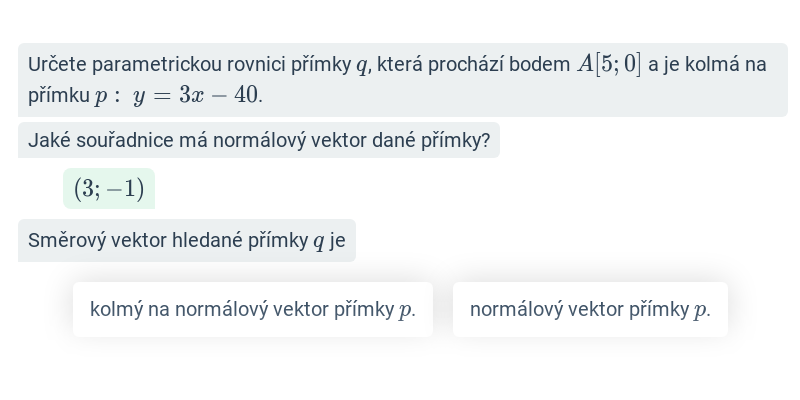
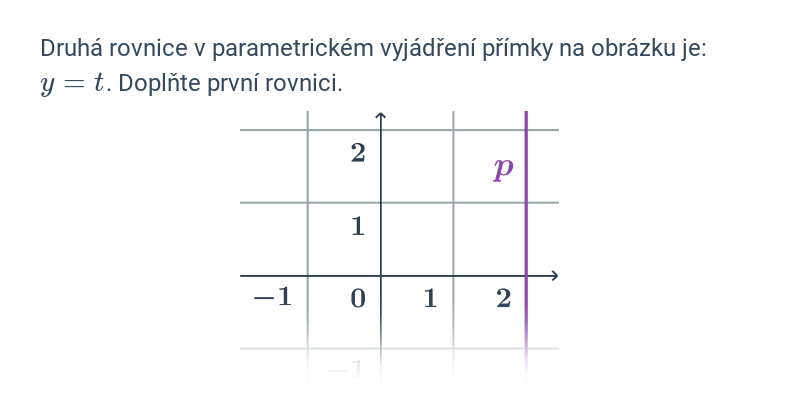
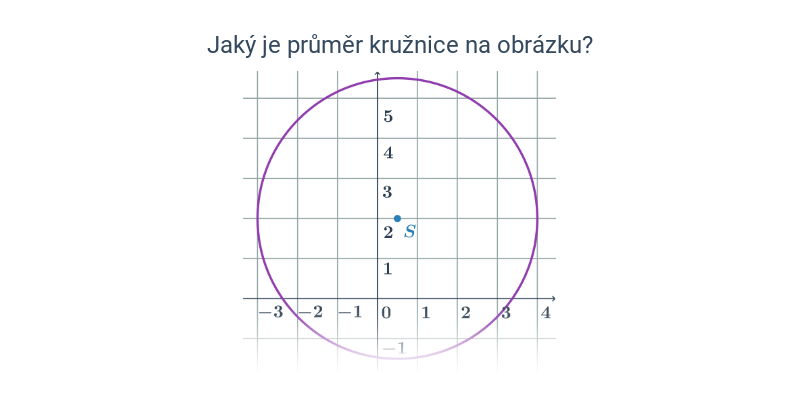
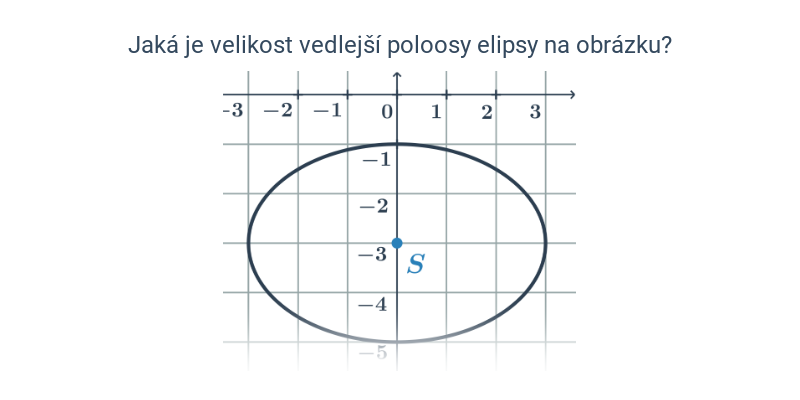
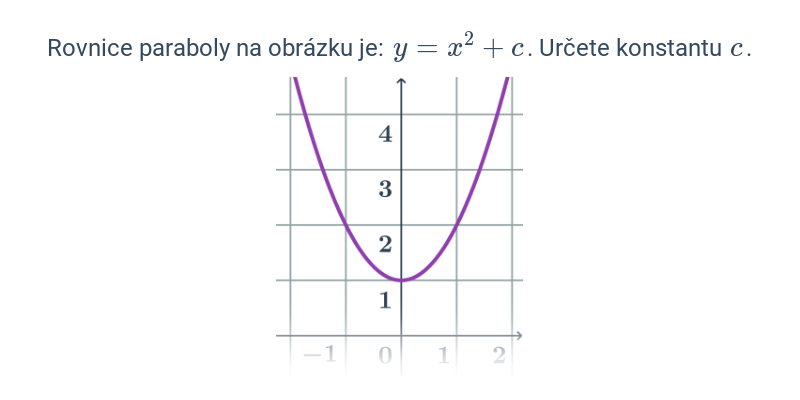
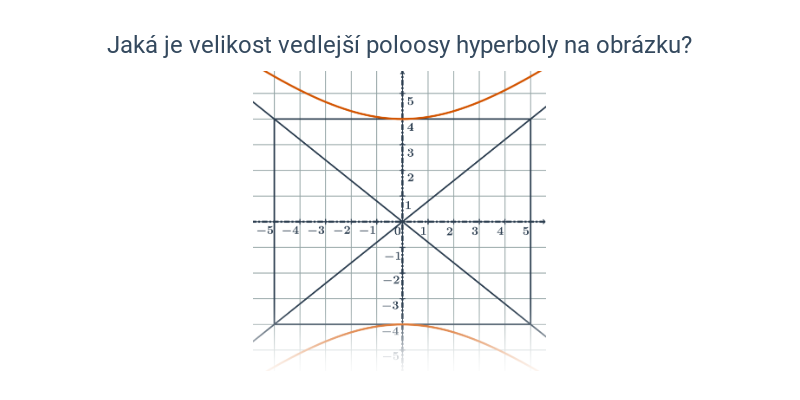
V případě přímek a rovin se pořád ještě jedná o objekty popsatelné lineárními rovnicemi nebo soustavami lineárních rovnic. Pokud se začneme zabývat i kvadratickými rovnicemi, dokážeme popsat i kuželosečky v rovině, například kružnici, elipsu, parabolu a hyperbolu.

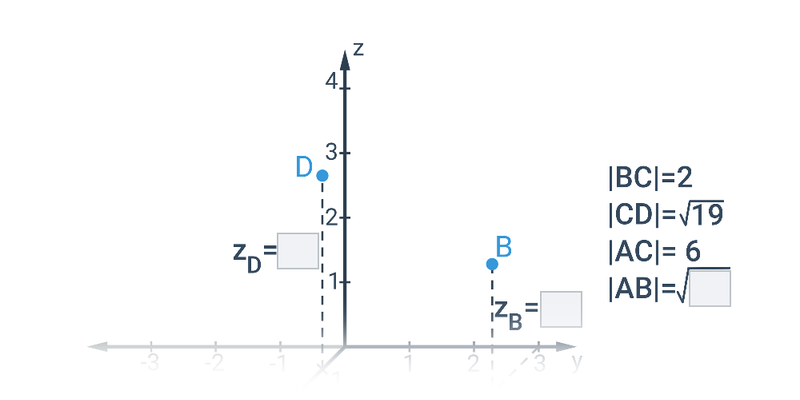
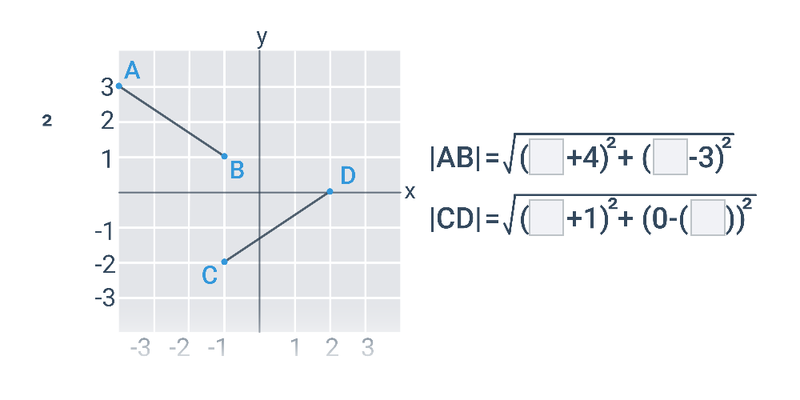
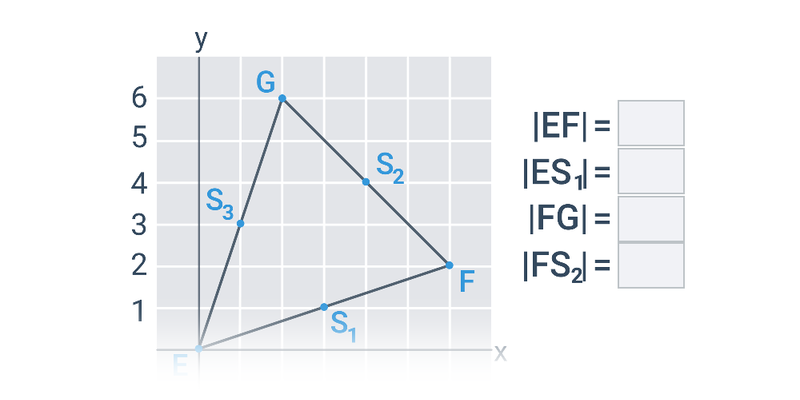
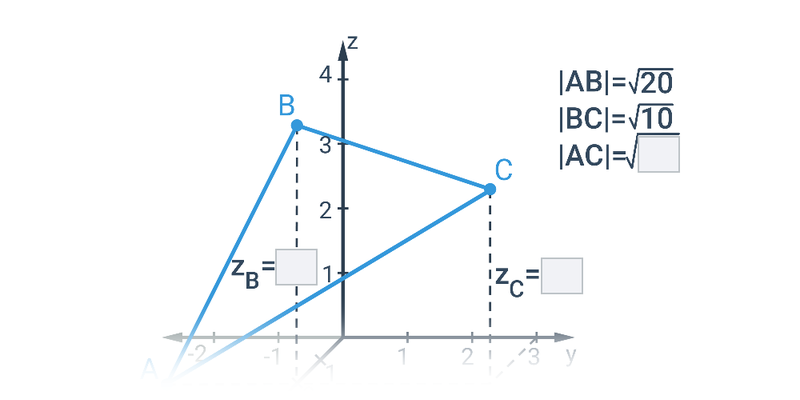
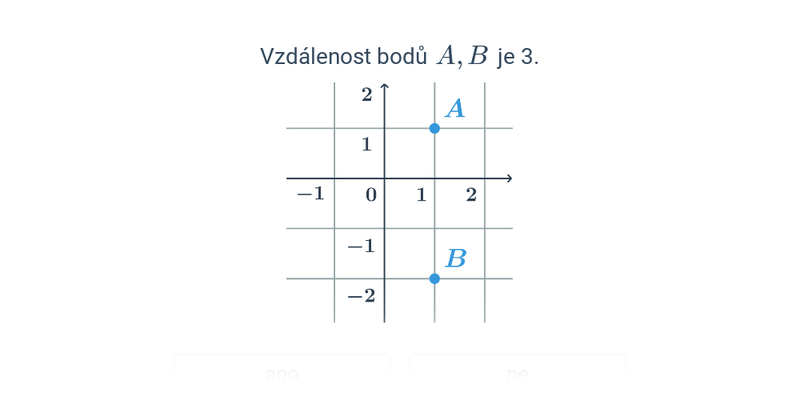
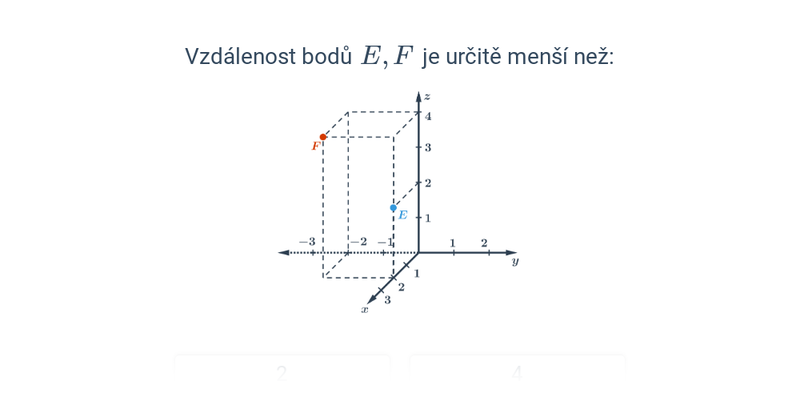
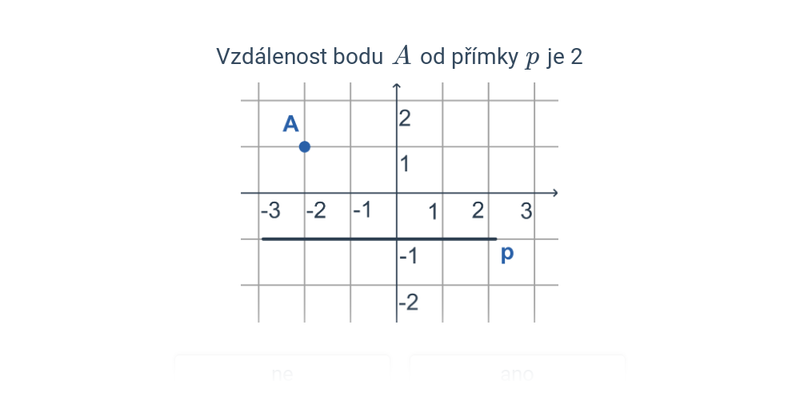
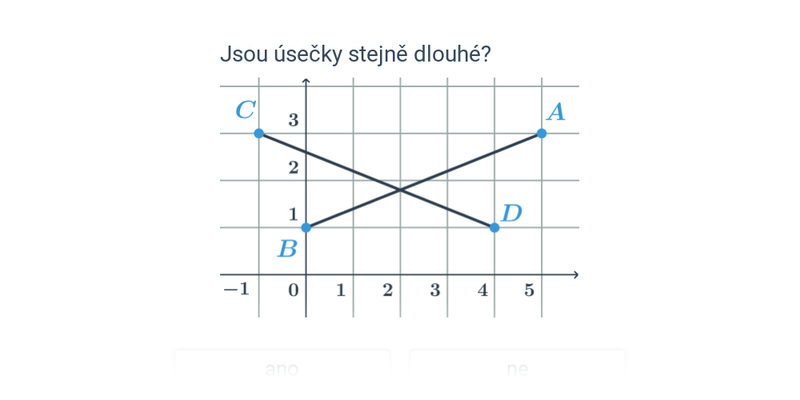
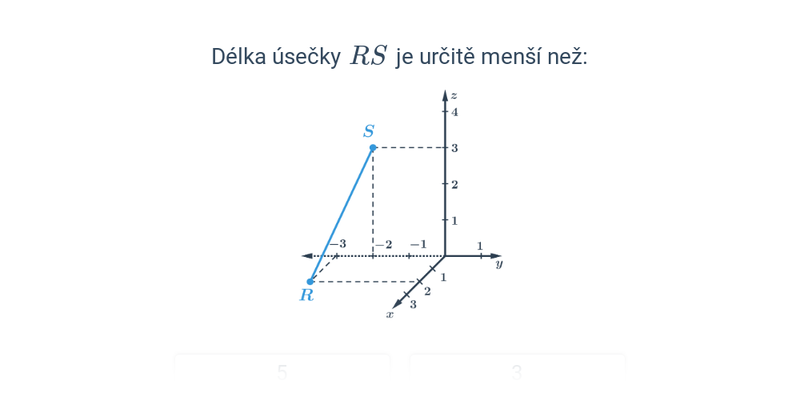
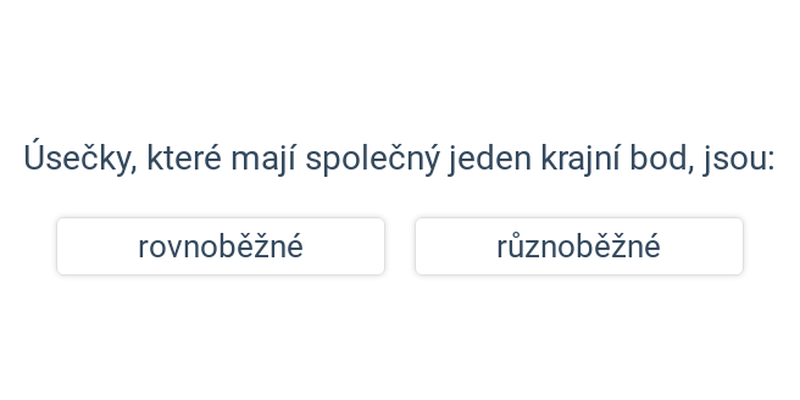
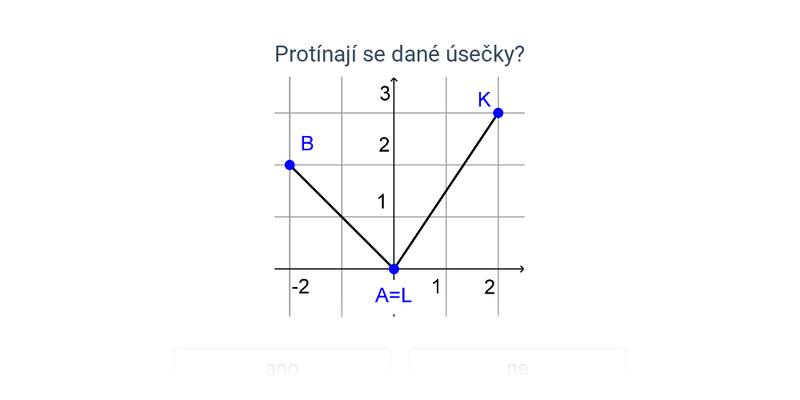
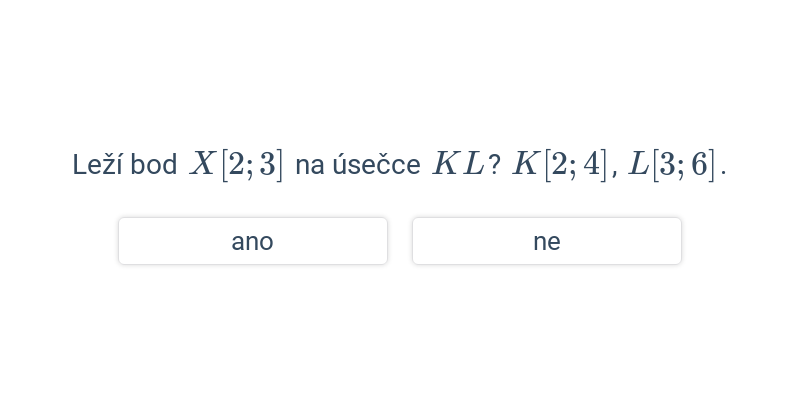
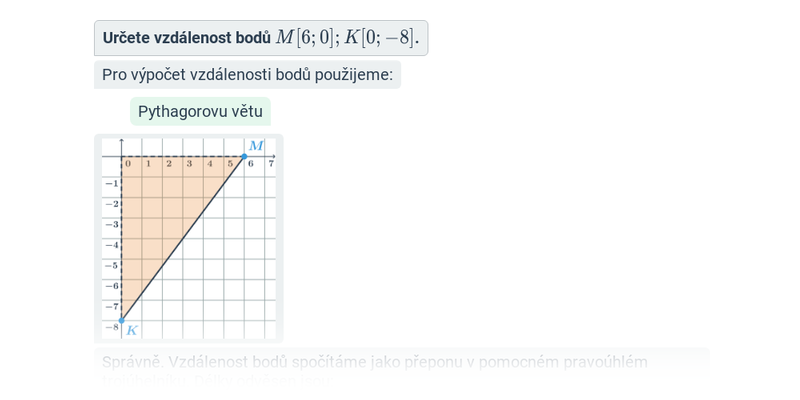
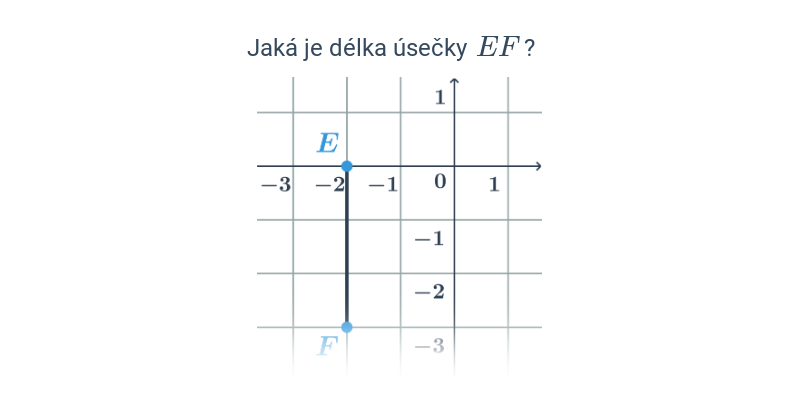
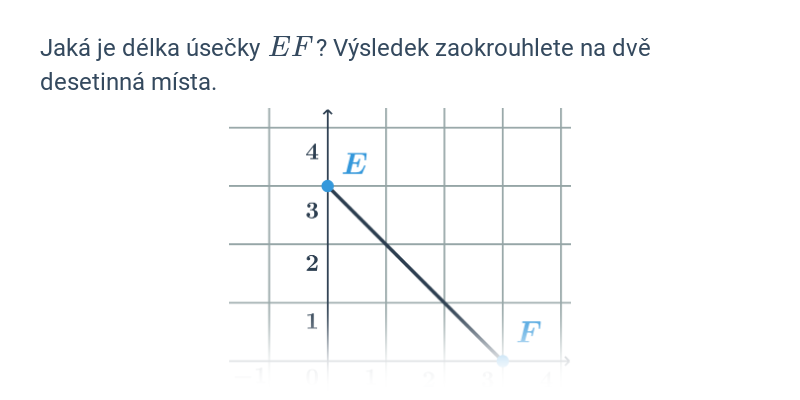
Dva významné typy problémů, které řešíme v rámci analytické geometrie jsou polohové úlohy, ve kterých vyšetřujeme vzájemnou polohu geometrických objektů, a metrické úlohy, ve kterých počítáme konkrétní číselnou hodnotu výsledku, jako je např. vzdálenost dvou bodů nebo úhel svíraný dvěma protínajícími se přímkami.

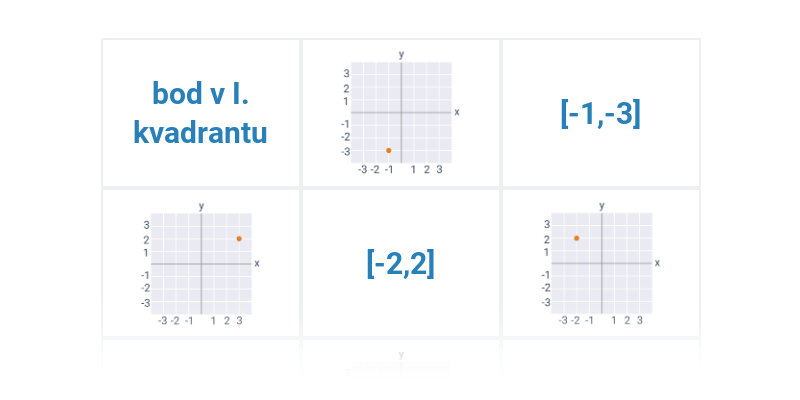
Přesouvání

Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.

Analytická geometrie

Body

Souřadnice bodů v rovině

Souřadnice bodů v rovině: první kvadrant

Souřadnice bodů v prostoru

Vzdálenost bodů v rovině

Vzdálenost bodů v prostoru

Úsečky

Délka úsečky v rovině

Střed úsečky v rovině

Délka úsečky v prostoru

Vektory

Souřadnice vektoru

Velikost vektoru

Velikost vektoru v rovině

Přímky

Parametrické rovnice přímky v rovině

Obecná rovnice přímky v rovině

Kuželosečky

Kuželosečky: pojmy

Kružnice (kuželosečka)

Kružnice: středová rovnice

Elipsa

Elipsa: středová rovnice

Parabola

Parabola: rovnice

Hyperbola

Hyperbola: středová rovnice

Kuželosečky: mix

Rovnice kuželoseček

Souřadnice bodů v rovině

Přesouvání • střední

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Analytická geometrie

Body

Souřadnice bodů v rovině

Souřadnice bodů v rovině: první kvadrant

Souřadnice bodů v prostoru

Vzdálenost bodů v rovině

Vzdálenost bodů v prostoru

Body: mix

Úsečky

Délka úsečky v rovině

Střed úsečky v rovině

Vzájemná poloha úseček v rovině

Délka úsečky v prostoru

Střed úsečky v prostoru

Vzájemná poloha úseček v prostoru

Úsečky: mix

Vektory

Vektory: pojmy

Souřadnice vektoru

Vektory: souřadnice v prostoru

Velikost vektoru

Vzájemná poloha vektorů

Vektory: mix

Operace s vektory

Vektory: násobení konstantou, součet, rozdíl

Vektory: skalární součin

Operace s vektory: mix

Přímky

Přímky: pojmy

Určení přímky

Parametrické rovnice přímky v rovině

Obecná rovnice přímky v rovině

Směrnicový tvar rovnice přímky

Vzájemná poloha přímek v rovině

Vzájemná poloha přímky a bodu v rovině

Přímky: mix

Roviny

Roviny: pojmy

Parametrické rovnice roviny

Obecná rovnice roviny

Vzájemná poloha bodu a roviny

Roviny: mix

Kuželosečky

Kuželosečky: pojmy

Kružnice: pojmy

Elipsa: pojmy

Parabola: pojmy

Hyperbola: pojmy

Kružnice (kuželosečka)

Kružnice: obecná rovnice

Kružnice: vzájemná poloha přímky a kružnice

Elipsa

Elipsa: středová rovnice

Elipsa: obecná rovnice

Elipsa: vzájemná poloha přímky a elipsy

Parabola

Parabola: rovnice

Parabola: tečna

Hyperbola

Hyperbola: středová rovnice

Hyperbola: obecná rovnice

Kuželosečky: mix

Délka úsečky v rovině

Rozhodovačka • lehké

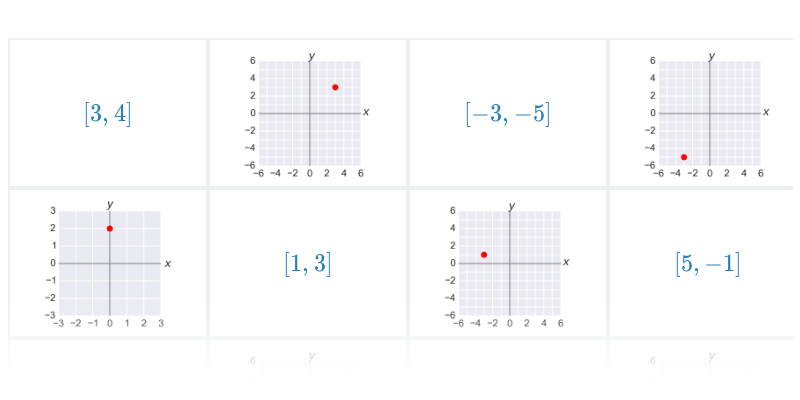
Pexeso

Hledání dvojic, které k sobě patří.

Analytická geometrie

Body

Souřadnice bodů v rovině

Úsečky

Délka úsečky v rovině

Délka úsečky

Vzájemná poloha úseček v rovině

Délka úsečky

Pexeso • střední

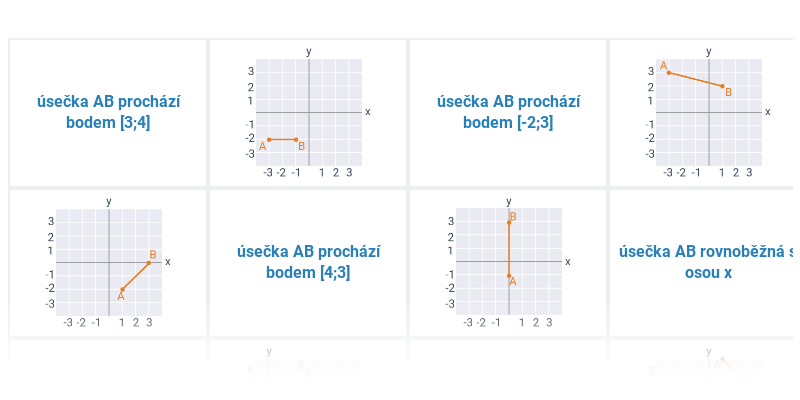
Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Analytická geometrie

Body

Vzdálenost bodů v rovině

Úsečky

Délka úsečky v rovině

Střed úsečky v rovině

Střed úsečky v prostoru

Přímky

Parametrické rovnice přímky v rovině

Obecná rovnice přímky v rovině

Vzájemná poloha přímek v rovině

Vzájemná poloha přímky a bodu v rovině

Přímky: mix

Polohové úlohy

Metrické úlohy

Vzdálenost bodu od přímky

Odchylka dvou přímek

Kuželosečky

Kružnice (kuželosečka)

Kružnice: středová rovnice

Kružnice: obecná rovnice

Kružnice: vzájemná poloha přímky a kružnice

Elipsa

Elipsa: středová rovnice

Elipsa: obecná rovnice

Elipsa: vzájemná poloha přímky a elipsy

Parabola

Parabola: rovnice

Parabola: tečna

Parabola: vzájemná poloha přímky a paraboly

Hyperbola

Hyperbola: obecná rovnice

Hyperbola: středová rovnice

Kuželosečky: mix

Určení kuželosečky

Vzdálenost bodů v rovině

Krok po kroku • lehké

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Analytická geometrie

Body

Souřadnice bodů v rovině

Souřadnice bodů v prostoru

Vzdálenost bodů v rovině

Vzdálenost bodů v prostoru

Body: mix

Úsečky

Délka úsečky v rovině

Střed úsečky v rovině

Délka úsečky v prostoru

Střed úsečky v prostoru

Úsečky: mix

Vektory

Souřadnice vektoru

Velikost vektoru

Vzájemná poloha vektorů

Vektory: mix

Operace s vektory

Vektory: skalární součin

Přímky

Parametrické rovnice přímky v rovině

Obecná rovnice přímky v rovině

Vzájemná poloha přímek v rovině

Vzájemná poloha přímky a bodu v rovině

Přímky: mix

Kuželosečky

Kružnice (kuželosečka)

Kružnice: středová rovnice

Elipsa

Elipsa: středová rovnice

Parabola

Hyperbola

Hyperbola: středová rovnice

Kuželosečky: mix

Velikost vektoru

Psaná odpověď • těžké

Grafař

Specializované cvičení na práci s grafem a funkcemi.

Analytická geometrie

Body

Souřadnice bodů v rovině

Grafař • lehké

Roboti

Závody na rychlost proti robotům. Jednoduché ovládání výběrem ze dvou možností.

Analytická geometrie

Body

Souřadnice bodů v rovině

Spustit

Filtr podle ročníku

Cvičení

Analytická geometrie

umime.to/F4Z

Přesouvání

Souřadnice bodů v rovině

Rozhodovačka

Délka úsečky v rovině

Pexeso

Délka úsečky

Krok po kroku

Vzdálenost bodů v rovině

Psaná odpověď

Velikost vektoru

Grafař

Souřadnice bodů v rovině

Roboti

Děkujeme za vaši zprávu, byla úspěšně odeslána.

Napište nám

Nevíte si rady?

Čeho se zpráva týká?

Filtr podle ročníku

Cvičení

Analytická geometrie

umime.to/F4Z

Přesouvání

Souřadnice bodů v rovině (střední) • GJM

zadání: 12

Souřadnice bodů v rovině: první kvadrant (lehké) • G4W

Souřadnice bodů v prostoru (střední) • GJ3

zadání: 10

Vzdálenost bodů v rovině (střední) • GKP

zadání: 12

Vzdálenost bodů v prostoru (střední) • GLO

zadání: 12

Délka úsečky v rovině (střední) • GMA

zadání: 10

Střed úsečky v rovině (střední) • GM6

zadání: 10

Délka úsečky v prostoru (střední) • GMV

zadání: 10

Souřadnice vektoru (střední) • GKV

zadání: 12

Velikost vektoru v rovině (střední) • GKZ

zadání: 12

Parametrické rovnice přímky v rovině (střední) • GLX

zadání: 12

Obecná rovnice přímky v rovině (střední) • GMW

zadání: 12

Kuželosečky: pojmy (střední) • FKL

zadání: 8

Kružnice: středová rovnice (střední) • GN1

zadání: 12

Elipsa: středová rovnice (střední) • GOW

zadání: 12

Parabola: rovnice (střední) • GSM

zadání: 12

Hyperbola: středová rovnice (střední) • GSA

zadání: 12

Rovnice kuželoseček (těžké) • FKM

zadání: 7

Souřadnice bodů v rovině

Rozhodovačka

Souřadnice bodů v rovině (lehké) • GMJ

zadání: 76

Souřadnice bodů v rovině (střední) • GMK

zadání: 60

Souřadnice bodů v rovině (těžké) • GJK

zadání: 80

Souřadnice bodů v rovině: první kvadrant (lehké) • G4D

Souřadnice bodů v prostoru (střední) • GJR

zadání: 47

Vzdálenost bodů v rovině (lehké) • GJS

zadání: 43

Vzdálenost bodů v rovině (střední) • GJT

zadání: 44

Vzdálenost bodů v prostoru (střední) • GLP

zadání: 45

Body: mix (lehké) • FSX

zadání: 131

Body: mix (střední) • FSN

zadání: 203

Délka úsečky v rovině (lehké) • GLZ

zadání: 43

Délka úsečky v rovině (střední) • GL1

zadání: 44

Střed úsečky v rovině (lehké) • GM3

zadání: 39

Střed úsečky v rovině (střední) • GM4

zadání: 44

Vzájemná poloha úseček v rovině (lehké) • GMX

zadání: 37

Vzájemná poloha úseček v rovině (střední) • GMZ

zadání: 46

Délka úsečky v prostoru (střední) • GML

zadání: 42

Střed úsečky v prostoru (střední) • GNH

zadání: 30

Vzájemná poloha úseček v prostoru (těžké) • GM2

zadání: 40

Úsečky: mix (lehké) • FSZ