Výpis souhrnů
Analytická geometrie
Podtémata
- Analytická geometrie
- Body
- Souřadnice bodů v rovině
- Souřadnice bodů v prostoru
- Vzdálenost bodů v rovině
- Vzdálenost bodů v prostoru
- Úsečky
- Délka úsečky v rovině
- Střed úsečky v rovině
- Vzájemná poloha úseček v rovině
- Délka úsečky v prostoru
- Střed úsečky v prostoru
- Vzájemná poloha úseček v prostoru
- Vektory
- Vektory: pojmy
- Souřadnice vektoru
- Velikost vektoru
- Vzájemná poloha vektorů
- Operace s vektory
- Vektory: násobení konstantou, součet, rozdíl
- Vektory: skalární součin
- Přímky
- Přímky: pojmy
- Určení přímky
- Parametrické rovnice přímky v rovině
- Obecná rovnice přímky v rovině
- Směrnicový tvar rovnice přímky
- Vzájemná poloha přímek v rovině
- Vzájemná poloha přímky a bodu v rovině
- Polohové úlohy
- Metrické úlohy
- Vzdálenost bodu od přímky
- Odchylka dvou přímek
- Roviny
- Roviny: pojmy
- Parametrické rovnice roviny
- Obecná rovnice roviny
- Vzájemná poloha bodu a roviny
- Kuželosečky
- Kružnice (kuželosečka)
- Elipsa
- Parabola
- Hyperbola
Analytická geometrie
Analytická geometrie nám dovoluje zapsat geometrické problémy algebraicky a vyřešit je pomocí rovnic.
Nejjednodušší objekty popsatelné analyticky jsou body, úsečky a vektory v rovině nebo v prostoru. Když už umíme manipulovat s vektory, můžeme je použít například k popisu přímky nebo roviny.
V případě přímek a rovin se pořád ještě jedná o objekty popsatelné lineárními rovnicemi nebo soustavami lineárních rovnic. Pokud se začneme zabývat i kvadratickými rovnicemi, dokážeme popsat i kuželosečky v rovině, například kružnici, elipsu, parabolu a hyperbolu.
Dva významné typy problémů, které řešíme v rámci analytické geometrie jsou polohové úlohy, ve kterých vyšetřujeme vzájemnou polohu geometrických objektů, a metrické úlohy, ve kterých počítáme konkrétní číselnou hodnotu výsledku, jako je např. vzdálenost dvou bodů nebo úhel svíraný dvěma protínajícími se přímkami.
NahoruUvažujeme‑li body v rovině nebo v prostoru, kde máme zavedenou kartézskou soustavu souřadnic (v rovině se dvěma osami x,y nebo v prostoru se třemi osami x,y,z), můžeme body popsat číselně souřadnicemi v rovině, případně souřadnicemi v prostoru.
Pomocí souřadnic pak umíme spočítat vzdálenost dvou bodů „vzdušnou čarou“ – délku úsečky v rovině, případně v prostoru.
NahoruSouřadnice bodů v rovině
Souřadnice bodů většinou zapisujeme pomocí kartézské soustavy souřadnic v rovině, která má jako osy dvě kolmé přímky. Vodorovná přímka se tradičně označuje x a souřadnice podél této osy se zapisuje první. Svislá přímka se tradičně označuje y a souřadnice podle této osy se zapisuje druhá. Přímky x, y se protínají v bodě [0;0].
Přímky x a y jsou souřadné osy, bod [0;0] je počátek soustavy souřadnic.
Příklad: Souřadnice bodu A
Bod A na obrázku je v dané soustavě souřadnic určen jako x=1, y=2, což můžeme zapsat jako A[1;2].
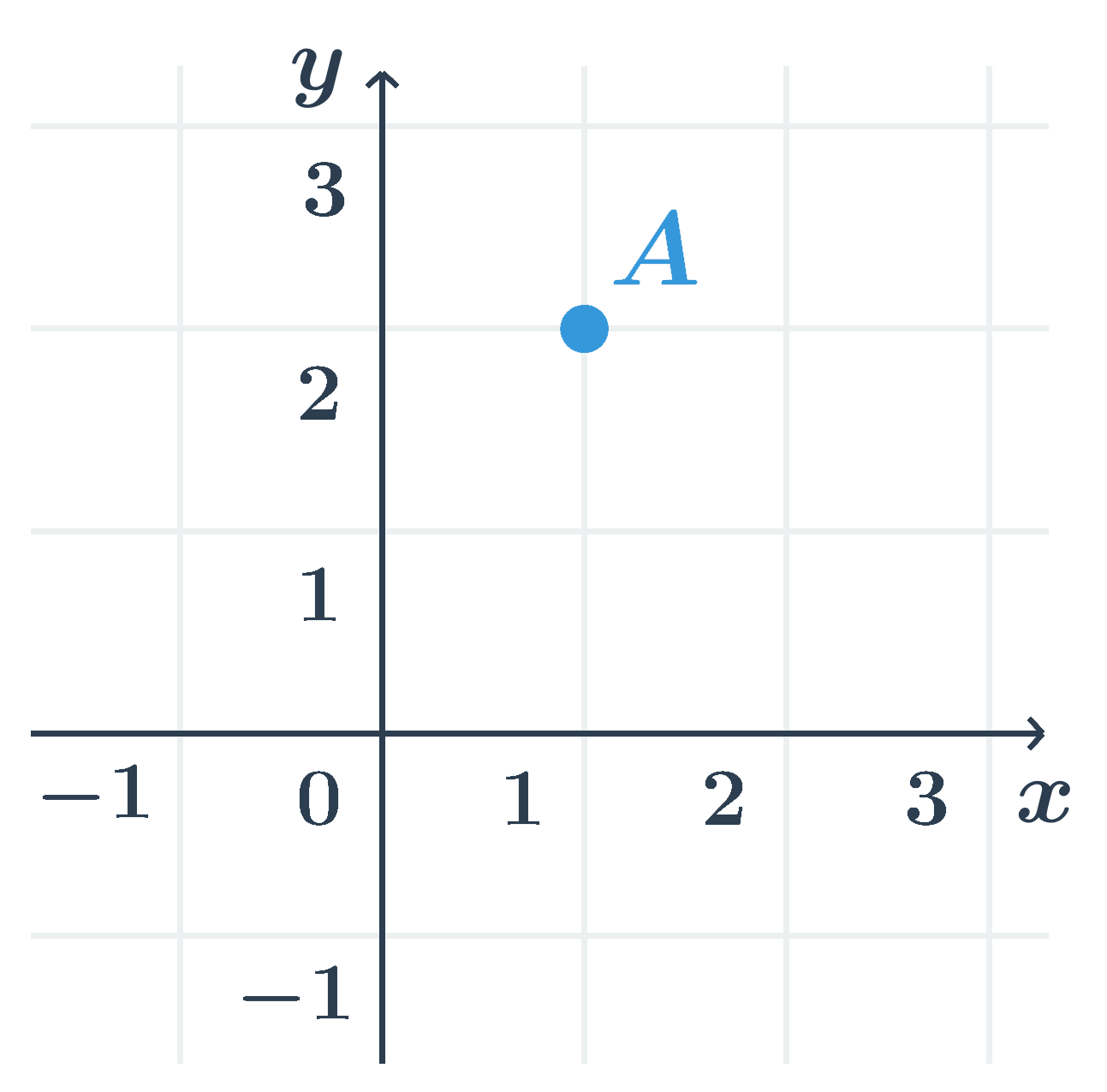
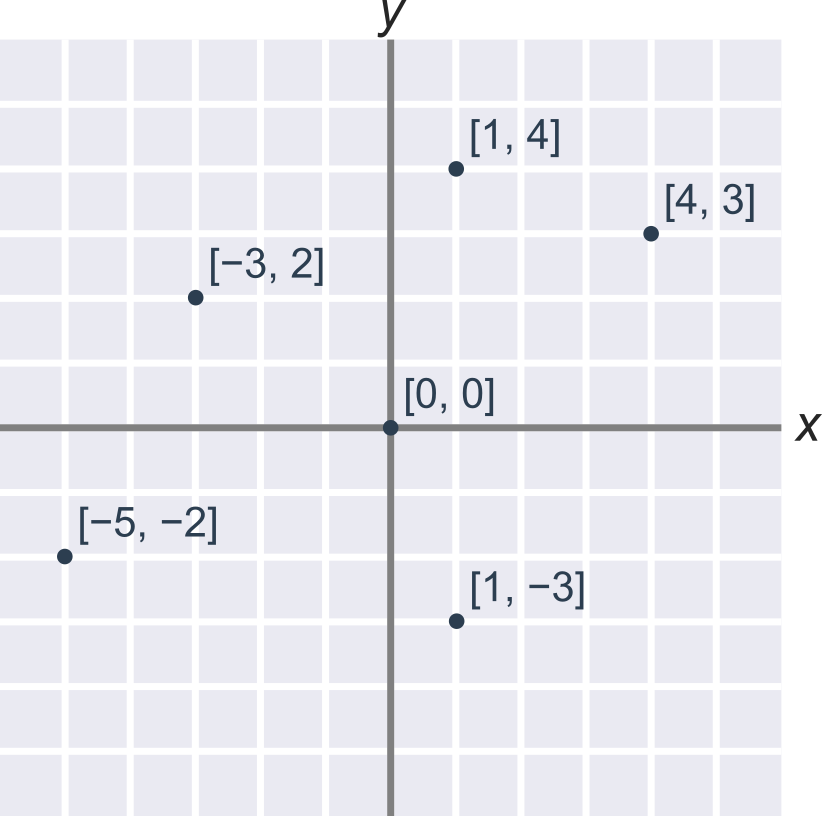
Další příklady souřadnic bodů
Souřadnice bodů v prostoru
Kartézská soustava souřadnic v rovině je daná trojicí navzájem kolmých číselných os x,y,z, které se protínají v bodě [0;0;0].
Přímky x,y,z jsou souřadné osy v prostoru, bod [0;0;0] je počátek soustavy souřadnic.
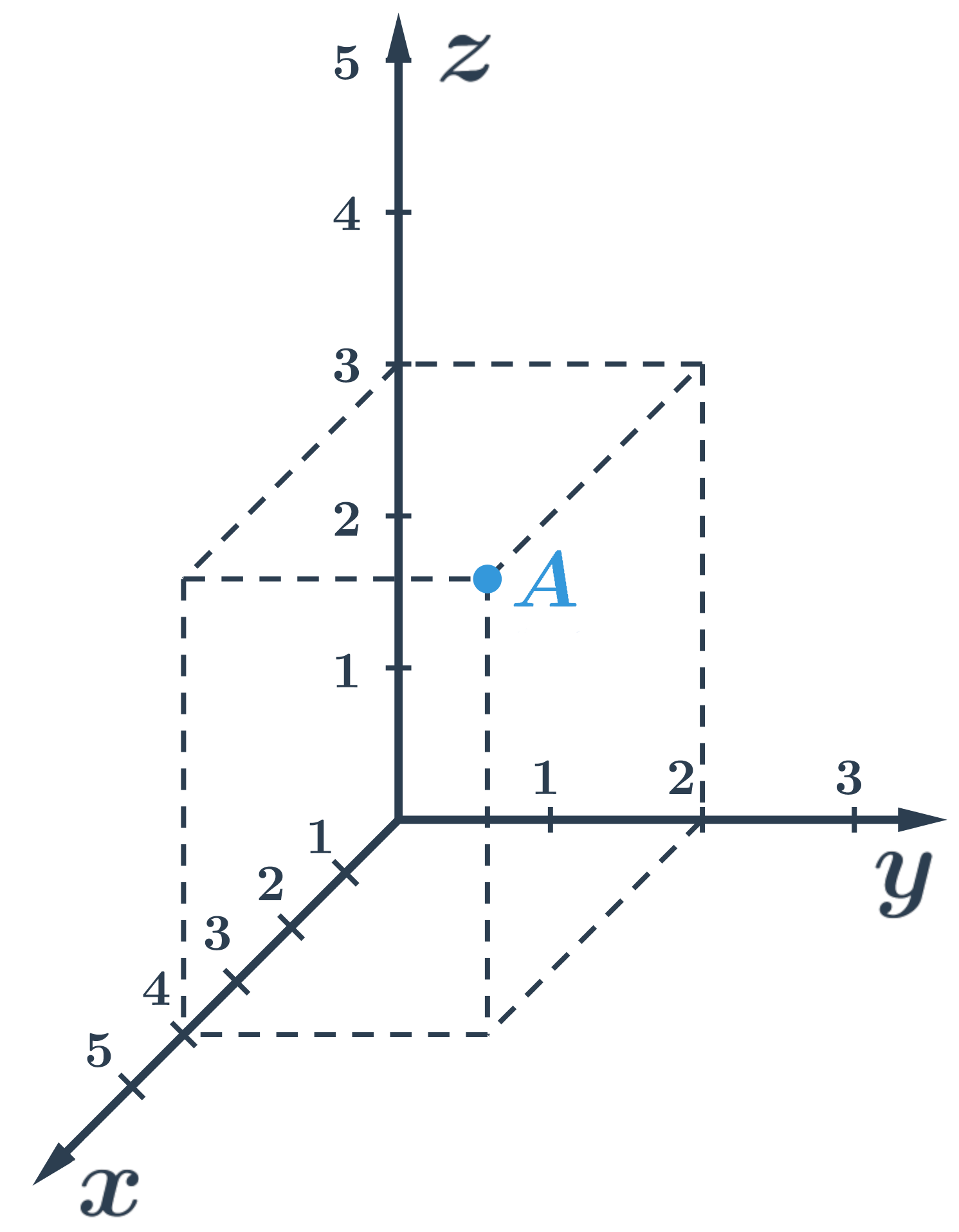
Příklad: Souřadnice bodu A
Bod A na obrázku je v dané soustavě souřadnic určen jako x=4, y=2, z=3, což můžeme zapsat jako A[4;2;3].
Vzdálenost bodů v rovině
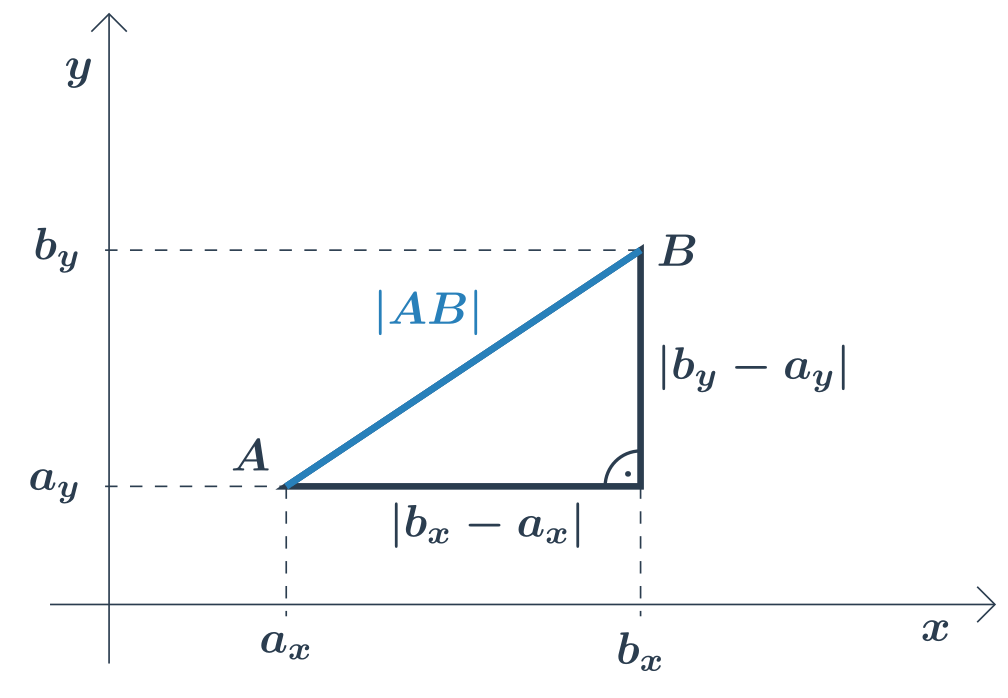
Vzdálenost dvou bodů v rovině můžeme spočítat, když známe jejich souřadnice.
Jsou‑li dány souřadnice A=[a_x,a_y], B=[b_x,b_y], je vzdálenost bodu A od bodu B:
|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2}
Vzoreček vychází z Pythagorovy věty. Všimněme si pravoúhlého trojúhelníku s délkami odvěsen (b_x-a_x) a (b_y-a_y), jehož přepona má délku |AB|.
Příklad: vzdálenost C[0;1],D[4;4]
- |CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2}
- Dosadíme souřadnice bodů C[0;1] a D[4;4]:
\sqrt{(4-0)^2 + (4-1)^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5 - Vzdálenost je: |CD|=5
Příklad: vzdálenost M[2;-1], N[-1;-2]
- |MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2}
- Dosadíme souřadnice bodů M[2;-1] a N[-1;-2]:
\sqrt{(-1-2)^2 + (-2-(-1))^2}=\sqrt{(-3)^2 + (-1)^2}=\sqrt{10} - Vzdálenost je: |MN|=\sqrt{10}
Vzdálenost bodů v prostoru
Vzdálenost dvou bodů v prostoru spočítáme podobně jako v rovině pomocí jejich souřadnic. Máme‑li souřadnice bodů A=[a_x,a_y,a_z], B=[b_x,b_y,b_z], můžeme jejich vzdálenost určit takto:
|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2 + (b_z-a_z)^2}
Podobným způsobem (dvakrát po sobě použijeme Pythagorovu větu) počítáme délku tělesové úhlopříčky kvádru.
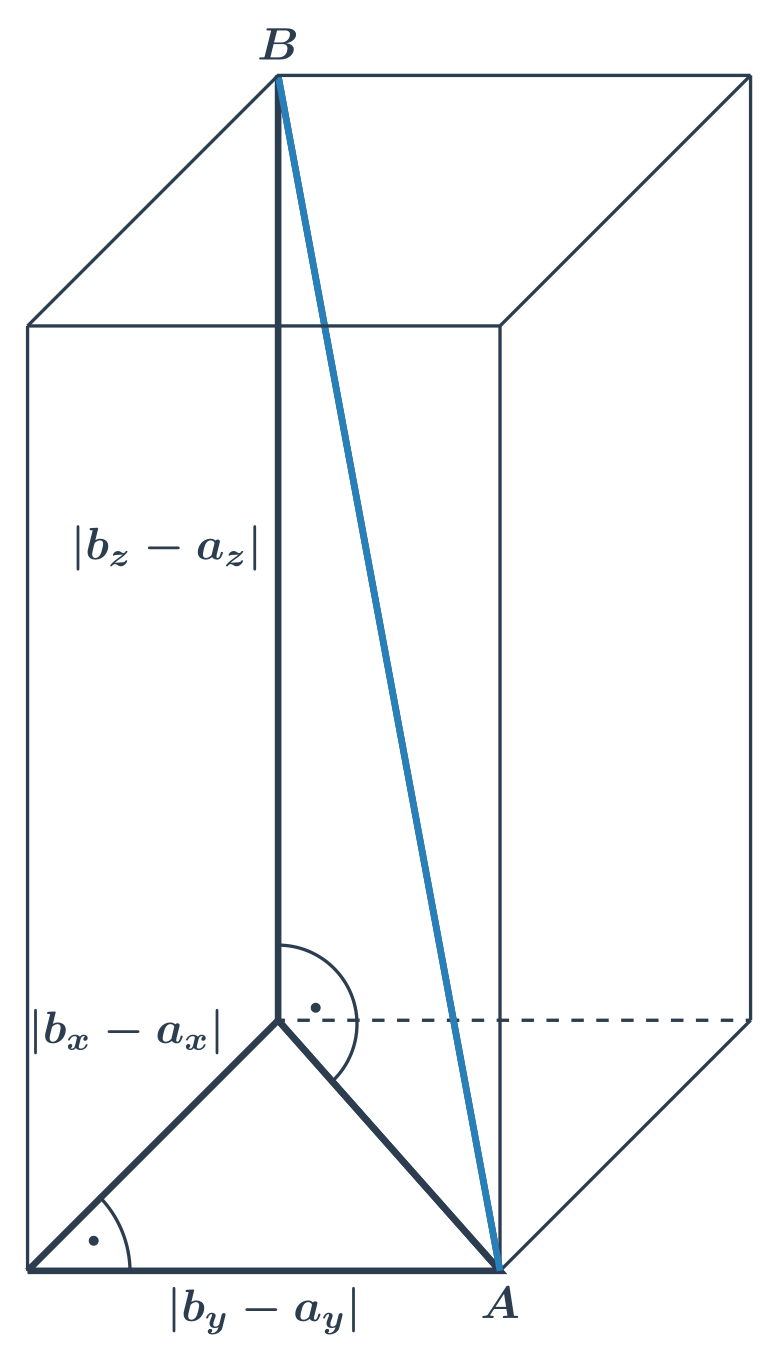
Příklad: vzdálenost C[1;2;0],D[4;5;1]
- |CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2 + (d_z-c_z)^2}
- Dosadíme souřadnice bodů C[1;2;0] a D[4;5;1]: \sqrt{(4-1)^2 + (5-2)^2 + (1-0)^2}=\sqrt{3^2 + 3^2 + 1^2}=\sqrt{19}
- Vzdálenost je: |CD|=\sqrt{19}
Příklad: vzdálenost M[0;-1;3], N[-4;1;-1]
- |MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2 + (n_y-m_y)^2}
- Dosadíme souřadnice bodů M[0;-1;3] a N[-4;1;-1]: \sqrt{(-4-0)^2 + (1-(-1))^2 + (-1-3)^2}=\sqrt{(-4)^2 + 2^2+(-4)^2}=\sqrt{36}=6
- Vzdálenost je: |MN|=6
Úsečka je část přímky mezi dvěma krajními body (včetně těchto bodů). Úsečka je v rovině i v prostoru jednoznačně zadaná svými krajními body.
NahoruDélka úsečky v rovině
Délku úsečky v rovině spočítáme stejně jako vzdálenost bodů v rovině.
Jsou‑li dány souřadnice A[x_A; y_A], B[x_B; y_B], je délka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzoreček vychází z Pythagorovy věty.
Je nutné počítat rozdíl souřadnic v pořadí „druhý bod mínus první“?
- Není. Výrazy x_B-x_A a x_A-x_B nejsou stejné. Ale jsou opačné a ve vzorci počítáme jejich druhé mocniny, které se rovnají.
- Navíc geometricky, délka úsečky AB je stejná jako délka úsečky BA.
- Důvodem zápisu právě v tomto tvaru je fakt, že délka úsečky je rovna velikosti vektoru \overrightarrow{AB} a u vektoru se jeho velikost vždy počítá „koncový bod mínus počáteční“.
Příklad: Délka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme souřadnice bodů E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Délka úsečky je: |EF|=5
Střed úsečky v rovině
Střed úsečky dělí úsečku na dvě stejné části. Pokud leží krajní body úsečky AB na číselné ose a jejich polohám odpovídají hodnoty a a b, potom jejímu středu S odpovídá číslo s=\frac{a+b}{2}. Střed úsečky je „průměrem“ jejích krajních bodů.
Pro úsečku v rovině bude situace následující. 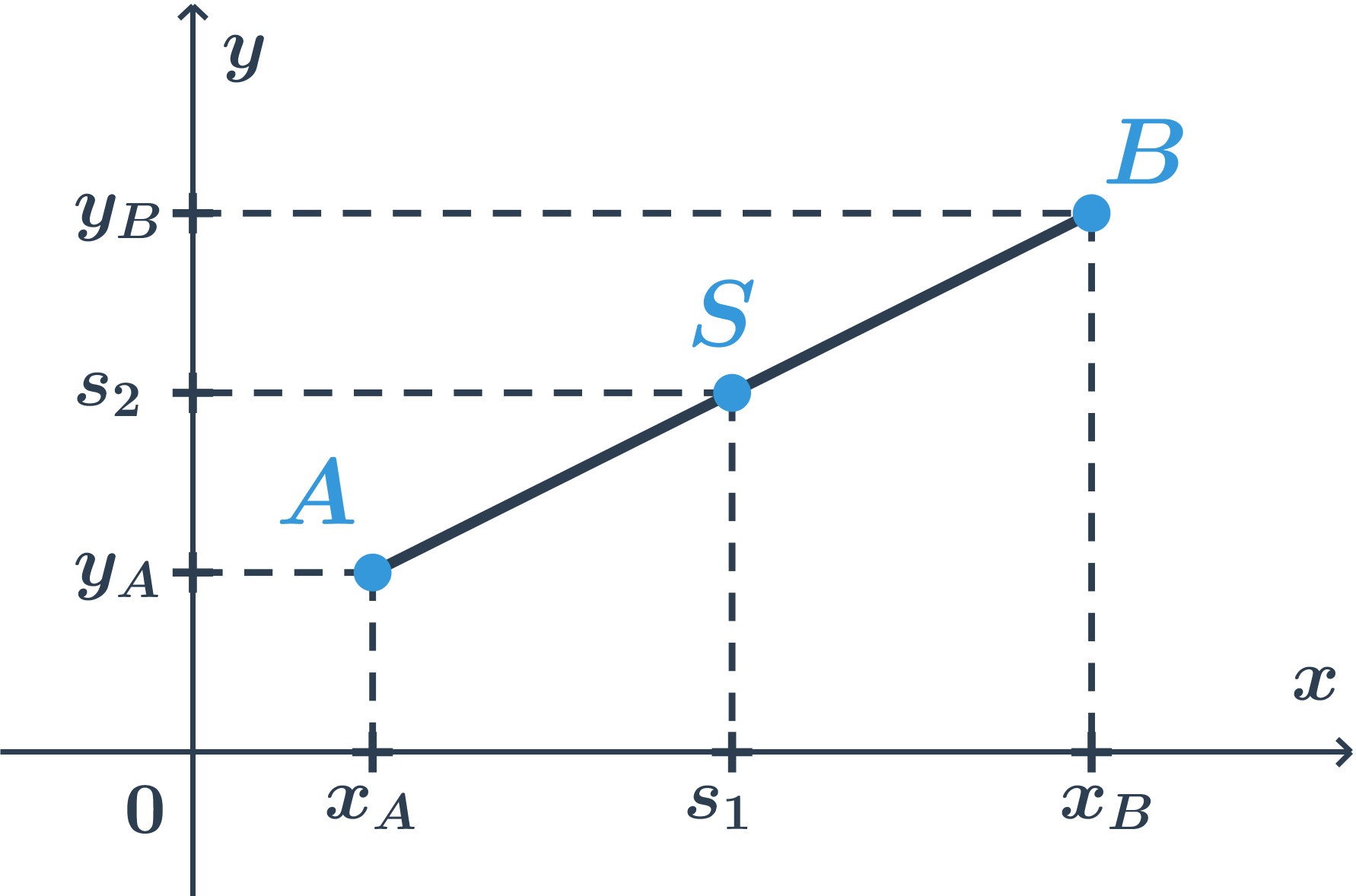 Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[6;-1], B[2;3]
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Střed úsečky AB je bod S[4;1]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je‑li dán bod A[-3;0] a její střed S[1;3].
- Pro souřadnice středu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme souřadnice bodů A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítáme neznámé x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má souřadnice [5;6].
Vzájemná poloha úseček v rovině
Dvě úsečky v rovině mohou mít společné krajní body, pak říkáme, že jsou totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.
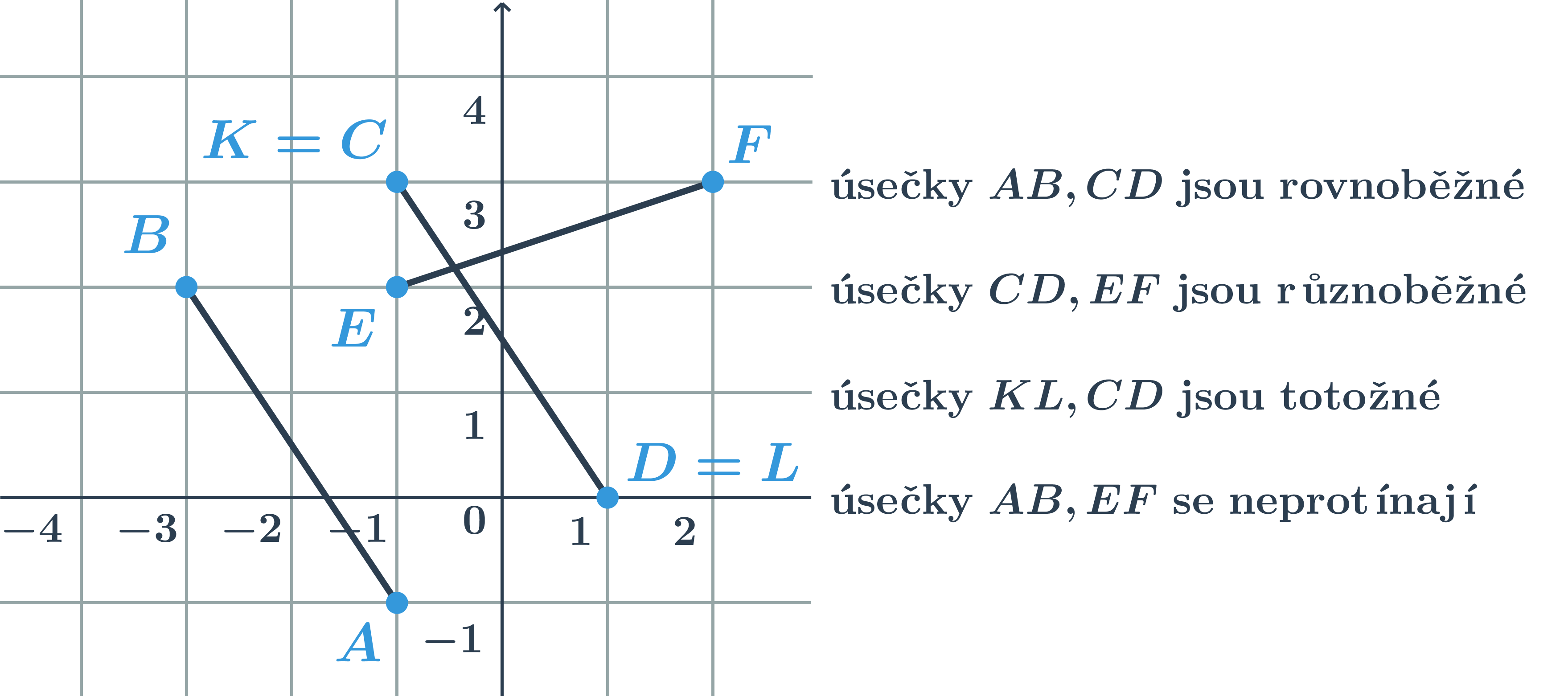
Délka úsečky v prostoru
Délku úsečky v prostoru spočítáme stejně jako vzdálenost bodů v prostoru.
Jsou‑li dány souřadnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je délka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}
Příklad: Délka úsečky EF: E[-2;0;1], F[-4;2;0]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
- Dosadíme souřadnice bodů EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3 - Délka úsečky je: |EF|=3
Střed úsečky v prostoru
Střed úsečky v prostoru spočítáme podobně jako střed úsečky v rovině. Spočítáme všechny souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.
Pro střed S[s_1;s_2;s_3] úsečky AB, kde A[x_A; y_A;z_A], B[x_B; y_B;z_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2} , s_3 = \frac{z_A+z_B}{2}
Příklad: určení středu úsečky
Najděte střed úsečky AB: A[2;1;-3], B[2;-3;3]
Pro souřadnice středu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme souřadnice bodů A[2;1;-3], B[2;-3;3].
- s_1 = \frac{2+2}{2}=2, s_2 = \frac{1-3}{2}=-1, s_3 = \frac{-3+3}{2}=0
Střed úsečky AB je bod S[2;-1;0]
Příklad: určení druhého krajního bodu úsečky
Určete souřadnice druhého krajního bodu úsečky AB, je-li dán bod A[1;2;4] a její střed S[1;-3;0].
- Pro souřadnice středu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme souřadnice bodů A[1;2;4], S[1;-3;0].
- 1 = \frac{1+x_B}{2}, -3 = \frac{2+y_B}{2}, 0 = \frac{4+z_B}{2}
- Dopočítáme neznámé x_B, y_B, z_B:
\begin{array}{rclcrcr} 2&=&1+x_B &\Rightarrow& x_B&=&1\\ -6&=&2+y_B &\Rightarrow& y_B&=&-8\\ 0&=&4+z_B &\Rightarrow& z_B&=&-4 \end{array}
- Bod B má souřadnice [2;-8;-4].
Vzájemná poloha úseček v prostoru
Podobně jako v rovině mohou mít dvě úsečky společné krajní body, pak říkáme, že jsou totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.
Tyto vzájemné polohy si dobře můžeme ilustrovat na krychli.
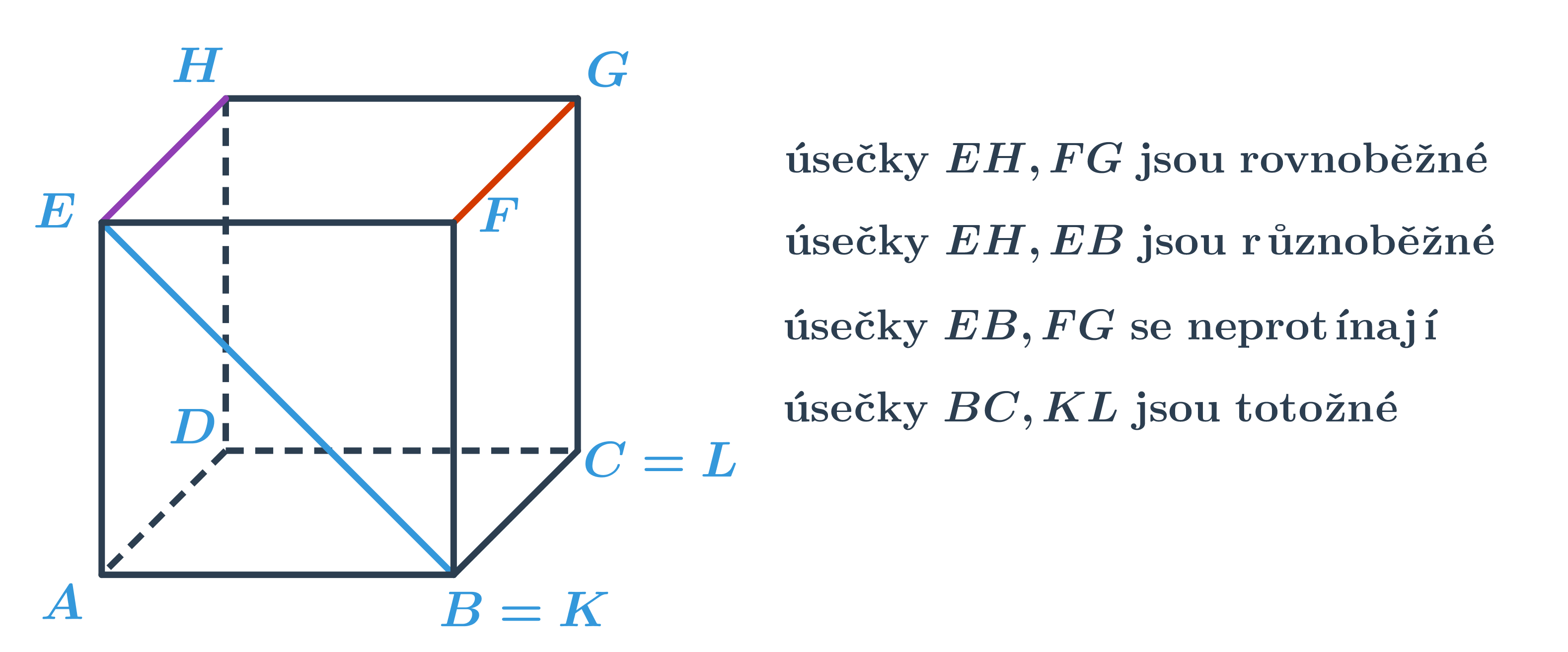
Vektory patří mezi základní objekty používané v analytické geometrii. Vektory mají hojné využití i ve fyzice. Intuitivně si je můžeme představit jako šipky, které udávají směr a současně mají určitou velikost.
Základní procvičování vektorů je rozdělené do několika témat:
- Vektory: pojmy – definice vektoru, vektory opačné, kolmé a kolineární, souřadnice vektoru, velikost vektoru
- Souřadnice vektoru – určování souřadnic vektorů, souvislost se souřadnicemi bodů
- Velikost vektoru – výpočet velikosti vektoru, aplikace Pythagorovy věty
- Vzájemná poloha vektorů – opačné, kolmé a kolineární vektory, určování vzájemné polohy na základě souřadnic
Vektory: pojmy
Vektor je množina všech shodně orientovaných úseček, které mají stejnou délku. Každou z těchto úseček nazýváme umístěním vektoru.
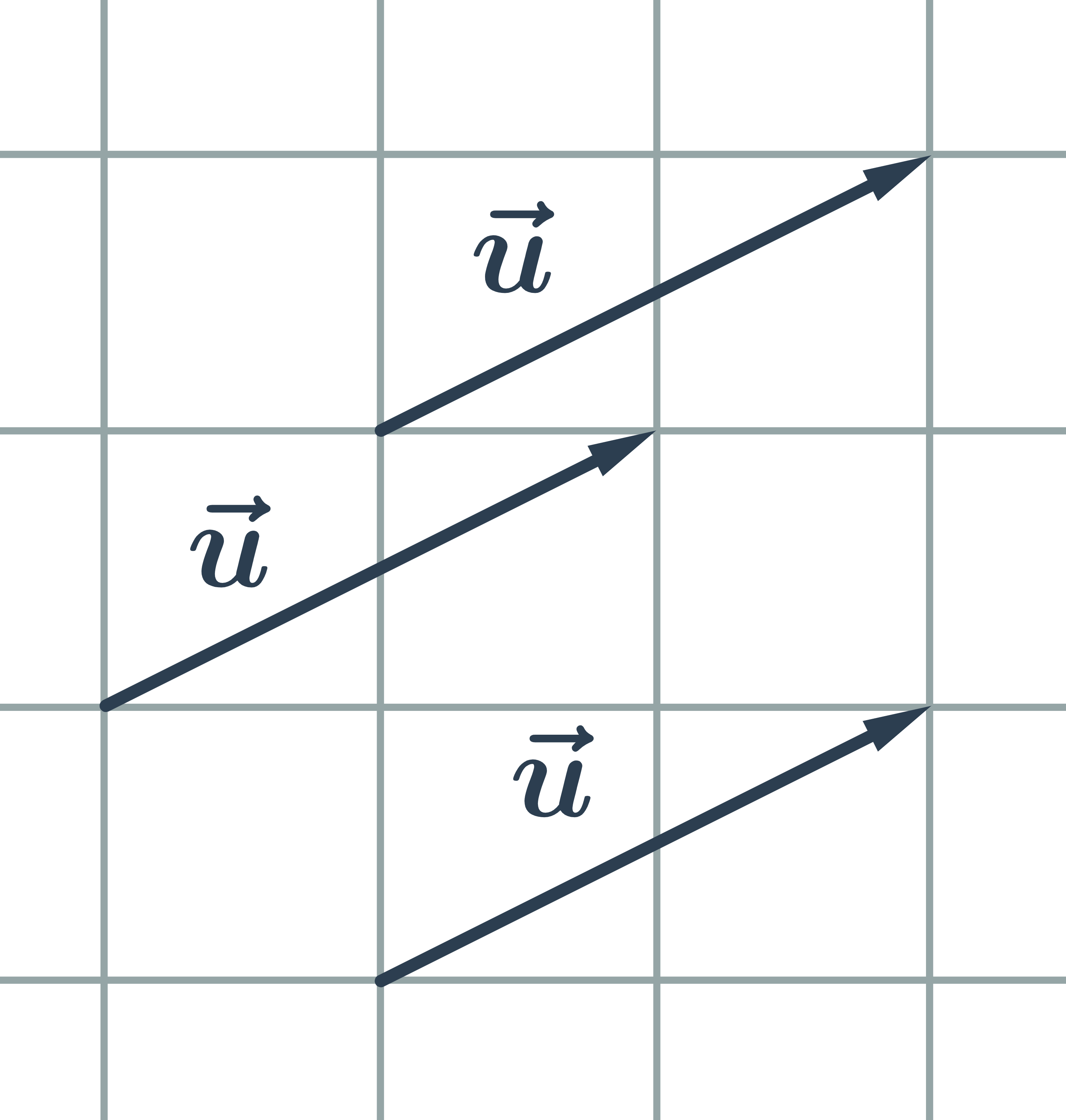
Vektor je určený počátečním a koncovým bodem, graficky znázorňujeme se šipkou u koncového bodu, zapisujeme: \vec{u}=\overrightarrow{AB}
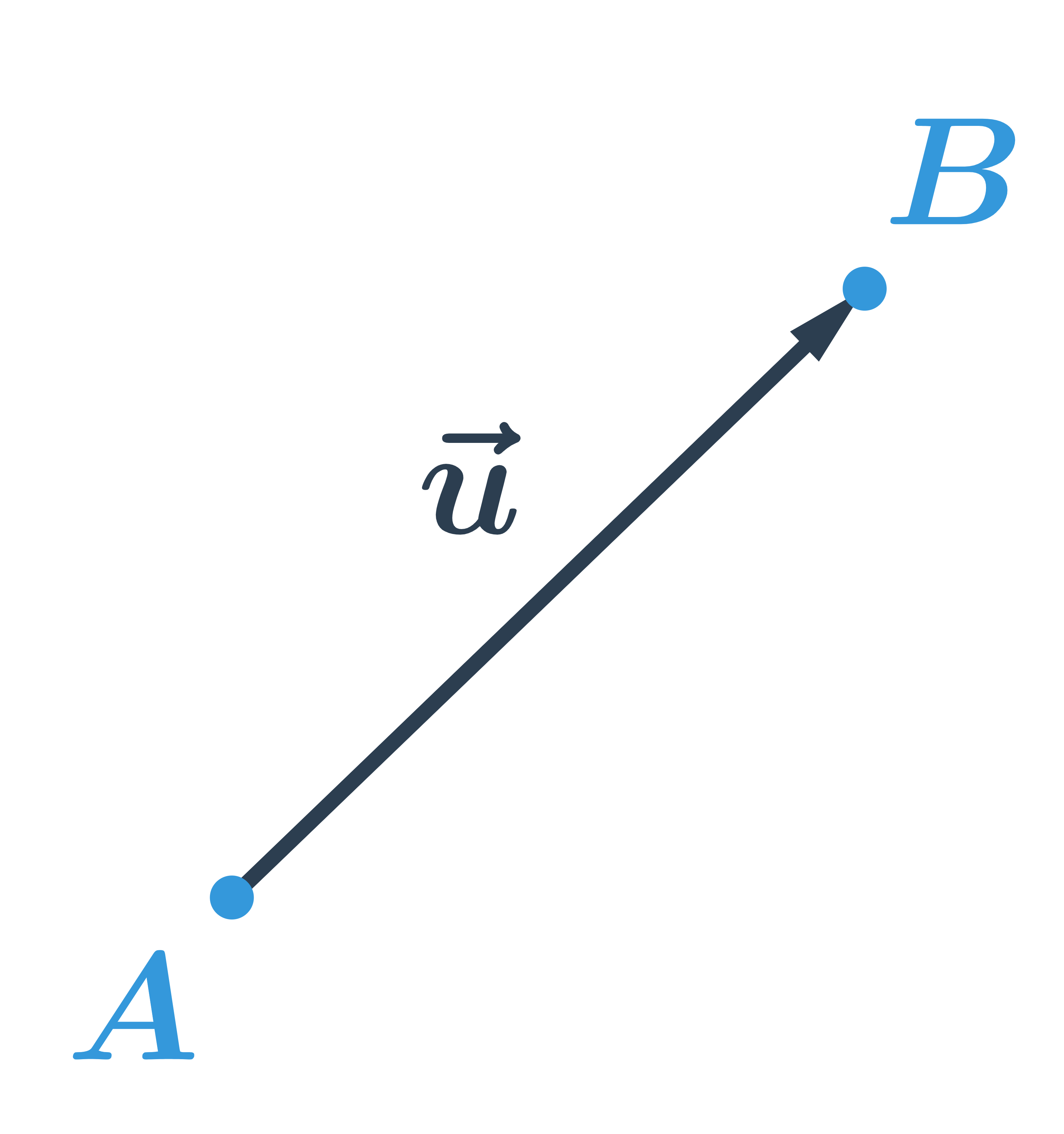
Na obrázku je A počáteční bod vektoru \vec{u}, B je koncový bod vektoru \vec{u}.
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci:
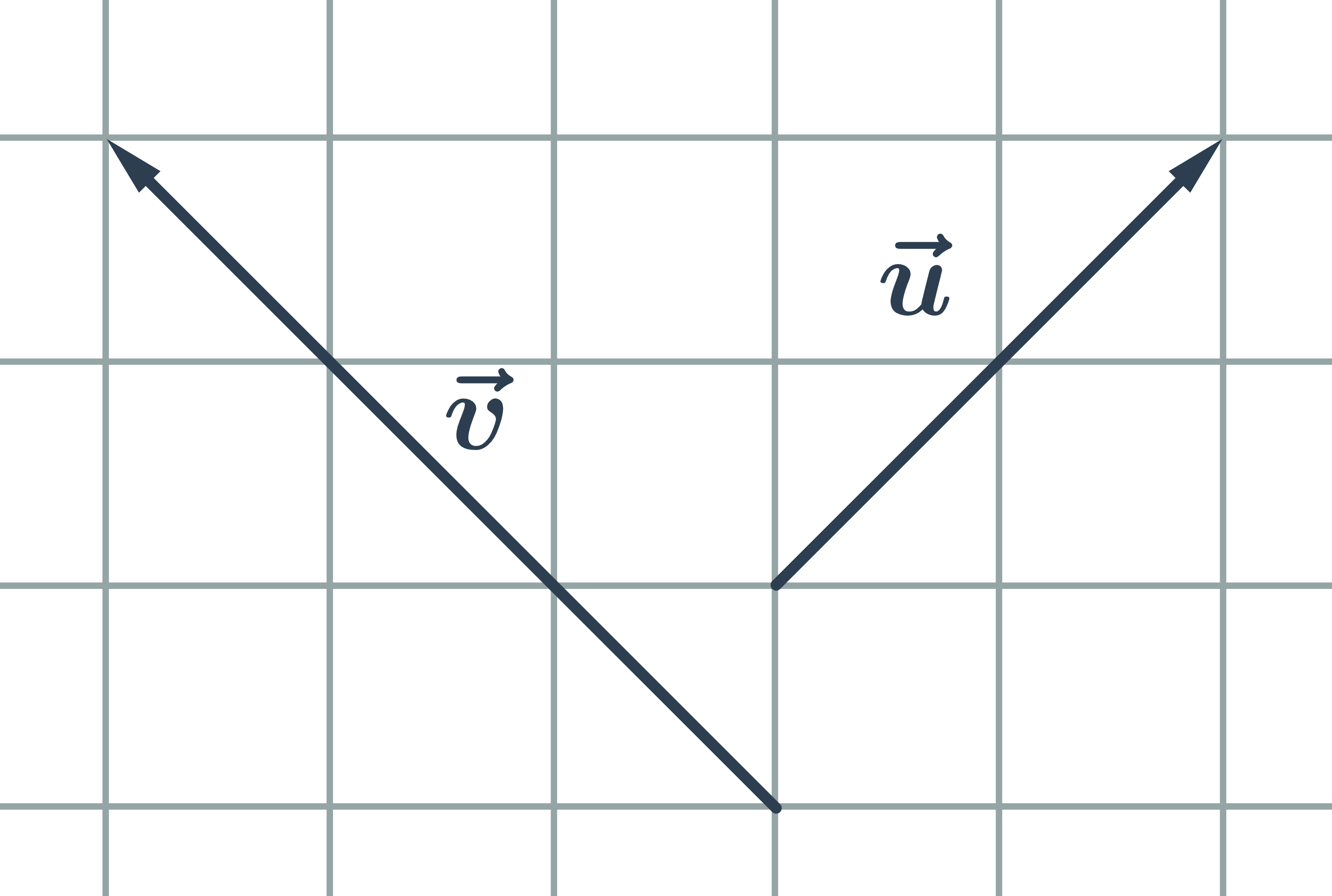
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. Tedy nemusí mít stejnou délku, mohou mít stejnou nebo opačnou orientaci:
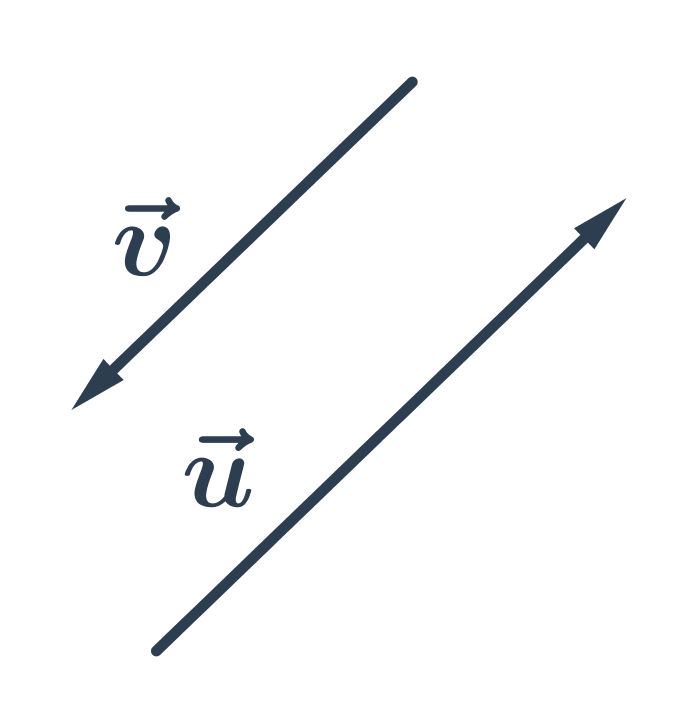
Kolmé vektory jsou vektory, které svírají pravý úhel:
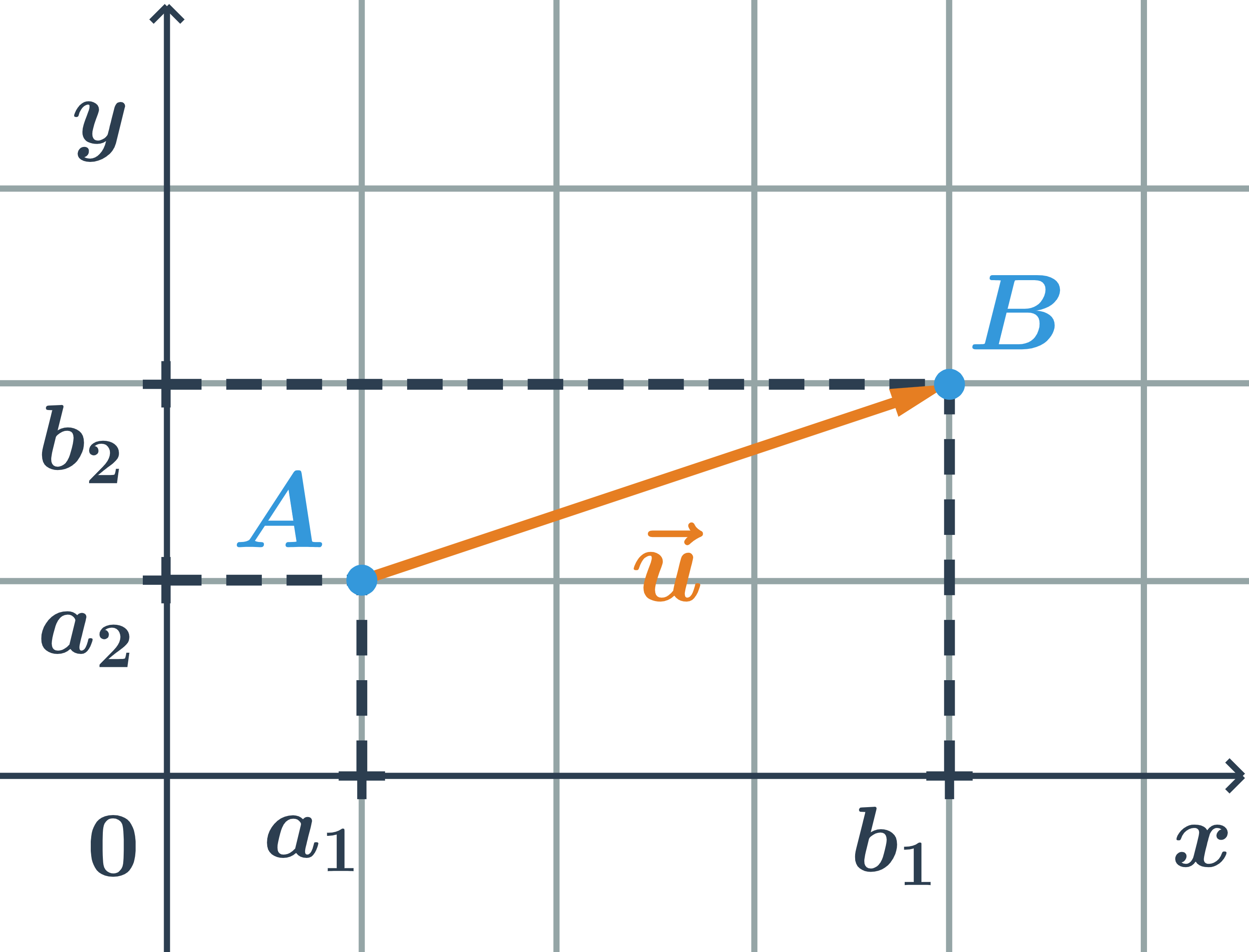
Souřadnice vektoru jsou pravoúhlé průměty vektoru do souřadných os, tedy vektor \vec{u}=\overrightarrow{AB} má souřadnice: \vec{u}=(u_1;u_2)=(b_1-a_1;b_2-a_2)
Velikost vektoru \vec {u}=\overrightarrow{AB} je délka úsečky AB, značíme \left| \vec{u} \right| a platí: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
Jednotkový vektor má délku 1.
Nulový vektor má nulovou délku, tedy splývá jeho počáteční a koncový bod.
NahoruSouřadnice vektoru
Již víme, že vektor je množina nekonečně mnoha orientovaných úseček, jedna z nich má počátek v počátku souřadného systému, v bodě O=[0;0]. Souřadnice koncového bodu jsou souřadnice daného vektoru.
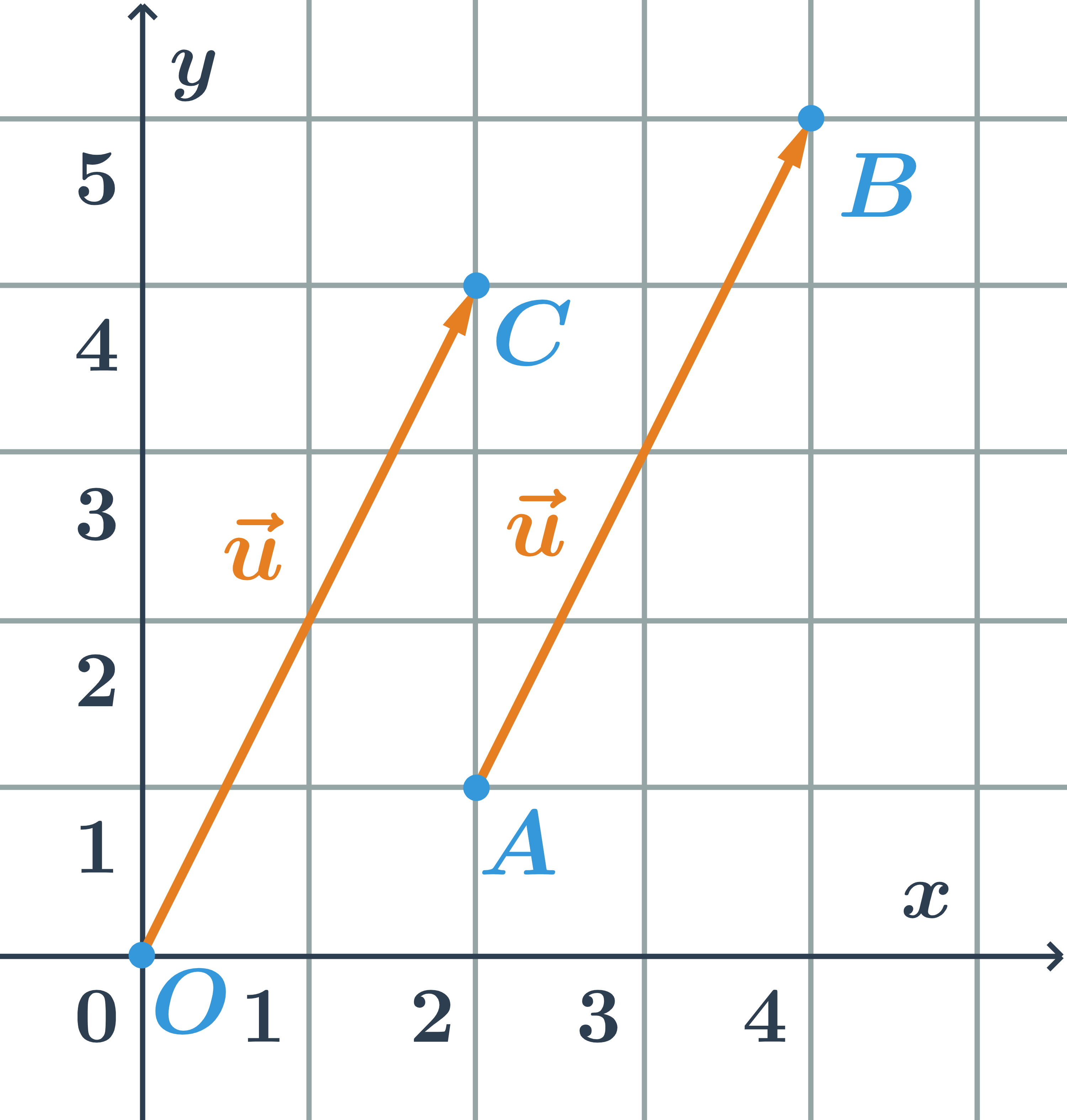
Souřadnice vektoru \overrightarrow{AB}
- Chceme-li vektor \overrightarrow{AB} posunout do počátku souřadného systému, posuneme ho o dva čtverečky vlevo a o jeden čtvereček dolů.
- Bod A se posune do bodu O, bod B se posune do bodu C. Tento posun můžeme vyjádřit takto:
- A se posune na [2-2;1-1]=[0;0]
- B se posune na [4-2;5-1]=[2;4]
- Souřadnice vektor na obrázku jsou: \vec{u}=\overrightarrow{AB}=\overrightarrow{OC}=(2;4)
Všimněte si, že souřadnice vektoru \overrightarrow{AB} jsme získali odečtením souřadnic bodu A od souřadnic bodu B
Pro souřadnice vektoru \overrightarrow{AB} určeného body A=[a_1;a_2], B=[b_1;b_2] platí: \overrightarrow{AB}=B-A=(b_1-a_1;b_2-a_2)
NahoruVelikost vektoru
Velikost vektoru \overrightarrow{AB} je délka úsečky AB. Vektor, který má délku 1, se nazývá jednotkový vektor:
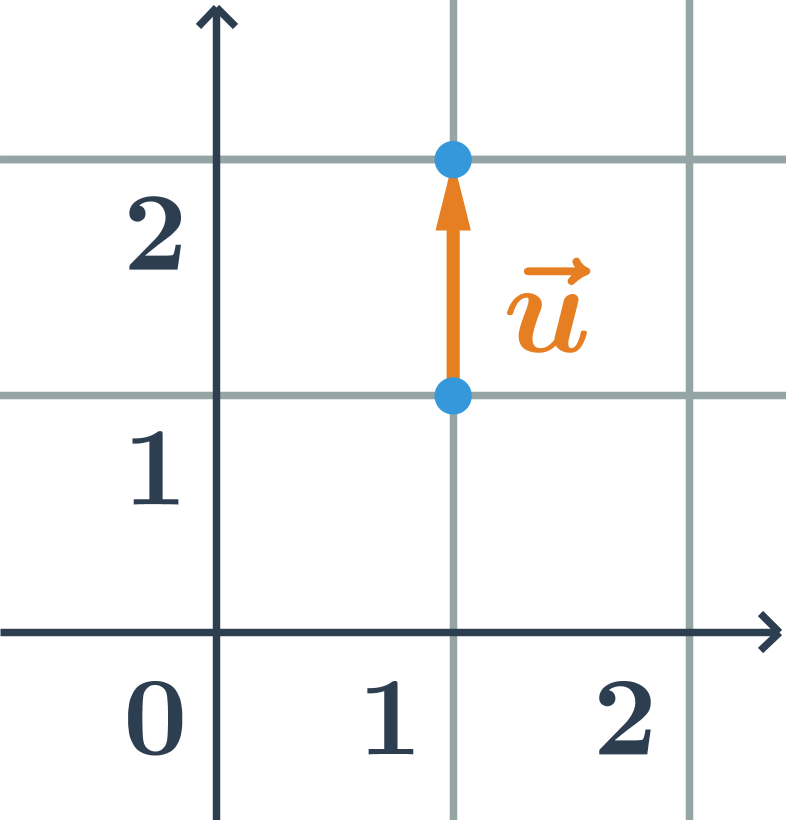
Vektor, který má nulovou délku (počáteční a koncový bod vektoru splývá) se nazývá nulový vektor:
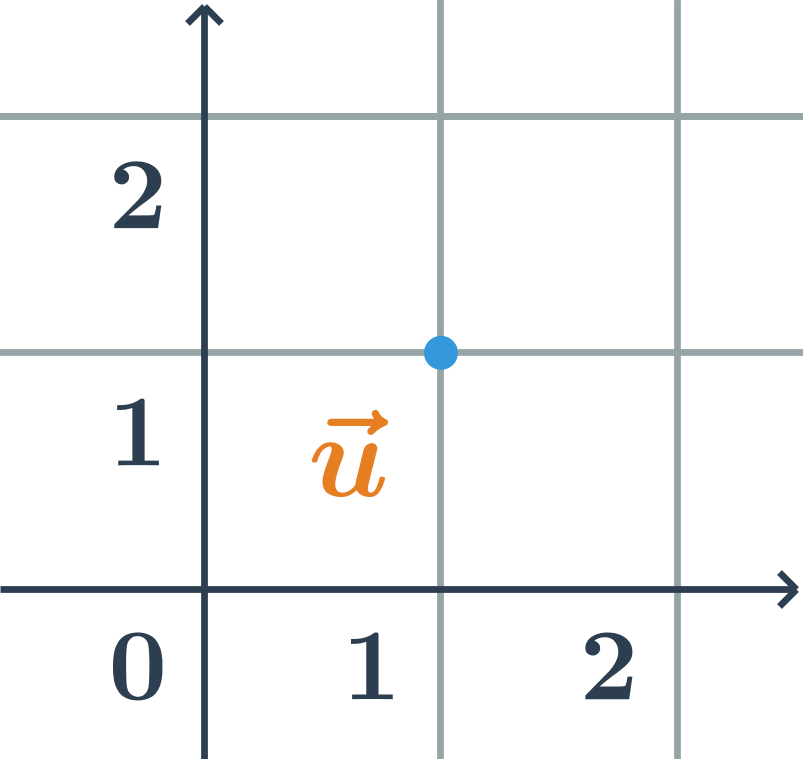
Velikost vektoru \vec{u}=(u_1;u_2) určíme s využitím Pythagorovy věty: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
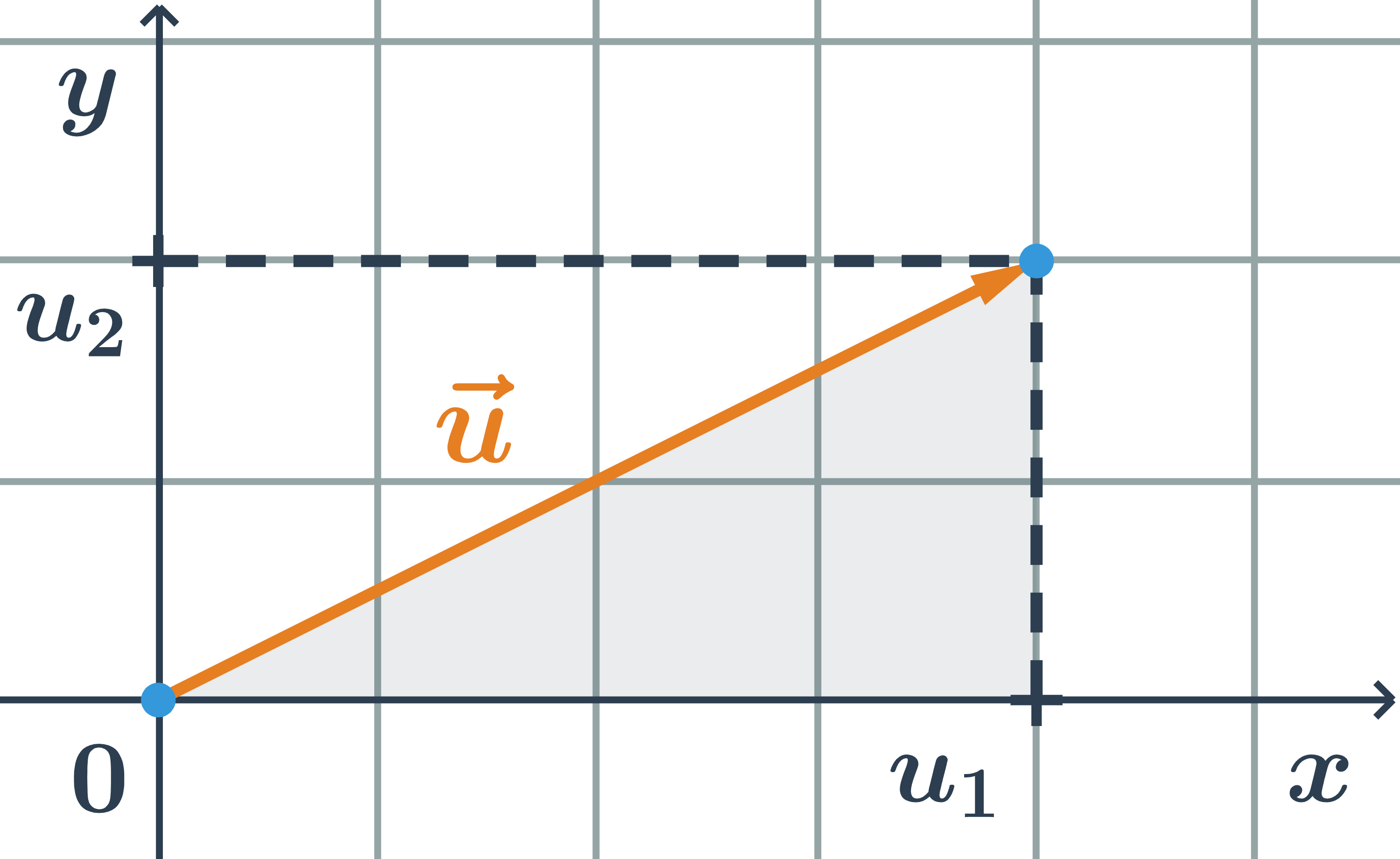
Ve vybarveném trojúhelníku je délka vektoru přepona, odvěsny mají délky u_1 a u_2.
Příklad: velikost vektoru
Určete velikost vektoru na obrázku:
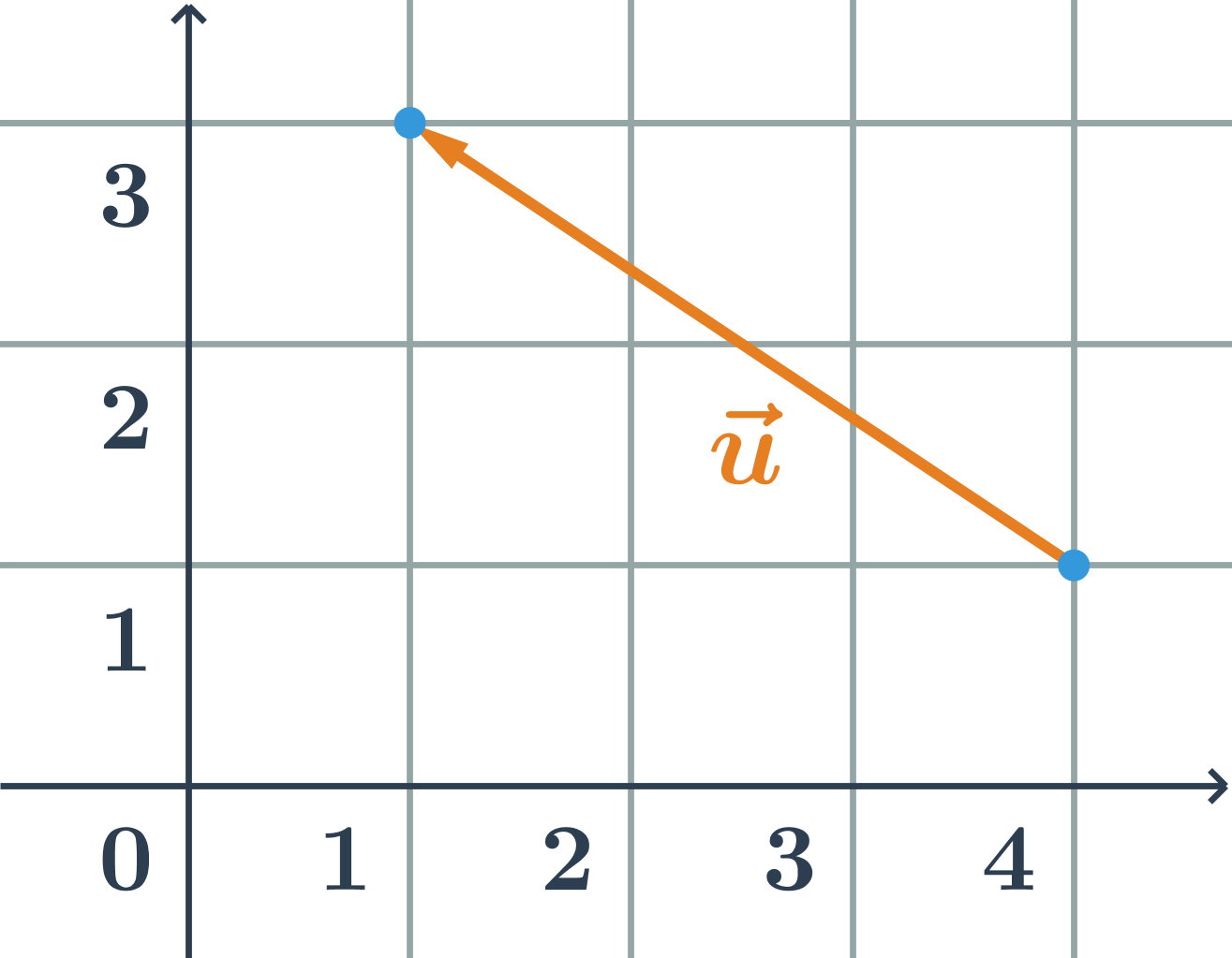
Vektor na obrázku má souřadnice \vec{u}=(-3;2), jeho velikost je \left| \vec{u} \right|=\sqrt{(-3)^2+2^2}=\sqrt{(-3)^2+2^2}=\sqrt{13}
Vzájemná poloha vektorů
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
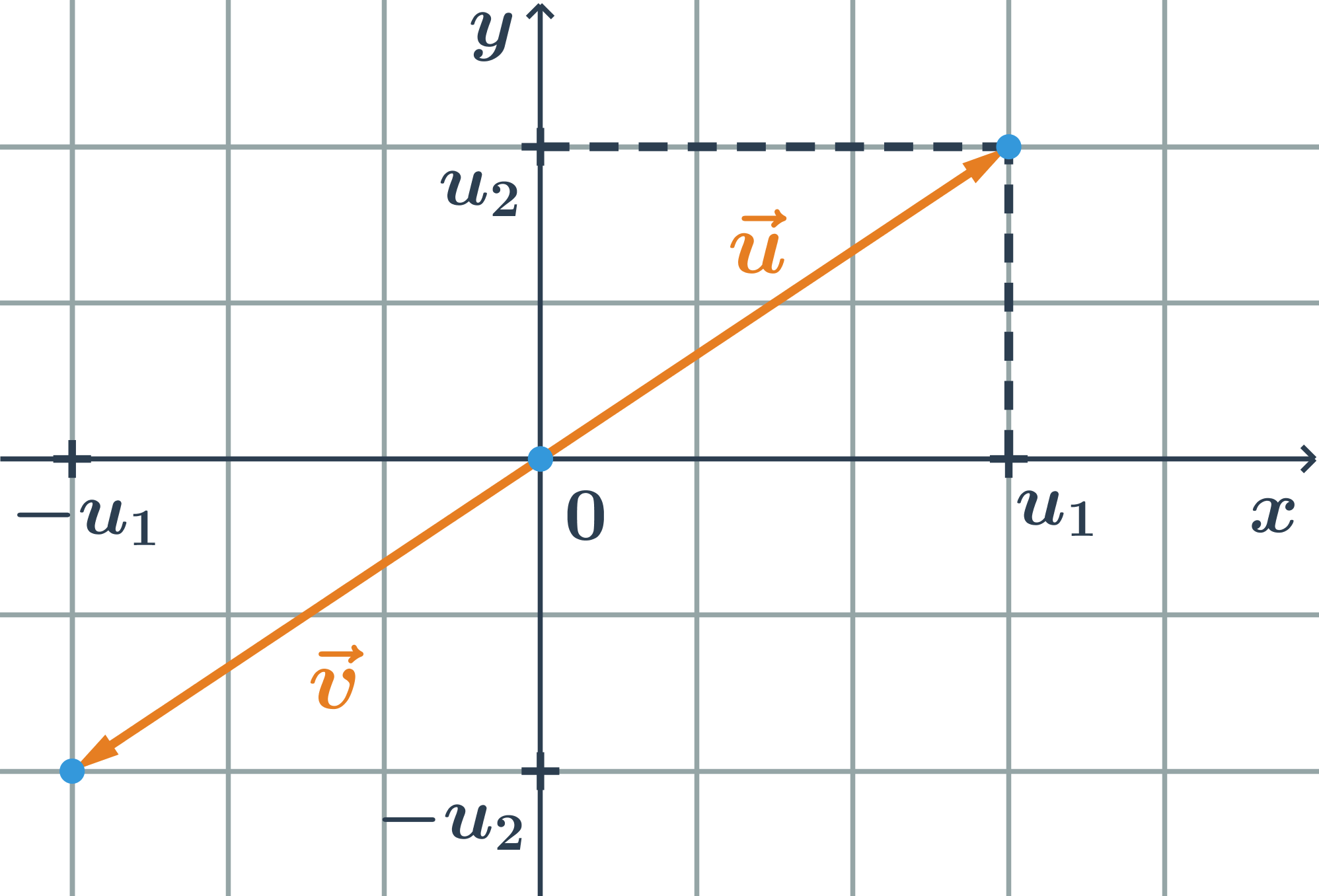
Příklad opačný vektor
- Určete opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má souřadnice: (-u_1;-u_2)=(-3;1)
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. S vektorem \vec{u}=(u_1;u_2) je kolineární každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálné nenulové číslo. Pro k \gt 0 vektory mají stejný směr, pro k \lt 0 mají vektory opačný směr.
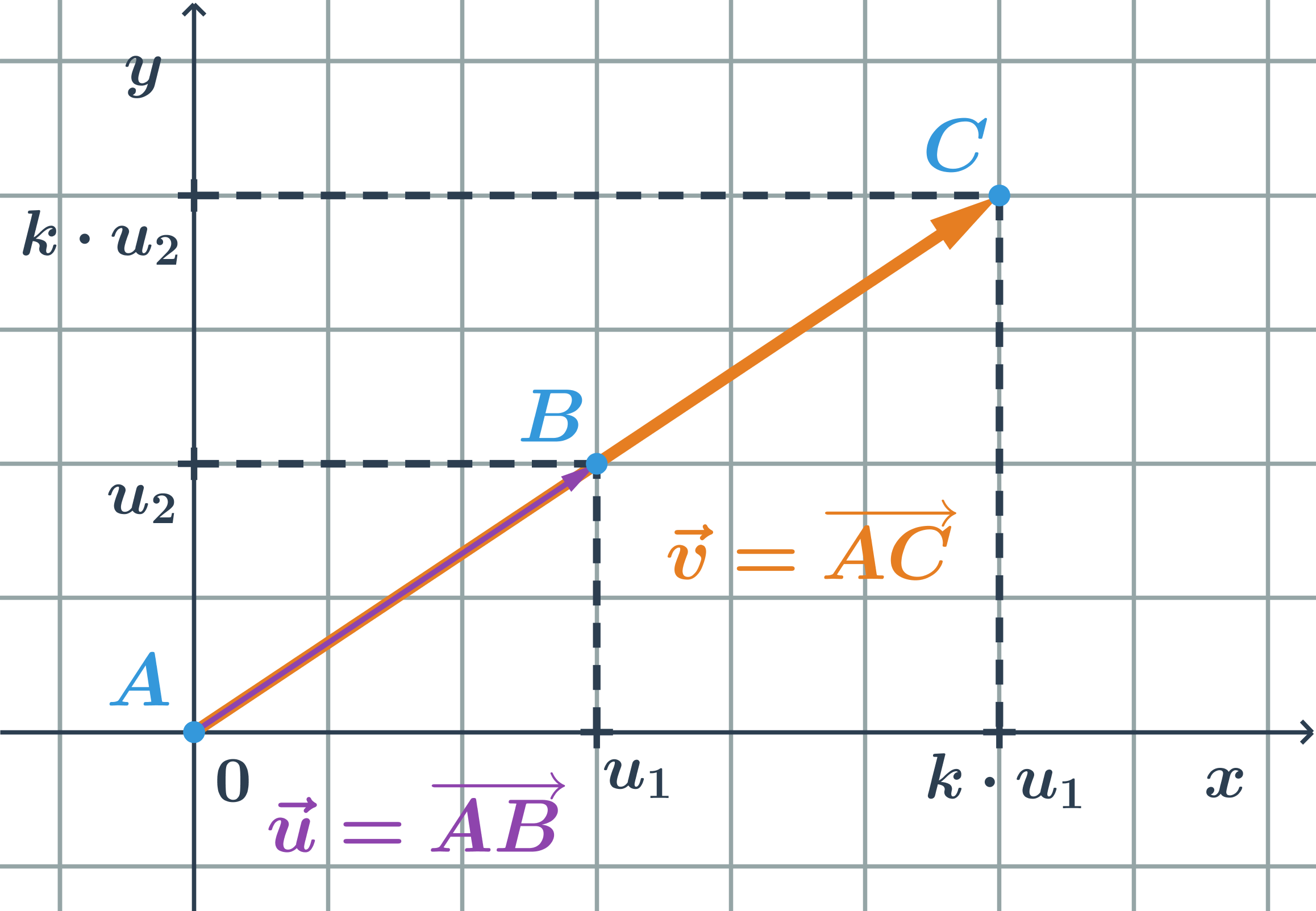
Příklad kolineární vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;3) tak, aby byl kolineární s vektorem \vec{u}=(2;-1).
- Pro druhou souřadnici platí: v_2=3, u_2=-1, tedy v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, tj. \vec{u} a \vec{v} mají opačnou orientaci
- Pro první souřadnici musí platit: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory jsou vektory, které svírají pravý úhel K vektoru \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálné nenulové číslo.
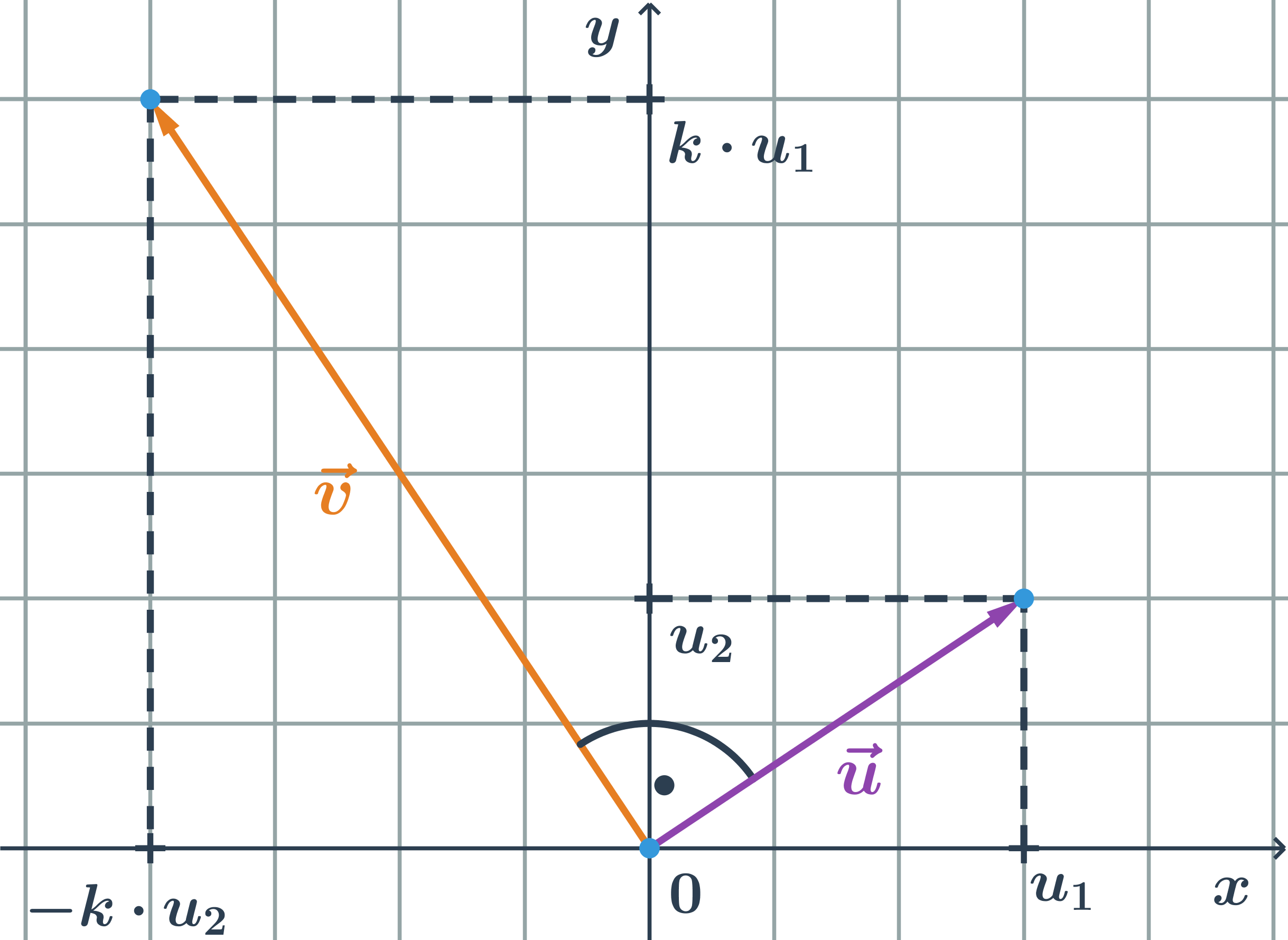
Příklad kolmý vektor
- Doplňte souřadnici vektoru \vec{v}=(v_1;4) tak, aby byl kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, tedy musí platit: v_1 = - 2 \cdot u_2.
- Máme tedy v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
Operace s vektory
Vektory v rovině mohou být zapsané jako dvojice čísel – souřadnic v rovině, podobně trojrozměrné vektory lze zapsat jako trojice čísel – souřadnic v prostoru.
Operace jako součet, rozdíl a vynásobení reálným číslem, které umíme jednoduše provádět s čísly, lze s vektory provádět po jednotlivých souřadnicích. Tím se zabývá kapitolka Vektory: násobení konstantou, součet, rozdíl. Příklady praktického použití těchto operací s vektory:
- vrabec letí stejným směrem jako moucha a dvakrát rychleji než moucha – vektor rychlosti vrabce získáme, když vektor rychlosti mouchy vynásobíme konstantou 2,
- satelitní snímky ukazují, že ráno ještě vozítko Marka Watneyho stálo na marsovské základně, za dnešek ujel 50 km na východ – jeho novou polohu získáme, když k souřadnicím základny přičteme vektor (50;0),
- šnek přelezl rovně po monitoru z levého horního rohu (souřadnice v pixelech [0;0]) do bodu [1007;555] – vektor, jehož souřadnice jsou počty pixelů, co šnek ulezl v horizontálním a vertikálním směru získáme jako rozdíl jeho umístění na konci pohybu a jeho umístění na začátku pohybu.
Speciální operace, kterou lze provést se dvěma vektory stejné dimenze (mají stejný počet souřadnic), je skalární součin. Vstup této operace jsou dva vektory, výstup je reálné číslo.
Díky skalárnímu součinu můžeme vypočítat kupříkladu jaký úhel vektory svírají, speciálně jestli jsou na sebe kolmé (v takovém případě jejich skalární součin vyjde nulový).
NahoruVektory: násobení konstantou, součet, rozdíl
Součet vektorů
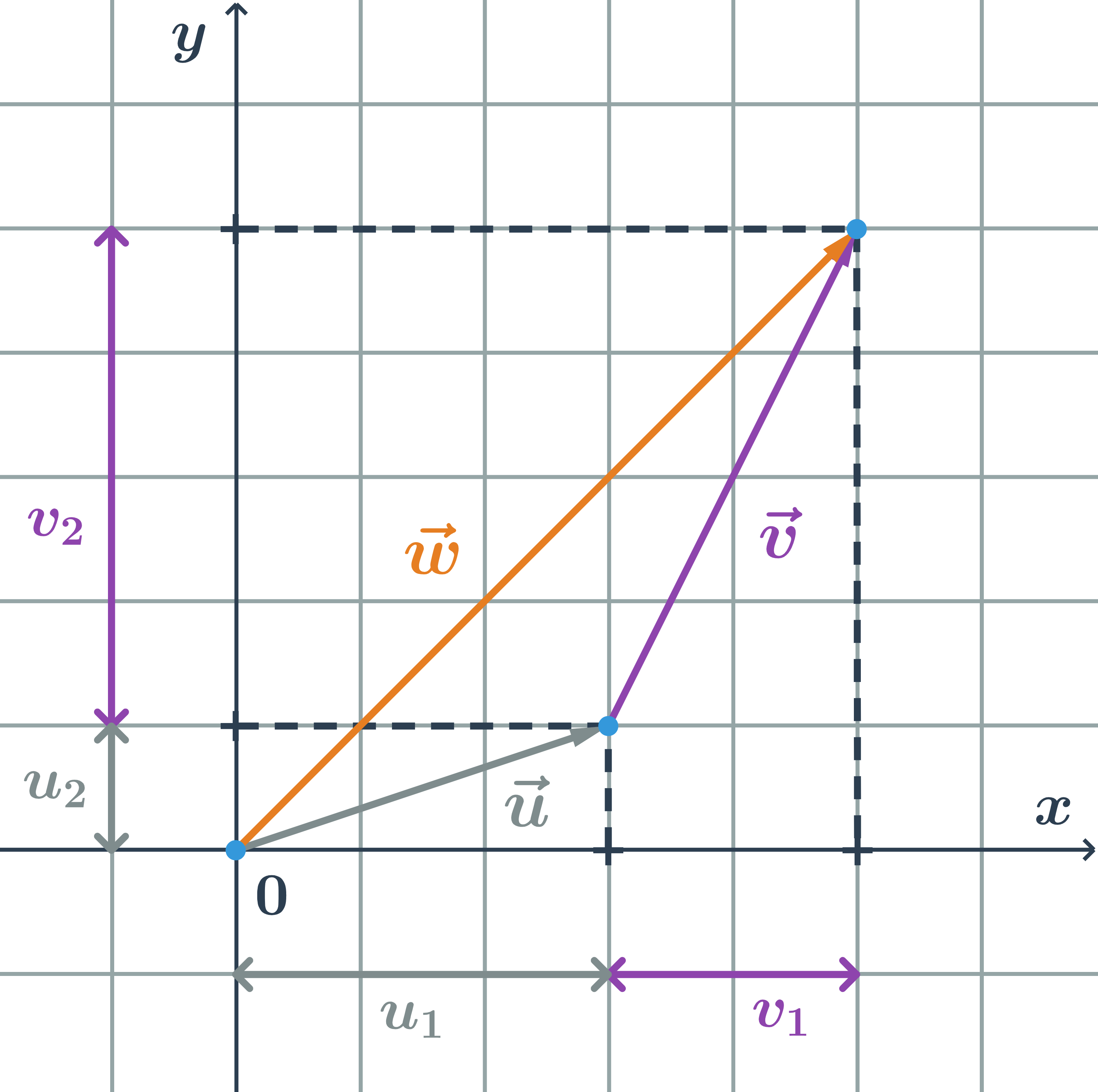
Vektory \vec{u} a \vec{v} sečteme takto: počáteční bod vektoru \vec{v} posuneme do koncového bodu vektoru \vec{u}. Součet vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má počáteční bod stejný jako vektor \vec{u} a koncový bod stejný jako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
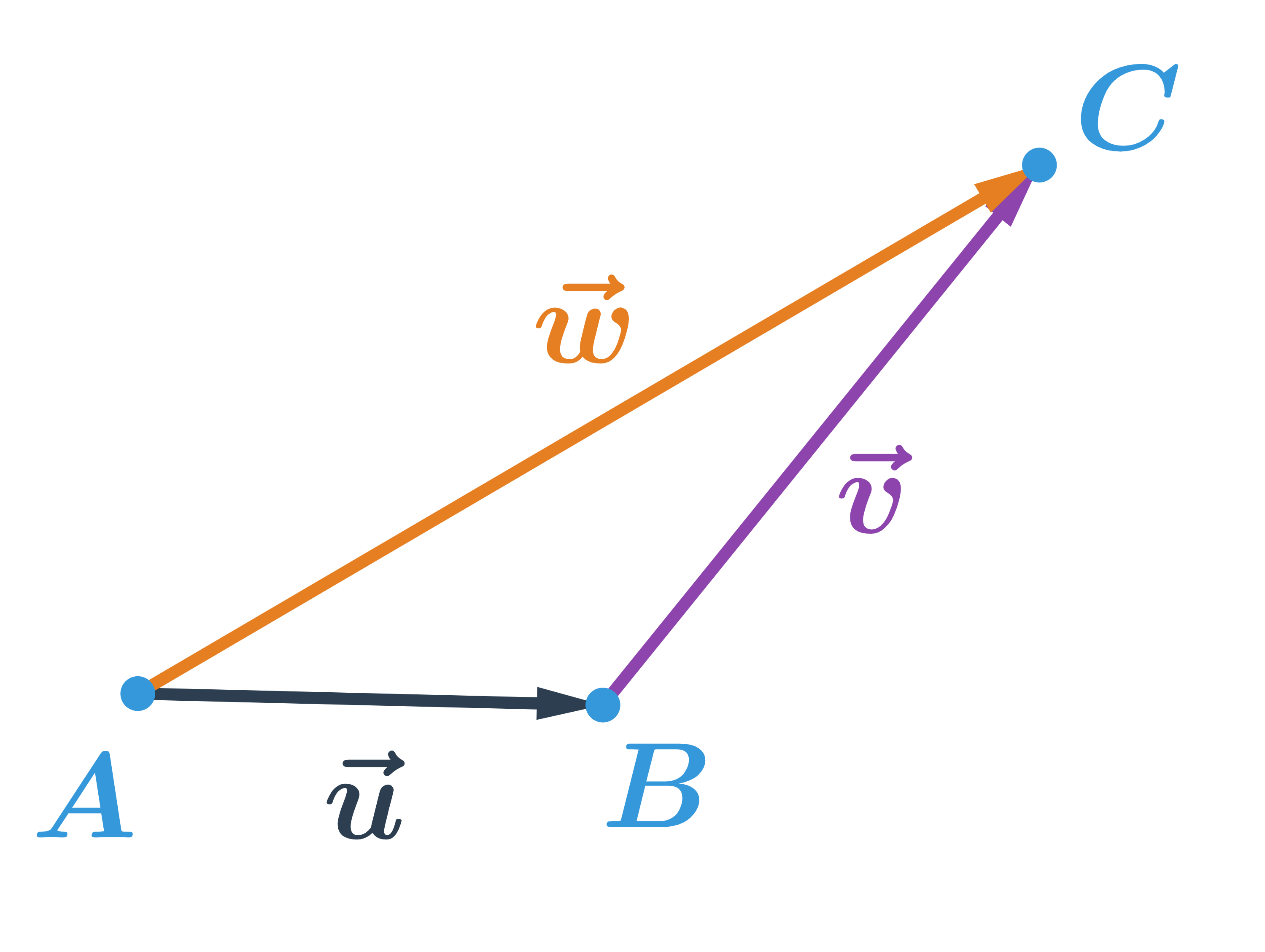
Vektory na obrázku jsou označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Součet těchto vektorů: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
Mějme vektory se souřadnicemi \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Pak součet vektorů \vec{u} a \vec{v} je vektor \vec{w} se souřadnicemi \vec{w}=(u_1+v_1; u_2+v_2).
Rozdíl vektorů
Rozdíl vektorů \vec{u} a \vec{v} je součet vektoru \vec{u} s vektorem opačným k \vec{v}. Tedy:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
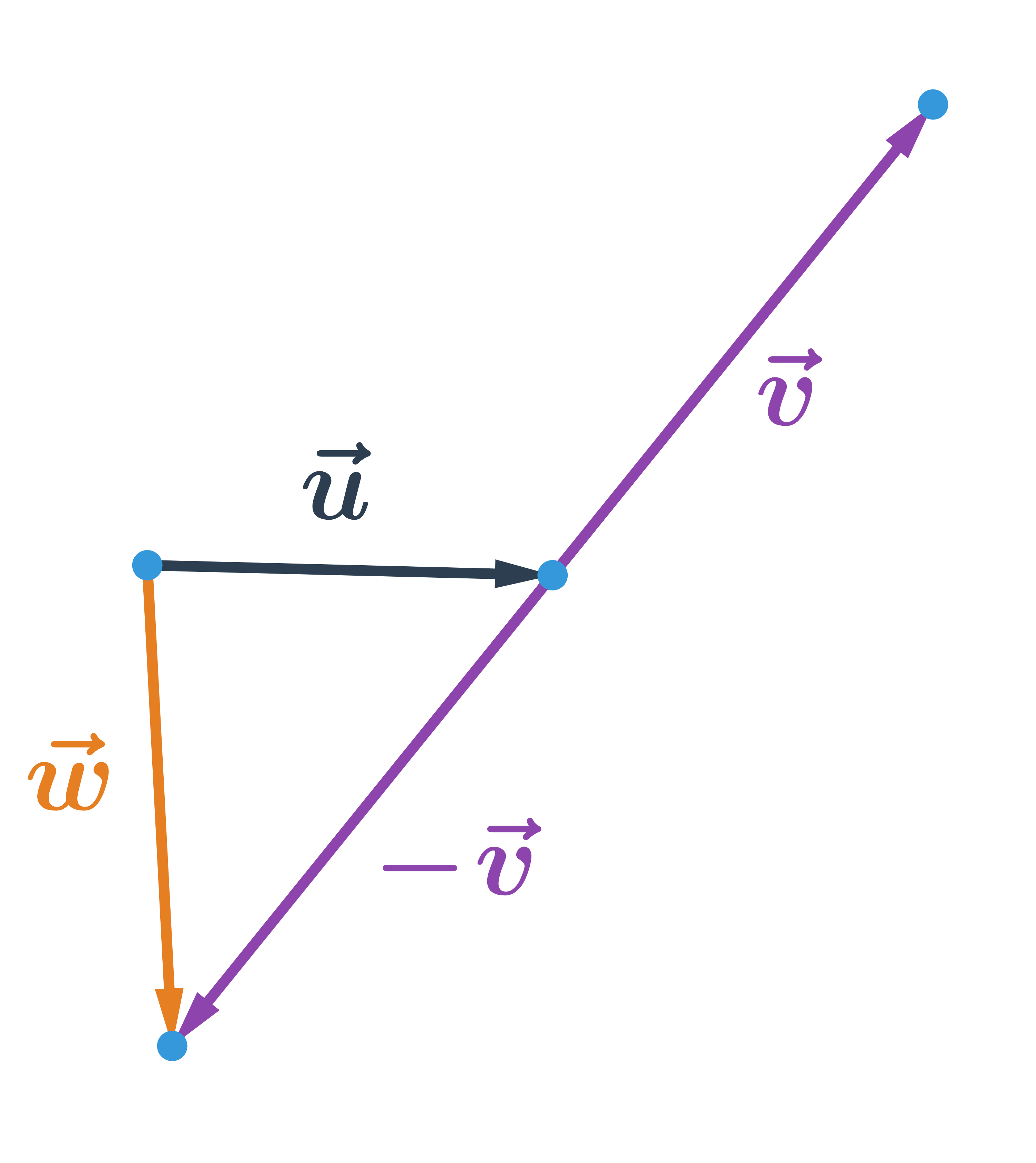
Máme-li souřadnice vektorů: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak rozdíl vektorů \vec{u} a \vec{v} je vektor \vec{w}, který má souřadnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobek vektoru
Vektor \vec{u} můžeme vynásobit libovolným reálným číslem k. Dostaneme vektor \vec{v}, kterému říkáme násobek vektoru. Píšeme \vec{v}=k \cdot \vec{u}
- Pokud k \gt 0, vektory \vec{u} a k \cdot \vec{u} mají stejný směr
- Pokud k \lt 0, vektory \vec{u} a k \cdot \vec{u} mají opačný směr
- Pokud k=0, vektor k \cdot \vec{u} je nulový vektor
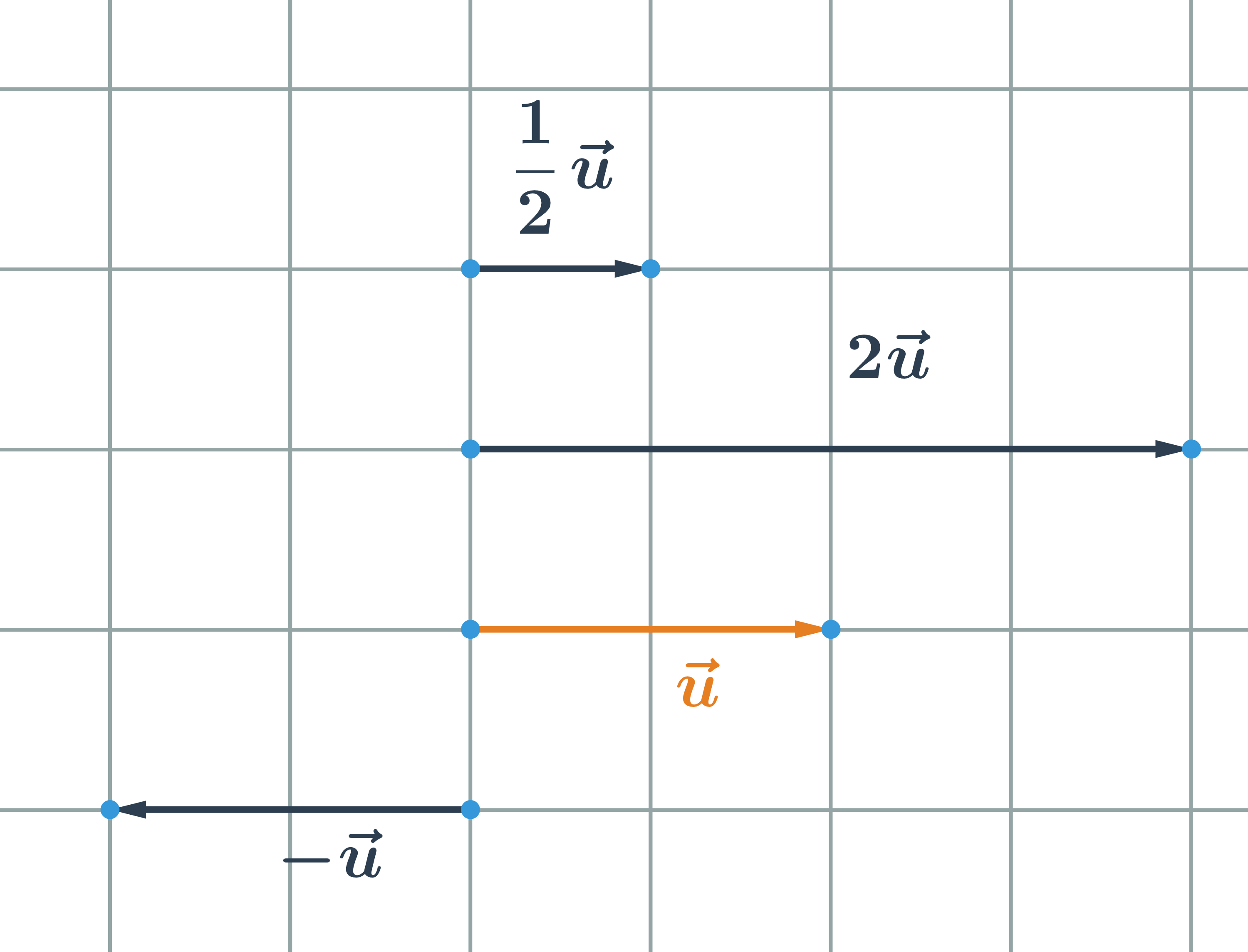
Máme-li souřadnice vektoru \vec{u}=(u_1;u_2), pak jeho násobek \vec{v}=k \cdot \vec{u} má souřadnice \vec{v}=(k \cdot u_1; k\cdot u_2).
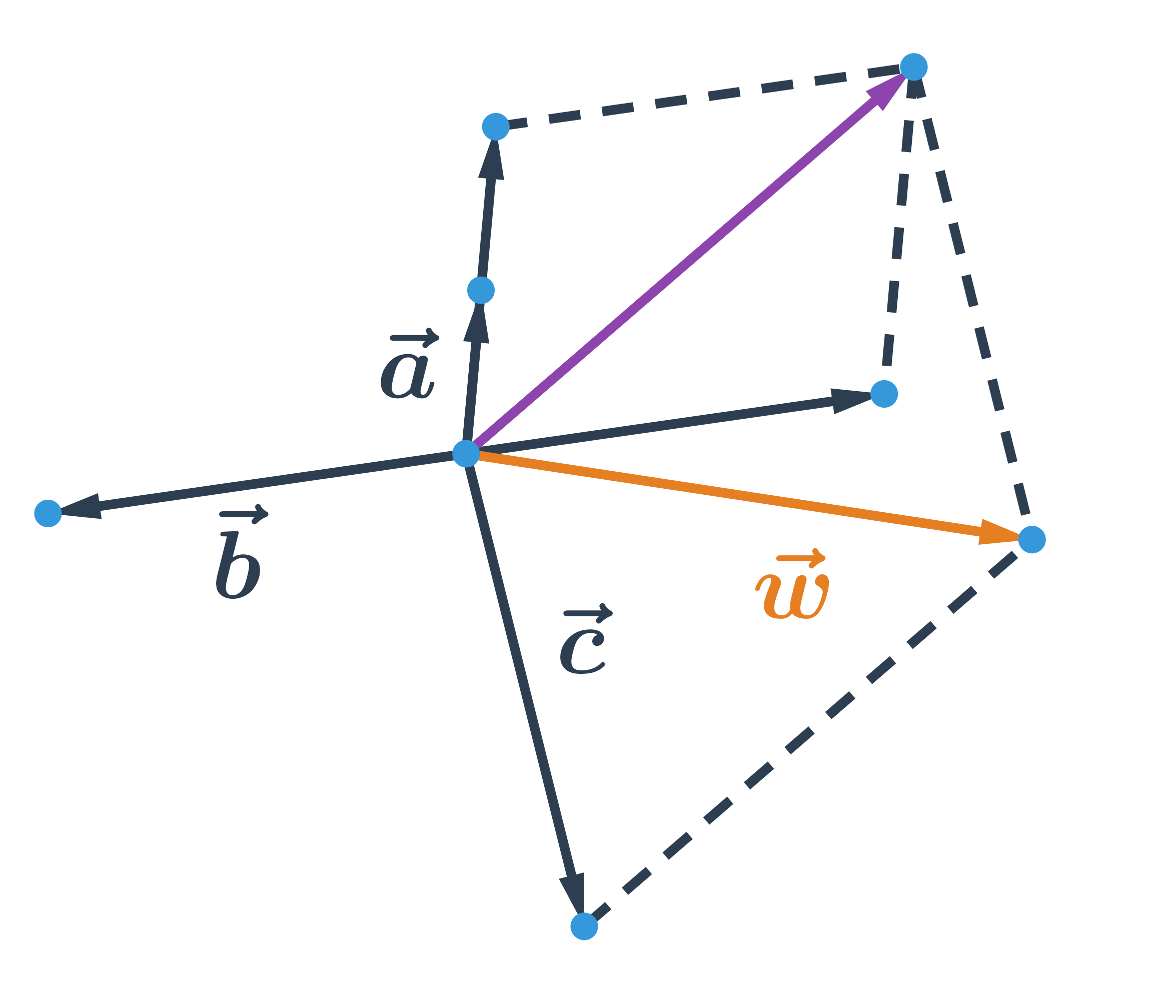
Příklad součet a násobek vektoru graficky
Načrtněte vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
Příklad součet a násobek vektoru v souřadnicích
Jsou dány vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určete souřadnice vektoru \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Vektory: skalární součin
Skalární součin vektorů \vec{u} a \vec{v} označujeme \vec{u}\cdot \vec{v}. Pro vektory \vec{u}, \vec{v} o velikostech \left| \vec{u} \right| a \left| \vec{v} \right|, které spolu svírají úhel \alpha, je skalární součin definován následovně:
\vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
Vlastnosti skalárního součinu
- Výsledkem skalárního součinu dvou vektorů je číslo (neboli skalár).
- Skalární součin nulového vektoru s libovolným jiným vektorem je vždy roven 0.
- Skalární součin vektorů, které jsou na sebe kolmé, je také roven nule.
Výpočet pomocí souřadnic
Máme-li souřadnice vektorů \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), pak hodnota jejich skalárního součinu je:
u_1\cdot v_1+u_2 \cdot v_2
Poznámka: další typy součinu vektorů
Kromě skalárního součinu existují i jiné typy součinu vektorů (vektorový, smíšený), proto je důležité psát o jaký součin se jedná.Příklad: skalární součin vektorů
Určete skalární součin vektorů, jestliže platí: \left| \vec{u} \right|=4, \left| \vec{v} \right|=3 a vektory svírají úhel 60°.
- Vzoreček: \vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
- Dosadíme známé hodnoty: \vec{u}\cdot \vec{v}=4\cdot3\cdot \cos 60°=4\cdot3\cdot\frac{1}{2}=6
Určení úhlu svíraného dvěma vektory
S využitím vztahu pro skalární součin můžeme určit úhel vektorů: \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}
Příklad: úhel svíraný vektory
Určete úhel vektorů \vec{u}=(3;3) a \vec{v}=(2;0).
- Platí \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}.
- Pomocí známých souřadnic vektorů umíme spočítat skalární součin \vec{u}\cdot\vec{v} a velikosti vektorů \left| \vec{u} \right|, \left| \vec{v} \right|:
- \vec{u}\cdot \vec{v}=u_1\cdot v_1+u_2 \cdot v_2=3\cdot2+3\cdot0=6
- \left| \vec{u} \right|=\sqrt{u_1^2 + u_2^2}=\sqrt{3^2+3^2}=\sqrt{18}
- \left| \vec{v} \right|=\sqrt{v_1^2 + v_2^2}=\sqrt{2^2+0^2}=\sqrt{4}
- Dosadíme tyto hodnoty do vztahu pro výpočet \cos \alpha:
- \cos \alpha =\frac {6}{\sqrt{18}\cdot\sqrt{4}}=\frac{6}{3\sqrt{2}\cdot2}=\frac{1}{\sqrt{2}}
- Úhel vektorů je 45°.
Přímka je jednoznačně určena bodem, který na ní leží a směrovým vektorem, což si můžete prakticky vyzkoušet v kapitole Určení přímky.
V rovině i v prostoru lze zapsat přímku jako množinu bodů, které splňují parametrickou rovnici. V rovině umíme pro danou přímku napsat také obecnou rovnici (ale v prostoru ne).
Máme-li přímku popsanou rovnicí, umíme určit vzájemnou polohu dvou přímek nebo vzájemnou polohu přímky a bodu výpočtem.
NahoruPřímky: pojmy
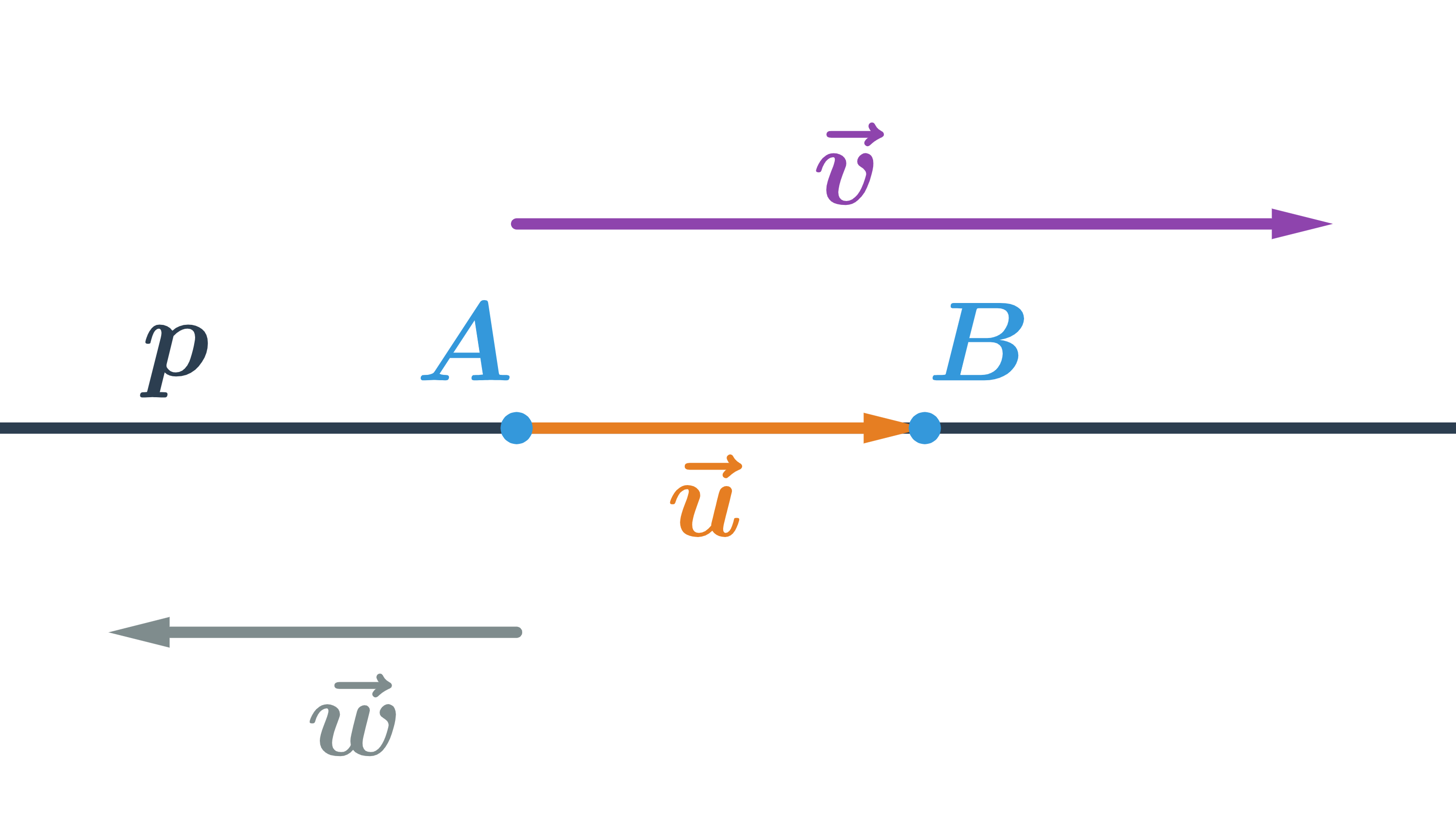
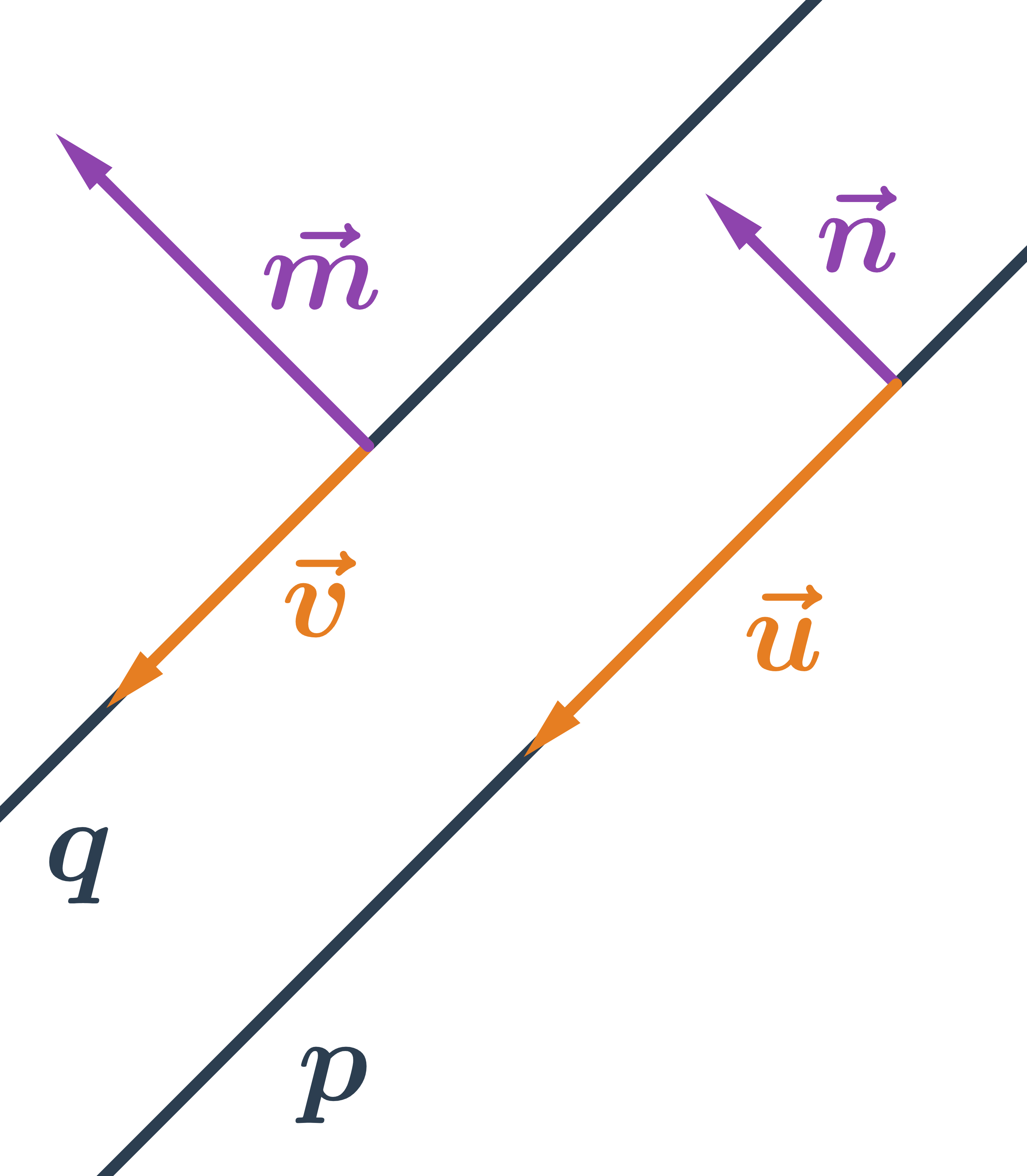
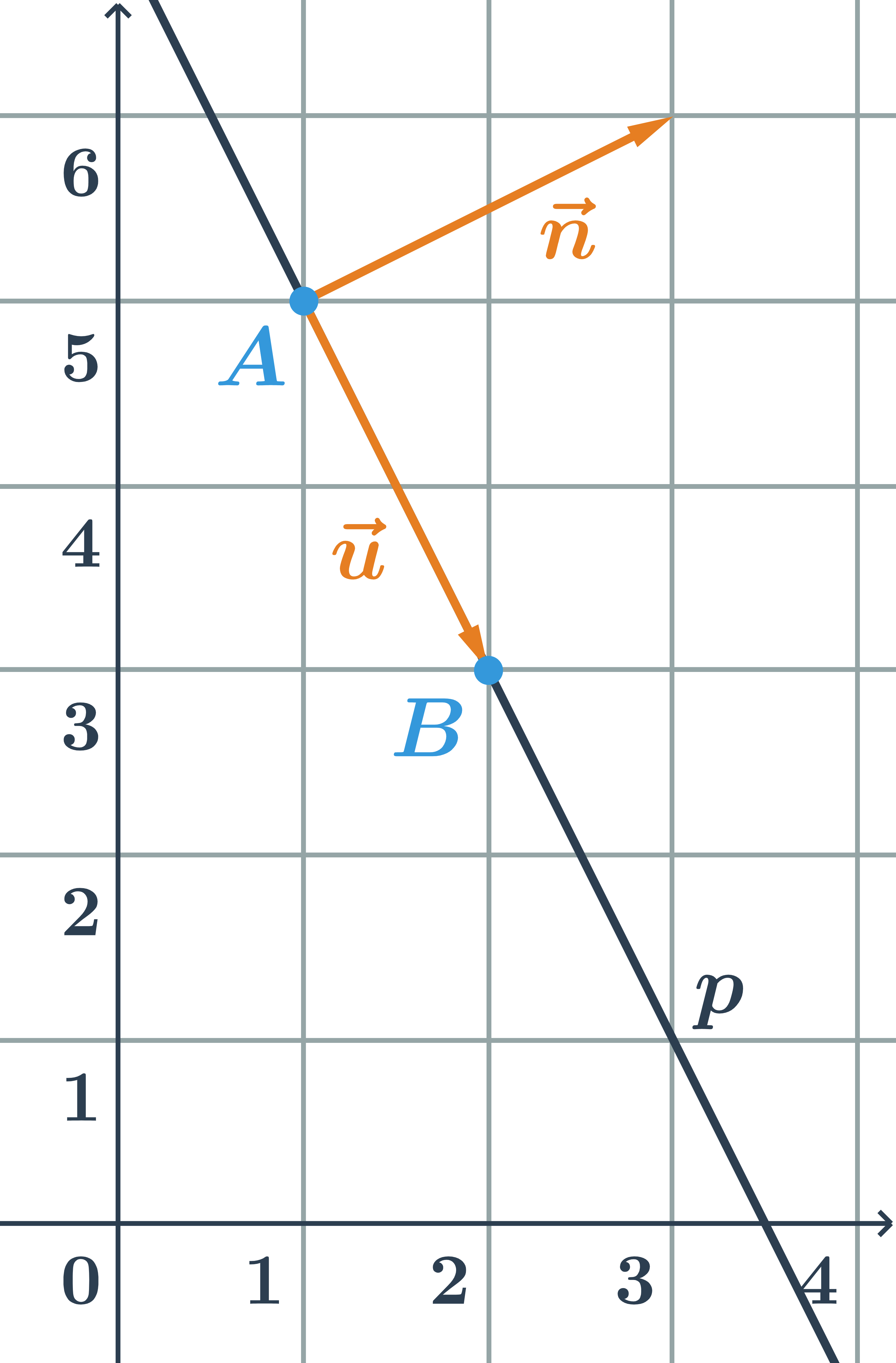
Přímka je jednoznačně určena dvěma body, na obrázku je přímka p určená body A a B. Každý vektor, který je rovnoběžný s vektorem \overrightarrow{AB} se nazývá směrový vektor přímky p. Kterýkoliv z vektorů na obrázku je směrový vektor přímky p. K tomu, abychom určili konkrétní přímku ještě potřebujeme znát jeden bod na přímce (přímka p na obrázku je určena bodem A a kterýmkoliv z vektorů \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice přímky
Přímka určená bodem A=[a_1;a_2] a vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr.
Jak souvisí hodnota parametru t s polohou bodu na přímce
- Přímka p je určená bodem A a vektorem \vec{u}=\overrightarrow{AB}, tedy p:X=A+t\vec{u}
- Pro hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pro hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pro hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pro hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (střed úsečky AB)
- Pro hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
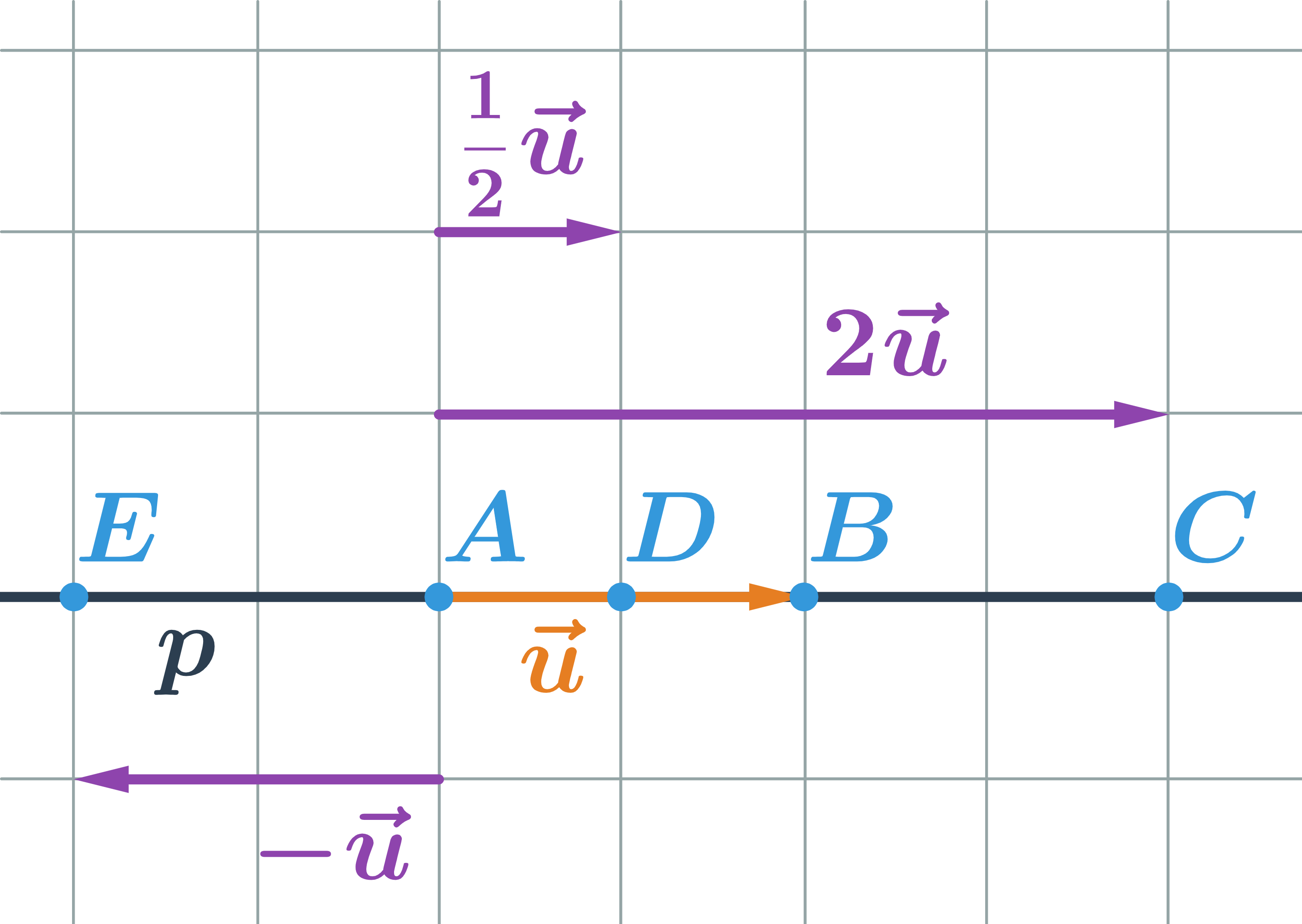
- Každá hodnota parametru určuje jeden bod na přímce, pro určení celé přímky tedy potřebujeme všechna reálná čísla, proto píšeme t\in\mathbb{R}.
- Body, které leží na úsečce AB (tedy body ležící mezi body A a B), vyjádříme parametricky, pokud do rovnice X=A+t\vec{u} dosadíme hodnoty parametru t splňující 0\leq t\leq1.
Obecná rovnice přímky
Každý vektor kolmý k přímce p se nazývá normálový vektor přímky p. Obecná rovnice přímky je rovnice ve tvaru: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.
Souřadnice směrového a normálového vektoru přímky p
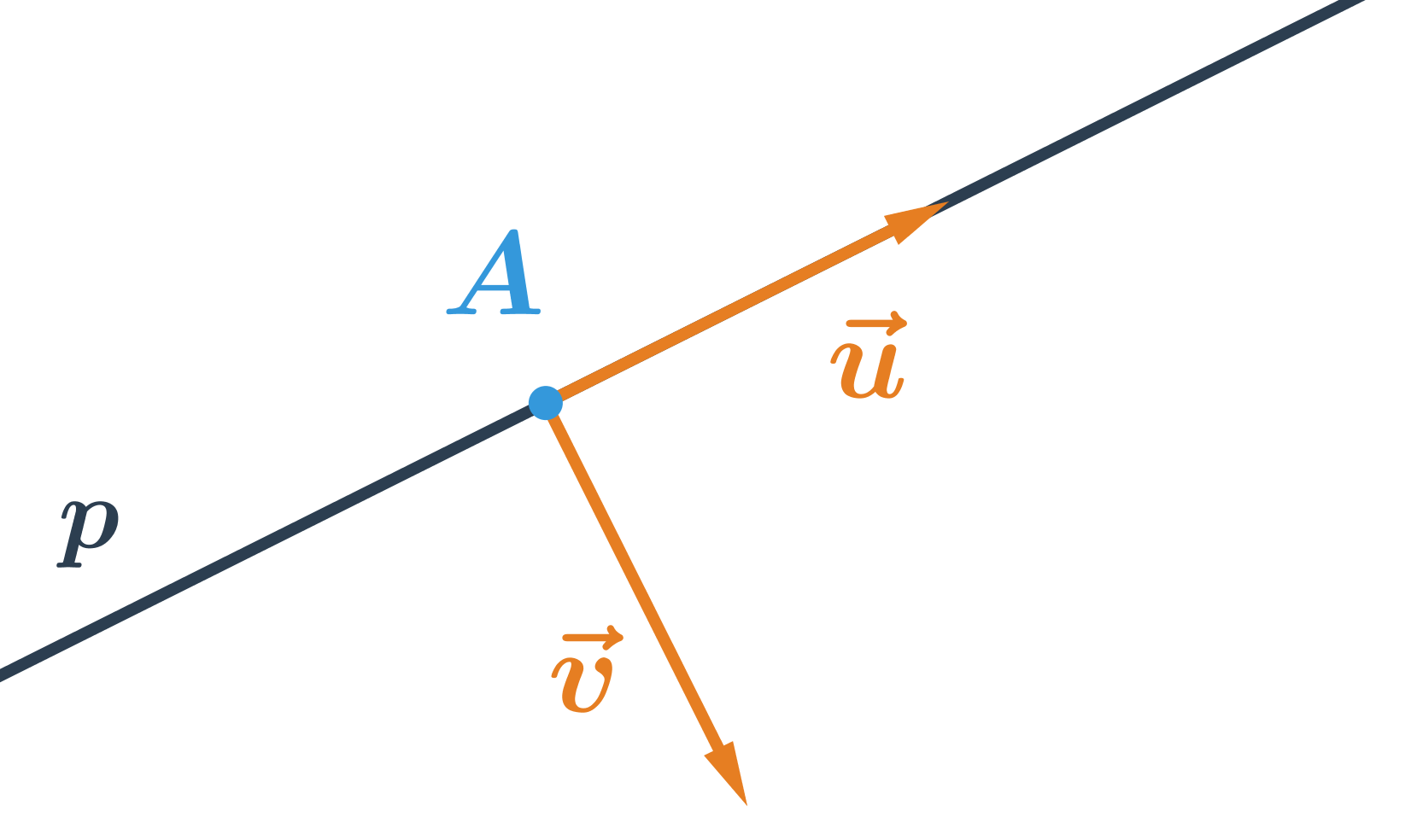
- Pro přímku danou obecnou rovnicí ax+by+c=0:
- \vec{v} je normálový vektor přímky p, jeho souřadnice jsou: \vec{v}=(a;b)
- \vec{u} je směrový vektor přímky p, protože je to vektor kolmý k vektoru \vec{v}=(a;b), jeho souřadnice jsou: \vec{u}=(-b;a)
- Pro přímku danou parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je směrový vektor přímky p, jeho souřadnice jsou: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor přímky p, protože je to vektor kolmý k vektoru \vec{u}=(u_1;u_2), jeho souřadnice jsou: \vec{v}=(-u_2;u_1)
Obecná rovnice přímky rovnoběžné s osou x
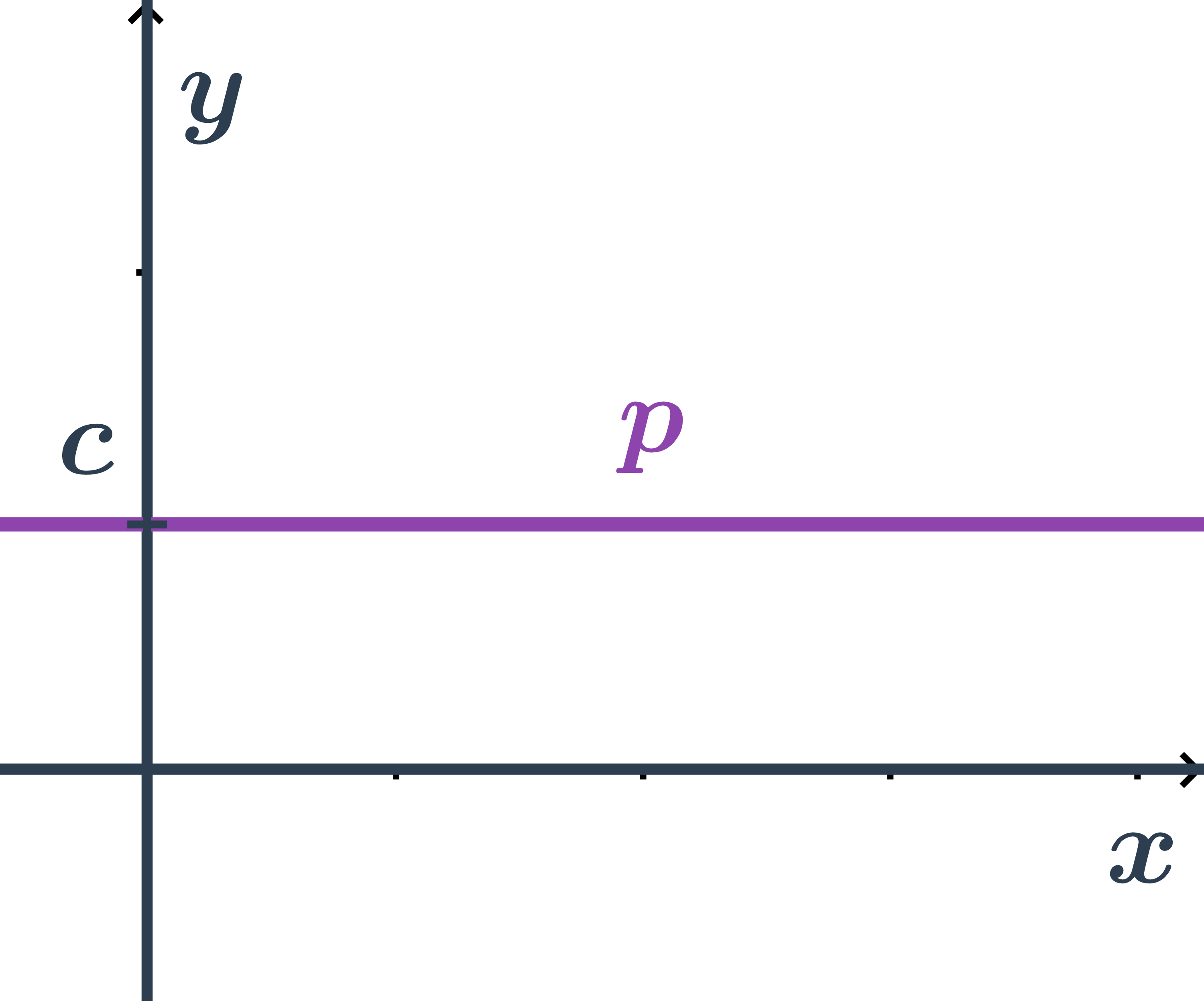
- Pro všechny body ležící na přímce je druhá souřadnice stejná a to: y=c
- Tedy přímka má obecnou rovnici: y-c=0
Obecná rovnice přímky rovnoběžné s osou y
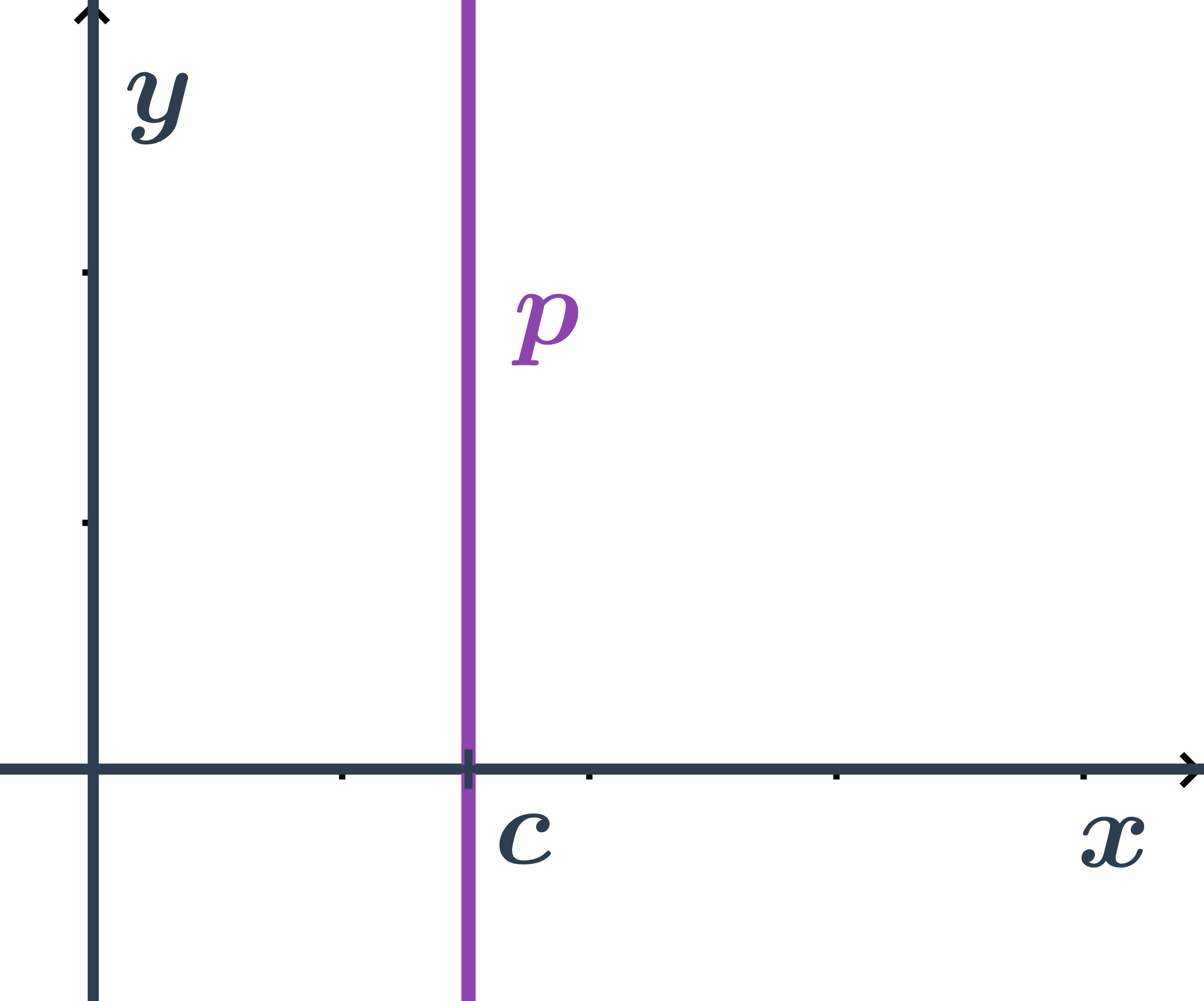
- Pro všechny body ležící na přímce je první souřadnice stejná a to: x=c
- Tedy přímka má obecnou rovnici: x-c=0
Bod a přímka
Bod M=[m_1;m_2] leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky. Pokud je přímka daná obecnou rovnicí ax+by+c=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c=0 Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t. (Více o vzájemné poloze bodu a přímky.)
Obecná rovnice přímky, která prochází počátkem
- Přímka prochází bodem O=[0;0], tedy souřadnice počátku splňují její obecnou rovnici ax+by+c=0.
- Dosadíme souřadnice bodu O a zkusíme zjistit nějaké informace o konstantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Proto přímka, která prochází počátkem má obecnou rovnici ax+by=0.
Dvě přímky
Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.
Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
Více o vzájemné poloze dvou přímek.
Přímka v prostoru
Přímku v prostoru nelze vyjádřit obecnou rovnicí. Parametrickou rovnici přímky v prostoru určíme obdobně jako v rovině na základě znalosti souřadnic směrového vektoru a jednoho bodu na přímce.
NahoruUrčení přímky
Přímka je obvykle určena bodem a vektorem, případně dvěma body.
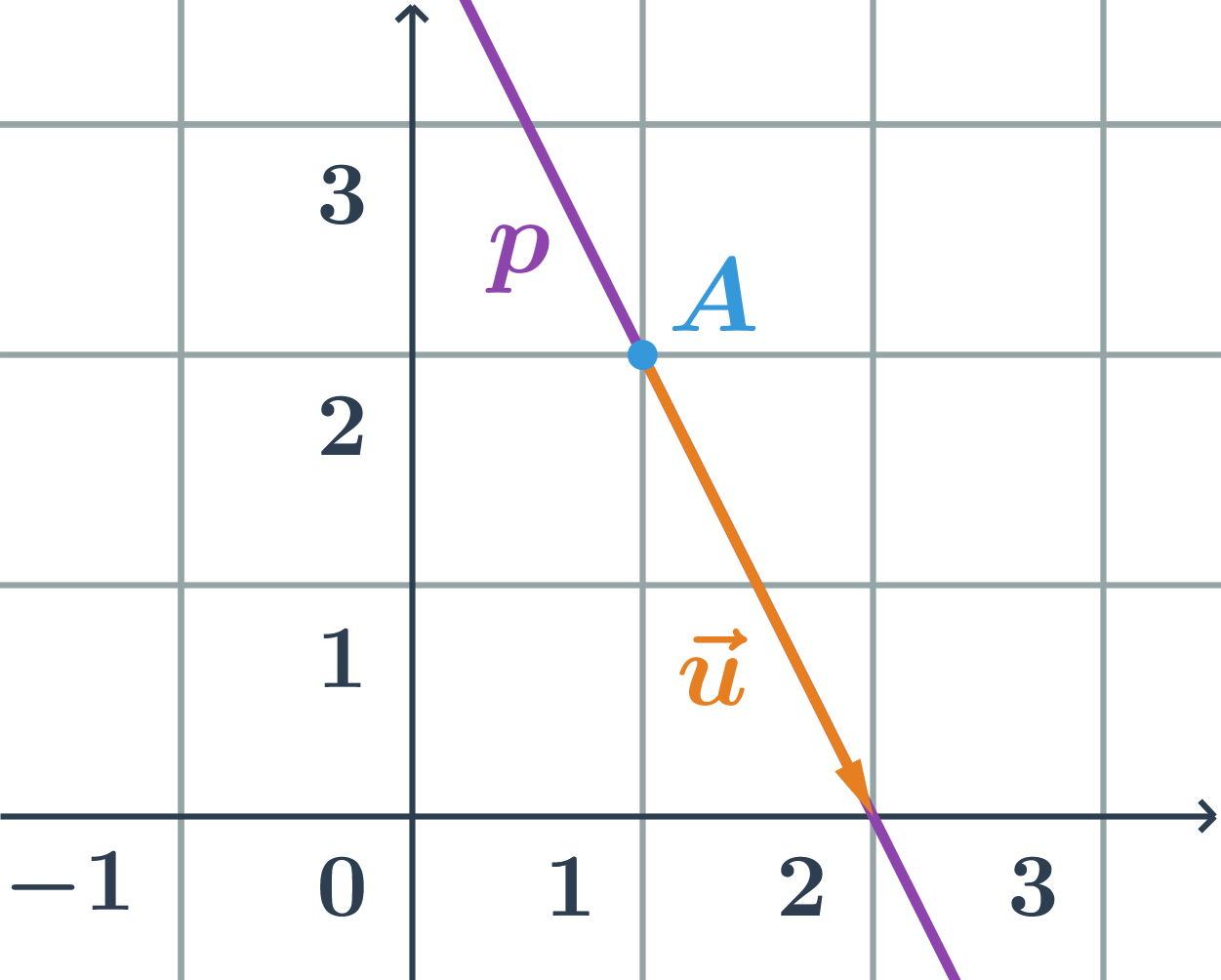
Přímka p na obrázku je určena například:
- bodem A=[1;2], který na ní leží a směrovým vektorem \vec{u}=(1;-2)
- nebo dvěma různými body [1;2] a [2;0], které na ní leží
Parametrické rovnice přímky v rovině
Přímka určená bodem A=[a_1;a_2] a směrovým vektorem \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit p:X=A+t\vec{u}, číslo t nazýváme parametr. Pokud známe dva body A, B ležící na přímce, směrový vektor je například \vec{u}=\overrightarrow{AB}.
Parametrické rovnice přímky p určené body A=[1;2] a B=[3;1]
- přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
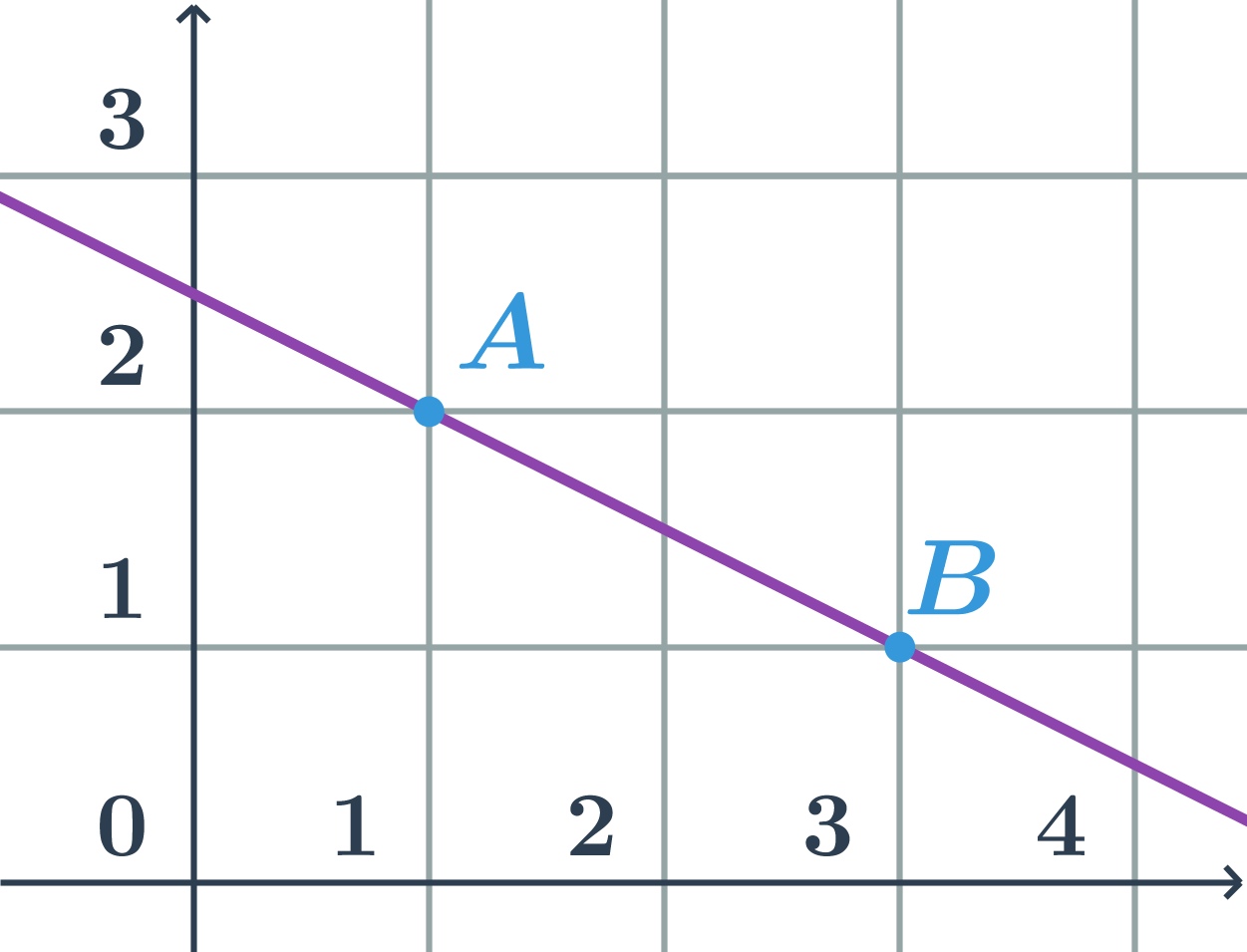
Různé parametrické rovnice přímky na obrázku
Určíme souřadnice směrového vektoru a jednoho bodu na přímce:
- například: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Další možnost parametrického vyjádření:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice přímky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Pro určení parametrických rovnic můžeme vybrat kterýkoliv bod ležící na přímce a jakýkoliv zápis souřadnic směrového vektoru, možností jak parametricky vyjádřit danou přímku je tedy nekonečně mnoho.
Obecná rovnice přímky v rovině
Obecná rovnice přímky v rovině má tvar: ax+by+c=0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý k dané přímce, tedy i kolmý ke směrovému vektoru přímky.
Obecná rovnice přímky p určené body A=[1;5] a B=[2;3]
- Přímka p je určená bodem A a směrovým vektorem \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;-2), tedy například vektor \vec{n}=(2;1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 2x+y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Obecná rovnice přímky p je: 2x+y-7=0
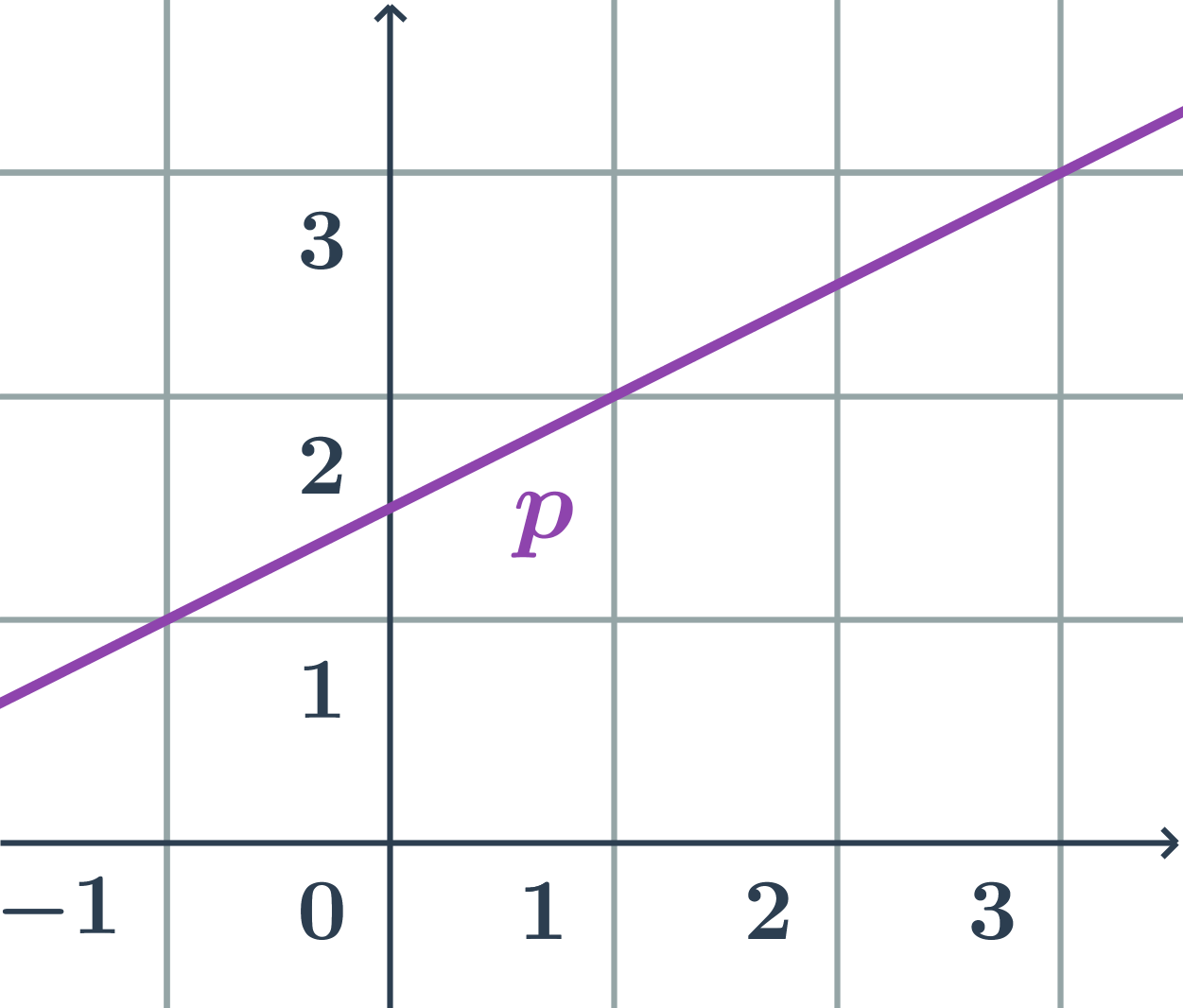
Obecná rovnice přímky dané parametricky
Určete obecnou rovnici přímky p, která je dána následující parametrickou soustavou rovnic: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Přímka p je určená bodem A=[1;4] a směrovým vektorem \vec{u}=(2;6).
- Souřadnice směrového vektoru můžeme upravit na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý k vektoru \vec{u}=(1;3), tedy například vektor \vec{n}=(3;-1).
- Souřadnice normálového vektoru jsou konstanty a a b v obecné rovnici přímky. Obecná rovnice má tvar: 3x-y+c=0
- Konstantu c dopočítáme dosazením souřadnic bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Obecná rovnice přímky p je: 3x-y+1=0
Parametrické vyjádření přímky dané obecnou rovnicí
Určete parametrické vyjádření přímky p, která má obecnou rovnici: 3x-2y+4=0.
- Přímka p má normálový vektor \vec{n}=(3;-2).
- Směrový vektor je kolmý k vektoru \vec{n}=(3;-2), tedy například vektor \vec{u}=(2;3).
- Určíme jeden bod na přímce p : jednu souřadnici můžeme zvolit, například x=0, druhou souřadnici dopočítáme: 3\cdot0-2y+4=0\Rightarrow y=2
- Z obecné rovnice jsme tedy zjistili, že na přímce leží bod A=[0;2].
- Parametrické vyjádření přímky p je: \begin{array}{rrl}x&=&0+2t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
Směrnicový tvar rovnice přímky
Každou přímku p, která není rovnoběžná s osou y, můžeme vyjádřit ve tvaru: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar se nazývá směrnicový tvar rovnice přímky.
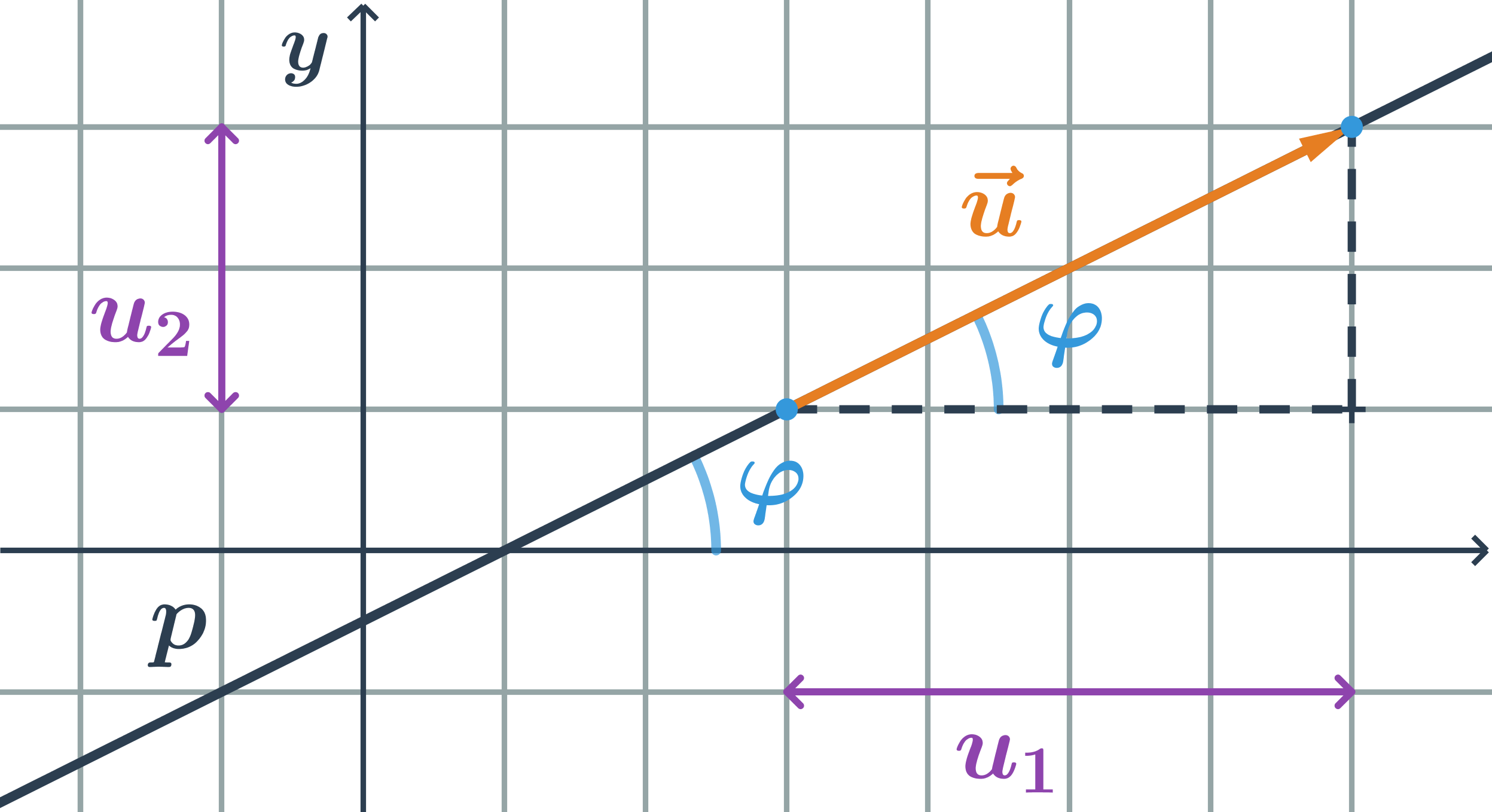
Konstanta k se nazývá směrnice a její hodnota je tangens úhlu, který svírá přímka p s kladnou částí osy x, tedy: k=\tan \varphi.
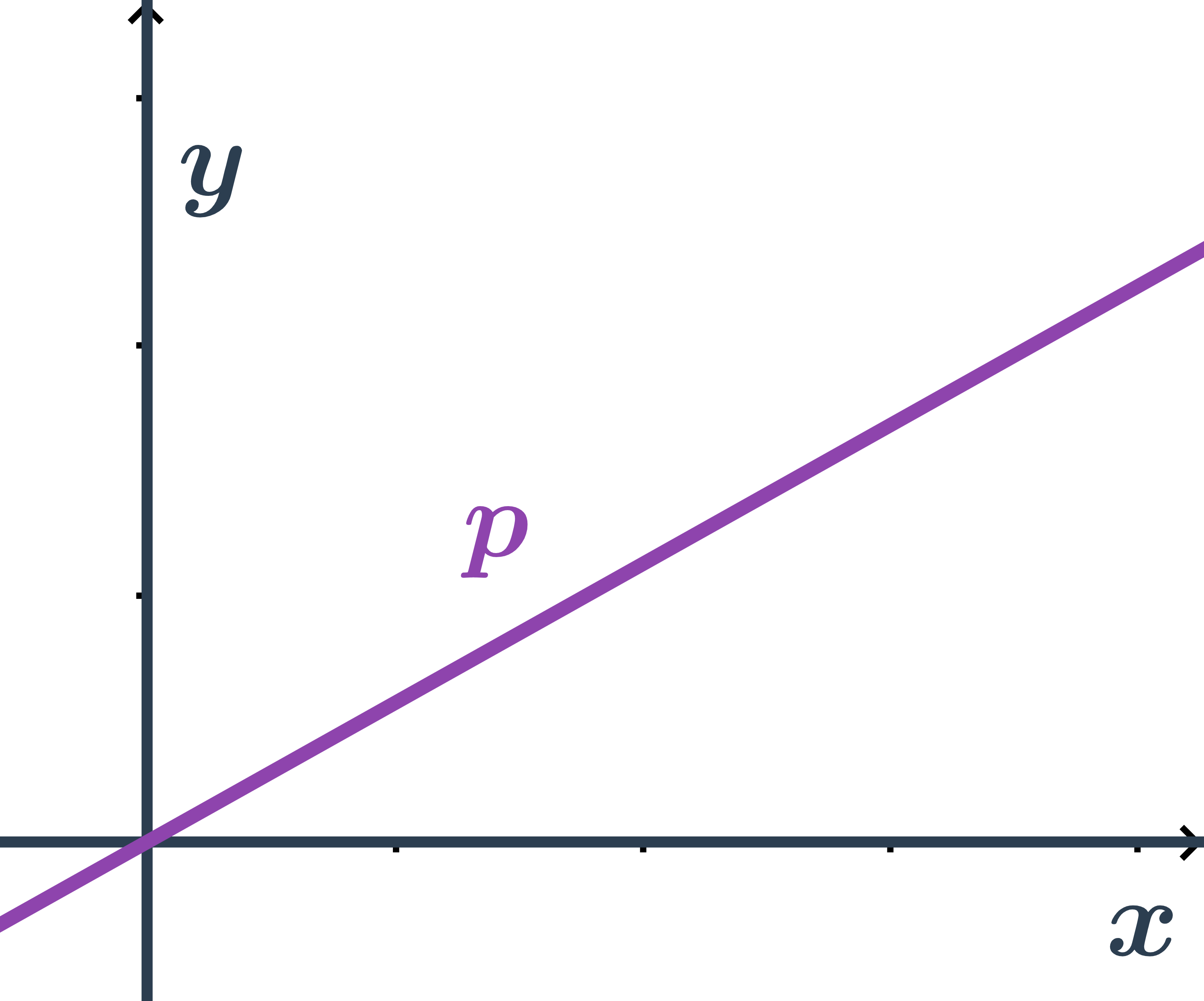
Konstanta q určuje průsečík přímky p s osou y, souřadnice průsečíku jsou: P=[0;q]. Pro přímku, která prochází počátkem, je q=0, tedy směrnicový tvar její rovnice je: y=kx.
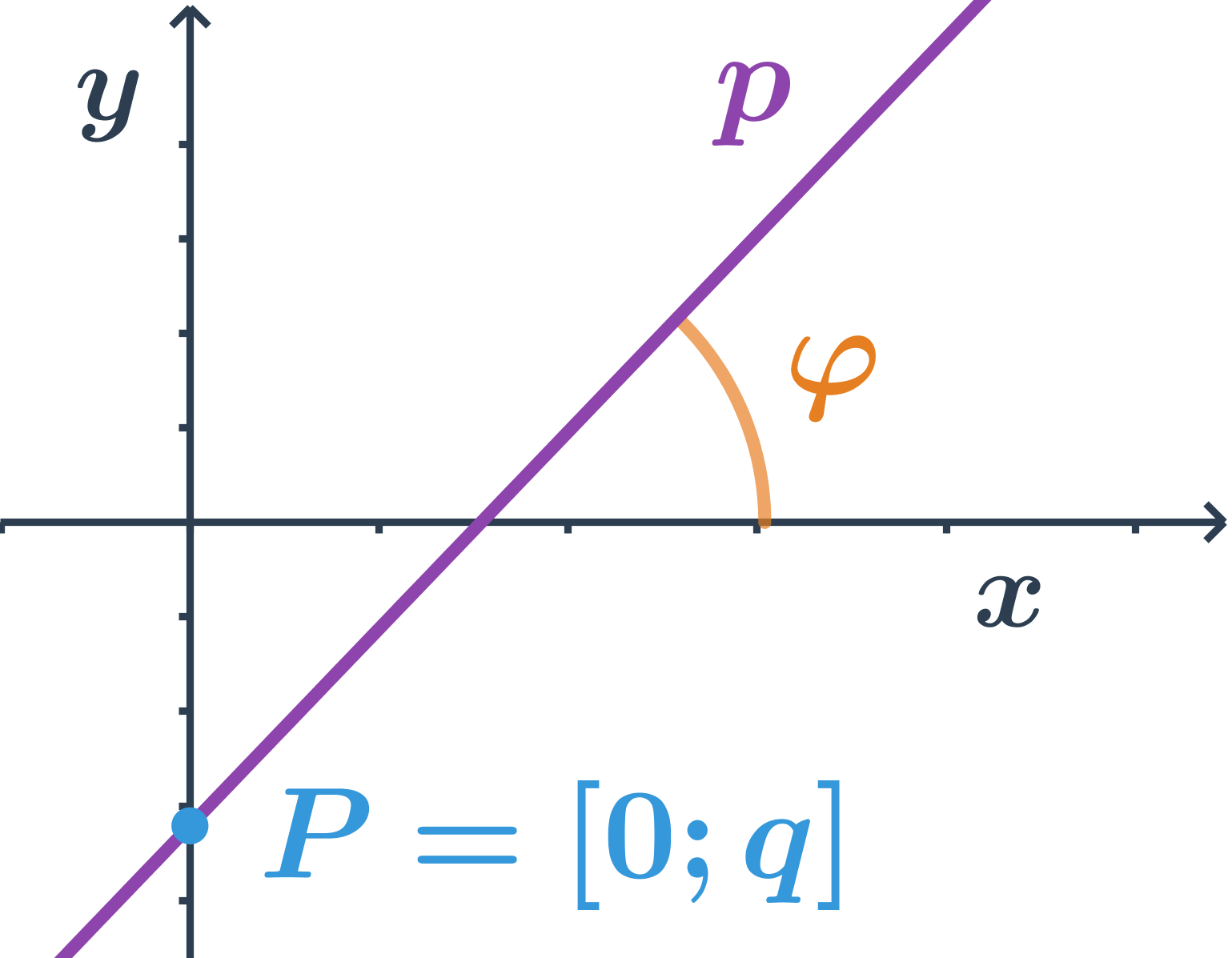
Směrnice přímky, která má směrový vektor \vec{u}=(u_1;u_2), je podíl souřadnic směrového vektoru:
k=\tan \varphi=\frac{u_2}{u_1}
Různé hodnoty směrnice
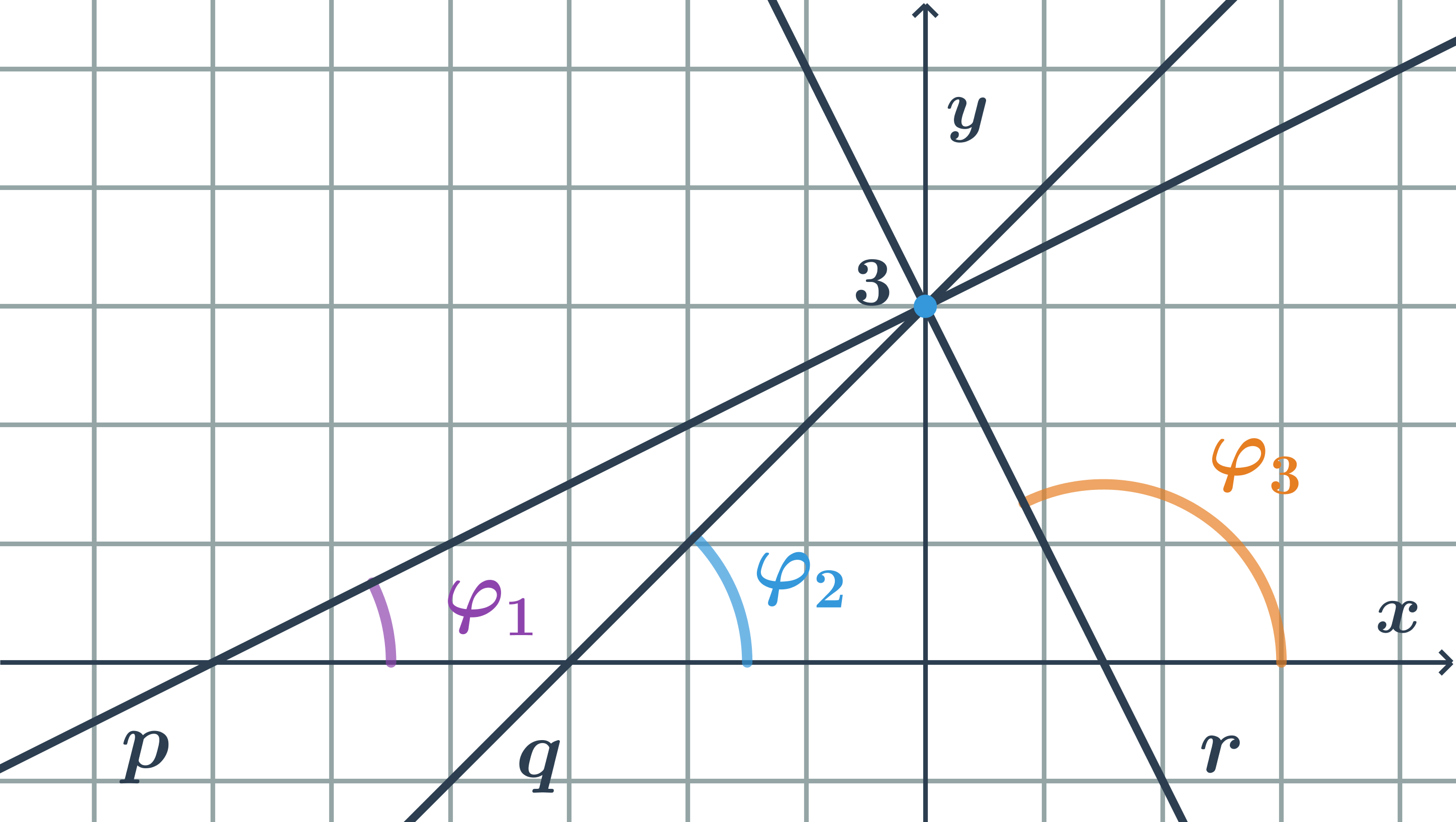
- Směrnice přímky p: k_1=\tan \varphi_1=\frac{1}{2}
- Směrnice přímky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Směrnice přímky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím větší odchylka od kladné části osy x, tím větší hodnota směrnice k.
- Přímka rovnoběžná s osou x svírá s kladnou částí osy x úhel 0^\circ a tedy její směrnice je \tan 0^\circ=0.
- Přímka rovnoběžná s osou y svírá s kladnou částí osy x úhel 90^\circ a pro tuto hodnotu funkce tangens není definována, proto nemůžeme určit směrnici.
Směrnicový tvar přímky z obrázku
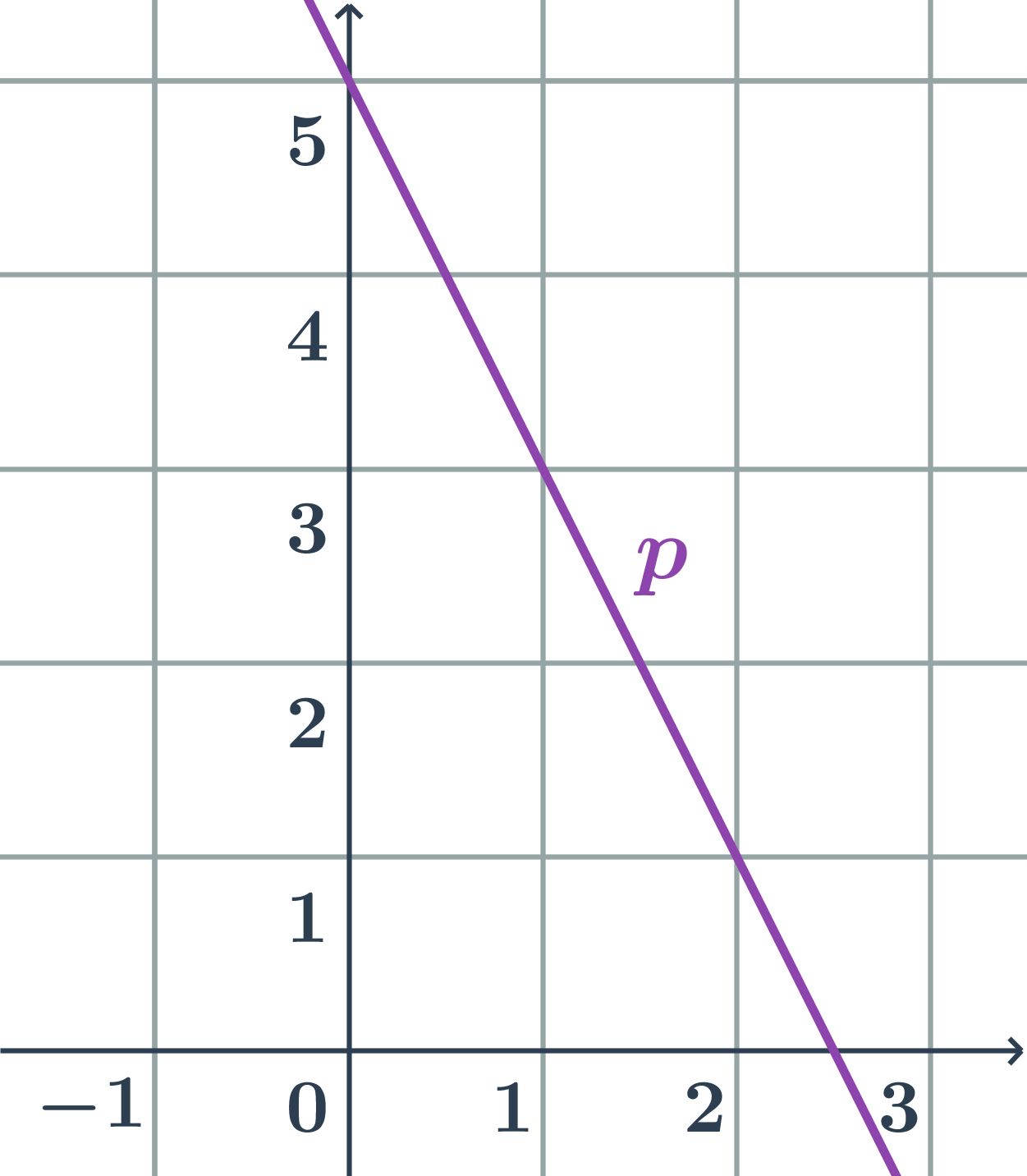
Hledáme směrnicový tvar rovnice přímky: y=kx+q.
- Pro nalezení konstant k a q určíme směrový vektor přímky p a průsečík s osou y.
- směrový vektor přímky: \vec{u}=(1;-2)
- směrnice: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- průsečík přímky s osou y: P=[0;5]
- konstanta q=y_P=5
- přímka na obrázku má směrnicový tvar y=-2x+5
Dvě přímky
Dvě rovnoběžné přímky svírají s kladnou částí osy x stejný úhel, mají tedy stejnou směrnici.
Pro dvě k sobě kolmé přímky platí:
- přímka p má směrový vektor \vec{u}=(u_1;u_2) a tedy směrnici: k=\frac{u_2}{u_1}
- každá přímka k ní kolmá má směrový vektor (-u_2;u_1) a tedy směrnici: \frac{u_1}{-u_2}=-\frac{1}{k}
Vzájemná poloha přímek v rovině
Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné. Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.
Rovnoběžky zadané parametrickými rovnicemi
Určete vzájemnou polohu dvou přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(3;1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[-3;2].
- Ověříme, že tento bod neleží na přímce q dosazením souřadnic bodu A do rovnic přímky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšly různé hodnoty parametru s, takže bod A neleží na q \Rightarrow přímky nejsou totožné
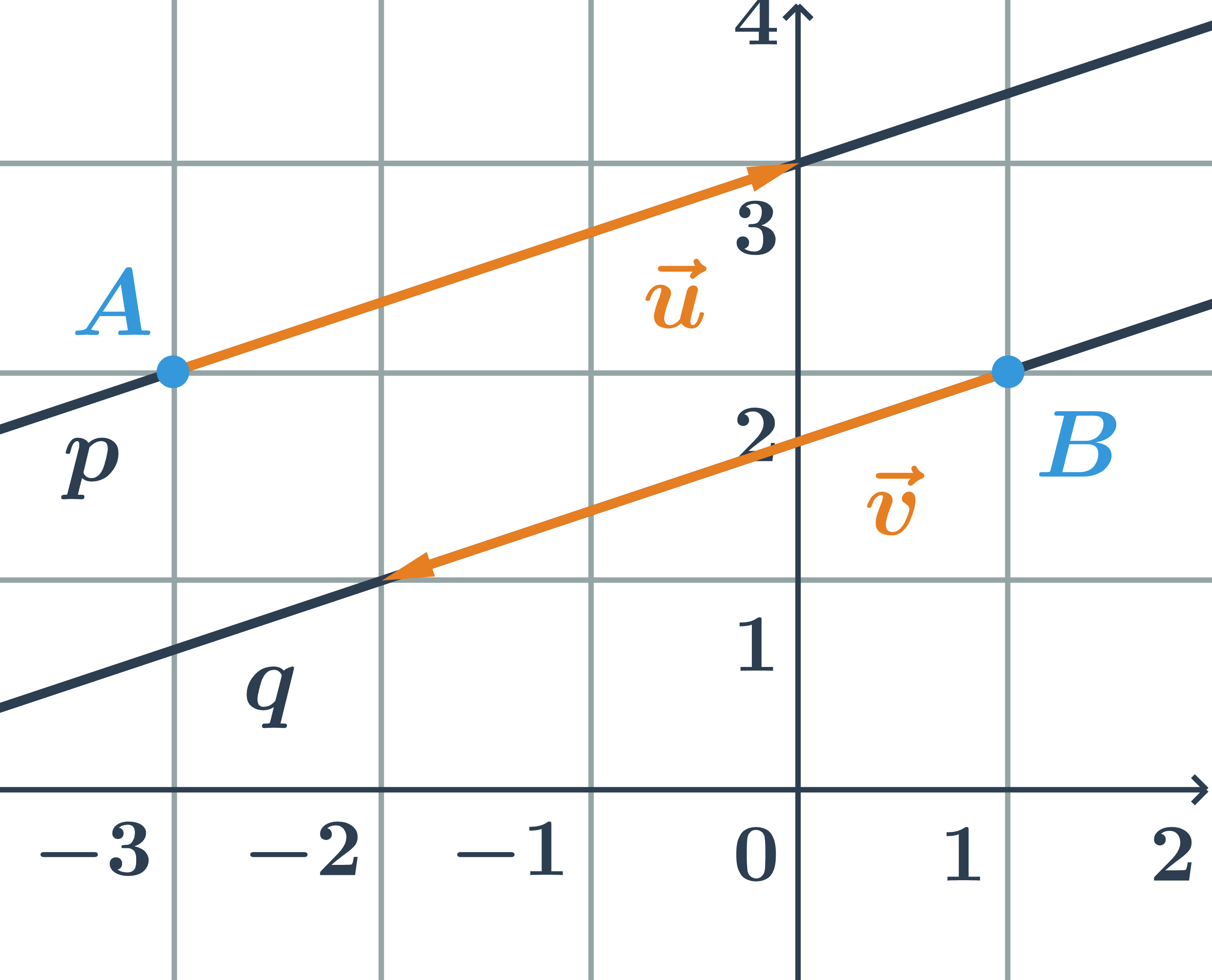
Rovnoběžky zadané obecnými rovnicemi
Určete vzájemnou polohu dvou přímek daných obecnými rovnicemi p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(4;2)
- Přímky p a q jsou rovnoběžné, protože jejich normálové vektory jsou kolineární.
- Ověříme, že přímky nejsou totožné. Stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce p leží například bod A=[0;1].
- Ověříme, zda A leží na p dosazením souřadnic bodu A do rovnice přímky p: 4\cdot0+2\cdot1+3\neq 0
- A nesplňuje rovnici, takže neleží na přímce q \Rightarrow přímky nejsou totožné
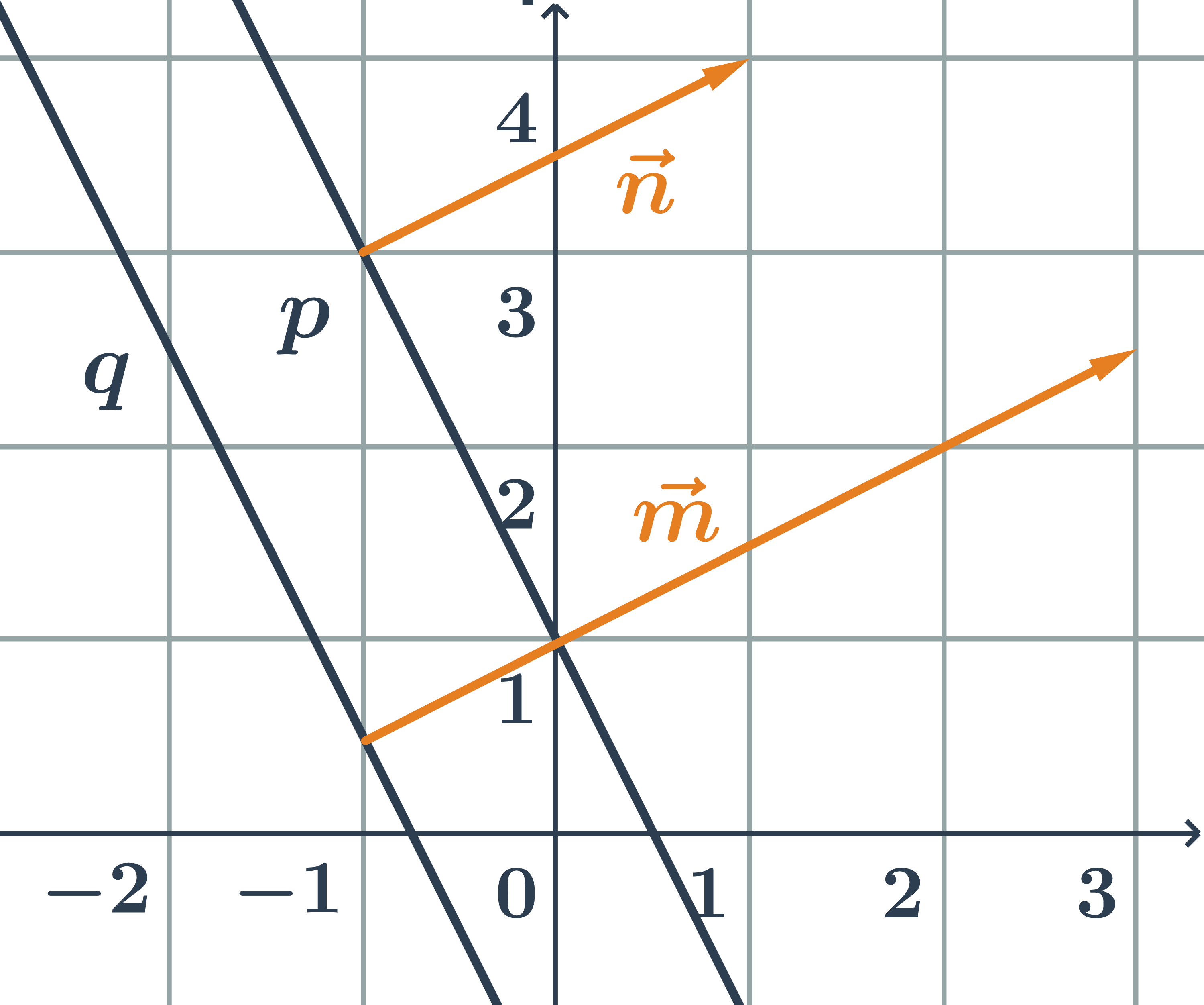
Různoběžky zadané parametrickými rovnicemi
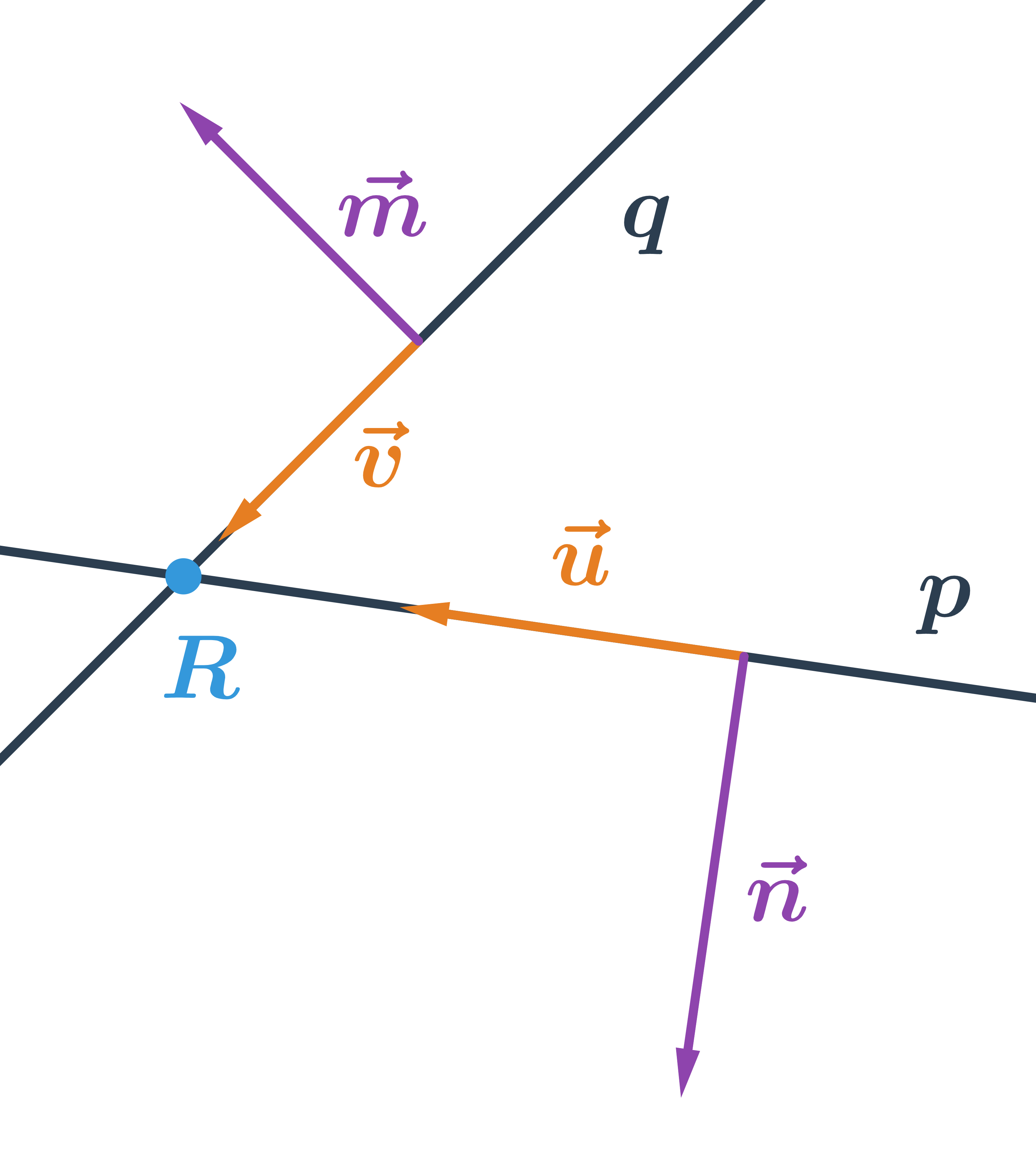
Určete vzájemnou polohu přímek p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
- směrový vektor přímky p:\hspace{0.25cm}\vec{u}=(1;2)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární.
Průsečík přímek splňuje rovnice obou přímek, tedy každou z jeho souřadnic lze vyjádřit dvěma způsoby, dostáváme následující soustavu rovnic: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
- Soustavu můžeme vyřešit sečtením obou rovnic: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
- Výsledný parametr t dosadíme do parametrických rovnic kterékoliv z přímek a dostaneme souřadnice x,y průsečíku.
Průsečík přímek p a q je bod R=[-2;1].
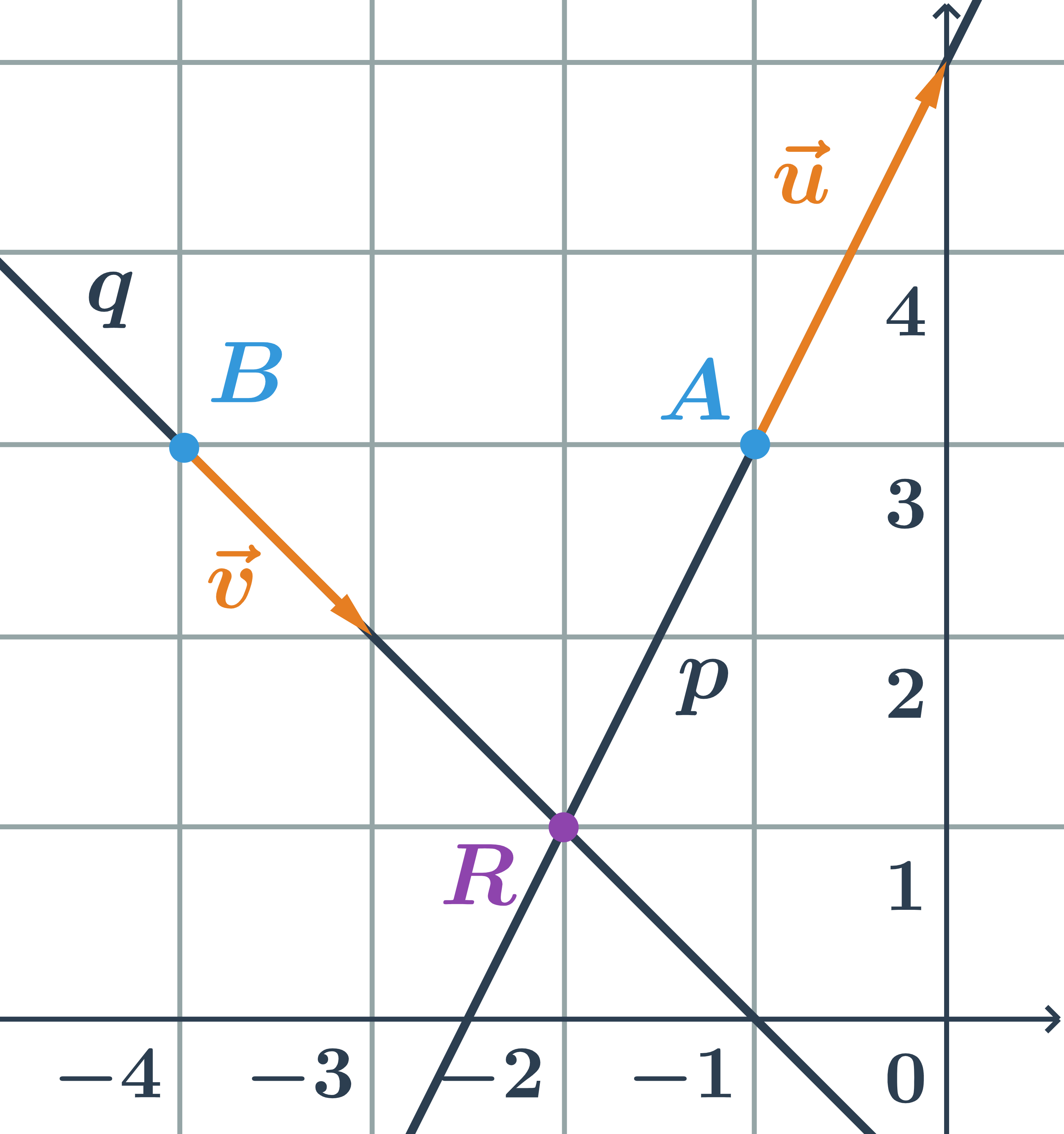
Různoběžky zadané obecnými rovnicemi
Určíme vzájemnou polohu dvou přímek zadaných obecnými rovnicemi p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor přímky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Přímky p a q jsou různoběžné, protože jejich normálové vektory nejsou kolineární.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice jsou řešením soustavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Můžeme vyřešit sečtením obou rovnic: 3x=0\Rightarrow x=0
- Průsečík přímek p a q je bod R=[0;1]
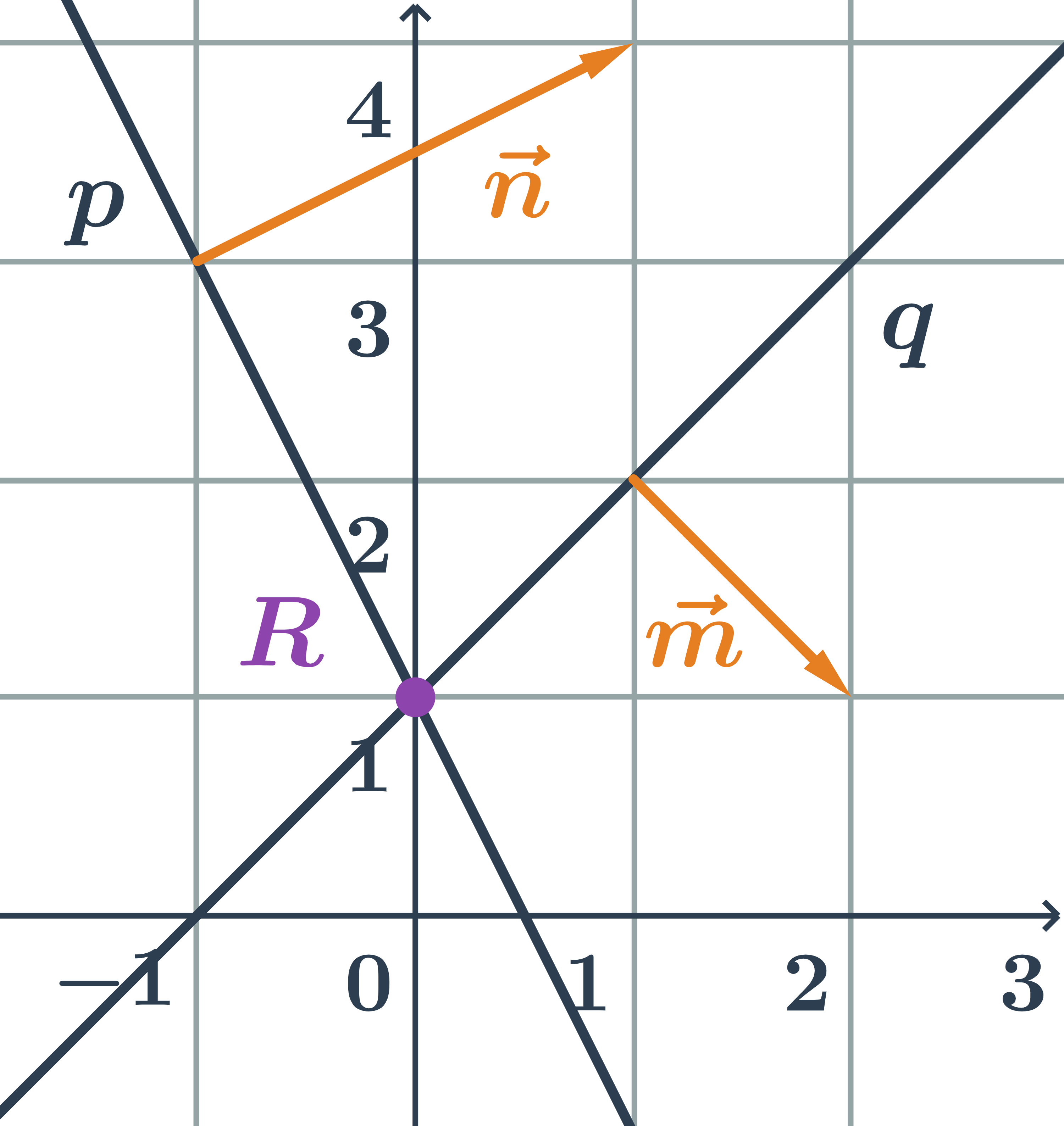
Přímka daná obecnou rovnicí a druhá parametricky – první příklad
Určete vzájemnou polohu přímek p,q zadaných takto:
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(2;-1)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(-2;-4)
- Přímky p a q jsou rovnoběžné, protože jejich směrové vektory jsou kolineární. Proto normálový vektor jedné přímky je kolmý ke směrovému vektoru druhé přímky.
- Ověříme, že přímky nejsou totožné: stačí určit, zda bod, který leží na jedné přímce neleží na přímce druhé.
- Na přímce q leží například bod B=[3;2].
- Na přímce p tento bod neleží, což zjistíme dosazením souřadnic bodu B do rovnice přímky: 2\cdot3-2+3\neq 0
- Bod B nesplňuje rovnici, takže neleží na přímce p \Rightarrow přímky nejsou totožné
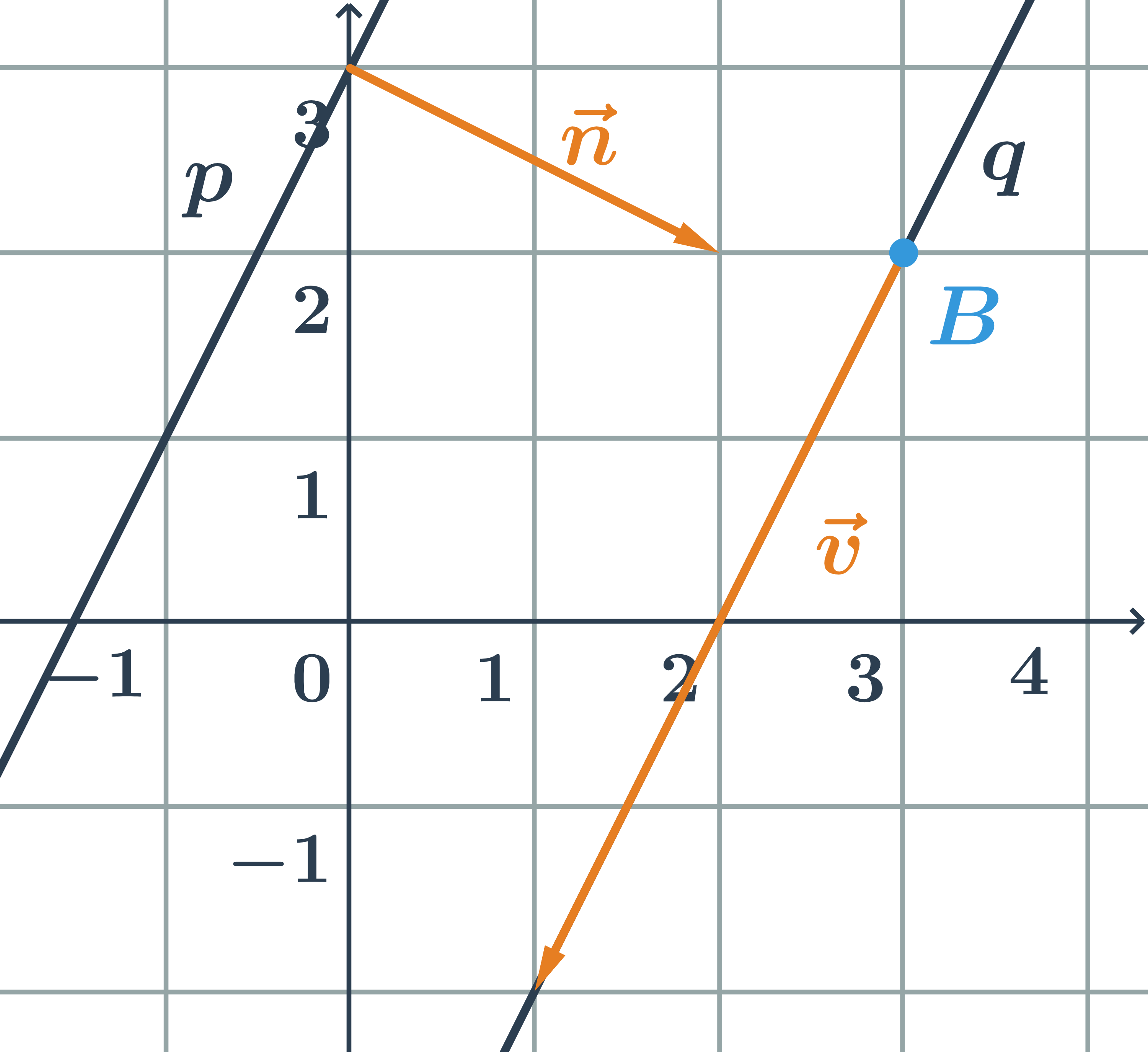
Přímka daná obecnou rovnicí a druhá parametricky – druhý příklad
Určete vzájemnou polohu přímek p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor přímky p:\hspace{0.25cm}\vec{n}=(1;-3)
- směrový vektor přímky q:\hspace{0.25cm}\vec{v}=(1;2)
- Přímky p a q jsou různoběžné, protože jejich směrové vektory nejsou kolineární. Vyplývá z toho, že normálový vektor jedné přímky není kolmý ke směrovému vektoru druhé přímky.
- Průsečík přímek splňuje rovnice obou přímek, tedy jeho souřadnice najdeme tak, že parametrické vyjádření přímky q dosadíme do obecné rovnice přímky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Průsečík přímek p a q je bod R=[3;2]
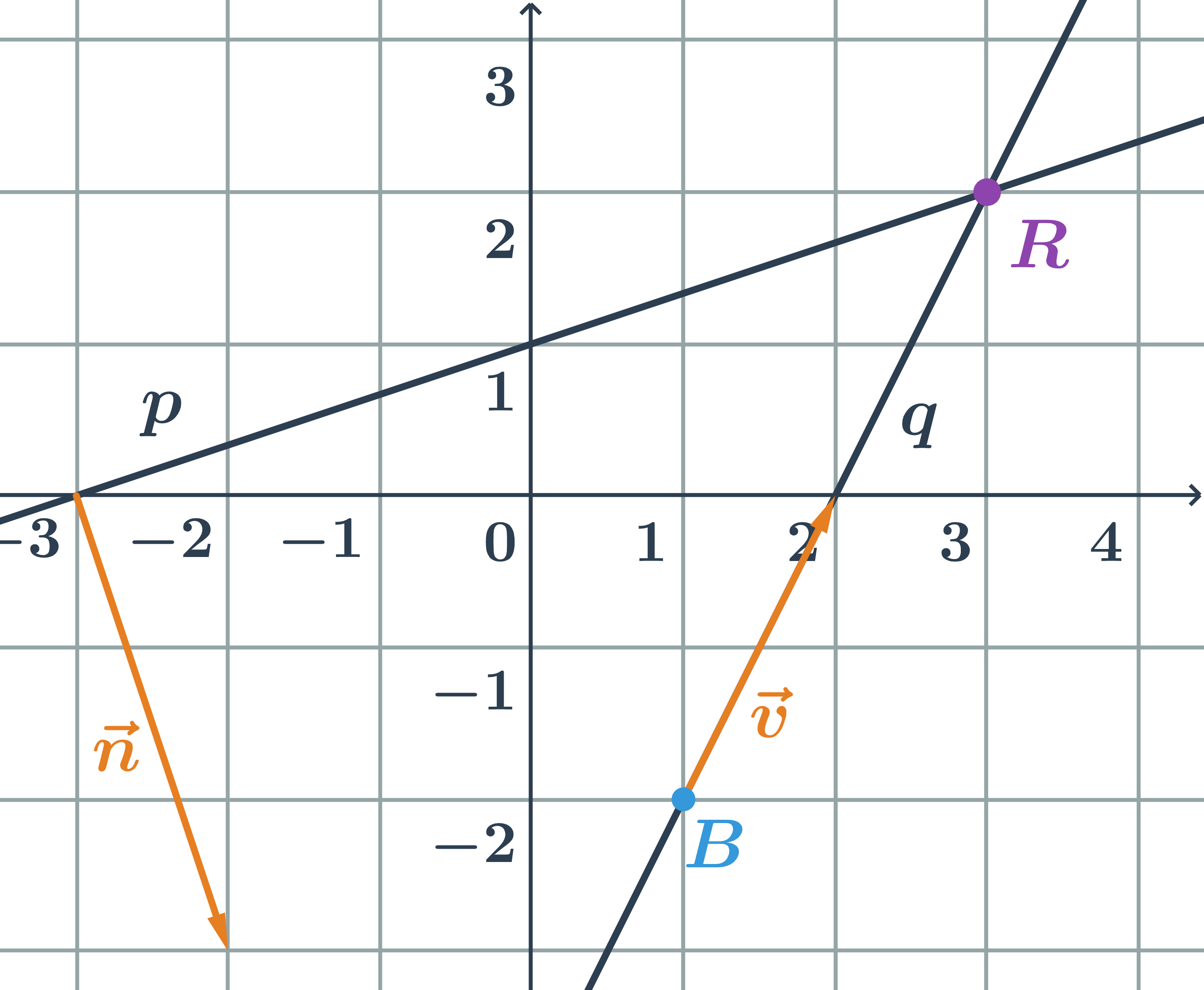
Souvislost počtu společných bodů přímek s počtem řešení soustavy rovnic
Pro určení společného bodu (bodů) dvou přímek, vždy řešíme soustavu rovnic. Tato soustava může mít:
- jedno řešení – přímky jsou různoběžné
- žádné řešení – přímky jsou rovnoběžné
- nekonečně mnoho řešení – přímky jsou totožné
Počet společných bodů – první příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno řešení \Rightarrow různoběžné přímky
Počet společných bodů – druhý příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žádné řešení \Rightarrow různé rovnoběžné přímky
Počet společných bodů – třetí příklad
Hledáme průsečík(y) přímek p,q zadaných jako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjádření do obecné rovnice a řešíme soustavu rovnic:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečně mnoho řešení \Rightarrow totožné přímky
Vzájemná poloha přímky a bodu v rovině
Bod leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky.
- Pokud je přímka daná obecnou rovnicí, po dosazení souřadnic bodu, který na přímce leží, do rovnice přímky nastane rovnost.
- Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t.
Bod a přímka daná obecnou rovnicí
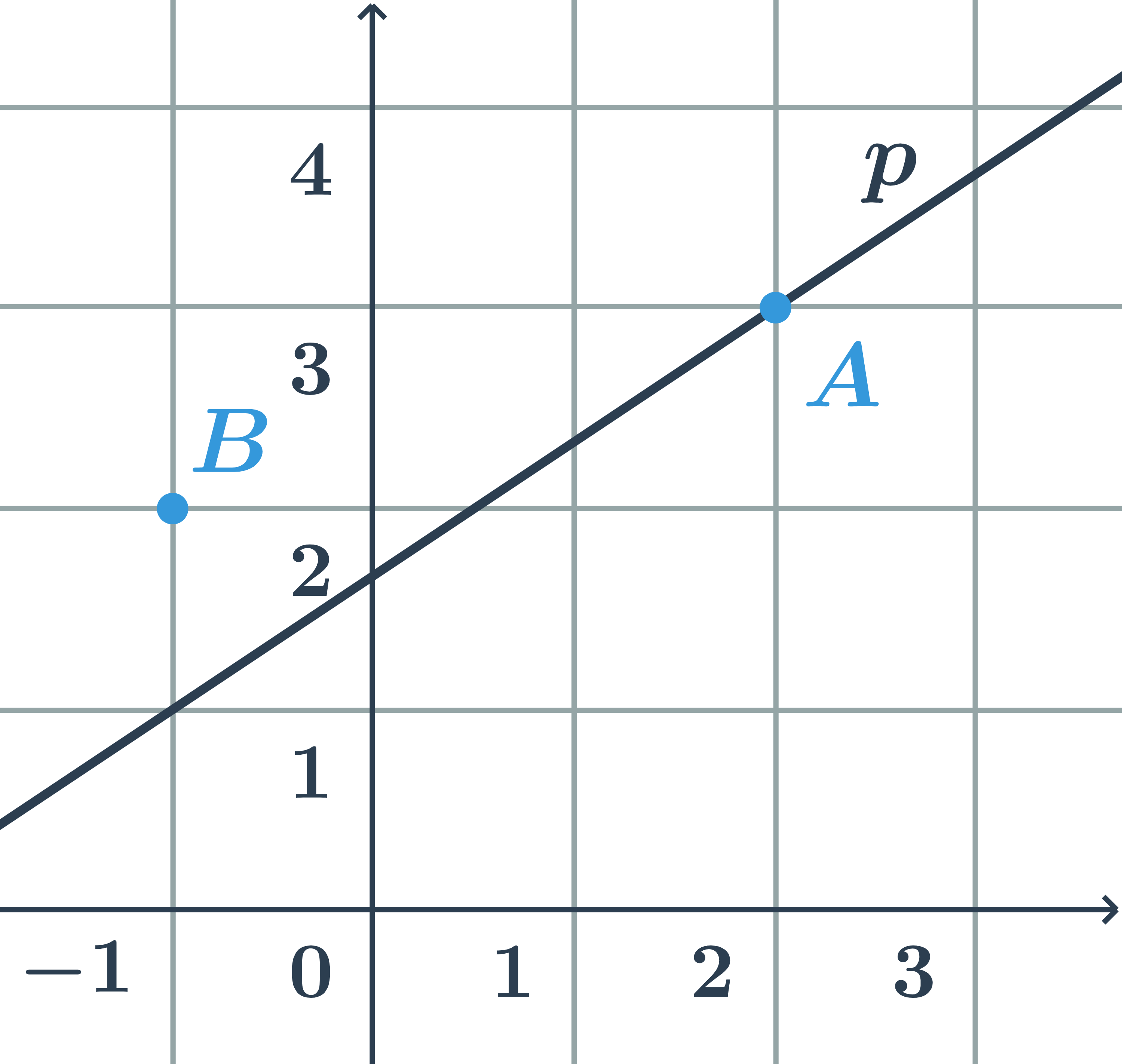
Určete, zda body A=[2;3] a B=[-1;2] leží na přímce p:2x-3y+5=0.
- Do rovnice přímky dosadíme souřadnice bodu A=[2;3]:
- 2\cdot 2-3\cdot3+5=0 \Rightarrow bod A leží na přímce p
- Do rovnice přímky dosadíme souřadnice bodu B=[-1;2]:
- 2\cdot (-1)-3\cdot2+5=-3 \Rightarrow bod B neleží na přímce p
Bod a přímka daná parametricky
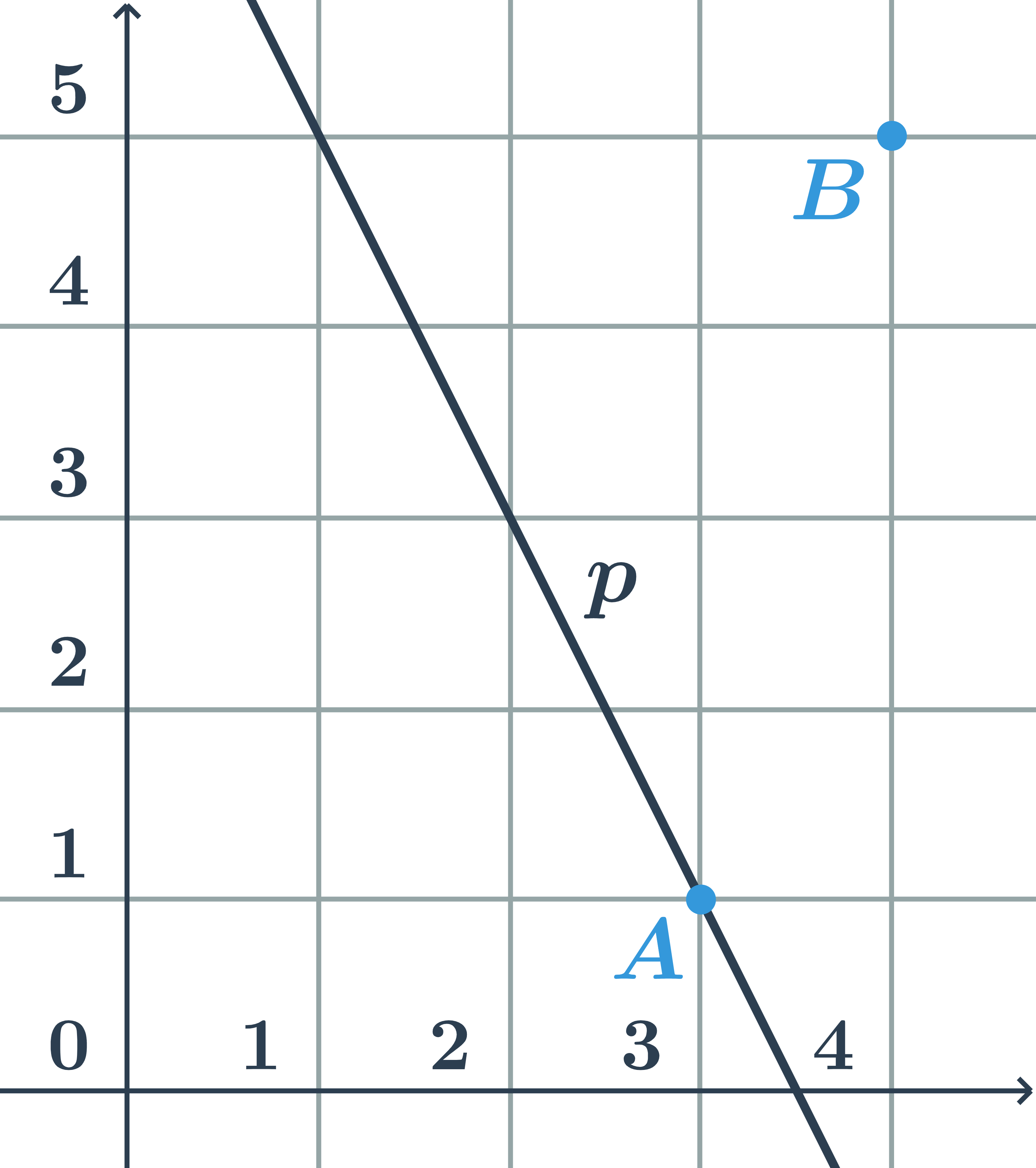
Určete, zda body A=[3;1] a B=[4;4] leží na přímce p dané parametricky: \begin{array}{rrl}x&=&2-t\\y&=&3+2t\\&&t\in\mathbb{R}\end{array}
- Do rovnic přímky dosadíme souřadnice bodu A=[3;1]:
\begin{array}{rrrr}3&=&2-t&\Rightarrow t=-1\\1&=&3+2t&\Rightarrow t=-1\end{array} \Rightarrow bod A leží na přímce p
- Do rovnice přímky dosadíme souřadnice bodu B=[4;5]:
\begin{array}{rrrl}4&=&2-t&\Rightarrow t=-2\\5&=&3+2t&\Rightarrow t=1\end{array}\Rightarrow bod B neleží na přímce p
Polohové úlohy
V polohových úlohách řešíme analyticky vzájemnou polohu geometrických útvarů v rovině. Nejčastěji jde o vzájemnou polohu dvou přímek nebo o vzájemnou polohu přímky a bodu.
NahoruMetrické úlohy
V metrických úlohách v analytické geometrii bývá úkolem spočítat konkrétní číselnou hodnotu veličin jako je:
- vzdálenost dvou objektů, např. vzdálenost bodu od přímky,
- odchylka dvou přímek v rovině.
Vzdálenost bodu od přímky
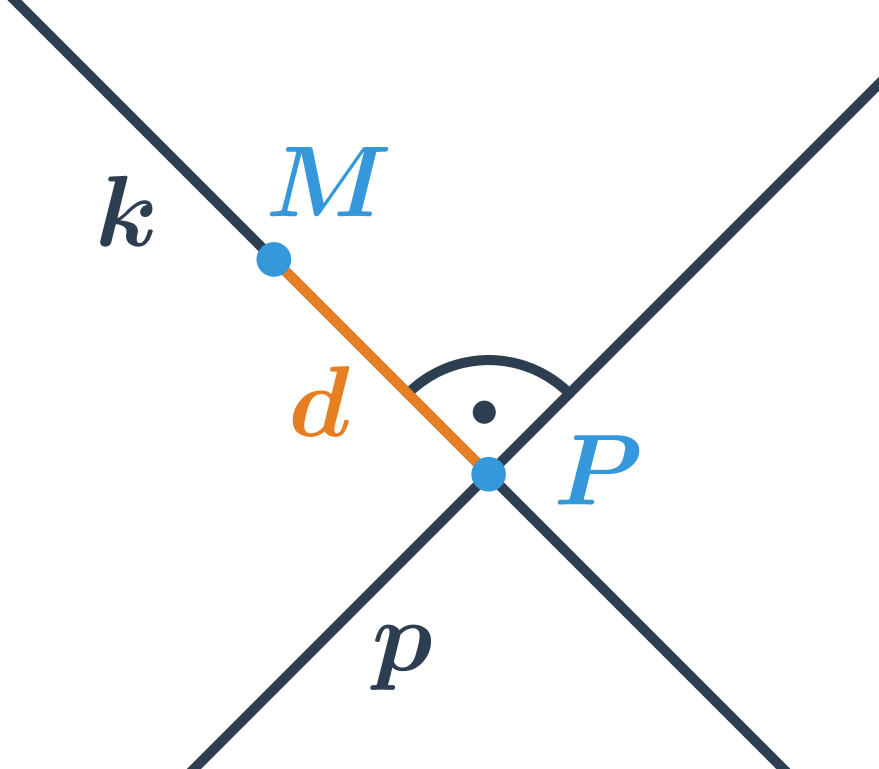
Vzdálenost bodu od přímky je délka nejkratší úsečky určené bodem M a bodem ležícím na přímce p. Jak je vidět z obrázku tato nejkratší úsečka leží na kolmici z bodu M k přímce p. Vzdálenost bodu od přímky tedy můžeme určit takto:
- najdeme přímku k, která prochází bodem M a je kolmá k přímce p
- určíme průsečík P přímky k s přímkou p
- vzdálenost bodu M od přímky p je délka úsečky PM
Příklad: vzdálenost bodu od přímky – pomocí kolmice
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0.
- Přímka k, která prochází bodem M a je kolmá k přímce p má směrový vektor kolineární s normálovým vektorem přímky p.
- Souřadnice směrového vektoru přímky k jsou: \vec{u}=(4;3).
- Přímka k má parametrické vyjádření: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Souřadnice průsečíku P přímky k s přímkou p určíme dosazením parametrického vyjádření přímky k do obecné rovnice přímky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Průsečík přímek k a p je bod P=[1;-1].
- Vzdálenost bodu M od přímky p je délka úsečky PM:
- Vzorec pro délku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme souřadnice bodů M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pro vzdálenost bodu od přímky dané obecnou rovnicí
Vzdálenost bodu M=[m_1;m_2] od přímky p dané obecnou rovnicí ax+by+c=0 je dána vzorcem: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Příklad: vzdálenost bodu od přímky – pomocí vzorce
Určete vzdálenost bodu M=[5;2] od přímky p:4x+3y-1=0 s využitím vzorce.
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[5;2] a koeficienty a a b z obecné rovnice přímky.
- Obecná rovnice pro p je 4x+3y-1=0, tedy a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdálenost dvou rovnoběžek
Umíme-li určit vzdálenost bodu od přímky, snadno určíme také vzdálenost dvou rovnoběžek. Stačí si uvědomit, že všechny body ležící na jedné přímce mají od druhé přímky stejnou vzdálenost. Proto je vzdálenost rovnoběžek stejná jako vzdálenost libovolného bodu na jedné přímce od přímky druhé.
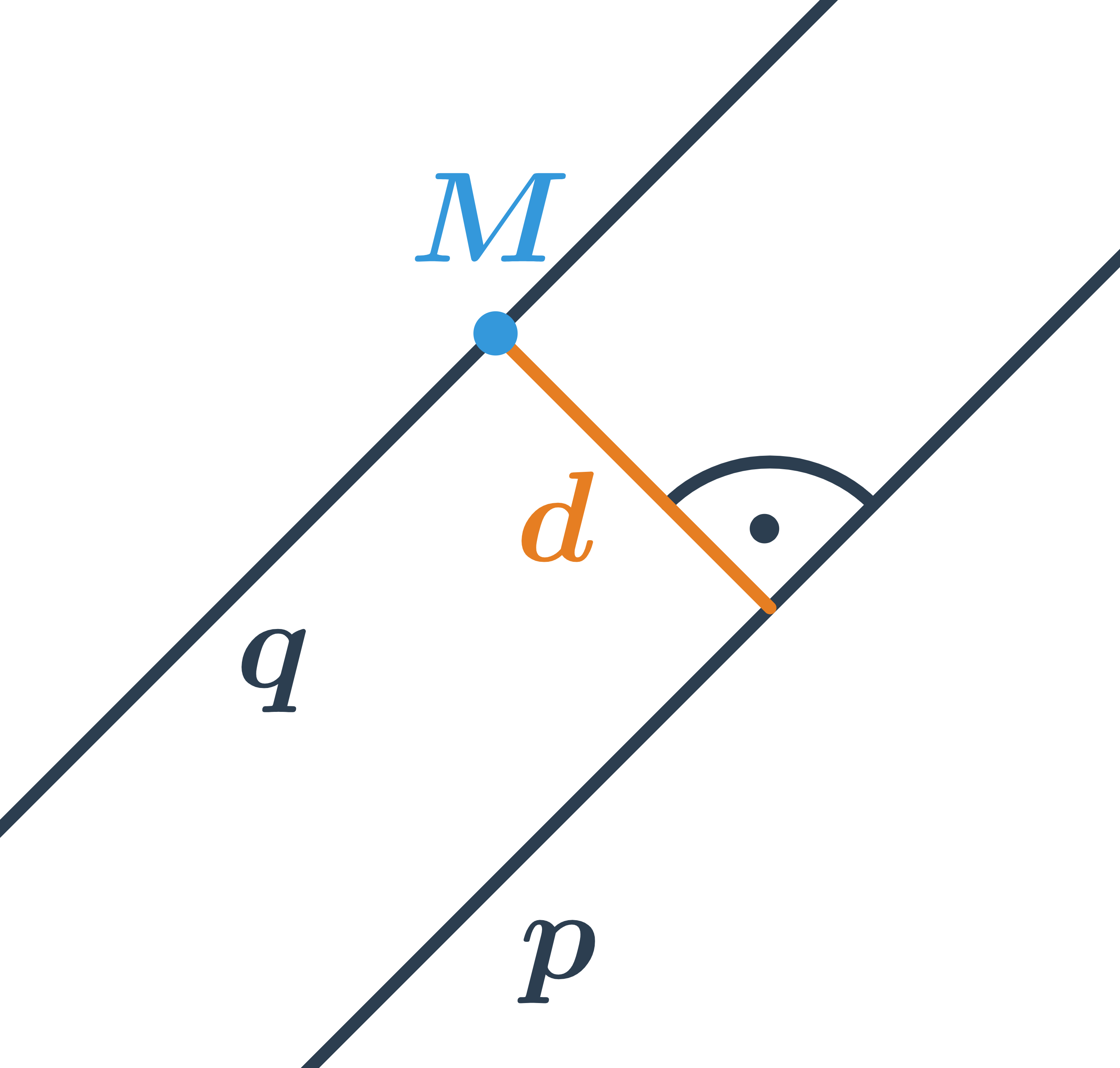
Příklad: vzdálenost rovnoběžek
Určete vzdálenost rovnoběžek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme souřadnice jednoho bodu (M) na přímce q tak, že jednu souřadnici zvolíme a druhou dopočítáme.
- Zvolíme například souřadnici y=0, pak x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorce d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} souřadnice bodu M=[-1;0] a koeficienty a a b z obecné rovnice přímky p.
- Obecná rovnice pro p je 2x-4y+3=0, tedy a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdálenost rovnoběžek p a q je: d=\frac{1}{\sqrt{20}}
Odchylka dvou přímek
Odchylka rovnoběžek je 0^\circ. Odchylka různoběžek je velikost ostrého nebo pravého úhlu, který přímky svírají.
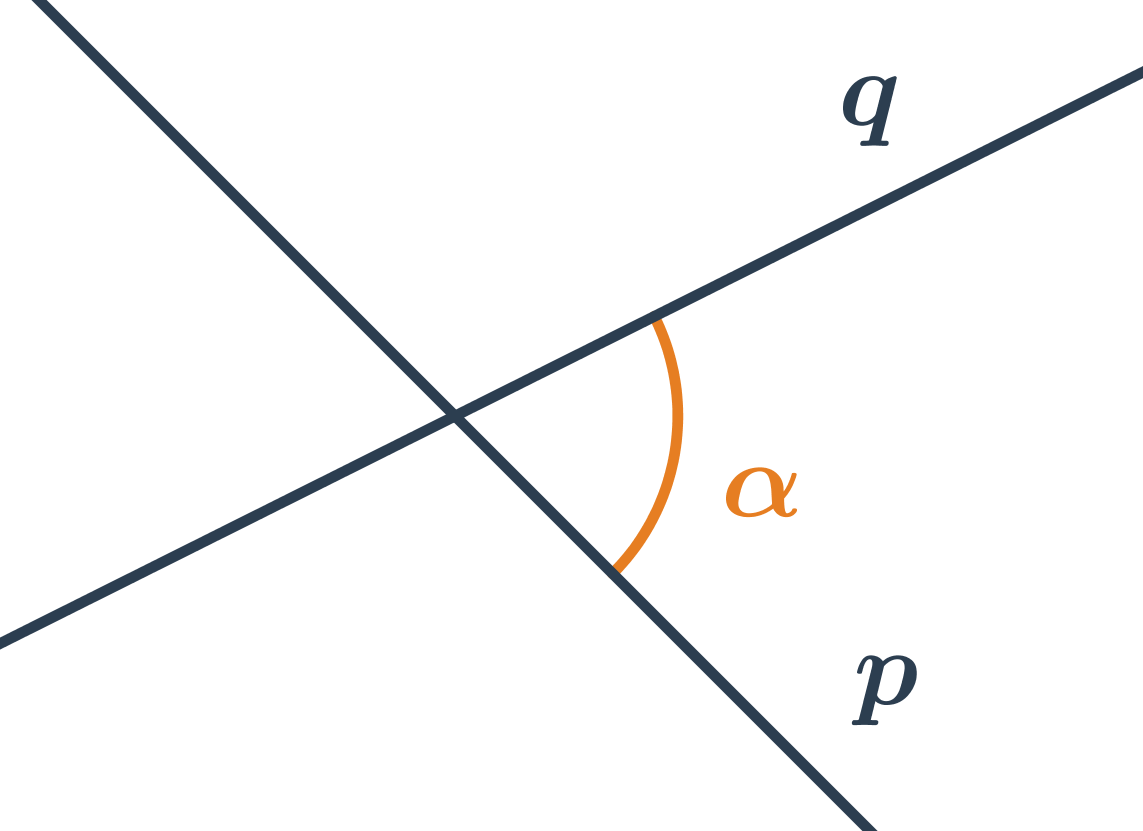
Odchylku různoběžek p a q můžeme vypočítat na základě znalosti směrových nebo normálových vektorů přímek. Vzorec pro výpočet úhlu různoběžek je obdobný jako vzorec pro výpočet úhlu vektorů
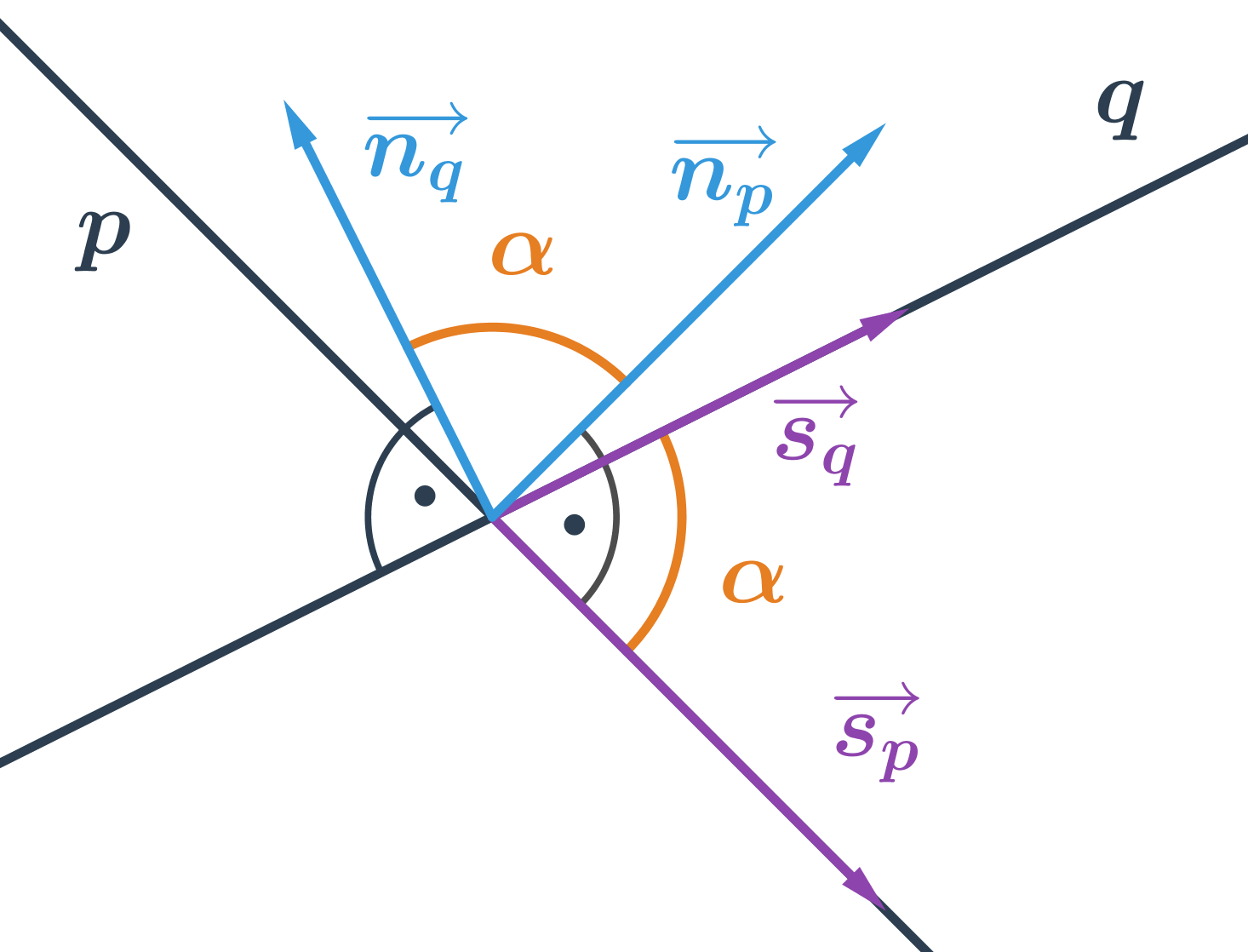
Odchylka různoběžek je úhel \alpha, pro který platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené ve vzorci jsou směrové vektory \overrightarrow{s_p} a \overrightarrow{s_q} nebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} přímek p a q.
Pro dvě k sobě kolmé přímky platí, že jejich odchylka \alpha=90^\circ a tedy \cos\alpha=0.
Proč musí být ve vzorci pro výpočet odchylky přímek absolutní hodnota?
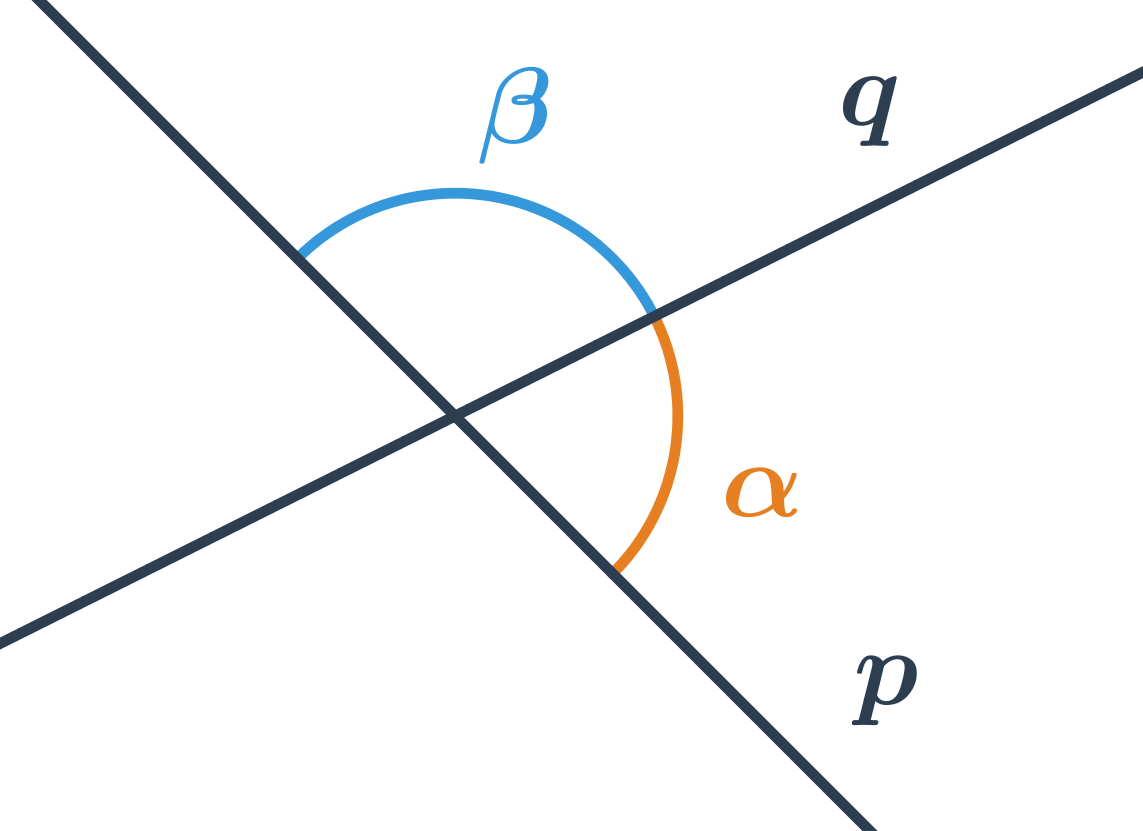
- Odchylka přímek p a q na obrázku je ostrý úhel \alpha, nikoliv tupý úhel \beta.
- \alpha a \beta jsou vedlejší úhly, pro které je hodnota funkce \cos opačná, tedy: \cos\alpha=-\cos\beta
- Pro úhel \alpha je \cos\alpha \gt 0, pro \beta je $$
- Absolutní hodnota ve vzorci nám zaručí, že najdeme úhel, kde hodnota funkce \cos je kladná, tedy úhel ostrý, který je odchylkou daných přímek.
Odchylka přímek a úhly v trojúhelníku
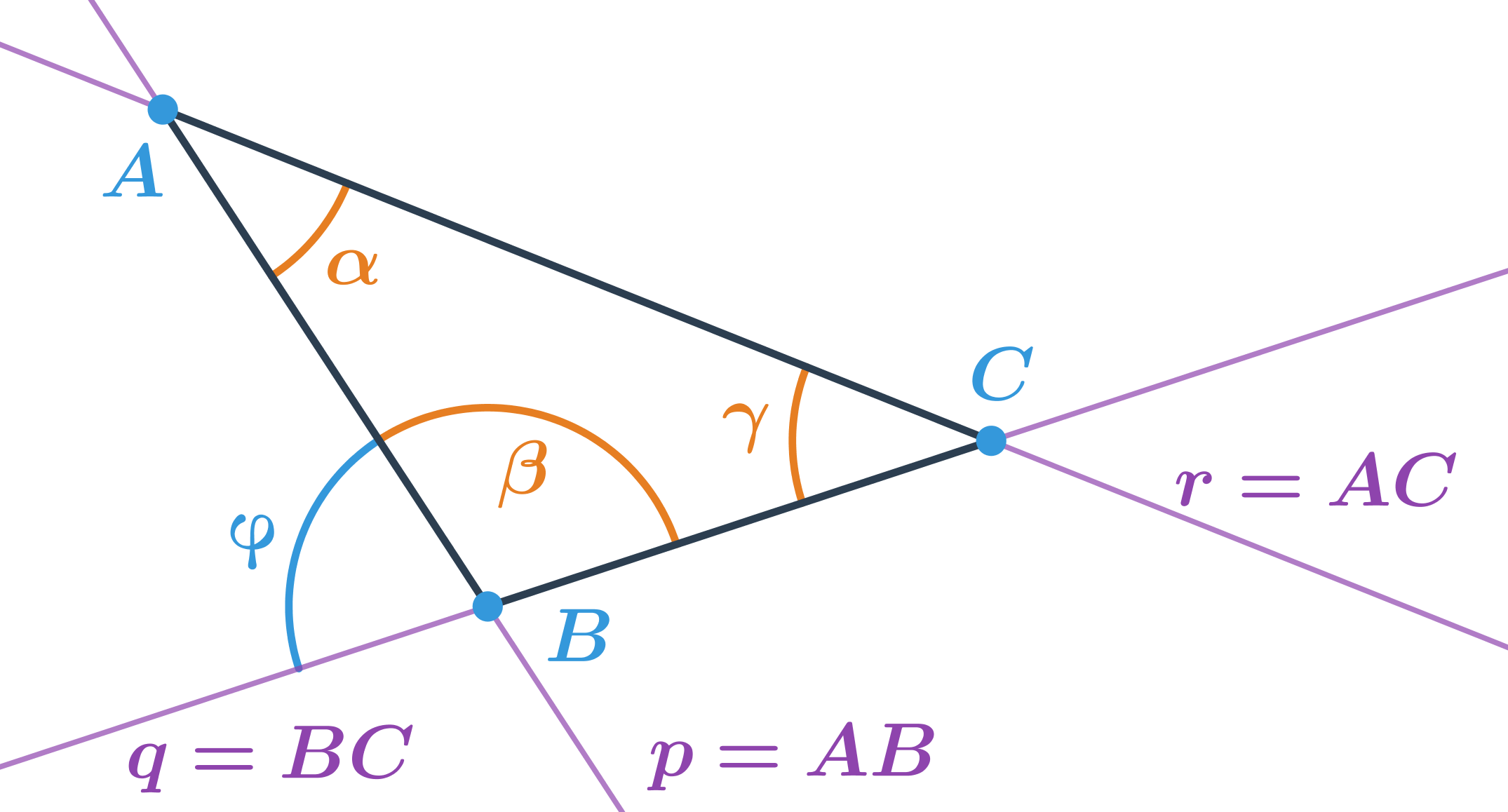
V trojúhelníku na obrázku:
- úhel \alpha je menší než 90^\circ a je to odchylka přímek AB a AC
- úhel \beta je větší než 90^\circ a není to odchylka přímek AB a BC
- úhel \gamma je menší než 90^\circ a je to odchylka přímek BC a AC
Velikost úhlů v trojúhelníku nemusí být stejná jako odchylka přímek, na kterých leží strany trojúhelníku. Úhly v trojúhelníku počítáme jako odchylku vektorů, které určují daný úhel. Tento úhel může být větší než 90^\circ, proto využijeme vzorec pro výpočet odchylky vektorů (ve vzorci nebude absolutní hodnota).
Odchylka přímek
Určete odchylku přímek p:x-2y+3=0 a q:2x-y+1=0
- Přímky jsou dané obecnými rovnicemi, proto pro výpočet jejich odchylky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorce: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocí funkce cos^{-1} na kalkulačce dopočítáme odchylku: \alpha=36^\circ
Rovina je určena třemi body, které neleží na jedné přímce. Z předchozích kapitol již víme, že dvojice bodů určuje přímku, případně vektor, proto je mnoho dalších způsobů jak určit rovinu:
- bodem a přímkou
- dvěma různoběžnými přímkami
- dvěma rovnoběžnými přímkami
- bodem a dvěma vektory
V prostoru lze zapsat rovinu jako množinu bodů, které splňují parametrickou rovnici nebo obecnou rovnici.
Máme-li rovinu popsanou rovnicí, umíme určit vzájemnou polohu roviny a bodu výpočtem.
NahoruRoviny: pojmy
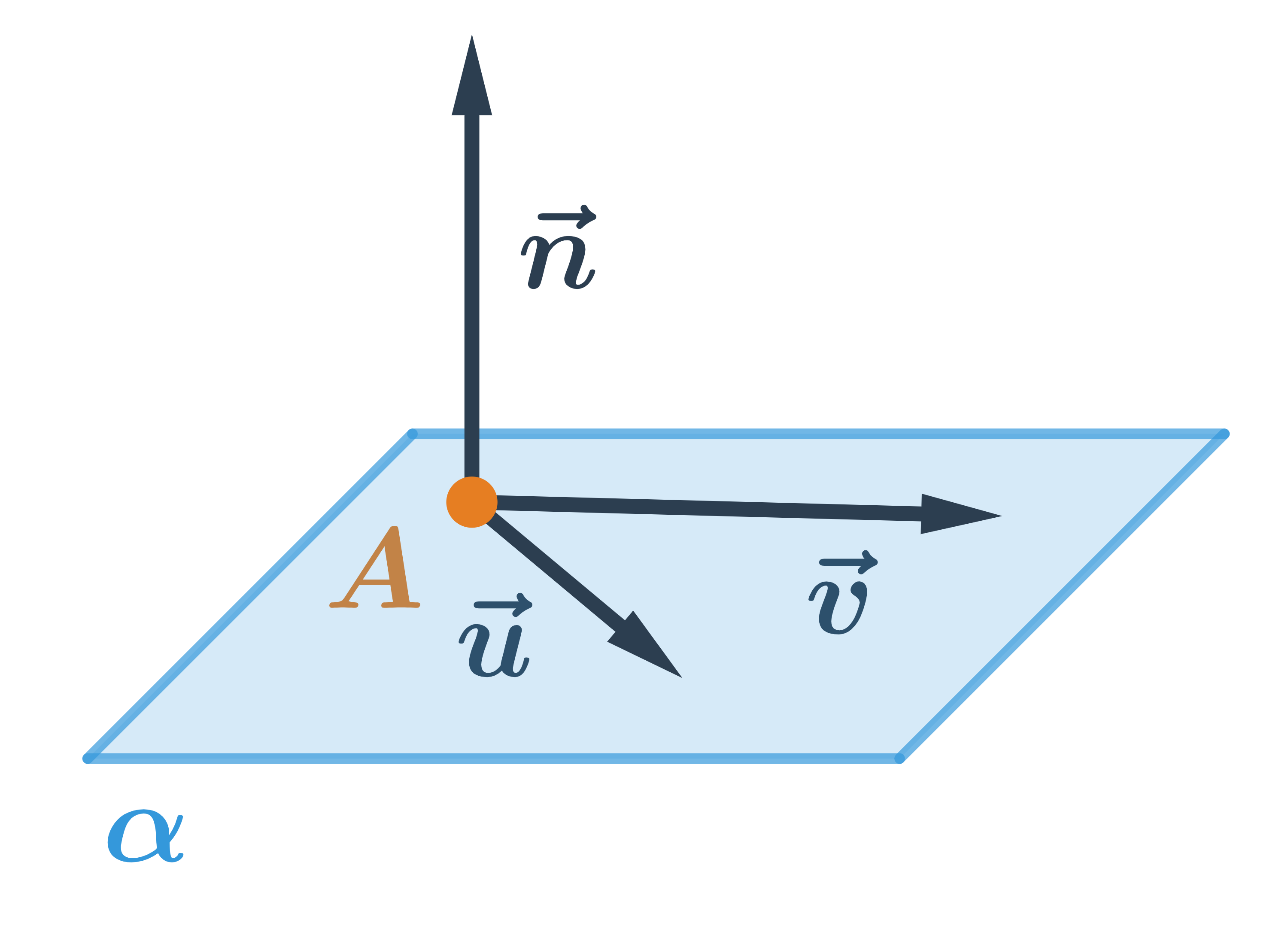
Přímka je jednoznačně určena bodem a dvěma vektory, které nejsou kolineární. Na obrázku je rovina \alpha určená bodem A a vektory \vec{u}, \vec{v}. Každý vektor, který je kolmý k rovině \alpha se nazývá normálový vektor roviny \alpha. Na obrázku je normálový vektor \vec{n}.
Parametrické rovnice roviny
Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t, s nazýváme parametry.
Obecná rovnice roviny
Obecná rovnice roviny je ve tvaru ax+by+cz+d=0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo.
Obecná rovnice roviny rovnoběžné s osami x a y
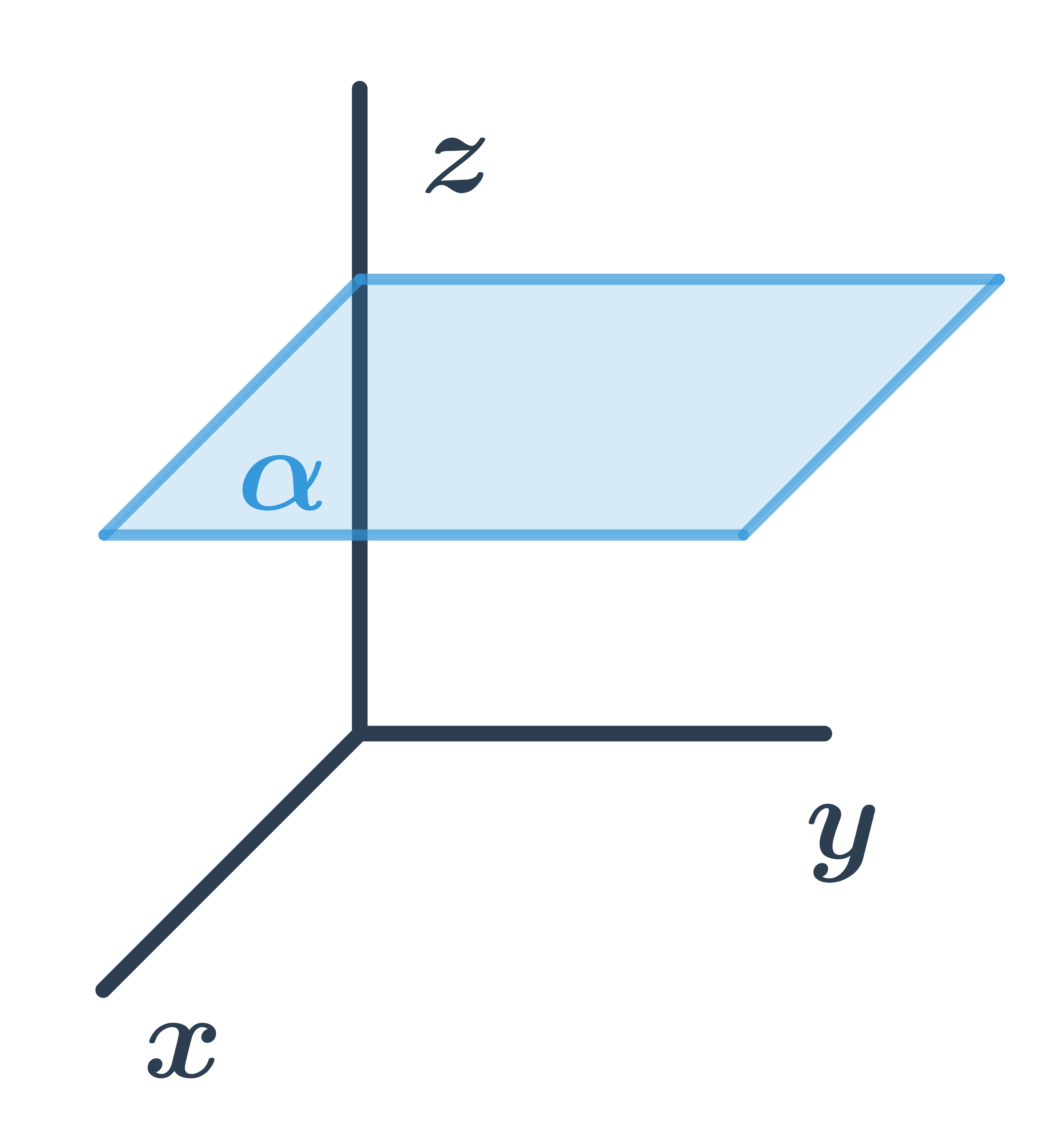
Pro všechny body ležící v rovině je třetí souřadnice stejná, tedy rovina má obecnou rovnici: z+d=0.
Obecná rovnice roviny rovnoběžné s osami x a z
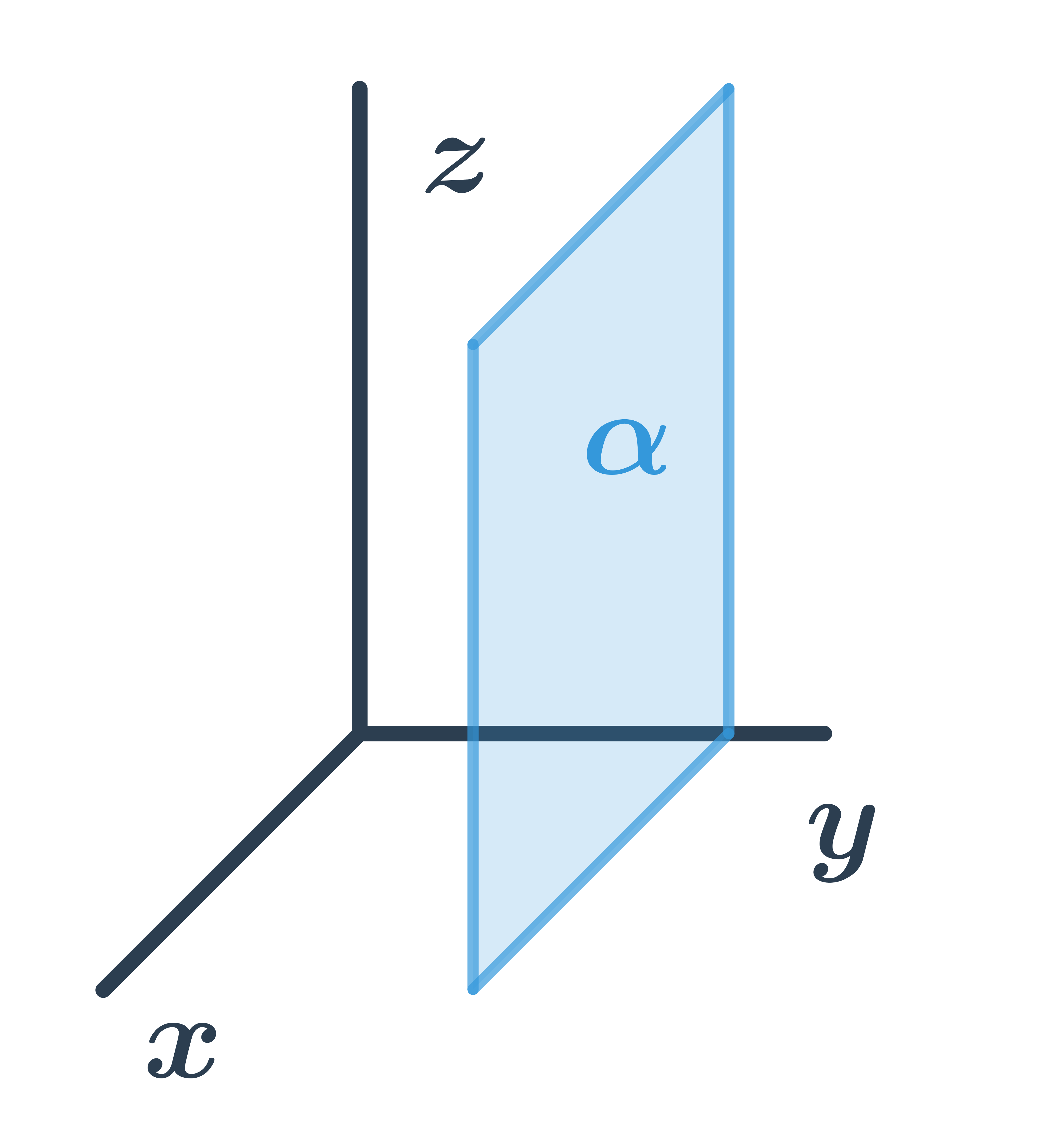
Pro všechny body ležící v rovině je druhá souřadnice stejná, tedy rovina má obecnou rovnici: y+d=0.
Obecná rovnice roviny rovnoběžné s osami y a z
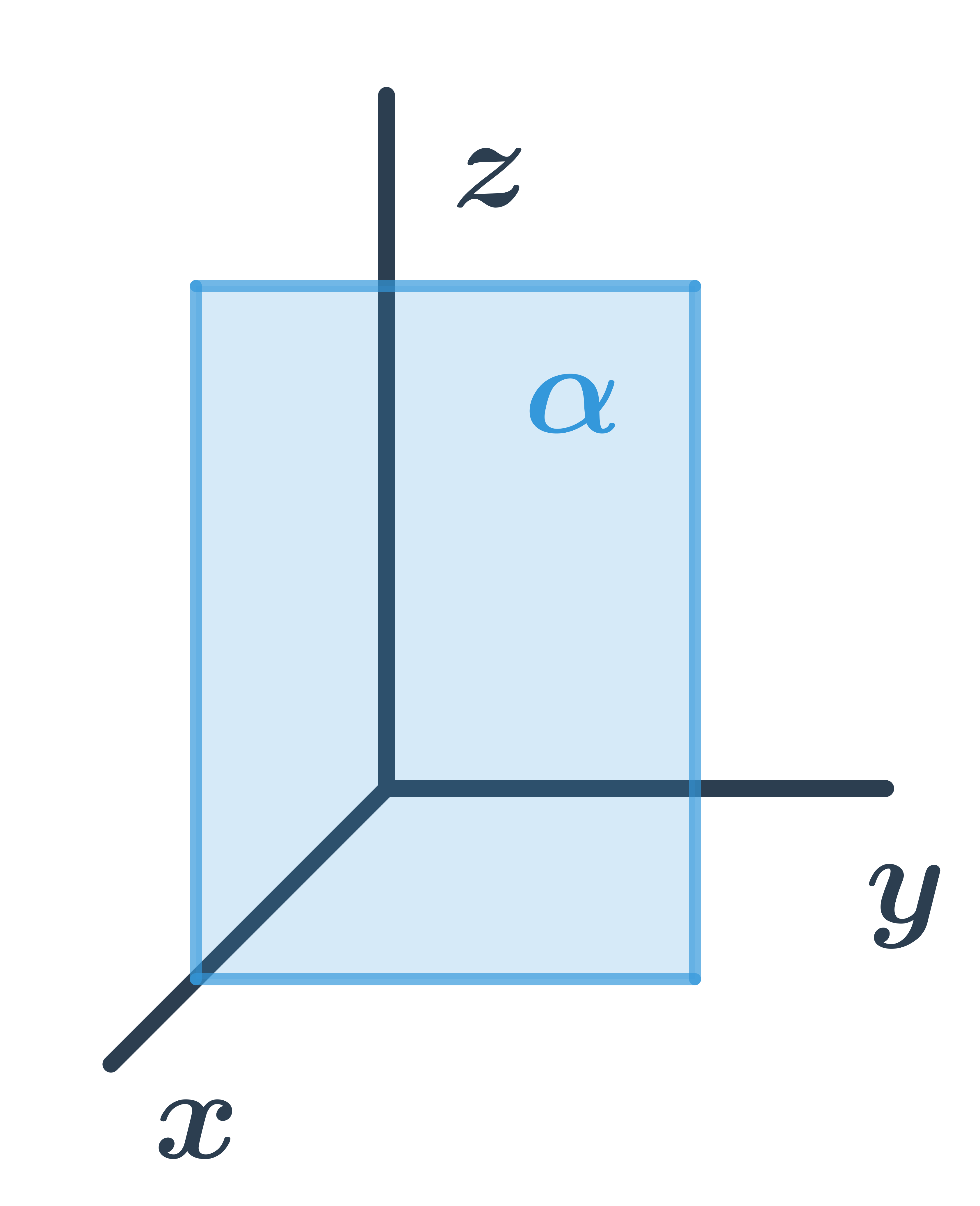
Pro všechny body ležící v rovině je první souřadnice stejná, tedy rovina má obecnou rovnici: z+d=0.
Bod a rovina
Bod M=[m_1;m_2;m_3] leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny.
- Pokud je rovina daná obecnou rovnicí ax+by+cz+d=0, pro souřadnice bodu, který leží na přímce platí: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Pokud je rovina daná parametricky, po dosazení souřadnic bodu do parametrických rovnic dostaneme soustavu tří rovnic pro dvě neznámé t, s, která má právě jedno řešení (dvojici reálných čísel).
Obecná rovnice roviny, která prochází počátkem
- Rovina prochází bodem O=[0;0;0], tedy musí platit: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Rovina, která prochází počátkem má obecnou rovnici: ax+by+cz=0.
Dvě rovnoběžné roviny
Normálové vektory dvou rovnoběžných rovin \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 jsou kolineární, tedy souřadnice jednoho vektoru jsou k-násobek souřadnic druhého vektoru. Pro konstanty v obecných rovnicích musí platit:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Pokud by platilo i d_2=k\cdot d_1 roviny jsou totožné.
NahoruParametrické rovnice roviny
Pro určení parametrických rovnic roviny potřebujeme znát souřadnice jednoho bodu a dvou nekolineárních vektorů v rovině \alpha. Rovina určená bodem A=[a_1;a_2;a_3] a vektory \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Zkráceně můžeme vyjádřit \alpha:X=A+t\vec{u}+s\vec{v}, kde t,s \in \mathbb{R} jsou parametry.
Parametrické rovnice roviny určené třemi body
Určete parametrické rovnice roviny \alpha určené body A=[3;2;1], B=[1;3;4], C=[2;-3;3].
- rovina \alpha je určená bodem A a vektory \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{AC}:
- \vec{u}=\overrightarrow{AB}=B-A=(-2;1;3)
- \vec{v}=\overrightarrow{AC}=C-A=(-1;-5;2)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&3-2t-s\\y&=&2+t-5s\\z&=&1+3t+2s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určené bodem a dvěma vektory
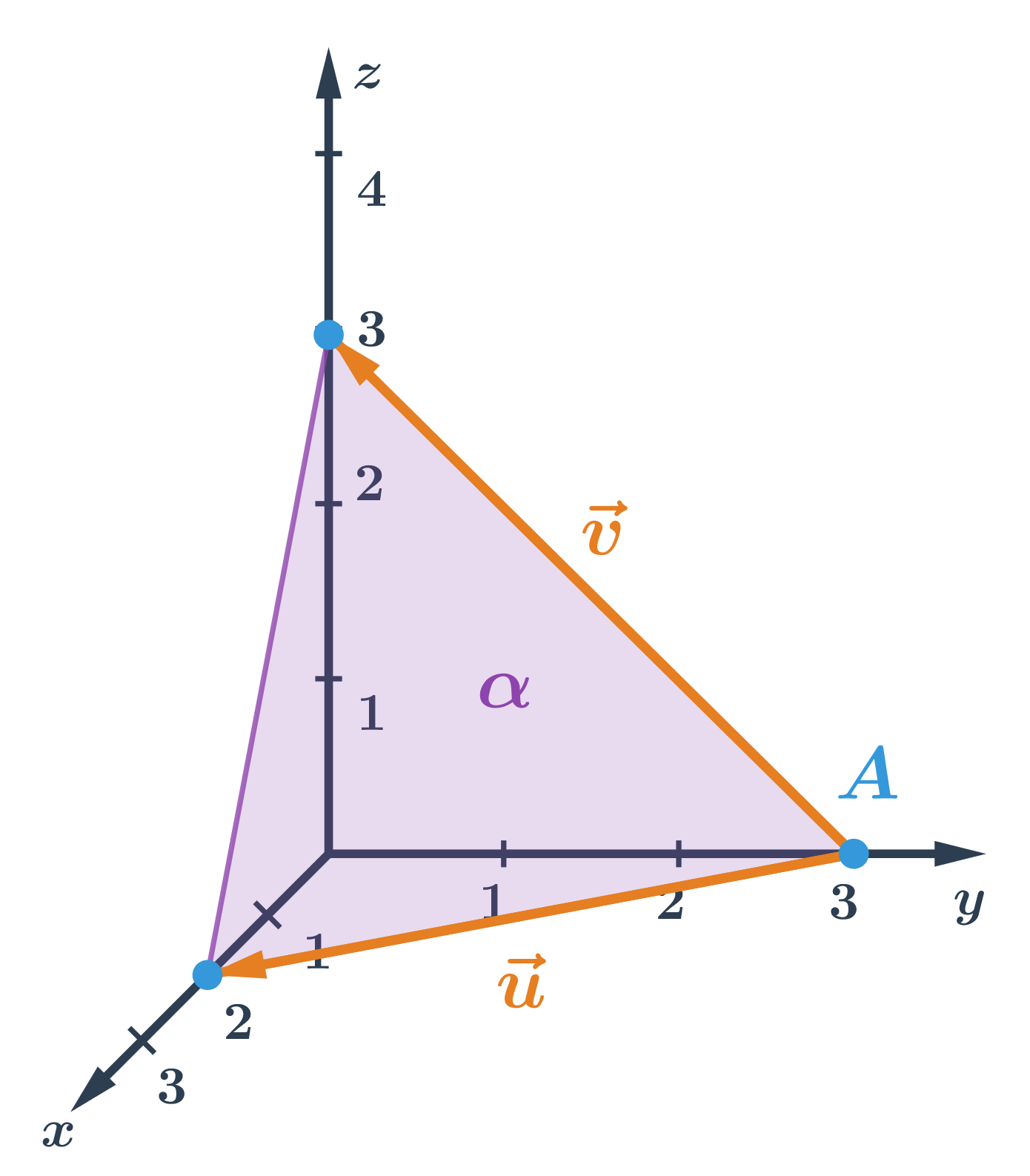
- rovina \alpha je určená bodem A a vektory \vec{u}, \vec{v}
- souřadnice určíme z obrázku:
- A=[0;3;0],
- \vec{u}=(2;-3;0),
- \vec{v}=(0;-3;3)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&2t\\y&=&3-3t-3s\\z&=&3s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určené různoběžkami p a q
Určete parametrické rovnice roviny určené dvěma různoběžkami s následujícími parametrickými rovnicemi:
p:\begin{array}{rrl}x&=&2+3t\\y&=&1+2t\\z&=&4-4t\\&&t\in\mathbb{R}\end{array}, q:\begin{array}{rrl}x&=&2+4s\\y&=&1-2s\\z&=&4-5s\\&&s\in\mathbb{R}\end{array}
- rovina \alpha je určená společným bodem různoběžek a směrovými vektory přímek p a q
- společný bod různoběžek: R=[2;1;4],
- směrový vektor přímky p:\vec{u}=(3;2;4),
- směrový vektor přímky q:\vec{v}=(4;-2;-5)
- parametrické rovnice roviny \alpha jsou:
\begin{array}{rrl}x&=&2+3t+4s\\y&=&1+2t-2s\\z&=&4-4t-5s\\&&t,s\in\mathbb{R}\end{array}
Obecná rovnice roviny
Obecná rovnice roviny má tvar ax+by+cz+d=0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo. Normálový vektor \vec{n}=(a;b;c) je vektor kolmý k dané rovině.
Obecná rovnice roviny určené bodem a normálovým vektorem
Určete obecnou rovnici roviny \alpha určené bodem A=[-3;1;2] a normálovým vektorem \vec{n}=(2;3;-4).
- Souřadnice normálového vektoru jsou konstanty a, b, c v obecné rovnici roviny, proto obecná rovnice bude mít tvar: 2x+3y-4z+d=0
- Konstantu d určíme dosazením souřadnic bodu A=[-3;1;2] do obecné rovnice: 2\cdot(-3)+3\cdot1-4\cdot 2+d=0\Rightarrow -11+d=0\Rightarrow d=11
- Obecná rovnice roviny \alpha je: 2x+3y-4z+11=0
Obecná rovnice roviny dané bodem a rovnoběžné s jinou rovinou
Obecná rovnice roviny \alpha, která prochází bodem A=[2;3;1] a je rovnoběžná s rovinou \beta:3x+y+4z+1=0.
- Dvě rovnoběžné roviny mají stejný normálový vektor, souřadnice normálového vektoru jsou souřadnice a, b, c v obecné rovnici roviny.
- Proto obecná rovnice hledané roviny \alpha bude mít tvar: 3x+y+4z+d=0
- Konstantu d určíme dosazením souřadnic bodu A=[2;3;1] do obecné rovnice: 3\cdot2+3+4\cdot 1+d=0\Rightarrow 13+d=0\Rightarrow d=-13
- Obecná rovnice roviny \alpha je: 3x+y+4z-13=0
Vzájemná poloha bodu a roviny
Bod leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny. Pokud je rovina daná obecnou rovnicí, po dosazení souřadnic bodu do rovnice roviny nastane rovnost. Pokud je rovina daná parametricky, po dosazení souřadnic bodu dostaneme soustavu tří rovnic pro dvě neznámé, která má právě jedno řešení.
Bod a rovina daná obecnou rovnicí
Určete, zda body A=[3;4;2] a B=[1;3;0] leží v rovině \alpha dané obecnou rovnicí 2x-y+3z+1=0.
- Do rovnice roviny dosadíme souřadnice bodu A=[3;4;2].
- 2\cdot 3-4+3\cdot2+1=0\Rightarrow9\neq 0, tedy bod A neleží v rovině \alpha.
- Do rovnice roviny dosadíme souřadnice bodu B=[1;3;0].
- 2\cdot 1-3+3\cdot0+1=0\Rightarrow0=0, tedy bod B leží v rovině \alpha.
Bod a rovina daná parametricky
Určete, zda body A=[2;3;4] a B=[0;2;2] leží v rovině \alpha dané parametrickými rovnicemi:
\begin{array}{rrl}x&=&1-t+s\\y&=&2+t+s\\z&=&3-t+s\\&&t,s\in\mathbb{R}\end{array}
- Do rovnic roviny dosadíme souřadnice bodu A=[1;3;4]: \begin{array}{rrrr}2&=&1-t+s\\3&=&2+t+s\\4&=&3-t+s\\\end{array}
- Z prvních dvou rovnic určíme hodnoty t a s, dosazením do třetí rovnice zjistíme, zda nalezené hodnoty jsou řešením soustavy a tedy zda bod leží v rovině:
- první a druhou rovnici sečteme: 5=3+2s\Rightarrow s=1
- hodnotu s=1 dosadíme do první rovnice: 1=1-t+1\Rightarrow t=1
- hodnoty s=1 a t=1 dosadíme do třetí rovnice: 4=3-1+1. Tato rovnost neplatí, tedy bod A neleží v rovině \alpha.
- Do rovnic roviny dosadíme souřadnice bodu B=[0;-3;2]: \begin{array}{rrrr}0&=&1-t+s\\-3&=&2+t+s\\2&=&3-t+s\\\end{array}
- Z prvních dvou rovnic určíme hodnoty t a s, dosazením do třetí rovnice zjistíme, zda nalezené hodnoty jsou řešením soustavy a tedy zda bod leží v rovině:
- první a druhou rovnici sečteme: -3=3+2s\Rightarrow s=-3
- hodnotu s=-3 dosadíme do první rovnice: 0=1-t-3\Rightarrow t=-2
- hodnoty s=-3 a t=-2 dosadíme do třetí rovnice: 2=3-(-2)-3. Tato rovnost platí, tedy bod B leží v rovině \alpha.
Kuželosečky
Jak již název napovídá, mají kuželosečky společný původ. Každá z nich vzikne jako řez rotační kuželové plochy rovinou. 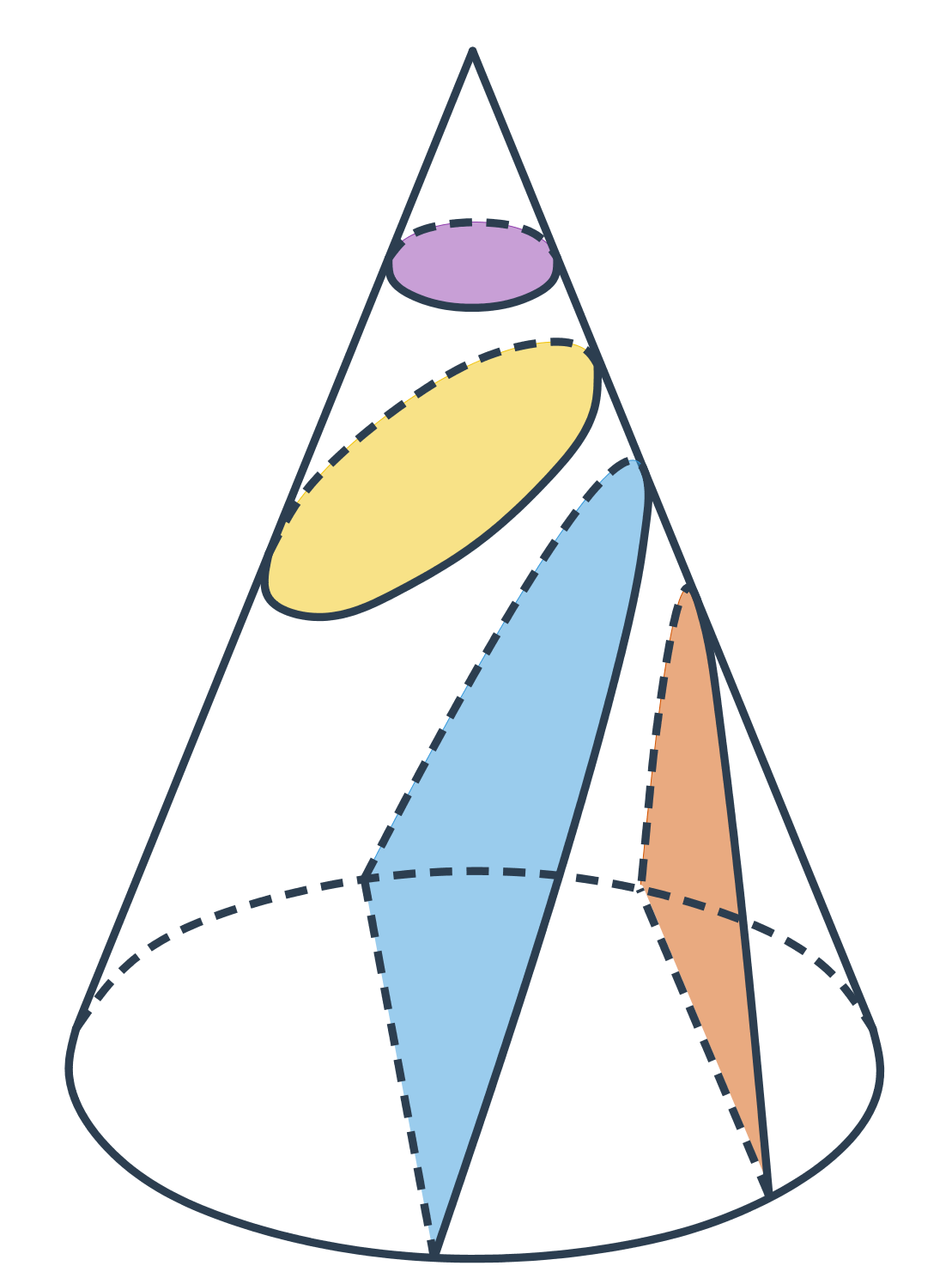
- Kružnice vznikne jako řez rovinou, která je kolmá na osu kuželové plochy.
- Pokud rovinu řezu trochu nakloníme, vznikne elipsa.
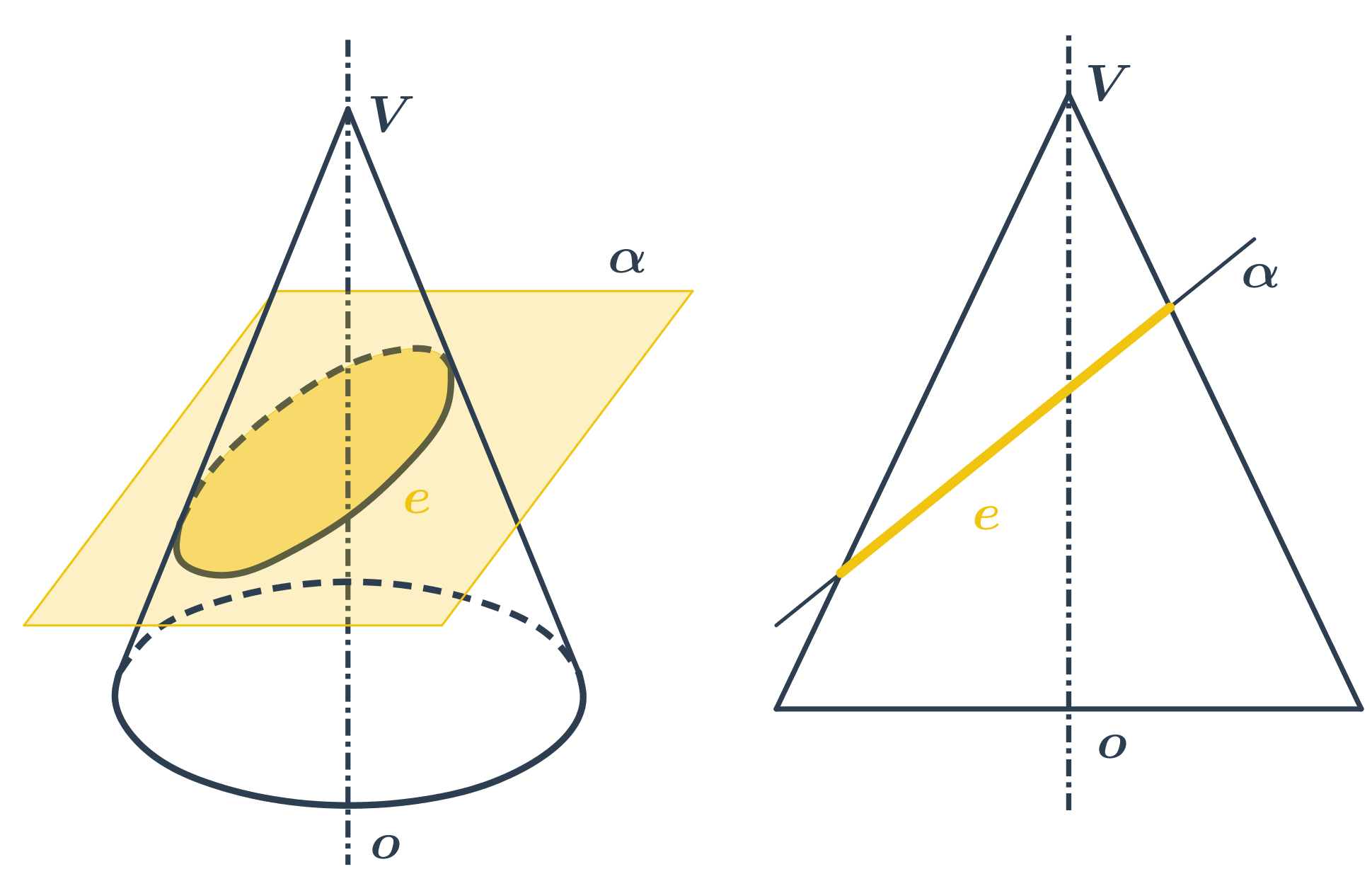
- Pokud rovinu řezu nakloníme tolik, že bude rovnoběžná s některou z přímek na kuželové ploše, vznikne parabola.
- Při dalším naklánění už rovina řezu protne obě části kuželové plochy a vznikne dvoudílná hyperbola.
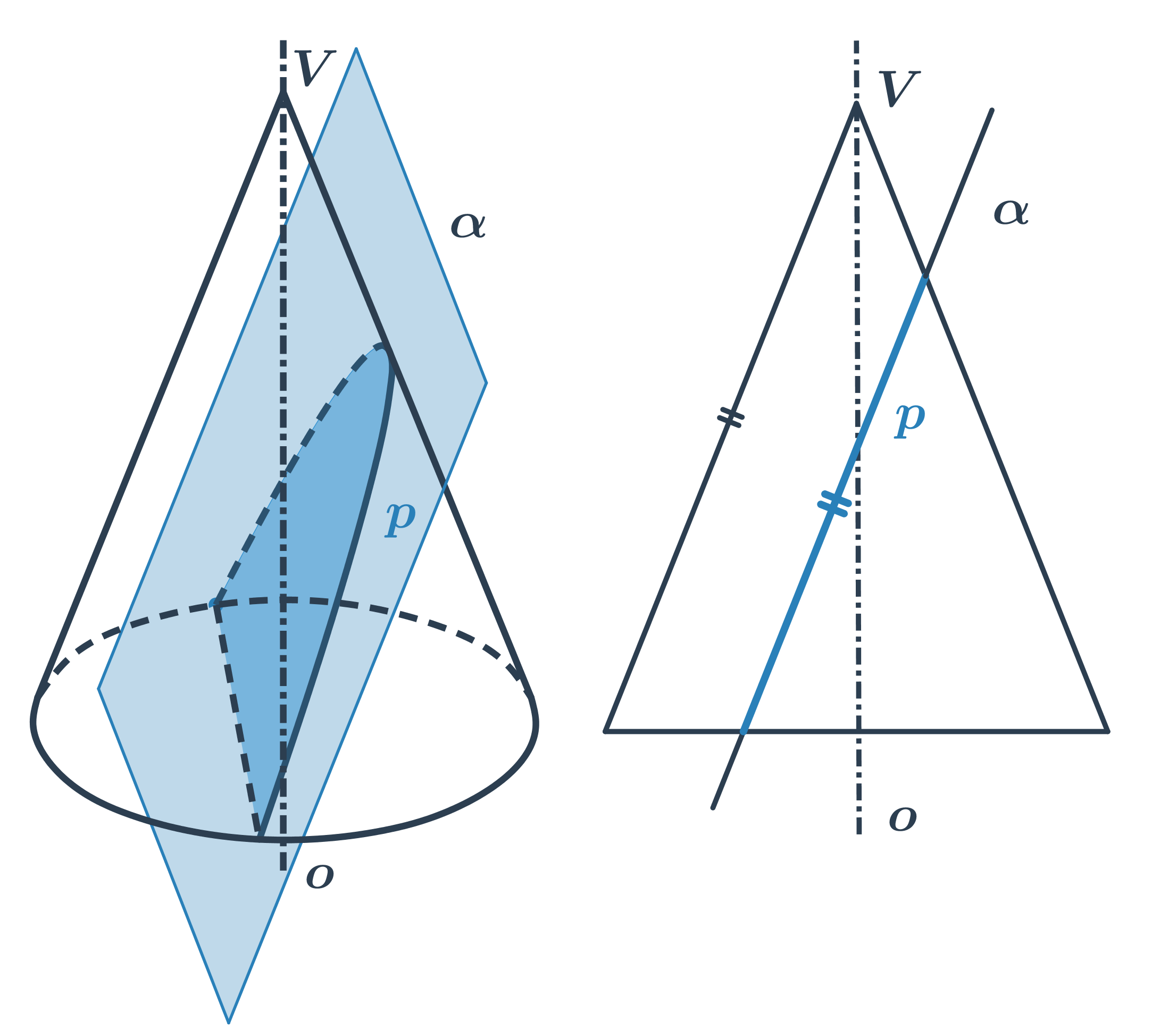
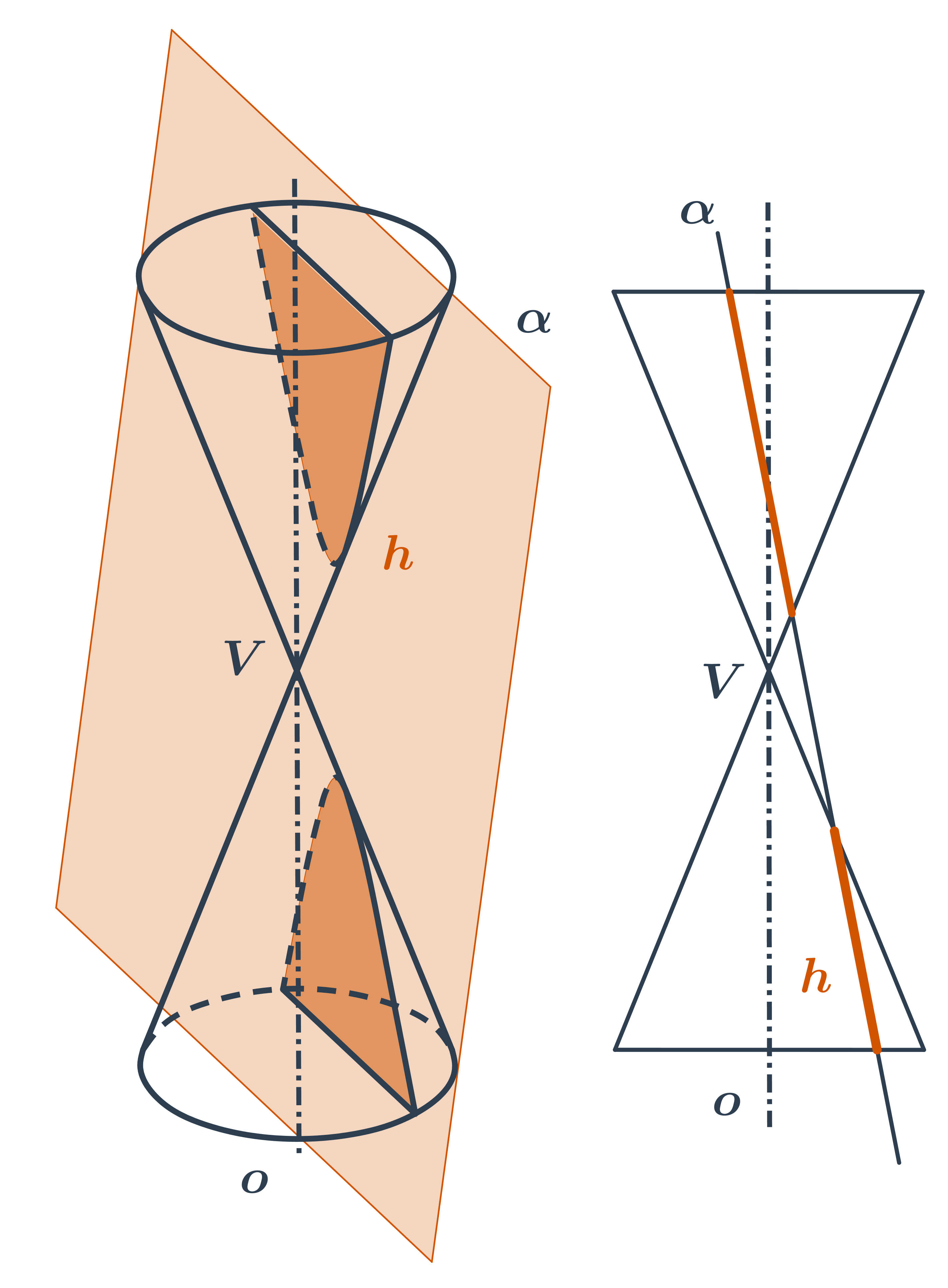
Na kuželosečky můžeme také hledět jako na množiny bodů dané vlastnosti. V analytické geometrii často zapisujeme tyto množiny pomocí rovnic.
NahoruKružnice (kuželosečka)
Kružnice je množina všech bodů v rovině, které mají od daného pevného bodu S stejnou vzdálenost r. Bod S nazýváme střed kružnice, hodnotu r nazveme poloměr kružnice. 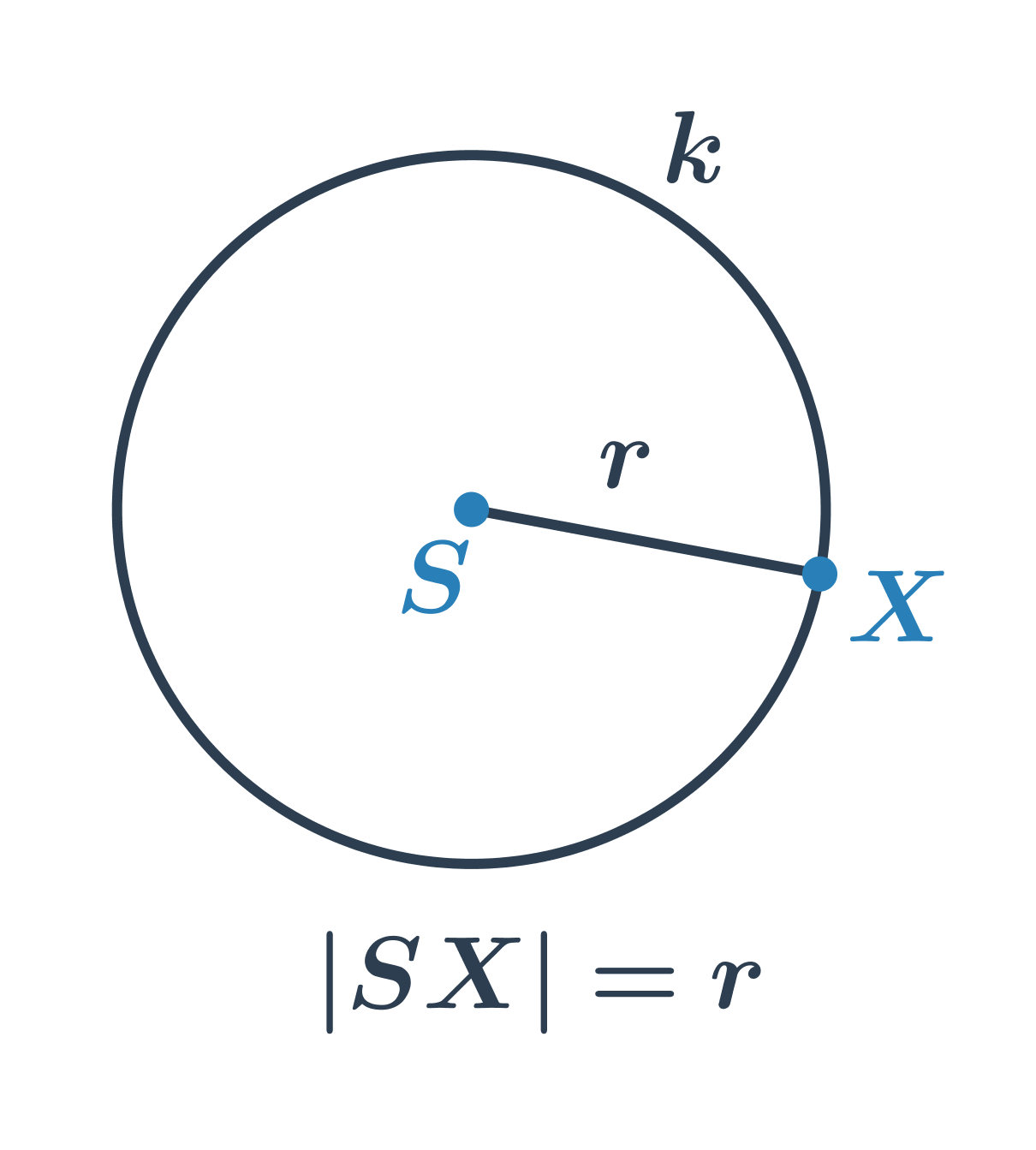
Středová rovnice kružnice
Středová rovnice kružnice o středu S[m;n] a poloměru r je ve tvaru: (x-m)^2 +(y-n)^2=r^2 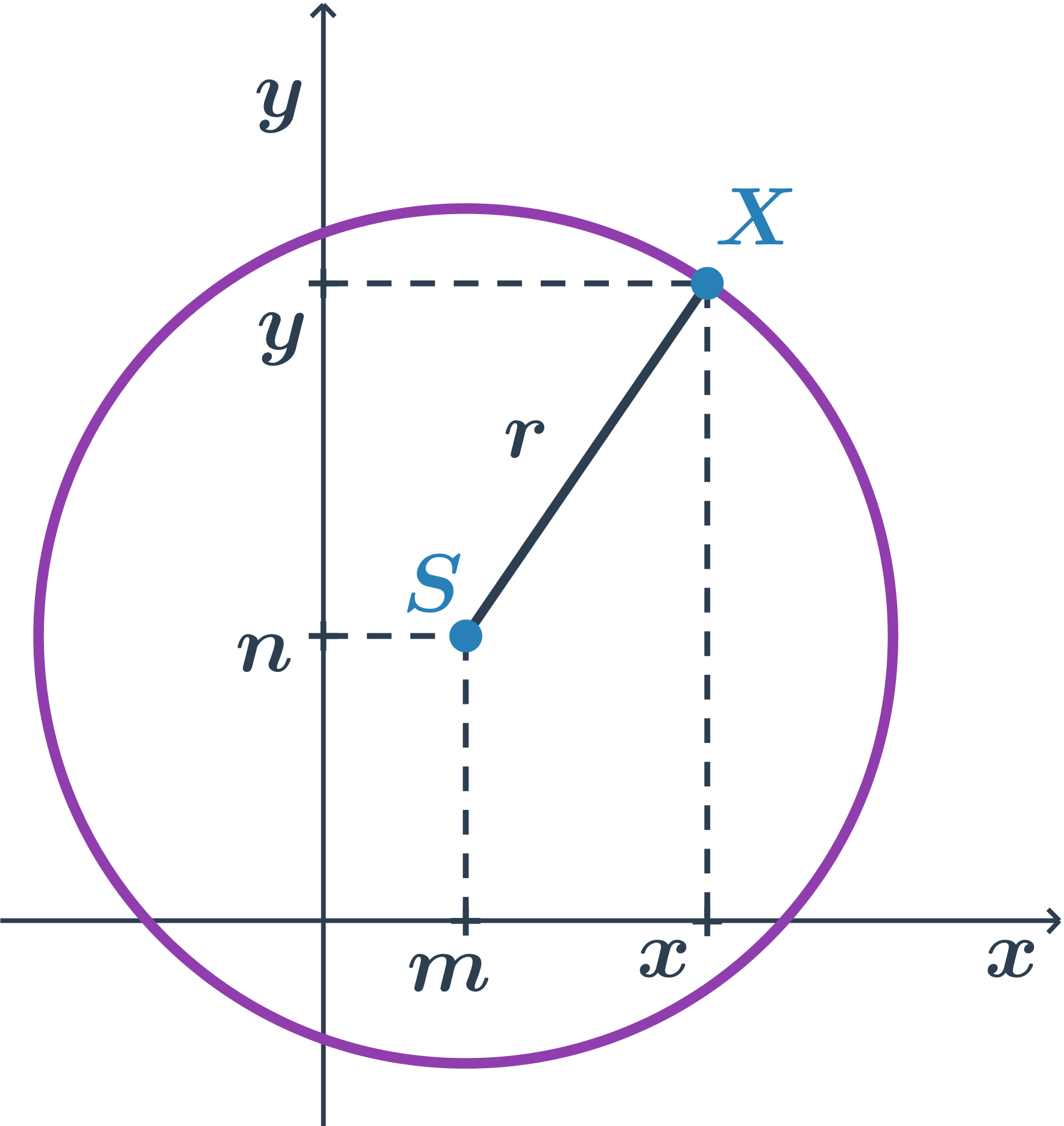
Příklad: Určete středovou rovnici kružnice se středem v bodě S[-1;2] a poloměrem r=3.
- Středová rovnice je ve tvaru: (x-m)^2 +(y-n)^2=r^2
- Dosadíme souřadnice středu a poloměr. Při dosazení si dáme pozor na to, že souřadnice středu ve středové rovnici odečítáme: (x-(-1))^2 +(y-2)^2=3^2
- Po úpravě: (x+1)^2 +(y-2)^2=9
Obecná rovnice kružnice
Podobně jako existuje několik tvarů rovnic přímky, můžeme i rovnici kružnice zapsat různými způsoby. Obecná rovnice kružnice je ve tvaru: x^2 +y^2-2mx-2ny+p=0.
Každá rovnice v tomto tvaru ale nemusí ještě být obecnou rovnicí kružnice. Pro obecnou rovnici kružnice musí platit, že výraz m^2+n^2-p je kladný. Praktické ověření, zda se jedná o kružnici, ale obvykle provádíme převedením na středovou rovnici kružnice.
Příklad: Najděte střed a poloměr kružnice dané obecnou rovnicí x^2+y^2+4x+6y-12=0.
- Nejprve si uspořádáme členy podle proměnných: x^2+4x+y^2-6y-12=0.
- Našim dalším cílem je upravit výraz na levé straně jako součet dvou druhých mocnin (čtverců), podle vzorečků a^2\pm 2ab+b^2=(a\pm b)^2.
- K oběma stranám rovnice přičteme konstanty 4 a 9, abychom součty členů s proměnnými x a y mohli upravit na druhé mocniny (provedeme v obou případech doplnění na čtverec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na závěr ještě převedeme -12 na druhou stranu rovnice: (x+2)^2 +(y-3)^2=25
- Tímto jsme převedli obecnou rovnici kružnice na středovou rovnici kružnice.
- Poloměr kružnice je r=\sqrt{25}=5.
- Souřadnice středu S[m,n] odčítáme ve středové rovnici od proměnných x a y, mají tedy opačná znaménka než konstanty v závorkách ve středové rovnici \Rightarrow S[-2;3].
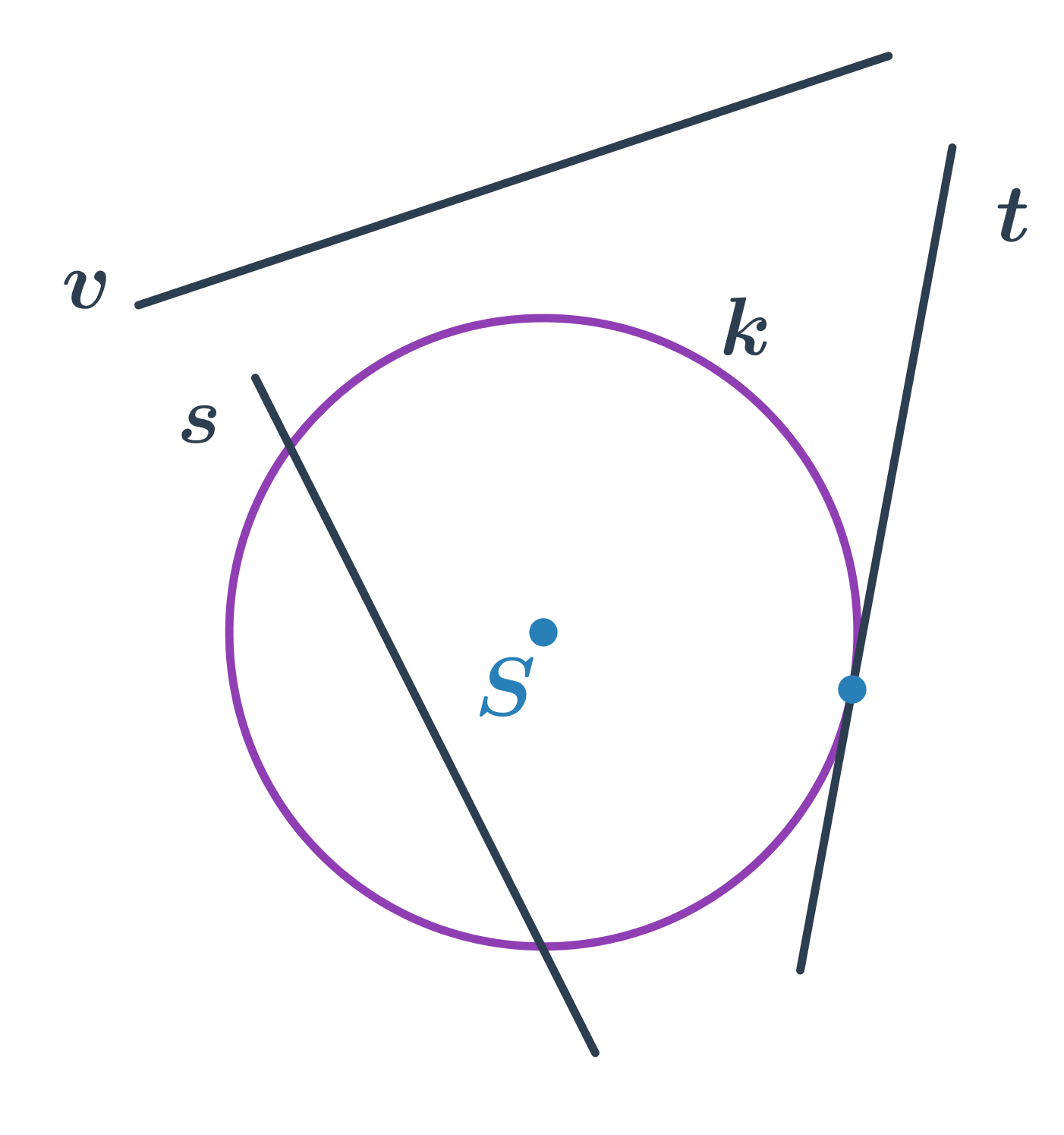
Kružnice a přímka
- přímka s protíná kružnici ve dvou bodech – sečna kružnice
- přímka t protíná kružnici v jednom bodě – tečna kružnice
- přímka v kružnici neprotíná – vnější přímka kružnice
Rovnice tečny kružnice v bodě, který leží na kružnici
Kružnice daná rovnicí (x-m)^2 +(y-n)^2=r^2 má v bodě T[x_0;y_0] tečnu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Jak si zapamatovat rovnici tečny
- Středová rovnice je ve tvaru (x-m)^2 +(y-n)^2=r^2.
- Závorky rozložíme na součiny dvoučlenů (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každém součinu zaměníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnici tečny (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Příklad: Určete rovnici tečny kružnice (x-1)^2+(y+2)^2=13 v jejím bodě T[3;1].
- Ověříme, zda bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Tečna má rovnici (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme souřadnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme závorky: 2x-2 +3y+6=13
- A dostaneme obecnou rovnici tečny 2x+3y-9=0
Polára kružnice
Z bodu R mimo kružnici můžeme sestrojit dvě tečny k dané kružnici. Přímka určená body dotyku tečen se nazývá polára kružnice vzhledem k bodu R. 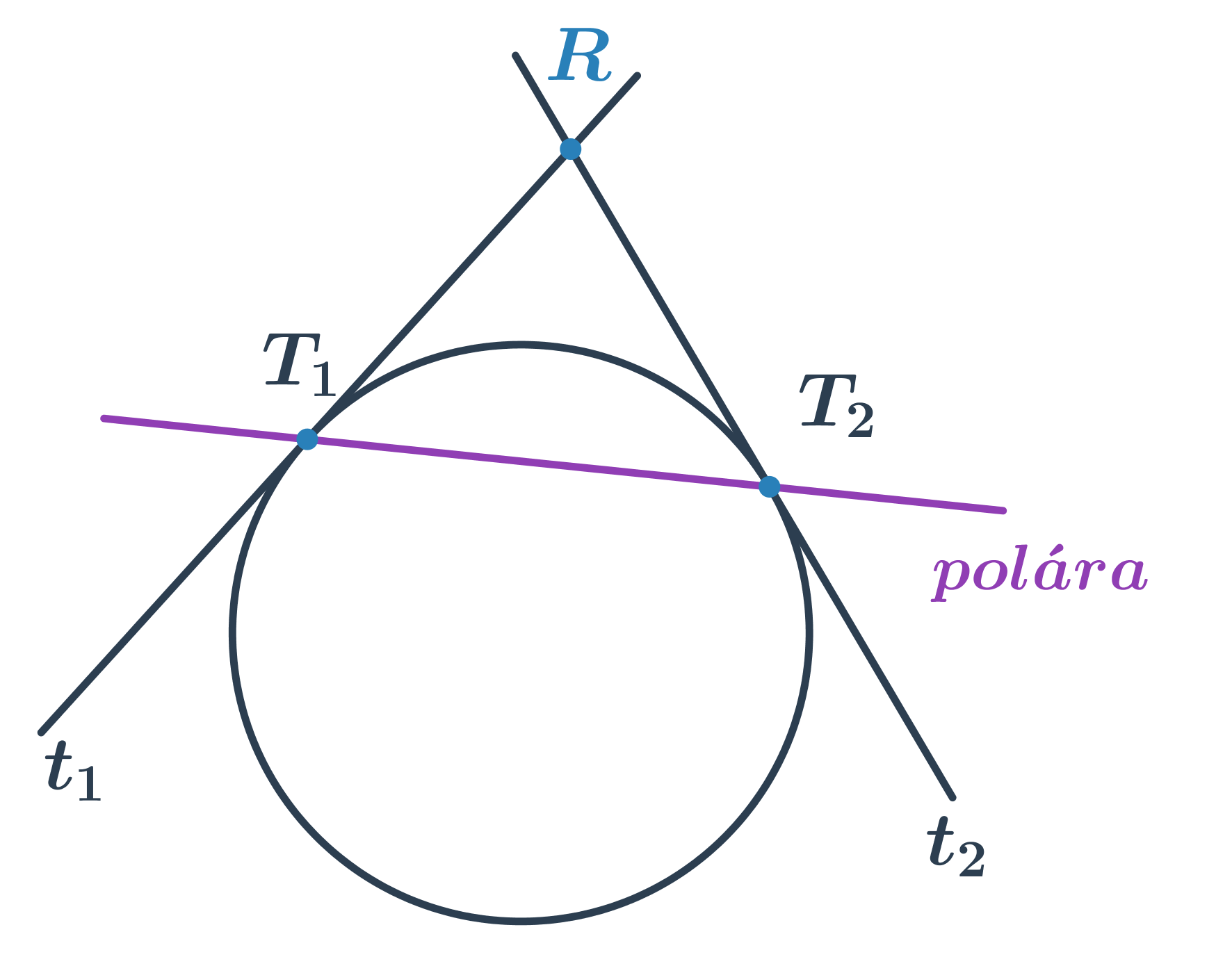
Rovnice poláry kružnice kružnice (x-m)^2 +(y-n)^2=r^2 vzhledem k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
K čemu poláru použijeme?
- Poláru využíváme ke konstrukci tečen ležících z bodu mimo kružnici.
- Podle vzorce určíme rovnici poláry, tedy přímky.
- Najdeme průsečíky poláry a kružnice – to jsou body dotyku hledaných tečen.
- Když známe body dotyku, určíme podle vztahu pro rovnici tečny v bodě kružnice obecné rovnice obou tečen.
Elipsa je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý součet vzdáleností 2a, který je větší než vzdálenost ohnisek. 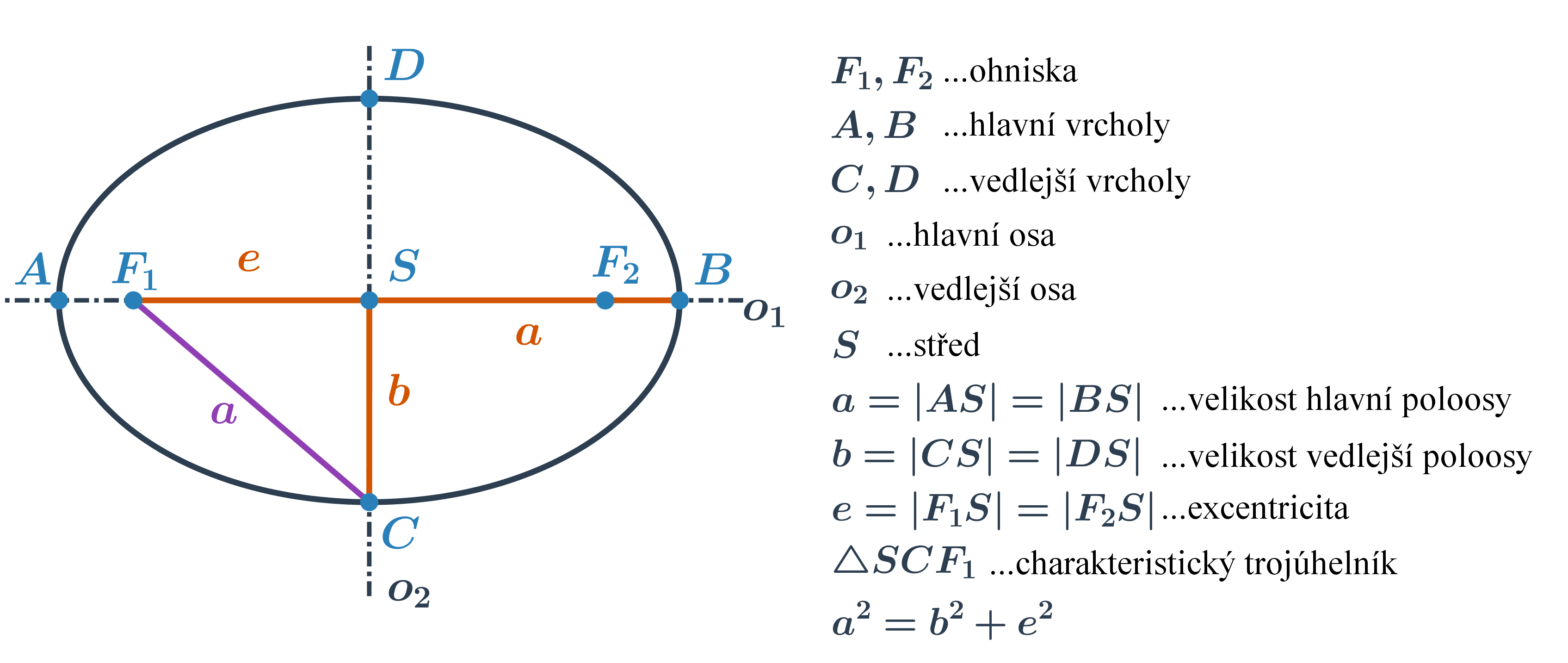
Středová rovnice elipsy
Tvar středové rovnice elipsy o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a a b závisí na poloze hlavní osy:
hlavní osa je rovnoběžná s osou x, rovnice je ve tvaru: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1
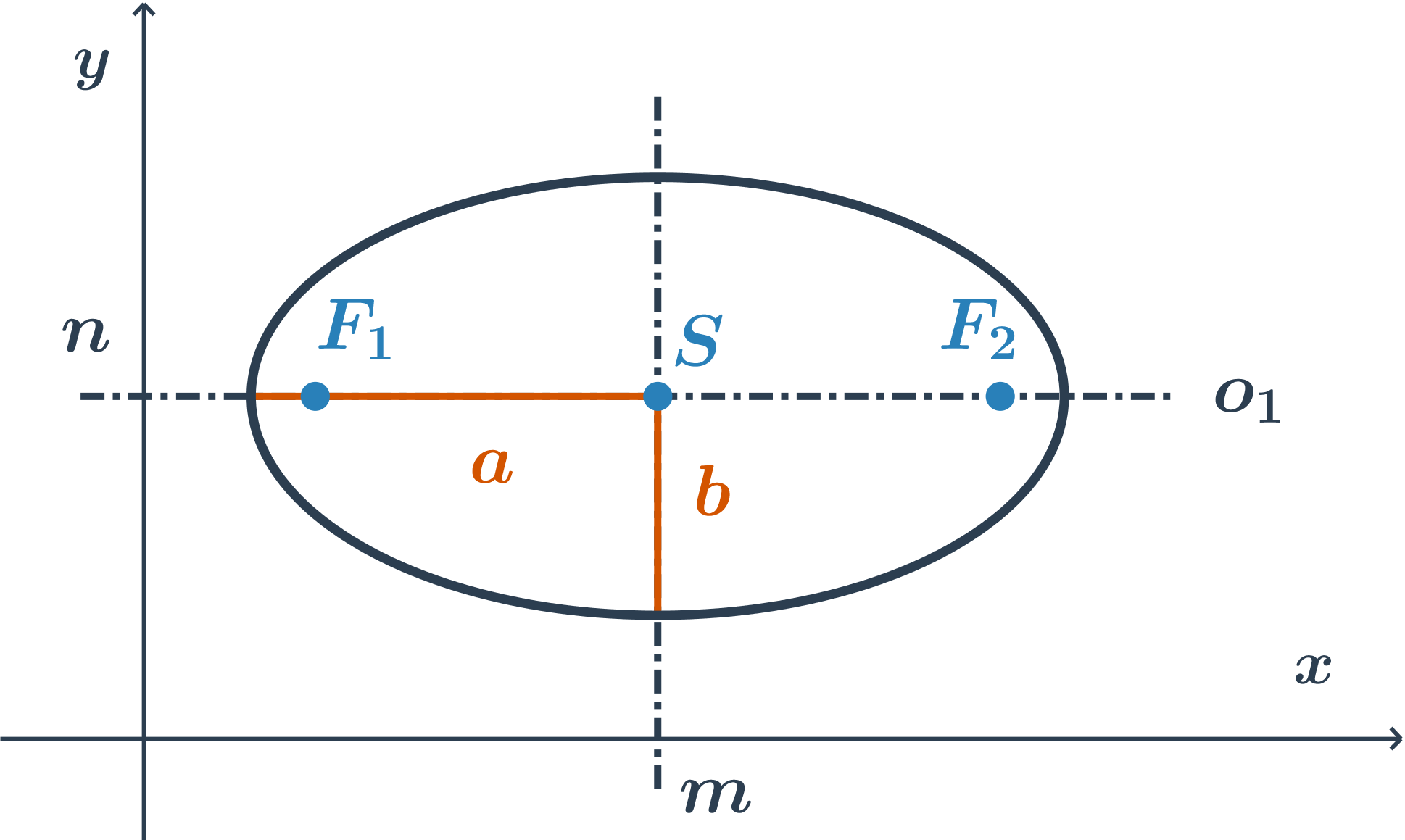
hlavní osa je rovnoběžná s osou y, rovnice je ve tvaru: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1
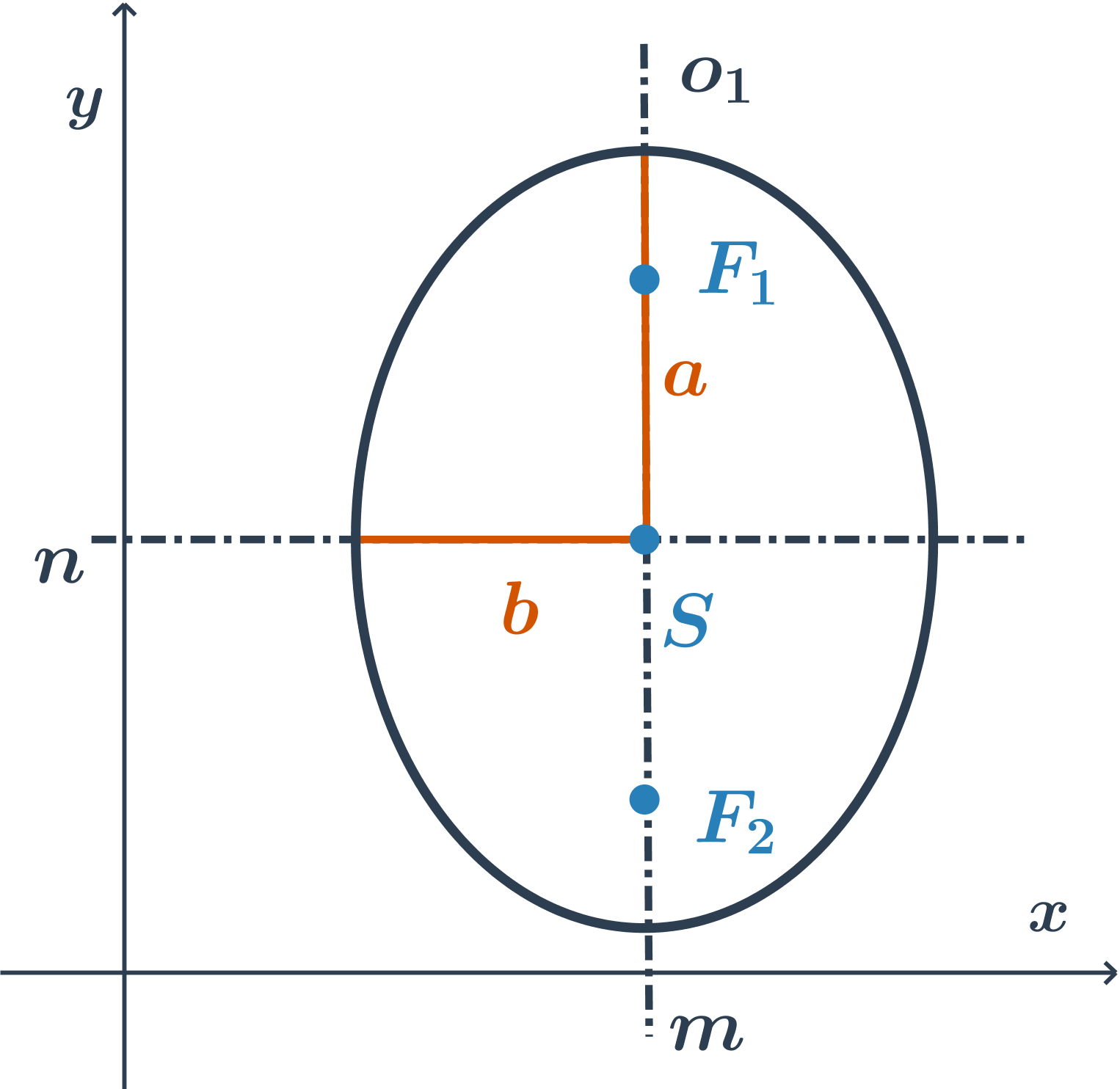
Návod: jak z rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa elipsy
- Podíváme se do jmenovatelů.
- Větší jmenovatel je druhá mocnina velikosti hlavní poloosy (a menší jmenovatel je druhá mocnina velikosti vedlejší poloosy).
- Proměnná v daném čitateli (zlomku s větším jmenovatelem) pak určuje, se kterou osou je hlavní osa elipsy rovnoběžná.
- Stručně řečeno: je‑li větší číslo například ve jmenovateli s proměnnou x, je hlavní osa rovnoběžná s osou x
Příklad: určení středové rovnice elipsy s daným středem, velikostmi poloos a směrem hlavní osy
Určete středovou rovnici elipsy se středem v bodě S[-2;3], je‑li a=3, b=2 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úpravě: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Obecná rovnice elipsy
Podobně jako existuje několik rovnic přímky, můžeme i rovnici elipsy zapsat jiným způsobem. Obecná rovnice elipsy je ve tvaru:
Ax^2 +By^2+Cx+Dy+E=0, A\ne B, A\cdot B>0.
Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí elipsy. Praktické ověření, zda se jedná o elipsu provádíme převedením na středovou rovnici.
Příklad: určuje daná rovnice elipsu?
Rozhodněte, zda rovnice x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Nejprve si uspořádáme členy: x^2+8x+3y^2-18y+31=0.
- Ze členů s proměnnou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K oběma stranám rovnice přičteme konstanty 16 a 27, abychom členy s proměnnými x a y mohli upravit podle vztahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Převedeme konstantu 31 na druhou stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na závěr rovnici vydělíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Jedná se tedy o elipsu.
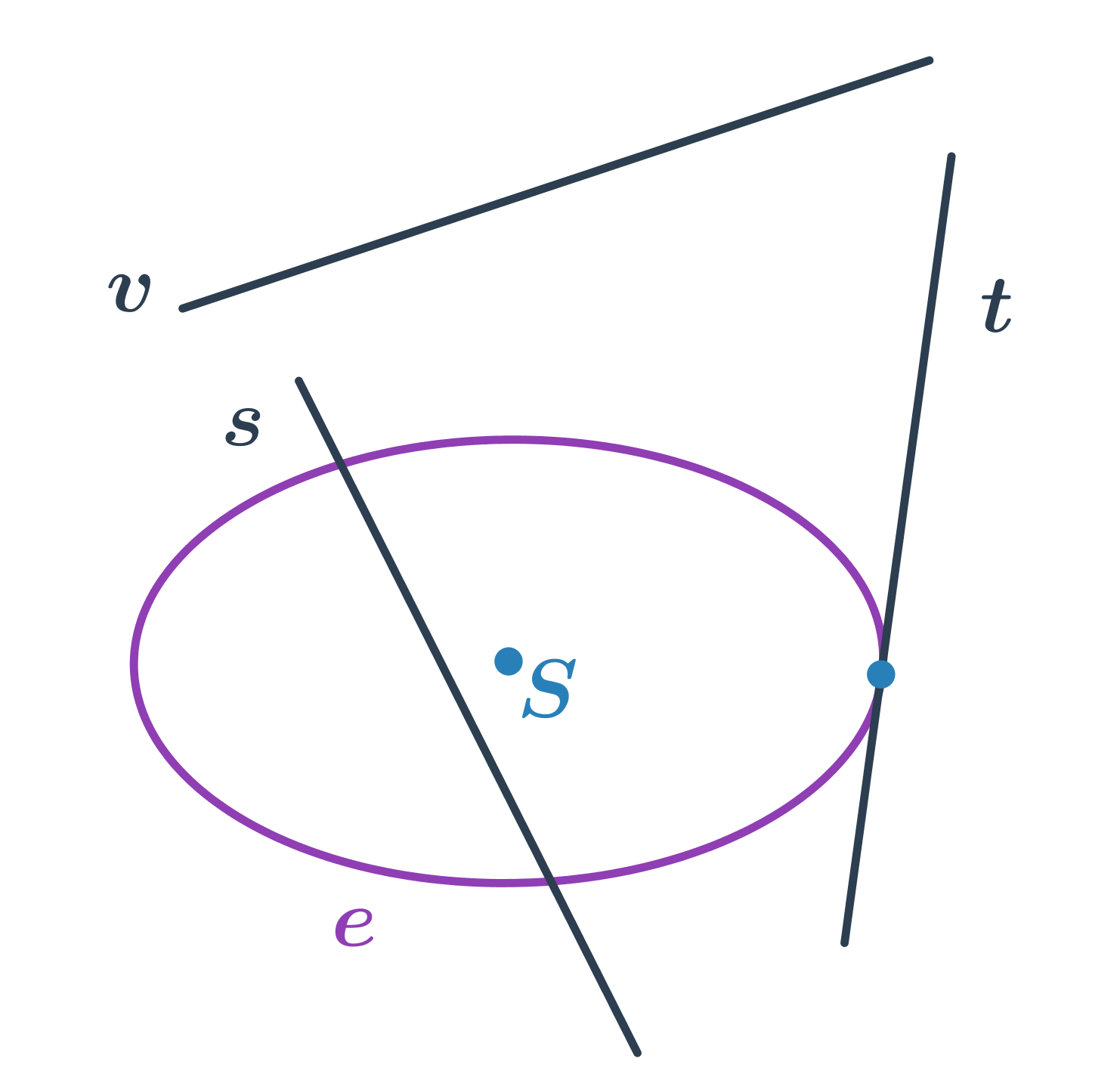
Elipsa a přímka
- přímka s protíná elipsu ve dvou bodech – sečna elipsy
- přímka t protíná elipsu v jednom bodě – tečna elipsy
- přímka v elipsu neprotíná – vnější přímka elipsy
Rovnice tečny elipsy v bodě, který leží na elipse
Elipsa daná rovnicí \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu určenou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobně můžeme zapsat i rovnici tečny elipsy, která má hlavní osu rovnoběžnou s osou y.
Příklad: určení rovnice tečny elipsy v jejím daném bodě
Určete rovnici tečny elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jejím bodě T[1;-2].
- Ověříme, zda bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Tečna má rovnici \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme souřadnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme se zlomků: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme závorky: -2x+4 -4y+8=18
- A dostaneme obecnou rovnici tečny: x+2y+3=0
Parabola je množina všech bodů roviny, které mají stejnou vzdálenost od daného bodu (ohnisko) a dané přímky (řídicí přímka)
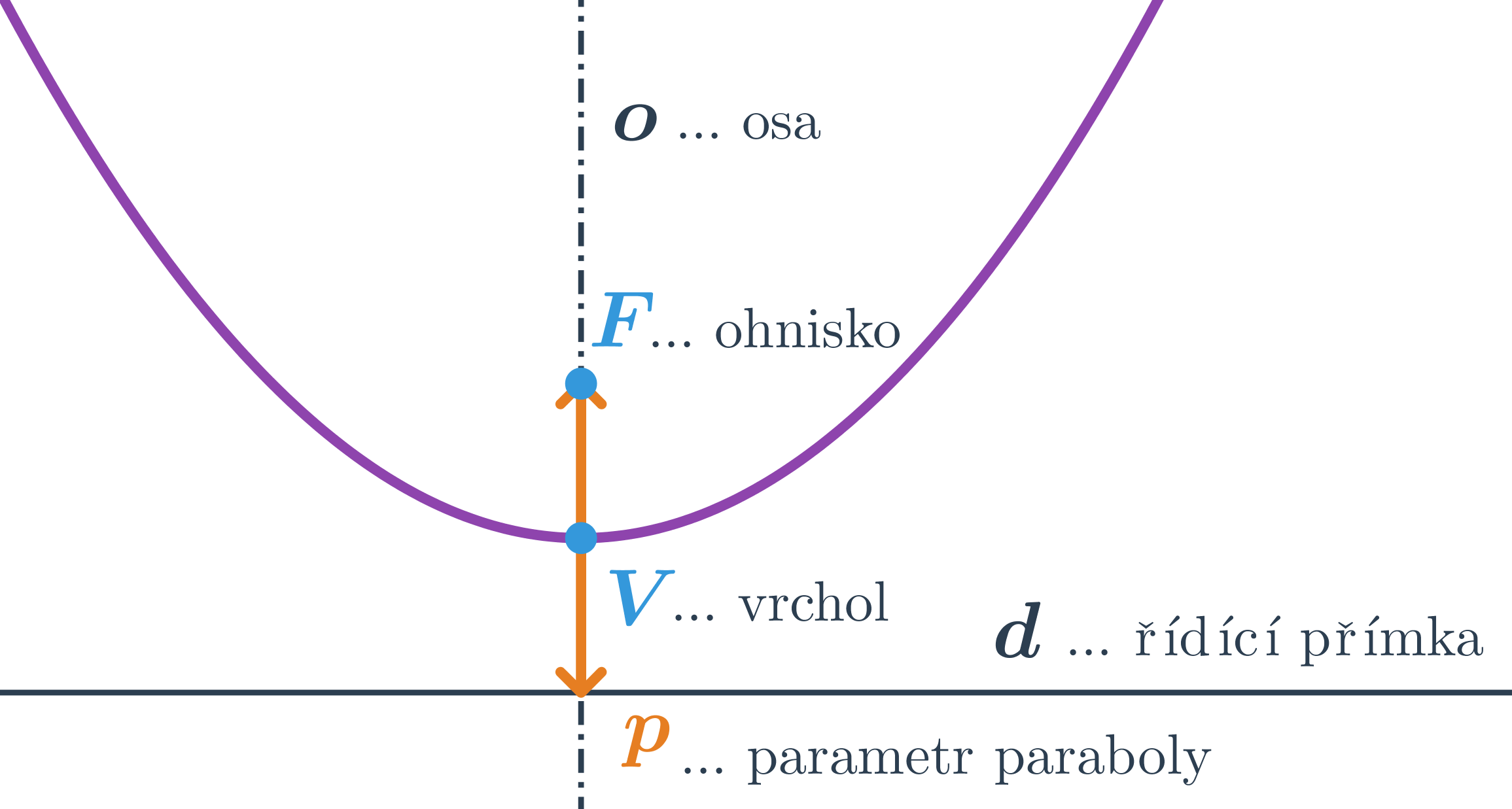
Vrcholová rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly rovnoběžná s osou y, vrcholová rovnice pak má tvar: (x-m)^2=\pm 2p(y-n)
- osa paraboly rovnoběžná s osou x, vrcholová rovnice pak má tvar: (y-n)^2=\pm 2p(x-m)
V rovnici paraboly označují m, n souřadnice vrcholu paraboly, tedy vrchol je bod V=[m;n]. Dále p je parametr paraboly = vzdálenost ohniska od řídicí přímky. Znaménko před parametrem závisí na poloze vrcholu vzhledem k bodům paraboly.
Příklad paraboly s osou rovnoběžnou s osou y
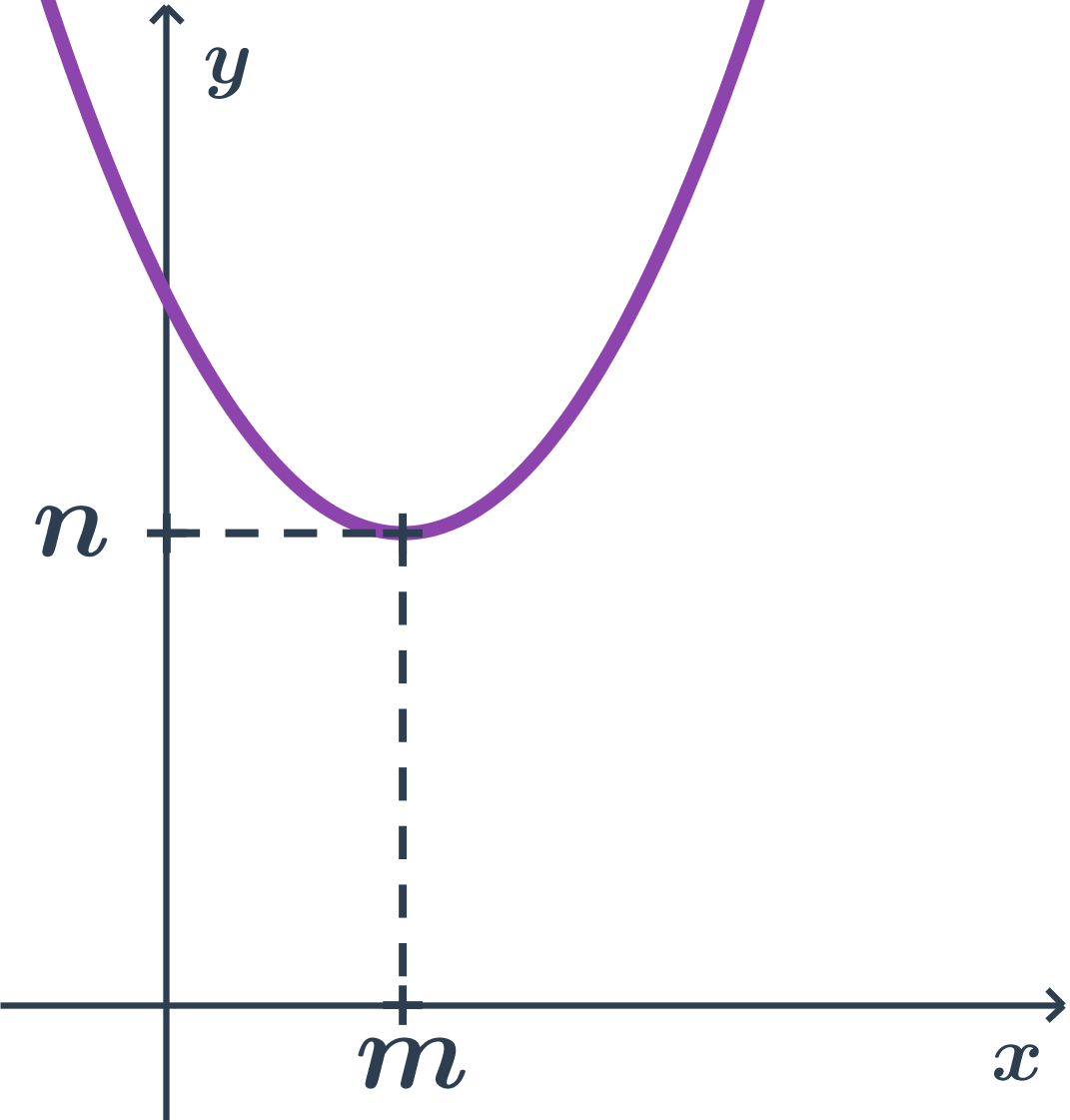
- body paraboly mají y souřadnici alespoň tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= + 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace
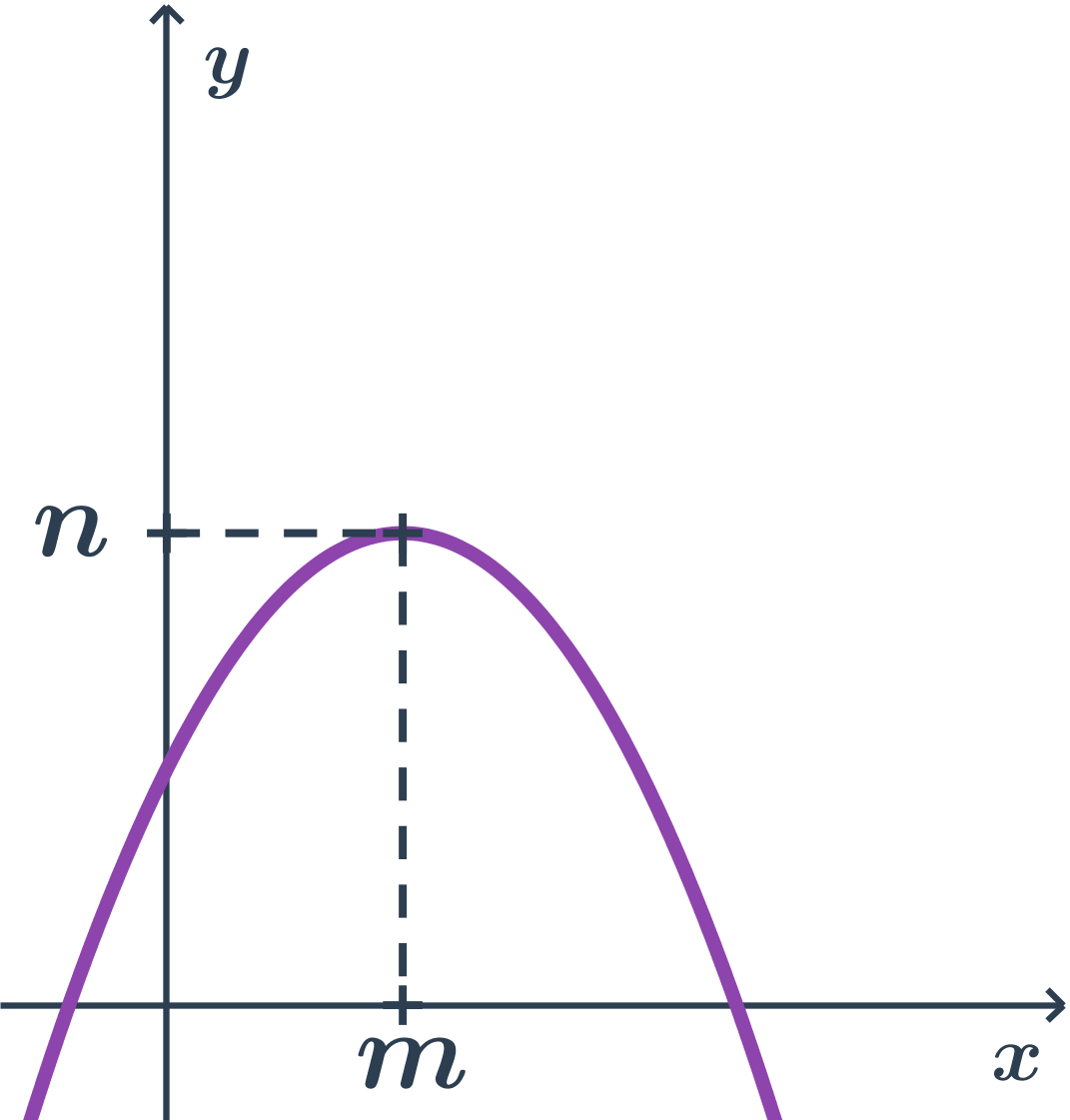
- body paraboly mají y souřadnici nejvýše tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= - 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou x
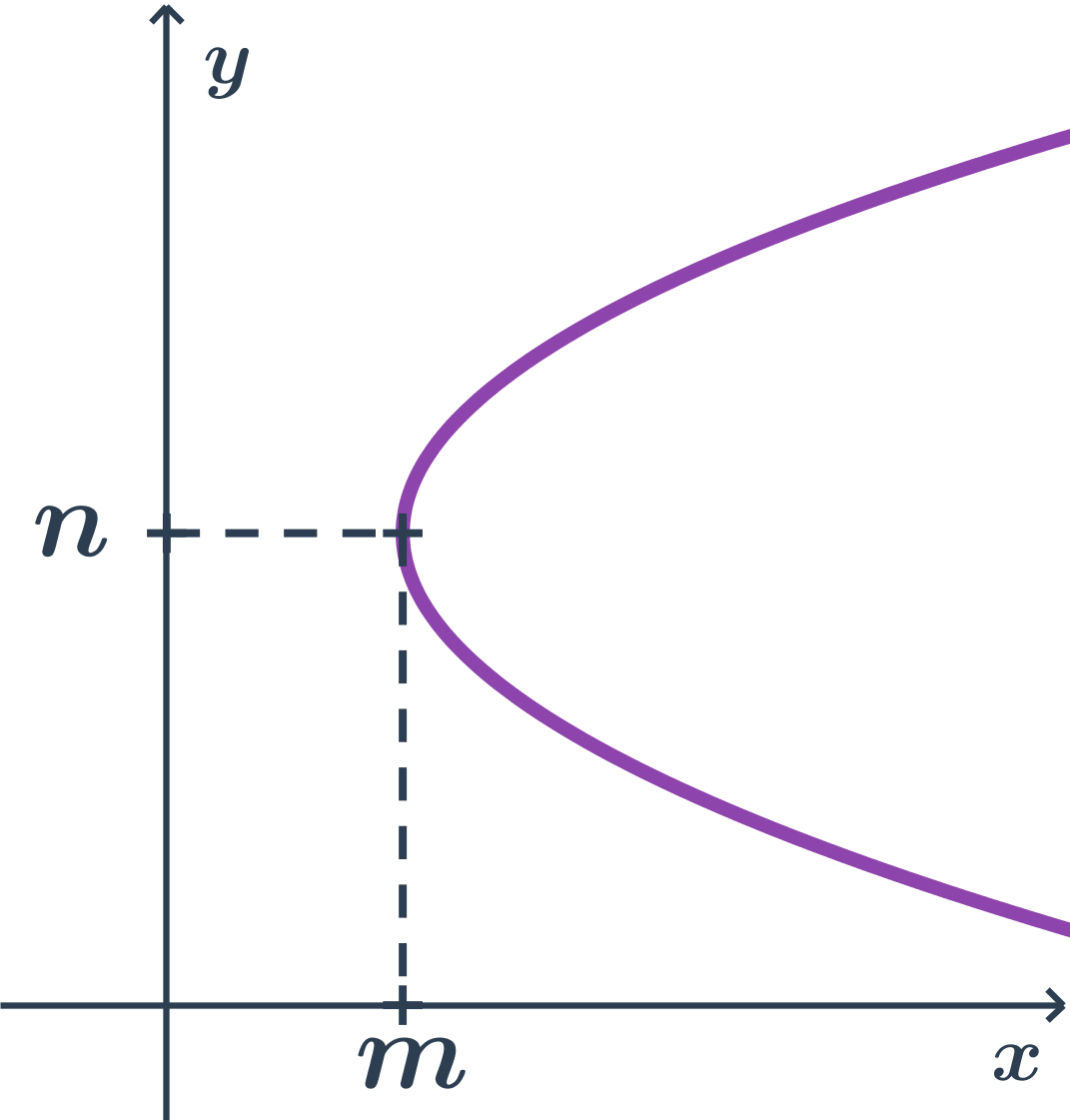
- body paraboly mají x souřadnici alespoň tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= + 2p(x-m)
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace
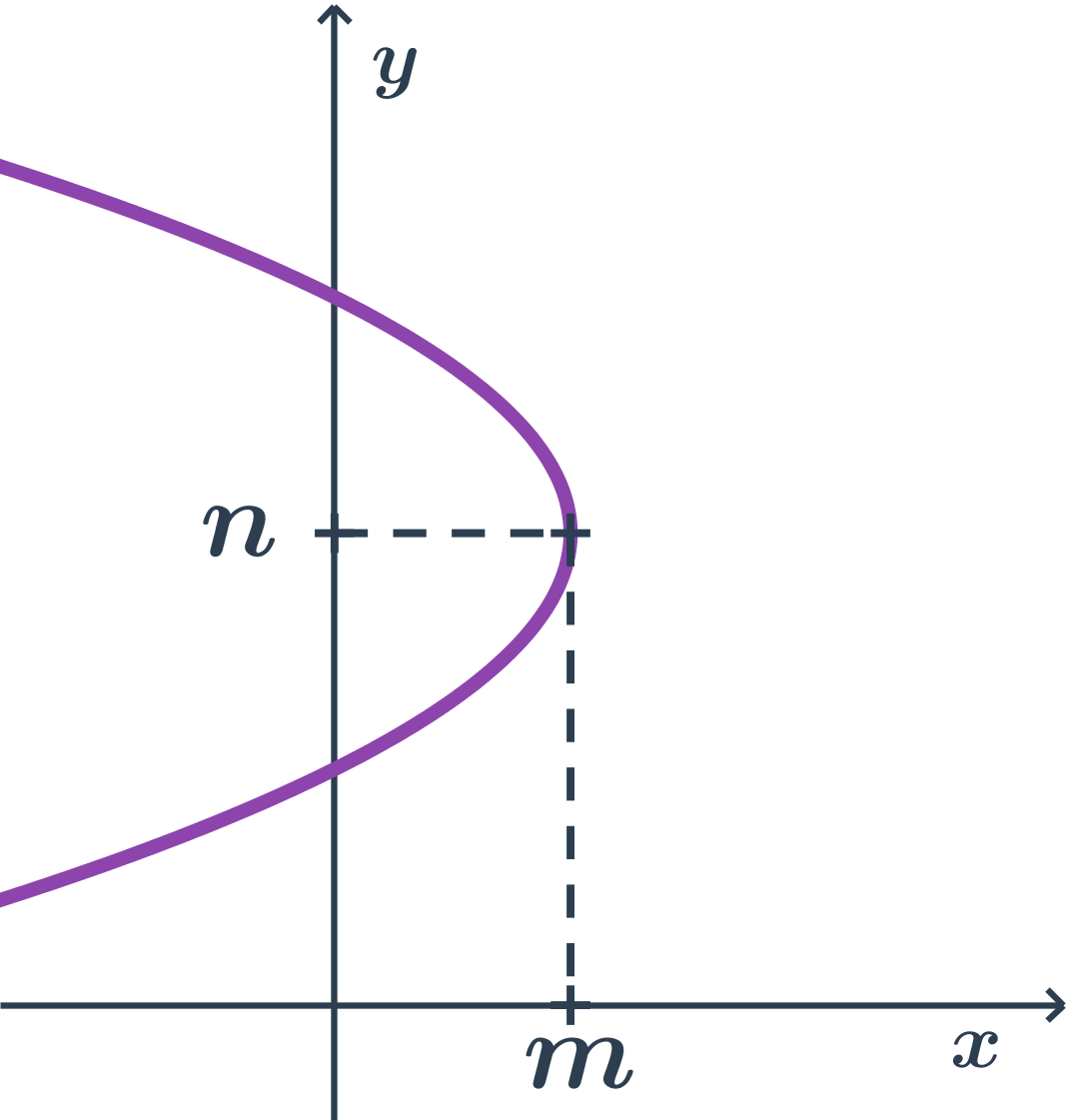
- body paraboly mají x souřadnici nejvýše tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= - 2p(x-m)
Obecná rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly je rovnoběžná s osou y: y=ax^2+bx+c
- osa paraboly je rovnoběžná s osou x: x=ay^2+by+c
Příklad paraboly s osou rovnoběžnou s osou y, obecná rovnice
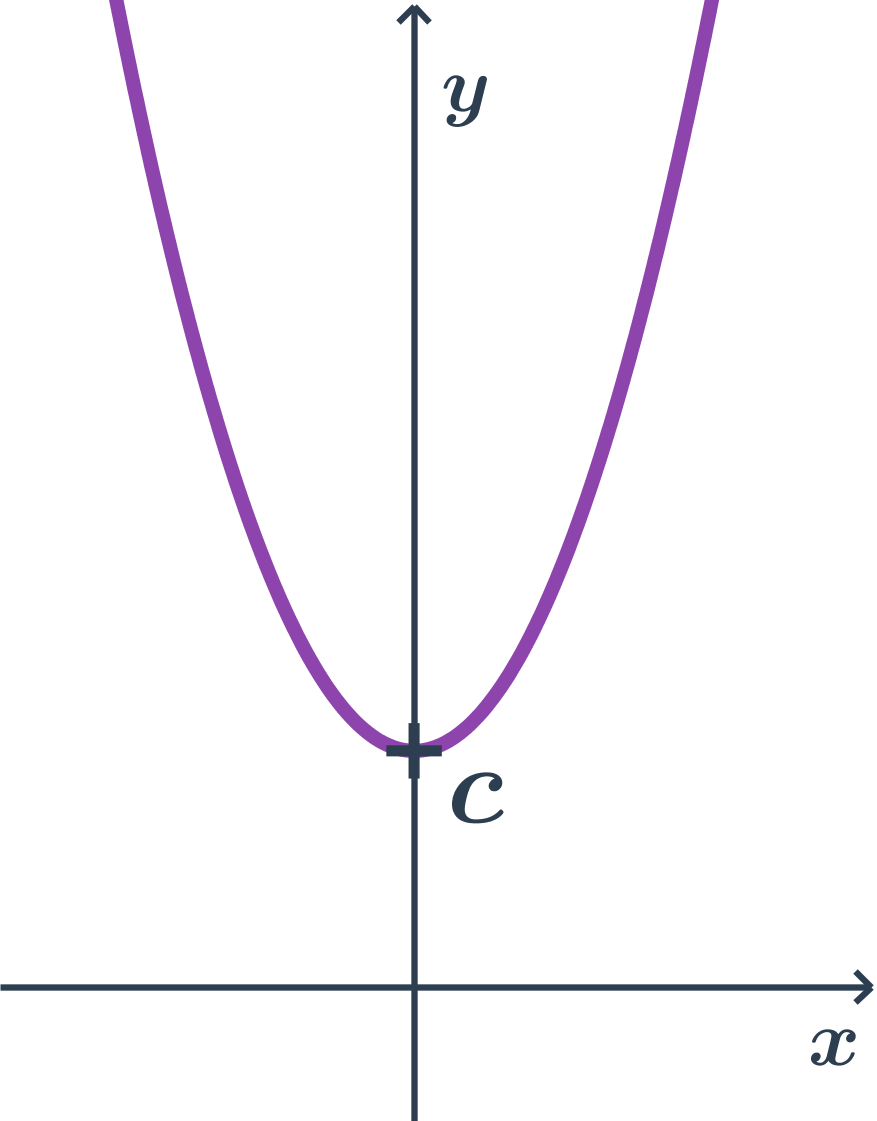
- obecná rovnice: y=ax^2+bx+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace, obecná rovnice
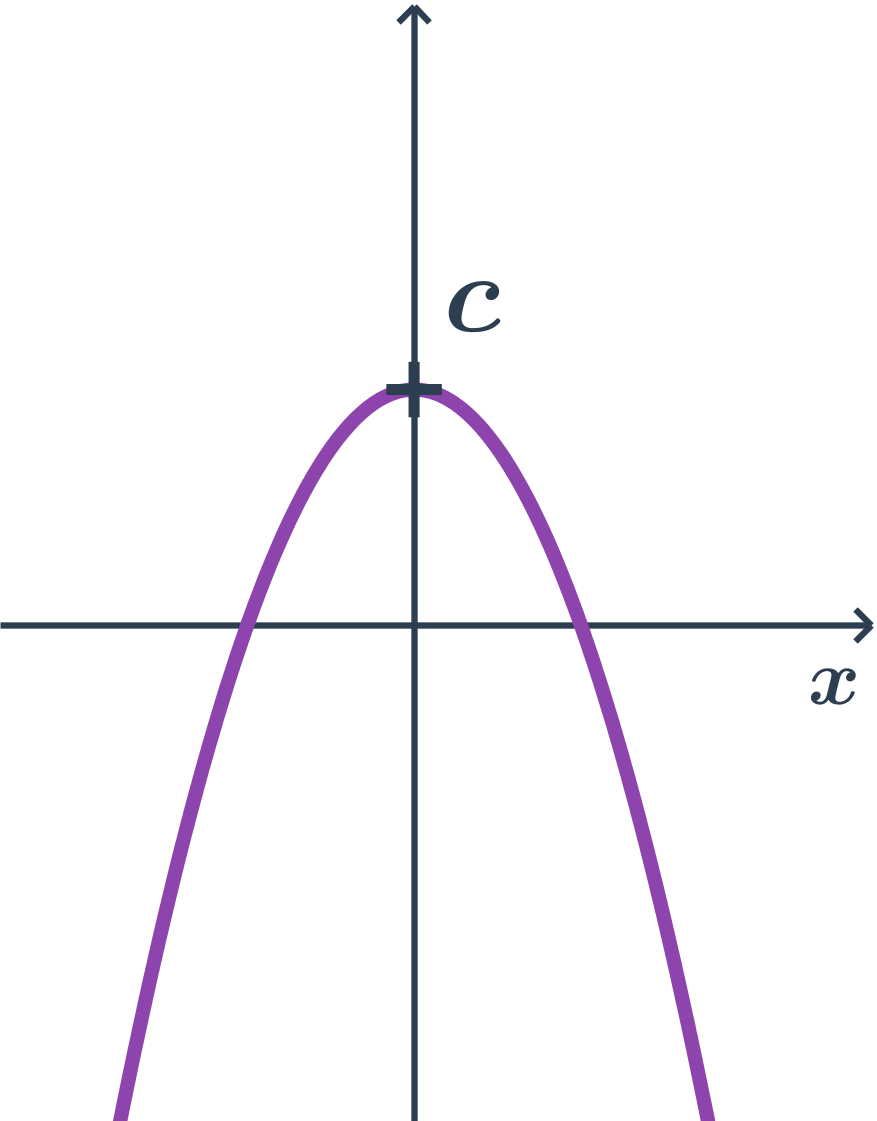
- obecná rovnice: y=ax^2+bx+c
- kde a \lt 0
Příklad paraboly s osou rovnoběžnou s osou x, obecná rovnice
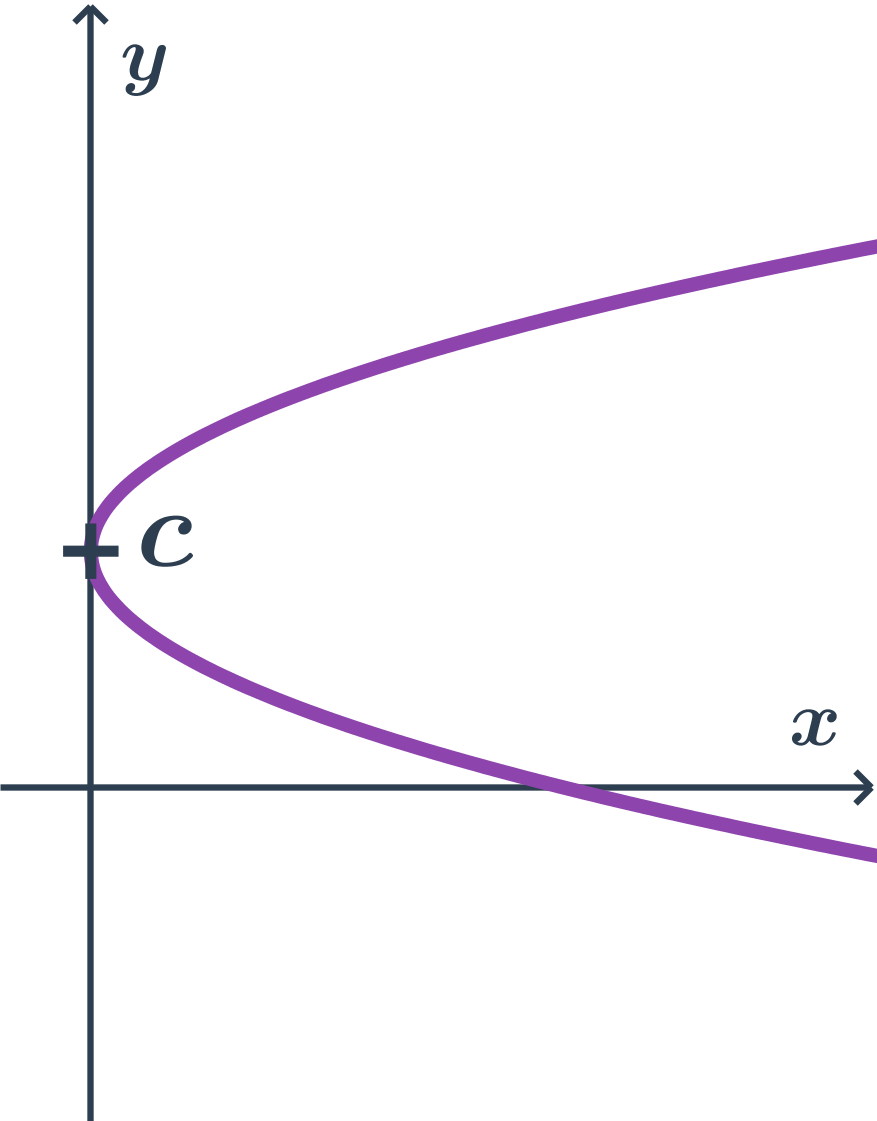
- obecná rovnice: x=ay^2+by+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace, obecná rovnice
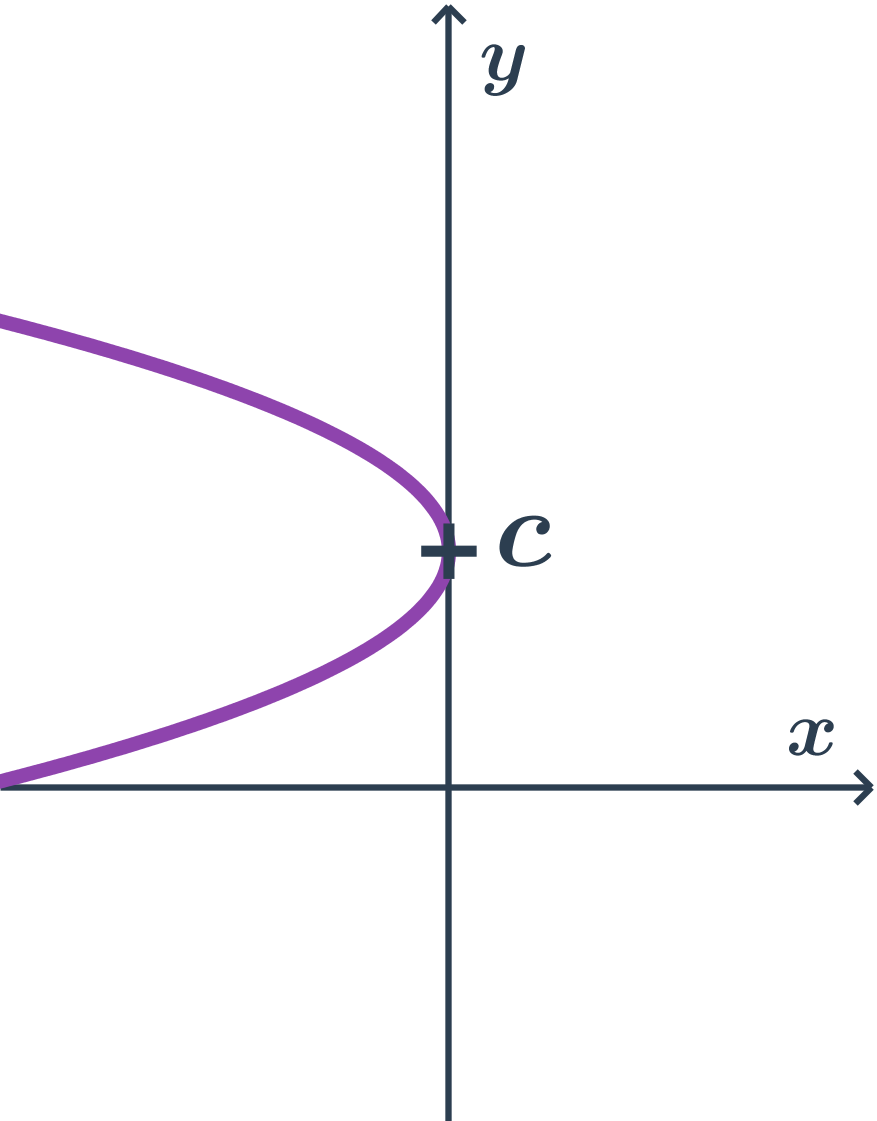
- obecná rovnice: x=ay^2+by+c
- kde a \lt 0
Přímka a parabola
- přímka b protíná parabolu ve dvou bodech – sečna paraboly
- přímka a se dotýká paraboly v jednom bodě – tečna paraboly
- přímka c neprotíná parabolu
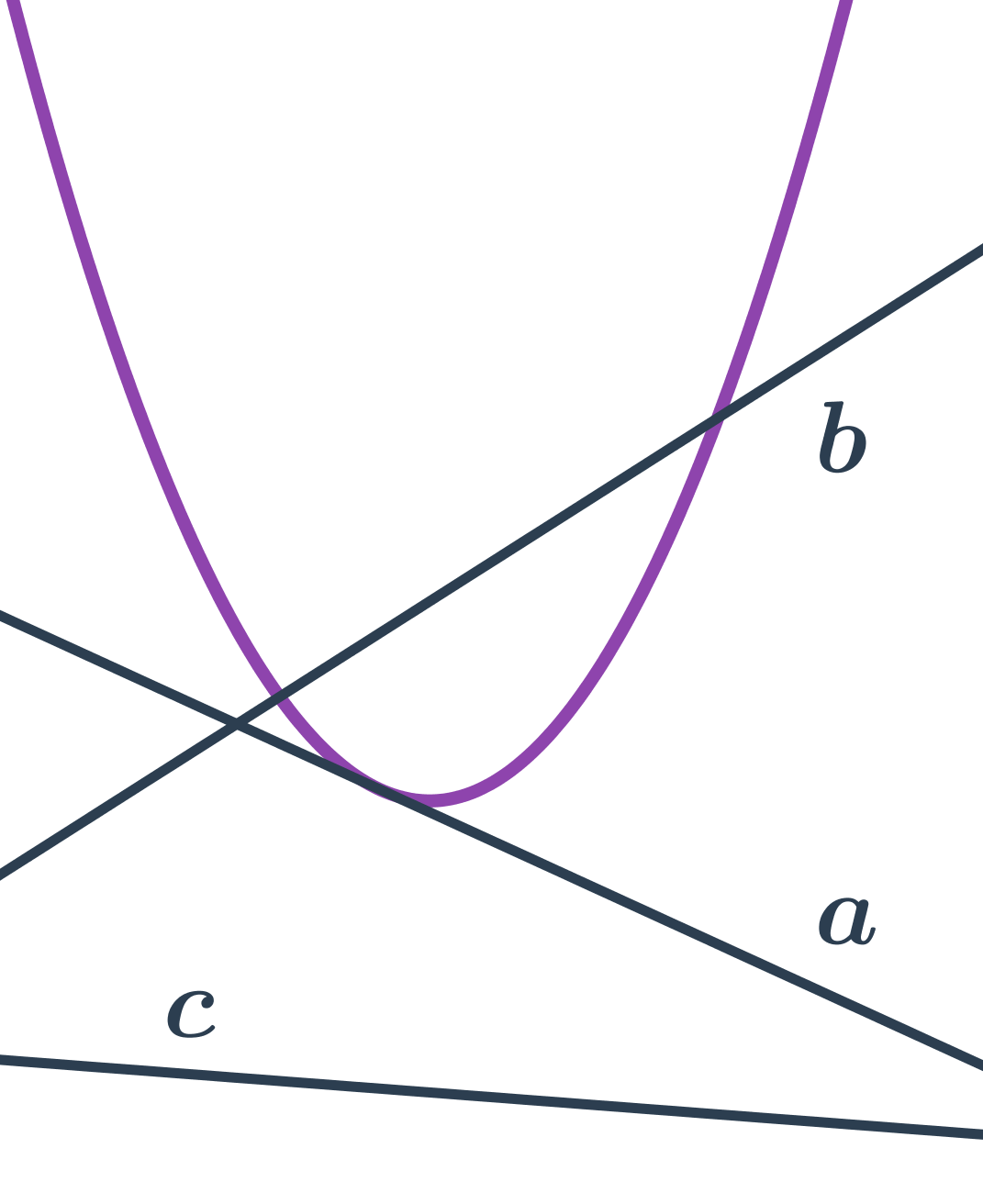
Rovnice tečny paraboly v bodě, který leží na parabole
- parabola daná rovnicí (x-m)^2=\pm 2p(y-n) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (x_0 - m)(x - m)=\pm p(y_0 - n) \pm p(y - n)
- parabola daná rovnicí (y-n)^2=\pm 2p(x-m) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (y_0 - n)(y - n)=\pm p(x_0 - m)\pm p(x - m)
Příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2=2(y-1)
- pro tuto parabolu je m=2, n=1, p=1
- na této parabole leží (souřadnice splňují rovnici) například bod T=[4;3]
- tečna dané paraboly v bodě T=[4;3] má rovnici: (4 - 2)(x - 2)= (3 - 1) + (y - 1)
- rovnici tečny můžeme zjednodušit na 2x-4 = y+1, tedy y = 2x-5
Druhý příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2= - 4(y-1)
- pro tuto parabolu je m=2, n=1, p=2, pravá strana je ve formě -2p(y-n)
- na této parabole leží (souřadnice splňují rovnici) například bod T=[6;-3]
- tečna dané paraboly v bodě T=[6;-3] má rovnici: (6-2)(x-2)= -2(-3-1)-2(y-1)
- rovnici tečny můžeme zjednodušit na 4x-8 = 8 -2y+2, tedy y = -2x+9
Speciální poloha přímky a paraboly
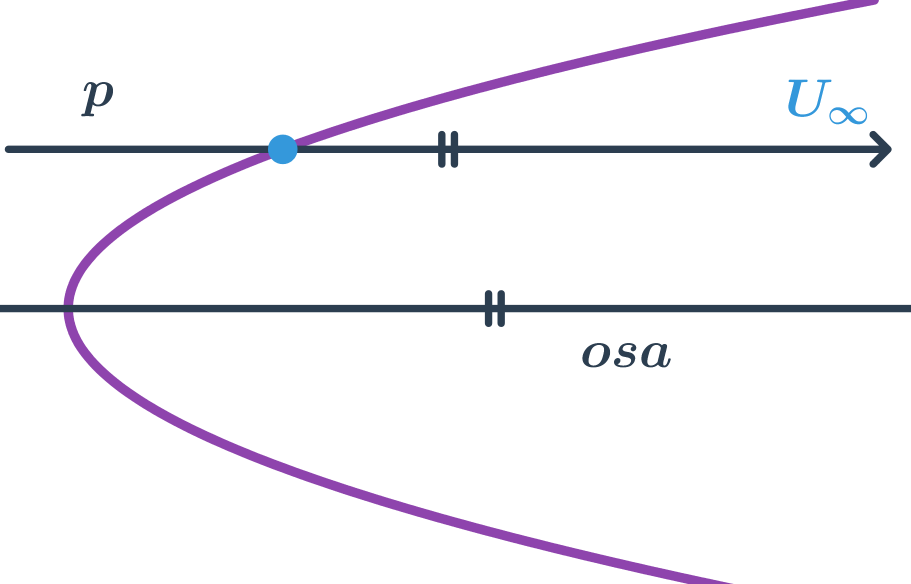
Přímka rovnoběžná s osou paraboly je sečna paraboly, přestože se zdá, že má s parabolou jeden společný bod. Druhý společný bod má tato přímka a parabola v nekonečnu.
Hyperbola
Hyperbola je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý rozdíl vzdáleností 2a, který je menší než vzdálenost ohnisek. Hyperbola se skládá ze dvou částí – větví hyperboly. Tyto dvě větve se blíží k přímkám, které nazýváme asymptoty. 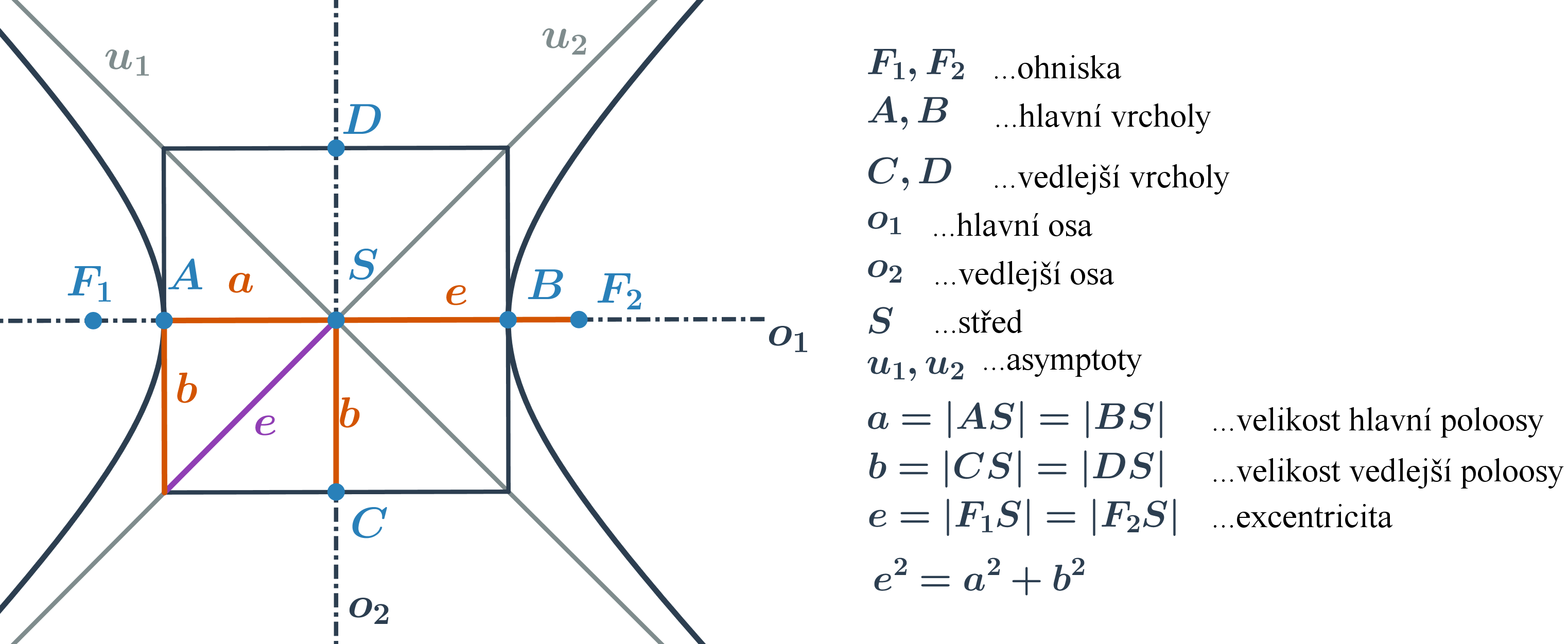
Středová rovnice hyperboly
Tvar středové rovnice hyperboly o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a,b závisí na poloze hlavní osy.
Středová rovnice hyperboly s hlavní osou rovnoběžnou s osou x
Pokud je hlavní osa rovnoběžná s osou x, rovnice je ve tvaru \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1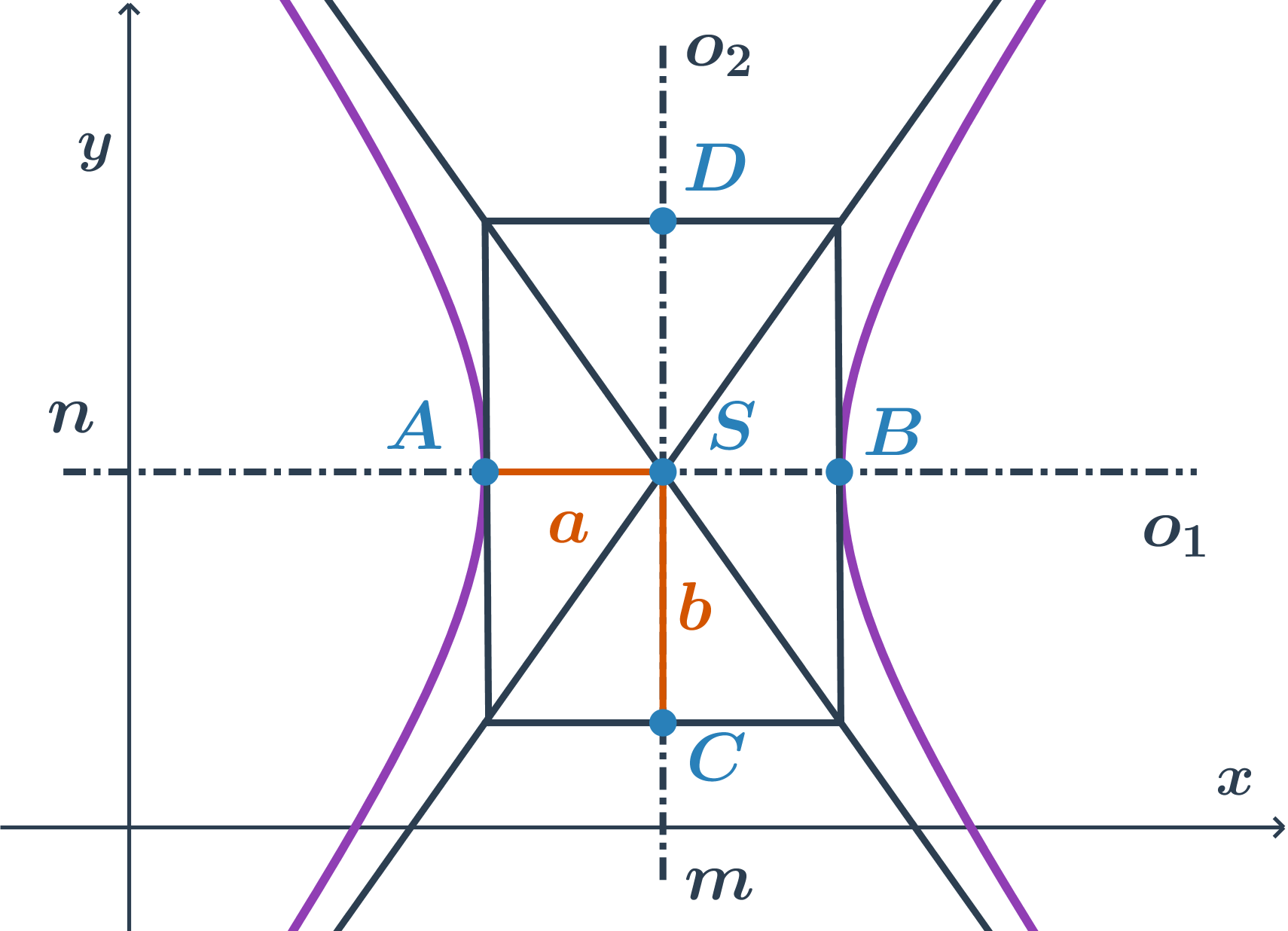
Středová rovnice hyperboly s hlavní osou rovnoběžnou s osou y
Pokud je hlavní osa rovnoběžná s osou y, rovnice je ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1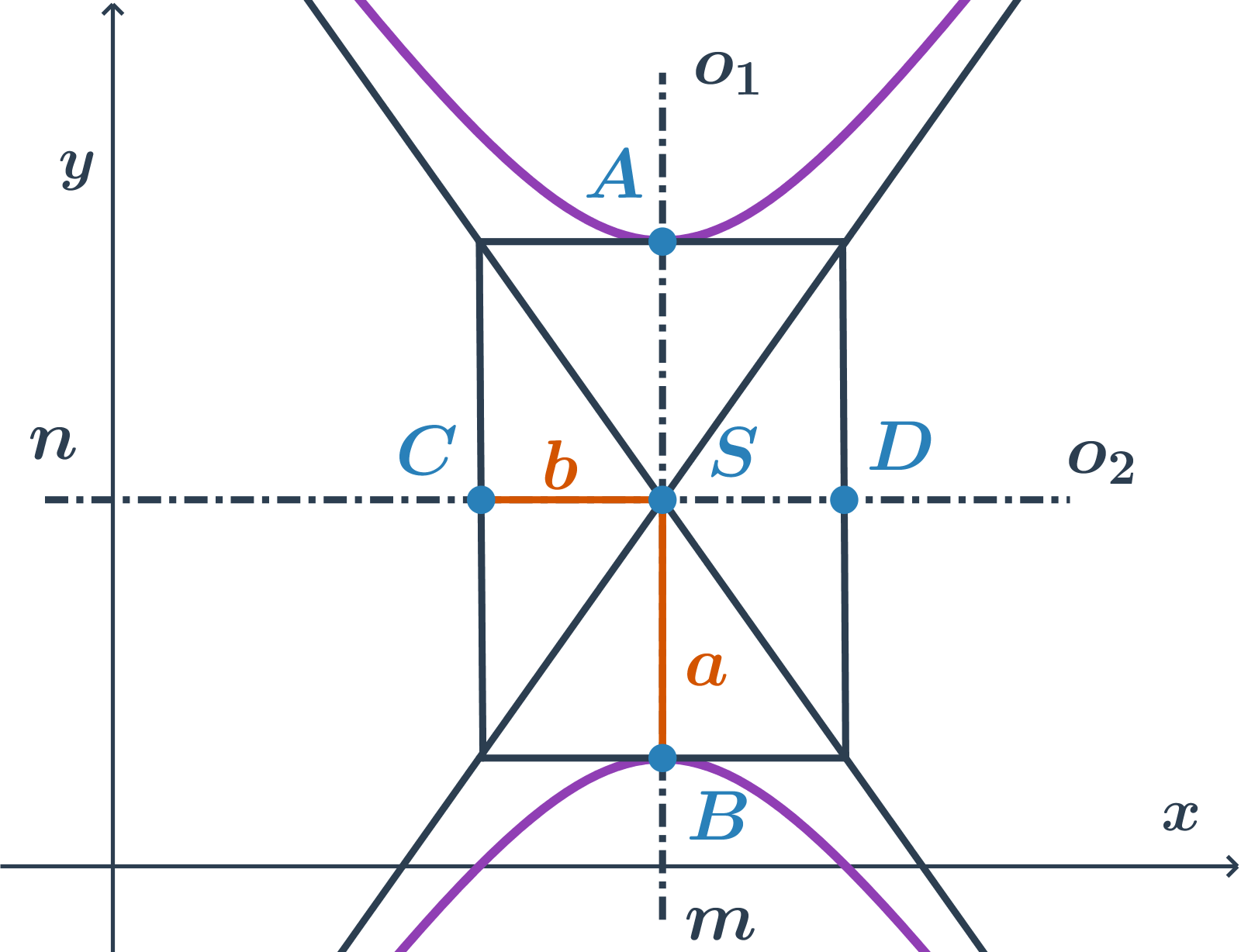
Na rozdíl od elipsy, nemusí být u hyperboly vždy hlavní poloosa a delší než vedlejší poloosa b. Pro rovnoosou hyperbolu dokonce platí a=b.
Jak ze středové rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa hyperboly?
- Podíváme se na znaménka členů s proměnnými x a y.
- Proměnná ve členu, který má před sebou znaménko plus udává, se kterou souřadnou osou je rovnoběžná hlavní osa hyperboly.
- Ve jmenovateli dané proměnné je pak (ve druhé mocnině) velikost hlavní poloosy.
- Stručně řečeno: je-li znaménko plus například u členu s proměnnou x, je hlavní osa rovnoběžná s osou x a ve jmenovateli je druhá mocnina velikosti hlavní poloosy a
Příklad: Určení středové rovnice hyperboly
Určete středovou rovnici hyperboly se středem v bodě S[1;-5], je-li velikost hlavní poloosy 2, velikost vedlejší poloosy 6 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1. Hlavní poloosa má velikost a, vedlejší b.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: -\frac{(x-1)^2}{6^2} +\frac{(y-(-5))^2}{2^2}=1
- Po úpravě: -\frac{(x-1)^2}{36} +\frac{(y+5)^2}{4}=1
Rovnice asymptot
Už víme, že asymptoty jsou přímky, ke kterým se hyperbola blíží. Pomohou při vykreslení hyperboly. Rovnice asymptot závisí na tvaru středové rovnice hyperboly.
Pro hyperbolu danou rovnicí ve tvaru \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 jsou rovnice asymptot:
y=\pm\frac{b}{a}(x-m)+n
Pro hyperbolu danou rovnicí ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 jsou rovnice asymptot:
y=\pm\frac{a}{b}(x-m)+n
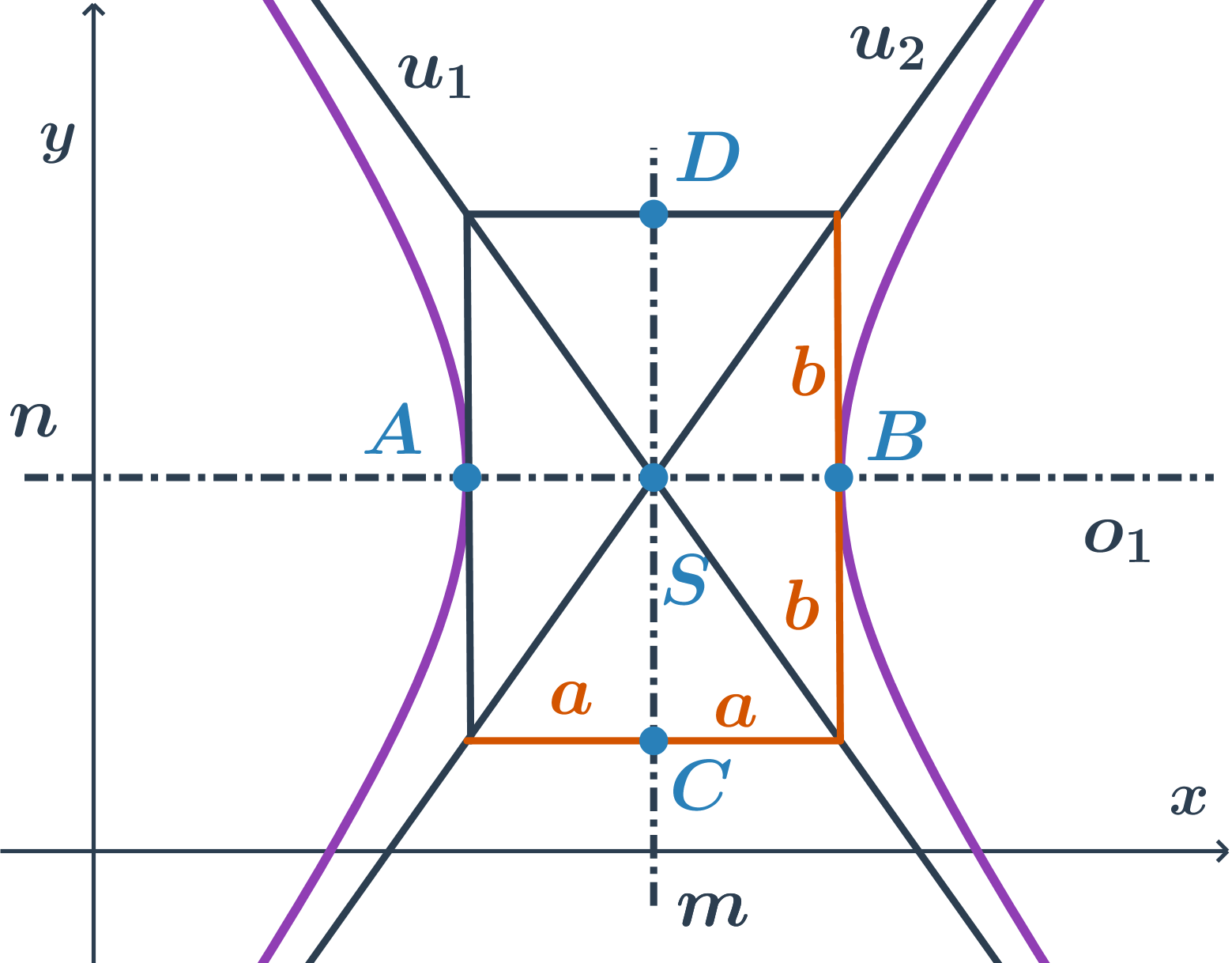
Jak načrtnout hyperbolu?
- Nejprve si vyznačíme střed, hlavní a vedlejší vrcholy.
- Poté sestrojíme charakteristický obdélník hyperboly. To je obdélník, který má strany rovnoběžné s osami a vrcholy hyperboly jsou středy jeho stran. Délky jeho stran jsou tedy 2a a 2b.
- Asymptoty jsou úhlopříčky charakteristického obdélníku.
Obecná rovnice hyperboly
Podobně jako existuje několik rovnic elipsy, můžeme i rovnici hyperboly zapsat různými způsoby. Obecná rovnice hyperboly je ve tvaru: Ax^2 +By^2+Cx+Dy+E=0, A\cdot B \lt 0. Podmínka A\cdot B \lt 0 zaručuje, že konstanty A, B mají opačná znaménka. Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí hyperboly. Praktické ověření, zda se jedná o hyperbolu provádíme převedením na středovou rovnici.
Příklad: Určuje daná rovnice hyperbolu?
Rozhodněte, zda rovnice -x^2+2y^2+8x-18y+31=0 určuje hyperbolu.
- Nejprve si uspořádáme členy: -x^2+8x+y^2-18y+40=0.
- Ze členů s proměnnou x vytkneme -1: -(x^2-8x)+y^2-18y+40=0
- K oběma stranám rovnice přičteme konstantu 81 a odečteme konstantu 16, abychom členy s proměnnými x a y mohli upravit podle vztahu pro (a\pm b)^2: -(x^2-8x+16)+y^2-18y+81+40=81-16
- A upravíme: -(x-4)^2 +(y-9)^2+40=65
- Převedeme konstantu 40 na druhou stranu rovnice: -(x-4)^2 +(y-9)^2 =25
- Na závěr rovnici vydělíme 25: -\frac{(x-4)^2}{25} +\frac{(y-9)^2}{25}=1
- Jedná se tedy o hyperbolu. Hlavní osa je rovnoběžná s osou y a a=b=5.
Hyperbola a přímka
- přímka s protíná hyperbolu ve dvou bodech – sečna hyperboly
- přímka t protíná hyperbolu v jednom bodě – tečna hyperboly
- přímka v hyperbolu neprotíná – vnější přímka hyperboly
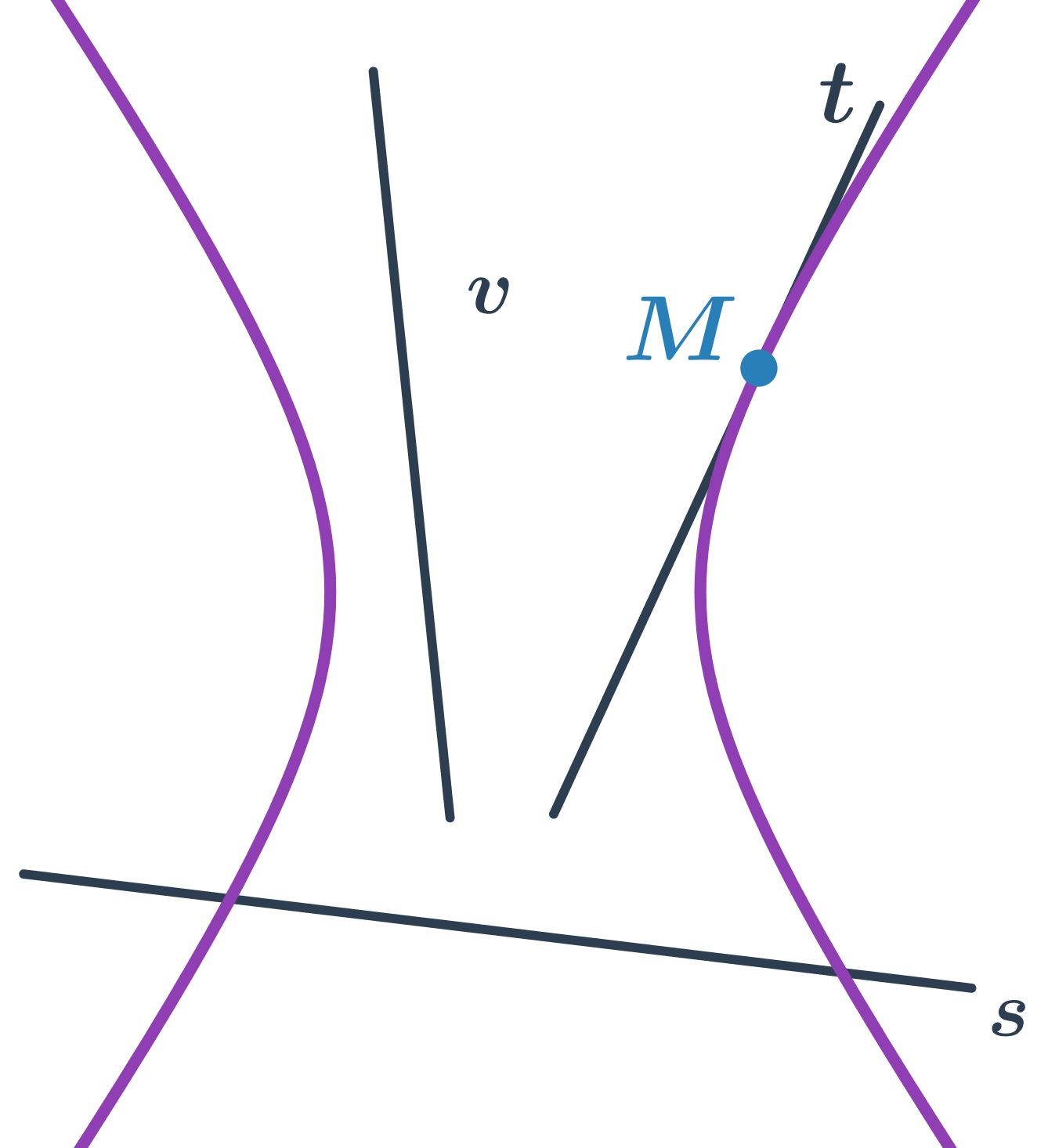
Speciální polohou sečny hyperboly je přímka, která je rovnoběžná s asymptotou. Taková sečna pak protíná hyperbolu v jednom bodě. 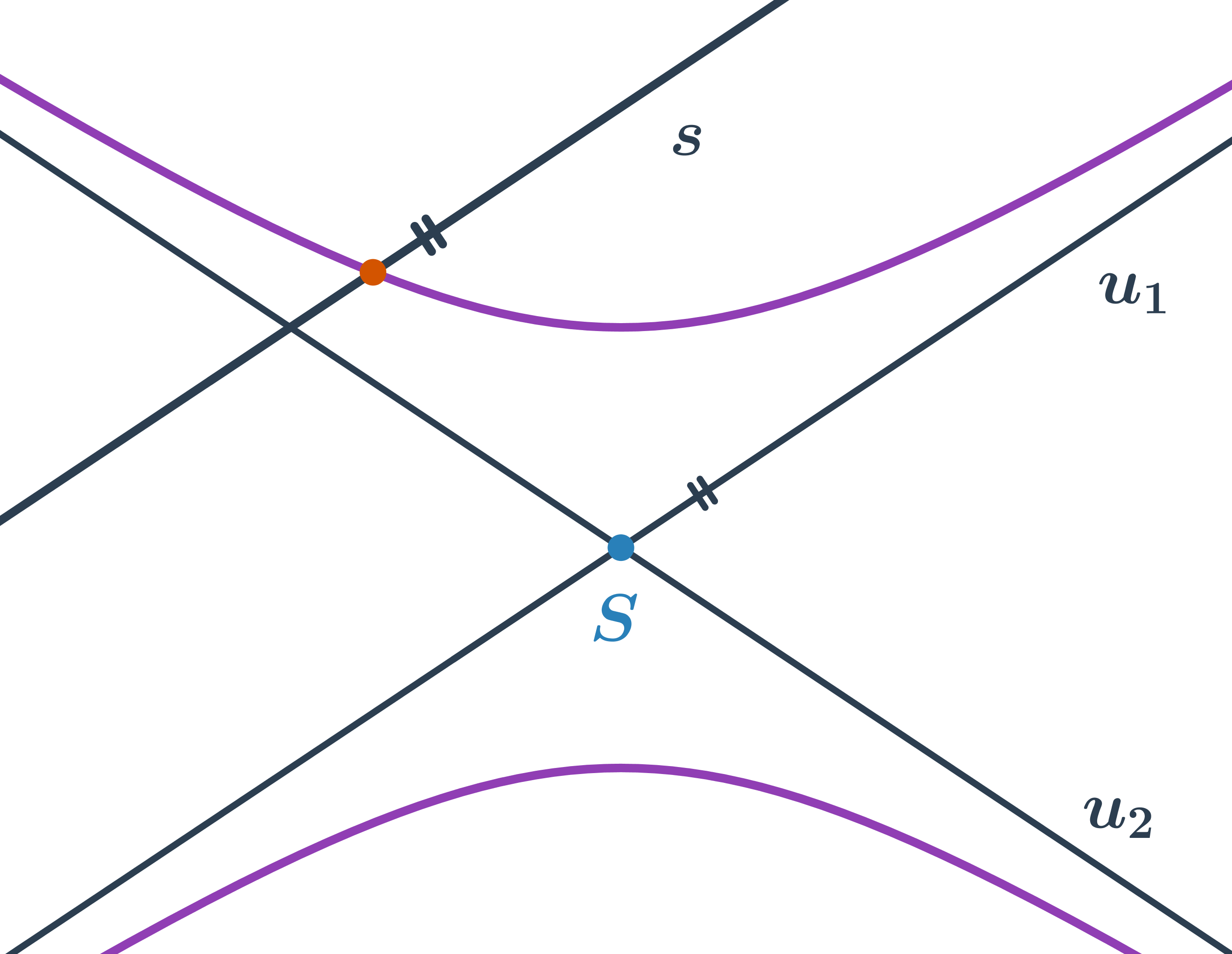
Jak rozlišit, je-li přímka tečna nebo sečna?
- Nejprve určíme vzájemnou polohu přímky a hyperboly.
- Pokud vyjdou dva průsečíky, jedná se o sečnu v obecné poloze.
- Pokud vyjde jeden průsečík, musíme ještě rozhodnout, jestli je přímka rovnoběžná s asymptotou. Pokud ne, jedná se o tečnu. V opačném případě jde o sečnu.
Rovnice tečny hyperboly v bodě, který leží na hyperbole
Hyperbola daná rovnicí \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu danou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} -\frac{(y-n)(y_0-n)}{b^2}=1.
Podobně můžeme zapsat i rovnici tečny hyperboly, která má hlavní osu rovnoběžnou s osou y.
Nahoru
