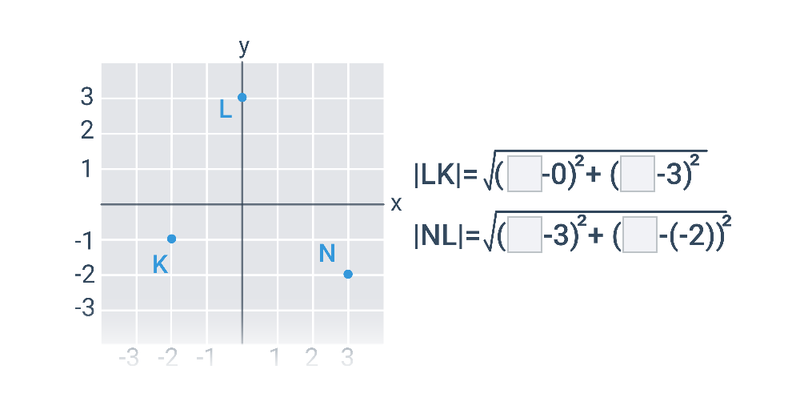Vzdálenost bodů v rovině

umime.to/GJW

Vzdálenost dvou bodů v rovině můžeme spočítat, když známe jejich souřadnice.

Jsou‑li dány souřadnice A=[a_x,a_y], B=[b_x,b_y], je vzdálenost bodu A od bodu B:

|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2}

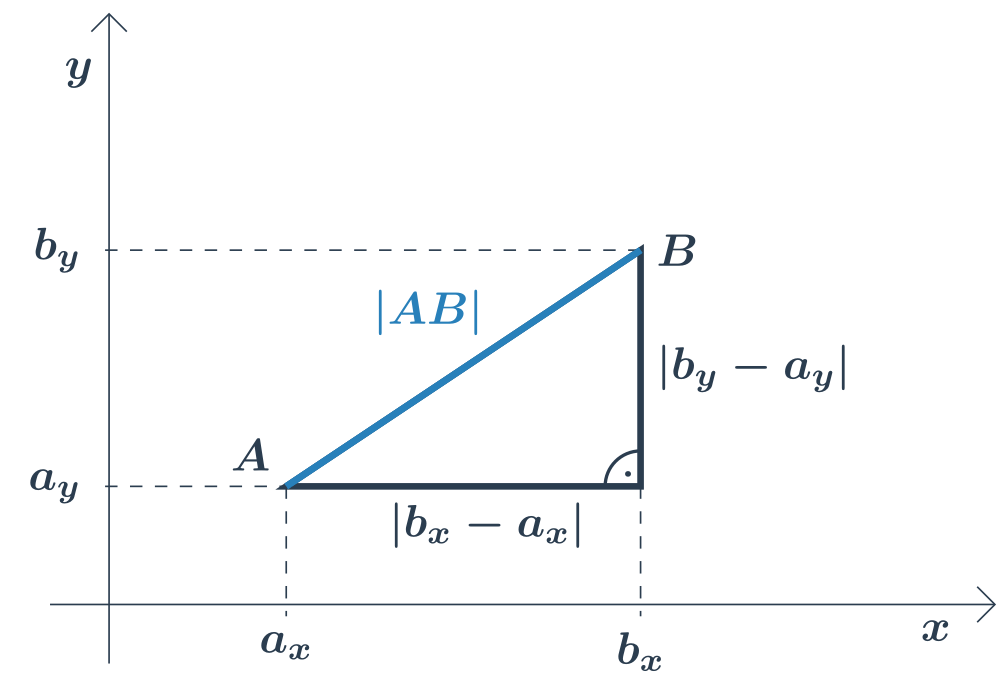
Vzoreček vychází z Pythagorovy věty. Všimněme si pravoúhlého trojúhelníku s délkami odvěsen (b_x-a_x) a (b_y-a_y), jehož přepona má délku |AB|.

Příklad: vzdálenost C[0;1],D[4;4]

|CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2}
Dosadíme souřadnice bodů C[0;1] a D[4;4]:
\sqrt{(4-0)^2 + (4-1)^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
Vzdálenost je: |CD|=5

Příklad: vzdálenost M[2;-1], N[-1;-2]

|MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2}
Dosadíme souřadnice bodů M[2;-1] a N[-1;-2]:
\sqrt{(-1-2)^2 + (-2-(-1))^2}=\sqrt{(-3)^2 + (-1)^2}=\sqrt{10}
Vzdálenost je: |MN|=\sqrt{10}

Přesouvání

Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.

Vzdálenost bodů v rovině

Přesouvání • střední

Rozhodovačka

Rychlé procvičování výběrem ze dvou možností.

Vzdálenost bodů v rovině

Rozhodovačka • lehké

Krok po kroku

Doplňování jednotlivých kroků v rozsáhlejším postupu.

Vzdálenost bodů v rovině

Krok po kroku • lehké

Psaná odpověď

Cvičení, ve kterém píšete odpověď na klávesnici.

Vzdálenost bodů v rovině

Psaná odpověď • lehké

Předcházející

Navazující

Cvičení

Vzdálenost bodů v rovině

umime.to/GJW

Přesouvání