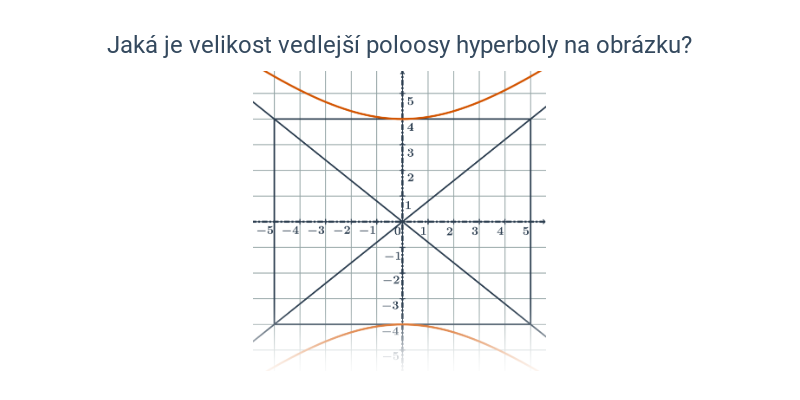
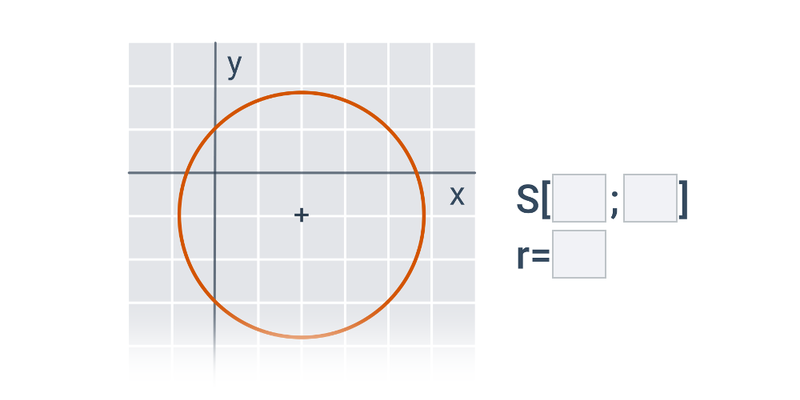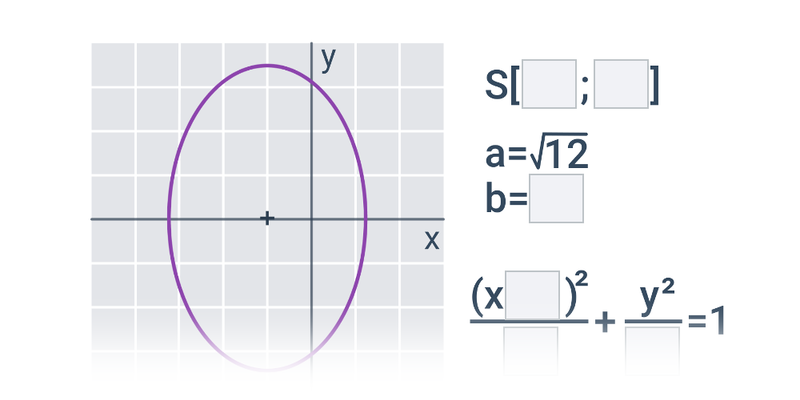Kuželosečky
F4PZkopírovat kód tématu
Zkopírovat krátkou adresu (umime.to/F4P)
Ukázat QR kód
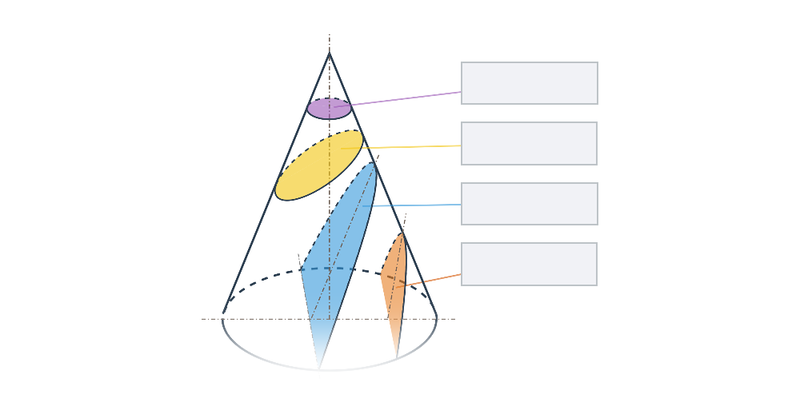
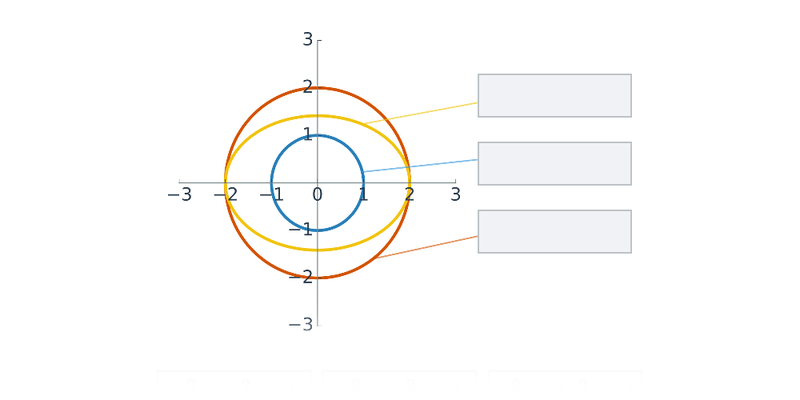
Všechny souhrnyJak již název napovídá, mají kuželosečky společný původ. Každá z nich vzikne jako řez rotační kuželové plochy rovinou. 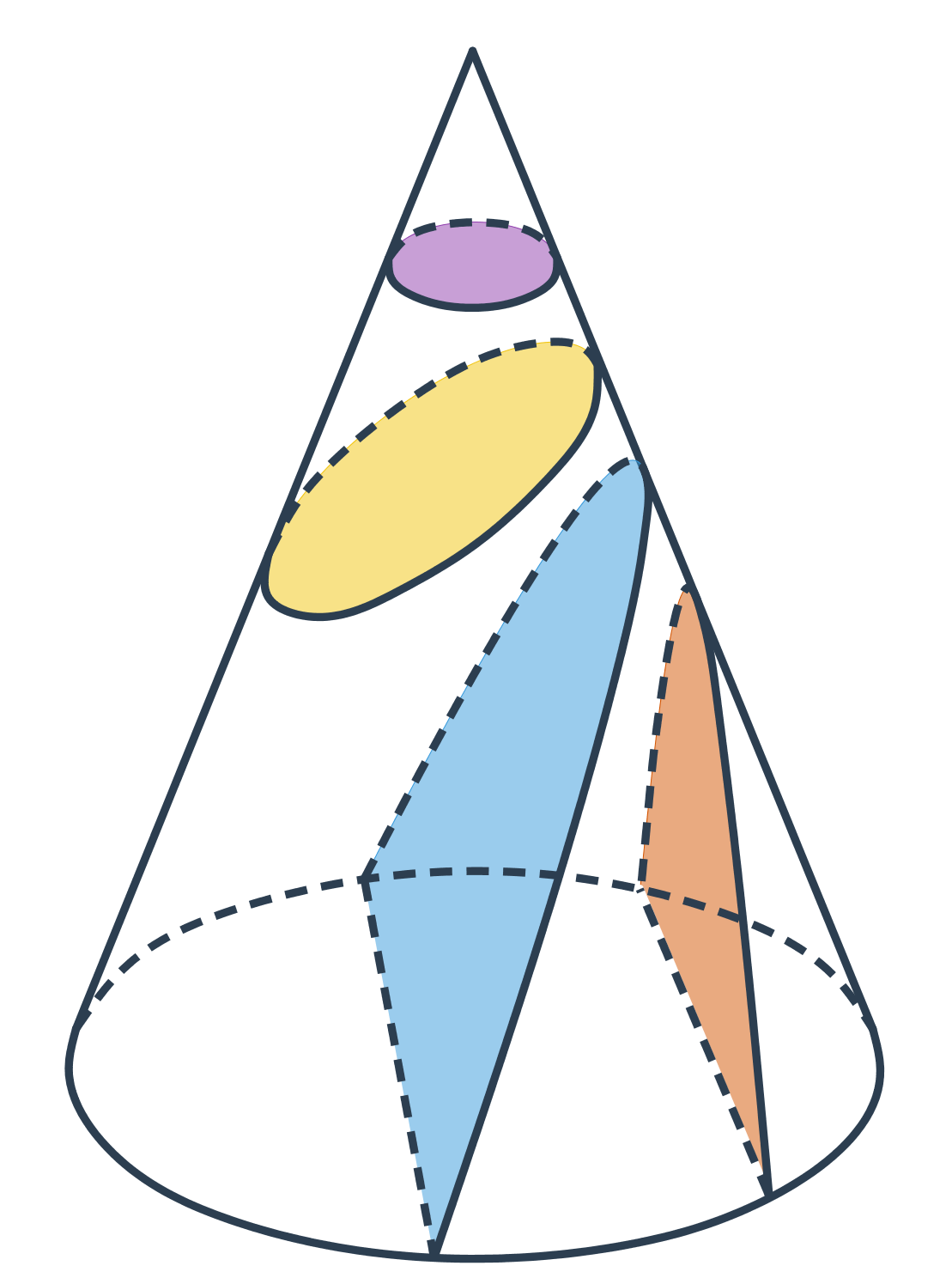
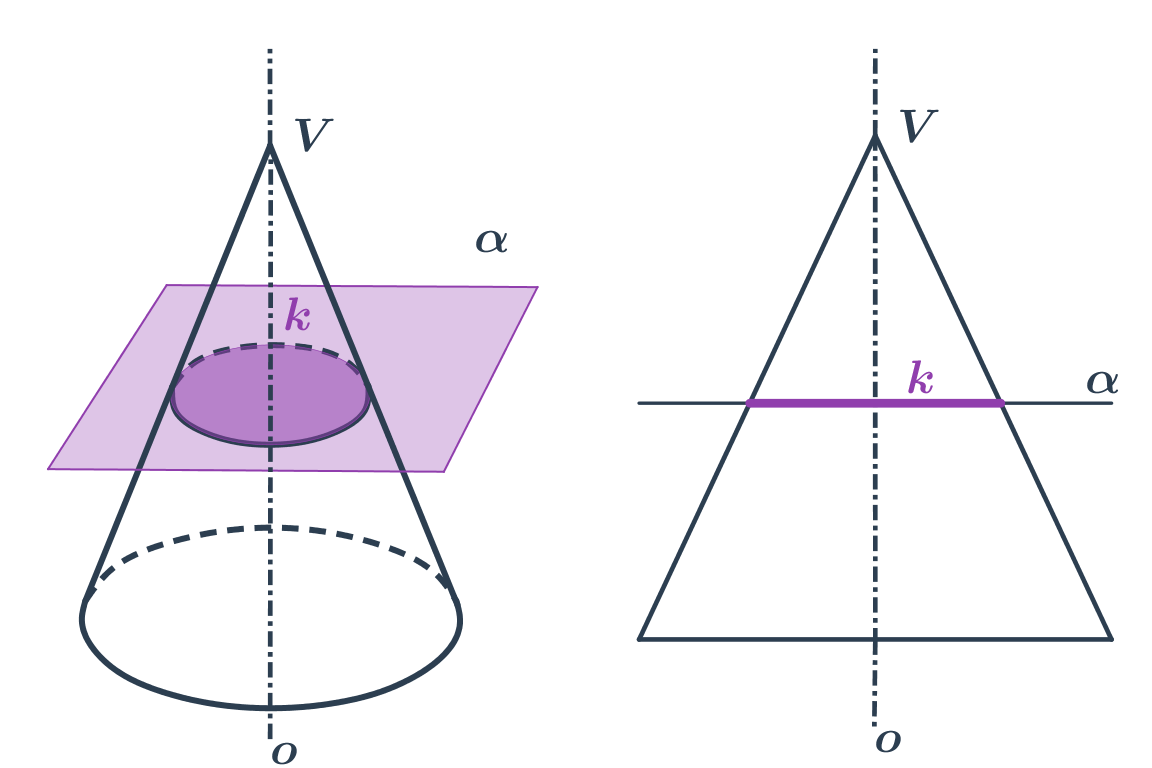
- Kružnice vznikne jako řez rovinou, která je kolmá na osu kuželové plochy.
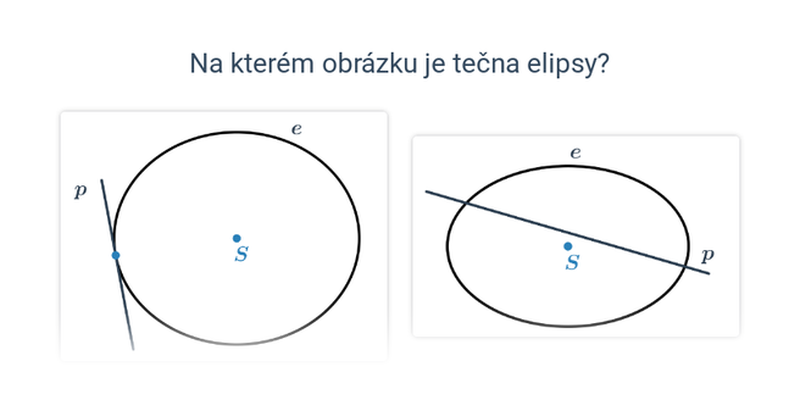
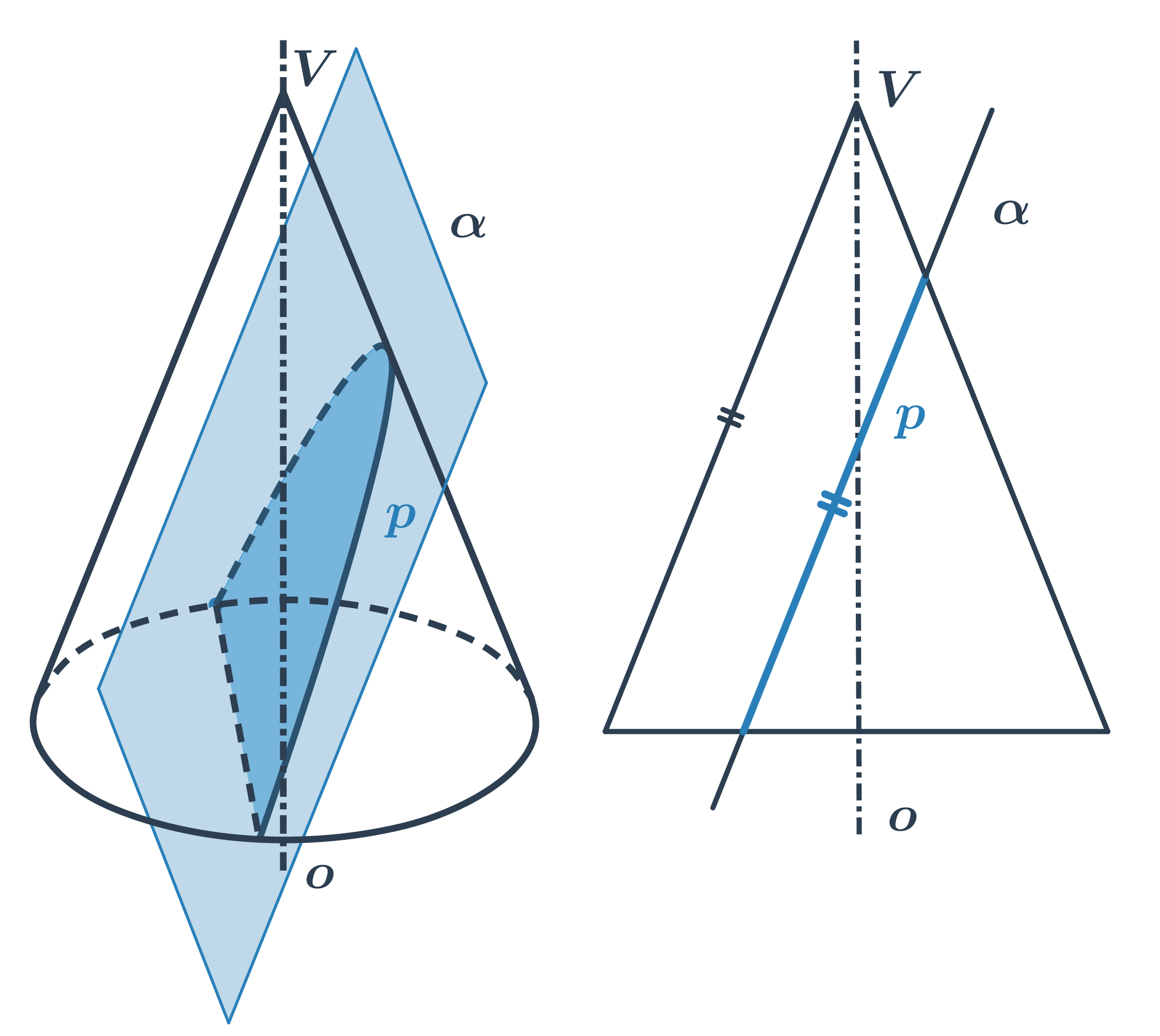
- Pokud rovinu řezu trochu nakloníme, vznikne elipsa.
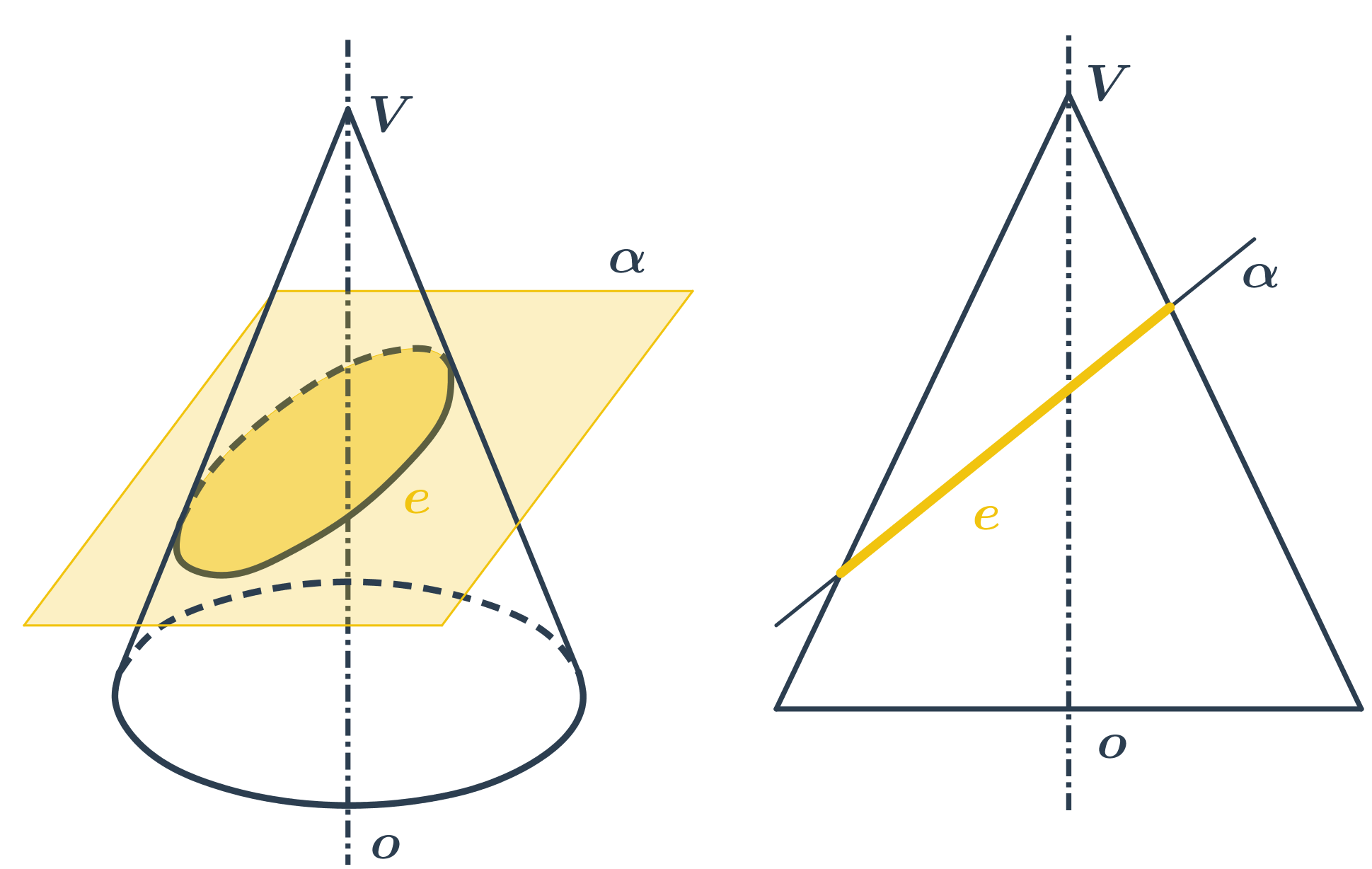
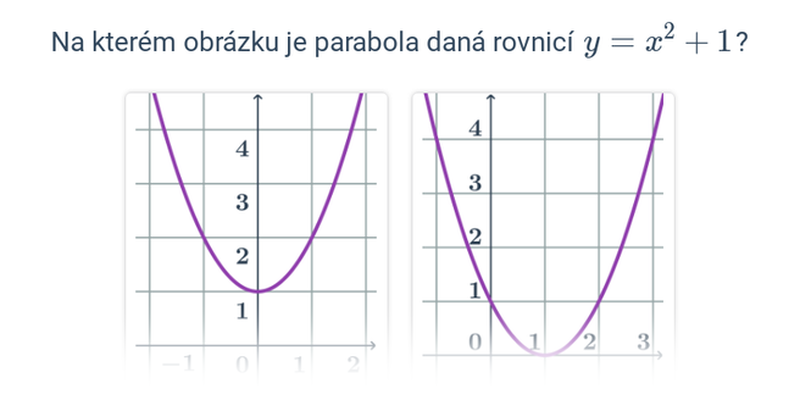
- Pokud rovinu řezu nakloníme tolik, že bude rovnoběžná s některou z přímek na kuželové ploše, vznikne parabola.
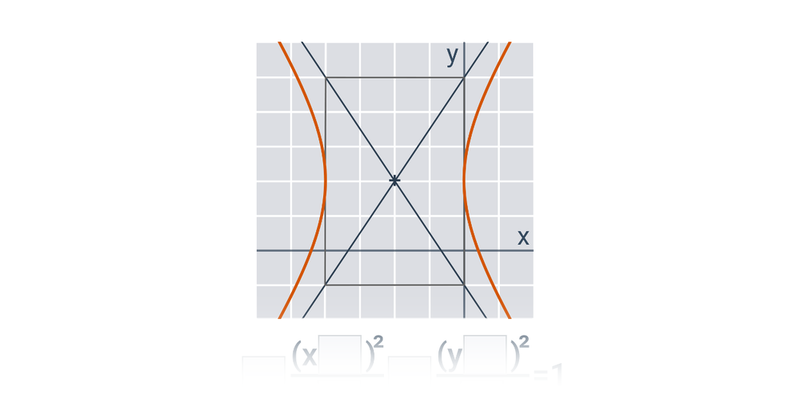
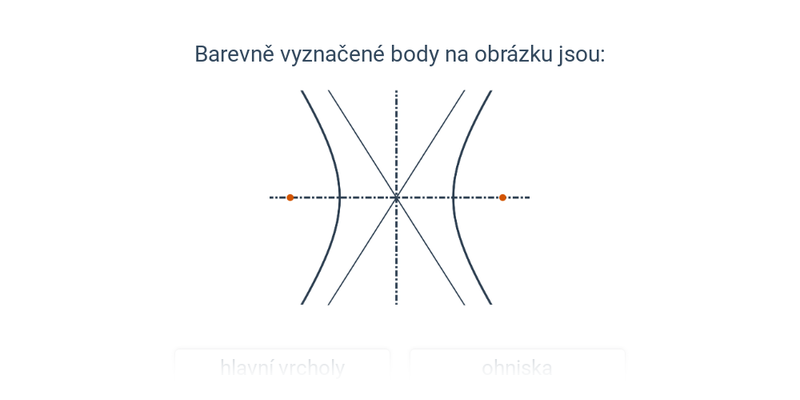
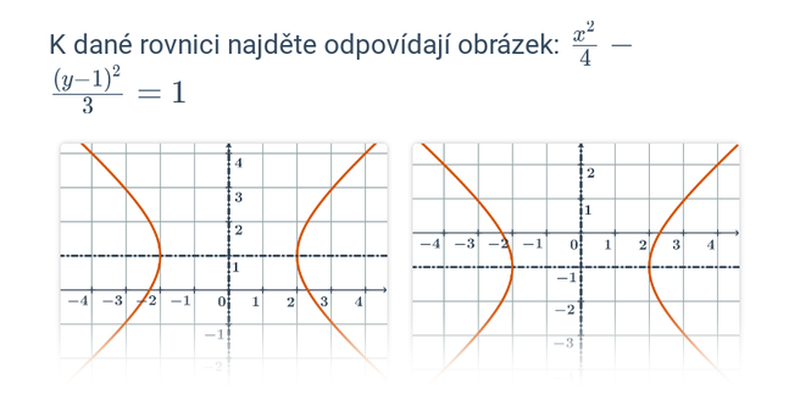
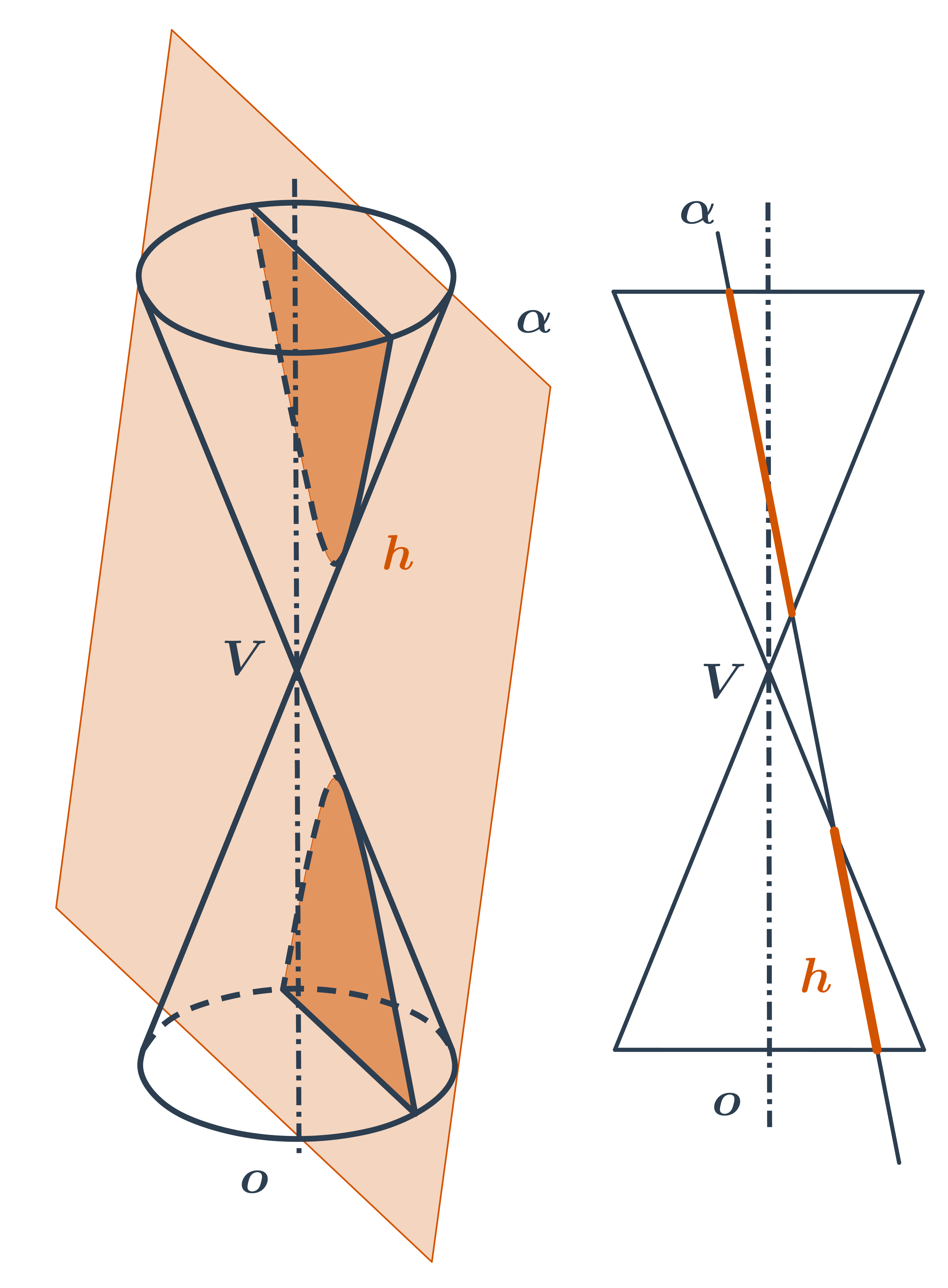
- Při dalším naklánění už rovina řezu protne obě části kuželové plochy a vznikne dvoudílná hyperbola.
Na kuželosečky můžeme také hledět jako na množiny bodů dané vlastnosti. V analytické geometrii často zapisujeme tyto množiny pomocí rovnic.
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Kuželosečky
Kuželosečky: pojmy
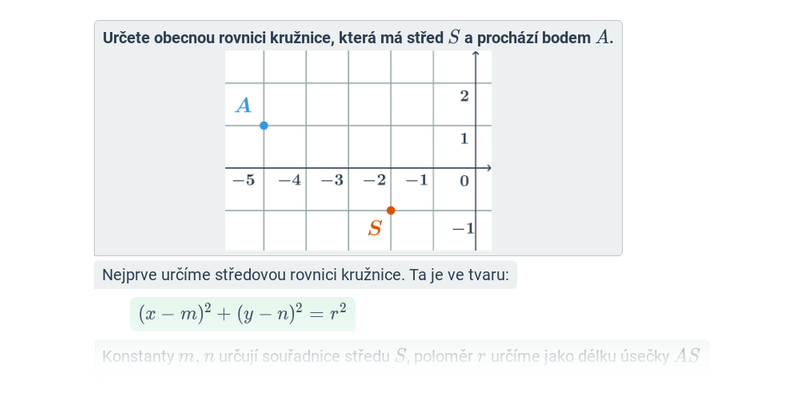
Kružnice: středová rovnice
Elipsa: středová rovnice
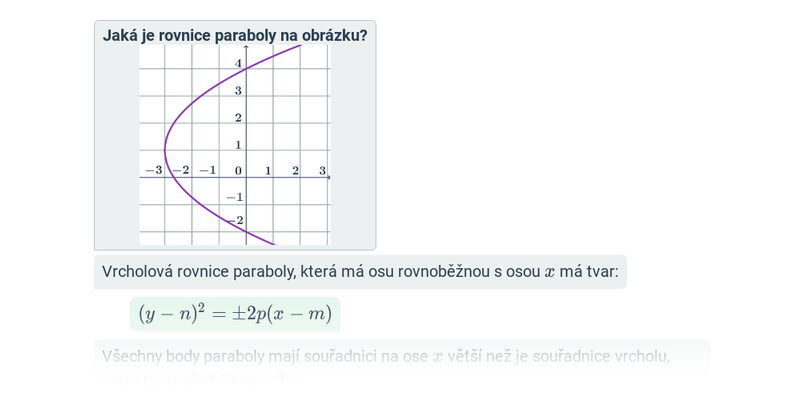
Parabola: rovnice
Hyperbola: středová rovnice
Kuželosečky: mix
Rovnice kuželoseček
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Kuželosečky
Kuželosečky: pojmy
Kružnice: pojmy
Elipsa: pojmy
Parabola: pojmy
Hyperbola: pojmy
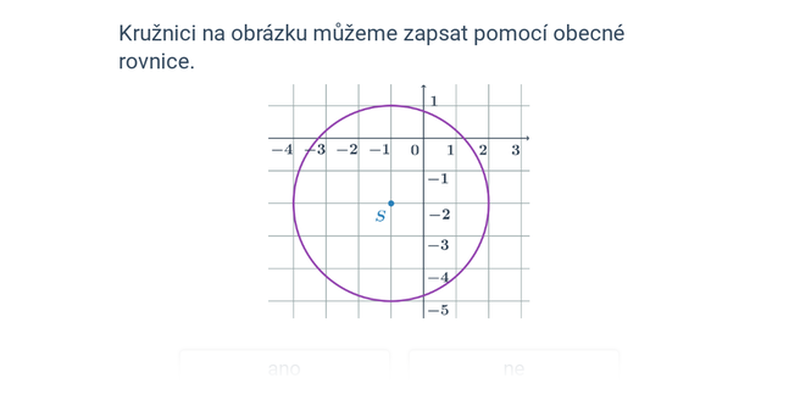
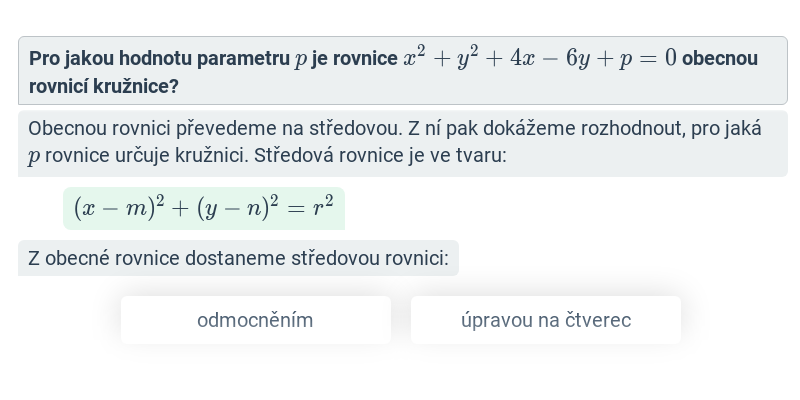
Kružnice: obecná rovnice
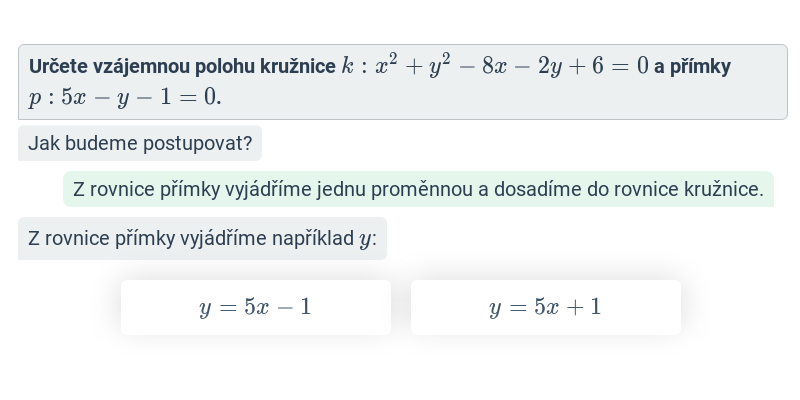
Kružnice: vzájemná poloha přímky a kružnice
Elipsa: středová rovnice
Elipsa: obecná rovnice
Elipsa: vzájemná poloha přímky a elipsy
Parabola: rovnice
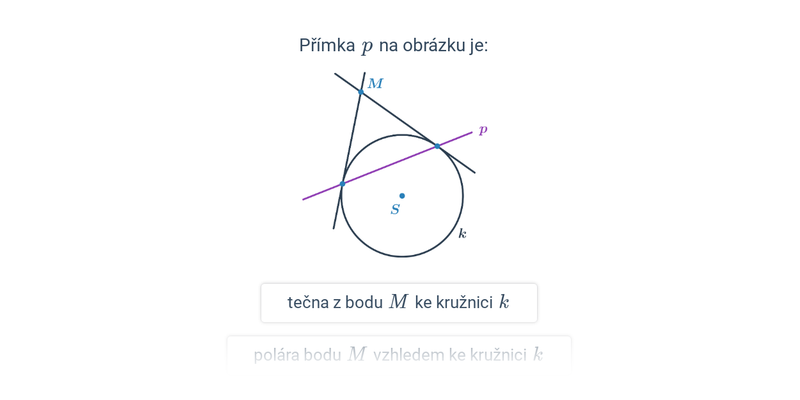
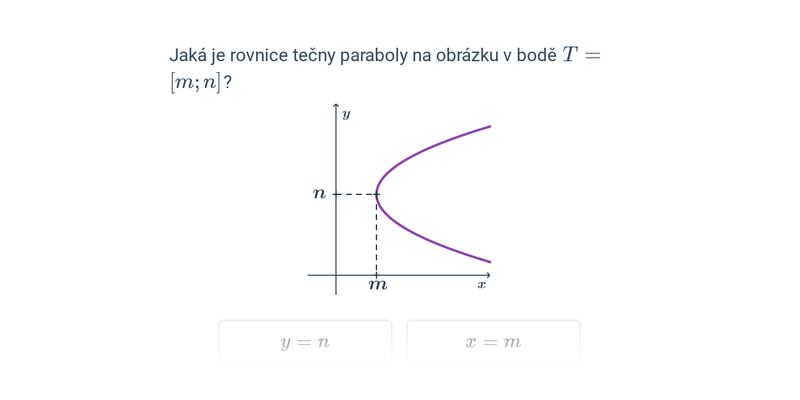
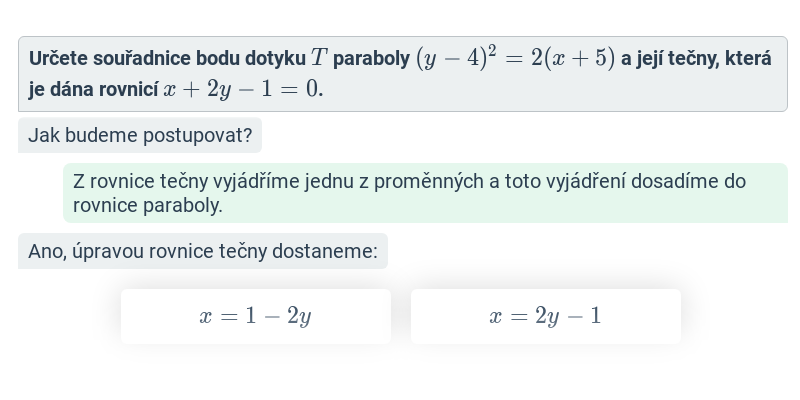
Parabola: tečna
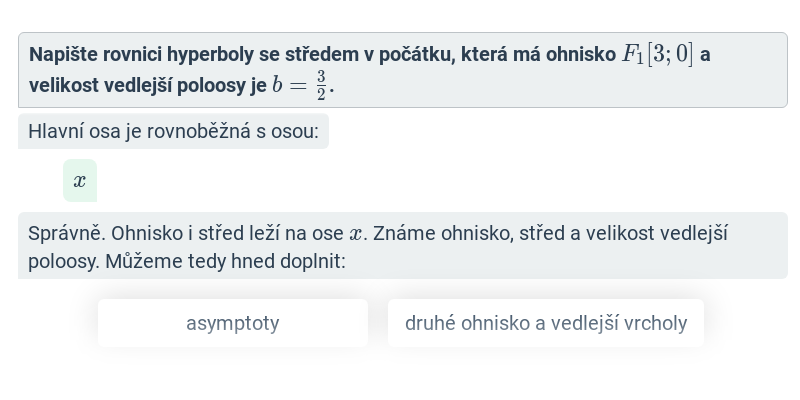
Hyperbola: středová rovnice
Hyperbola: obecná rovnice
Kuželosečky: mix
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Kuželosečky
Kružnice: středová rovnice
Kružnice: obecná rovnice
Kružnice: vzájemná poloha přímky a kružnice
Elipsa: středová rovnice
Elipsa: obecná rovnice
Elipsa: vzájemná poloha přímky a elipsy
Parabola: rovnice
Parabola: tečna
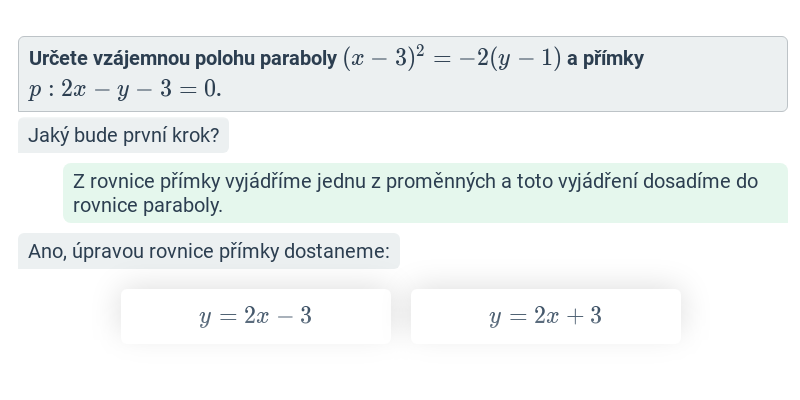
Parabola: vzájemná poloha přímky a paraboly
Hyperbola: obecná rovnice
Hyperbola: středová rovnice
Kuželosečky: mix
Určení kuželosečky
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Kuželosečky
Kružnice: středová rovnice
Elipsa: středová rovnice
Hyperbola: středová rovnice
Kuželosečky: mix