Výpis souhrnů
Kuželosečky
Podtémata
Kuželosečky
Jak již název napovídá, mají kuželosečky společný původ. Každá z nich vzikne jako řez rotační kuželové plochy rovinou. 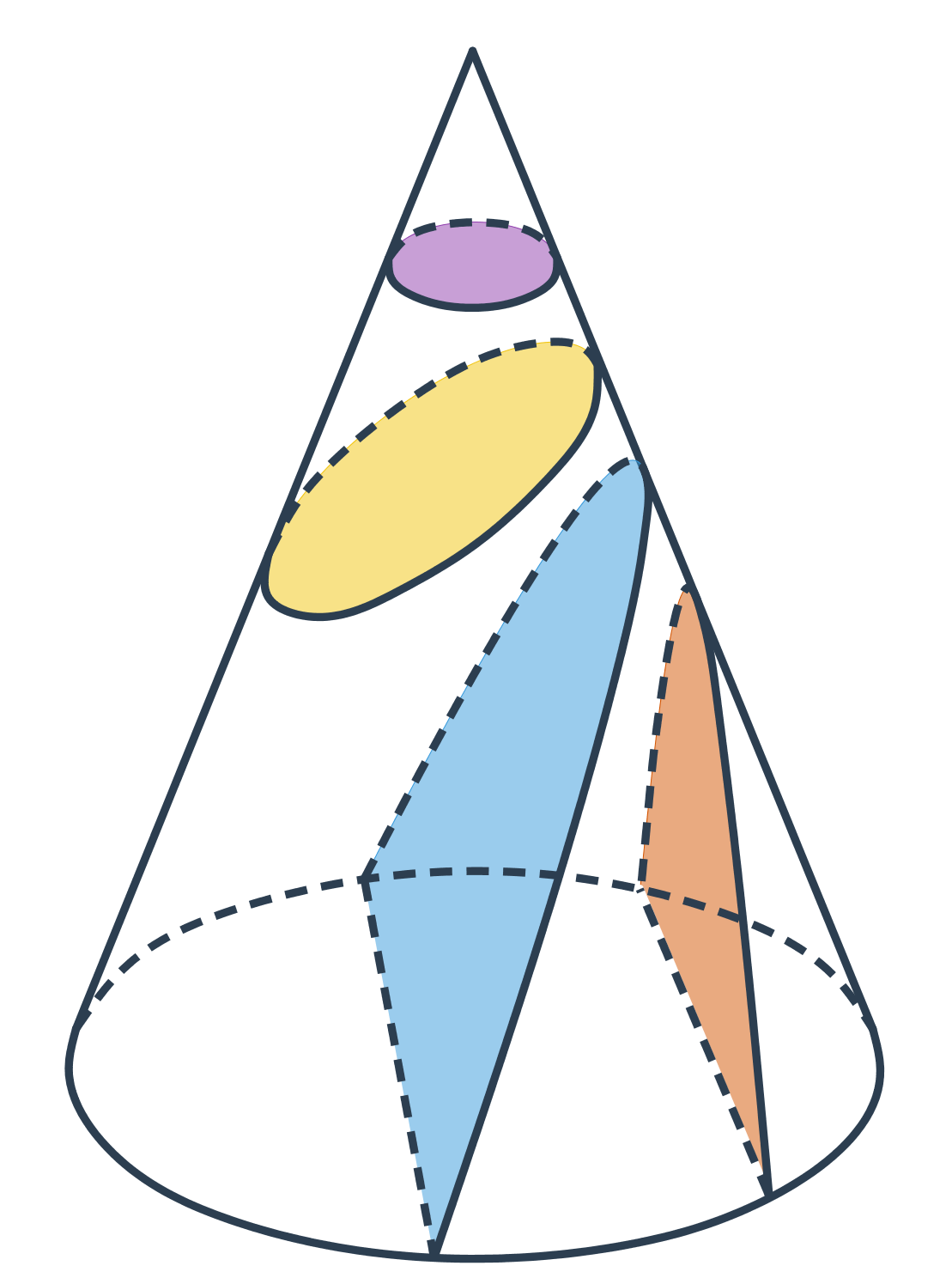
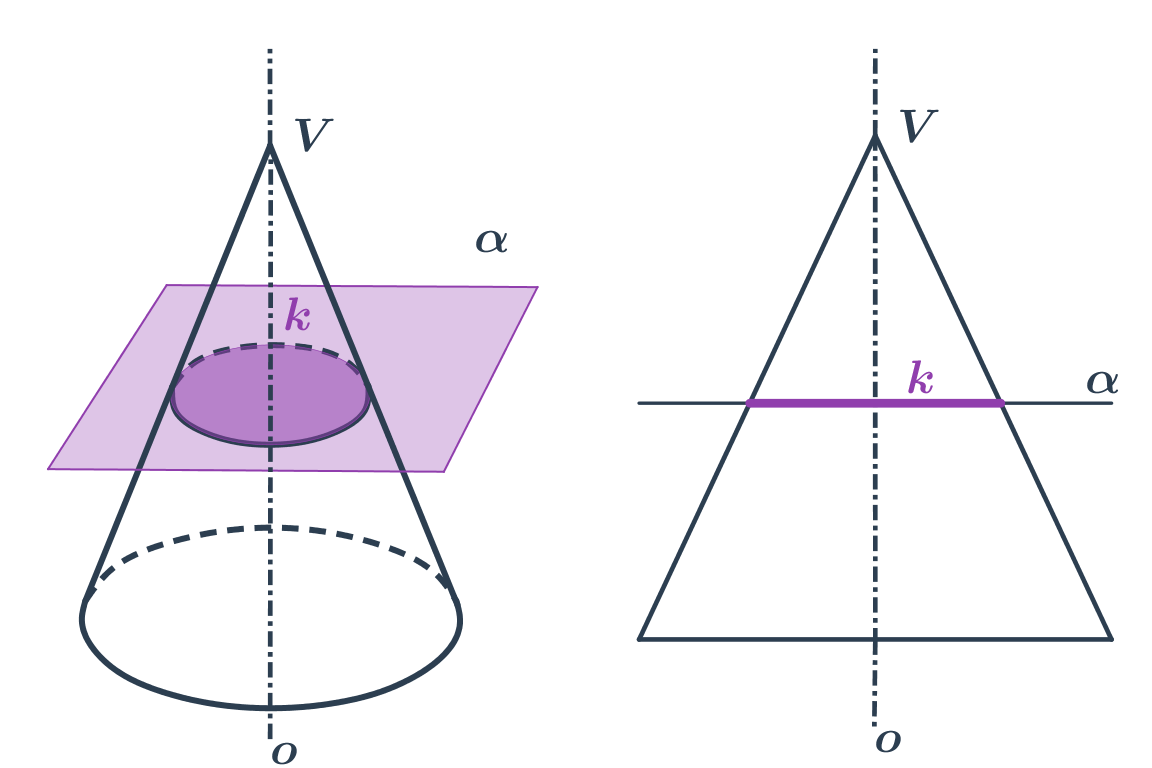
- Kružnice vznikne jako řez rovinou, která je kolmá na osu kuželové plochy.
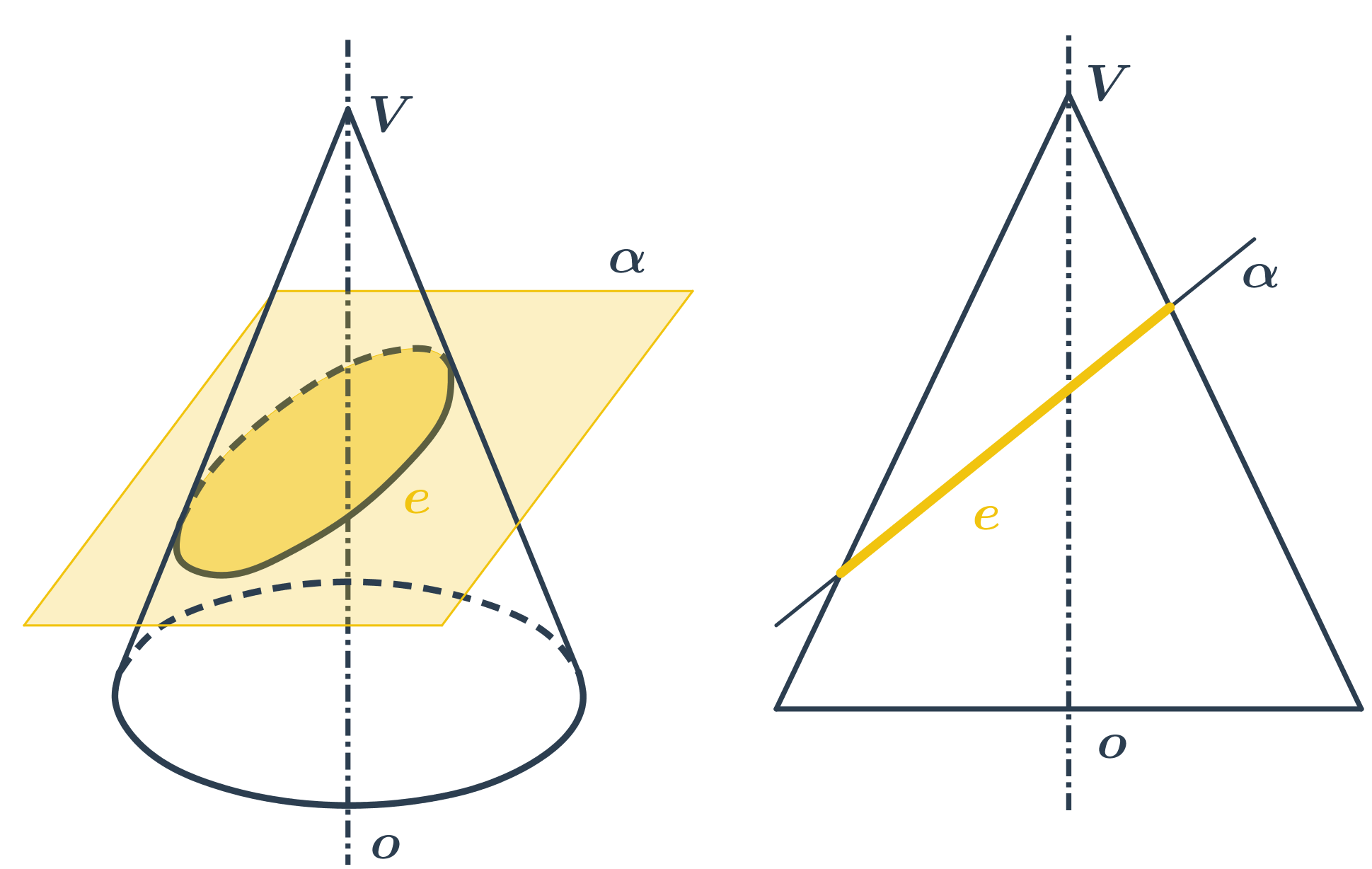
- Pokud rovinu řezu trochu nakloníme, vznikne elipsa.
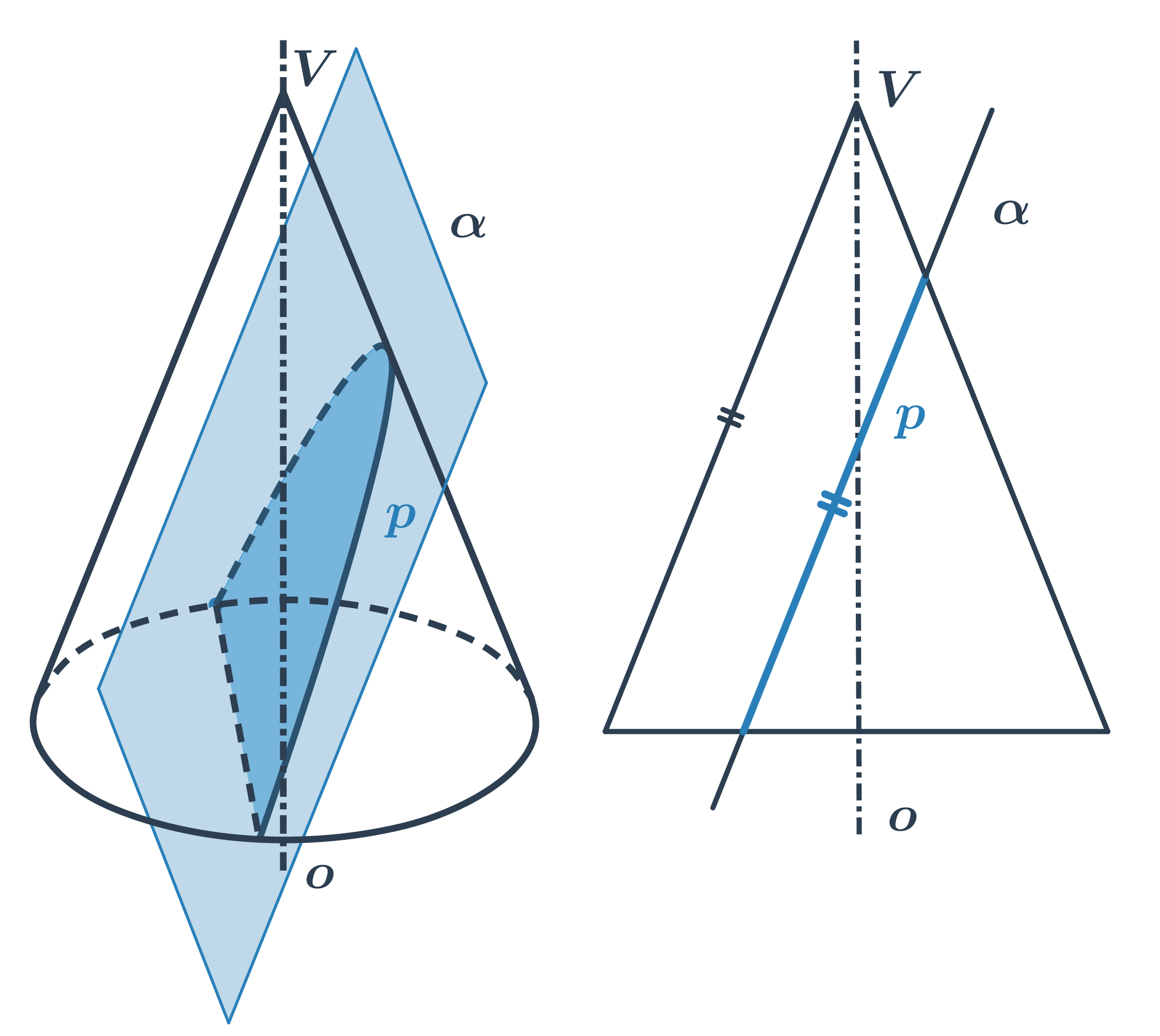
- Pokud rovinu řezu nakloníme tolik, že bude rovnoběžná s některou z přímek na kuželové ploše, vznikne parabola.
- Při dalším naklánění už rovina řezu protne obě části kuželové plochy a vznikne dvoudílná hyperbola.
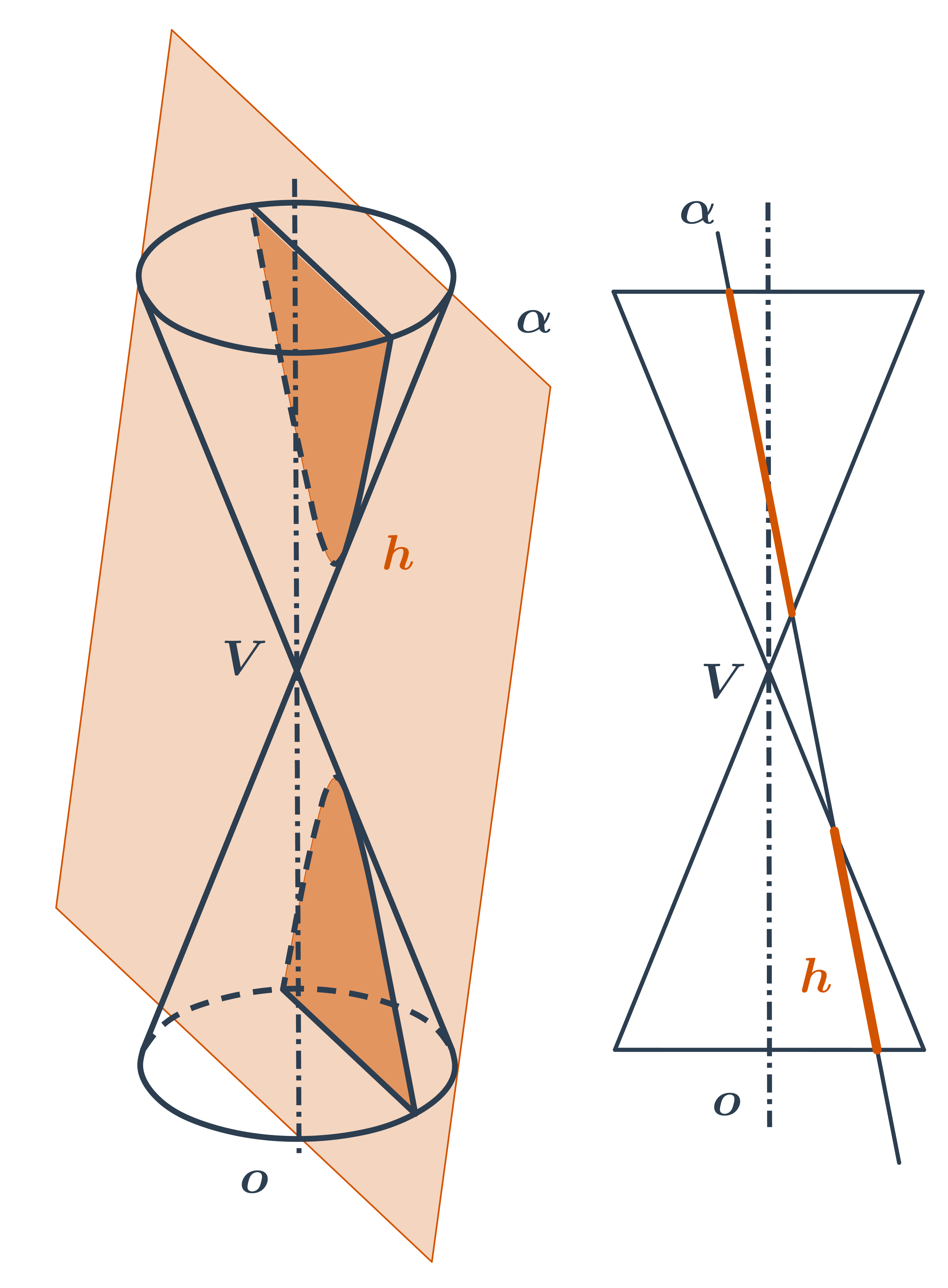
Na kuželosečky můžeme také hledět jako na množiny bodů dané vlastnosti. V analytické geometrii často zapisujeme tyto množiny pomocí rovnic.
NahoruKružnice (kuželosečka)
Kružnice je množina všech bodů v rovině, které mají od daného pevného bodu S stejnou vzdálenost r. Bod S nazýváme střed kružnice, hodnotu r nazveme poloměr kružnice. 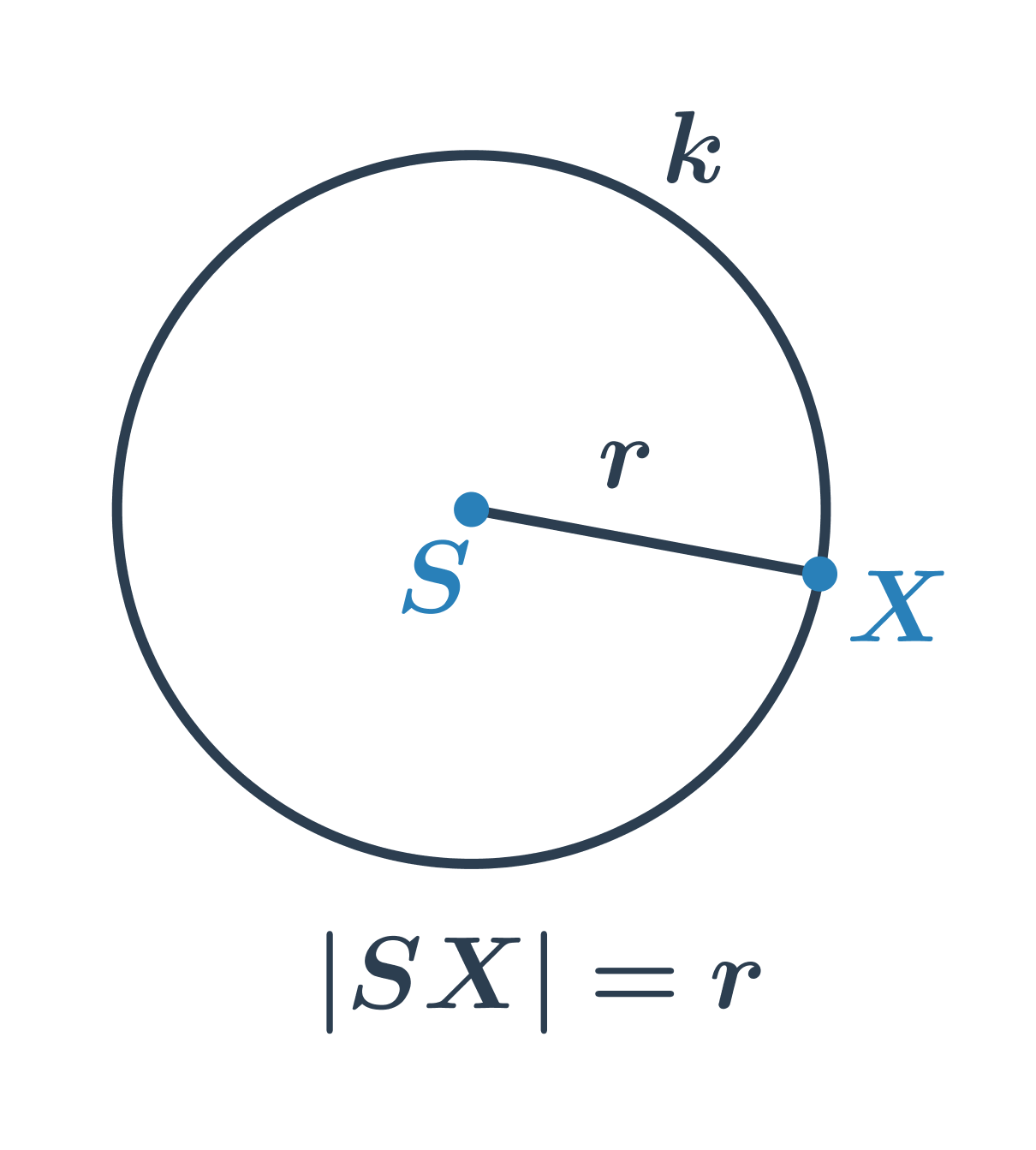
Středová rovnice kružnice
Středová rovnice kružnice o středu S[m;n] a poloměru r je ve tvaru: (x-m)^2 +(y-n)^2=r^2 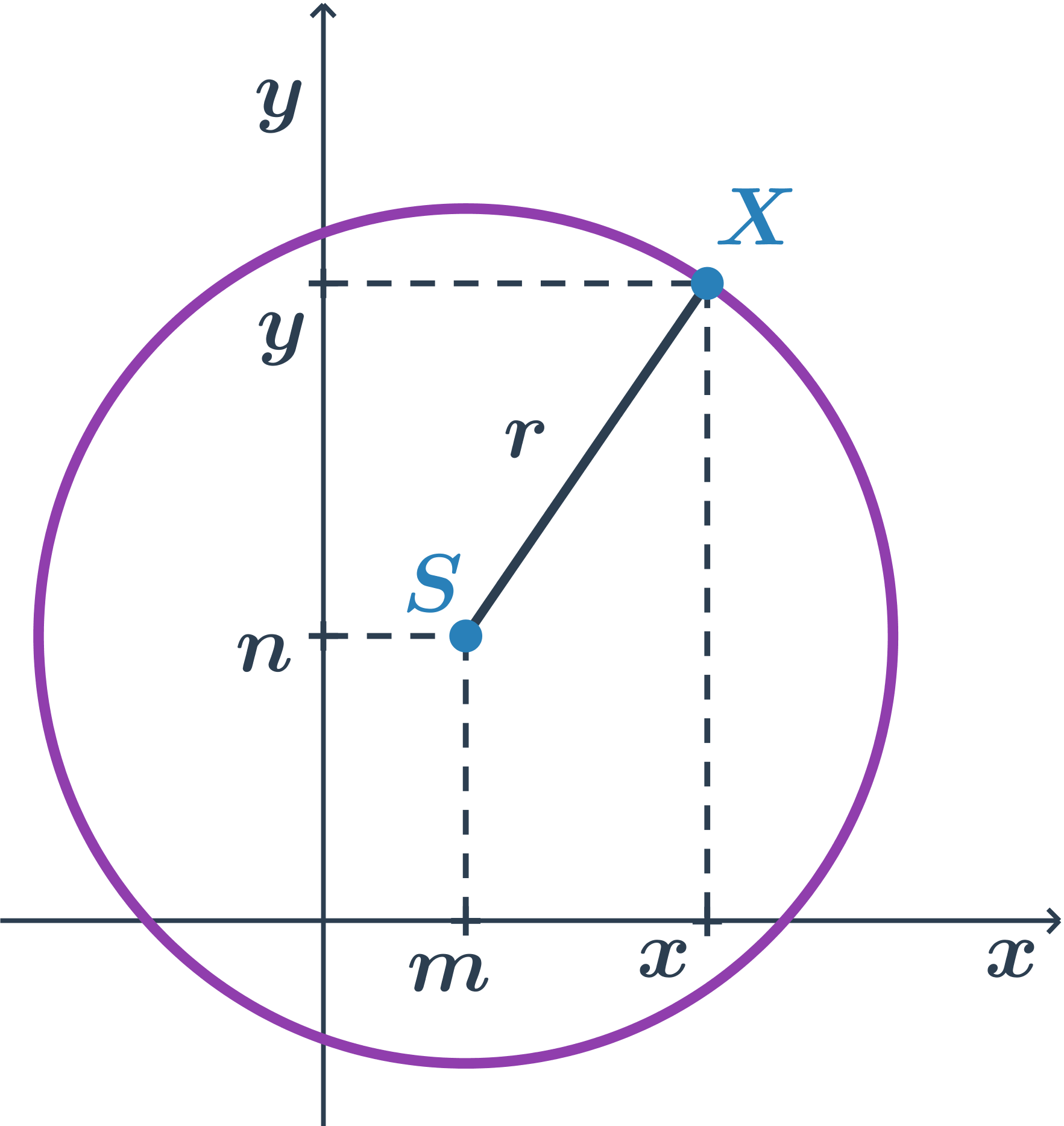
Příklad: Určete středovou rovnici kružnice se středem v bodě S[-1;2] a poloměrem r=3.
- Středová rovnice je ve tvaru: (x-m)^2 +(y-n)^2=r^2
- Dosadíme souřadnice středu a poloměr. Při dosazení si dáme pozor na to, že souřadnice středu ve středové rovnici odečítáme: (x-(-1))^2 +(y-2)^2=3^2
- Po úpravě: (x+1)^2 +(y-2)^2=9
Obecná rovnice kružnice
Podobně jako existuje několik tvarů rovnic přímky, můžeme i rovnici kružnice zapsat různými způsoby. Obecná rovnice kružnice je ve tvaru: x^2 +y^2-2mx-2ny+p=0.
Každá rovnice v tomto tvaru ale nemusí ještě být obecnou rovnicí kružnice. Pro obecnou rovnici kružnice musí platit, že výraz m^2+n^2-p je kladný. Praktické ověření, zda se jedná o kružnici, ale obvykle provádíme převedením na středovou rovnici kružnice.
Příklad: Najděte střed a poloměr kružnice dané obecnou rovnicí x^2+y^2+4x+6y-12=0.
- Nejprve si uspořádáme členy podle proměnných: x^2+4x+y^2-6y-12=0.
- Našim dalším cílem je upravit výraz na levé straně jako součet dvou druhých mocnin (čtverců), podle vzorečků a^2\pm 2ab+b^2=(a\pm b)^2.
- K oběma stranám rovnice přičteme konstanty 4 a 9, abychom součty členů s proměnnými x a y mohli upravit na druhé mocniny (provedeme v obou případech doplnění na čtverec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na závěr ještě převedeme -12 na druhou stranu rovnice: (x+2)^2 +(y-3)^2=25
- Tímto jsme převedli obecnou rovnici kružnice na středovou rovnici kružnice.
- Poloměr kružnice je r=\sqrt{25}=5.
- Souřadnice středu S[m,n] odčítáme ve středové rovnici od proměnných x a y, mají tedy opačná znaménka než konstanty v závorkách ve středové rovnici \Rightarrow S[-2;3].
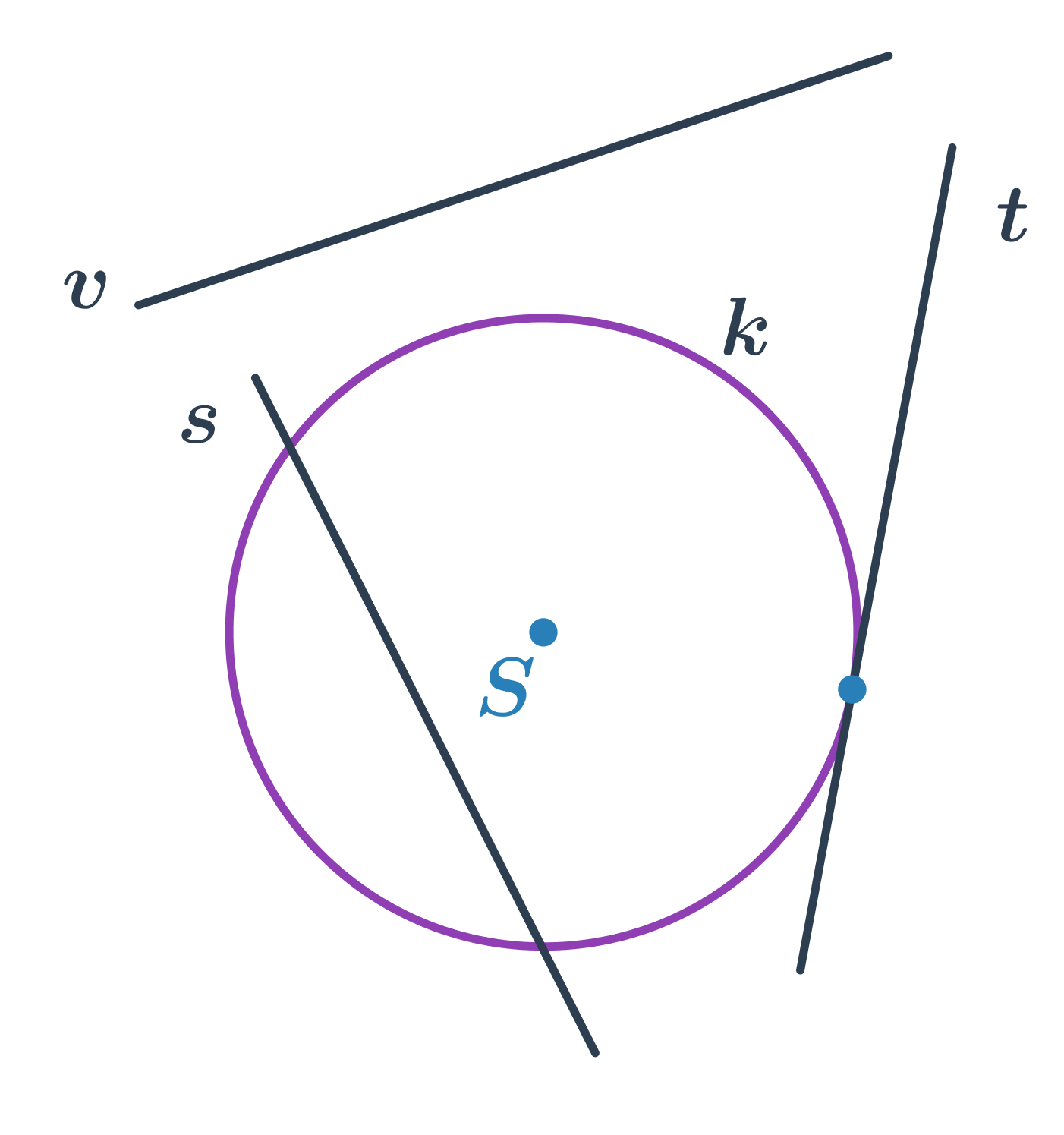
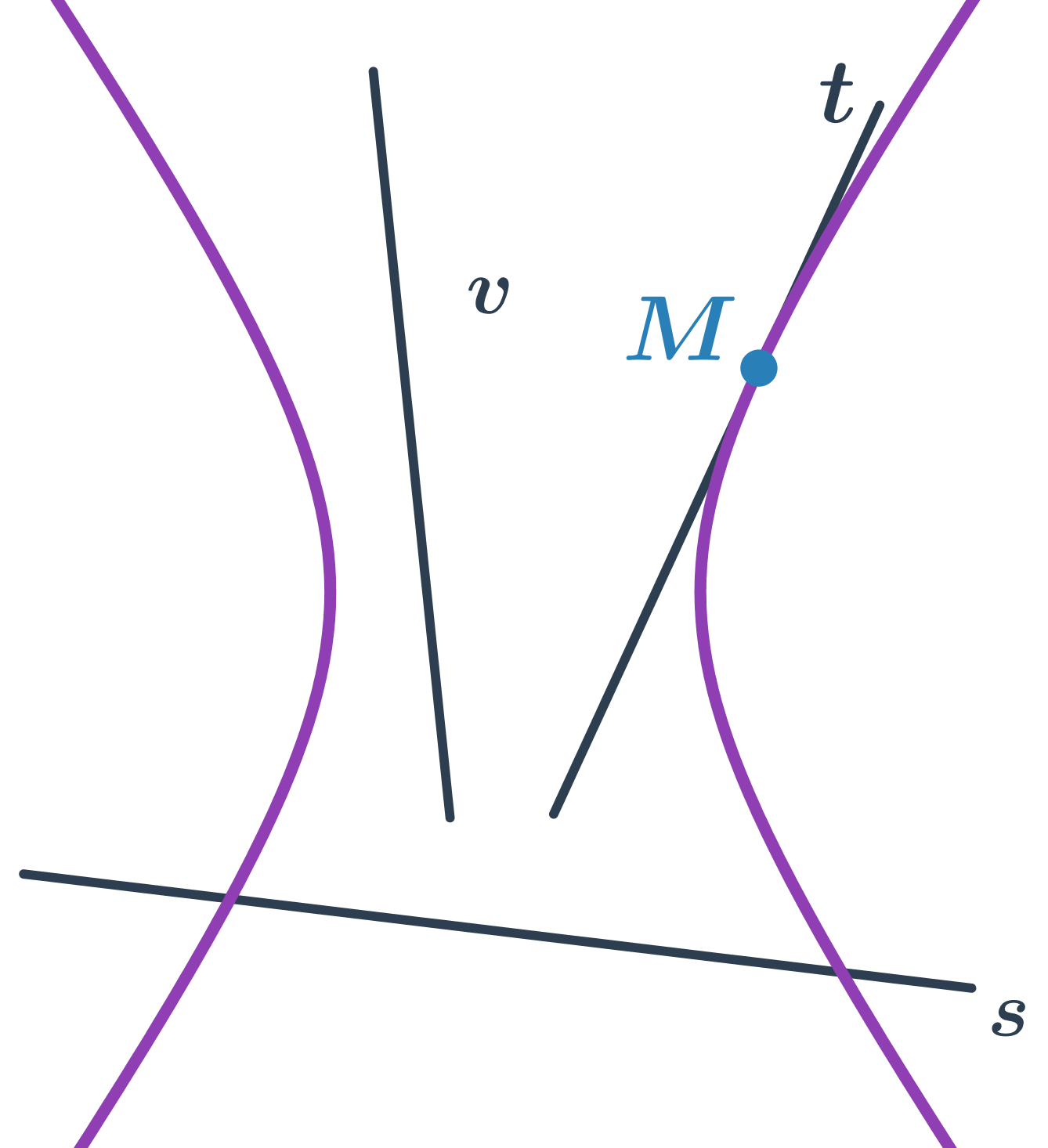
Kružnice a přímka
- přímka s protíná kružnici ve dvou bodech – sečna kružnice
- přímka t protíná kružnici v jednom bodě – tečna kružnice
- přímka v kružnici neprotíná – vnější přímka kružnice
Rovnice tečny kružnice v bodě, který leží na kružnici
Kružnice daná rovnicí (x-m)^2 +(y-n)^2=r^2 má v bodě T[x_0;y_0] tečnu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Jak si zapamatovat rovnici tečny
- Středová rovnice je ve tvaru (x-m)^2 +(y-n)^2=r^2.
- Závorky rozložíme na součiny dvoučlenů (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každém součinu zaměníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnici tečny (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Příklad: Určete rovnici tečny kružnice (x-1)^2+(y+2)^2=13 v jejím bodě T[3;1].
- Ověříme, zda bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Tečna má rovnici (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme souřadnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme závorky: 2x-2 +3y+6=13
- A dostaneme obecnou rovnici tečny 2x+3y-9=0
Polára kružnice
Z bodu R mimo kružnici můžeme sestrojit dvě tečny k dané kružnici. Přímka určená body dotyku tečen se nazývá polára kružnice vzhledem k bodu R. 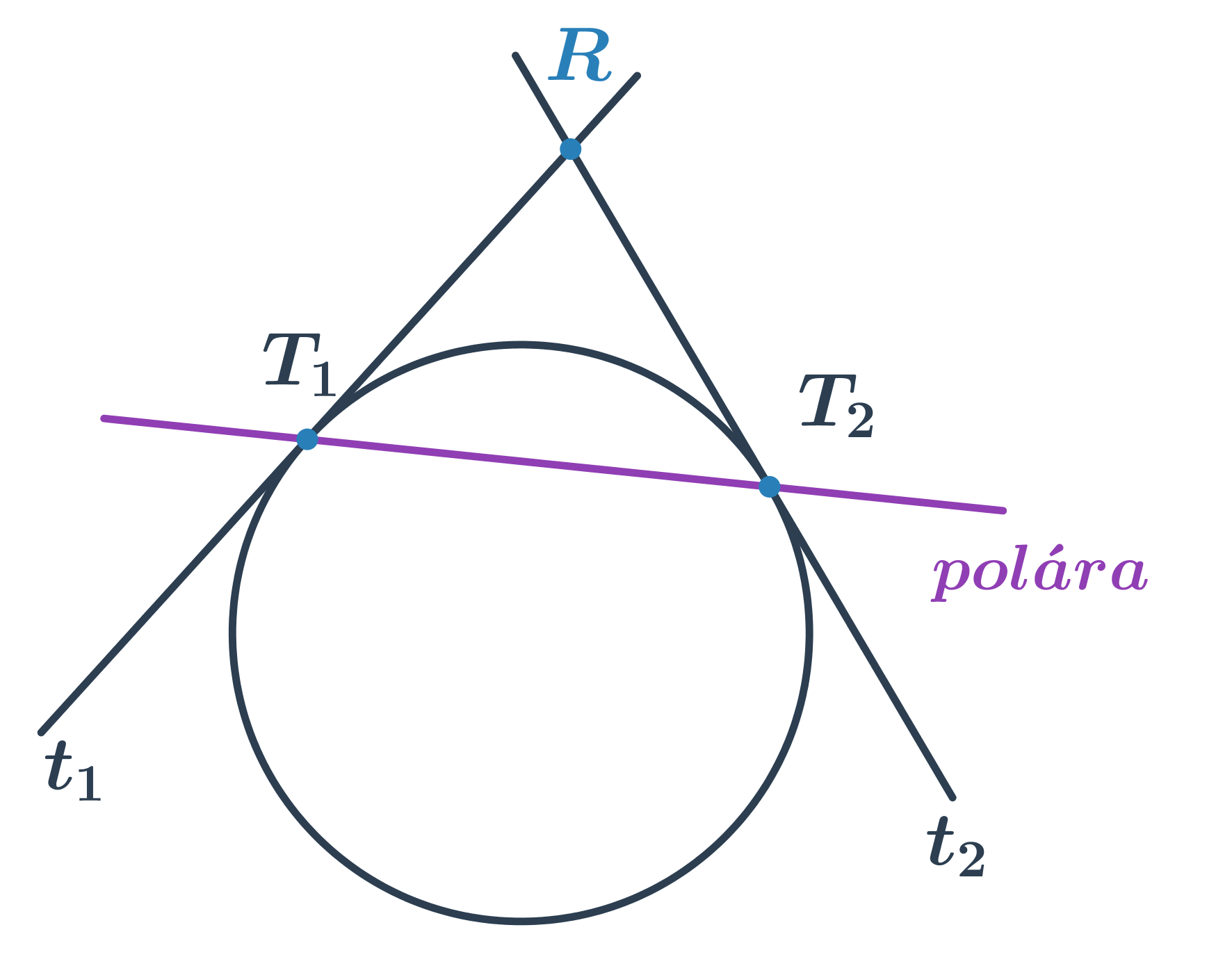
Rovnice poláry kružnice kružnice (x-m)^2 +(y-n)^2=r^2 vzhledem k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
K čemu poláru použijeme?
- Poláru využíváme ke konstrukci tečen ležících z bodu mimo kružnici.
- Podle vzorce určíme rovnici poláry, tedy přímky.
- Najdeme průsečíky poláry a kružnice – to jsou body dotyku hledaných tečen.
- Když známe body dotyku, určíme podle vztahu pro rovnici tečny v bodě kružnice obecné rovnice obou tečen.
Elipsa je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý součet vzdáleností 2a, který je větší než vzdálenost ohnisek. 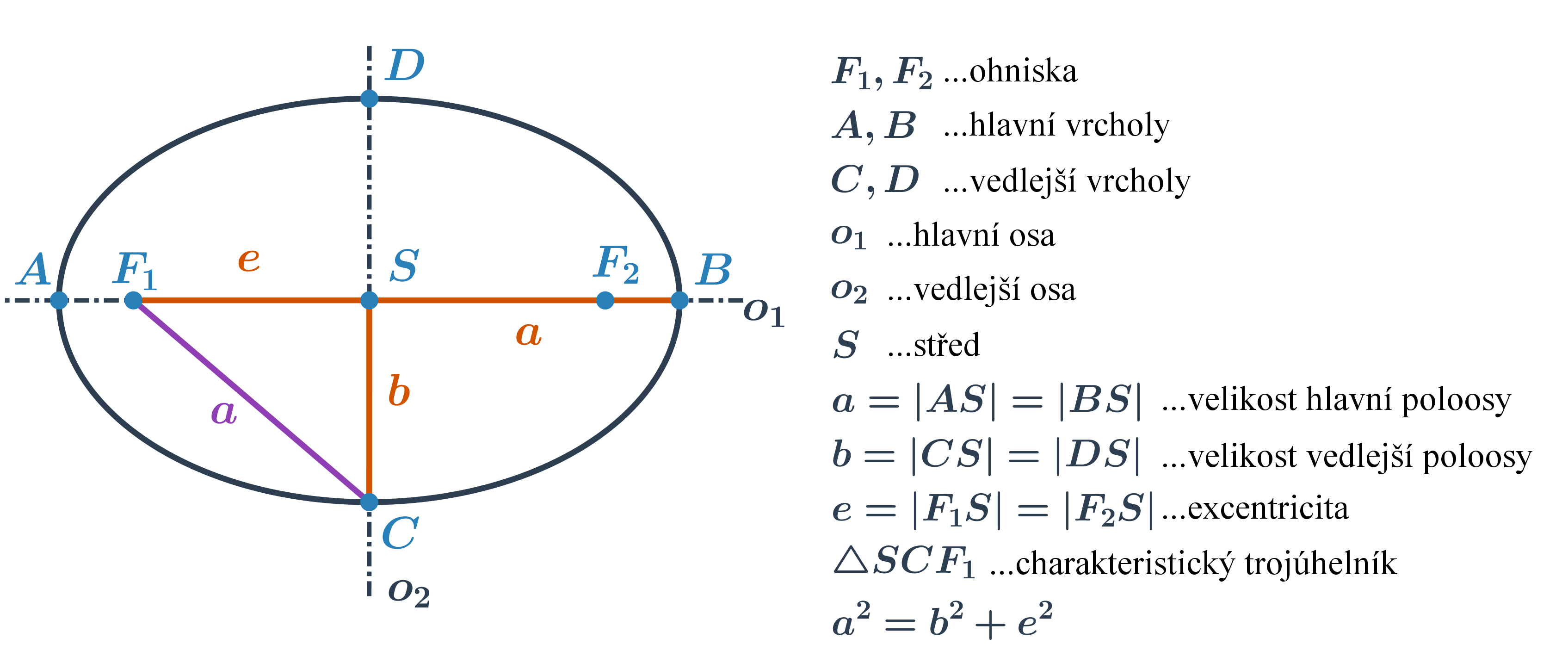
Středová rovnice elipsy
Tvar středové rovnice elipsy o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a a b závisí na poloze hlavní osy:
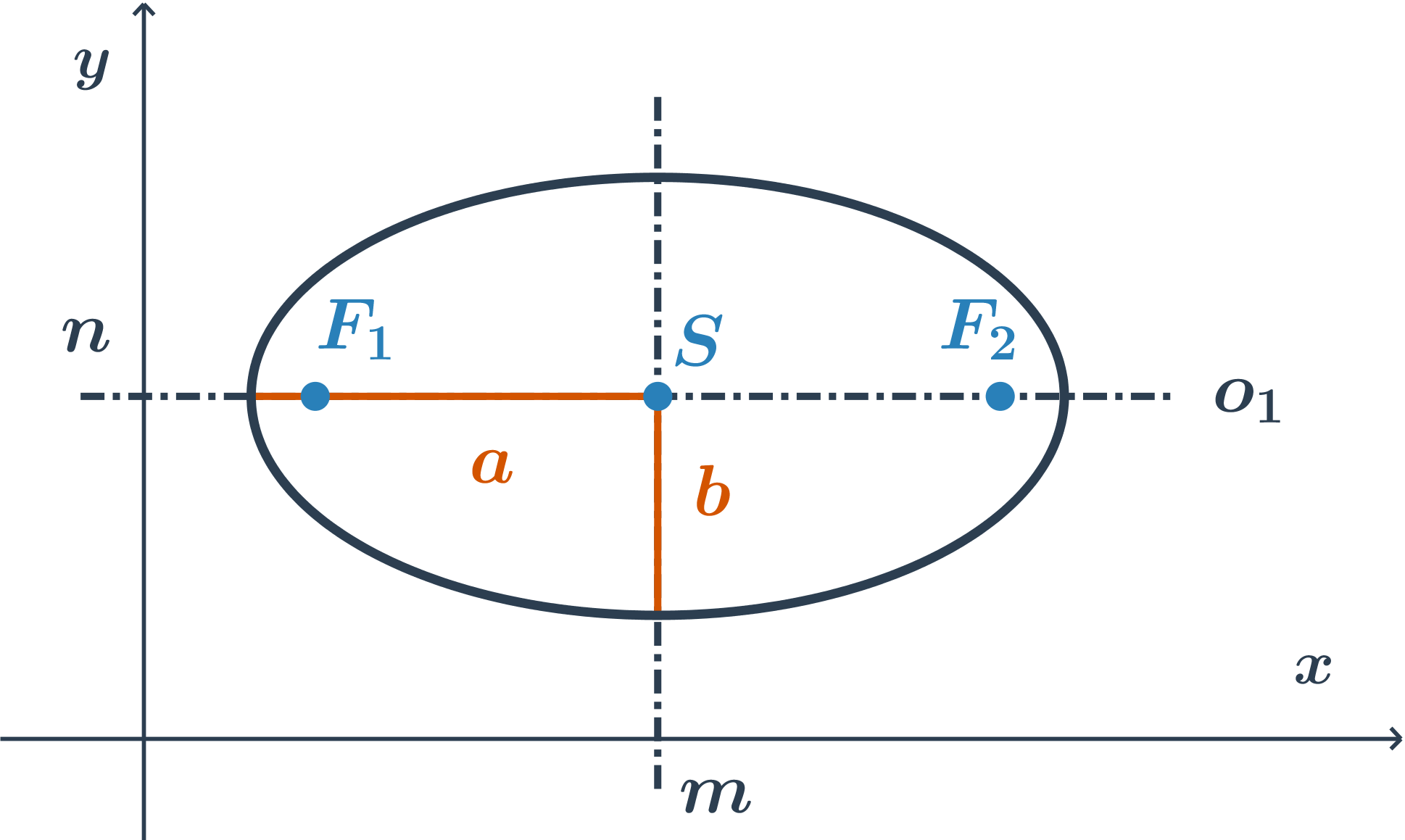
hlavní osa je rovnoběžná s osou x, rovnice je ve tvaru: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1
hlavní osa je rovnoběžná s osou y, rovnice je ve tvaru: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1
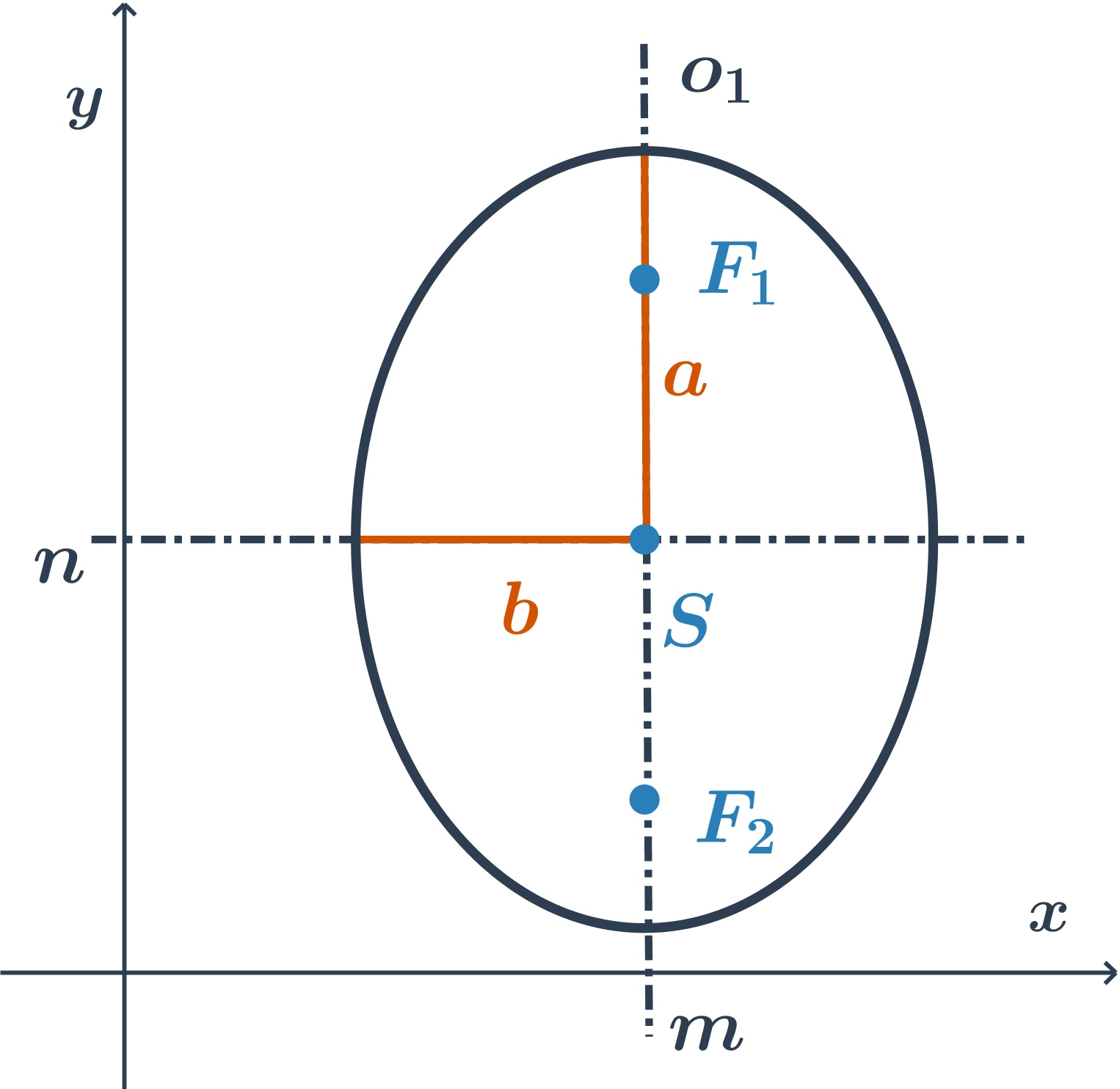
Návod: jak z rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa elipsy
- Podíváme se do jmenovatelů.
- Větší jmenovatel je druhá mocnina velikosti hlavní poloosy (a menší jmenovatel je druhá mocnina velikosti vedlejší poloosy).
- Proměnná v daném čitateli (zlomku s větším jmenovatelem) pak určuje, se kterou osou je hlavní osa elipsy rovnoběžná.
- Stručně řečeno: je‑li větší číslo například ve jmenovateli s proměnnou x, je hlavní osa rovnoběžná s osou x
Příklad: určení středové rovnice elipsy s daným středem, velikostmi poloos a směrem hlavní osy
Určete středovou rovnici elipsy se středem v bodě S[-2;3], je‑li a=3, b=2 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úpravě: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Obecná rovnice elipsy
Podobně jako existuje několik rovnic přímky, můžeme i rovnici elipsy zapsat jiným způsobem. Obecná rovnice elipsy je ve tvaru:
Ax^2 +By^2+Cx+Dy+E=0, A\ne B, A\cdot B>0.
Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí elipsy. Praktické ověření, zda se jedná o elipsu provádíme převedením na středovou rovnici.
Příklad: určuje daná rovnice elipsu?
Rozhodněte, zda rovnice x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Nejprve si uspořádáme členy: x^2+8x+3y^2-18y+31=0.
- Ze členů s proměnnou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K oběma stranám rovnice přičteme konstanty 16 a 27, abychom členy s proměnnými x a y mohli upravit podle vztahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Převedeme konstantu 31 na druhou stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na závěr rovnici vydělíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Jedná se tedy o elipsu.
Elipsa a přímka
- přímka s protíná elipsu ve dvou bodech – sečna elipsy
- přímka t protíná elipsu v jednom bodě – tečna elipsy
- přímka v elipsu neprotíná – vnější přímka elipsy
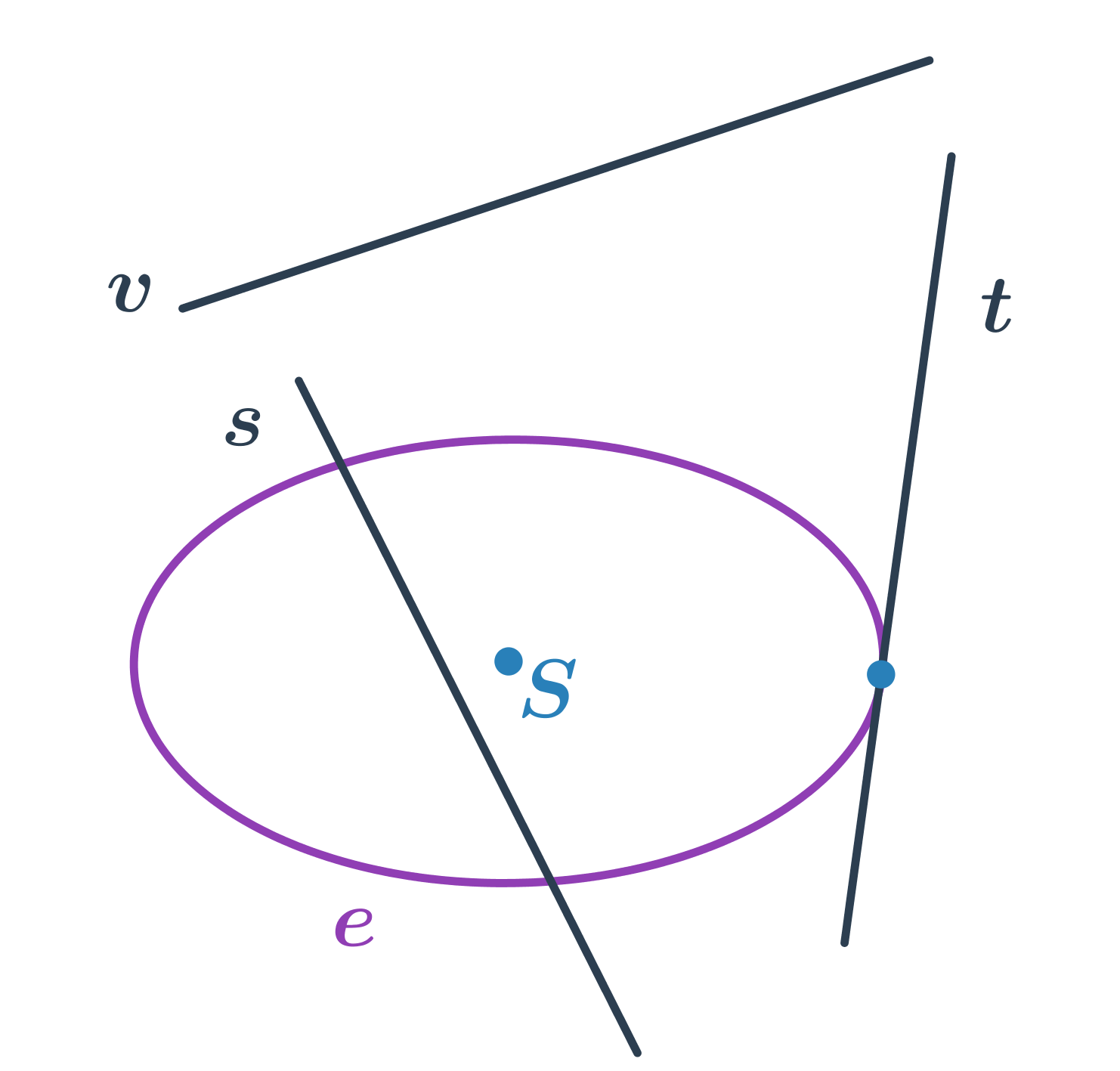
Rovnice tečny elipsy v bodě, který leží na elipse
Elipsa daná rovnicí \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu určenou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobně můžeme zapsat i rovnici tečny elipsy, která má hlavní osu rovnoběžnou s osou y.
Příklad: určení rovnice tečny elipsy v jejím daném bodě
Určete rovnici tečny elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jejím bodě T[1;-2].
- Ověříme, zda bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Tečna má rovnici \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme souřadnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme se zlomků: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme závorky: -2x+4 -4y+8=18
- A dostaneme obecnou rovnici tečny: x+2y+3=0
Parabola je množina všech bodů roviny, které mají stejnou vzdálenost od daného bodu (ohnisko) a dané přímky (řídicí přímka)
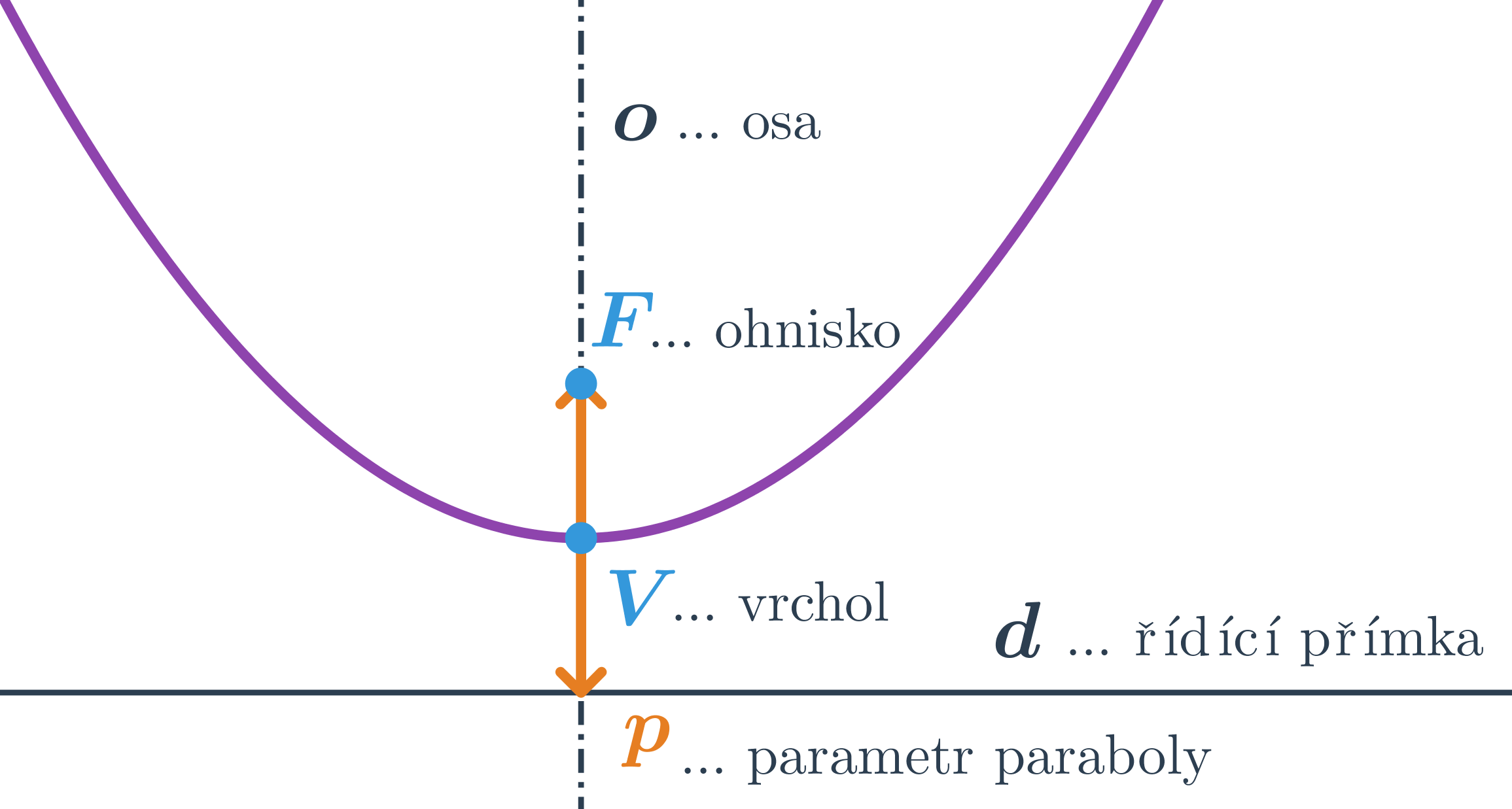
Vrcholová rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly rovnoběžná s osou y, vrcholová rovnice pak má tvar: (x-m)^2=\pm 2p(y-n)
- osa paraboly rovnoběžná s osou x, vrcholová rovnice pak má tvar: (y-n)^2=\pm 2p(x-m)
V rovnici paraboly označují m, n souřadnice vrcholu paraboly, tedy vrchol je bod V=[m;n]. Dále p je parametr paraboly = vzdálenost ohniska od řídicí přímky. Znaménko před parametrem závisí na poloze vrcholu vzhledem k bodům paraboly.
Příklad paraboly s osou rovnoběžnou s osou y
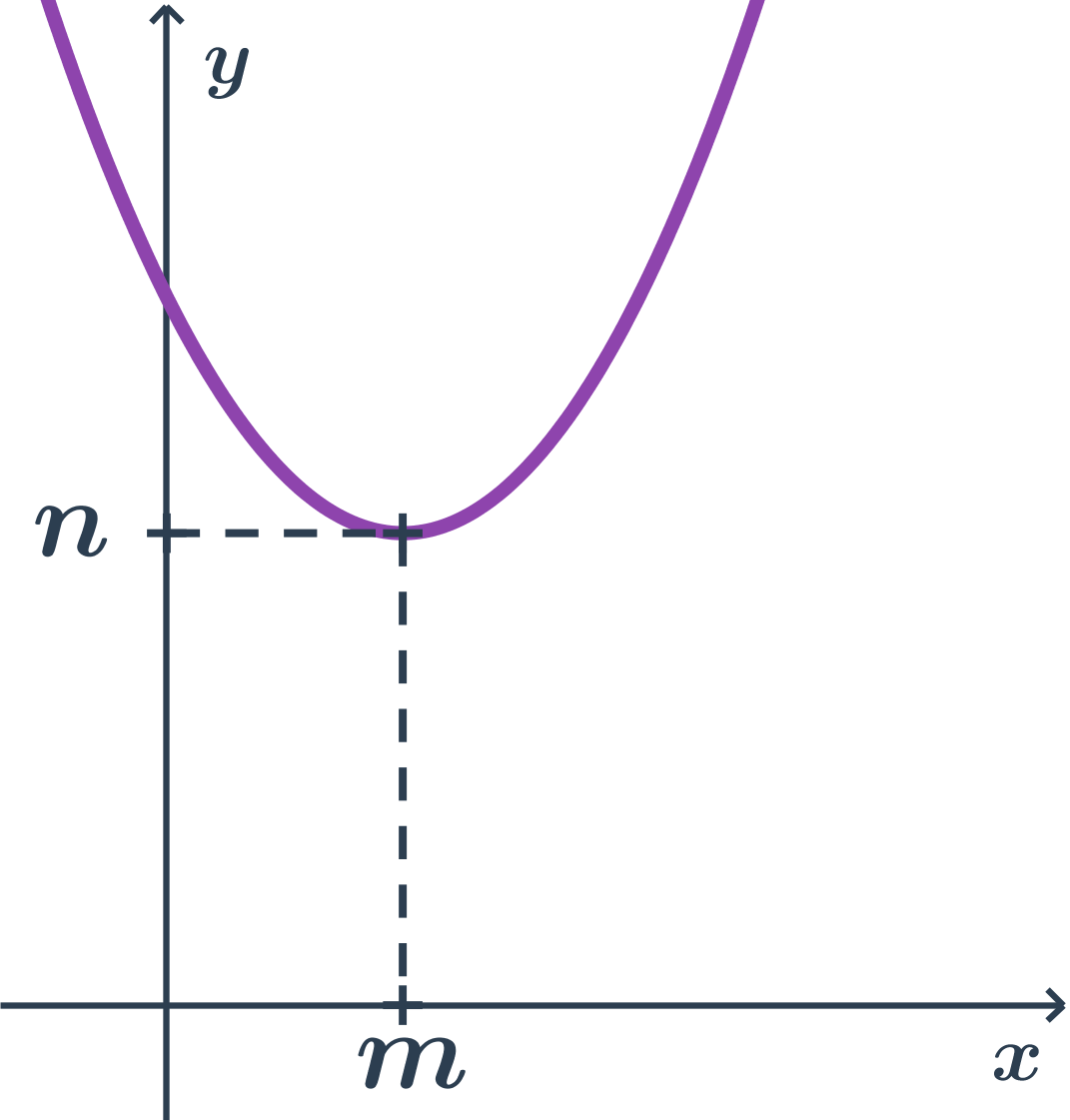
- body paraboly mají y souřadnici alespoň tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= + 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace
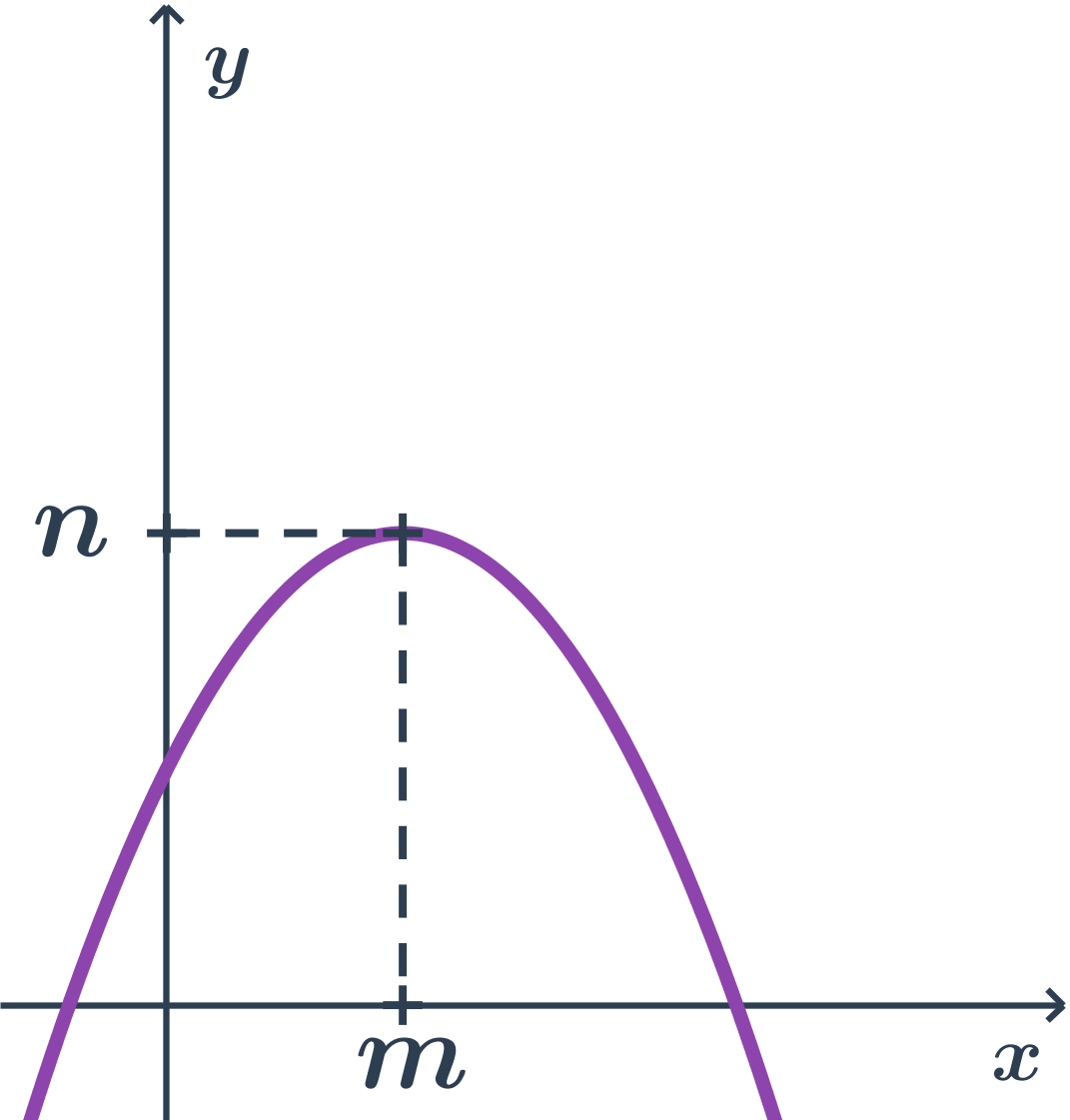
- body paraboly mají y souřadnici nejvýše tak velkou jako vrchol (tj. n)
- vrcholová rovnice: (x-m)^2= - 2p(y-n)
Příklad paraboly s osou rovnoběžnou s osou x
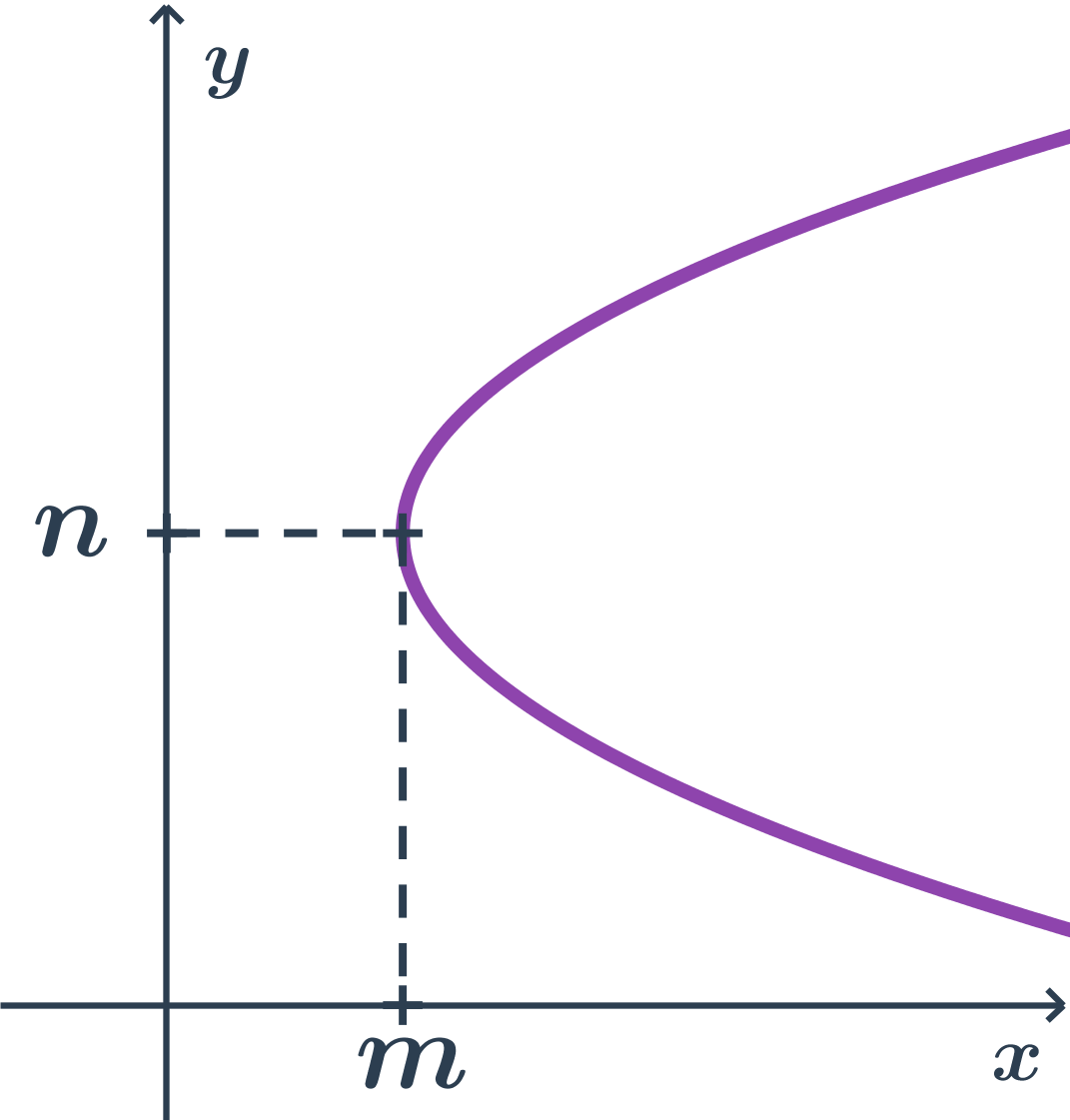
- body paraboly mají x souřadnici alespoň tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= + 2p(x-m)
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace
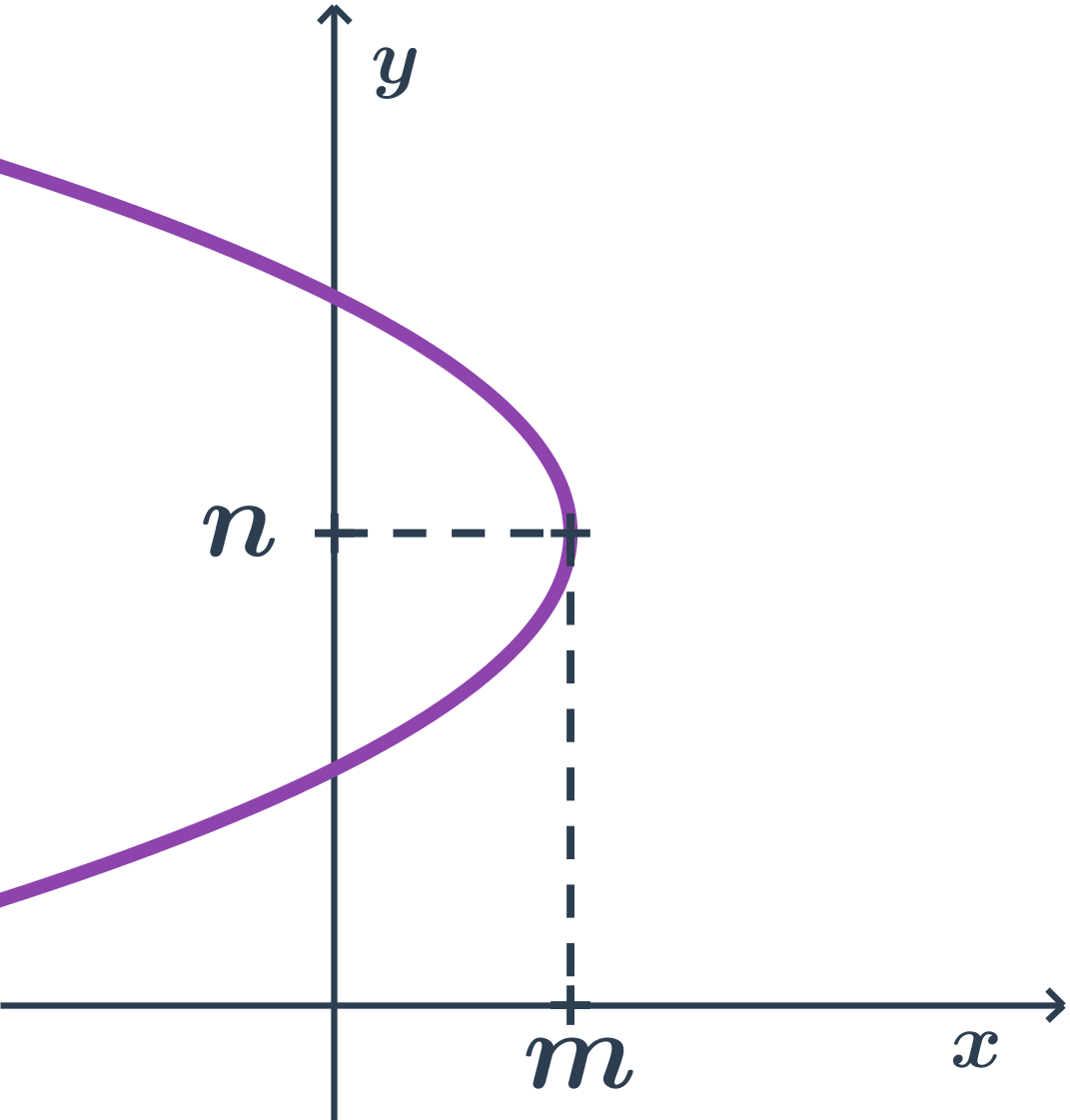
- body paraboly mají x souřadnici nejvýše tak velkou jako vrchol (tj. m)
- vrcholová rovnice: (y-n)^2= - 2p(x-m)
Obecná rovnice paraboly
Tvar rovnice závisí na umístění osy:
- osa paraboly je rovnoběžná s osou y: y=ax^2+bx+c
- osa paraboly je rovnoběžná s osou x: x=ay^2+by+c
Příklad paraboly s osou rovnoběžnou s osou y, obecná rovnice
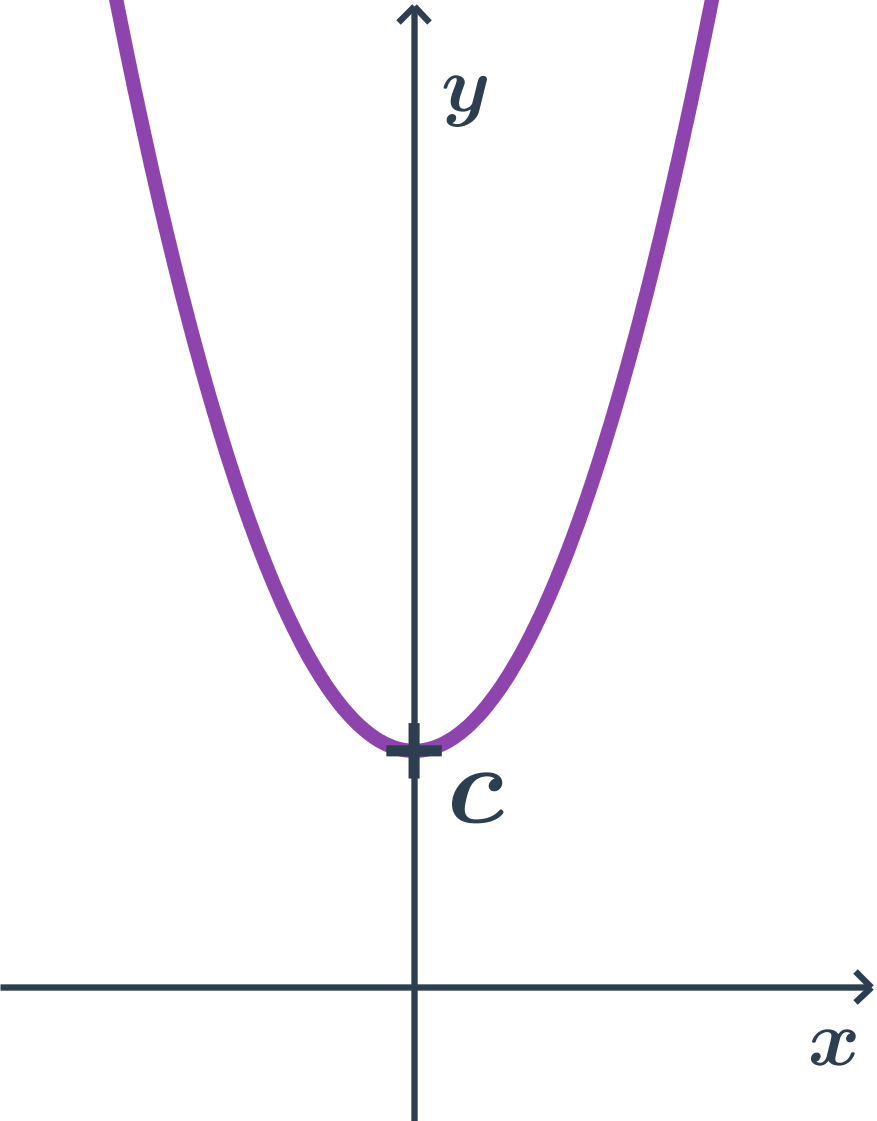
- obecná rovnice: y=ax^2+bx+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou y, druhá orientace, obecná rovnice
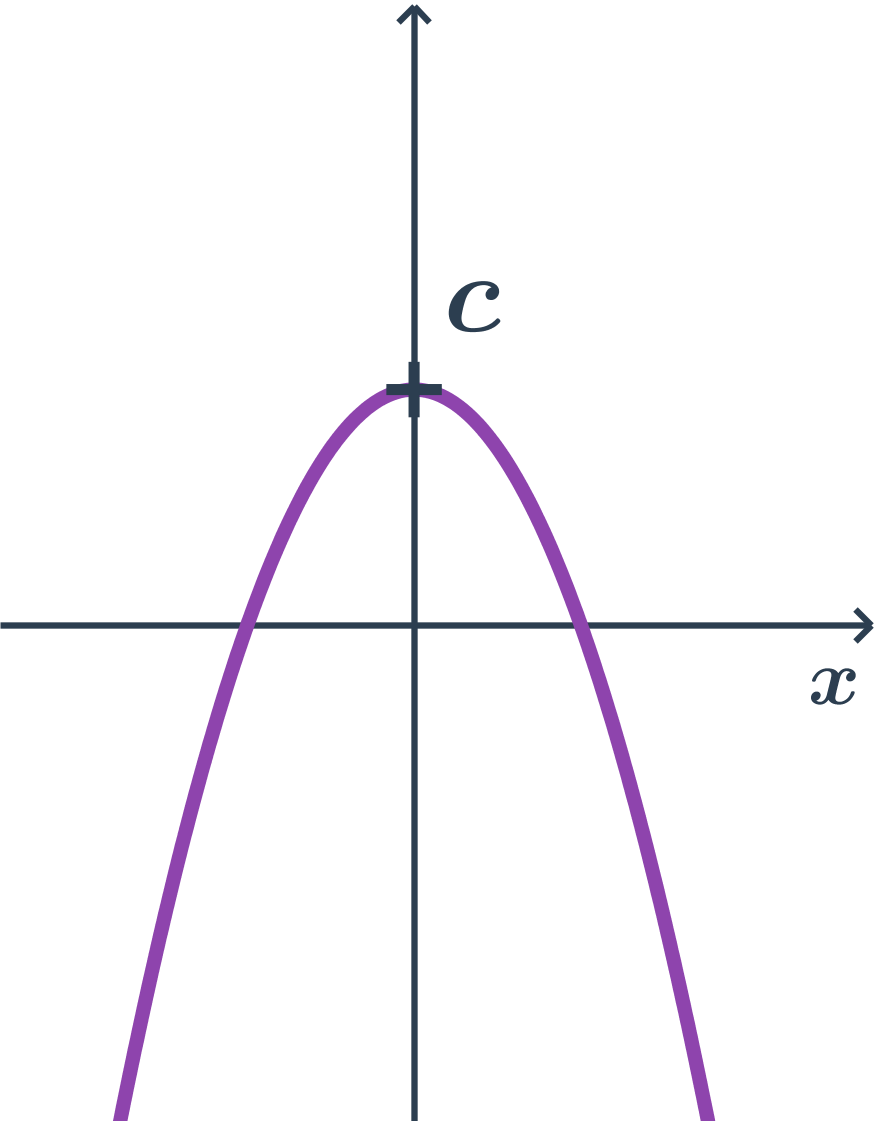
- obecná rovnice: y=ax^2+bx+c
- kde a \lt 0
Příklad paraboly s osou rovnoběžnou s osou x, obecná rovnice
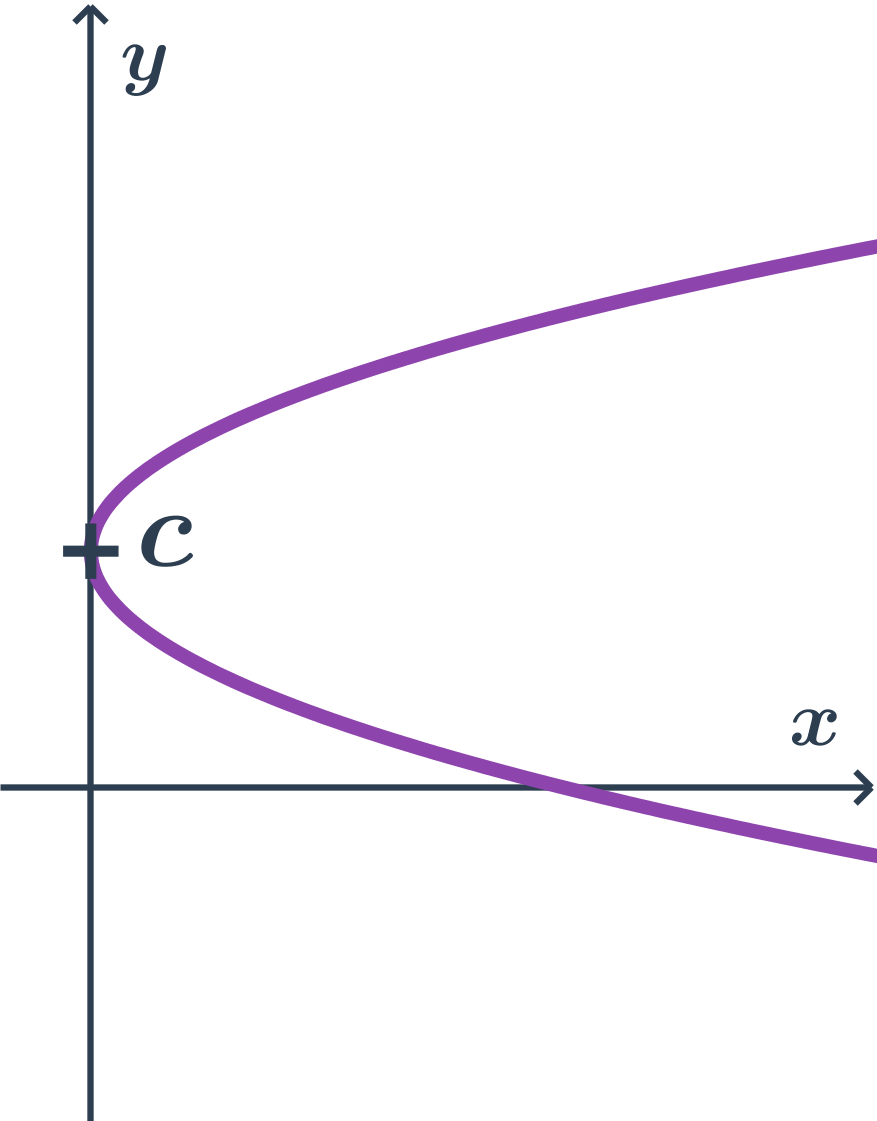
- obecná rovnice: x=ay^2+by+c
- kde a \gt 0
Příklad paraboly s osou rovnoběžnou s osou x, druhá orientace, obecná rovnice
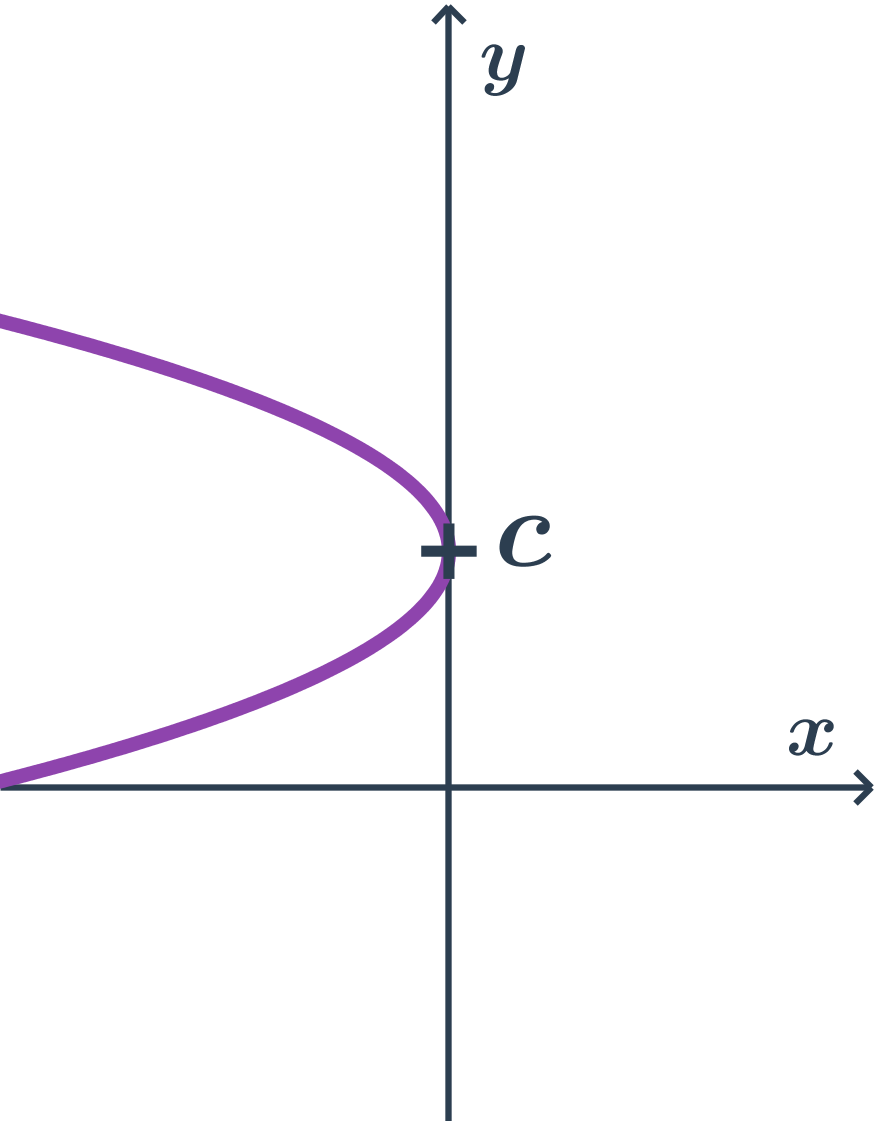
- obecná rovnice: x=ay^2+by+c
- kde a \lt 0
Přímka a parabola
- přímka b protíná parabolu ve dvou bodech – sečna paraboly
- přímka a se dotýká paraboly v jednom bodě – tečna paraboly
- přímka c neprotíná parabolu
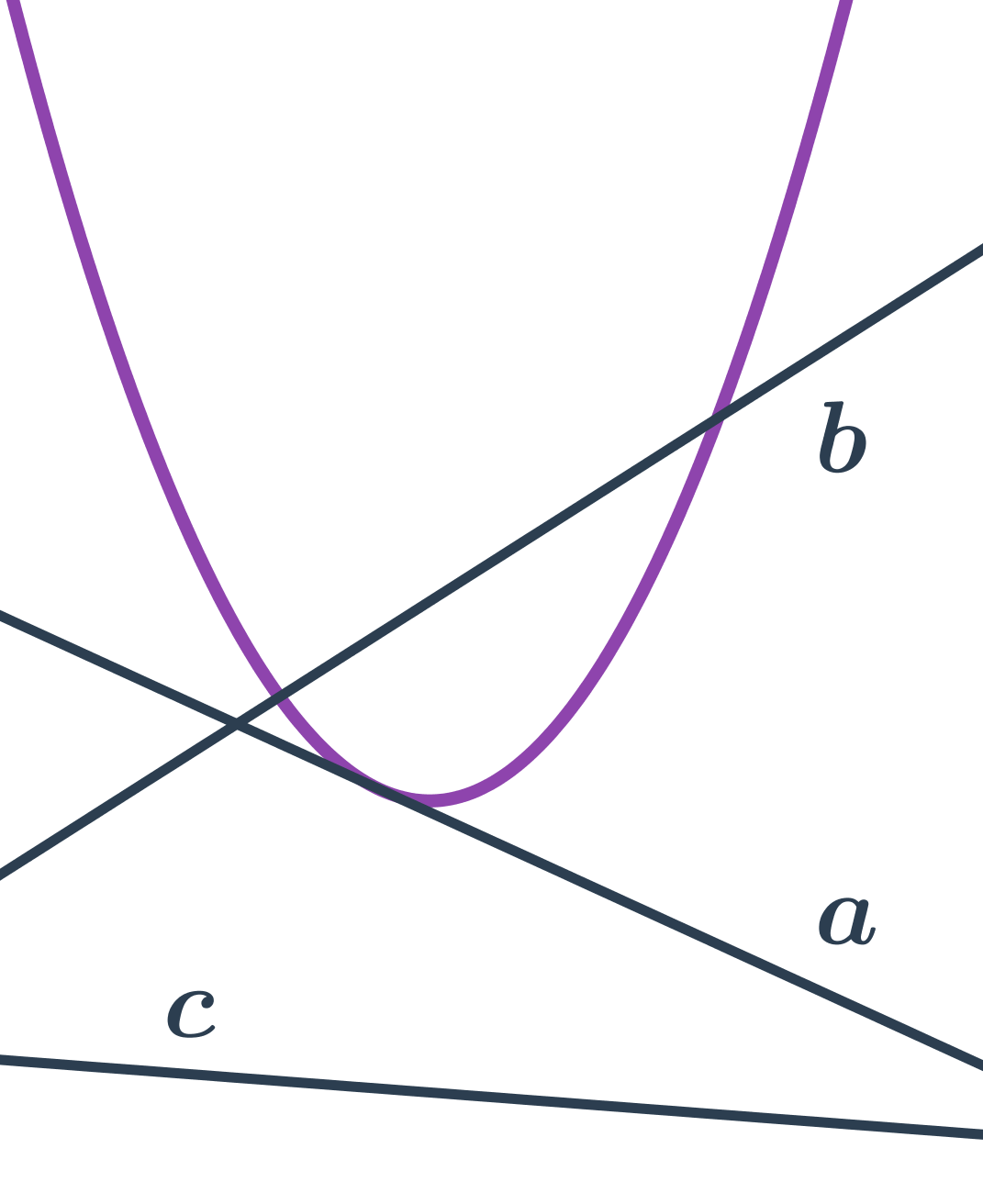
Rovnice tečny paraboly v bodě, který leží na parabole
- parabola daná rovnicí (x-m)^2=\pm 2p(y-n) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (x_0 - m)(x - m)=\pm p(y_0 - n) \pm p(y - n)
- parabola daná rovnicí (y-n)^2=\pm 2p(x-m) má v bodě T=[x_0;y_0] tečnu danou rovnicí: (y_0 - n)(y - n)=\pm p(x_0 - m)\pm p(x - m)
Příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2=2(y-1)
- pro tuto parabolu je m=2, n=1, p=1
- na této parabole leží (souřadnice splňují rovnici) například bod T=[4;3]
- tečna dané paraboly v bodě T=[4;3] má rovnici: (4 - 2)(x - 2)= (3 - 1) + (y - 1)
- rovnici tečny můžeme zjednodušit na 2x-4 = y+1, tedy y = 2x-5
Druhý příklad tečny paraboly v bodě
- mějme parabolu danou vrcholovou rovnicí: (x-2)^2= - 4(y-1)
- pro tuto parabolu je m=2, n=1, p=2, pravá strana je ve formě -2p(y-n)
- na této parabole leží (souřadnice splňují rovnici) například bod T=[6;-3]
- tečna dané paraboly v bodě T=[6;-3] má rovnici: (6-2)(x-2)= -2(-3-1)-2(y-1)
- rovnici tečny můžeme zjednodušit na 4x-8 = 8 -2y+2, tedy y = -2x+9
Speciální poloha přímky a paraboly
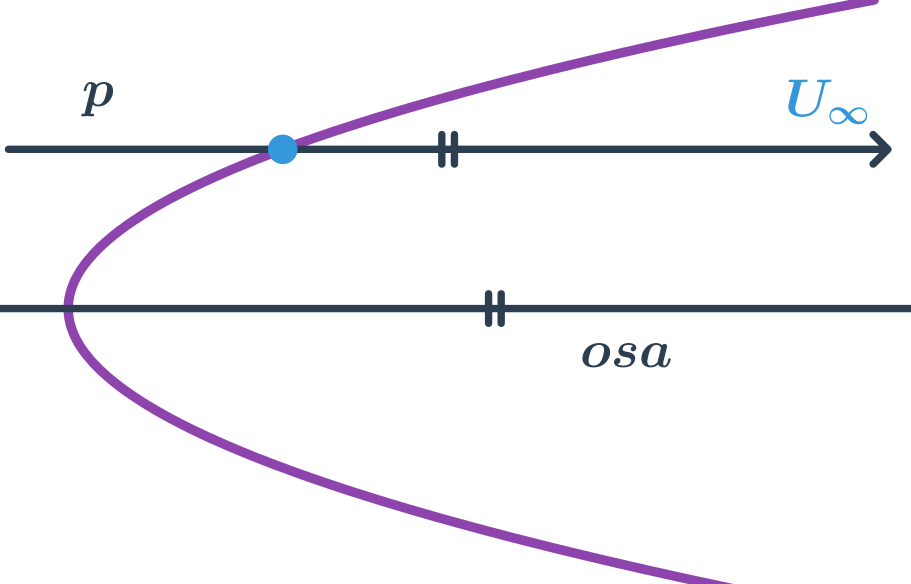
Přímka rovnoběžná s osou paraboly je sečna paraboly, přestože se zdá, že má s parabolou jeden společný bod. Druhý společný bod má tato přímka a parabola v nekonečnu.
Hyperbola
Hyperbola je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý rozdíl vzdáleností 2a, který je menší než vzdálenost ohnisek. Hyperbola se skládá ze dvou částí – větví hyperboly. Tyto dvě větve se blíží k přímkám, které nazýváme asymptoty. 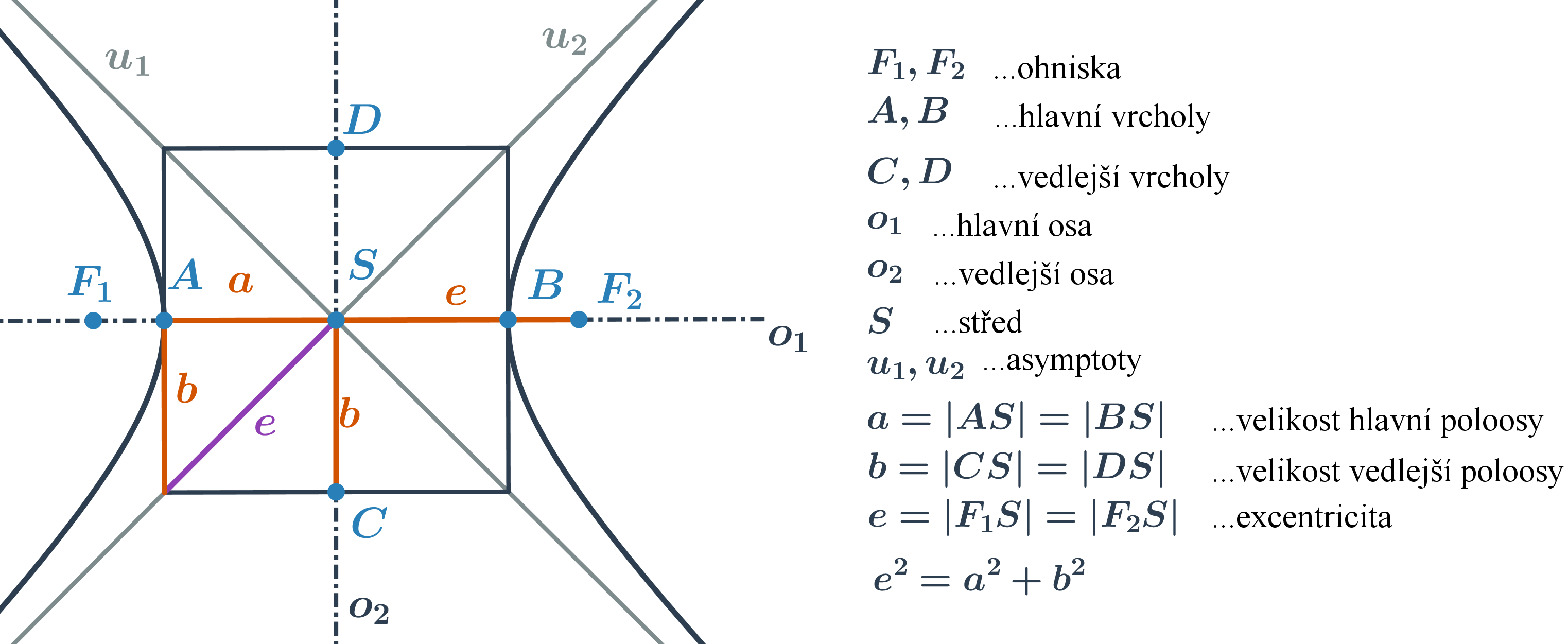
Středová rovnice hyperboly
Tvar středové rovnice hyperboly o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a,b závisí na poloze hlavní osy.
Středová rovnice hyperboly s hlavní osou rovnoběžnou s osou x
Pokud je hlavní osa rovnoběžná s osou x, rovnice je ve tvaru \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1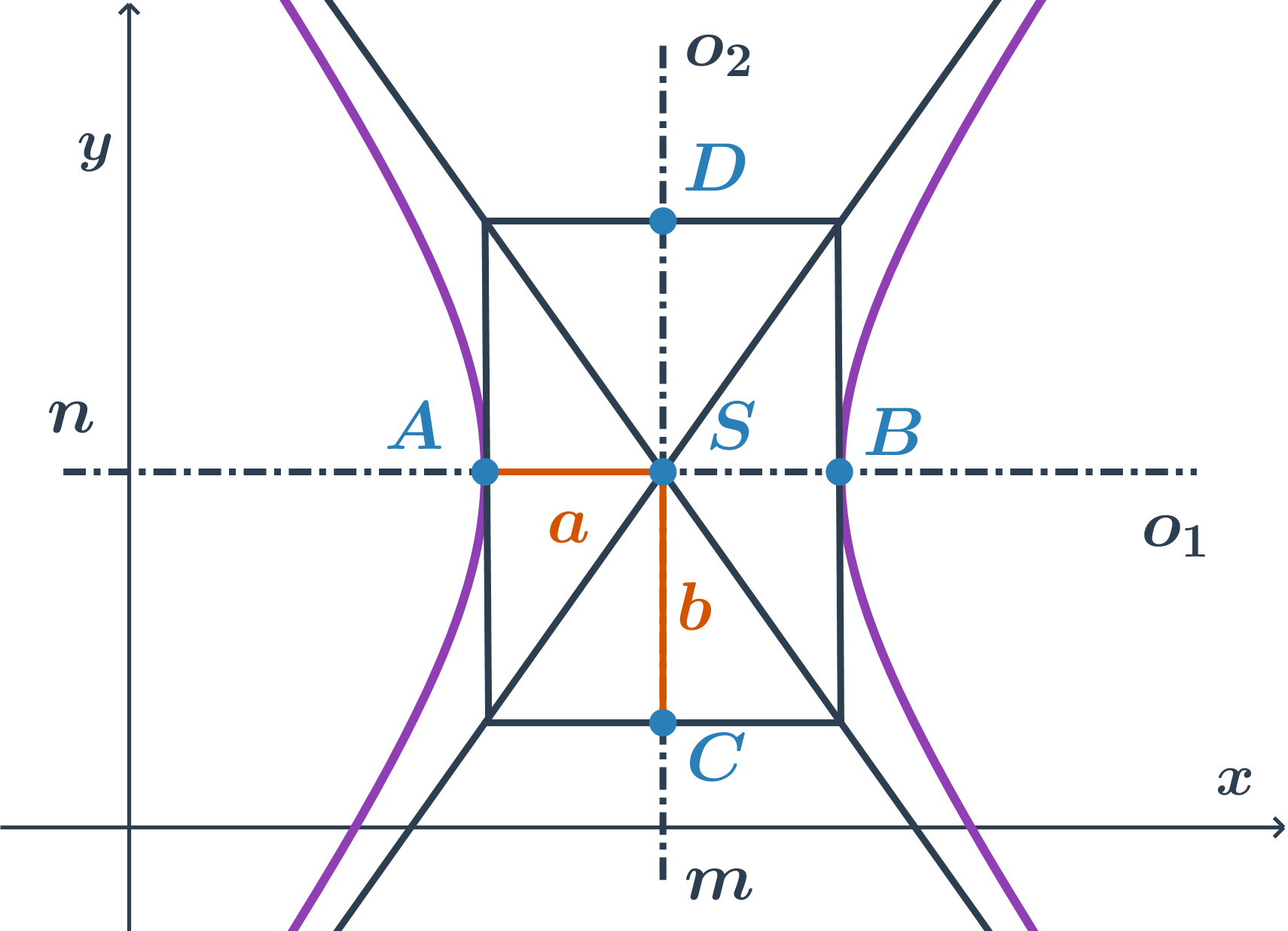
Středová rovnice hyperboly s hlavní osou rovnoběžnou s osou y
Pokud je hlavní osa rovnoběžná s osou y, rovnice je ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1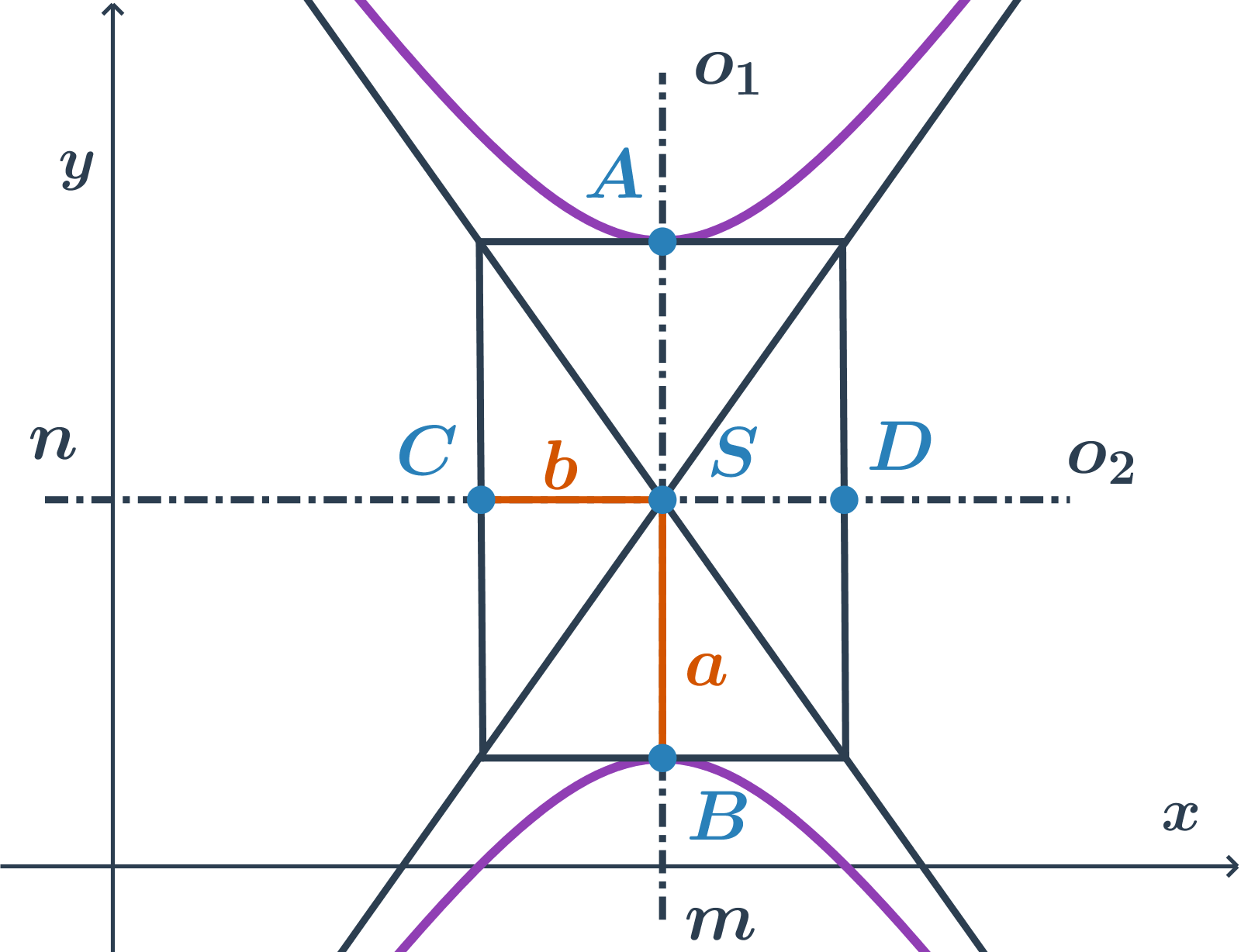
Na rozdíl od elipsy, nemusí být u hyperboly vždy hlavní poloosa a delší než vedlejší poloosa b. Pro rovnoosou hyperbolu dokonce platí a=b.
Jak ze středové rovnice poznat, se kterou souřadnou osou je rovnoběžná hlavní osa hyperboly?
- Podíváme se na znaménka členů s proměnnými x a y.
- Proměnná ve členu, který má před sebou znaménko plus udává, se kterou souřadnou osou je rovnoběžná hlavní osa hyperboly.
- Ve jmenovateli dané proměnné je pak (ve druhé mocnině) velikost hlavní poloosy.
- Stručně řečeno: je-li znaménko plus například u členu s proměnnou x, je hlavní osa rovnoběžná s osou x a ve jmenovateli je druhá mocnina velikosti hlavní poloosy a
Příklad: Určení středové rovnice hyperboly
Určete středovou rovnici hyperboly se středem v bodě S[1;-5], je-li velikost hlavní poloosy 2, velikost vedlejší poloosy 6 a hlavní osa je rovnoběžná s osou y.
- Středová rovnice je ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1. Hlavní poloosa má velikost a, vedlejší b.
- Dosadíme souřadnice středu a velikosti hlavní a vedlejší poloosy. Při dosazení si dáme pozor na to, že souřadnice středu odčítáme: -\frac{(x-1)^2}{6^2} +\frac{(y-(-5))^2}{2^2}=1
- Po úpravě: -\frac{(x-1)^2}{36} +\frac{(y+5)^2}{4}=1
Rovnice asymptot
Už víme, že asymptoty jsou přímky, ke kterým se hyperbola blíží. Pomohou při vykreslení hyperboly. Rovnice asymptot závisí na tvaru středové rovnice hyperboly.
Pro hyperbolu danou rovnicí ve tvaru \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 jsou rovnice asymptot:
y=\pm\frac{b}{a}(x-m)+n
Pro hyperbolu danou rovnicí ve tvaru -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 jsou rovnice asymptot:
y=\pm\frac{a}{b}(x-m)+n
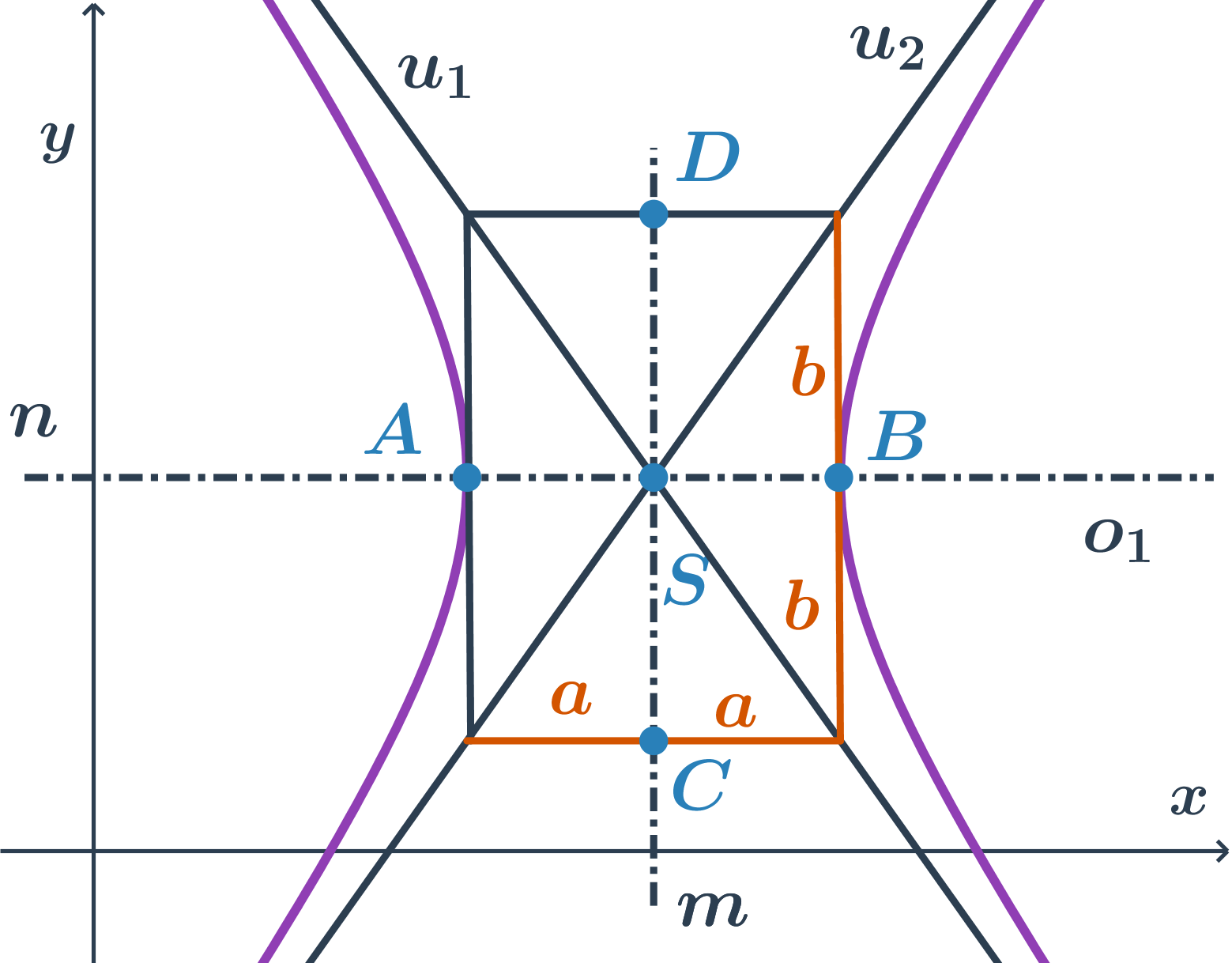
Jak načrtnout hyperbolu?
- Nejprve si vyznačíme střed, hlavní a vedlejší vrcholy.
- Poté sestrojíme charakteristický obdélník hyperboly. To je obdélník, který má strany rovnoběžné s osami a vrcholy hyperboly jsou středy jeho stran. Délky jeho stran jsou tedy 2a a 2b.
- Asymptoty jsou úhlopříčky charakteristického obdélníku.
Obecná rovnice hyperboly
Podobně jako existuje několik rovnic elipsy, můžeme i rovnici hyperboly zapsat různými způsoby. Obecná rovnice hyperboly je ve tvaru: Ax^2 +By^2+Cx+Dy+E=0, A\cdot B \lt 0. Podmínka A\cdot B \lt 0 zaručuje, že konstanty A, B mají opačná znaménka. Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí hyperboly. Praktické ověření, zda se jedná o hyperbolu provádíme převedením na středovou rovnici.
Příklad: Určuje daná rovnice hyperbolu?
Rozhodněte, zda rovnice -x^2+2y^2+8x-18y+31=0 určuje hyperbolu.
- Nejprve si uspořádáme členy: -x^2+8x+y^2-18y+40=0.
- Ze členů s proměnnou x vytkneme -1: -(x^2-8x)+y^2-18y+40=0
- K oběma stranám rovnice přičteme konstantu 81 a odečteme konstantu 16, abychom členy s proměnnými x a y mohli upravit podle vztahu pro (a\pm b)^2: -(x^2-8x+16)+y^2-18y+81+40=81-16
- A upravíme: -(x-4)^2 +(y-9)^2+40=65
- Převedeme konstantu 40 na druhou stranu rovnice: -(x-4)^2 +(y-9)^2 =25
- Na závěr rovnici vydělíme 25: -\frac{(x-4)^2}{25} +\frac{(y-9)^2}{25}=1
- Jedná se tedy o hyperbolu. Hlavní osa je rovnoběžná s osou y a a=b=5.
Hyperbola a přímka
- přímka s protíná hyperbolu ve dvou bodech – sečna hyperboly
- přímka t protíná hyperbolu v jednom bodě – tečna hyperboly
- přímka v hyperbolu neprotíná – vnější přímka hyperboly
Speciální polohou sečny hyperboly je přímka, která je rovnoběžná s asymptotou. Taková sečna pak protíná hyperbolu v jednom bodě. 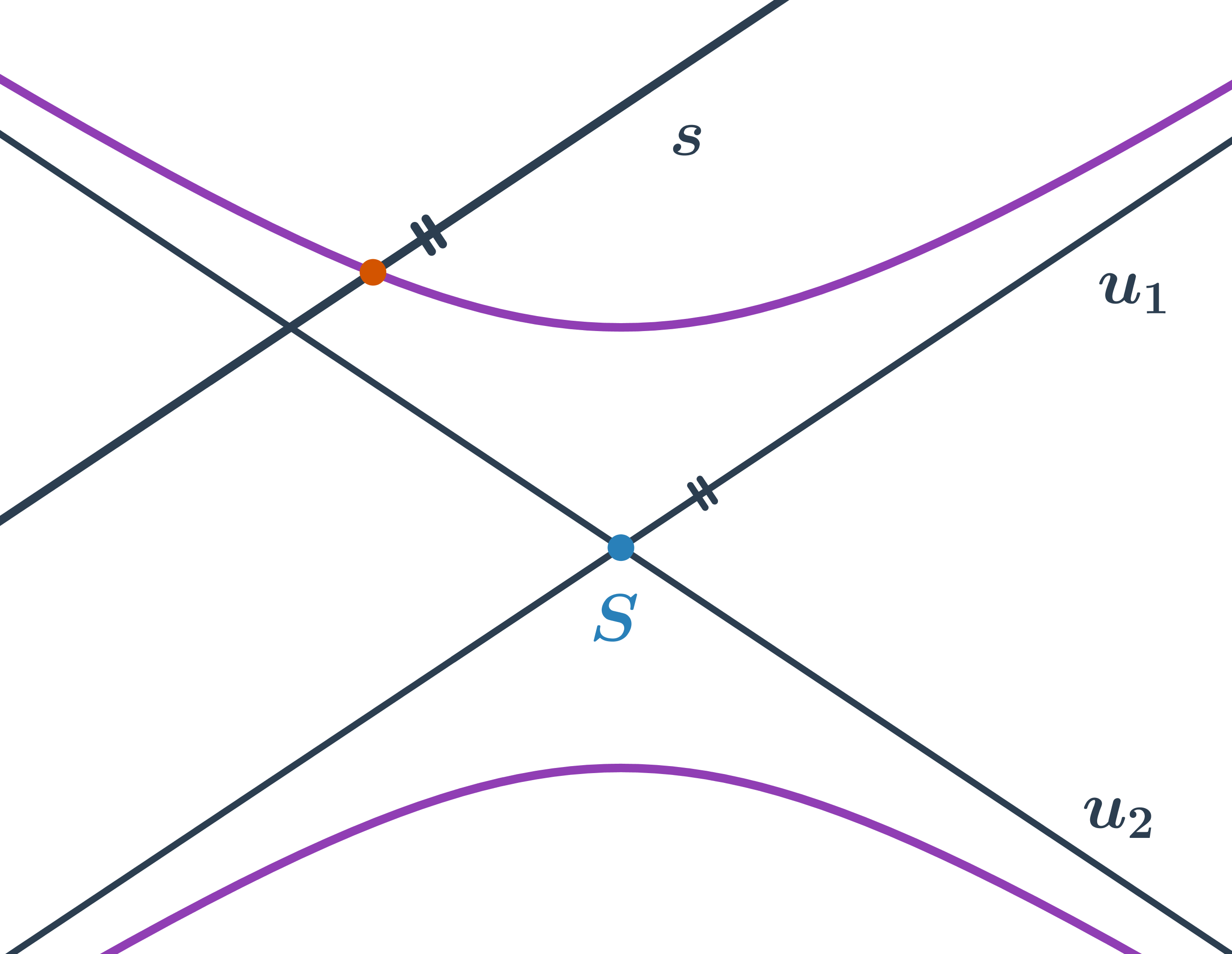
Jak rozlišit, je-li přímka tečna nebo sečna?
- Nejprve určíme vzájemnou polohu přímky a hyperboly.
- Pokud vyjdou dva průsečíky, jedná se o sečnu v obecné poloze.
- Pokud vyjde jeden průsečík, musíme ještě rozhodnout, jestli je přímka rovnoběžná s asymptotou. Pokud ne, jedná se o tečnu. V opačném případě jde o sečnu.
Rovnice tečny hyperboly v bodě, který leží na hyperbole
Hyperbola daná rovnicí \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 má v bodě T[x_0;y_0] tečnu danou rovnicí:
\frac{(x-m)(x_0-m)}{a^2} -\frac{(y-n)(y_0-n)}{b^2}=1.
Podobně můžeme zapsat i rovnici tečny hyperboly, která má hlavní osu rovnoběžnou s osou y.
Nahoru
