Krok po kroku – 9. ročník
V tomto cvičení doplňujete jednotlivé kroky v rozsáhlejším postupu – například jednotlivé kroky v úpravě výrazů nebo při řešení rovnic. Cvičení je dobrou rozcvičkou na samostatné řešení kompletních příkladů.
Filtr podle ročníku
Zlomky, procenta, desetinná čísla

Desetinná čísla, mocniny, odmocniny (lehké) • G4S
zadání: 15
Typicky zabere: 8 min

Geometrie

Obsah šedé oblasti (střední) • FJM
zadání: 20
Typicky zabere: 10 min
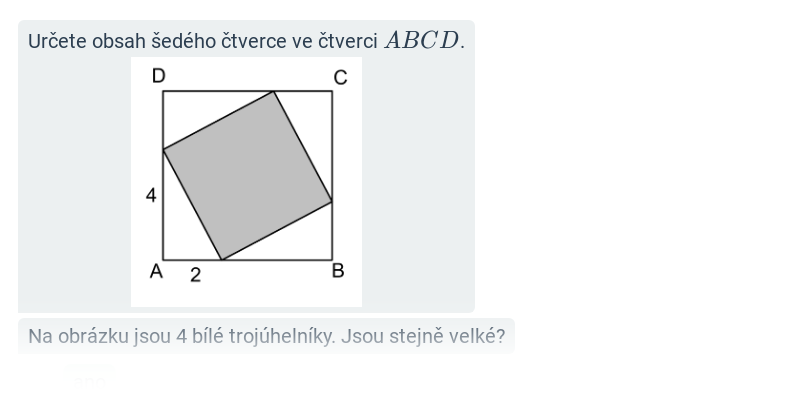

Obsah šedé oblasti (těžké) • FJT
zadání: 15
Typicky zabere: 10 min
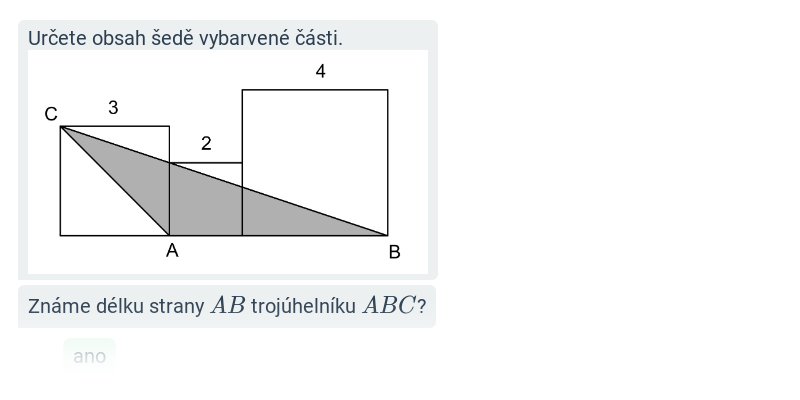

Objem a povrch: koule, válec, kužel (střední) • FTF
zadání: 15
Typicky zabere: 10 min


Objem a povrch: kvádr, jehlan, hranol (střední) • FKE
zadání: 16
Typicky zabere: 9 min
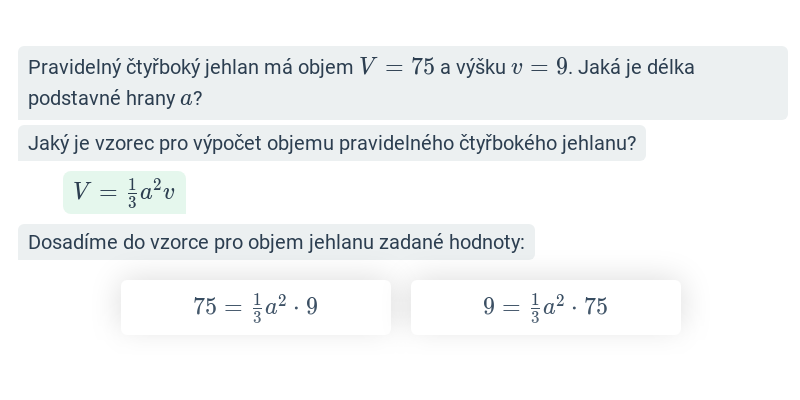

Konstrukce: osová a středová souměrnost (střední) • G26
zadání: 12
Typicky zabere: 7 min
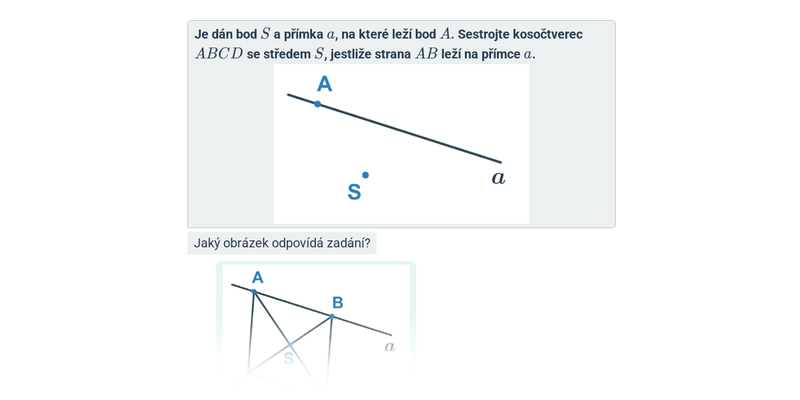
Elementární algebra

Úpravy výrazů s jednou proměnnou (těžké) • FJU
zadání: 23
Typicky zabere: 8 min


Úpravy výrazů s více proměnnými (těžké) • FJV
zadání: 22
Typicky zabere: 8 min
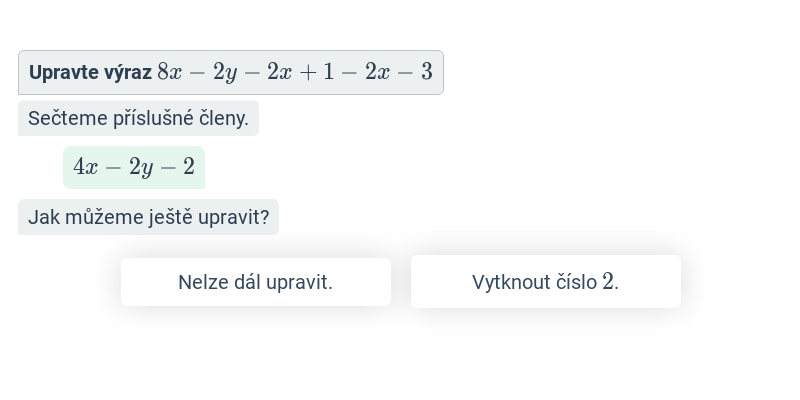

Podmínky lomených výrazů (lehké) • FTD
zadání: 23
Typicky zabere: 8 min
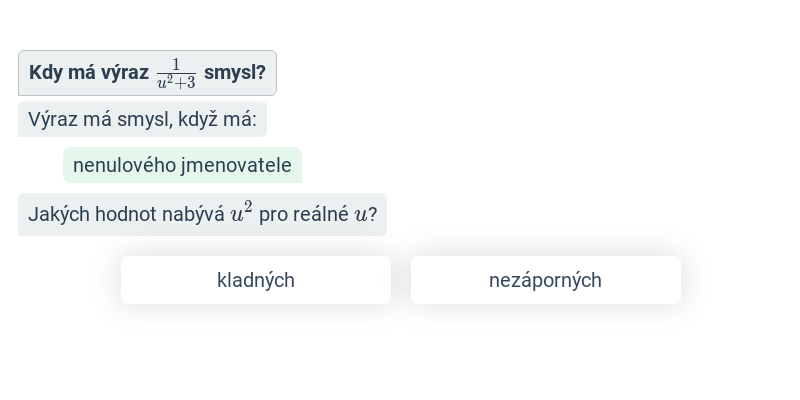

Podmínky lomených výrazů (střední) • FTE
zadání: 20
Typicky zabere: 9 min
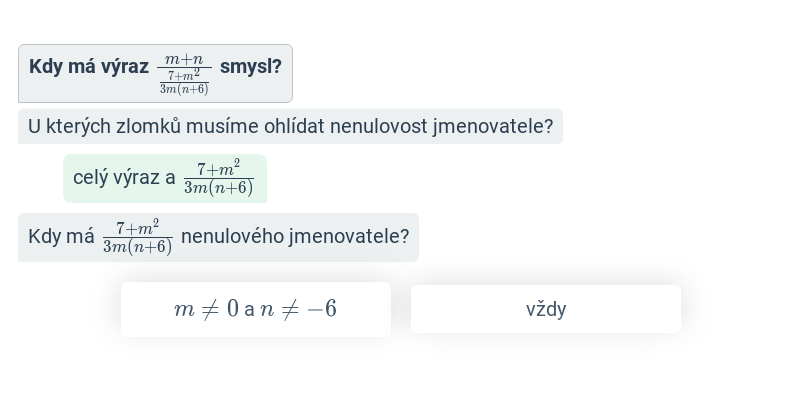

Podmínky lomených výrazů (těžké) • E3H
zadání: 22
Typicky zabere: 8 min
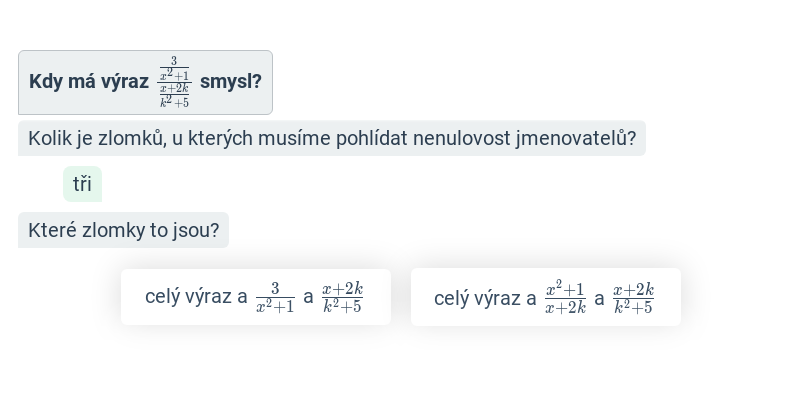

Početní operace s lomenými výrazy (lehké) • F7K
zadání: 10
Typicky zabere: 7 min


Lomené výrazy: mix (lehké) • F7P
zadání: 30
Typicky zabere: 9 min
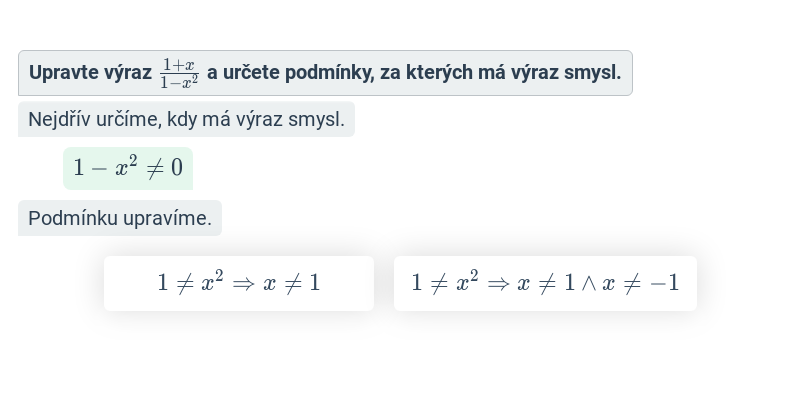

Rovnice se závorkami (těžké) • FH7
zadání: 52
Typicky zabere: 7 min


Rovnice s neznámou ve jmenovateli (střední) • E42
zadání: 15
Typicky zabere: 6 min
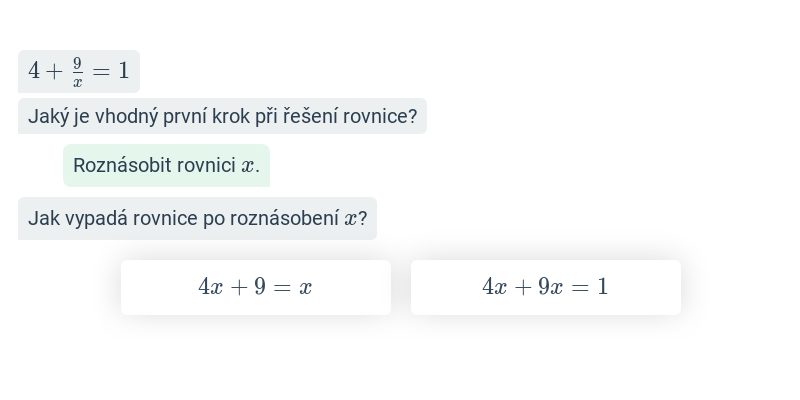

Rovnice se zlomky (těžké) • FHM
zadání: 21
Typicky zabere: 10 min


Rovnice s lomenými výrazy (lehké) • F9F
zadání: 15
Typicky zabere: 7 min


Rovnice s lomenými výrazy (střední) • F9G
zadání: 15
Typicky zabere: 7 min
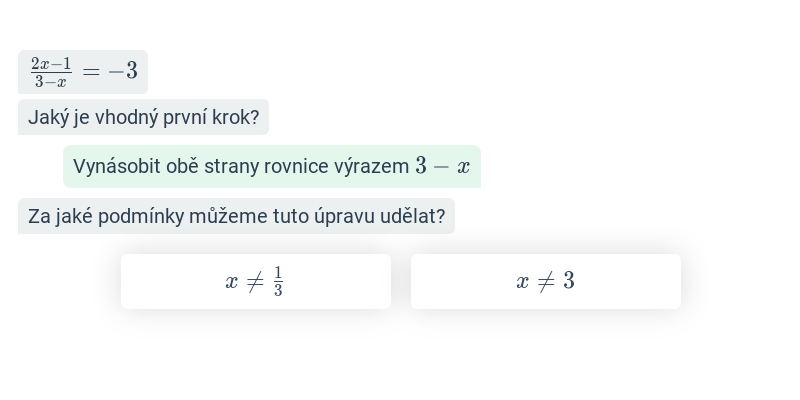

Rovnice s lomenými výrazy (těžké) • FGX
zadání: 15
Typicky zabere: 8 min
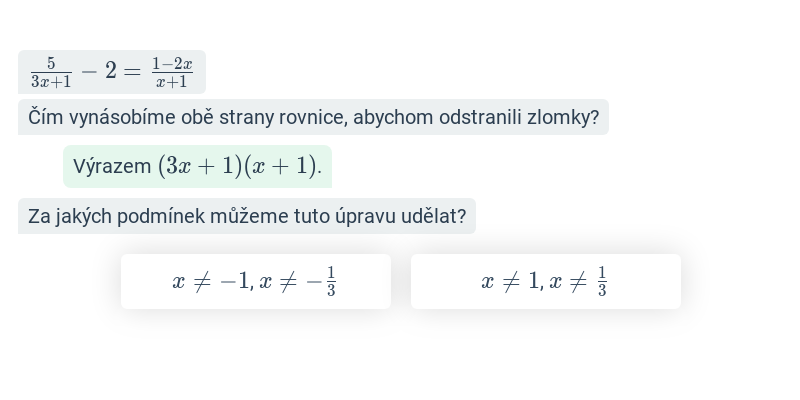

Soustava dvou rovnic: sčítací metoda řešení (lehké) • GHR
zadání: 20
Typicky zabere: 8 min
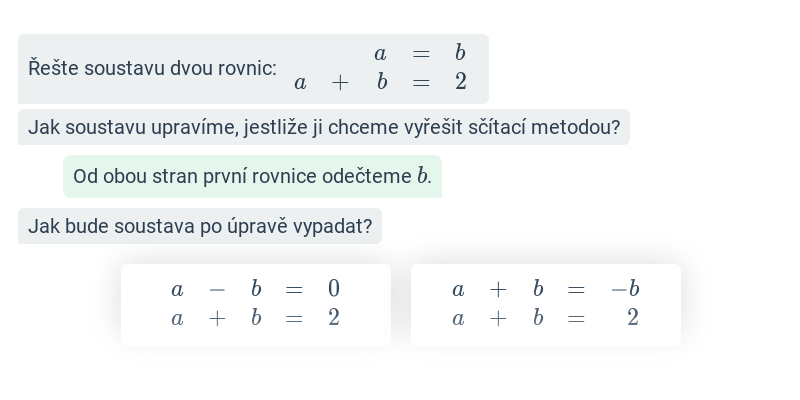

Soustava dvou rovnic: sčítací metoda řešení (střední) • FAL
zadání: 44
Typicky zabere: 8 min
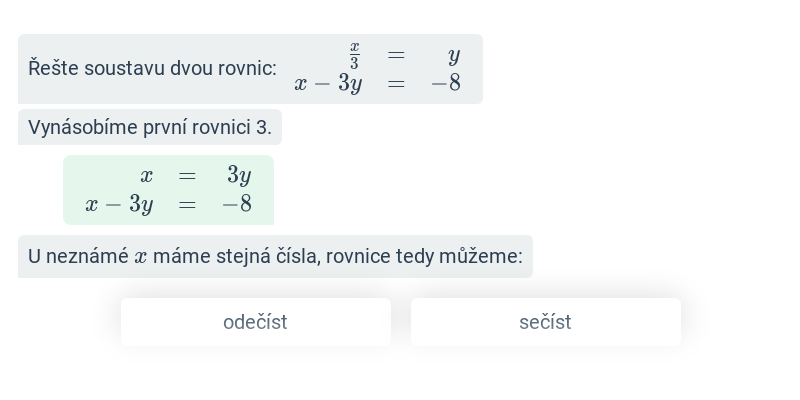

Soustava dvou rovnic: dosazovací metoda řešení (lehké) • GJF
zadání: 25
Typicky zabere: 6 min
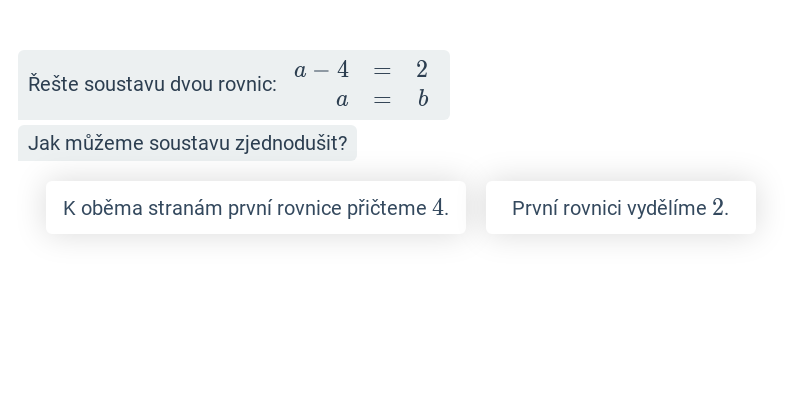

Soustava dvou rovnic: dosazovací metoda řešení (střední) • FAM
zadání: 59
Typicky zabere: 10 min
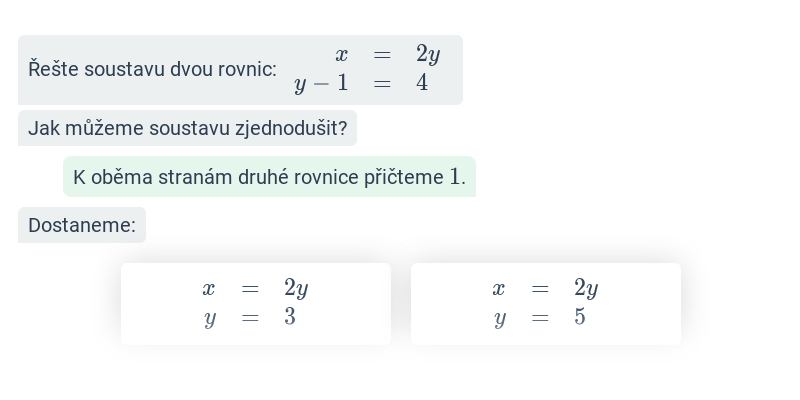

Soustava dvou rovnic: dosazovací metoda řešení (těžké) • FJD
zadání: 20
Typicky zabere: 9 min


Úlohy o směsích (střední) • E2T
zadání: 12
Typicky zabere: 13 min

Funkce

Grafy lineárních funkcí (lehké) • GZJ
zadání: 15
Typicky zabere: 9 min
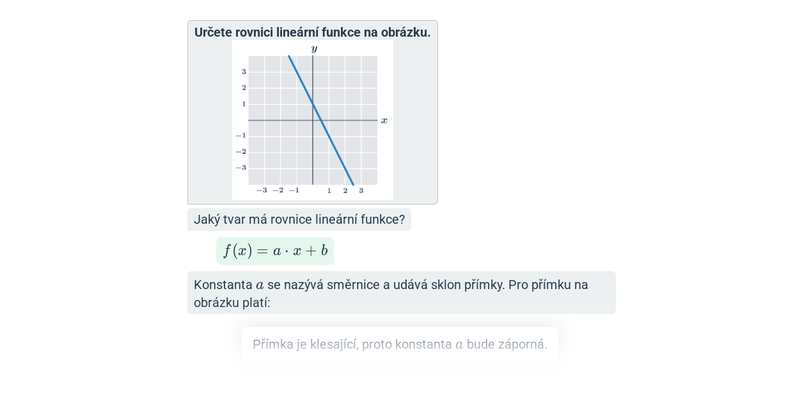
Finanční gramotnost

Sleva, daň, přirážka, jednoduchý úrok (střední) • GGL
zadání: 15
Typicky zabere: 11 min
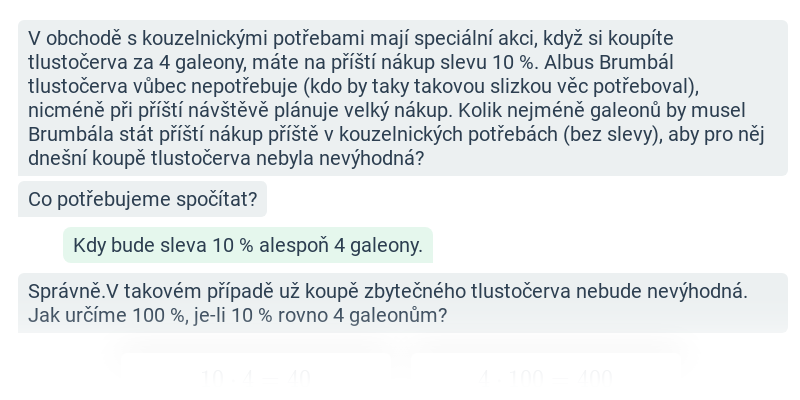

Jednoduché úročení: výpočty s daní (lehké) • GXE
zadání: 10
Typicky zabere: 10 min
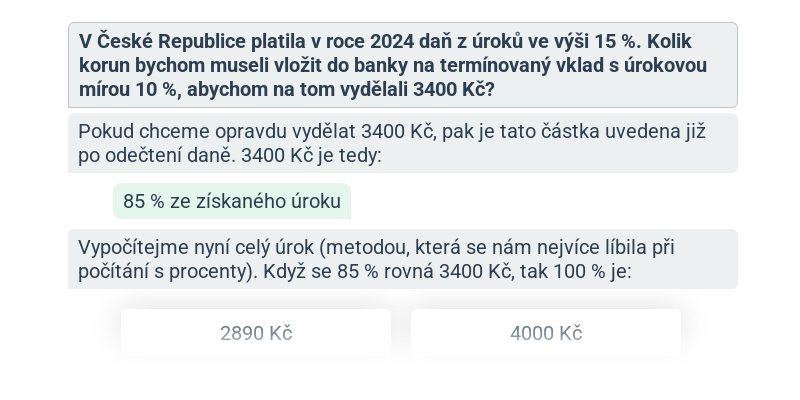

Složené úročení (střední) • GXF
zadání: 11
Typicky zabere: 8 min



 Čeština
Čeština Angličtina
Angličtina Informatika
Informatika Biologie
Biologie Němčina
Němčina Umíme to
Umíme to Zeměpis
Zeměpis Chemie
Chemie Dějepis
Dějepis Fyzika
Fyzika ZSV
ZSV
