Výpis souhrnů
Zlomky, procenta, desetinná čísla
Podtémata
- Zlomky, procenta, desetinná čísla
- Zlomky
- Zlomky: základy
- Poznávání zlomků
- Zlomky na číselné ose
- Porovnávání zlomků
- Smíšená čísla
- Výpočty se zlomky
- Krácení zlomků
- Sčítání a odčítání zlomků
- Násobení a dělení zlomků
- Zlomky a procenta
- Zlomky a desetinná čísla
- Pokročilé počítání se zlomky
- Zlomky, mocniny, odmocniny
- Úpravy výrazů se zlomky
- Rovnice se zlomky
- Procenta
- Procenta: poznávání
- Počítání s procenty
- Desetinná čísla
- Desetinná čísla: základy
- Desetinná čísla slovně
- Porovnávání desetinných čísel
- Zaokrouhlování desetinných čísel
- Desetinná čísla na číselné ose
- Výpočty s desetinnými čísly
- Sčítání a odčítání desetinných čísel
- Násobení desetinných čísel
- Dělení desetinných čísel
- Rovnice s desetinnými čísly
Zlomky, procenta, desetinná čísla
Zlomky, procenta a desetinná čísla na první pohled vypadají úplně jinak, nicméně spolu úzce souvisí – umožňují nám vyjadřovat části celku.
- Zlomky – zápis části z celku pomocí čitatele a jmenovatele, např. \frac{1}{2}
- Procenta – vyjádření jako část ze sta, např. 50 %
- Desetinná čísla – zápis čísel za využití desetinné čárky, např. 0,5
Společně nám tyto pojmy umožňují lépe rozumět matematice v každodenním životě, třeba správně rozumět slevám v obchodech.
Příklad: pizza
Máme na oběd pizzu a jednu čtvrtinu jsme již snědli. Zbývají nám tedy tři čtvrtiny, což můžeme zapsat:
- zlomkem: \frac{3}{4}
- procenty: 75 %
- desetinným číslem: 0,75
Výukové moduly
Konkrétní náměty, jakým způsobem učivo procvičovat a v jakém pořadí, poskytují výukové moduly:
| 4.–6. ročník | základní intuitivní porozumění jednotlivým zápisům a vzájemným vztahům | |
| 6.–8. ročník | početní operace, zaokrouhlování, umístění na číselnou osu | |
| 7.–9. ročník | složitější výpočty, převody, aplikace |
Zlomky jsou způsobem, jak vyjádřit část celku pomocí čitatele a jmenovatele. Často se s nimi setkáváme nejen v matematice, ale také v běžném životě, např. když po oslavě zbyde \frac13 dortu, na výletě jste urazili \frac78 cesty nebo když na vás při dělbě práce vyjde \frac25 umývání nádobí (což asi není zrovna spravedlivé, pokud jste na práci čtyři).
Zlomky nám pomáhají nejen při dělení jídla nebo výpočtech práce, ale také v geometrii, kde je třeba počítat části obrazců, nebo v algebře při práci s výrazy. Umění pracovat se zlomky je důležité pro pochopení dalších matematických oblastí, jako jsou desetinná čísla, procenta, poměry nebo rovnice.
Práce se zlomky je rozsáhlá oblast, kterou pro přehlednost dělíme na několik témat:
- Zlomky: základy – poznávání a porovnávání zlomků, umístění zlomků na číselné ose, práce se smíšenými čísly
- Výpočty se zlomky – základní operace se zlomky (krácení, sčítání, odčítání, násobení a dělení), převody mezi zlomky, procenty a desetinnými čísly
- Pokročilé počítání se zlomky – složitější operace zahrnující algebraické výrazy se zlomky, rovnice se zlomky, mocniny a odmocniny
Komiks pro zpestření

Zlomky: základy
Zlomky zapisujeme ve tvaru \frac{a}{b}, kde a se nazývá čitatel a b jmenovatel. Aby měl zlomek smysl, nesmí být jmenovatel nula. Význam zlomku odpovídá dělení. Příklad: ve zlomku \frac32 je čitatelem číslo 3 a jmenovatelem číslo 2, hodnota zlomku \frac32 se rovná dělení 3:2 = 1{,}5 („jedna a půl“).
Zlomek \frac{a}{b} je v základním tvaru, pokud jsou čísla a, b nesoudělná (tj. jejich jediný kladný společný dělitel je číslo 1). Na základní tvar převádíme zlomky pomocí krácení. Příklady:
- Zlomek \frac64 není v základním tvaru, protože čísla 6 a 4 jsou soudělná – mají společného dělitele 2, kterým jde zlomek krátit, čímž dostáváme základní tvar \frac32.
- Zlomek \frac34 je v základním tvaru, protože čísla 3 a 4 jsou nesoudělná.
Základy práce se zlomky si můžete procvičit v těchto tématech:
| téma | příklady |
|---|---|
| Poznávání zlomků | přiřazení zápisu zlomků ke grafickému vyjádření obrázkem |
| Zlomky na číselné ose | umisťování zlomků na číselnou osu, intuitivní představa o jejich velikosti |
| Porovnávání zlomků | porovnávání \frac{3}{11} a \frac{7}{11}, porovnání \frac{2}{3} a \frac{4}{7} |
| Smíšená čísla | převod 3\frac{1}{4} na \frac{13}{4} |
Komiks pro zpestření

Poznávání zlomků
Zlomky vyjadřují „části z celku“. Můžeme je graficky vyjádřit mnoha způsoby:

Kromě níže uvedených interaktivních cvičení je k dispozici také pracovní list – materiál určený k vytištění a rozstříhání:
NahoruZlomky na číselné ose
Zlomek můžeme na číselnou osu umístit tak, že ho převedeme na desetinné číslo (vydělíme prostě čitatele jmenovatelem) a pak postupujeme stejně jako u desetinných čísel. Například \frac{6}{5} = 1{,}2, tj. zlomek \frac{6}{5} leží dvě desetiny za jedničkou. Další příklady:
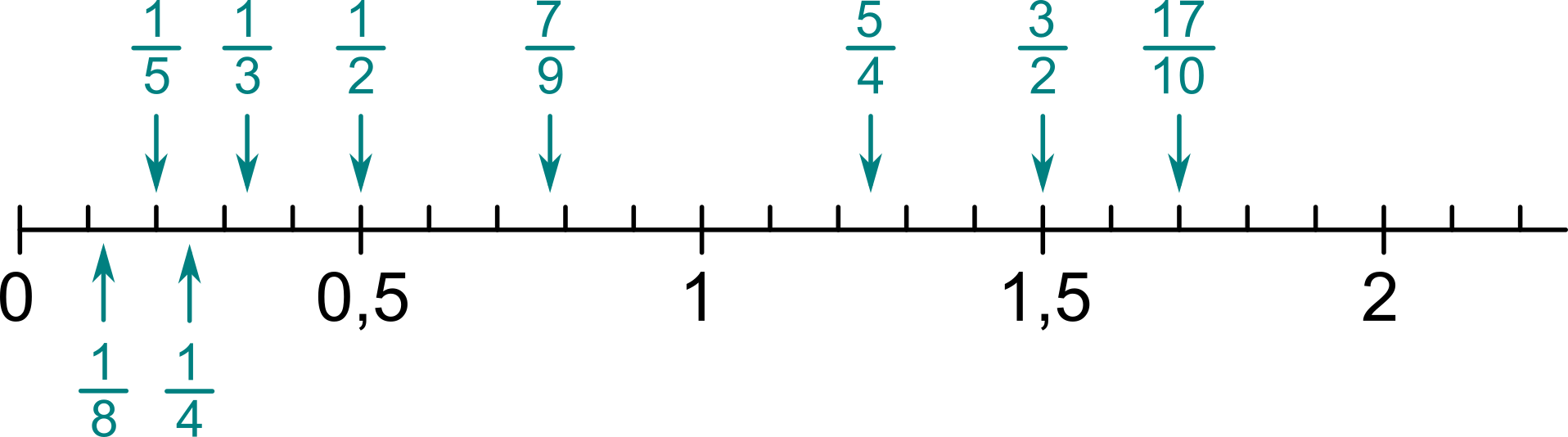
Zlomky menší než 1 můžeme umisťovat na číselnou osu také přímo (bez převodu na desetinné číslo) díky představě „část z celku“. Pokud máme umístit zlomek \frac{3}{7}, představíme si, jak bychom rozdělili úsečku od 0 po 1 na sedm stejných dílků. Zlomek \frac{3}{7} pak umístíme na třetí pozici.
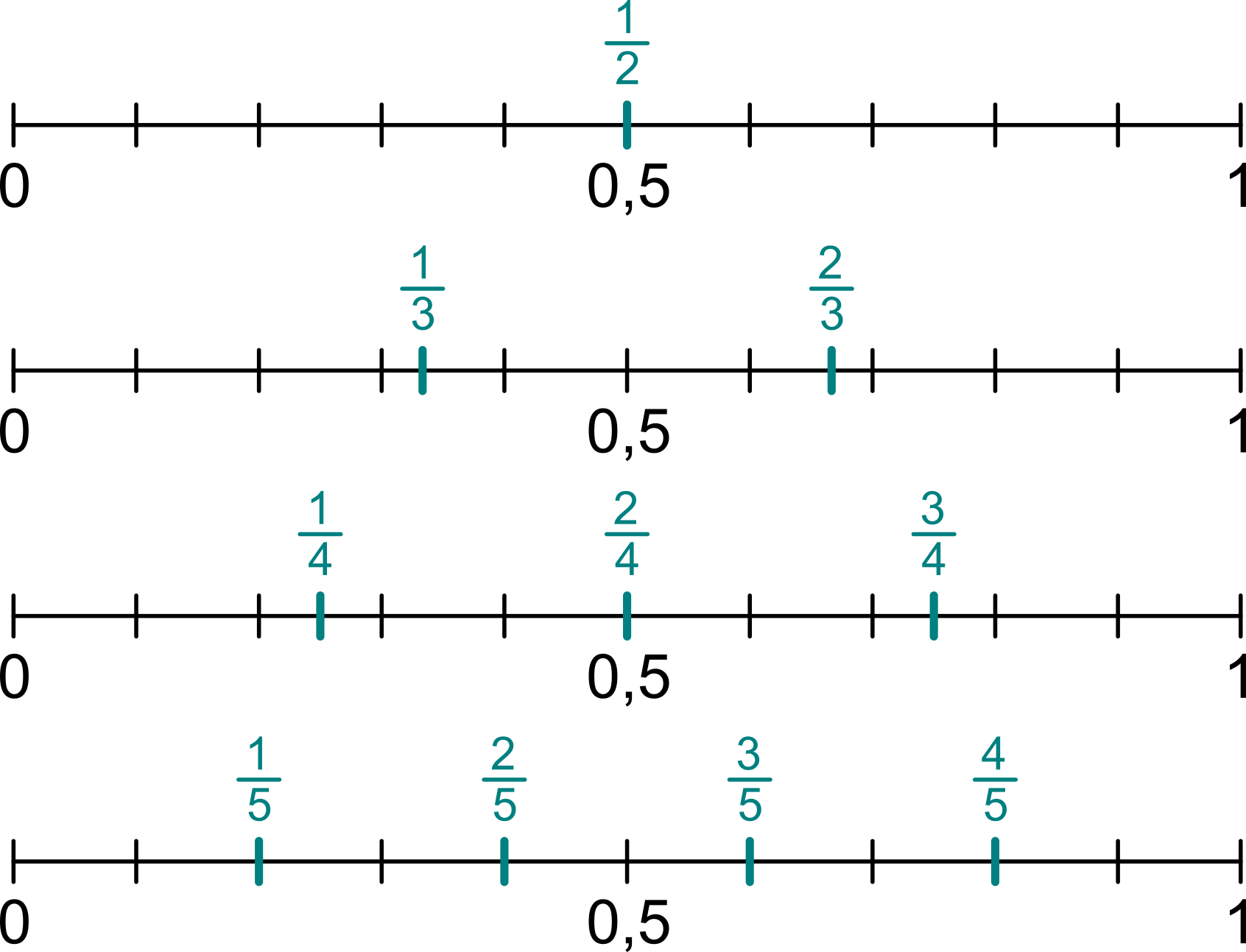
Hodí se vybudovat si dobrou představu zejména pro zlomky s malým jmenovatelem:
Porovnávání zlomků
Než se pustíme do porovnávání zlomků, je dobré mít jasno v tom, co je čitatel („to nahoře“) a jmenovatel („to dole“). Ve zlomku \frac{3}{7} je číslo 3 čitatelem, číslo 7 jmenovatelem.
Porovnávání zlomků se stejným jmenovatelem
Porovnávání zlomků se stejným jmenovatelem je jednoduché: stačí prostě porovnat čitatele. Pokud například porovnáváme zlomky \frac{3}{7} a \frac{5}{7}, je větší druhý zlomek. Oba zlomky vyjadřují sedminy z celku a je prostě víc, když máme sedmin pět.
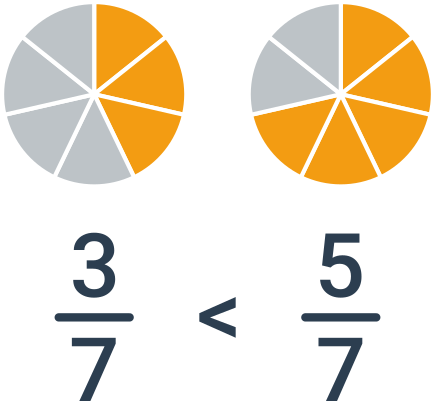
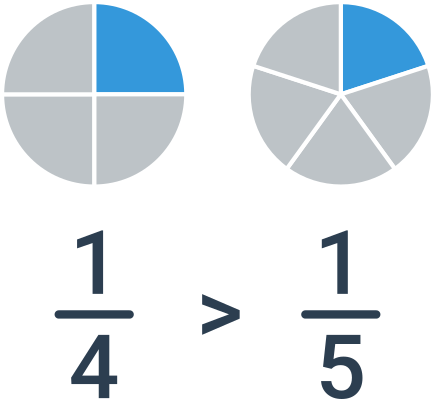
Porovnávání zlomků se stejným čitatelem
Pokud mají zlomky stejné čitatele, pak stačí porovnat jmenovatele. V tomto případě je však pořadí zlomků opačné než pořadí jmenovatelů. Pokud porovnáváme třeba zlomky \frac{1}{4} a \frac{1}{5}, je větší jedna čtvrtina: dostanu větší kousek pizzy, pokud se bude dělit mezi 4 lidi, než když se bude dělit mezi 5 lidí.
Jmenovatel různý od čitatele
V tomto případě potřebujeme zlomky nejprve převést na společného jmenovatele a teprve následně provést porovnání podle čitatelů. Příklad: porovnání zlomků \frac{2}{3} a \frac{4}{7}. Nejmenší společný jmenovatel je 21, po rozšíření dostáváme dvojici zlomků \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} a \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Protože 14 \gt 12, je větší první zlomek, tj. \frac{2}{3}.
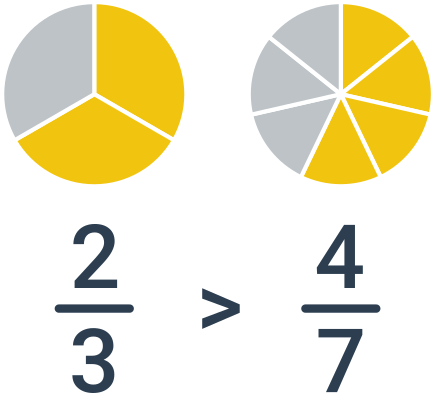
Porovnání bez výpočtu
Často můžeme provést porovnání i bez detailního výpočtu, pokud si zlomky správně představíme nebo porovnáme s vhodnou hodnotou „mezi“:
Zlomky \frac{2}{3} a \frac{7}{6}. První z nich je menší než 1, druhý je větší než 1. Platí tedy \frac{2}{3} \lt \frac{7}{6}.
Zlomky \frac{1}{3} a \frac{4}{5}. První z nich je určitě menší než polovina, druhý je výrazně větší než polovina. Platí tedy \frac{1}{3} \lt \frac{4}{5}.
Smíšená čísla
Pokud je u zlomku jmenovatel větší než čitatel (zlomek je menší než jedna), označuje se zlomek jako pravý. Nepravé zlomky (tedy ty, které jsou větší než jedna) můžeme zapsat pomocí smíšeného čísla. Smíšené číslo a\frac{b}{c} je zápis součtu a + \frac{b}{c}, kde \frac{b}{c} je kladný zlomek menší než jedna.
Převod smíšeného čísla na zlomek uděláme na základě pozorování, že jednotku můžeme zapsat jako \frac{c}{c}.

Příklady: převod smíšeného čísla na zlomek
- 3\frac14 = 3\cdot\frac44 + \frac14 = \frac{12}{4}+\frac14 = \frac{13}{4}
- 1\frac{1}{2} = \frac{3}{2}
- 2\frac{3}{5} = \frac{13}{5}
Převod nepravého zlomku na smíšené číslo uděláme pomocí dělení se zbytkem. Celá část smíšeného čísla odpovídá podílu, čitatel zbylého zlomku odpovídá zbytku.
Příklady: převod nepravého zlomku na smíšené číslo
- \frac{17}{3} = 5\frac23, protože 17:3 je 5 a zbytek 2.
- \frac{15}{7}= 2\frac17, protože 15:7 je 2 a zbytek 1.
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruVýpočty se zlomky
Základní výpočty se zlomky jsou následující:
- Zlomky se krátí tak, že čitatele i jmenovatele vydělíme jejich společným dělitelem.
- Zlomek \frac{9}{12} můžeme zkrátit na \frac{3}{4}, protože čitatel i jmenovatel mají společného dělitele 3.
- Pro sčítání a odčítání zlomků je nutné převést zlomky na společného jmenovatele.
- \frac{1}{4} + \frac{1}{6} převedeme na společného jmenovatele 12 a dostaneme \frac{3}{12} + \frac{2}{12} = \frac{5}{12}.
- Násobení se provádí tak, že vynásobíme čitatele i jmenovatele mezi sebou.
- \frac{2}{3} \cdot \frac{3}{4} = \frac{6}{12} = \frac{1}{2}
- Dělení se provádí násobením převráceného zlomku.
- \frac{2}{3} : \frac{3}{4} = \frac{2}{3} \cdot \frac{4}{3} = \frac{8}{9}
- Převod zlomku na procenta se provádí pomocí násobení 100.
- \frac{3}{4} = 0{,}75 = 75 \%
- Zlomky převedeme na desetinná čísla tak, že čitatele vydělíme jmenovatelem. Naopak desetinné číslo lze převést na zlomek pomocí roznásobení čísly jako 10, 100, 1000 … (mocninami desítky).
- \frac{2}{5} = 2 : 5 = 0{,}4
- 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, což po zkrácení dává \frac{1}{4}
- Zadání kombinující různé aritmetické operace se zlomky.
Krácení zlomků
Stejnou hodnotu můžeme vyjádřit mnoha zlomky, například \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Jen jedno možné vyjádření ovšem považujeme za základní tvar. Zlomek je v základním tvaru, pokud jsou čitatel a jmenovatel nesoudělní, tj. nemají žádného společného dělitele kromě jedničky. V uvedeném příkladě je v základním tvaru zlomek \frac23.
Jako krácení zlomku se označuje operace, kdy čitatele i jmenovatele vydělíme stejným, nenulovým číslem. Krácení zachovává hodnotu zlomku. Pokud chceme zlomek převést do základního tvaru, krátíme největším společným dělitelem čitatele a jmenovatele.
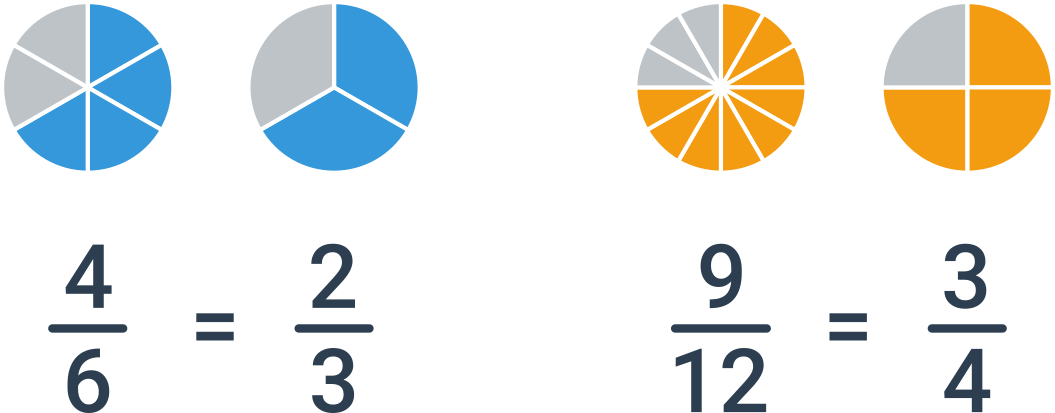
Opačnou operací je rozšíření zlomku, kdy čitatele i jmenovatele vynásobíme stejným nenulovým číslem. Rozšíření zlomku se používá při sčítání a odčítání zlomků.
Příklady krácení zlomků
- Zlomek \frac{15}{28} je v základním tvaru, protože čísla 15 a 28 nemají společného dělitele (jsou nesoudělná).
- Zlomek \frac{25}{30} můžeme krátit číslem 5, čímž dostaneme zlomek \frac{5}{6}, který je v základním tvaru.
- Zlomek \frac{12}{18} můžeme krátit číslem 2, čímž dostaneme zlomek \frac{6}{9}. Pokud chceme krátit na základní tvar, najdeme největšího společného dělitele čísel 12 a 18, což je 6. Po krácení číslem 6 dostáváme zlomek \frac{2}{3}.
Komiks pro zpestření
Sčítání a odčítání zlomků
Než se pustíme do sčítání zlomků, je dobré mít jasno v tom, co je čitatel („to nahoře“) a jmenovatel („to dole“). Ve zlomku \frac{3}{7} je 3 čitatel, 7 jmenovatel.
Sčítání zlomků se stejným jmenovatelem
Pokud mají sčítané zlomky stejného jmenovatele, stačí prostě sečíst čitatele. Jmenovatele necháme stejného, tedy \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.
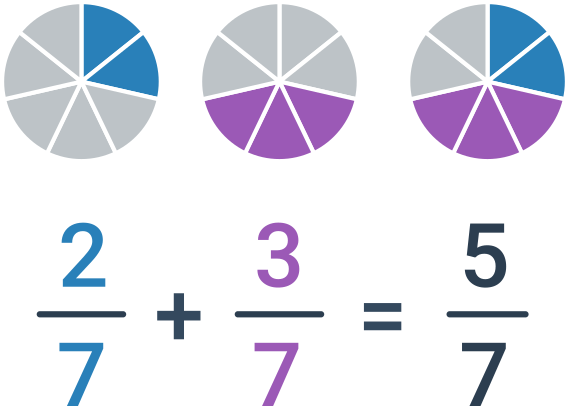
Sčítání zlomků s různými jmenovateli
Pokud mají sčítané zlomky různého jmenovatele, musíme je nejprve rozšířit tak, aby měly stejného jmenovatele. Nejvýhodnější je rozšířit zlomky na nejmenší společný násobek původních jmenovatelů. Jakmile mají zlomky stejného jmenovatele, sečteme je výše uvedeným postupem.
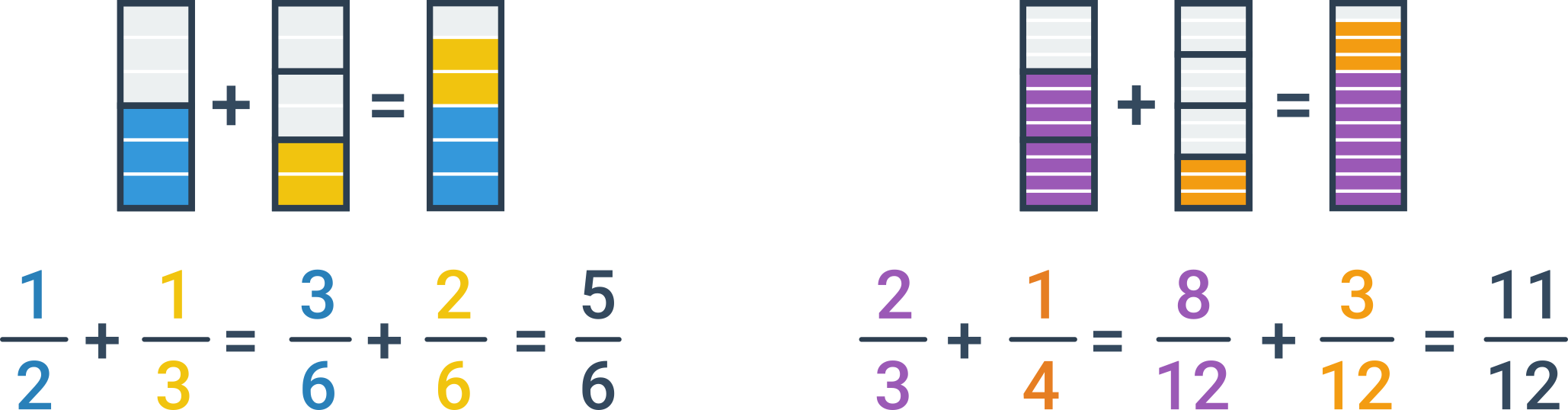
Úpravy a odčítání
Výsledný zlomek většinou ještě krátíme, abychom dostali výsledek v základním tvaru. Odčítání zlomků funguje stejným způsobem.
Příklady
Příklady se stejným jmenovatelem, bez nutnosti krácení
\frac{2}{5} + \frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}
\frac{5}{7} - \frac{2}{7} = \frac{5-2}{7} = \frac{3}{7}
Příklady se stejným jmenovatelem, kdy výsledek krátíme
\frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}
\frac{8}{9} - \frac{2}{9} = \frac{8-2}{9} = \frac{6}{9} = \frac{2}{3}
Příklad s různými jmenovateli: \frac{5}{6} - \frac{3}{4}
- Nejmenší společný násobek jmenovatelů 6 a 4 je 12, rozšíříme tedy zlomky na jmenovatele 12.
- \frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}
Příklady s různými jmenovateli: \frac{7}{8} + \frac{2}{5}
- Nejmenší společný násobek jmenovatelů 8 a 5 je 40, rozšíříme tedy zlomky na jmenovatele 40.
- \frac{7}{8} + \frac{2}{5} = \frac{7 \cdot 5}{8 \cdot 5} + \frac{2 \cdot 8}{5 \cdot 8} = \frac{35}{40} + \frac{16}{40} = \frac{51}{40}
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření
Násobení a dělení zlomků
Násobení zlomků si můžeme představit skrze čokoládu. Pokud násobíme \frac45\cdot \frac23 je to jako bychom brali čtyři z pěti sloupečků a dva ze tří řádků. Kolik čtverečků čokolády takto vezmeme? Osm z patnácti, tedy \frac{8}{15}.

Při násobení zlomků tedy prostě vynásobíme čitatele prvního zlomku a čitatele druhého zlomku a dostaneme výsledný čitatel, podobně pro jmenovatele: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Pokud si chceme ušetřit násobení velkých čísel, můžeme zlomky krátit, a to i „do kříže“.
Příklady násobení zlomků
- \frac{2}{3}\cdot\frac{1}{5} = \frac{2\cdot 1}{3\cdot 5}=\frac{2}{15}
- \frac{2}{3}\cdot\frac{3}{4} = \frac{2\cdot 3}{3\cdot 4}=\frac{2}{4}=\frac{1}{2} (všimněte si, že neroznásobujeme, ale hned krátíme)
Dělení zlomků je to stejné jako násobení převráceným zlomkem: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}.
Příklady dělení zlomků
- \frac13:\frac12 =\frac13\cdot \frac21 = \frac23
- \frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot \frac{4}{3} = \frac{2\cdot 4}{5\cdot 3} = \frac{8}{15}
Zlomky a procenta
Převod procent na zlomek v základním tvaru
Jedno procento je to stejné jako jedna setina, tj. \frac{1}{100}. Vynásobíme tedy číslo (udávající procenta) zlomkem \frac{1}{100} a následně zlomek vykrátíme (pomocí dělení největším společným dělitelem) na základní tvar. Příklady:
- 45\ \% = 45 \cdot \frac{1}{100} = \frac{45}{100} = \frac{5\cdot 9}{5\cdot 20}= \frac{9}{20}
- 12\ \% = 12 \cdot \frac{1}{100} = \frac{12}{100} = \frac{4\cdot 3}{4\cdot 25}= \frac{3}{25}
Převod zlomku na procenta
Chceme zlomek \frac{a}{b} vyjádřit jako p\ \%. Protože jedno procento je jedna setina, musí tedy platit \frac{a}{b} = \frac{p}{100}. Takže p = \frac{a}{b}\cdot 100. Stačí tedy zlomek vynásobit číslem 100. Příklady:
- \frac{2}{5} = \frac{2}{5} \cdot 100\ \% = \frac{200}{5}\ \% = 40\ \%
- \frac{3}{20} = \frac{3}{20} \cdot 100\ \% = \frac{300}{20}\ \% = 15\ \%
Zlomky a desetinná čísla
Převod desetinného čísla na zlomek
Desetinné číslo roznásobíme pomocí mocniny desítky tak, abychom se „zbavili“ desetinné čárky. Následně zlomek vykrátíme (největším společným dělitelem), abychom dostali zlomek v základním tvaru. Příklady:
1{,}5 = 1{,}5\cdot \frac{10}{10} = \frac{1{,}5\cdot 10}{10} = \frac{15}{10} = \frac{3}{2}
1{,}25 = 1{,}25 \cdot \frac{100}{100} = \frac{1{,}25\cdot 100}{100} = \frac{125}{100} = \frac{5}{4}
Počítání nám může usnadnit, když si zapamatujeme některé užitečné převody, s jejichž pomocí vhodné úvahy vyřešit i další příklady:
0{,}01 = \frac{1}{100}
0{,}1 = \frac{1}{10}
0{,}2 = \frac{1}{5}
0{,}25 = \frac{1}{4}
0{,}333\ldots = \frac{1}{3}
0{,}5 = \frac{1}{2}
Převod zlomku na desetinné číslo
Význam zlomku je prostě podíl čitatele a jmenovatele. Zlomek tedy vyjádříme jako desetinné číslo prostě tak, že podělíme čitatele jmenovatelem (může se hodit postup pro „dělení pod sebou“). Příklady:
\frac{3}{4} = 3:4 = 0{,}75
\frac{6}{5} = 6:5 = 1{,}2
\frac{3}{20} = 3:20 = 0{,}15
Pokročilé počítání se zlomky
Mezi pokročilejší výpočty se zlomky patří jejich umocňování a použití v algebraických výrazech a rovnicích.
| téma | příklady |
|---|---|
| Zlomky, mocniny, odmocniny | \large(\frac{2}{3}\large)^2, \ \sqrt{\frac{2}{3}}, \ 2^\frac{2}{3} |
| Úpravy výrazů se zlomky | \frac{3x+6}{15}, \ \frac{x}{2}+\frac{x}{3} |
| Rovnice se zlomky | \frac{x}{2} - \frac{x}{3} = 2 |
Zlomky, mocniny, odmocniny
Umocňování a odmocňování zlomku
Při umocňování (odmocňování) zlomku prostě umocníme (odmocníme) čitatele i jmenovatele:
\large(\frac{2}{3}\large)^2 = \frac{2^2}{3^2} = \frac{4}{9}
\sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}}
\large(\frac{4}{5}\large)^{-1} = \frac{4^{-1}}{5^{-1}} = \frac{5}{4} (umocňování na -1 odpovídá prohození čitatele a jmenovatele)
Umocňování na zlomek
Umocňování na zlomek odpovídá tomu, že vezmeme mocninu podle čitatele a odmocninu podle jmenovatele, tj. x^\frac{a}{b} = \sqrt[b]{x^a}. Příklady:
2^\frac{2}{3} = \sqrt[3]{2^2} = \sqrt[3]{4} = 1{,}587\ldots
4^\frac{1}{2} = \sqrt{4^1} = 2
81^\frac{3}{4} = \sqrt[4]{81^3} = \sqrt[4]{81}^3 = 3^3 = 27
Úpravy výrazů se zlomky
Úpravy výrazů se zlomky provádíme stejnými základními postupy jako ostatní úpravy výrazů, pouze při tom používáme navíc operace specifické pro zlomky, např. krácení zlomků, sčítání a odčítání zlomků, násobení a dělení zlomků. Příklady úprav:
| Popis | Výraz | Upravený výraz |
|---|---|---|
| Krácení zlomku | \frac{3x+6}{15} | =\frac{x+2}{5} |
| Součet zlomků | \frac{x}{2}+\frac{x}{3} | =\frac{3x}{6}+\frac{2x}{6} = \frac{5x}{6} |
| Násobení zlomků | \frac{x+1}{2} \cdot \frac{1}{3} | =\frac{x+1}{6} |
Rovnice se zlomky
Rovnice se zlomky řešíme stejnými postupy jako základní rovnice, pouze při tom používáme operace se zlomky.
Často se můžeme operacím se zlomky vyhnout tak, že celou rovnici nejprve roznásobíme společným násobkem všech jmenovatelů zlomků.
Řešený příklad
| Zadání: | \frac{x}{2} - \frac{x}{3} = 2 |
| Jmenovatelé ve zlomcích jsou 2 a 3, společný násobek je 6. Roznásobíme tedy rovnici číslem 6: | 3x - 2x = 12 |
| Řešení: | x=12 |
Procento (%) je bezrozměrná jednotka vyjadřující jednu setinu celku. Například zápis „42 %“ (42 procent) je to stejné jako zlomek \frac{42}{100} nebo desetinné číslo 0,42.
Promile (‰) je jedna desetina procenta, tedy jedna tisícina celku.
Základní využití procent je pro vyjádření části celku, například:
- jaká část obyvatel pracuje v zemědělství,
- kolik studentů úspěšně splnilo zkoušku,
- kolik alkoholu obsahuje láhev vína.
Další oblasti využití procent jsou:
- vyjadřování pravděpodobnosti (jaká je šance, že bude zítra pršet),
- finanční vztahy (slevy, úroky),
- zpracování a prezentování statistických dat.
Procvičování tohoto tématu je rozdělené na několik podtémat:
- Procenta: poznávání – základní představa o tom, co různé počty procent znamenají
- Počítání s procenty – výpočty s procenty, např. 70 % z 30 kilometrů, sleva 20 % z 450 Kč
- Zlomky a procenta – vztahy mezi procenty a zlomky, převádění z jednoho zápisu na druhý
Komiks pro zpestření
Procenta: poznávání
Pro dobré ovládnutí procent se hodí vybudovat si základní intuici o tom, co procenta znamenají a jak odpovídají jednotlivé hodnoty grafickému znázornění. Pro některé často se vyskytující hodnoty se hodí zapamatovat si význam zpaměti:
| 10 % | = | jedna desetina |
| 20 % | = | jedna pětina |
| 25 % | = | jedna čtvrtina |
| 33 % | = | jedna třetina |
| 50 % | = | jedna polovina |
| 75 % | = | tři čtvrtiny |
| 80 % | = | čtyři pětiny = celek bez jedné pětiny |
| 90 % | = | devět desetin = celek bez jedné desetiny |
Počítání s procenty
Pro počítání s procenty je nejdůležitější si uvědomit, že procento je jedna setina, tj. \frac{1}{100}. Pokud tedy chceme vypočítat například „15 % z 300“, počítáme takto: 15\ \% \textrm{ z } 300 = \frac{15}{100} \cdot 300 = 15 \cdot 3 = 45.
Pro některá často se vyskytující procenta si můžeme výpočet usnadnit:
- 50 % = jedna polovina, tj. dělíme číslem 2
- 25 % = jedna čtvrtina, tj. dělíme číslem 4
- 10 % = jedna desetina, tj. dělíme číslem 10
- 90 % = bez jedné desetiny
Komiks pro zpestření
Desetinná čísla
Desetinné číslo je způsob zápisu čísla pomocí celé části a desetinné části, která je oddělená desetinnou čárkou. Například v zápisu 154,28 je 154 celou částí a 28 desetinnou částí. Na prvním místě za desetinnou čárkou jsou desetiny, na druhém setiny, na třetím tisíciny.
Pro větší přehlednost dělíme procvičování desetinných čísel na několik dílčích témat:
- Desetinná čísla: základy – slovní vyjádření, porovnávání, zaokrouhlování, umístění desetinných čísel na číselné ose
- Výpočty s desetinnými čísly – základní aritmetické operace s desetinnými čísly (sčítání, odčítání, násobení, dělení), převod na zlomky
- Pokročilé počítání s desetinnými čísly – mocniny a odmocniny, rovnice s desetinnými čísly
Desetinná čárka a tečka
V češtině se používá k zápisu desetinných čísel desetinná čárka. V anglosaském světě se místo ní však používá desetinná tečka, tj. místo 154,28 se píše 154.28. Tento způsob zápisu se používá ve výpočetní technice všude na světě.
Desetinná čísla: základy
Pomocí desetinných čísel vyjadřujeme čísla, která nejsou „celá“. Příklad: Pokud rozdělíme 6 koláčů spravedlivě mezi 4 děti, dostane každé dítě „jeden a půl“ koláče, což zapisujeme jako 1,5.
Toto téma se zabývá základním porozuměním desetinným číslům:
- Desetinná čísla slovně – převod mezi slovním pojmenováním a číselným zápisem
- Porovnávání desetinných čísel – porovnávání kladných i záporných čísel s desetinnou částí
- Zaokrouhlování desetinných čísel – zaokrouhlování čísel na různé počty desetinných míst
- Desetinná čísla na číselné ose – dobrá představa o umístění čísel na číselnou osu pomáhá i s jinými operacemi (např. zaokrouhlování a porovnání)
Navazující téma pak řeší výpočty s desetinnými čísly.
NahoruDesetinná čísla slovně
Desetinná čísla můžeme číst mnoha různými způsoby. První je „přímočaré čtení“, kdy pouze místo „čárka“ říkáme „celá“. Desetinnou část můžeme přečíst jako jedno číslo, nebo vyjmenovat po cifrách:
| 4,23 | = | „čtyři celá dvacet tři“ |
| 21,508 | = | „dvacet jedna celá pět nula osm“ |
Dále můžeme desetinné číslo přečíst pomocí desetin, setin, tisícin:
| 0,1 | = | „jedna desetina“ |
| 0,01 | = | „jedna setina“ |
| 0,001 | = | „jedna tisícina“ |
| 3,4 | = | „tři a čtyři desetiny“ |
| 0,25 | = | „dvě desetiny a pět setin“ = „dvacet pět setin“ |
| 42,007 | = | „čtyřicet dva a sedm tisícin“ |
Někdy také desetinné číslo můžeme pojmenovat podle zlomku, který mu přísluší:
| 0,5 | = | „jedna polovina“ |
| 3,5 | = | „tři a půl“ |
| 0,25 | = | „jedna čtvrtina“ |
Porovnávání desetinných čísel
Při porovnávání desetinných čísel najdeme tu „nejdůležitější“ část, ve které se liší, a podle ní srovnání provedeme. Tedy nejprve porovnáváme celou část. Pokud jsou celé části shodné, porovnáváme desetiny, následně setiny, tisíciny a tak dále. Nezapomeneme též zkontrolovat znaménko, které má stejný vliv jako u celých čísel. Příklady:
15{,}3 \lt 17{,}9987 – liší se celá část, takže pro účely porovnání můžeme desetinná místa zcela ignorovat.
0{,}2 \gt 0{,}17 – celá část je stejná, rozhodujeme tedy podle desetin, kde 2 \gt 1. u příkladů tohoto typu se často chybuje, protože to vypadá, že 17 \gt 2, což je ovšem chybná úvaha. Pro lepší představu si můžeme doplnit nulu zprava: 0{,}20 \gt 0{,}17.
3{,}21 \gt -3{,}22 – zde vůbec nehrají roli desetinná místa, protože první číslo je kladné a druhé záporné.
-4{,}2791 \lt -4{,}2758 – porovnávání provádíme podle cifer na pozici tisícin (9 a 5), výsledek je „naopak“, protože jde o záporná čísla.
Zaokrouhlování desetinných čísel
Zaokrouhlování desetinných čísel funguje podobně jako zaokrouhlování celých čísel, pouze pracujeme i s částí za desetinnou čárkou. U desetinných čísel je téma zaokrouhlování obzvlášť důležité, protože se mu občas nemůžeme vyhnout – některá čísla v desítkové soustavě totiž nelze přesně zapsat, například \frac{1}{3} = 0{,}3333\ldots, \sqrt{2} = 1{,}4142\ldots, \pi = 3{,}14 159\ldots
Zaokrouhlování na desetiny znamená, že číslo nahradíme nejbližším násobkem čísla 0,1 (tj. číslem s jednou cifrou za desetinnou čárkou). Zaokrouhlování na setiny znamená, že číslo nahradíme nejbližším násobkem čísla 0,01 (tj. číslem s dvěma ciframi za desetinnou čárkou). Podobně zaokrouhlujeme i s vyšší přesností. Stejně jako při zaokrouhlování celých čísel i u desetinných čísel zaokrouhlujeme čísla končící číslicí 5 nahoru. Příklady:
3,628 zaokrouhleno na desetiny je 3,6.
3,628 zaokrouhleno na setiny je 3,63.
12,25 zaokrouhleno na desetiny je 12,3.
4,8975 zaokrouhleno na celé číslo je 5.
84,15 zaokrouhleno na desítky je 80 (pozor na rozdíl mezi zaokrouhlováním na „desetiny“ a „desítky“).
Desetinná čísla na číselné ose
Podobně jako na jiných číselných osách, první krok je určit, jaké jsou rozestupy mezi značkami na číselné ose. Při práci s desetinnými čísly bývá často rozestup 0,1 (jedna desetina), ale nemusí to tak být nutně.
Příklad:

Výpočty s desetinnými čísly
Toto téma se zabývá aritmetickými operacemi s desetinnými čísly. Základem je dobré zvládnutí základních aritmetických operací s přirozenými čísly, navíc musíme dávat pozor na správnou práci s desetinnou čárkou, např. při sčítání a odčítání musíme nejdříve zarovnat čísla podle desetinné čárky.
| téma | příklad |
|---|---|
| Sčítání a odčítání desetinných čísel | 3{,}75 + 1{,}2 = 4{,}95 |
| Násobení desetinných čísel | 1{,}2 \cdot 3{,}4 = 4{,}08 |
| Dělení desetinných čísel | 4{,}5 : 1{,}5 = 45 : 15 = 3 |
| Desetinná čísla a zlomky | 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100} = \frac{1}{4} |
| Kombinace operací s desetinnými čísly | (1{,}1-1)\cdot (1{,}1+1) = 0{,}1\cdot 2{,}1 = 0{,}21 |
Sčítání a odčítání desetinných čísel
Při sčítání a odčítání desetinných čísel postupujeme stejně jako při běžném sčítání a odčítání, pouze musíme mít čísla „zarovnaná“ podle desetinné čárky. Jako vhodná pomůcka (zejména při sčítání a odčítání pod sebou) může být doplnit si nuly zprava, aby obě čísla měla stejný počet cifer za desetinnou čárkou. Příklady:
1{,}2+2{,}3 = 3{,}5
3{,}457+4{,}2 = 3{,}457+4{,}200 = 7{,}657
1{,}3-0{,}8 = 0{,}5
0{,}001+0{,}01+0{,}1 = 0{,}001+0{,}010+0{,}100 = 0{,}111
2{,}01-0{,}1 = 2{,}01 - 0{,}10 = 1{,}91
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
NahoruNásobení desetinných čísel
Násobení desetinných čísel můžeme udělat následovně: 1) Obě čísla vynásobíme, jako kdyby desetinnou čárku vůbec neměla. 2) Do výsledku umístíme desetinnou čárku tak, aby měl výsledek tolik desetinných míst jako oba činitelé dohromady. Tento postup odpovídá násobení a následnému dělení mocninami desítky. Příklady:
5 \cdot 0{,}4 – násobíme 5\cdot 4 = 20, výsledek posuneme o 0+1=1 desetinné místo, dostáváme 2{,}0.
2{,}5 \cdot 0{,}05 – násobíme 25\cdot 5=125, výsledek posuneme o 1+2=3 desetinná místa, dostáváme 0,125.
0{,}9 \cdot 0{,}8 – násobíme 9\cdot 8=72, výsledek posuneme o 1+1=2 desetinná místa, dostáváme 0,72.
Výsledek je dobré zkontrolovat pomocí rychlého odhadu pomocí zaokrouhlených čísel. Například při násobení 0{,}9 \cdot 0{,}8 jsou oba činitelé „trochu menší než 1“, takže i výsledek by měl být „trochu menší než 1\cdot 1“, při násobení 4{,}92\cdot 3{,}06 můžeme snadno odhadnout, že výsledek by měl být přibližně 5\cdot 3=15.
NahoruDělení desetinných čísel
Při dělení desetinných čísel se můžeme desetinné části snadno zbavit tak, že dělence i dělitele vynásobíme dostatečně velkou mocninou desítky. Následně pak čísla dělíme stejně jako přirozená čísla.
Příklady: dělení desetinnými čísly
- 8:0{,}2 = 80:2 = 40
- 1:0{,}05 = 100:5 = 20
Příklady: dělení desetinných čísel
- 2{,}5:2 = 25:20 = 1{,}25
- 1{,}6:8 = 16:80 = 0{,}2
Příklady: dělení desetinných čísel desetinnými čísly
- 0{,}36 : 1{,}2 = 36 : 120 = 0{,}3
- 4{,}2 : 0{,}01= 420 : 1 = 420
Rovnice s desetinnými čísly
Rovnice s desetinnými čísly řešíme stejnými postupy jako základní rovnice, pouze při tom máme na paměti pravidla pro sčítání, odčítání, násobení a dělení desetinných čísel. Často si můžeme řešení usnadnit tím, že celou rovnici vynásobíme deseti (případně vyšší mocninou desítky).
Řešený příklad
| Zadání: | 0{,}2x+2{,}1x=4{,}6 |
| Vynásobíme deseti: | 2x+21x=46 |
| Řešíme jako základní rovnici: | 23x = 46 |
| x = 2 |

