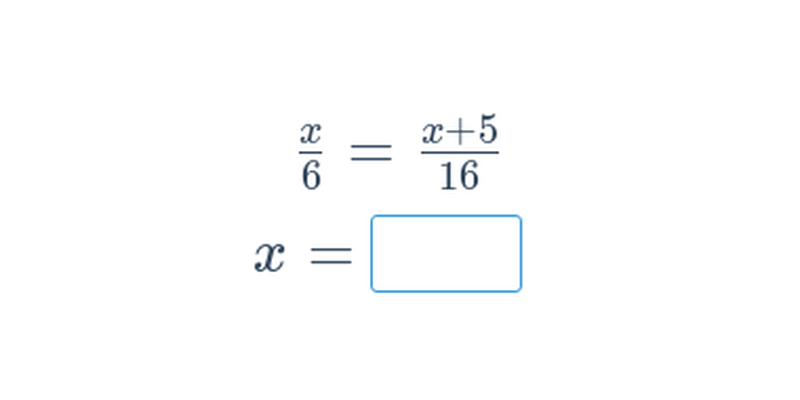Děkujeme za Vaše hodnocení.

Rovnice s lomenými výrazy

umime.to/FZN

Nadřazené	Elementární algebra » Rovnice » Rovnice s lomenými výrazy
Předcházející	Rovnice s neznámou ve jmenovateli, Lomené výrazy
Navazující	Exponenciální rovnice

Cvičení

Krok po kroku

Psaná odpověď

Rovnice s lomenými výrazy řešíme stejnými postupy jako základní rovnice.

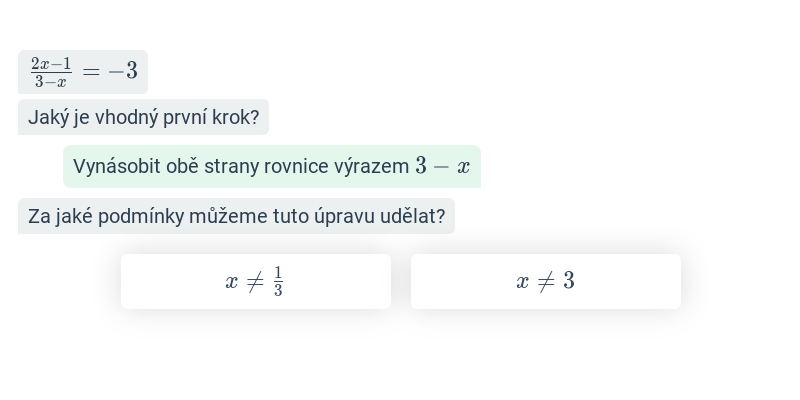
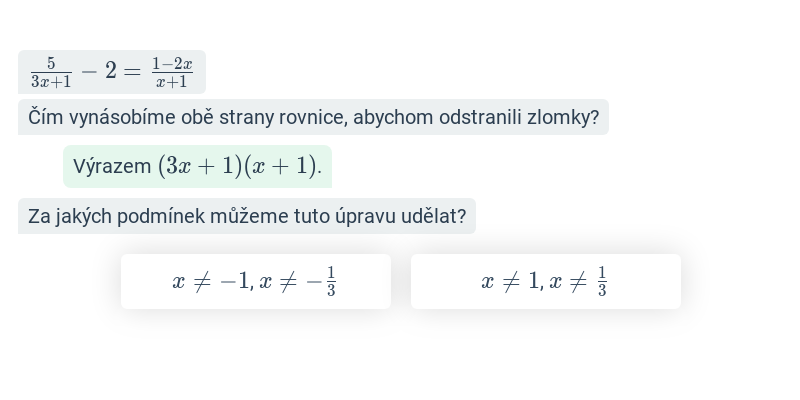
Užitečným (avšak ne vždy nezbytným) prvním krokem bývá roznásobení obou stran rovnice společným násobkem všech jmenovatelů lomených výrazů.

Podmínky řešitelnosti

Aby lomený výraz dával smysl, nesmí být jmenovatel roven nule. Po vyřešení rovnice tedy musíme zkontrolovat, že výsledné řešení tuto podmínku splňuje pro všechny jmenovatele v rovnici.

Řešený příklad

Zadání:	\frac{-1}{2} = \frac{x+1}{1-x}
Jmenovatelé jsou 2 a 1-x, společný násobek je 2(1-x). Roznásobíme tedy rovnici 2(1-x).	\frac{-1}{2}\cdot 2(1-x) = \frac{x+1}{1-x} \cdot 2(1-x)
Pokrátíme obě strany.	(-1)\cdot (1-x) = (x+1)\cdot 2
Roznásobíme obě strany.	x-1 = 2x +2
Převedeme x na jednu stranu, konstanty na druhou.	x = -3