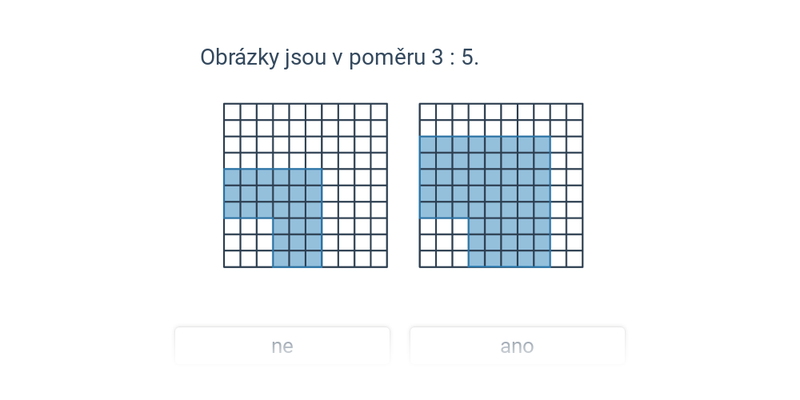
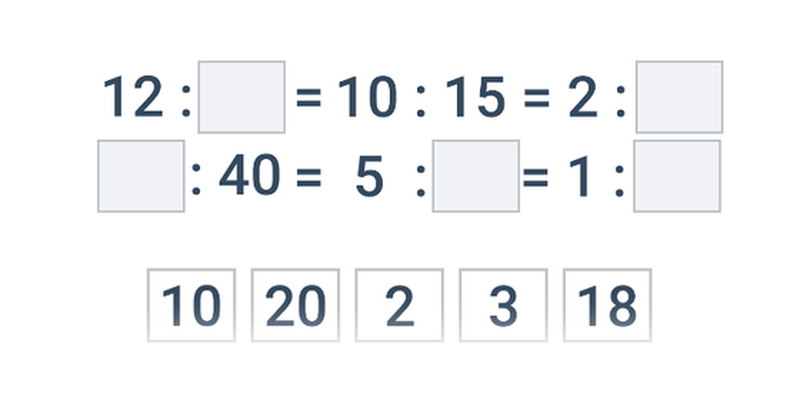Poměry
F6LPoměr dvou nebo více čísel vyjadřuje vztah jejich velikostí – tedy kolikrát je jedno číslo větší (nebo menší) než druhé. S poměry se setkáváme v běžném životě i v matematice: určují například poměr stran obrazovky (16 : 9), měřítko mapy (1 : 50 000) nebo směs dvou látek v určitém poměru. Poměry úzce souvisejí se zlomky nebo pojmem podobnost v geometrii.
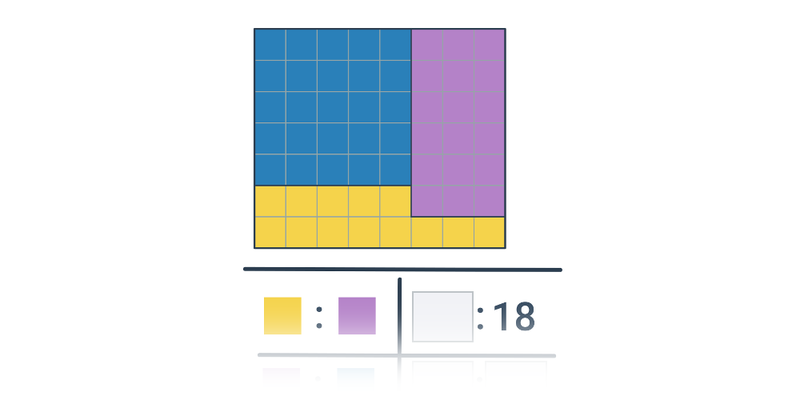
- Základy poměrů – zápis poměru, základní tvar, postupný a převrácený poměr, vztah ke zlomkům
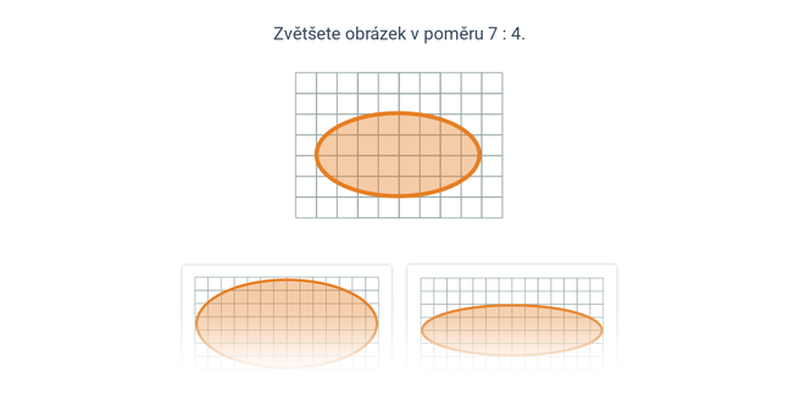
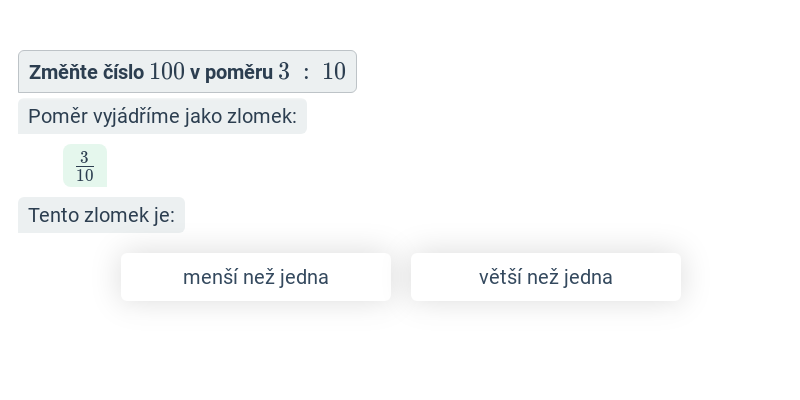
- Změna a rozdělení čísla – zvětšení nebo zmenšení čísla v daném poměru, rozdělení čísla v poměru (např. rozdělit 12 v poměru 1 : 3 na 3 a 9)
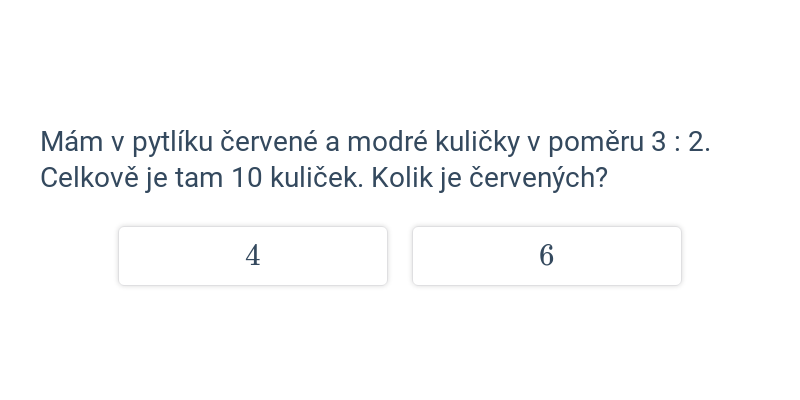
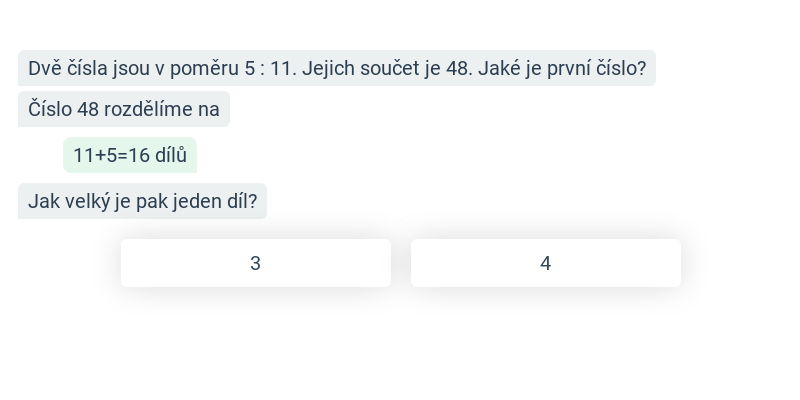
- Výpočty s poměry – výpočty při znalosti součtu nebo rozdílu částí, příklady s poměry a rovnicemi
- Měřítko mapy – použití poměrů při práci s mapami, plány nebo modely, převody skutečných a zmenšených vzdáleností
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
Rozhodovačka
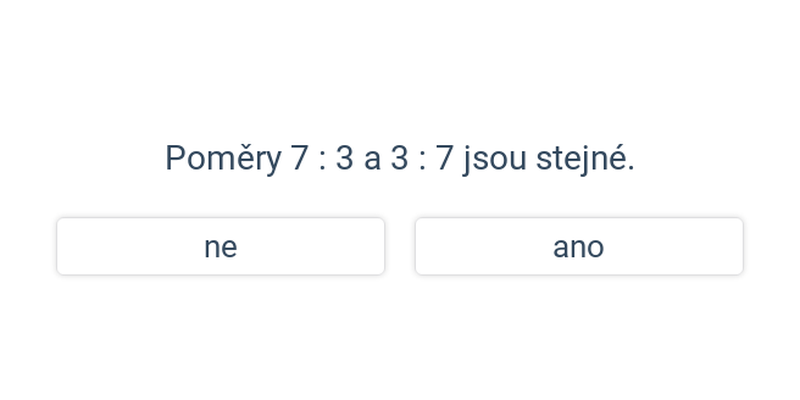
Rychlé procvičování výběrem ze dvou možností.
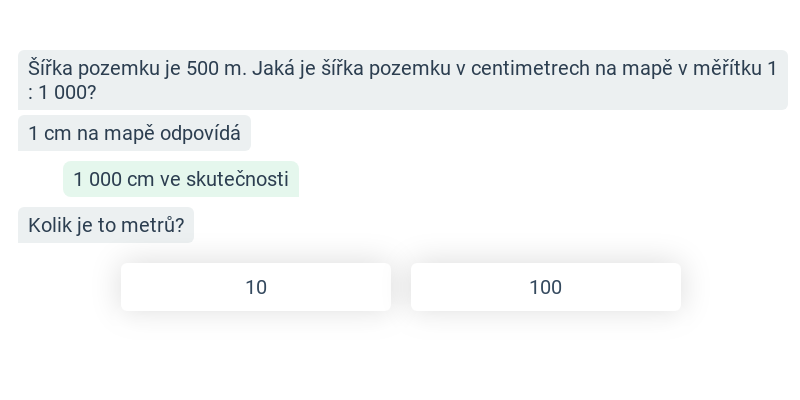
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.
Slovní úlohy
Klasické procvičování slovních úloh, s pestrou nabídkou zadání a vysvětlujícími texty.