Výpis souhrnů
Objem a povrch
Podtémata
Objem a povrch
Objem tělesa vyjadřuje kolik místa v prostoru těleso zaujímá. Můžeme si jej představit jako množství vody, které bychom potřebovali, kdybychom chtěli těleso „napustit“. Pro vyjádření objemu využíváme jednotky objemu.
Povrch tělesa je součet obsahů všech ploch, které těleso ohraničují. Můžeme si jej představit jako velikost barevného papíru, který potřebujeme na „polepení“ tělesa. Pro vyjádření povrchu využíváme jednotky obsahu.
Značení ve vzorcích
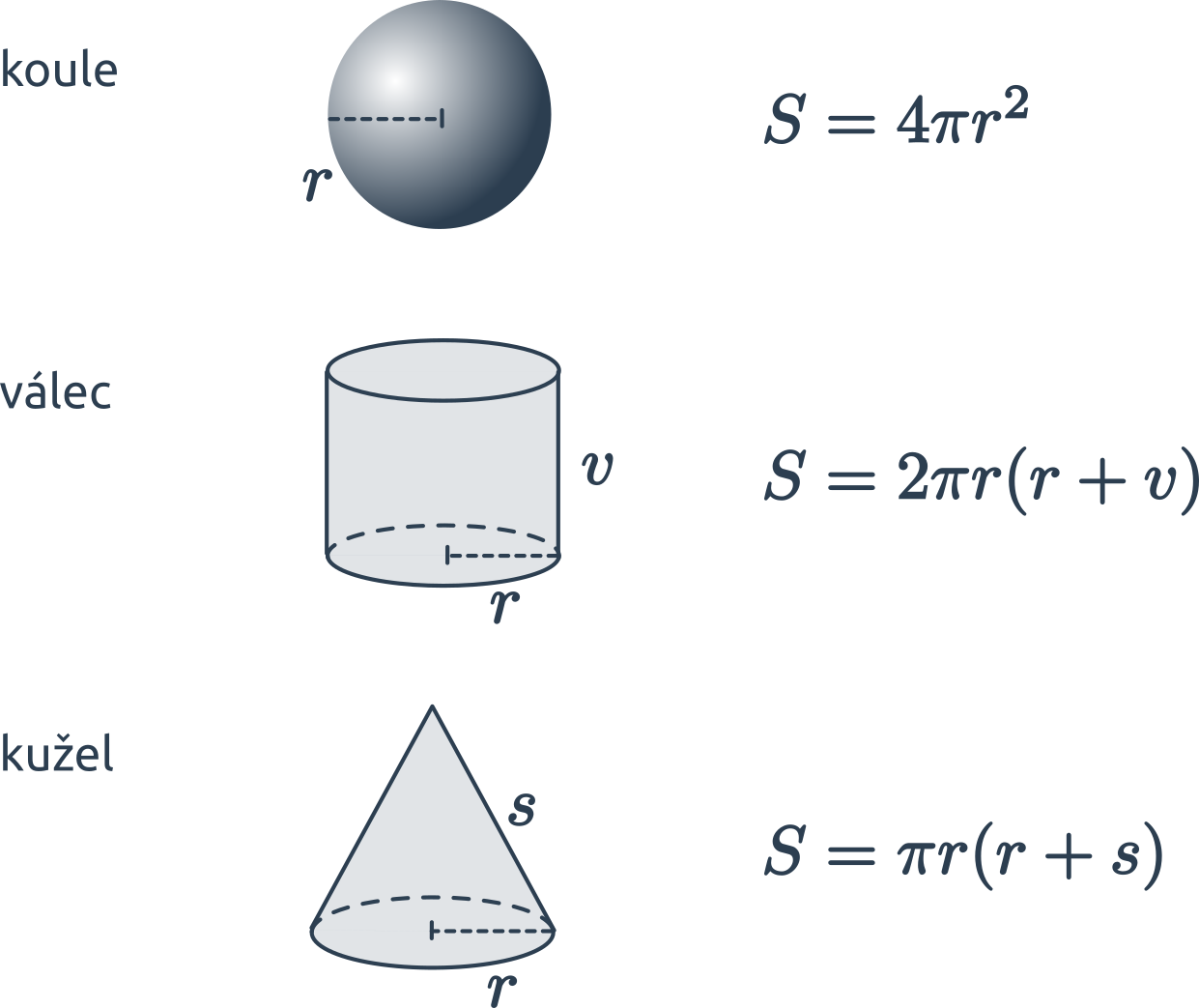
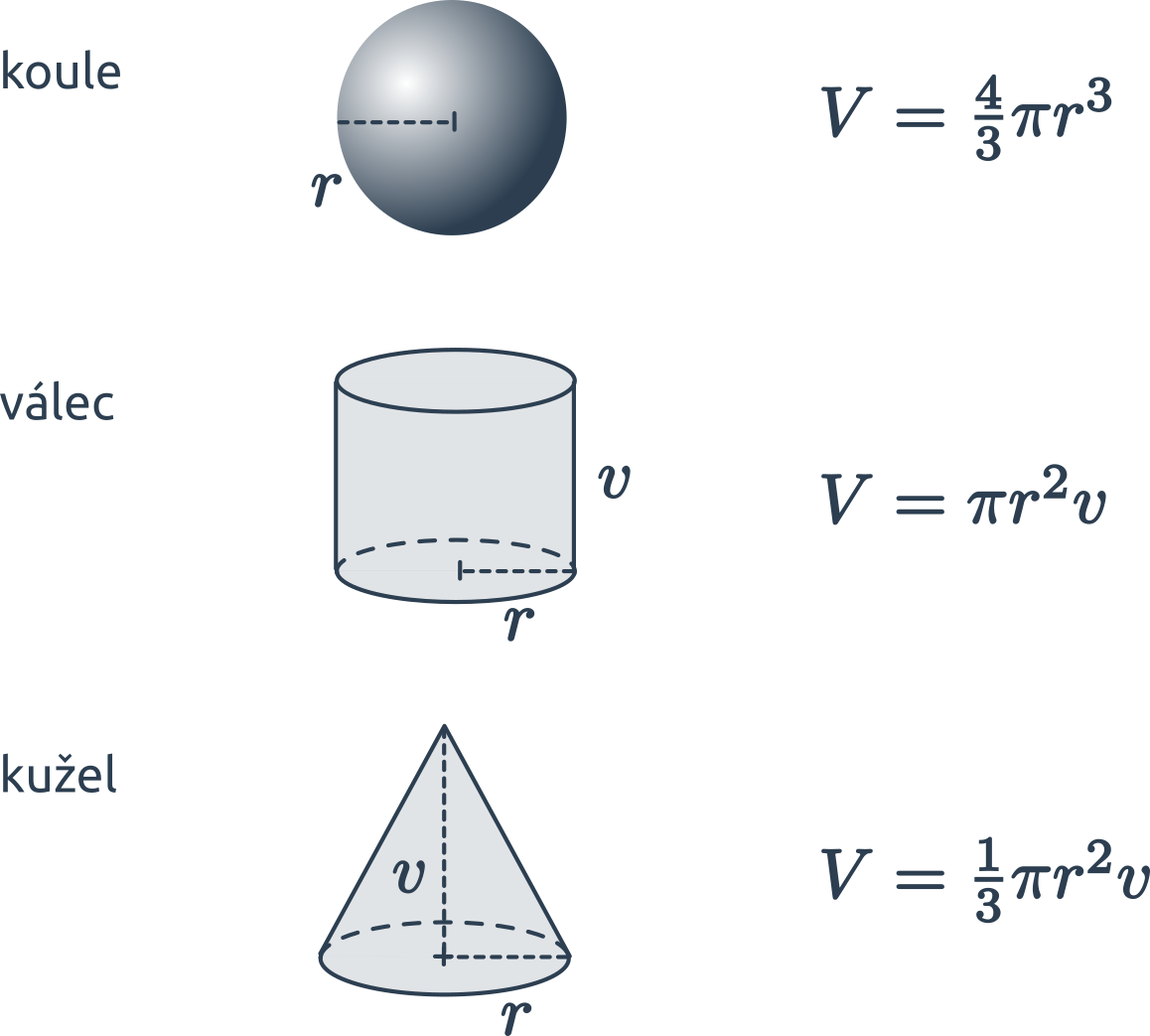
| V | objem |
| S | povrch |
| S_p | obsah podstavy |
| S_{pl} | obsah pláště |
| a, b, c | délky stran |
| r | poloměr |
| v | výška |
| s | strana kužele |
Vzorce
| Útvar | Objem | Povrch |
|---|---|---|
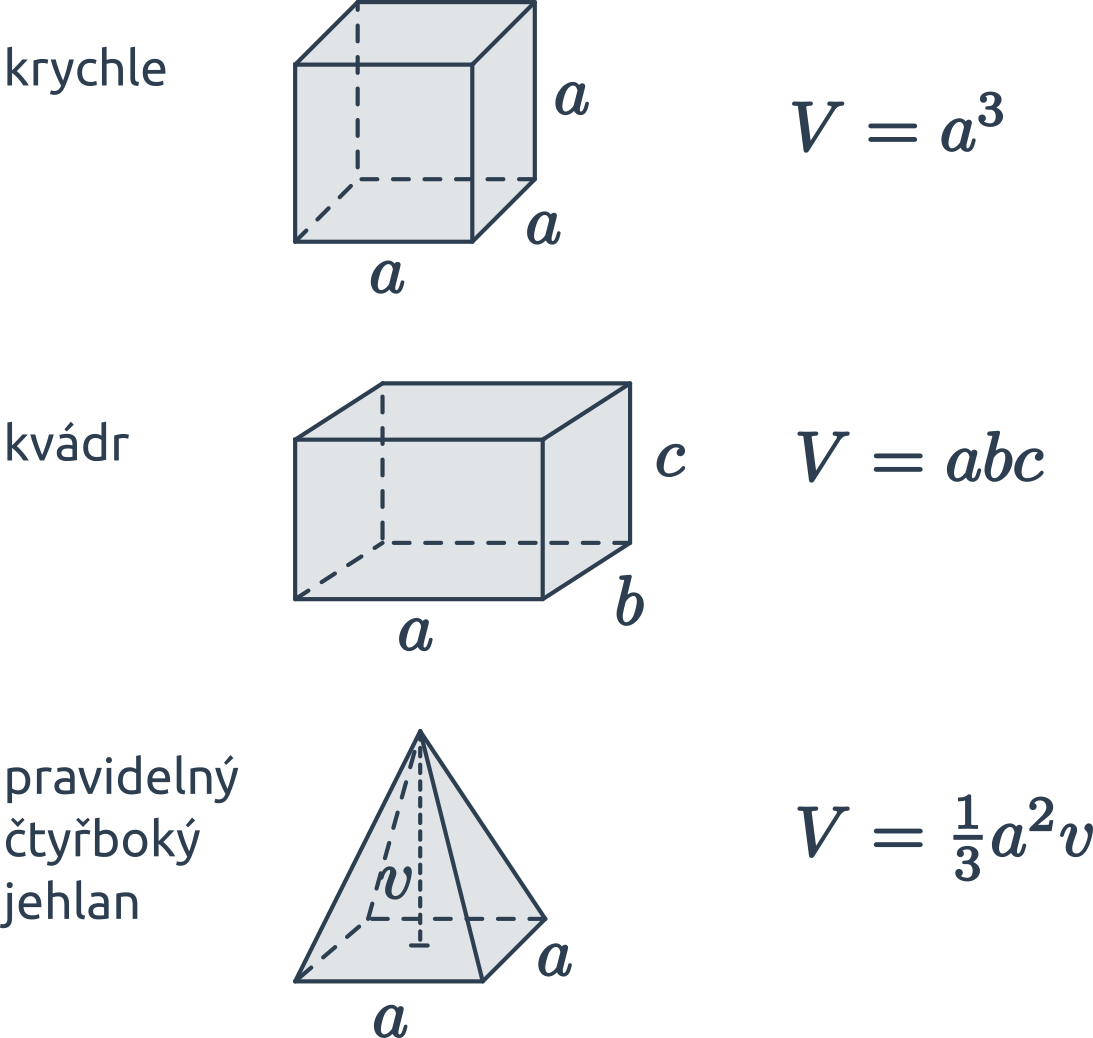
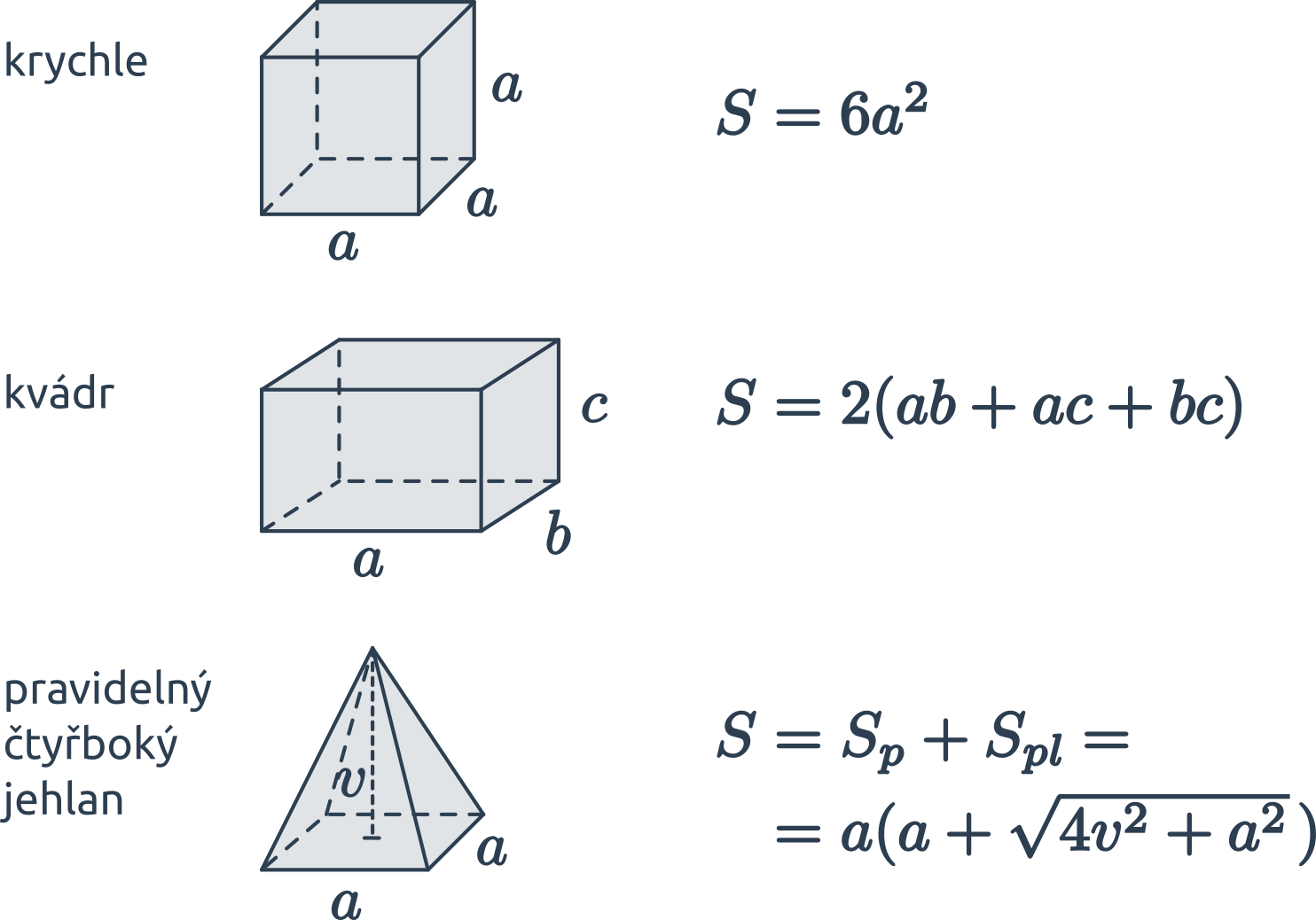
| krychle | V = a \cdot a \cdot a = a^3 | S= 6\cdot a \cdot a =6 a^2 |
| kvádr | V = abc | S = 2(ab+ac+bc) |
| koule | V=\frac43\pi r^3 | S=4\pi r^2 |
| válec | V=S_p\cdot v =\pi r^2 v | S=2S_p+S_{pl} =2\pi r(r+v) |
| kužel | V=\frac{1}{3}S_p\cdot v =\frac13 \pi r^2 v | S =S_p+S_{pl} =\pi r(r+\sqrt{r^2+v^2})=\pi r^2 +\pi rs |
| jehlan | V=\frac{1}{3}S_p\cdot v | S=S_p+S_{pl} |
| pravidelný čtyřboký jehlan | V=\frac{1}{3}S_p\cdot v=\frac{1}{3} a^2v | |
| hranol | V= S_p\cdot v | S=2\cdot S_p+S_{pl} |
Komiks pro zpestření
Objem krychle a kvádru
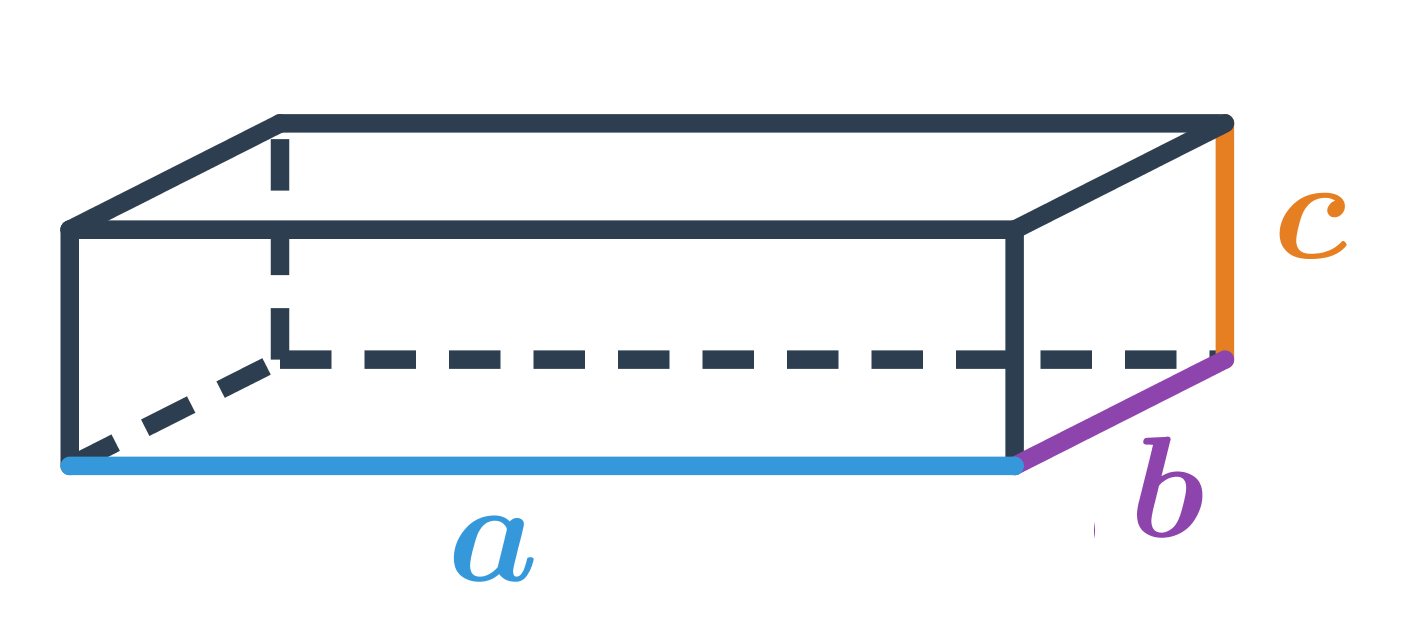
Objem kvádru s délkami hran a,b,c je: V=a\cdot b\cdot c
Objem krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy: V=a\cdot a\cdot a=a^3
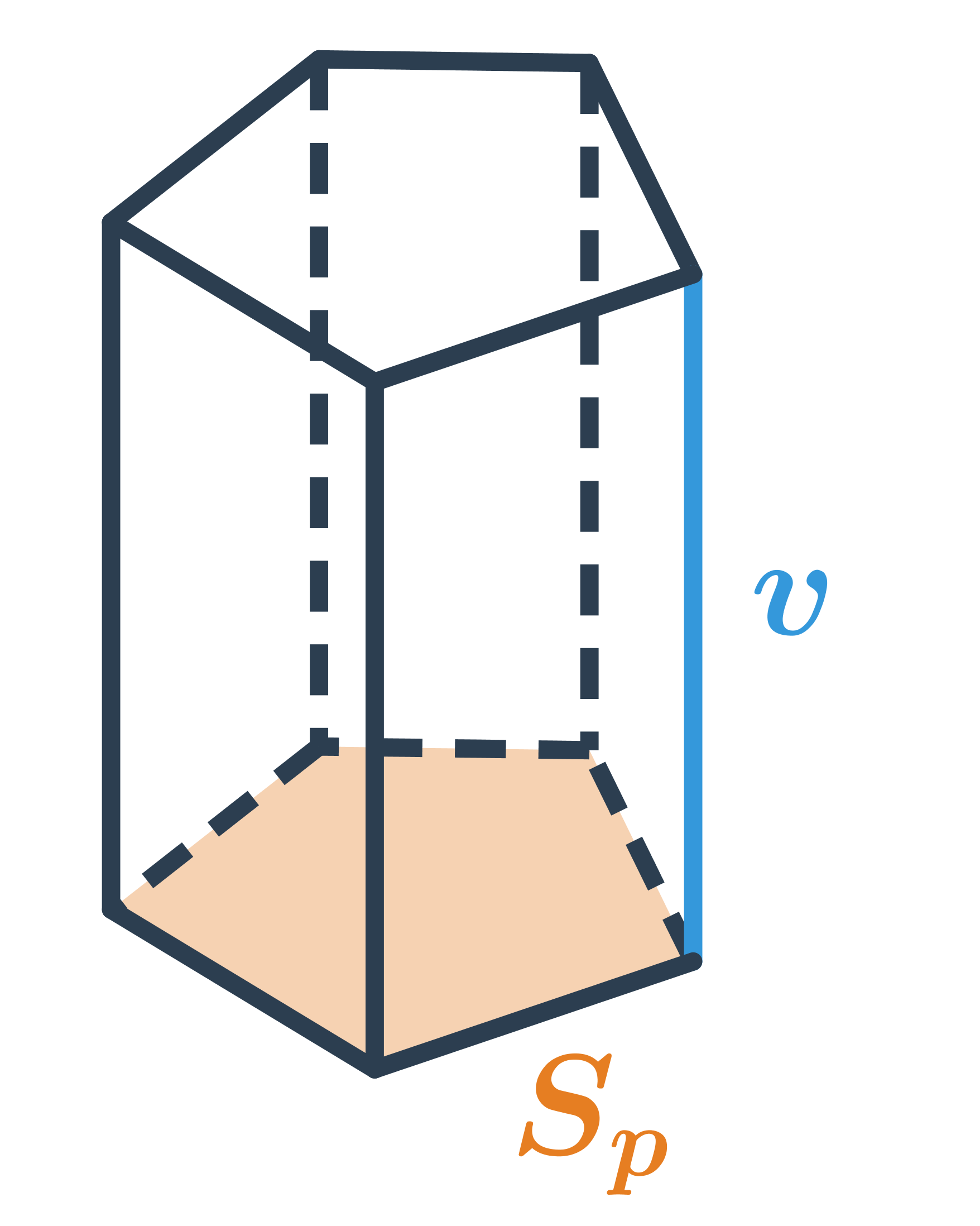
NahoruObjem hranolu
Objem hranolu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=S_p \cdot v.
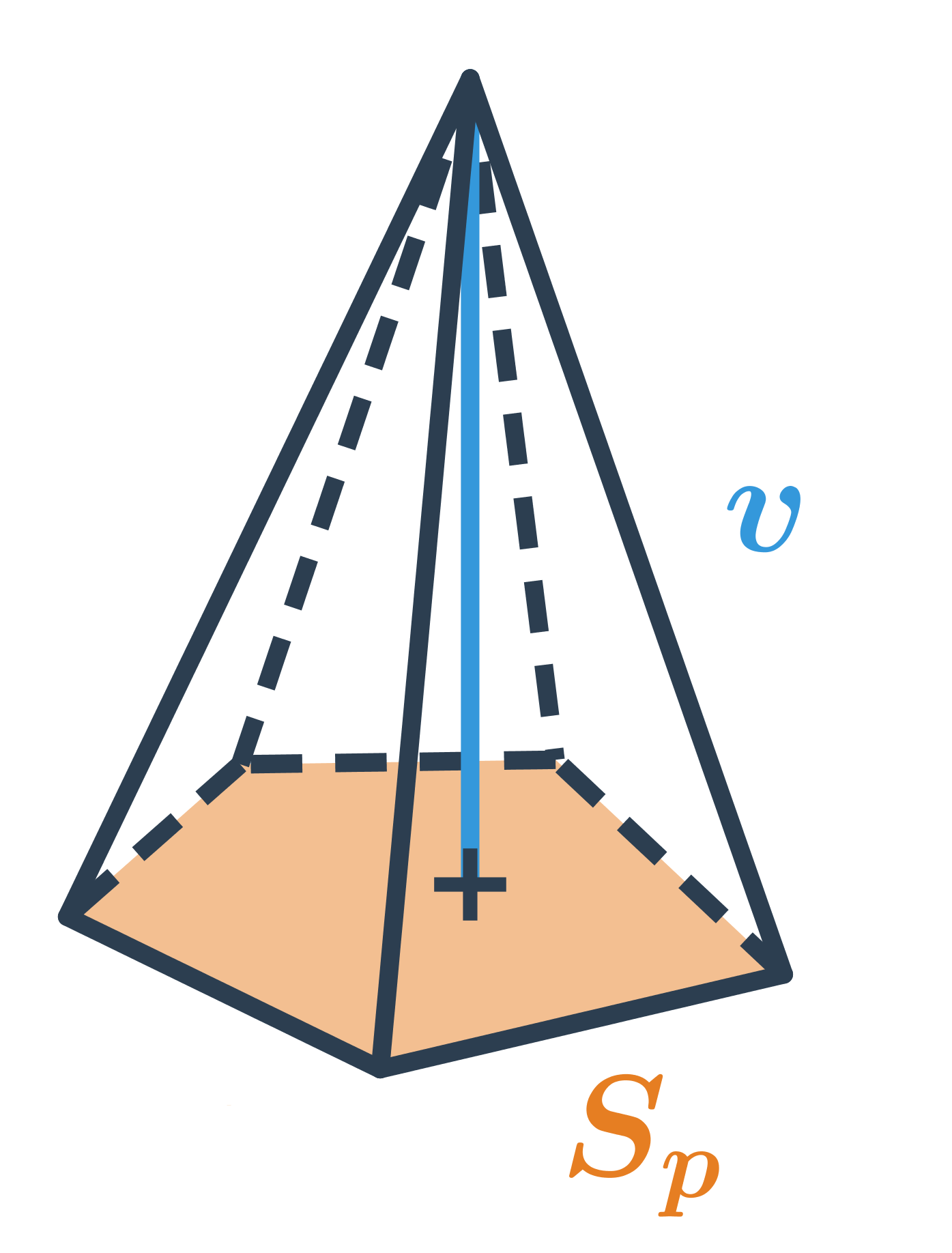
Objem jehlanu
Objem jehlanu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=\frac{1}{3} S_p \cdot v.
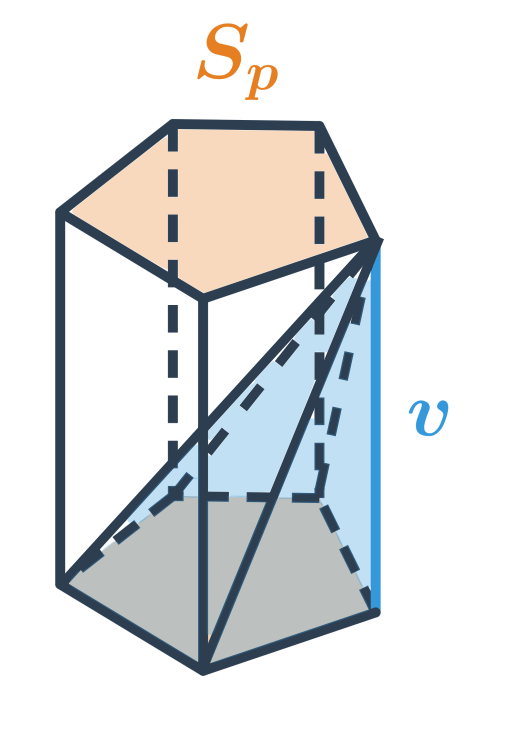
Oproti hranolu se stejnou výškou a tvarem podstavy má jehlan třikrát menší objem.
Objem hranatých těles
Vzorce pro objem „hranatých“ těles vychází z obsahu podstavy a výšky tělesa.
Objem libovolného hranolu je součin obsahu podstavy a výšky: V=S_p\cdot v.
Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = abc. Objem krychle vypočítáme stejným způsobem. Protože v krychli jsou všechny hrany stejně dlouhé, výraz se zjednoduší na V = a^3.
Příklad: objem krychle
Určete objem krychle o hraně délky 4 m.
- Objem krychle o hraně délky a spočítáme jako V=a^3.
- Dosadíme za a známou délku hrany.
- Takže daná krychle má objem V = 4^3 = 64 m³.
Délka hrany je zadaná v metrech, proto je výsledný objem krychle v metrech krychlových.
Příklad: objem kvádru
Určete objem kvádru s hranami 3, 6 a 10 cm.
- Objem kvádru s hranami a,b,c spočítáme jako V=a\cdot b\cdot c.
- Dosadíme za a,b,c známé délky hran.
- Takže daný kvádr má objem V = 3\cdot 6 \cdot 10 = 180 cm³.
Délky hran jsou zadány v centimetrech, proto je výsledný objem kvádru v centimetrech krychlových.
Objem jehlanu je jedna třetina součinu obsahu podstavy a výšky, tj. V=\frac{1}{3}S_p\cdot v. Pro pravidelný čtyřboký jehlan pak tedy V=\frac{1}{3} a^2v.
Příklad: objem pravidelného čtyřbokého jehlanu
Určete objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany 6 cm a výškou 4 cm.
- Objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany a a výškou v spočítáme jako V=\frac{1}{3} \cdot a^2 \cdot v.
- Dosadíme za a a v známé hodnoty.
- Takže daný jehlan má objem V=\frac{1}{3} 6^2 \cdot 4 = 48 cm³.
Délka hran podstavy a velikost výšky jsou zadány v centimetrech, proto je výsledný objem jehlanu v centimetrech krychlových.
Objem válce
Objem válce s poloměrem podstavy r a výškou v spočítáme jako: V=\pi \cdot r^2 \cdot v
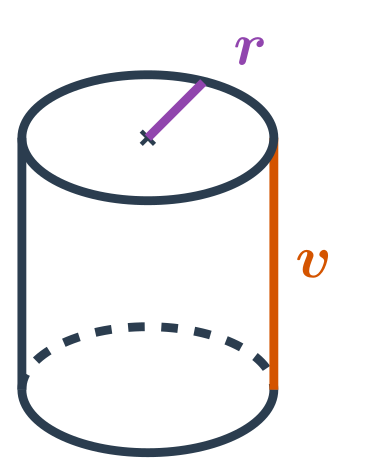
Platí V=S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
NahoruObjem kužele
Objem kužele s poloměrem podstavy r a výškou v spočítáme jako: V=\frac{1}{3} \pi \cdot r^2 \cdot v
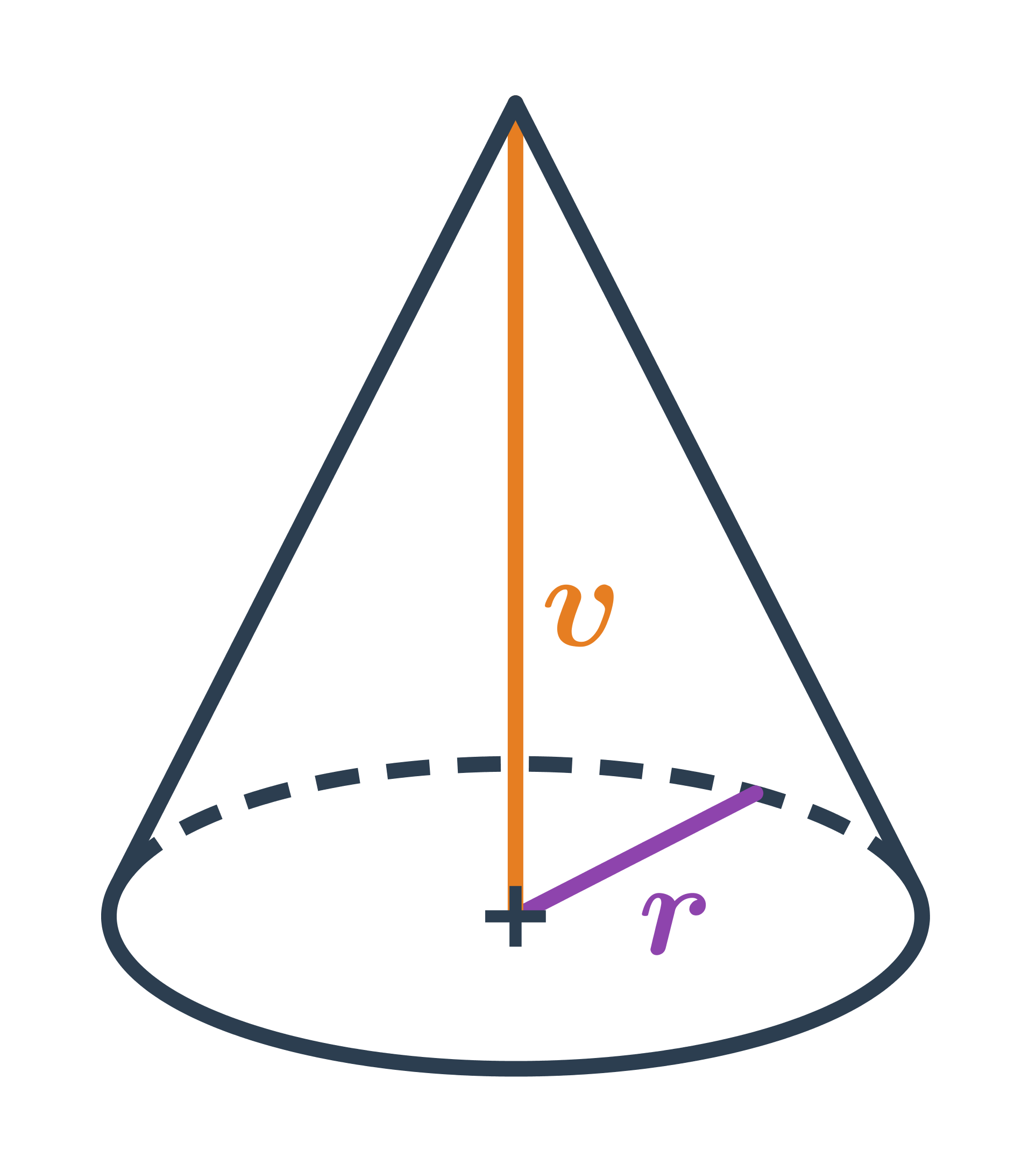
Pro kužel platí V=\frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
Oproti válci se stejnou výškou a poloměrem podstavy má kužel třikrát menší objem.
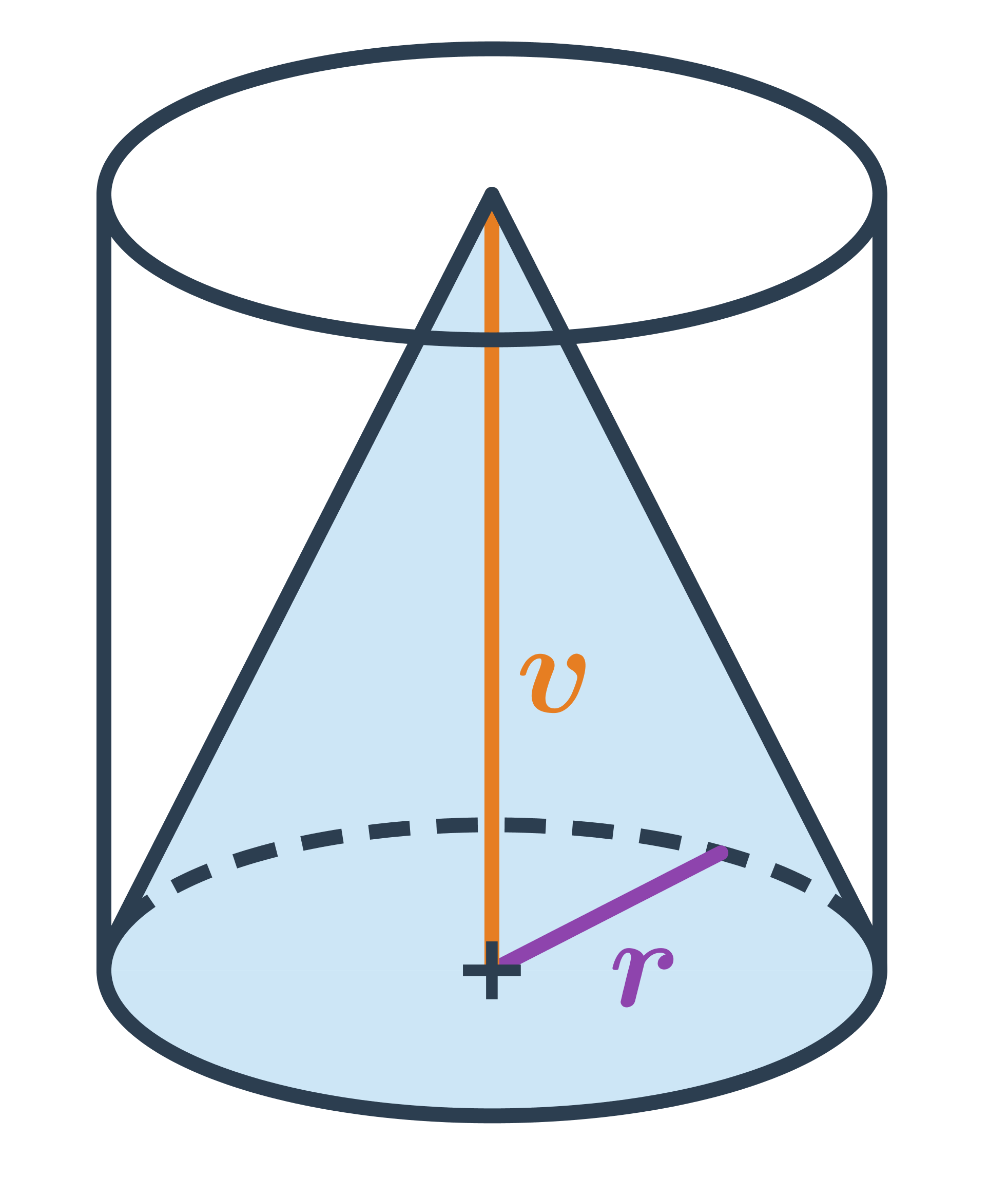
Objem kulatých těles
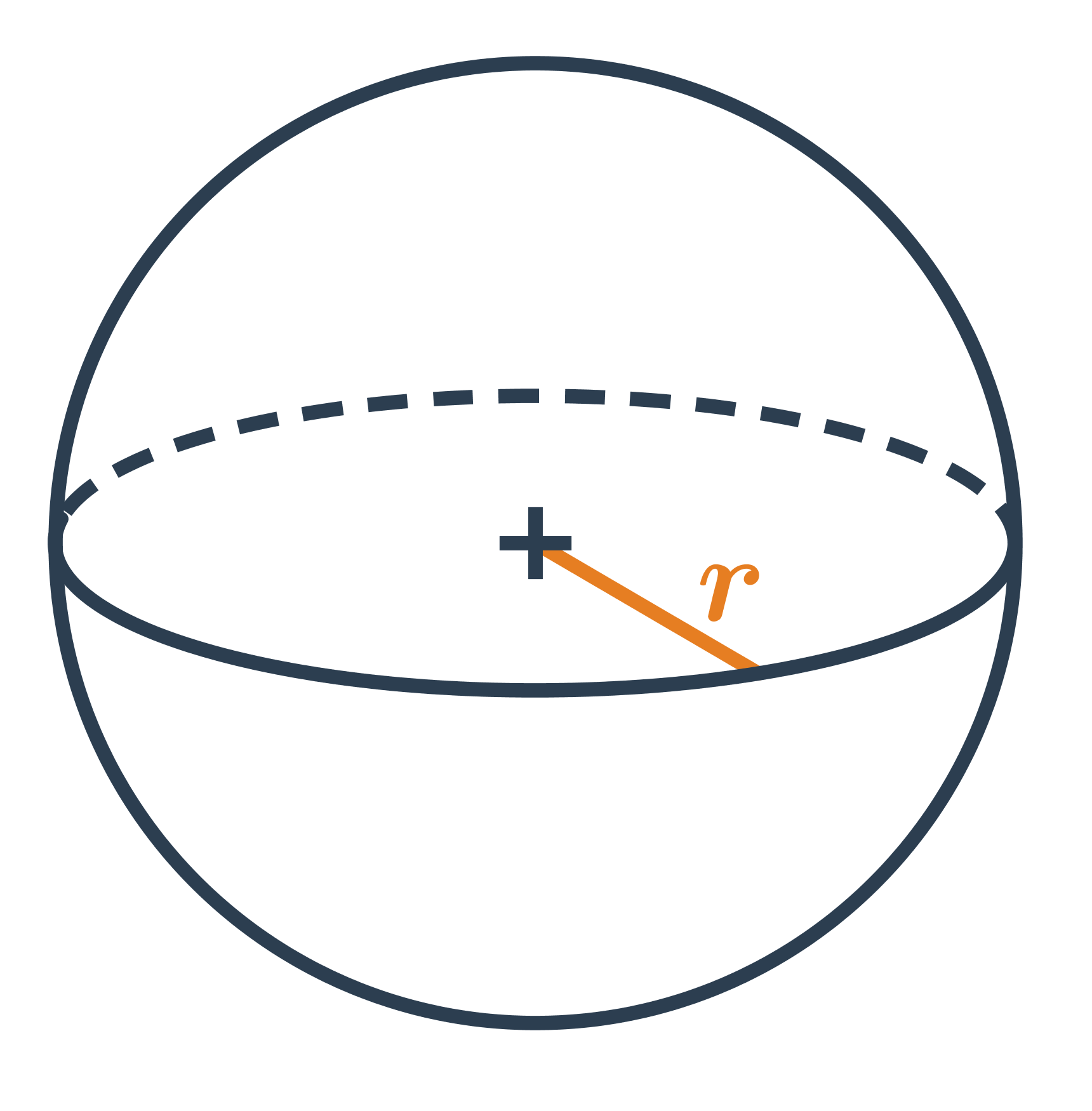
Objem „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14 159 265. Ve vzorcích označuje r poloměr (koule či podstavy) a v výšku válce.
- Objem koule je V = \frac43 \pi r^3.
- Objem válce je obsah (kruhové) podstavy vynásobený výškou, tedy V = S_p \cdot v = \pi r^2 v.
- Objem kužele je jedna třetina obsahu podstavy vynásobeného výškou, tedy V = \frac13 S_p \cdot v = \frac13 \pi r^2 v.
Příklad: objem koule s daným poloměrem
Určete objem koule o poloměru 3 m.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Dosadíme za r známou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 3^3 m³ = 36 \pi m³ \doteq 113 m³
Velikost poloměru je zadaná v metrech, proto je výsledný objem koule v metrech krychlových.
Příklad: objem koule s daným průměrem
Určete objem koule o průměru 4 dm.
- Objem koule o poloměru r spočítáme jako: V = \frac43 \pi r^3
- Známe průměr, proto umíme určit poloměr koule jako polovinu průměru r=\frac42=2 dm
- Dosadíme za r spočítanou velikost poloměru.
- Takže daná koule má objem: V = \frac43 \pi \cdot 2^3 dm³ = \frac{32}{3} \pi dm³ \doteq 33{,}5 dm³
Velikost průměru je zadaná v decimetrech, proto je výsledný objem koule v decimetrech krychlových.
Příklad: objem válce
Určete objem válce o poloměru podstavy 5 mm a výšce 0{,}1 cm.
- Poloměr podstavy a výšku máme v různých jednotkách. Převedeme velikost výšky na milimetry, abychom měli všechny údaje v mm.
- r=5 mm, v=0{,}1 cm = 1 mm
- Objem válce se známým poloměrem podstavy r a výškou v spočítáme jako: V = \pi r^2 v
- Dosadíme za r a v známé hodnoty v mm.
- Daný válec má objem: V = \pi \cdot 5^2 \cdot 1 mm³ = 25 \pi mm³ \doteq 78{,}5 mm³
Výpočty provádíme s velikostí poloměru i výšky v milimetrech, proto je výsledný objem válce v milimetrech krychlových.
Povrch krychle a kvádru
Povrch kvádru s délkami hran a,b,c spočítáme jako součet obsahů všech jeho stěn. Tedy: S=2 (a\cdot b + a\cdot c + b \cdot c)
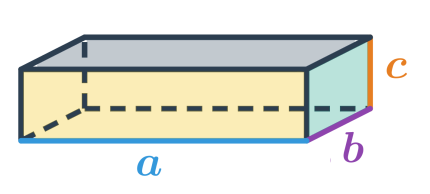
Povrch krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako povrch kvádru s a=b=c, tedy šestkrát obsah jedné čtvercové stěny krychle: S = 6\cdot a\cdot a = 6a^2
NahoruPovrch hranolu
Povrch hranolu, který má podstavu o obsahu S_p plášť o obsahu S_{pl}, spočítáme jako S=2S_p + S_{pl}. Plášť hranolu je tvořen všemi jeho stěnami kromě dvou podstav.
Povrch pravidelného n‑bokého hranolu, který má dvě podstavy ve tvaru pravidelných n‑úhelníků a potom n stejných obdélníkových stěn (obsah jedné označme S_1), spočítáme takto: S=2S_p + n\cdot S_1
NahoruPovrch jehlanu
Povrch jehlanu spočítáme jako součet obsahu jeho podstavy S_p a obsahu jeho pláště S_{pl}. Obsah pláště spočítáme jako součet obsahů stěn jehlanu, které tvoří plášť (tj. všechny stěny jehlanu kromě jeho podstavy).
Povrch pravidelného n‑bokého jehlanu, který má podstavu ve tvaru pravidelného n‑úhelníka a potom n stejných trojúhelníkových stěn (obsah jedné označme S_1), spočítáme takto: S= S_p + n\cdot S_1
NahoruPovrch hranatých těles
Povrch „hranatých“ těles je prostě součet obsahů jednotlivých stran.
Hranol má dvě stejné podstavy a plášť, povrch je tedy S=2\cdot S_p+S_{pl}. Jehlan má jednu podstavu a plášť, povrch je tedy S=S_p+S_{pl}.
Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2(ab+ac+bc).
Krychle má šest stěn — jde o šest stejných čtverců. Povrch je S=6a^2.
Povrch válce
Povrch válce s poloměrem podstavy r a výškou v spočítáme jako: S = 2\pi r \cdot(r + v)
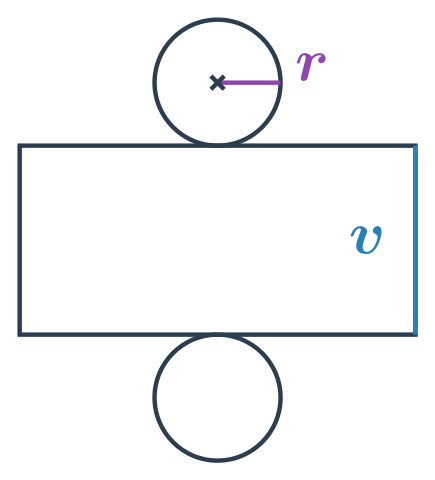
Platí S=2S_p + S_{pl}, kde S_p je obsah podstavy válce a S_{pl} obsah pláště válce. Podstava válce má tvar kruhu s poloměrem r a plášť válce je obdélník o stranách v a 2\pi r. Celkem máme:
- Obsah podstavy: S_p = \pi \cdot r^2
- Obsah pláště: S_{pl}=2\pi r \cdot v
- Povrch válce: S=2\pi r \cdot (r + v)
Povrch kužele
Povrch kužele s poloměrem podstavy r a délkou strany s spočítáme takto: V=\pi r^2 + \pi r s = \pi r \cdot (r+s)
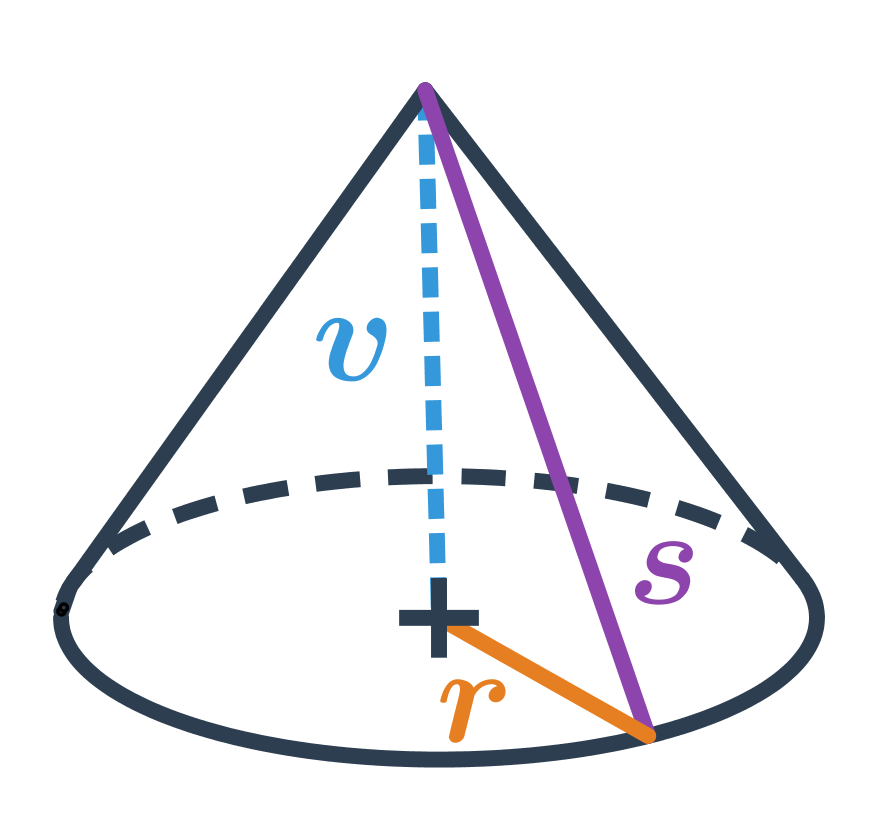
Může se stát, že známe poloměr r podstavy kužele a jeho výšku v, ale nemáme zadanou jeho stranu s. Potom si stranu můžeme dopočítat jako přeponu pravoúhlého trojúhelníka s odvěsnami o délkách v a r. Platí: s=\sqrt{v^2+r^2}
- Obsah podstavy kužele: \pi r^2
- Obsah pláště kužele: \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s
Povrch kulatých těles
Povrch „kulatých“ těles vypočítáme za využití konstanty \pi \approx 3{,}14 159 265. Ve vzorcích označuje r poloměr (koule či podstavy), v výšku válce, s stranu kužele.
- Povrch koule je S = 4\pi r^2.
- Povrch válce se skládá z podstavy (dvakrát) a pláště: S = 2\cdot \pi r^2 + 2\pi r v = 2\pi r (r+v).
- Povrch kužele se skládá z podstavy a pláště: S = \pi r^2 + \pi rs= \pi r(r+s).