Objem hranatých těles

umime.to/F4B

Vzorce pro objem „hranatých“ těles vychází z obsahu podstavy a výšky tělesa.

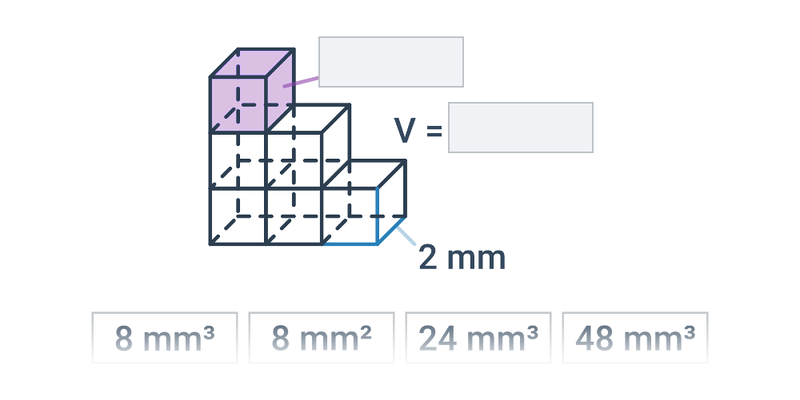
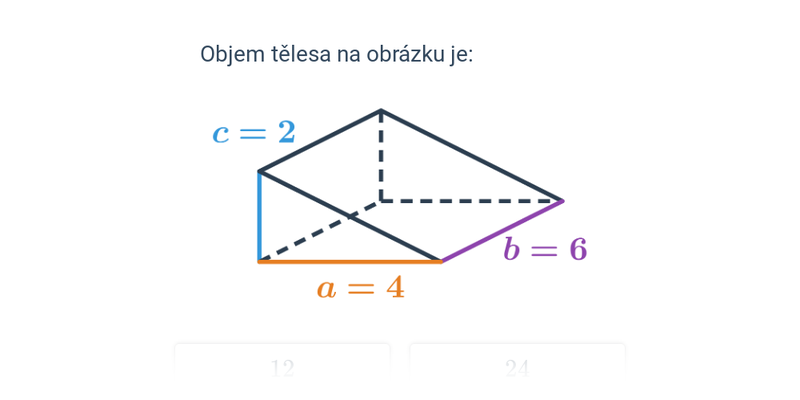
Objem libovolného hranolu je součin obsahu podstavy a výšky: V=S_p\cdot v.

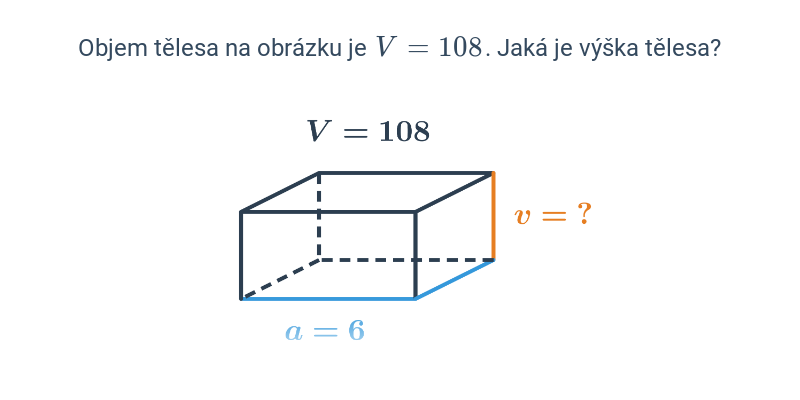
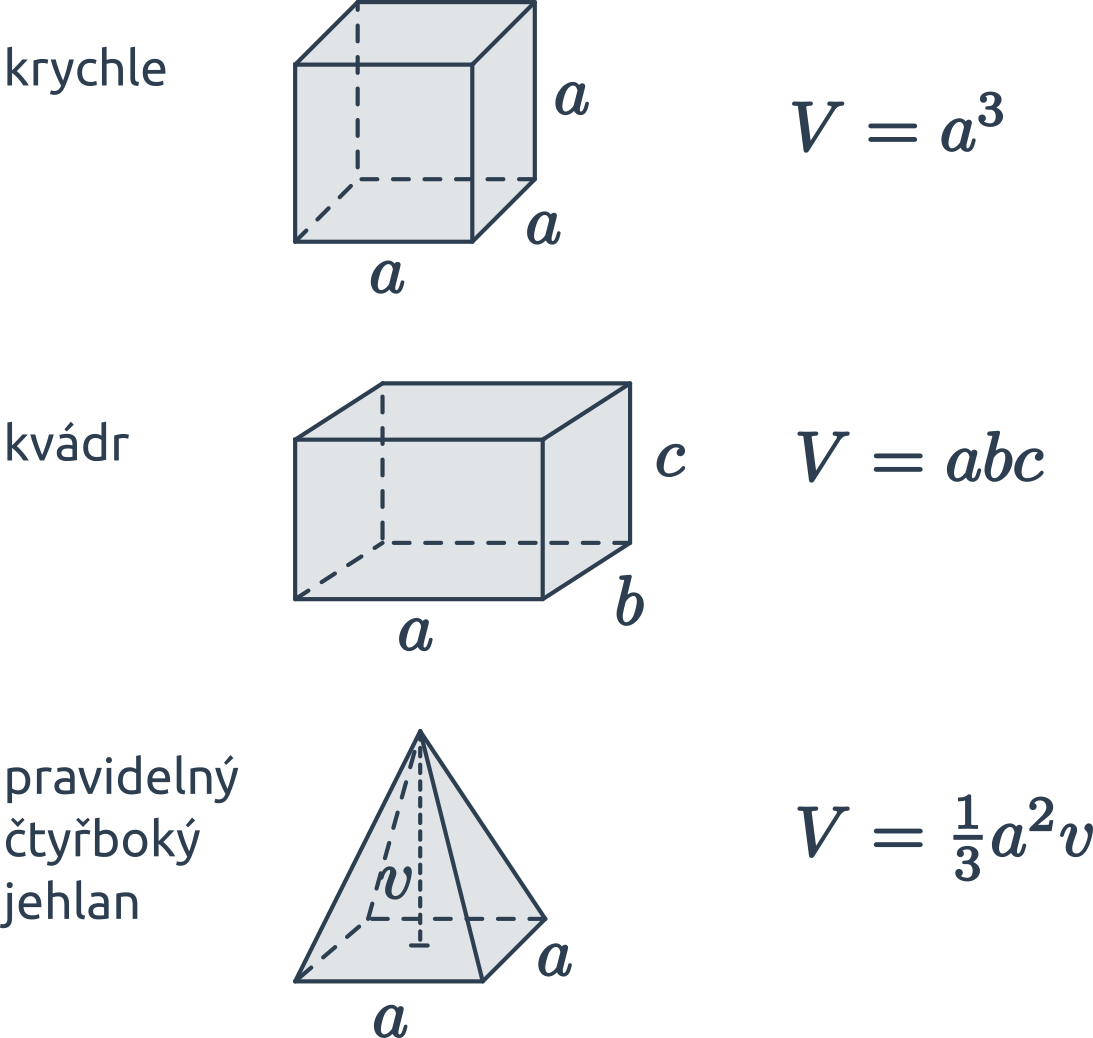
Kvádr a krychle jsou speciální případy hranolu, jejich podstava je obdélník (čtverec) a výška je zbývající hrana. Objem kvádru je tedy součin délek jeho hran: V = abc. Objem krychle vypočítáme stejným způsobem. Protože v krychli jsou všechny hrany stejně dlouhé, výraz se zjednoduší na V = a^3.

Příklad: objem krychle

Určete objem krychle o hraně délky 4 m.

Objem krychle o hraně délky a spočítáme jako V=a^3.
Dosadíme za a známou délku hrany.
Takže daná krychle má objem V = 4^3 = 64 m³.

Délka hrany je zadaná v metrech, proto je výsledný objem krychle v metrech krychlových.

Příklad: objem kvádru

Určete objem kvádru s hranami 3, 6 a 10 cm.

Objem kvádru s hranami a,b,c spočítáme jako V=a\cdot b\cdot c.
Dosadíme za a,b,c známé délky hran.
Takže daný kvádr má objem V = 3\cdot 6 \cdot 10 = 180 cm³.

Délky hran jsou zadány v centimetrech, proto je výsledný objem kvádru v centimetrech krychlových.

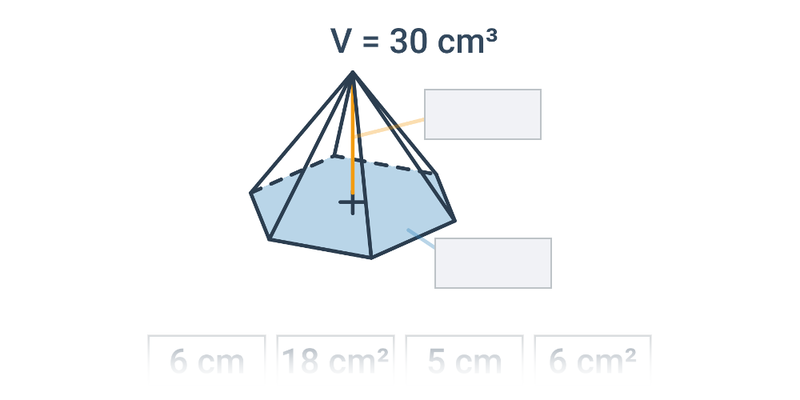
Objem jehlanu je jedna třetina součinu obsahu podstavy a výšky, tj. V=\frac{1}{3}S_p\cdot v. Pro pravidelný čtyřboký jehlan pak tedy V=\frac{1}{3} a^2v.

Příklad: objem pravidelného čtyřbokého jehlanu

Určete objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany 6 cm a výškou 4 cm.

Objem pravidelného čtyřbokého jehlanu s podstavou o délce hrany a a výškou v spočítáme jako V=\frac{1}{3} \cdot a^2 \cdot v.
Dosadíme za a a v známé hodnoty.
Takže daný jehlan má objem V=\frac{1}{3} 6^2 \cdot 4 = 48 cm³.

Délka hran podstavy a velikost výšky jsou zadány v centimetrech, proto je výsledný objem jehlanu v centimetrech krychlových.