Čeština
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Aritmetika
Zlomky, procenta, desetinná čísla
Geometrie
Elementární algebra
Funkce
Jednotky, míry
Diskrétní matematika
Finanční gramotnost
Rozhodovačka
Pexeso
Krok po kroku
Psaná odpověď
Grafař
Porozumění
Označování
Přesouvání
Mřížkovaná
Rozdělovačka
Rozbitá kalkulačka
Roboti
Střílečka
Příšerky
Závody
Územíčka
Tipovačka
Týmovka
Můj účet
Odhlásit sePro zjednodušení popisu uvažujeme v tomto shrnutí pouze funkce, jejichž definiční obor tvoří všechna reálná čísla.
Funkce f se nazývá sudá, právě když pro každé x je f(-x) = f(x). Graf sudé funkce je souměrný podle osy y.
Příklady sudých funkcí
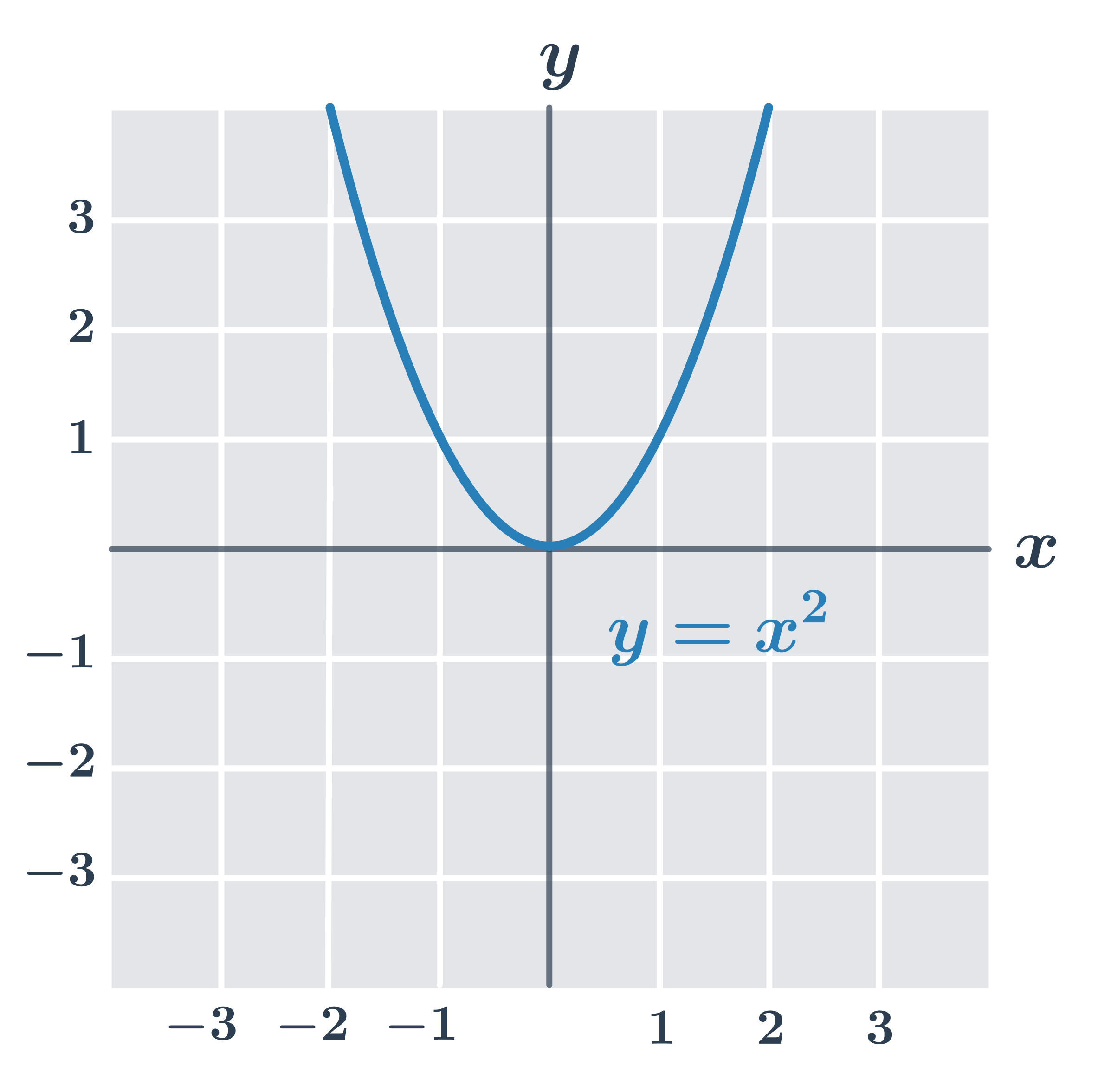
- f_1(x) = x^2
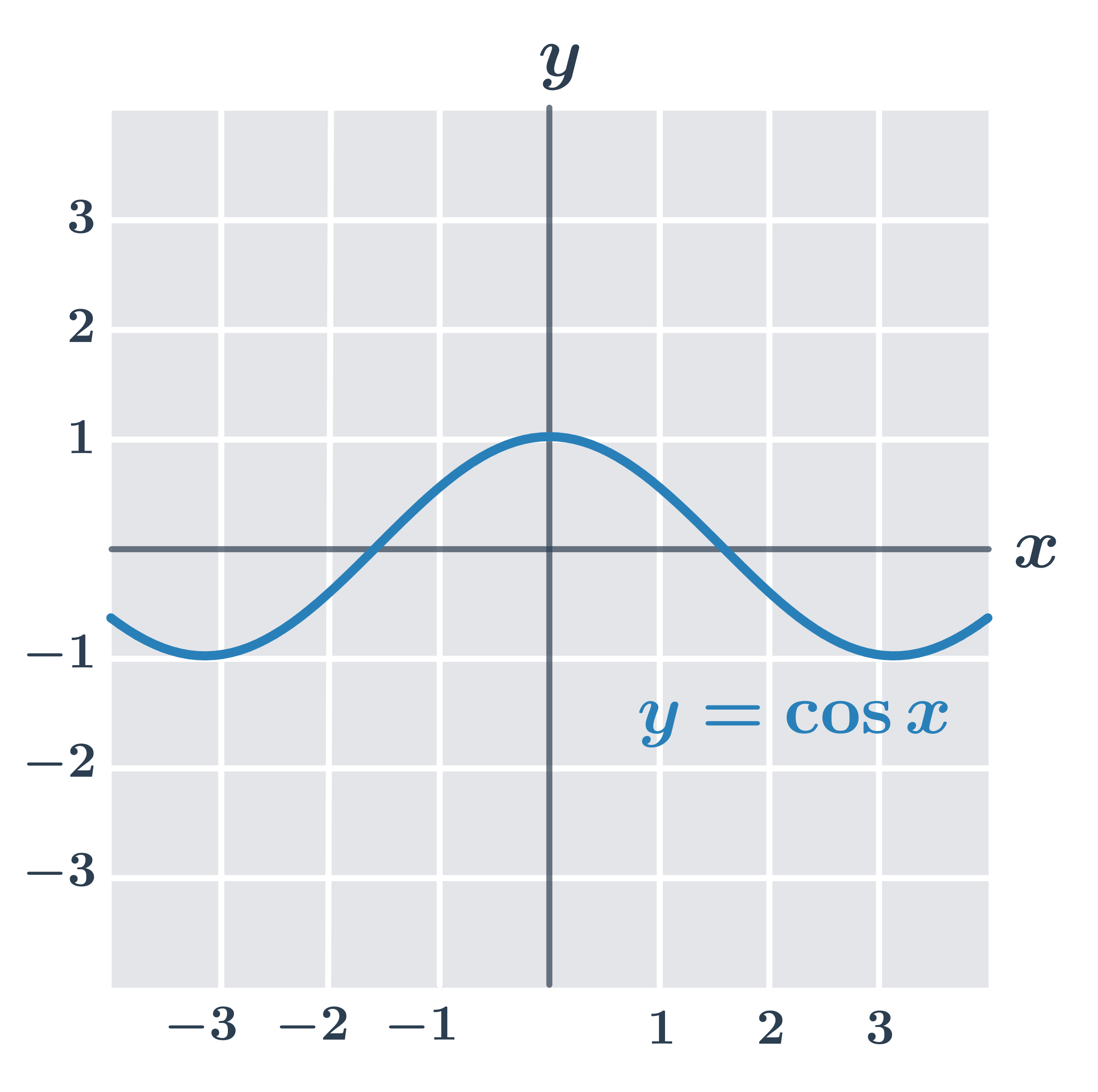
- f_2(x) = \cos x
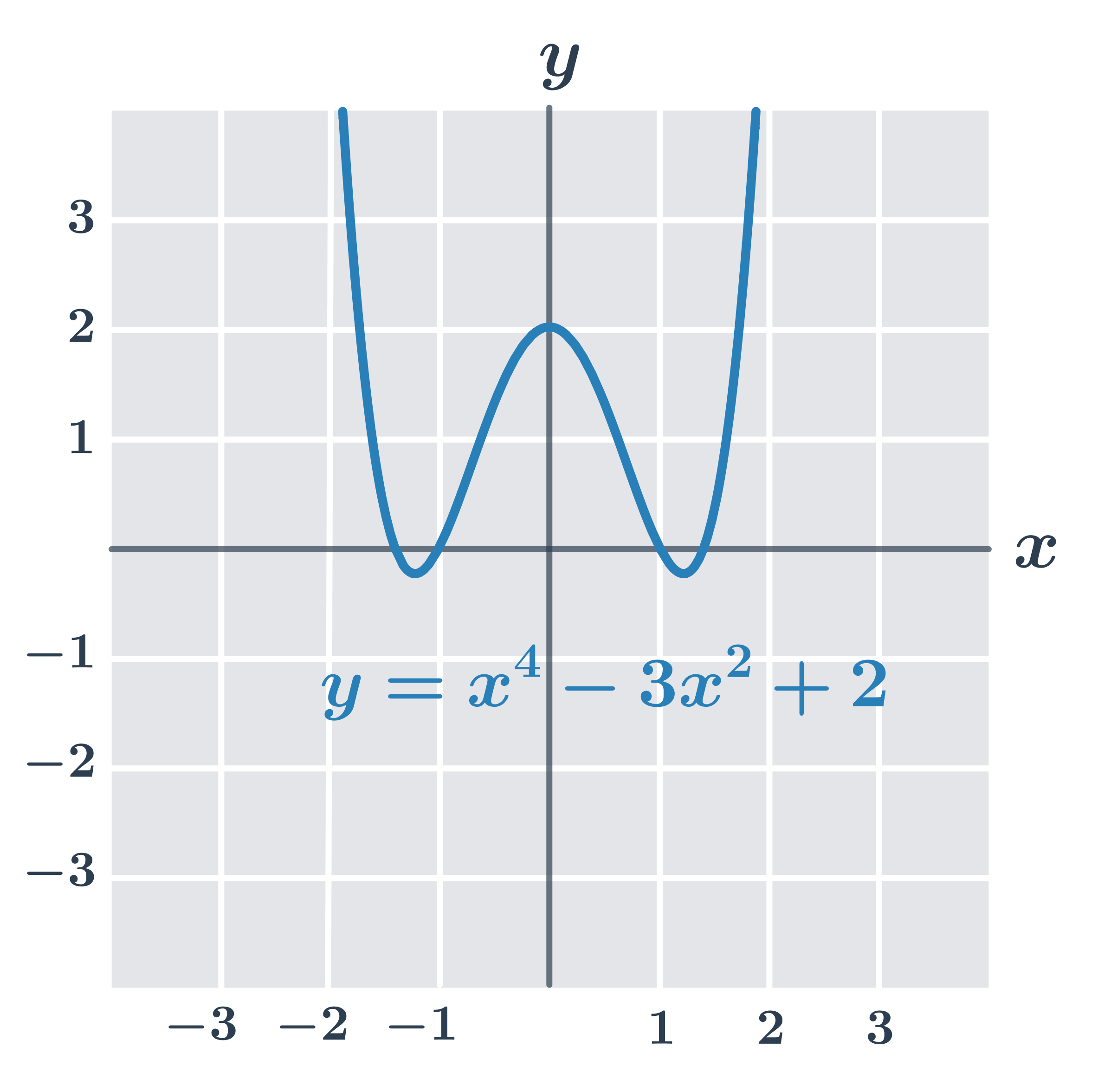
- f_3(x) = x^4-3x^2+2
Funkce f se nazývá lichá, právě když pro každé x je f(-x) = -f(x). Graf liché funkce je středově souměrný podle počátku soustavy souřadnic.
Příklady lichých funkcí
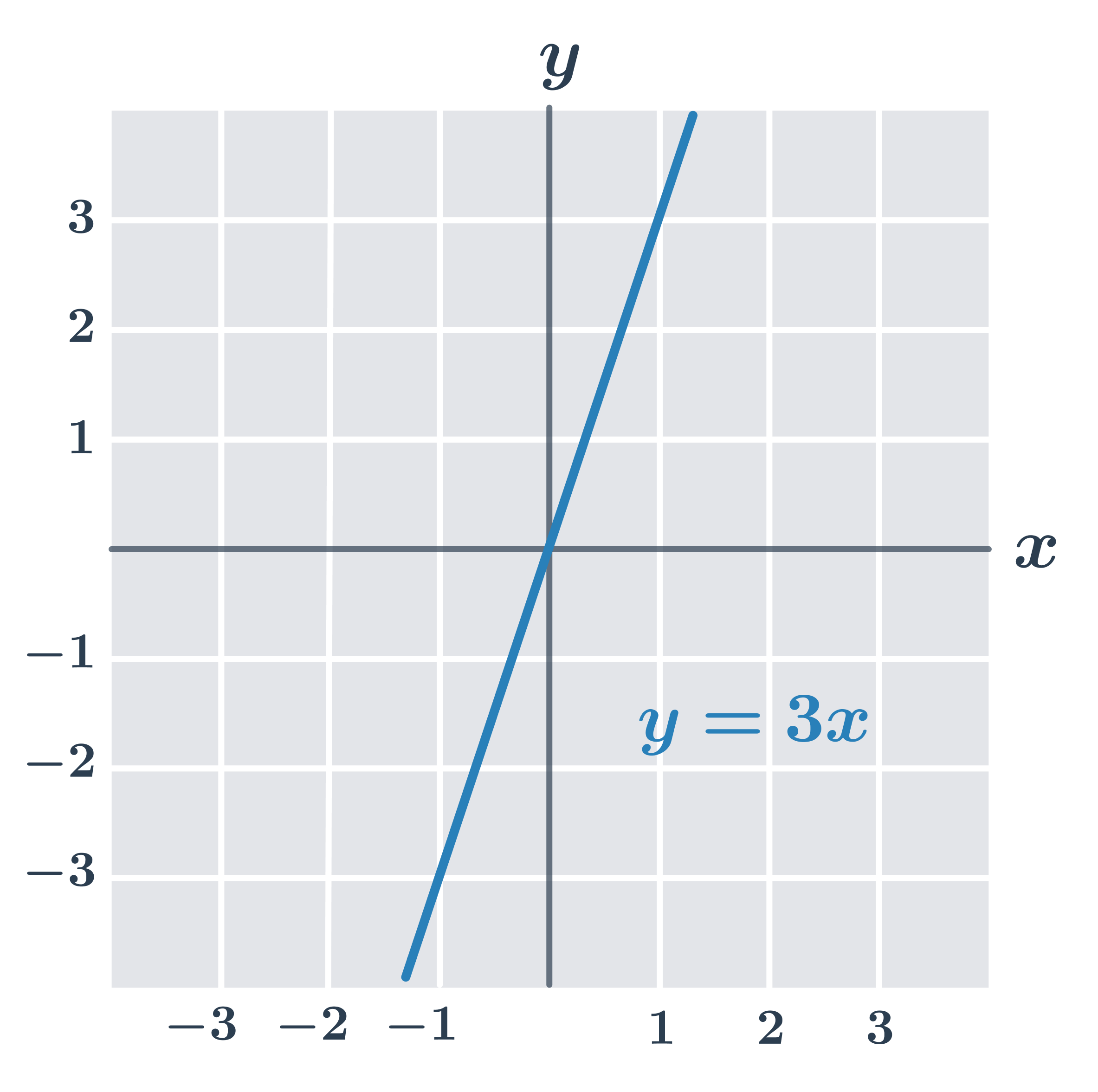
- f_1(x) = 3x
- f_2(x) = \sin x
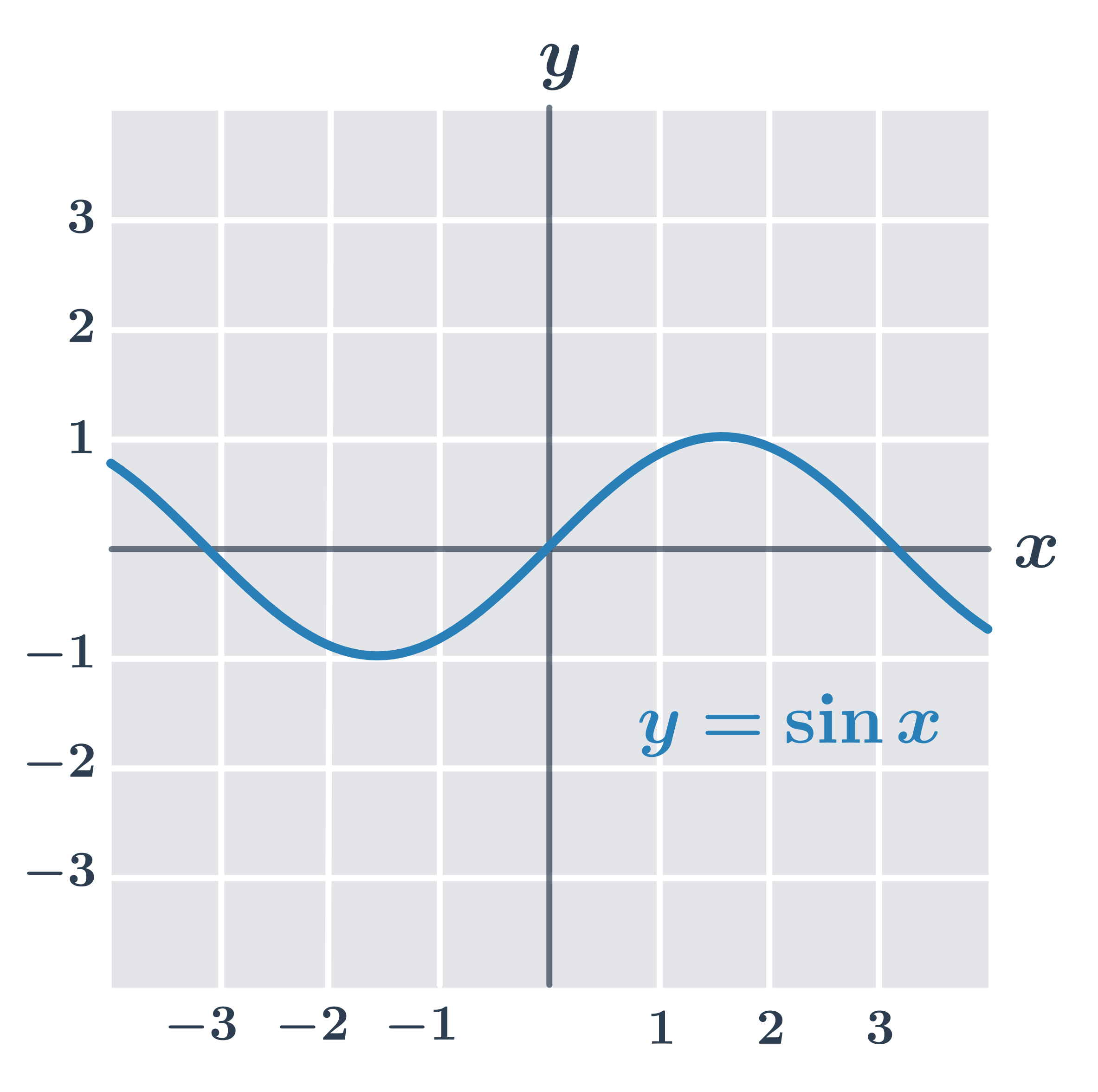
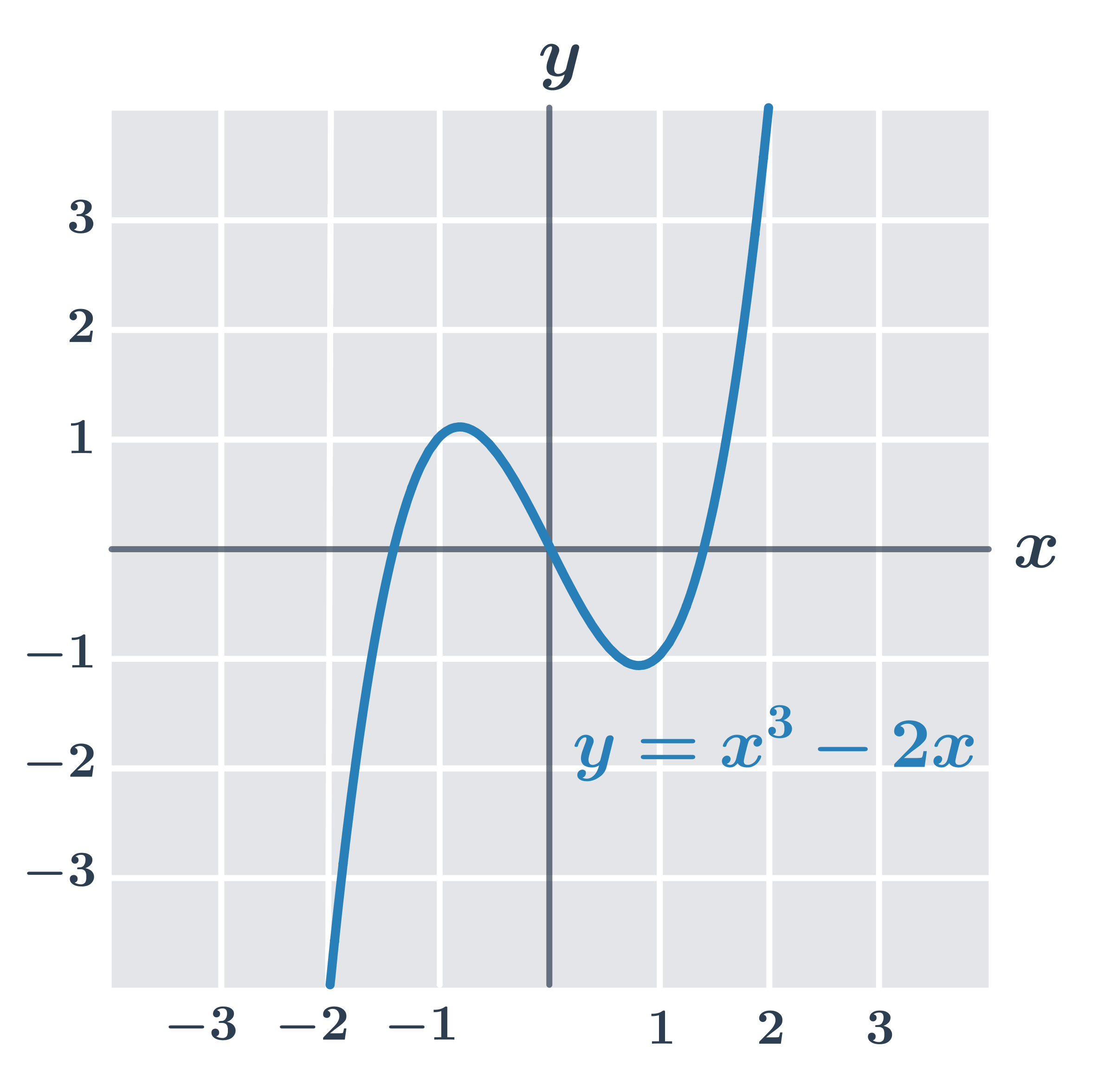
- f_3(x) = x^3-2x
Funkce f se nazývá periodická, právě když existuje číslo p \neq 0 (perioda funkce) takové, že pro každé x platí f(x+p)=f(x). Typickými příklady periodických funkcí jsou funkce goniometrické. Naopak třeba polynomy periodické nejsou (s výjimkou konstantní funkce).
Funkce f se nazývá zdola omezená, právě když existuje takové číslo k, že pro každé x platí f(x) \geq k. Funkce f se nazývá shora omezená, právě když existuje takové číslo k, že pro každé x platí f(x) \leq k. Funkce f se nazývá omezená, pokud je současně omezená shora i zdola.
Příklady (ne)omezených funkcí
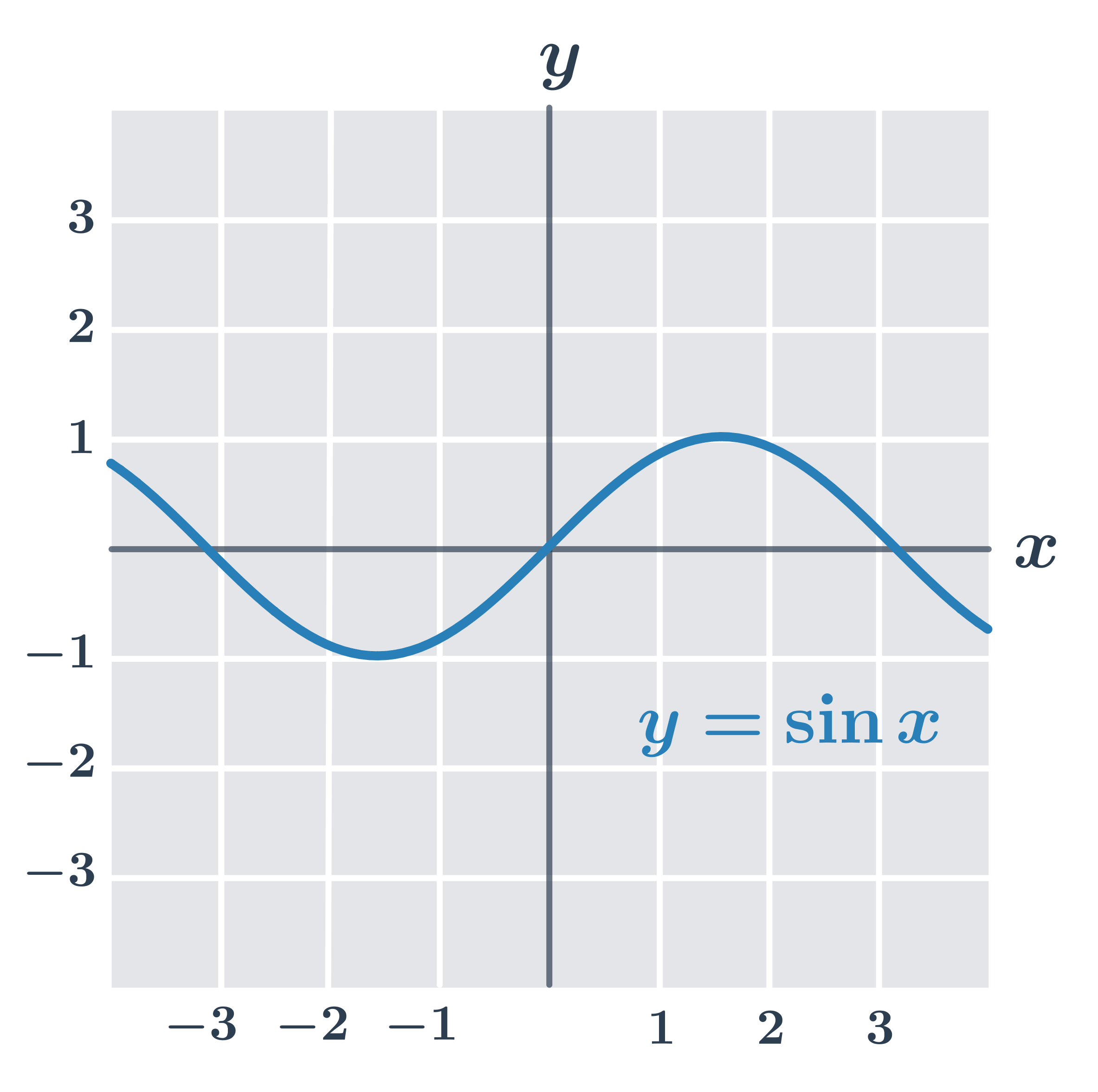
- Funkce f(x) = \sin x je omezená.
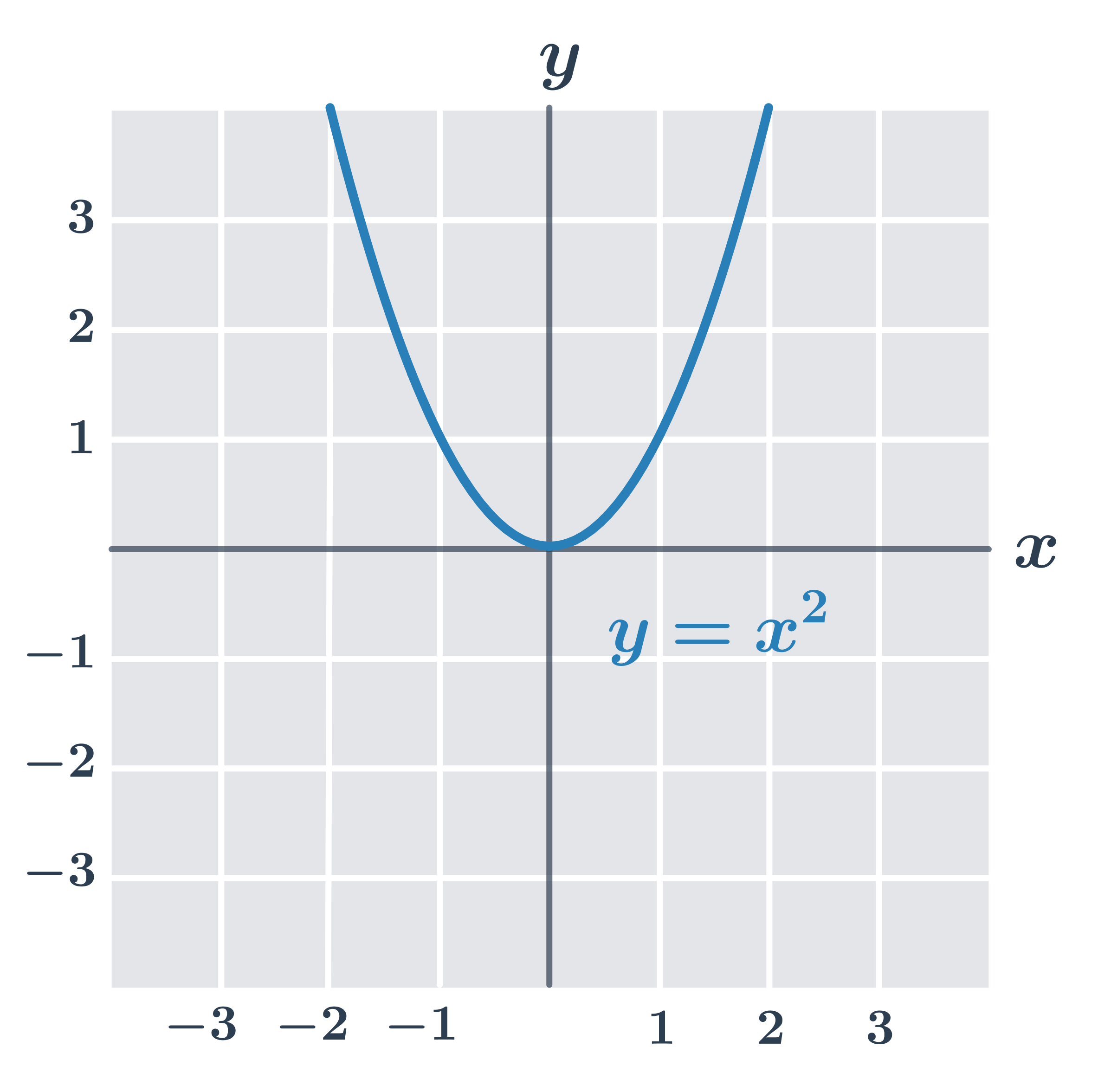
- Funkce f(x) = x^2 je omezená zdola (protože \forall x: f(x) \geq 0), ale není omezená shora.
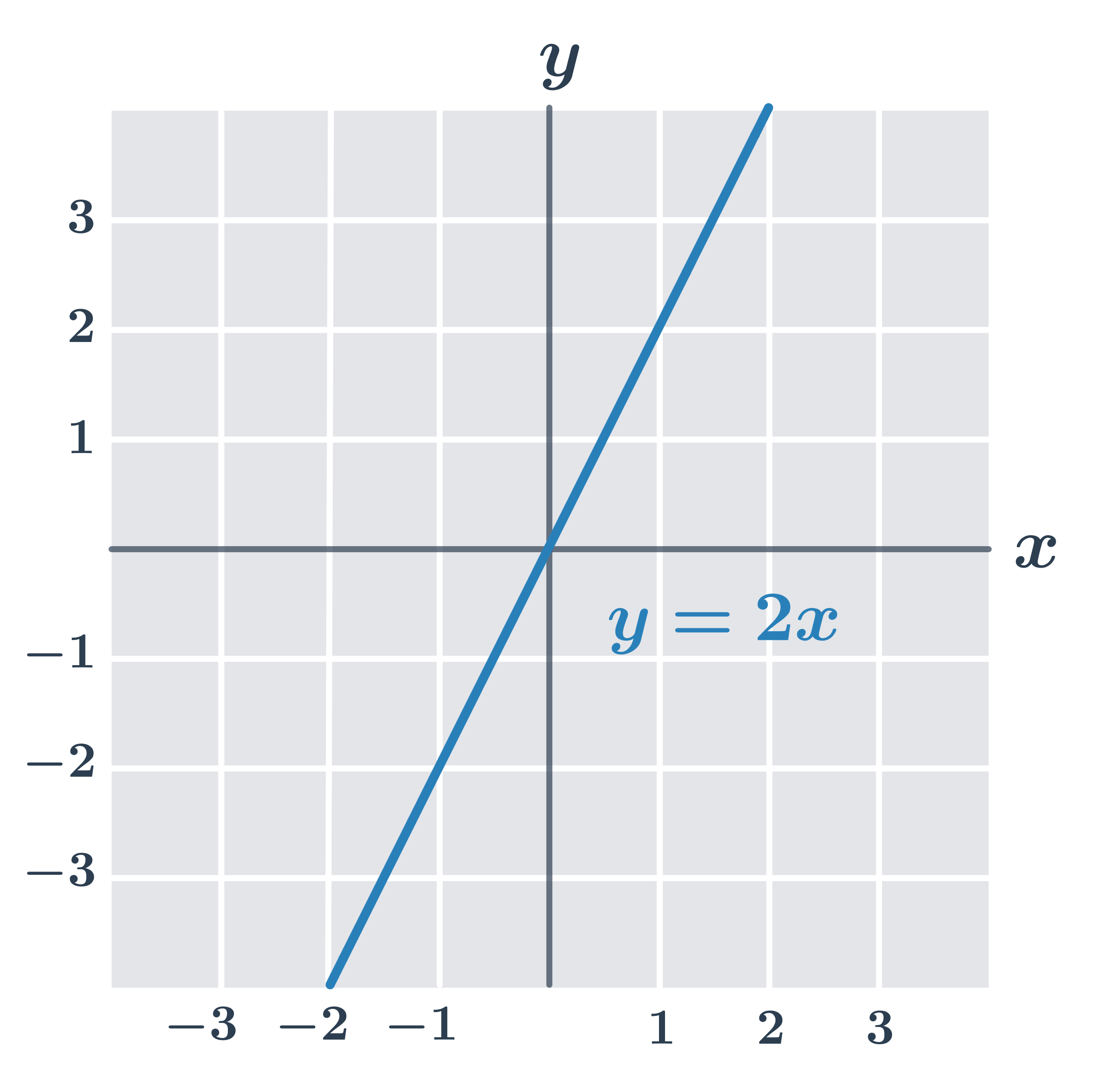
- Funkce f(x) = 2x není omezená ani shora, ani zdola.
Funkce f se nazývá prostá, právě když pro každou dvojici x_1 \neq x_2 platí f(x_1) \neq f(x_2).
Funkce f se nazývá rostoucí, právě když pro každou dvojici x_1 \lt x_2 platí f(x_1) \lt f(x_2).
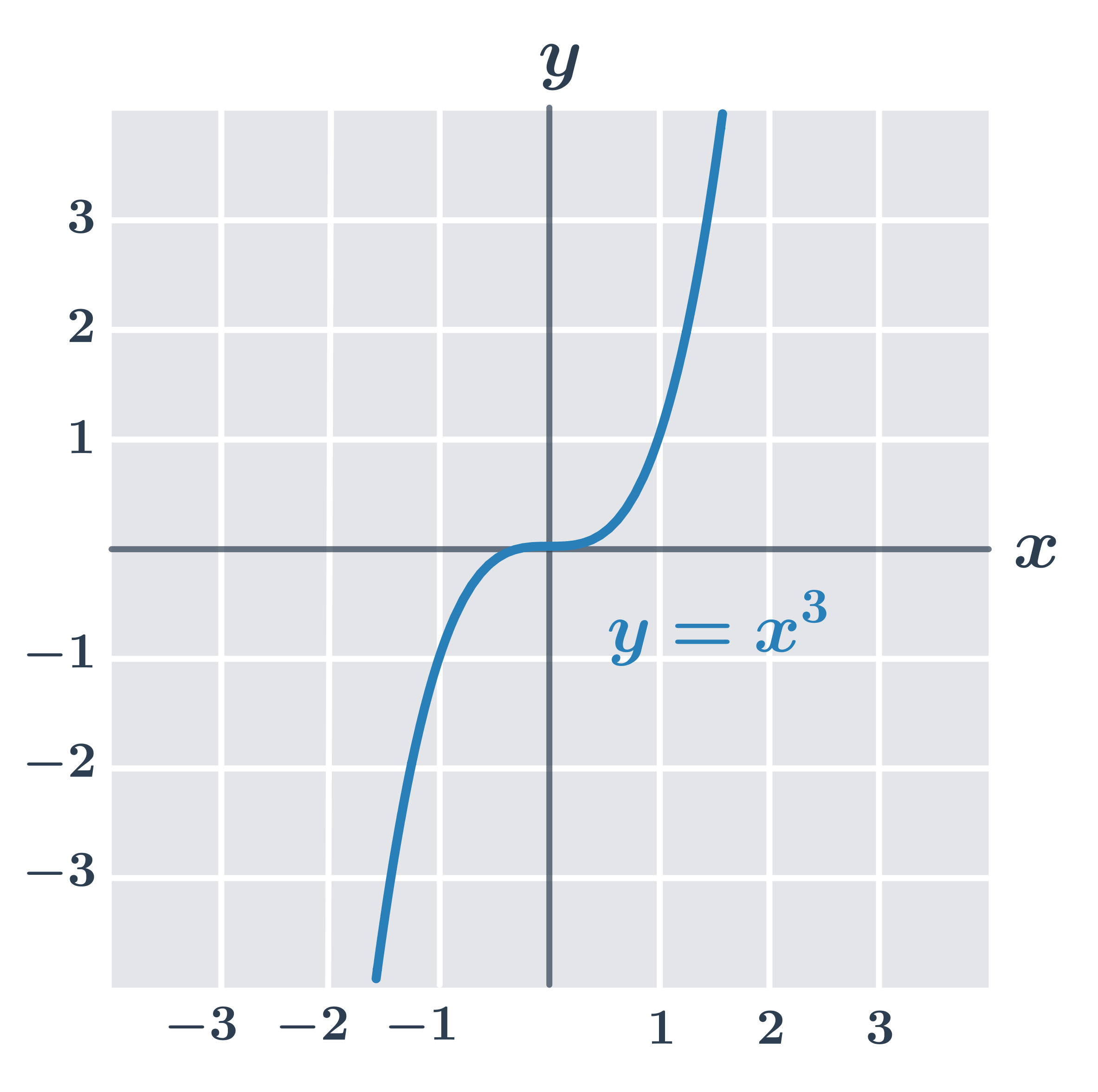
Příklad: funkce f(x) = x^3
Funkce f(x)=x^3 s definičním oborem D(f) = \mathbb{R} je prostá a rostoucí.
Funkce f se nazývá klesající, právě když pro každou dvojici x_1 \lt x_2 platí f(x_1) \gt f(x_2).
Příklad: funkce f(x) = \frac{1}{x}
Funkce f(x)= \frac{1}{x} s definičním oborem D(f) = (-\infty,0) \cup (0,\infty):
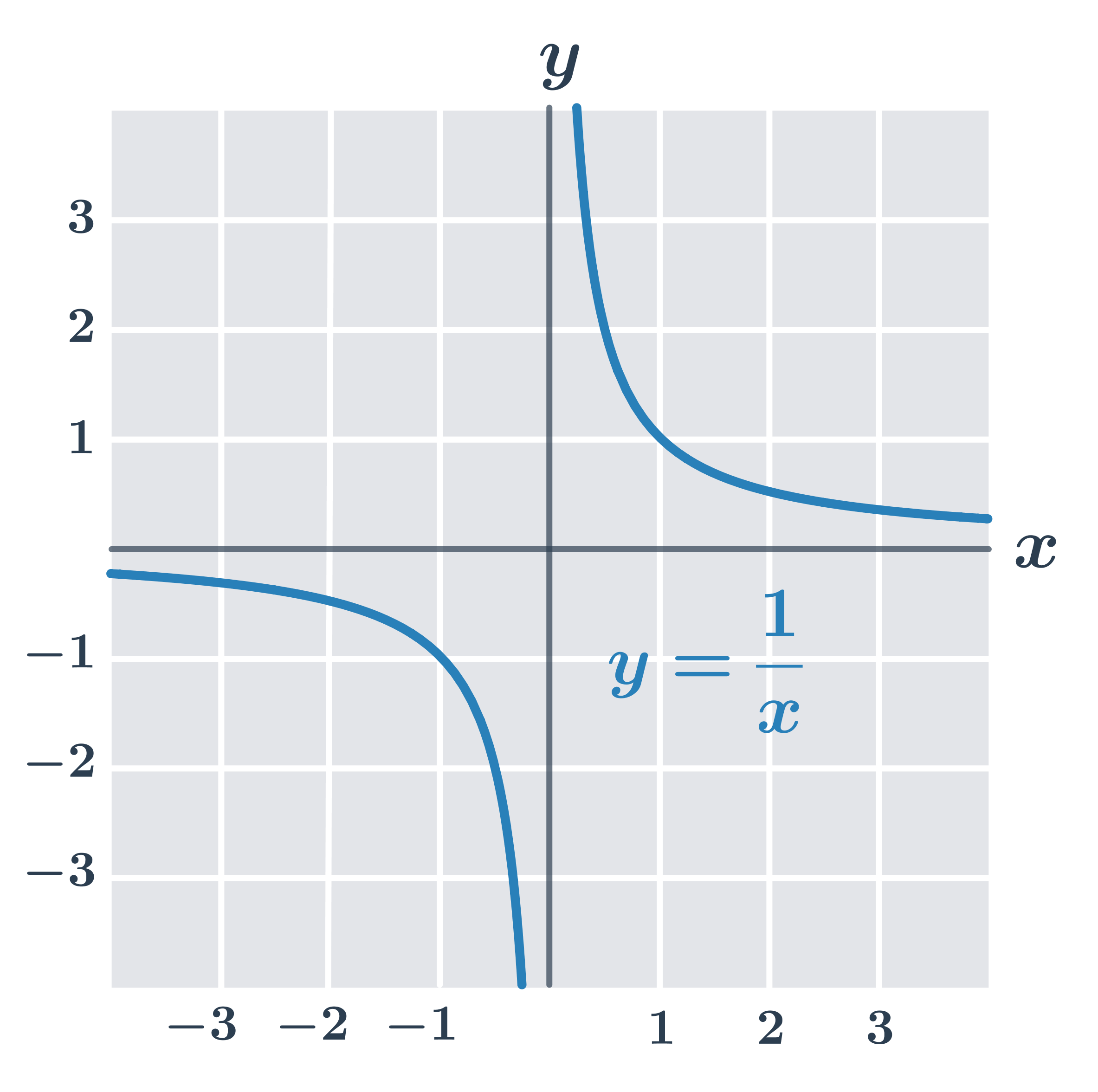
- funkce klesá na intervalu (-\infty,0)
- funkce také klesá na intervalu (0,\infty)
- ale funkce není klesající na celém D(f), např. -1 \lt 1, ale f(-1) \lt f(1)
Funkce f má v bodě x_0 maximum, jestliže pro každé x \in D(f) je f(x) \leq f(x_0). Maximum je tedy bod, ve kterém je funkční hodnota maximální (takových bodů může být i víc než jeden, např. u funkce sinus).
Funkce f má v bodě x_0 minimum, jestliže pro každé x \in D(f) je f(x) \geq f(x_0). Minimum je tedy bod, ve kterém je funkční hodnota minimální (takových bodů opět může být i více než jeden).
Maximum a minimum se nazývají extrémy funkce.
Příklad: maximum funkce f(x)=1-x^2
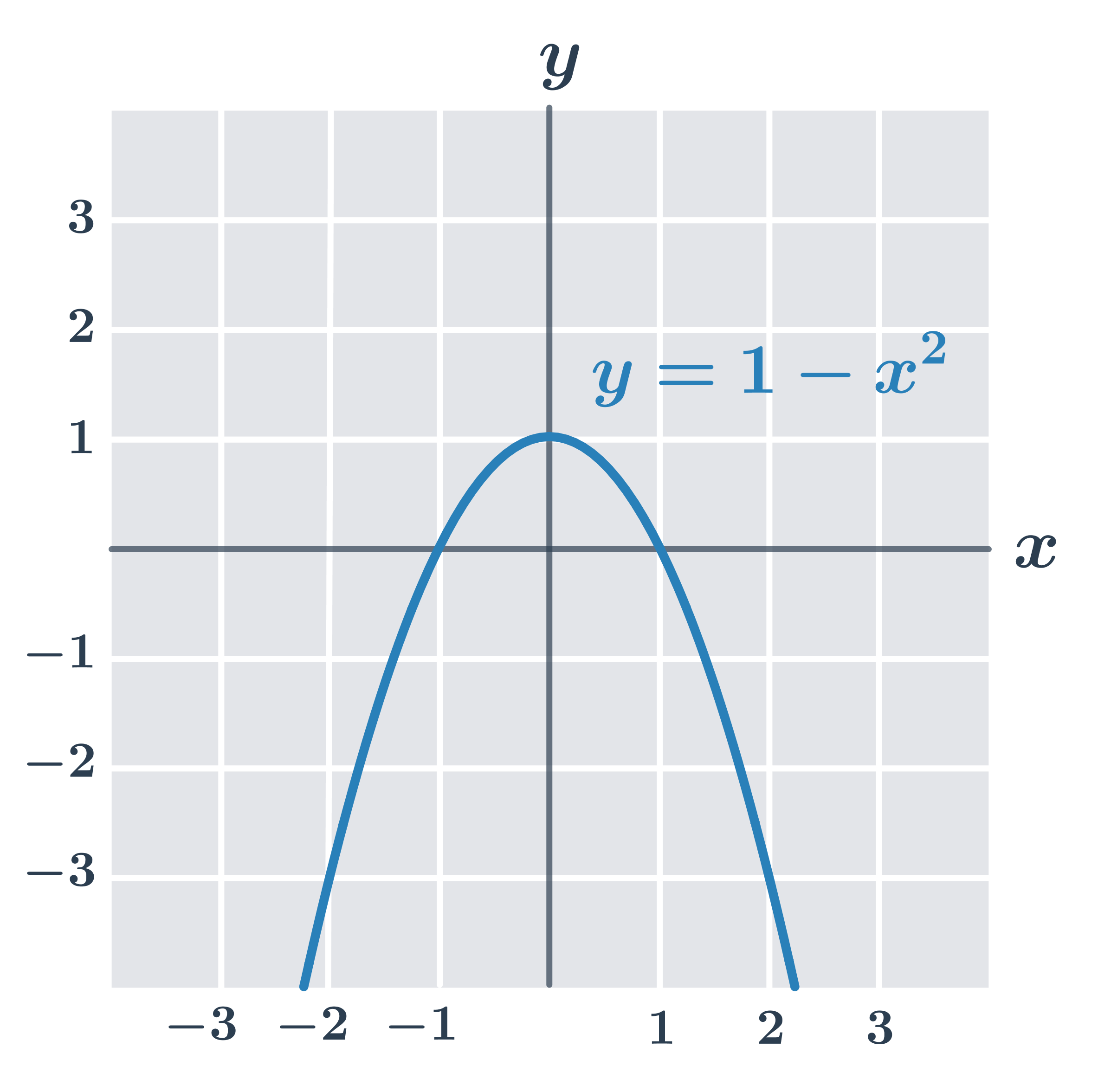
- Funkce f:y=1-x^2 má ze všech reálných čísel nejvyšší hodnotu v bodě x=0, je f(0)=1 a pro libovolné reálné číslo x je f(x) \leq 1.
- Funkce tedy nabývá maxima pro x=0. Minimum tato funkce nemá.
Příklad: minimum funkce f(x)=(x-1)^2
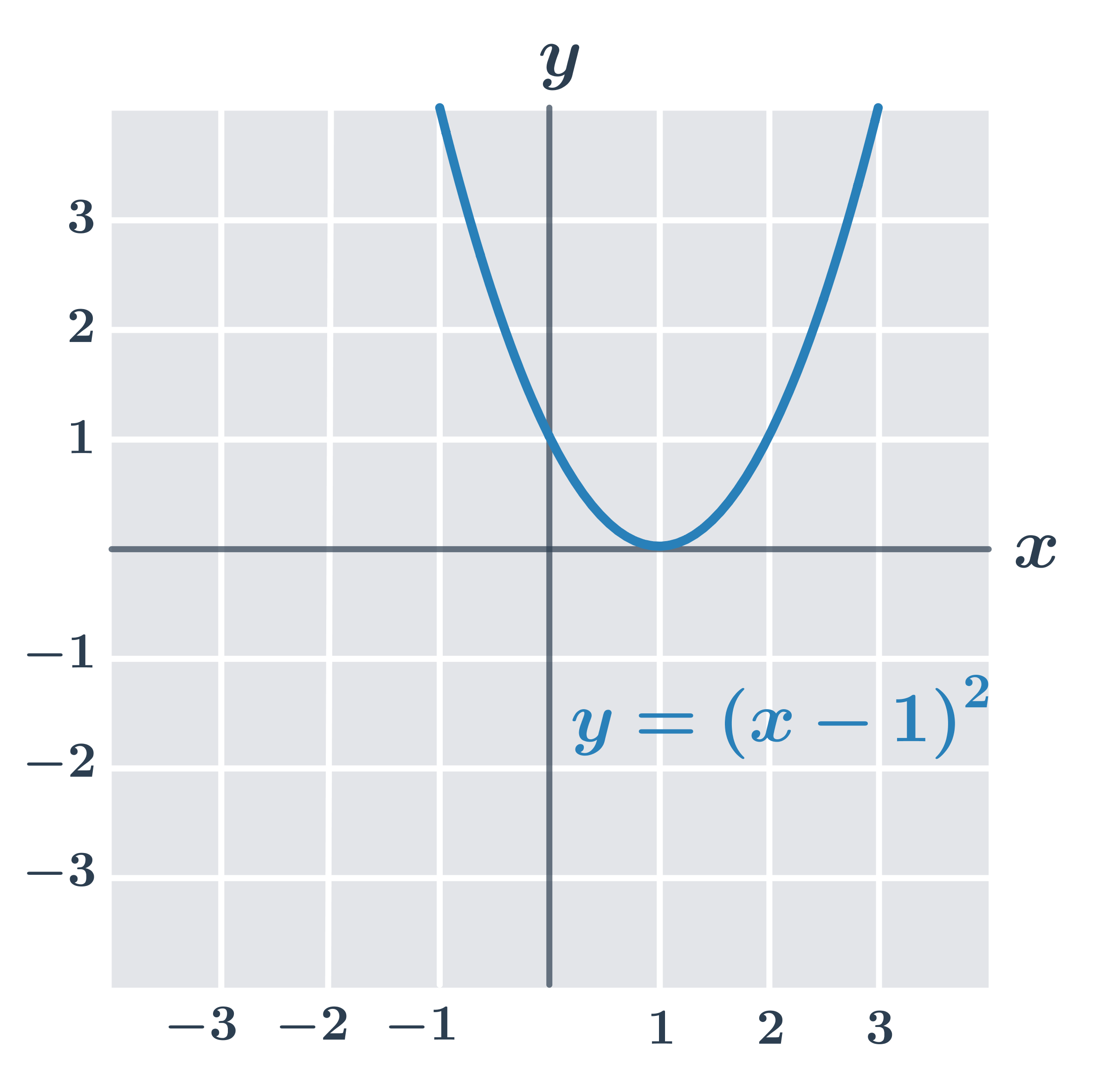
- Funkce f:y=(x-1)^2 má nejnižší hodnotu v bodě x=1, máme f(1) = 0 a pro libovolné reálné číslo x je f(x) \geq 0.
- Funkce tedy má v bodě x=1 minimum. Maximum tato funkce nemá.
