Logaritmus – 9. třída (9. ročník)

Definice a využití logaritmu

Logaritmus je inverzní operace k umocňování. Logaritmus kladného čísla x při základu a je takové reálné číslo y = \log_a(x), pro které platí a^y = x. Číslo a se nazývá základ logaritmu (báze). Procvičením této základní definice se zabývá téma Logaritmus: výpočet.

Logaritmus o základu e=2{,}71 828 182... (Eulerovo číslo) se nazývá přirozený logaritmus a značí se většinou \ln. Logaritmus o základu 10 se nazývá dekadický logaritmus (a někdy se značí \mathit{lg}).

Logaritmy mají velmi široké využití v mnoha oblastech matematiky. Historicky se využívaly jako užitečná početní pomůcka („logaritmické pravítko“), která využívala faktu, že logaritmus součinu je součet logaritmů. Dnes na logaritmy často narazíme například v informatice při návrhu a analýze algoritmů.

Vlastnosti logaritmů

Při práci s logaritmy, například při práci na tématu Výrazy s logaritmy, často využijeme následující vlastnosti logaritmů:

• Logaritmus je definován pouze pro kladná čísla.
• Logaritmus o základu 1 není definován.
• Logaritmus jedničky je nula, \log_a(1)=0.
• Logaritmus o stejném základu a argumentu je 1, \log_a{a}=1.
• Logaritmus součinu je součet logaritmů, \log_a(x\cdot y)=\log_a{x}+\log_a{y}.
• Logaritmus podílu je rozdíl logaritmů, \log_a\left(\frac{x}{y}\right)=\log_a{x}-\log_a{y}.
• Logaritmus je inverzní funkcí k exponenciální funkci o stejném základu, \log_a{x}=y \Leftrightarrow a^y=x.
• Logaritmus mocniny je součin exponentu a logaritmu základu mocniny, \log_a(x^n)=n\log_a{x}.

Graf logaritmu

Graf zobrazuje logaritmus o základu 2:

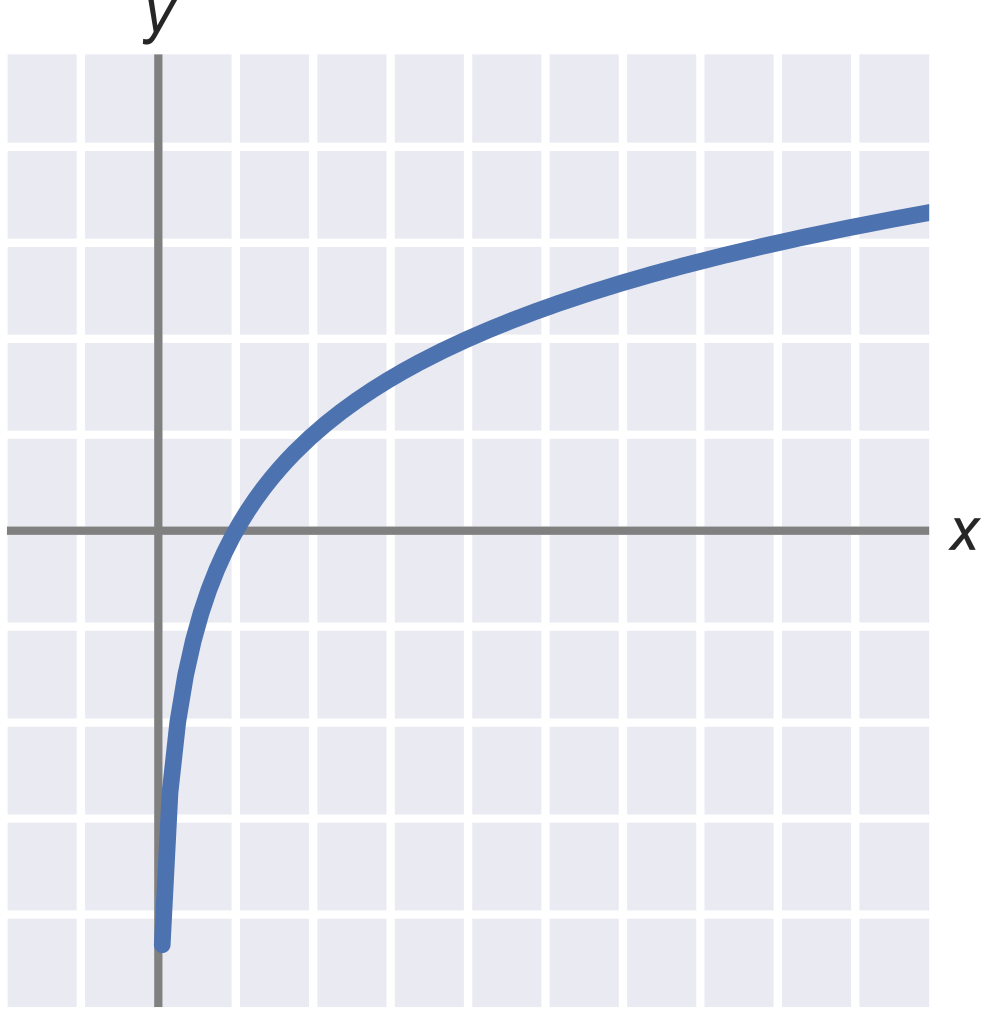
Podrobněji se grafy logaritmu zabývá téma Grafy exponenciálních a logaritmických funkcí.