Výpis souhrnů
Logaritmus
Podtémata
Logaritmus
Definice a využití logaritmu
Logaritmus je inverzní operace k umocňování. Logaritmus kladného čísla x při základu a je takové reálné číslo y = \log_a(x), pro které platí a^y = x. Číslo a se nazývá základ logaritmu (báze). Procvičením této základní definice se zabývá téma Logaritmus: výpočet.
Logaritmus o základu e=2{,}71 828 182... (Eulerovo číslo) se nazývá přirozený logaritmus a značí se většinou \ln. Logaritmus o základu 10 se nazývá dekadický logaritmus (značíme \log, v cizojazyčných textech se vyskytuje také zápis \lg).
Logaritmy mají velmi široké využití v mnoha oblastech matematiky. Historicky se využívaly jako užitečná početní pomůcka („logaritmické pravítko“), která využívala faktu, že logaritmus součinu je součet logaritmů. Dnes na logaritmy často narazíme například v informatice při návrhu a analýze algoritmů.
Vlastnosti logaritmů
Při práci s logaritmy, například při práci na tématu Výrazy s logaritmy, často využijeme následující vlastnosti logaritmů:
- Logaritmus je definován pouze pro kladná čísla.
- Logaritmus o základu 1 není definován.
- Logaritmus jedničky je nula, \log_a(1)=0.
- Logaritmus o stejném základu a argumentu je 1, \log_a{a}=1.
- Logaritmus součinu je součet logaritmů, \log_a(x\cdot y)=\log_a{x}+\log_a{y}.
- Logaritmus podílu je rozdíl logaritmů, \log_a\left(\frac{x}{y}\right)=\log_a{x}-\log_a{y}.
- Logaritmus je inverzní funkcí k exponenciální funkci o stejném základu, \log_a{x}=y \Leftrightarrow a^y=x.
- Logaritmus mocniny je součin exponentu a logaritmu základu mocniny, \log_a(x^n)=n\log_a{x}.
Graf logaritmu
Graf zobrazuje logaritmus o základu 2:
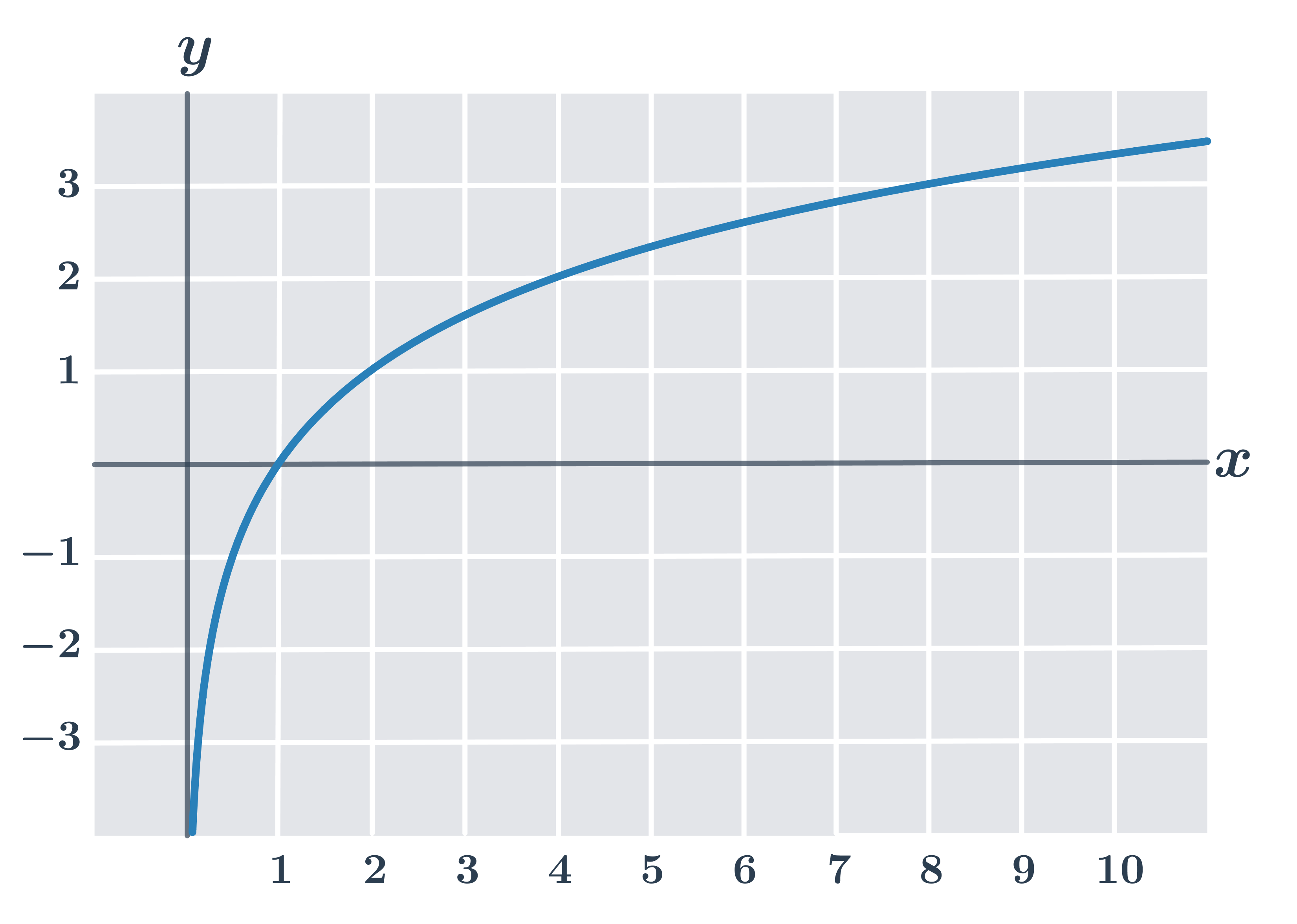
Podrobněji se grafy logaritmu zabývá téma Grafy logaritmických funkcí.
Komiks pro zpestření

Logaritmus: výpočet
Logaritmus kladného čísla x při základu a je takové reálné číslo y = \log_a(x), pro které platí a^y = x. Příklady:
| \log_{10}(100) = 2 | protože 10^2 = 100 |
| \log_2(32) = 5 | protože 2^5 = 32 |
| \log_5(125) = 3 | protože 5^3 = 125 |
| \log_7(1) = 0 | protože 7^0 = 1 |
| \log_2(0{,}5) = -1 | protože 2^{-1} = \frac{1}{2} = 0{,}5 |
Výrazy s logaritmy
Některé základní vlastnosti logaritmů vyjádřené pomocí vzorců:
- \log_a(a)=1
- \log_a(1)=0
- \log_a(x\cdot y) = \log_a(x) + \log_a(y) (logaritmus součinu je součet logaritmů)
- \log_a(\frac{x}{y}) = \log_a(x) - \log_a(y) (logaritmus podílu je rozdíl logaritmů)
- \log_a(x^k)=k\log_a(x)
- \log_a(x)=\frac{\log_b(x)}{\log_b(a)}
Logaritmické rovnice
Logaritmická rovnice je taková, kde neznámá vystupuje jako argument logaritmické funkce, např. 2 \cdot \log_6(x-2) = \log_6(14-x).
U logaritmických rovnic musíme dávat pozor na podmínky řešení. Argument každého logaritmu totiž musí být vždy kladné číslo. V uvedeném příkladě tedy musí platit x-2>0 a současně 14-x > 0.
Logaritmické rovnice řešíme za využití vlastností logaritmické funkce a jejího vztahu k exponenciální funkci. Dílčí způsoby, jak řešit logaritmické rovnice:
- Převedeme rovnici na tvar \log_a f(x) = c. Pak musí platit f(x) = a^c.
- Převedeme rovnici na tvar \log_a f(x) = \log_a g(x). Pak musí platit f(x) = g(x).
Grafy exponenciálních funkcí
Grafem exponenciální funkce je křivka jménem exponenciála. Na obrázku jsou grafy exponenciálních funkcí se základy 2 a e = 2{,}7 182 818 284\ldots. Vidíme také, že grafy funkcí e^x a e^{-x} jsou spolu souměrné podle osy y.
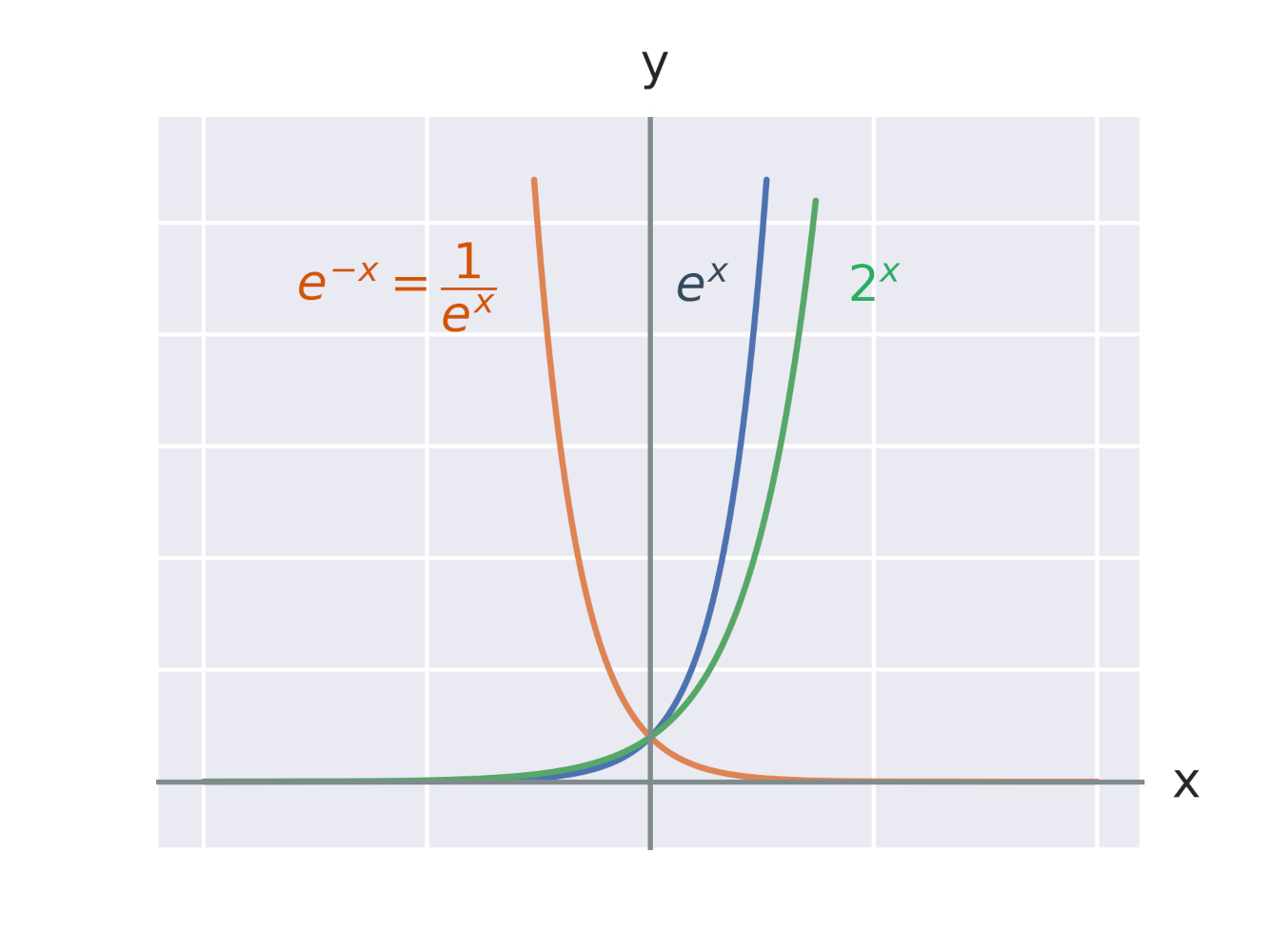
Graf každé exponenciální funkce tvaru f:y =a^x prochází bodem [0,1], protože pro libovolnou konstantu a platí: a^0=1.
Efekt přičtení konstanty k exponenciální funkci
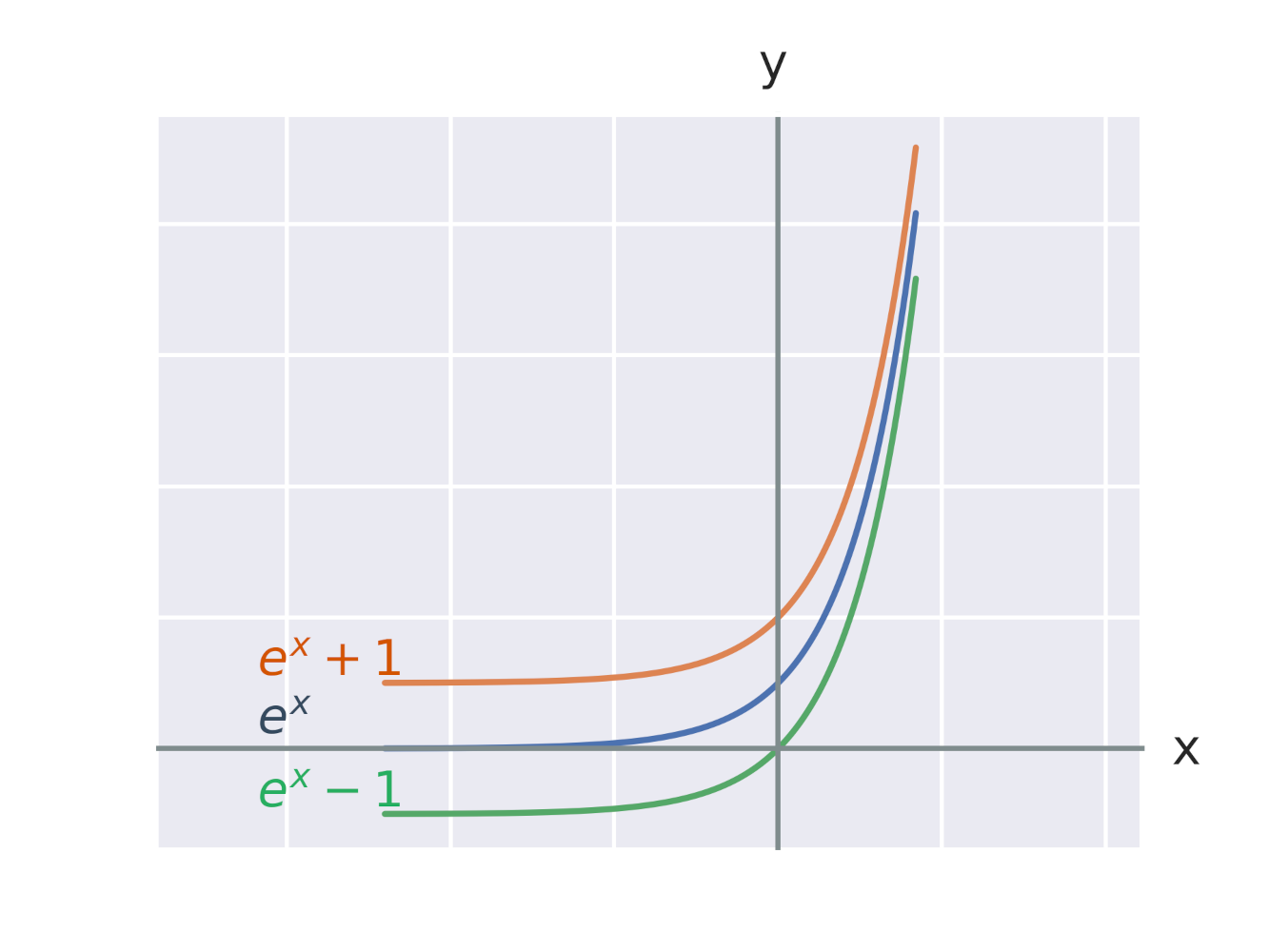
Efekt přičtení konstanty k exponentu
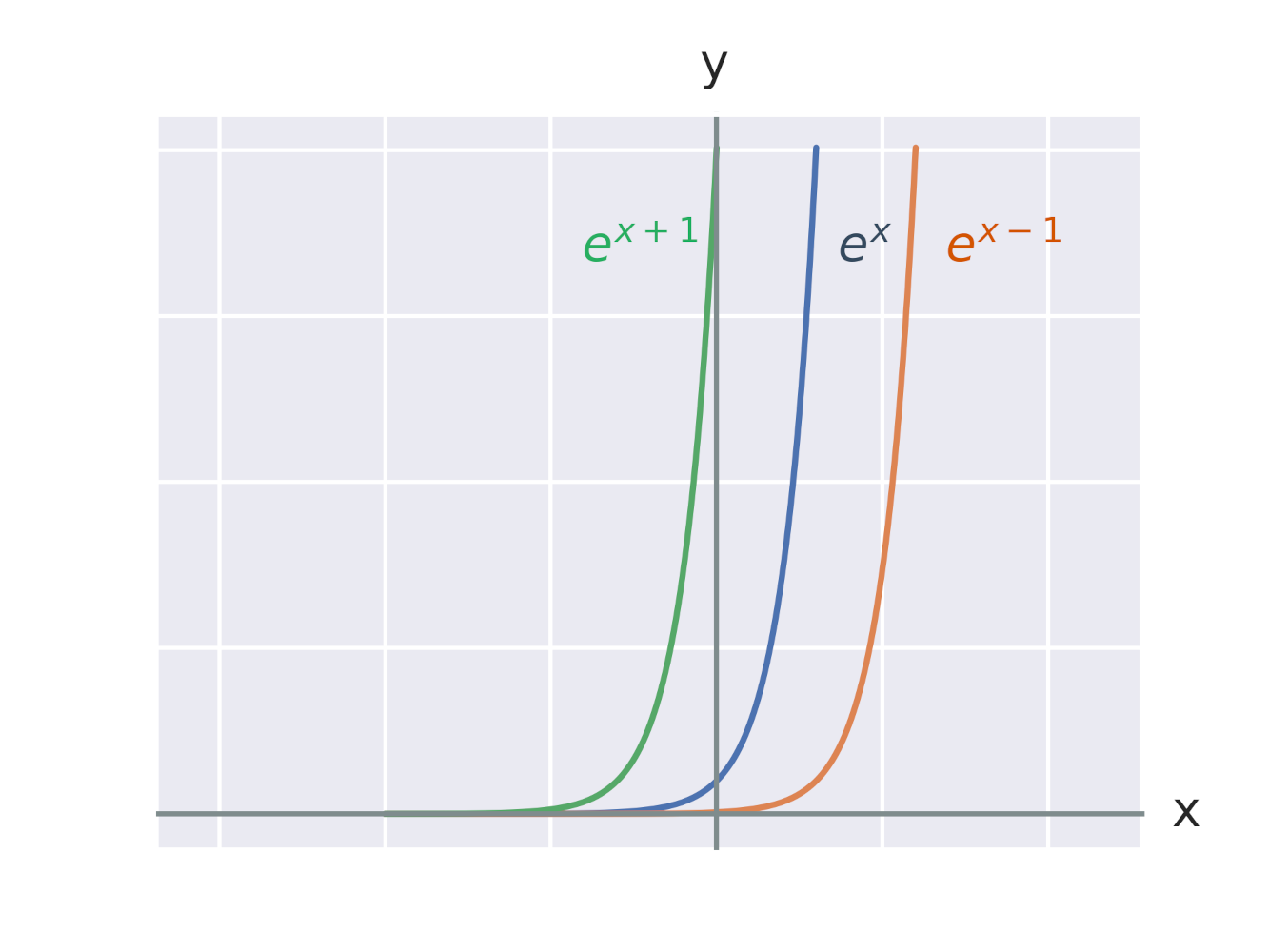
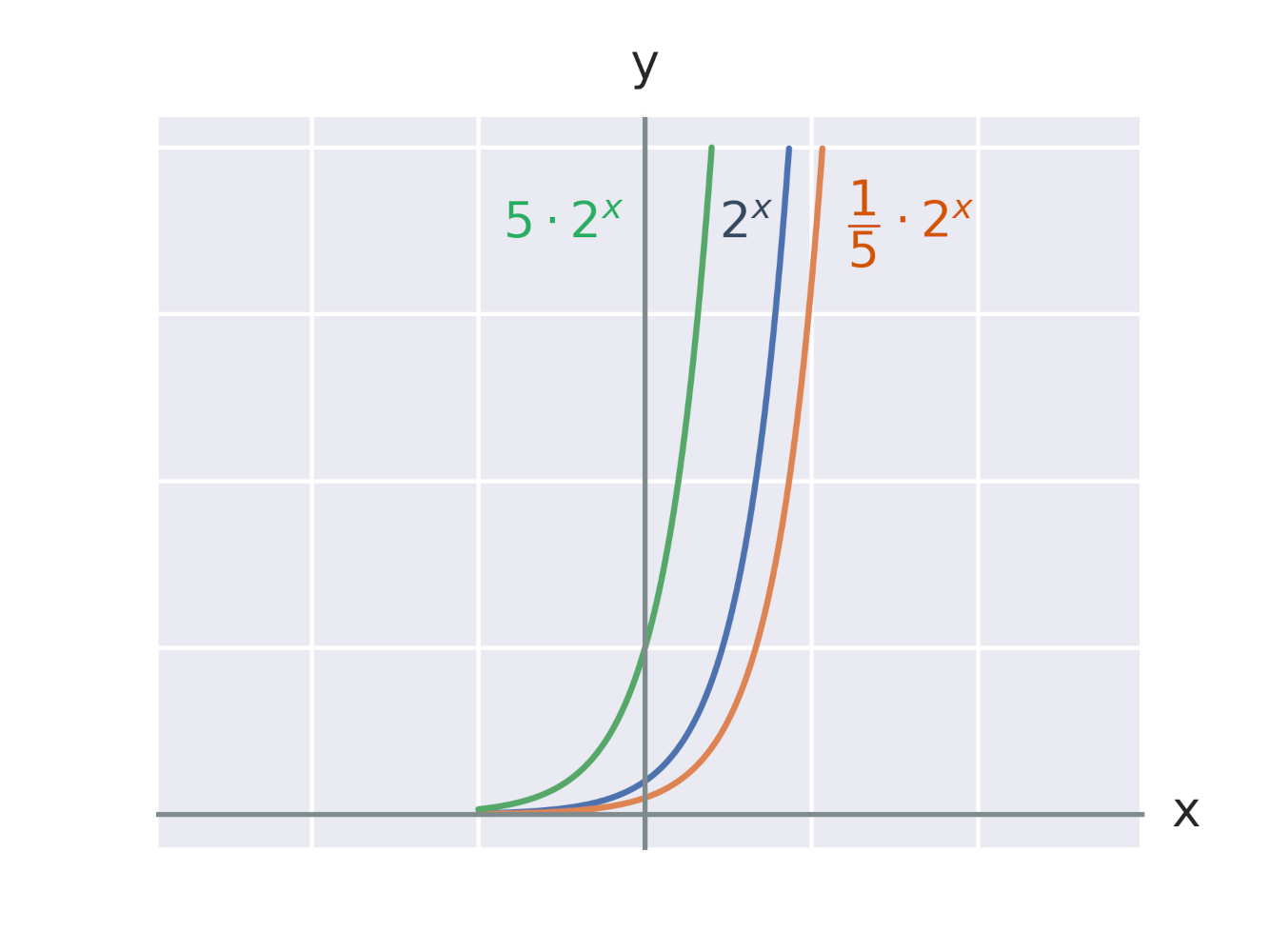
Efekt vynásobení exponenciální funkce konstantou
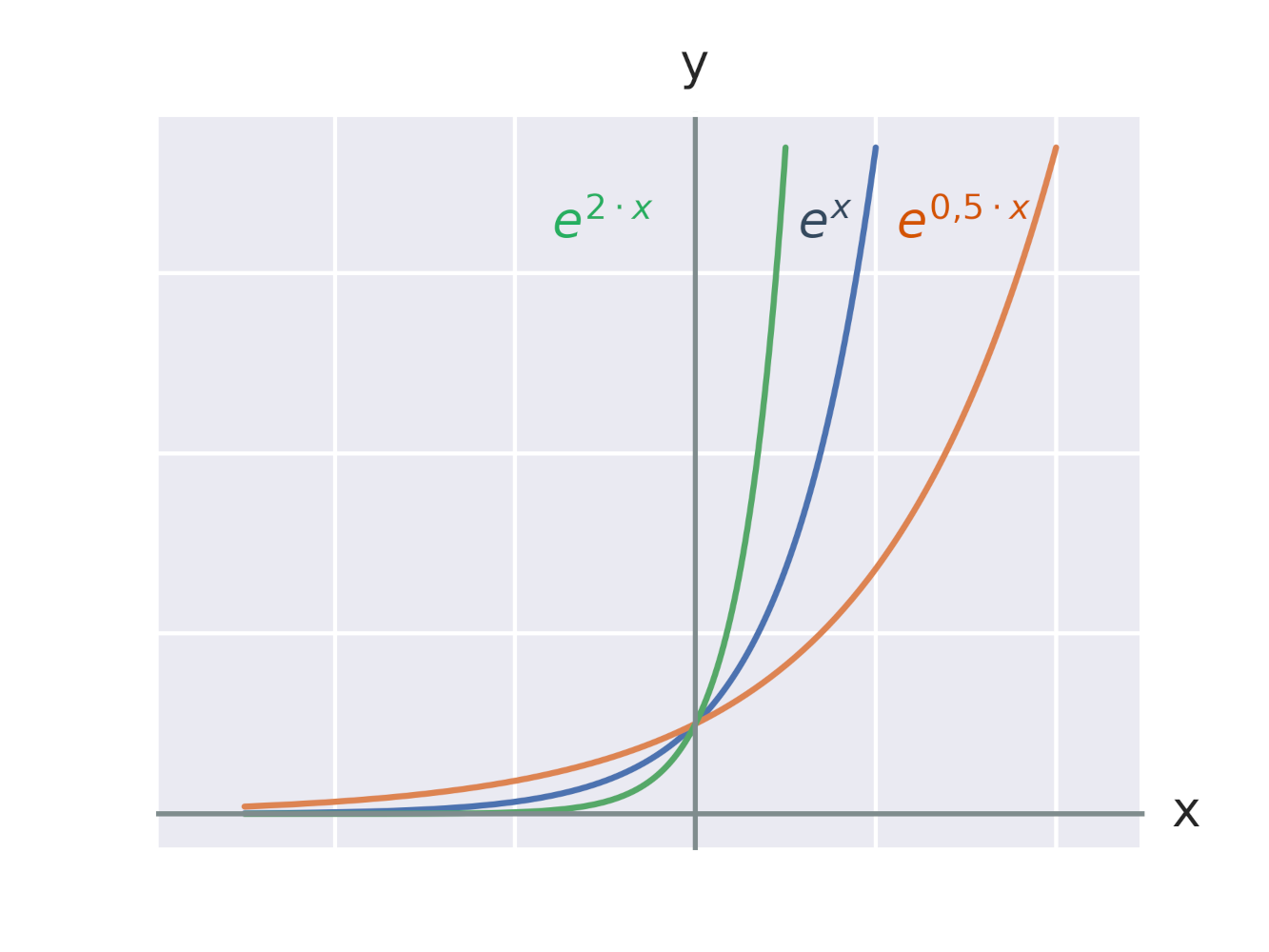
Efekt vynásobení exponentu konstantou
Grafy logaritmických funkcí
Logaritmická funkce je inverzní k exponenciální funkci o stejném základu. Grafy dvou navzájem inverzních funkcí jsou osově souměrné podle osy prvního kvadrantu (tj. přímky splňující x=y).
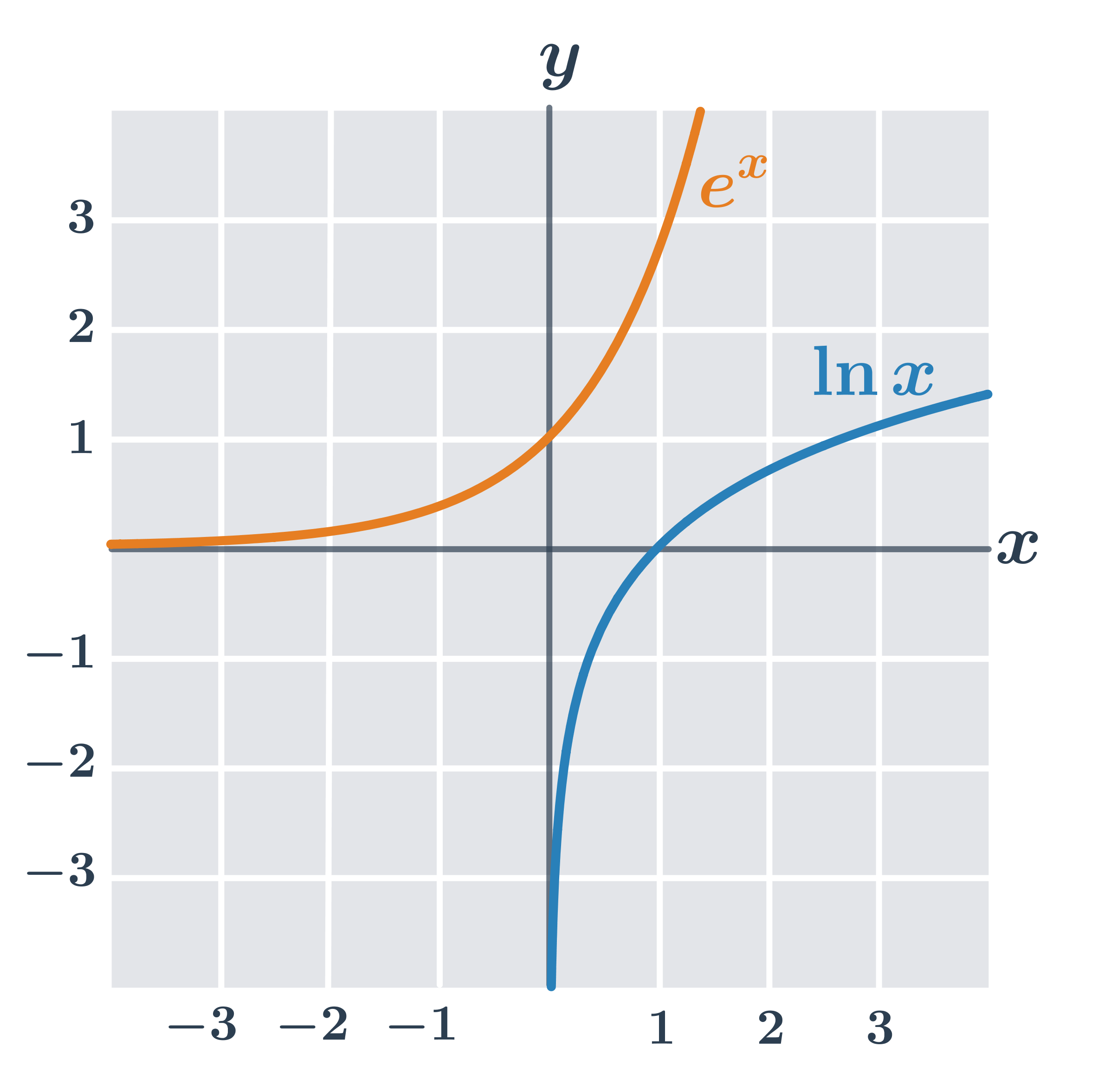
Graf každé logaritmické funkce tvaru y=\log_a x prochází bodem [1,0], protože pro libovolnou konstantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcí s různými základy 2, e, 10.
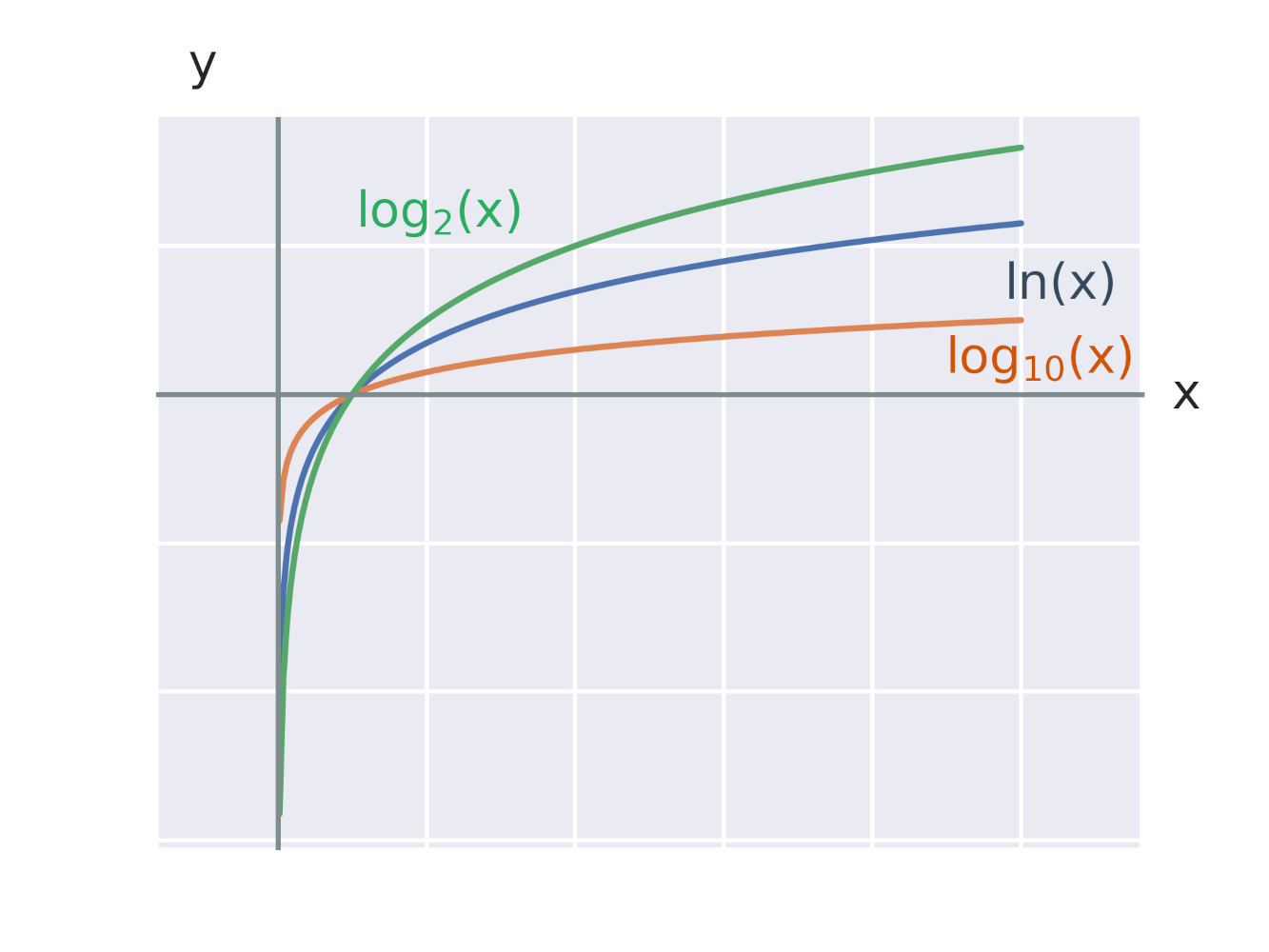
Značení některých význačných logaritmických funkcí:
| funkce | popis | další možná značení |
|---|---|---|
| \log_a x | obecně logaritmus x o základu a pro nějaké a >0, a\neq 1 | |
| \ln x | přirozený logaritmus x, tj. logaritmus x o základu e | v angl. textech někdy \log x |
| \log x | dekadický logaritmus x, tj. logaritmus x o základu 10 | \log_{10}x |
| \log_2 x | binární logaritmus x, tj. logaritmus x o základu 2 | někdy se objevuje \mathrm{lb}\;x |
Efekt přičtení konstanty k logaritmické funkci
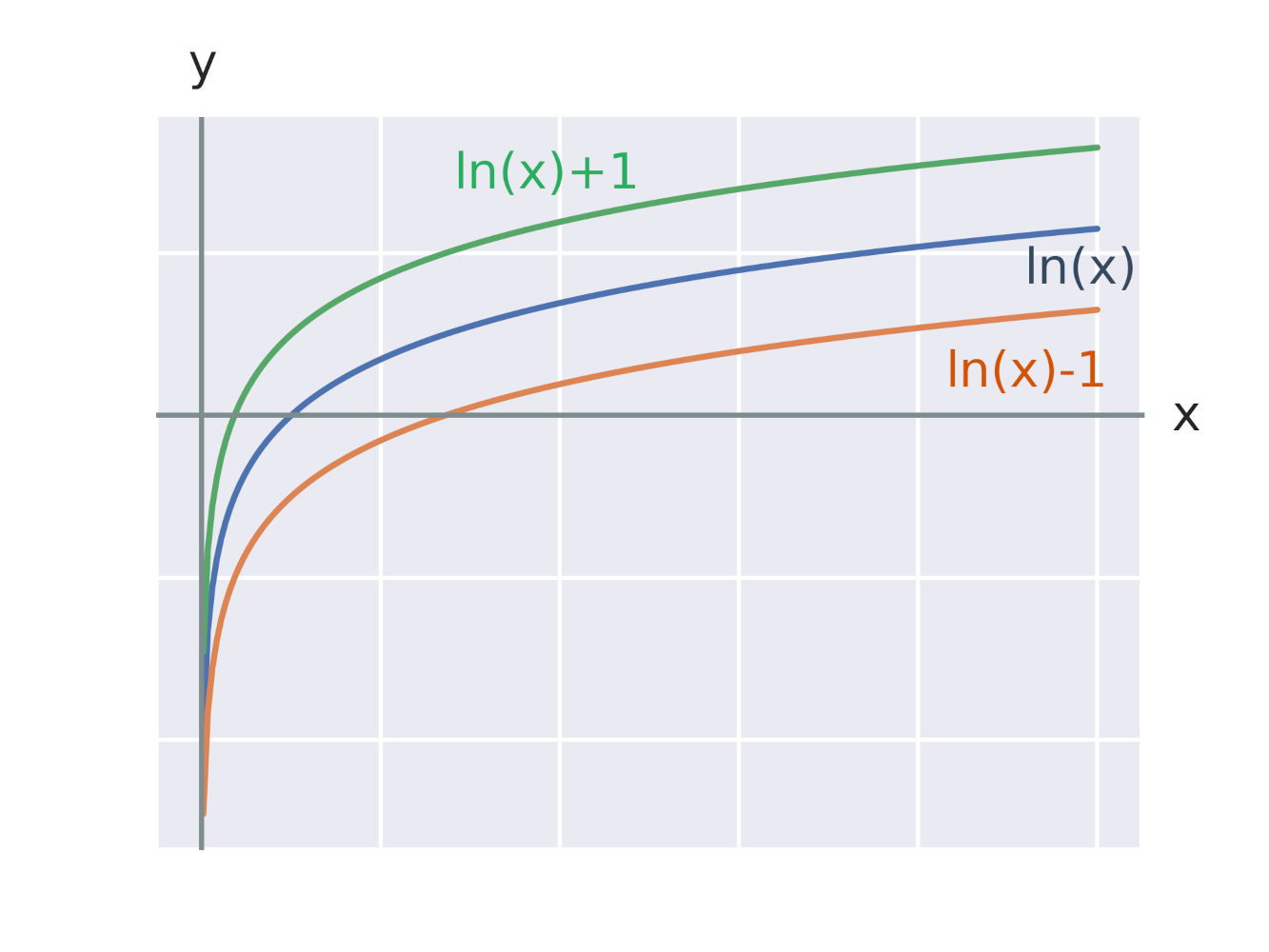
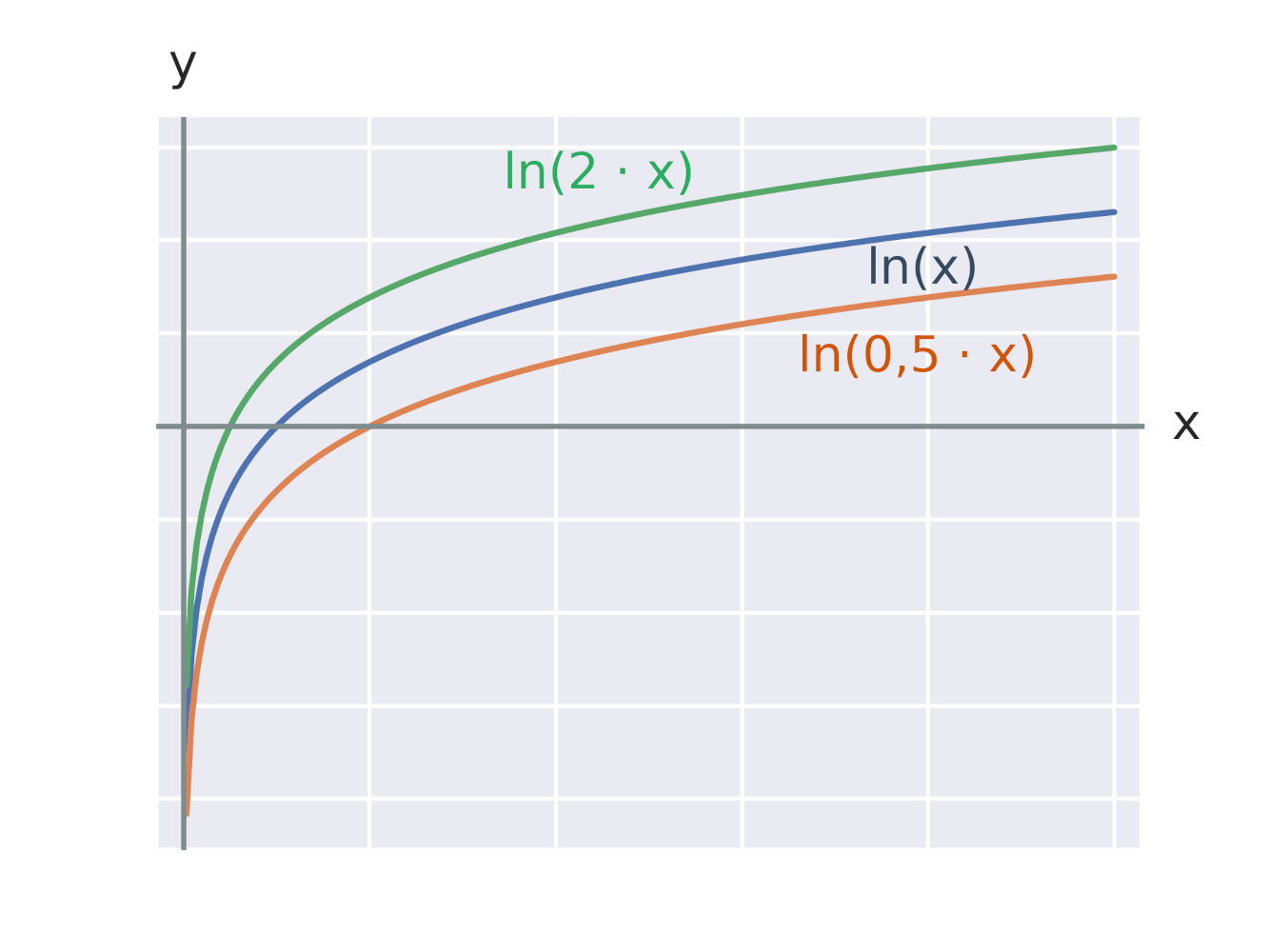
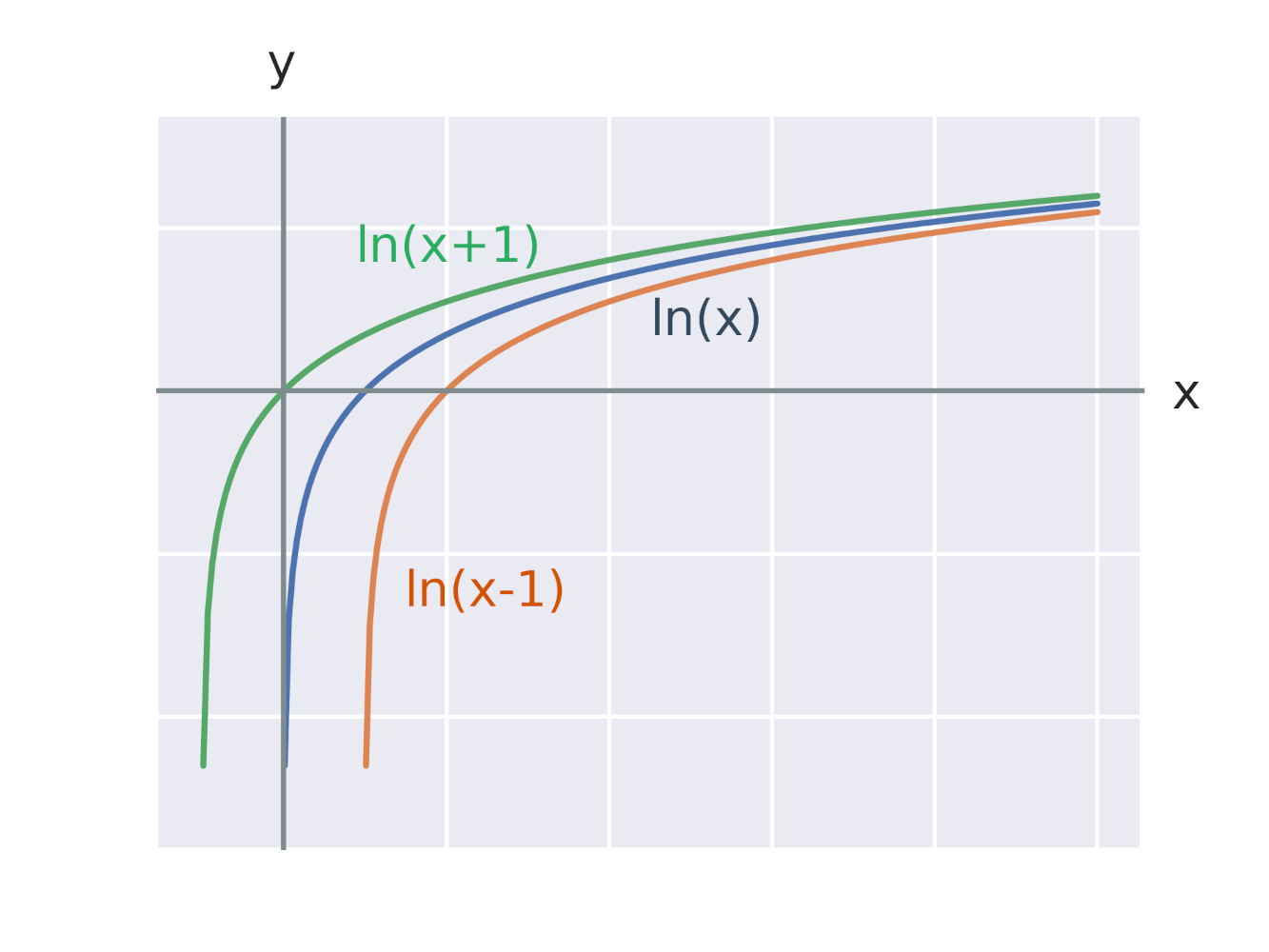
Efekt přičtení konstanty k argumentu logaritmické funkce
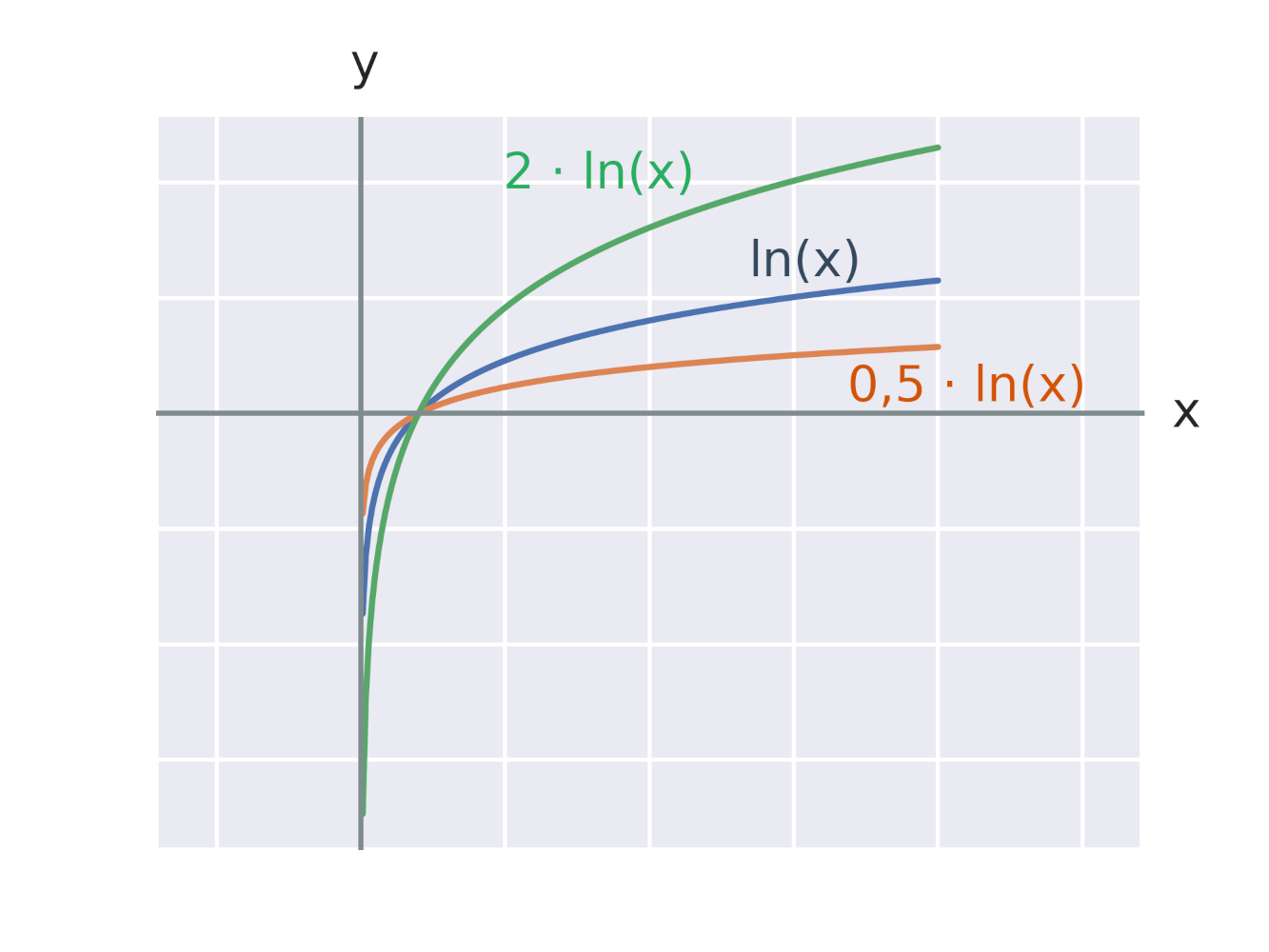
Efekt vynásobení logaritmické funkce konstantou
Efekt vynásobení argumentu logaritmické funkce konstantou