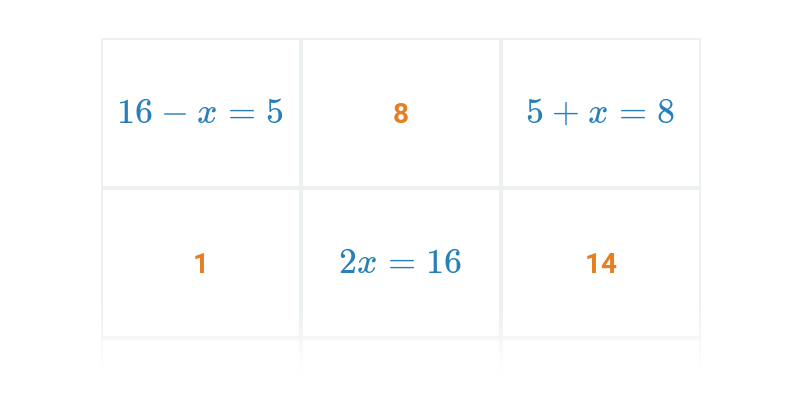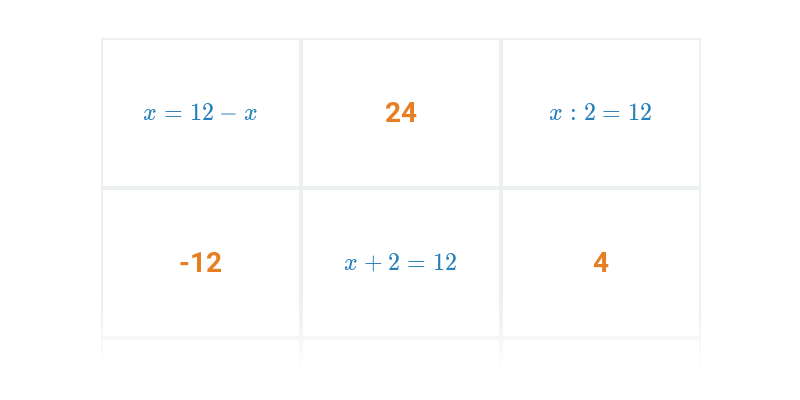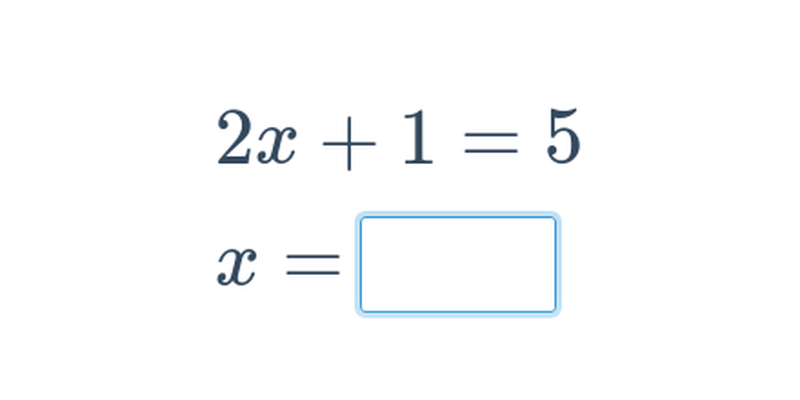Lineární funkce – 6. třída
FWJFunkce f je lineární, pokud ji lze vyjádřit ve tvaru f(x) = a\cdot x + b, kde a a b jsou konstanty. Grafem lineární funkce je přímka. Parametr a je směrnice (též nazývaná sklon), parametr b určuje její svislý posun (též nazývaný absolutní člen).
Příklady lineárních funkcí
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,}2
Aby byla funkce lineární, nemusí být nutně přímo zapsána ve tvaru f(x) = a\cdot x + b. Stačí, když jde na tento tvar upravit.
Příklady lineárních funkcí v jiném tvaru
- f(x) = 2-x můžeme přepsat jako f(x)= -1x + 2, což je lineární funkce se směrnicí −1 a absolutním členem 2.
- f(x) = 5(3-x) můžeme přepsat jako f(x)= -5x + 15, což je lineární funkce se směrnicí −5 a absolutním členem 15.
- f(x) = x^2 + 7 - x(x-1) vypadá na první pohled jako kvadratická funkce, ale můžeme ji upravit na f(x)= x + 7 (kvadratický člen se vyruší), takže jde o lineární funkci.
S lineárními funkcemi souvisí následující dílčí témata:
- Grafy lineárních funkcí – grafický význam směrnice a absolutního členu, zakreslení grafu podle funkčního předpisu, odvození funkčního předpisu podle grafu
- Vlastnosti lineární funkce – ujasnění obecných vlastností funkcí (např. definiční obor, obor hodnot, rostoucí a klesající funkce) v případě lineární funkce
- Základní rovnice s jednou neznámou – základní rovnice s jednou neznámou odpovídají rovnosti lineárních funkcí a můžeme je ztvárnit graficky pomocí přímek, které představují grafy těchto funkcí
Pexeso
Hledání dvojic, které k sobě patří.
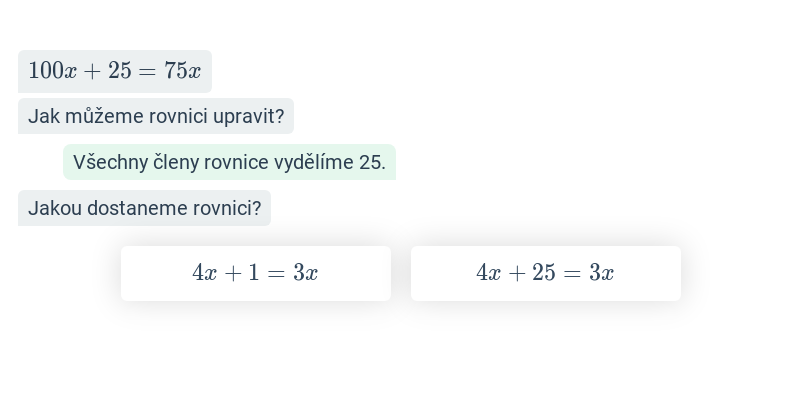
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.