Výpis souhrnů
Lineární funkce
Podtémata
Lineární funkce
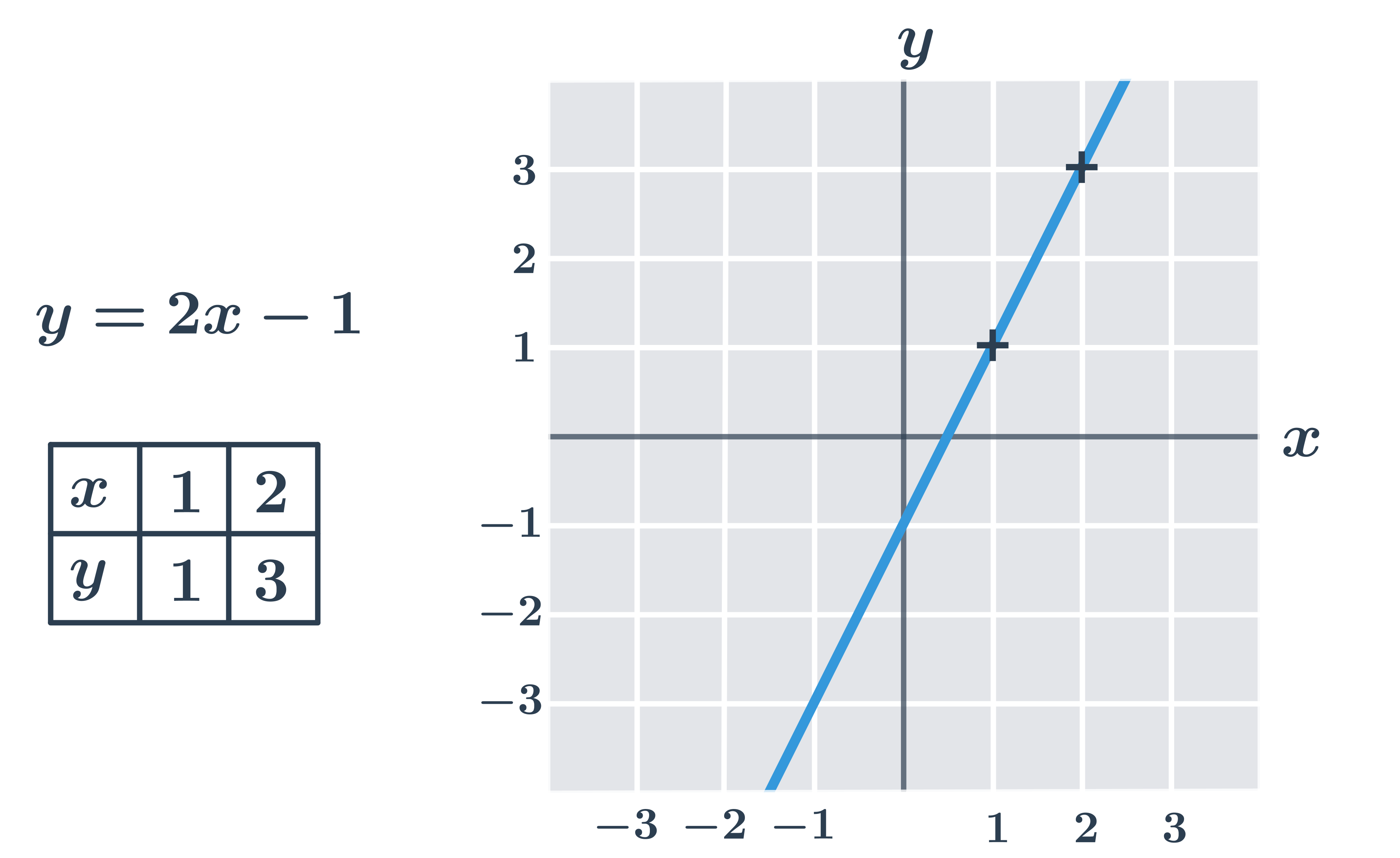
Funkce f je lineární, pokud ji lze vyjádřit ve tvaru f(x) = a\cdot x + b, kde a a b jsou konstanty. Grafem lineární funkce je přímka. Parametr a je směrnice (též nazývaná sklon), parametr b určuje její svislý posun (též nazývaný absolutní člen).
Příklady lineárních funkcí
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,}2
Aby byla funkce lineární, nemusí být nutně přímo zapsána ve tvaru f(x) = a\cdot x + b. Stačí, když jde na tento tvar upravit.
Příklady lineárních funkcí v jiném tvaru
- f(x) = 2-x můžeme přepsat jako f(x)= -1x + 2, což je lineární funkce se směrnicí −1 a absolutním členem 2.
- f(x) = 5(3-x) můžeme přepsat jako f(x)= -5x + 15, což je lineární funkce se směrnicí −5 a absolutním členem 15.
- f(x) = x^2 + 7 - x(x-1) vypadá na první pohled jako kvadratická funkce, ale můžeme ji upravit na f(x)= x + 7 (kvadratický člen se vyruší), takže jde o lineární funkci.
S lineárními funkcemi souvisí následující dílčí témata:
- Grafy lineárních funkcí – grafický význam směrnice a absolutního členu, zakreslení grafu podle funkčního předpisu, odvození funkčního předpisu podle grafu
- Vlastnosti lineární funkce – ujasnění obecných vlastností funkcí (např. definiční obor, obor hodnot, rostoucí a klesající funkce) v případě lineární funkce
- Základní rovnice s jednou neznámou – základní rovnice s jednou neznámou odpovídají rovnosti lineárních funkcí a můžeme je ztvárnit graficky pomocí přímek, které představují grafy těchto funkcí
Vlastnosti lineární funkce
Funkce f je lineární, pokud ji lze vyjádřit ve tvaru f(x) = a\cdot x + b, kde a a b jsou konstanty. Definiční obor lineární funkce je celá množina reálných čísel.
Speciálním případem lineární funkce je funkce konstantní. Tu dostáváme v případě, že a=0.
Pokud a \neq 0, pak pro lineární funkci platí:
- je prostá,
- není shora ani zdola omezená,
- nemá maximum ani minimum,
- není periodická,
- obor hodnot je množina reálných čísel.
Pro a \gt 0 je funkce f rostoucí, pro a \lt 0 je funkce f klesající.
Pro b=0 je funkce f lichá.
Grafem lineární funkce je přímka. Průsečík grafu s osou y je v bodě [0, b]. Průsečík grafu s osou x je v bodě [-\frac{b}{a}, 0].
NahoruZákladní rovnice s jednou neznámou
Nejjednodušší rovnice obsahují pouze lineární výrazy, tj. vyskytují se v nich pouze konstanty a násobky proměnné x. Rovnici upravujeme pomocí ekvivalentních úprav: přičítání a odčítání stejného výrazu k oběma stranám rovnice, úpravy výrazů na levé a pravé straně. Pomocí takových úprav ji převedeme do tvaru x = a, kde a je řešení.
Řešený příklad: 3x-1=2x+5
| Od obou stran rovnice odečteme 2x. | 3x-1-2x=2x+5-2x |
| x-1=5 | |
| K oběma stranám rovnice přičteme 1. | x-1+1=5+1 |
| x=6 | |
| Řešení rovnice je x=6. |
Řešený příklad: 2x-7 = 5-4x
| K oběma stranám rovnice přičteme 4x. | 2x - 7 + 4x = 5 - 4x + 4x |
| 6x - 7 = 5 | |
| K oběma stranám rovnice přičteme 7. | 6x - 7 + 7 = 5 + 7 |
| 6x = 12 | |
| Obě strany rovnice vydělíme číslem 6. | 6x : 6 = 12 : 6 |
| x = 2 | |
| Řešení rovnice je x=2. |
Počet řešení
U základních lineárních rovnic mohou nastat tři případy:
- Rovnice nemá žádné řešení, např. x+2=x+3.
- Rovnice má nekonečně mnoho řešení, např. u rovnice x+1+x = 2x+1 je řešením rovnice je libovolné číslo.
- Rovnice má právě jedno řešení, např. výše uvedená rovnice 2x-7 = 5-4x má jediné řešení x=2.
Časté chyby
Mezi časté chyby při řešení rovnic patří:
- provedení úpravy (přičtení čísla, vydělení čísel) pouze na jedné straně rovnice,
- chybné zkombinování konstant a výrazů s proměnnou x, např. úprava 3x + 2 na 5x,
- špatné znaménko u výrazu při převádění z jedné strany rovnice na druhou.
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Komiks pro zpestření

Grafy lineárních funkcí
Lineární funkci můžeme vždy zapsat ve tvaru f(x)= a \cdot x + b, kde a a b jsou konstanty. Číslo a je směrnice (též nazývaná sklon), konstanta b je absolutní člen. Grafem lineární funkce je přímka, kterou snadno sestrojíme pomocí dvou bodů.
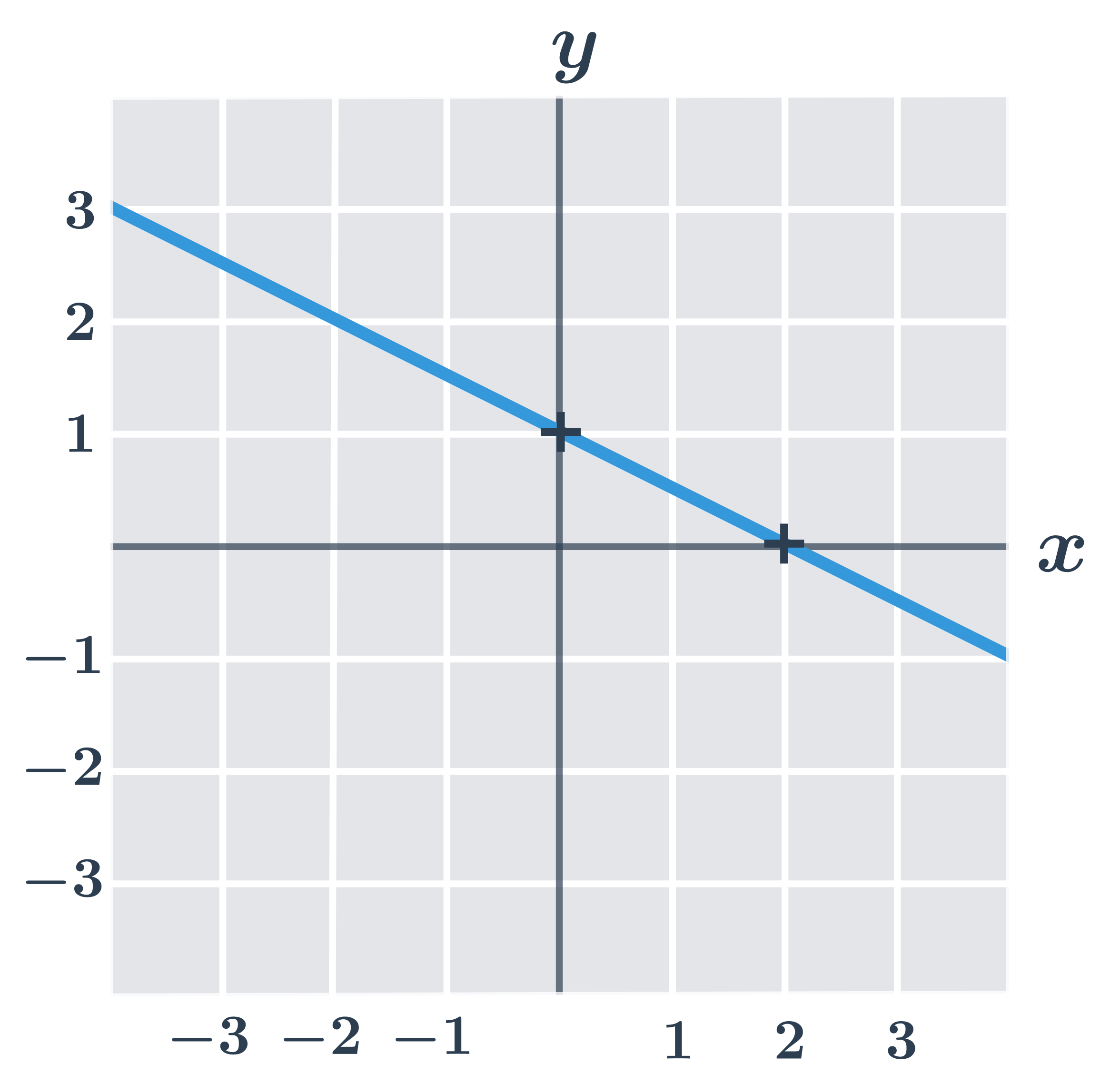
Příklad: graf funkce y=-0{,}5x+1.
- Zvolíme si dvě libovolné hodnoty proměnné x. Vhodnou volbou je x=0, tím zároveň určíme i průsečík s osou y.
- Pro x=0 dopočítáme hodnotu y, tedy: y=-0{,}5\cdot 0+2=0+1=1
- Dále zvolíme například x=2 a dosadíme: y=-0{,}5\cdot 2+1=-1+1=0
- Graf funkce y=-0{,}5x+1 pak prochází body [0;1] a [2;0].
Přímku, která je grafem funkce f(x)=a\cdot x+b můžeme sestrojit také pomocí konstant a a b, přičemž platí:
- Absolutní člen b udává „svislý posun“. Je to průsečík přímky s osou y. V uvedených příkladech je vyznačen oranžovou barvou.
- Směrnice a udává sklon přímky, což můžeme vyjádřit jako „o kolik jednotek na ose y se po dané přímce posuneme, když se posuneme o jednu jednotku na ose x“. V uvedených příkladech je směrnice vyznačena žlutou barvou.
Důležitá jsou znamínka (naznačená v obrázcích šipkami). Kladný absolutní člen znamená posun nahoru, záporný absolutní člen znamená posun dolů. Kladná směrnice znamená stoupající přímku, záporná směrnice znamená klesající přímku.
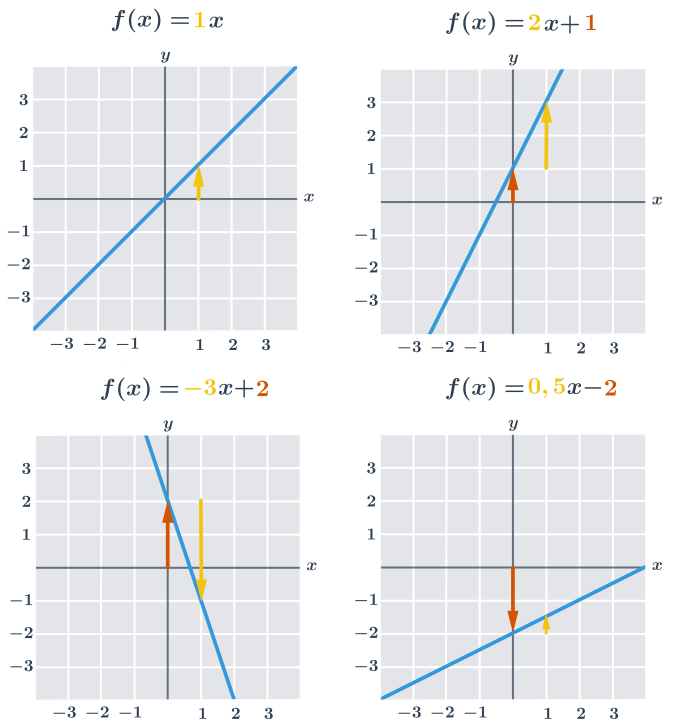
Pracovní list
Kromě interaktivního procvičování je k dispozici také pracovní list pro tisk:
Nahoru
