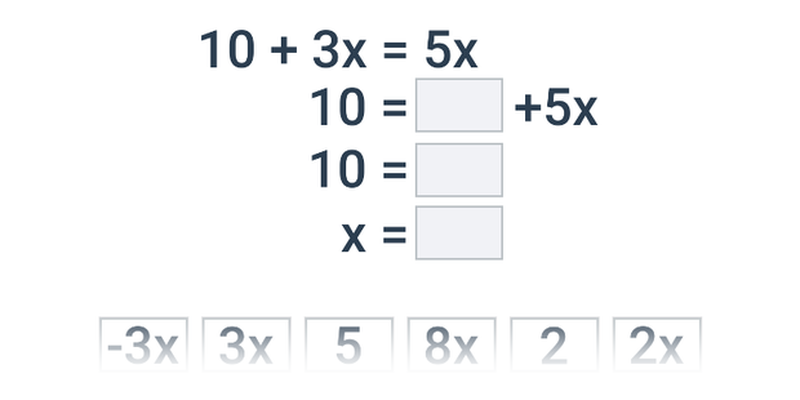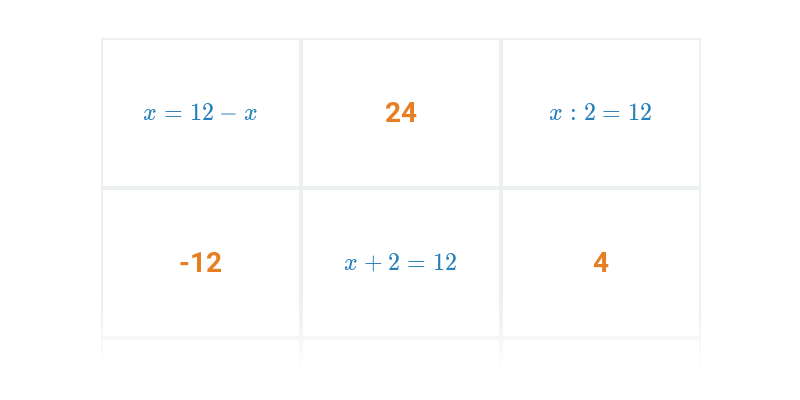Funkce – 8. třída
F21Pro snadnější pochopení pojmu funkce uvedeme příklad: Děti ve třídě mají napsat měsíc svého narození. Každému dítěti je tak daným pravidlem přiřazen měsíc.
Funkce je zde předpis, který každému x (dítě) z nějaké množiny D (všechny děti ze třídy) přiřazuje právě jednu funkční hodnotu y (měsíc, ve kterém se dané dítě narodilo). Daný předpis je funkce, protože každému x je přiřazena právě jedna hodnota y – každé dítě má právě jeden měsíc, ve kterém se narodilo.
Přitom ale nemusí každému y odpovídat právě jedna hodnota x. Dva různé prvky z množiny D mohou mít stejnou funkční hodnotu – dvě děti mohou mít stejný měsíc narození.
Příklad: souvislost s informatikou
Funkci můžeme chápat také jako vztah, který přiřazuje každému vstupu právě jeden výstup. Jako intuitivní příklad funkce může posloužit „obarvovač na modro“ – na vstup bere kostku, na výstup dává kostku obarvenou na modro.
Takové pojetí funkcí najdeme v informatice, kde funkce pomáhají definovat různé operace a jsou počítány pomocí algoritmů.
V matematice obvykle pracujeme s funkcemi nad množinami čísel, kde vztah mezi x a y popisuje matematický výraz, píšeme ve tvaru y=f(x). Definiční obor je množina všech hodnot x, které uvažujeme (např. množina všech x pro která má výraz f(x) smysl), označujeme D(f). Obor hodnot je množina všech funkčních hodnot y, označujeme H(f).
Mezi základní typy funkcí, se kterými se v matematice setkáme, patří:
| Typ | Příklad |
|---|---|
| Lineární funkce | f(x) = 3x + 1 |
| Lineární lomené funkce | f(x) = \frac{2x -4}{x+3} |
| Kvadratické funkce | f(x) = x^2 - 4x + 3 |
| Goniometrické funkce | f(x) = \sin x |
| Mocninné funkce | f(x) = x^3, f(x) = \sqrt{x} |
| Exponenciální a logaritmické funkce | f(x) = 2^x, f(x) = \log x |
Téma typy a vlastnosti funkcí se zabývá podrobnějším rozlišováním mezi jednotlivými typy funkcí a jejich vlastnostmi, jako jsou periodičnost či omezenost.
Funkce pro lepší pochopení často zakreslujeme graficky, což nám umožňuje lépe vidět vztah mezi x a f(x). Téma grafy funkcí zastřešuje procvičování v tomto ztvárnění.
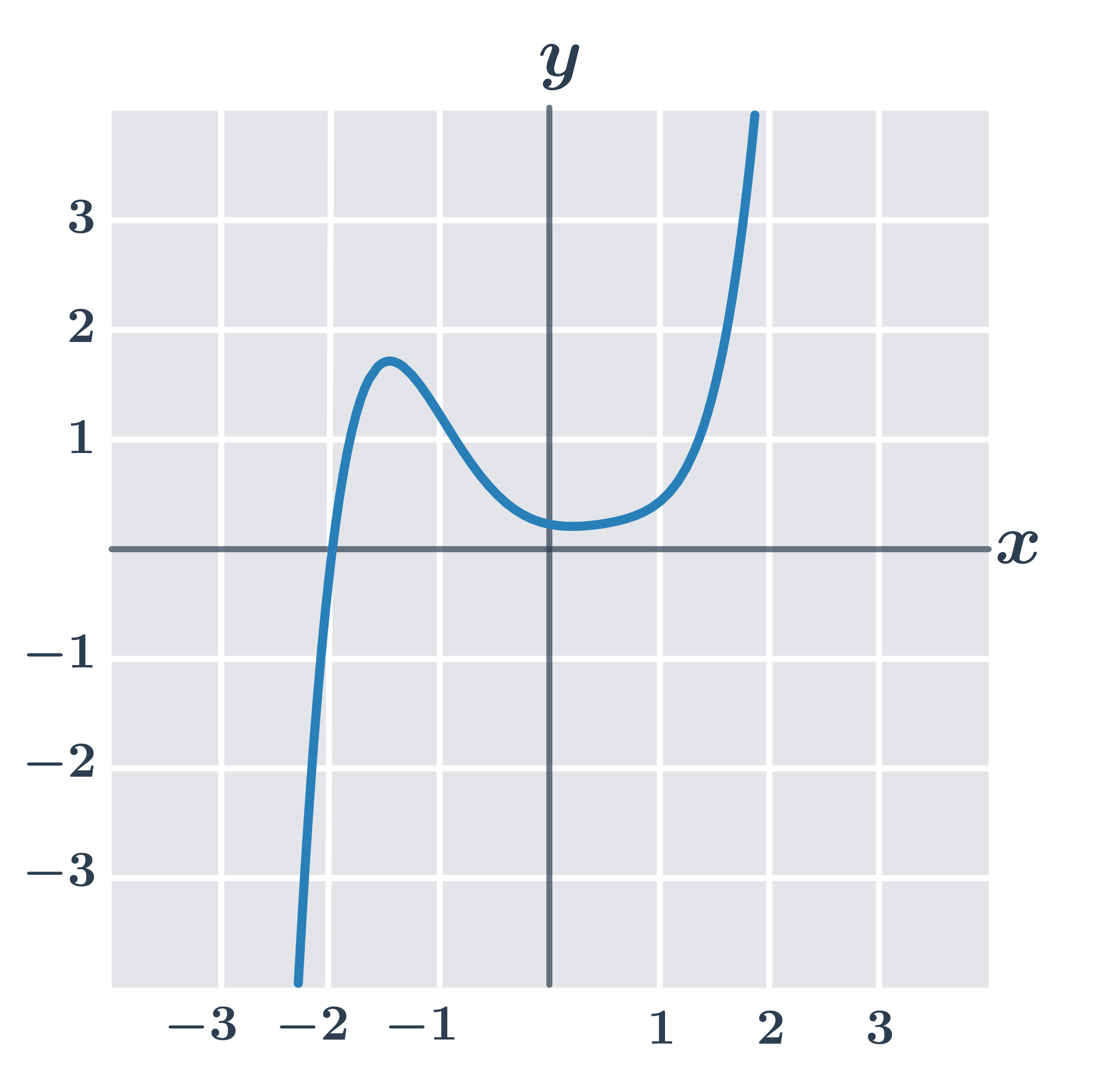
Příklad: graf funkce
Každému číslu x v definičním oboru funkce odpovídá právě jedna funkční hodnota y=f(x).
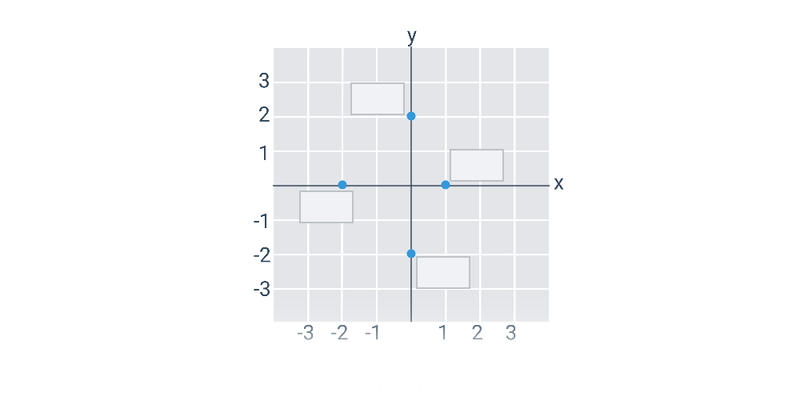
Příklad: toto není graf funkce
Na následujícím obrázku není graf funkce:
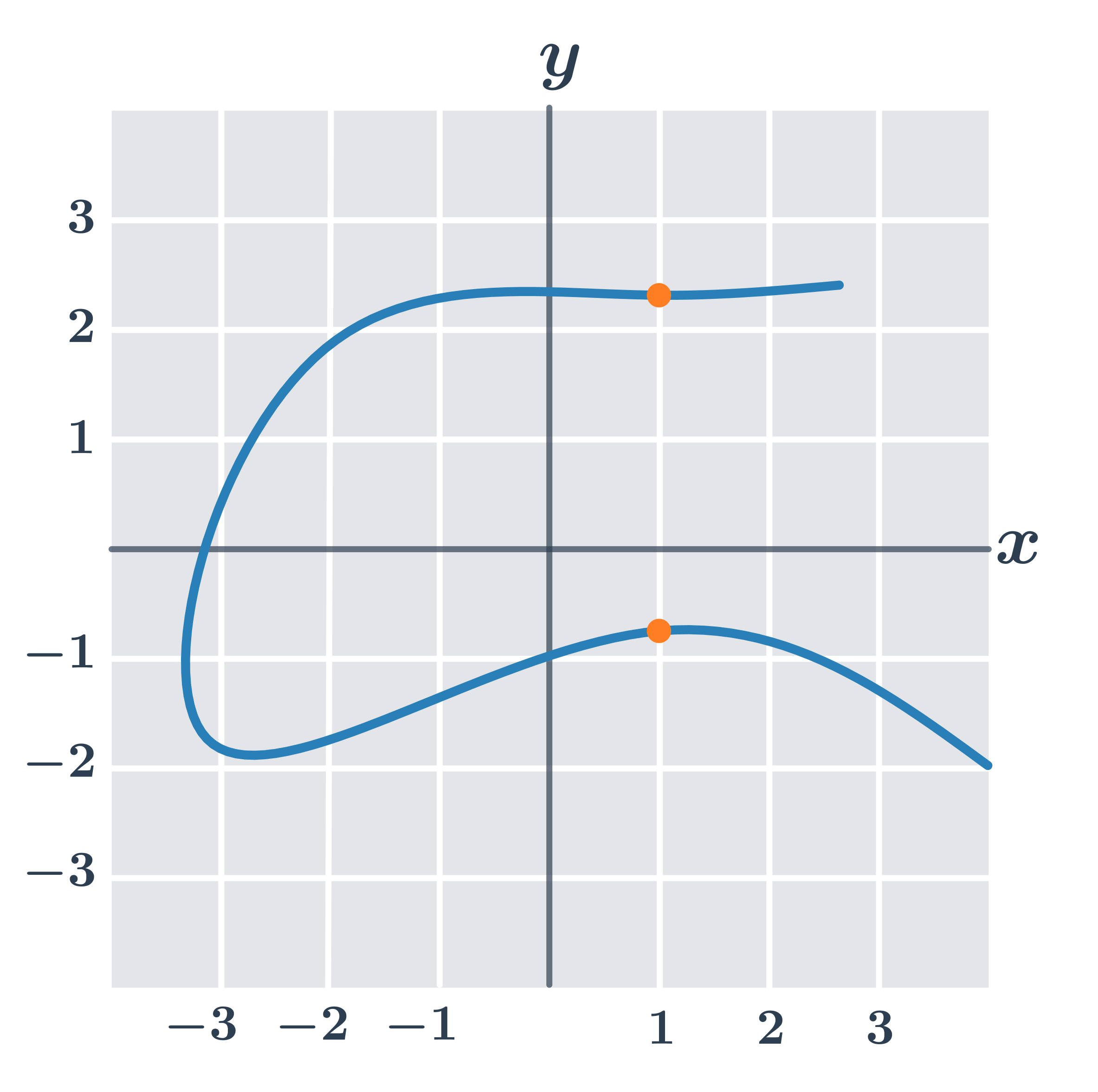
Například pro x=1 bychom neměli jednoznačně danou hodnotu y=f(x) (máme dva oranžově zvýrazněné body s x=1, ale dvěma různými souřadnicemi y).
Přesouvání
Přesouvání kartiček na správné místo. Jednoduché ovládání, zajímavé a neotřelé úlohy.
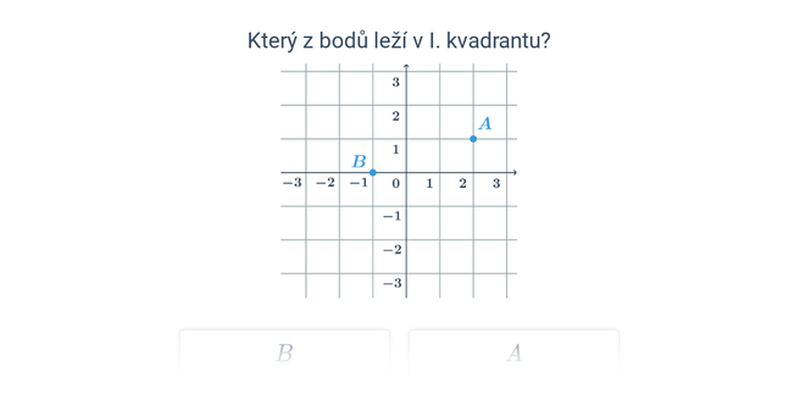
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Pexeso
Hledání dvojic, které k sobě patří.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.