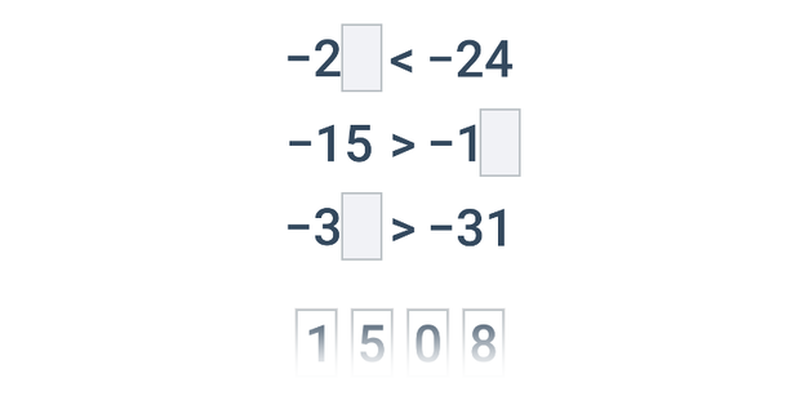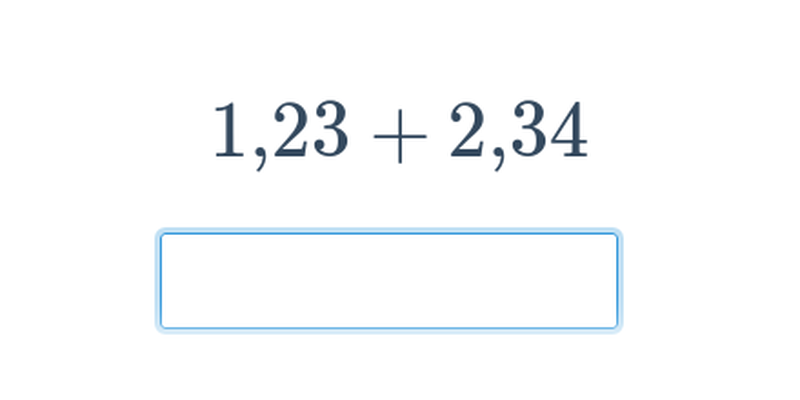Příprava na přijímací zkoušky na osmiletá gymnázia, matematika
Zpět na rozcestník k přípravě na přijímací zkoušky
Procvičování v Umíme doporučujeme kombinovat s řešením testových zadání z předchozích let. Zadání v Umíme jsou vhodná především pro přípravu a učení, testová zadání pak pro seznámení s formální podobou testů.
Uvedený výběr témat k procvičování pokrývá všechny oblasti uvedené v oficiální specifikaci požadavků k jednotné přijímací zkoušce. Systém Umíme nabízí velmi bohaté možnosti procvičování a uvedený výběr zdaleka nezmiňuje všechny dostupné možnosti. Tato stránka uvádí pouze výběr cvičení, která jsou nejvíce užitečná pro přípravu na přijímací zkoušky. Při výběru bylo zohledněno mimo jiné i to, jaké úlohy byly používané v přijímacích zkouškách v minulých letech.
Pokud budete potřebovat k některému tématu důkladnější procvičení, můžete najít další cvičení skrze vyhledávání názvu tématu. Systém vám bude také automaticky doporučovat další návaznosti. Lze také použít kompletní výpis témat pro 5. ročník.
Následující tabulka uvádí časový odhad při pravidelném procvičování 15 minut denně.
| Varianta procvičování | Rozsah výpisu | Komentář | Časový rozsah procvičování |
|---|---|---|---|
| Základní | 56 sad | Základní procvičování, které má smysl si určitě projít pro osvěžení všech témat, která se ve zkouškách vyskytují. | měsíc |
| S rozcvičením | 95 sad | Základní procvičování rozšířené o přípravná cvičení zaměřená na témata, která často dělají problémy. | 2–3 měsíce |
| S bonusem | 83 sad | Základní procvičení rozšířené o náročnější cvičení, která pomohou s průpravou i na náročnější příklady ze zkoušek. | 2–3 měsíce |
| Důkladné | 122 sad | Kombinace předchozího, tj. od přípravných cvičení až po bonusy. | 3 a více měsíců |
- Čísla, zaokrouhlování
- Násobení, dělení
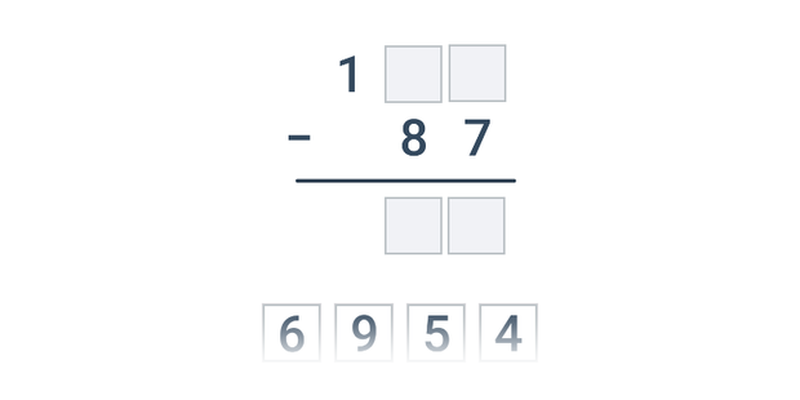
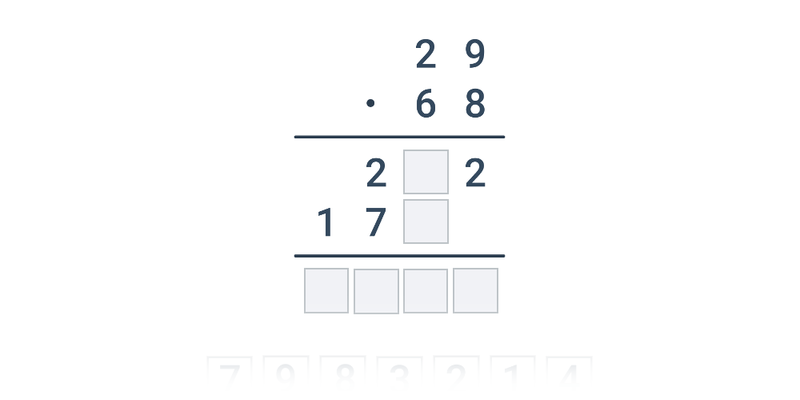
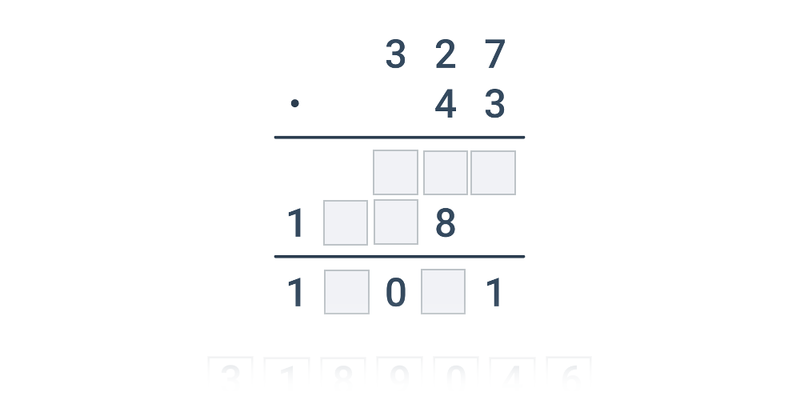
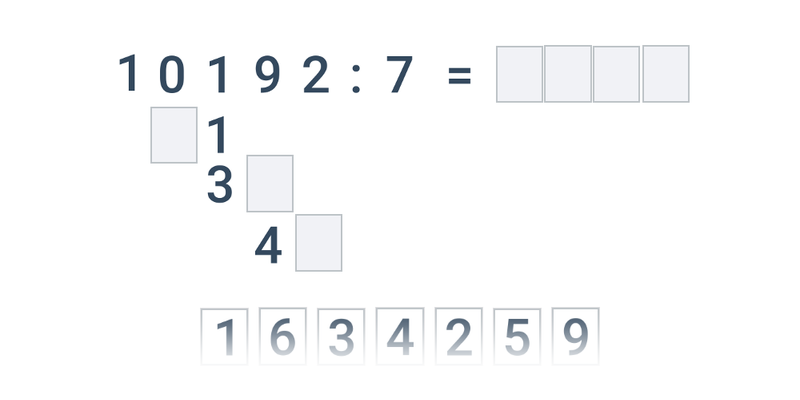
- Počítání pod sebou
- Pořadí operací, závorky
- Počítání a logické myšlení
- Zlomky a desetinná čísla
- Převody jednotek
- Obsah a obvod
- Osová souměrnost
- Konstrukční úlohy
- Prostorová představivost
1. Čísla, zaokrouhlování
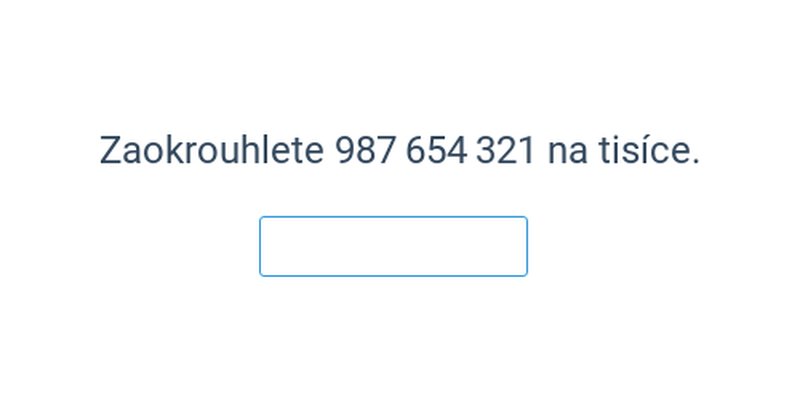
Základem k matematice je dobré porozumění číslům. Mezi partie, které stojí pro zkoušky za procvičení, patří především záporná čísla, porovnávání čísel a zaokrouhlování.
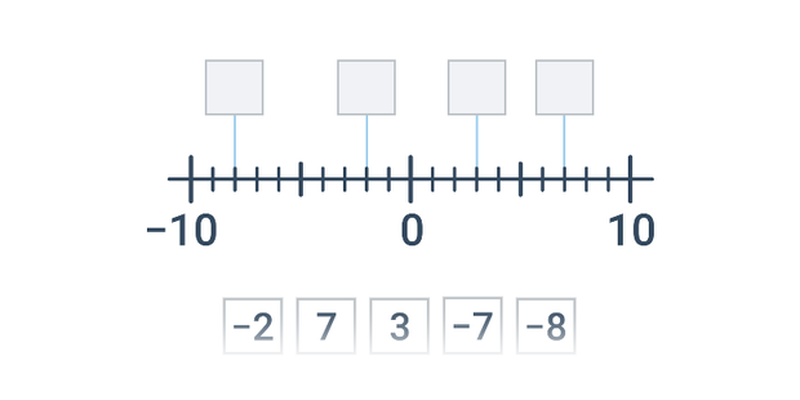
| Přesouvání | Číselná osa: kladná a záporná čísla | ||
| Přesouvání | Porovnávání celých čísel | ||
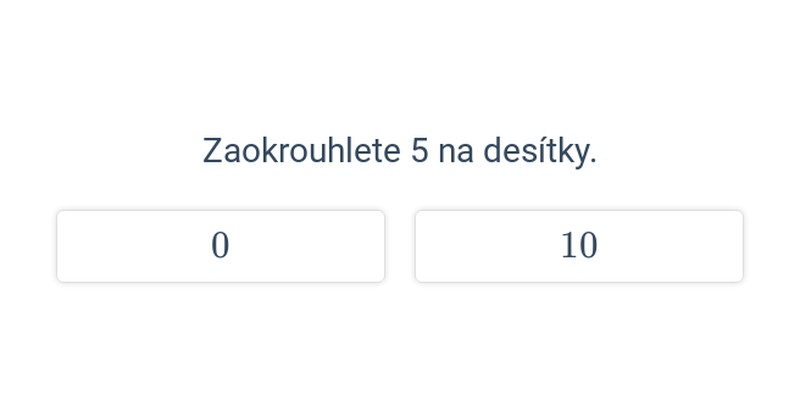
| Rozhodovačka | Zaokrouhlování na desítky a stovky | ||
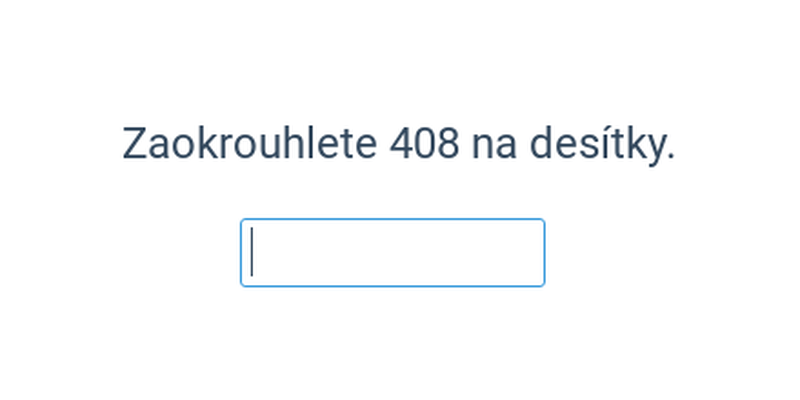
| Psaná odpověď | Zaokrouhlování na desítky a stovky | ||
| Psaná odpověď | Zaokrouhlování velkých čísel | ||
| Rozhodovačka | Čísla: mix |
2. Násobení, dělení
Důkladné pamětné zvládnutí násobení a dělení tvoří klíčový základ. Sice není přímo v samostatných zkouškových otázkách, ale pro zvládnutí matematických příkladů je důležité se nezasekávat na základních počtech (to platí nejen pro přijímačky).
| Slovní úlohy | Malá násobilka | ||
| Psaná odpověď | Násobení víceciferné | ||
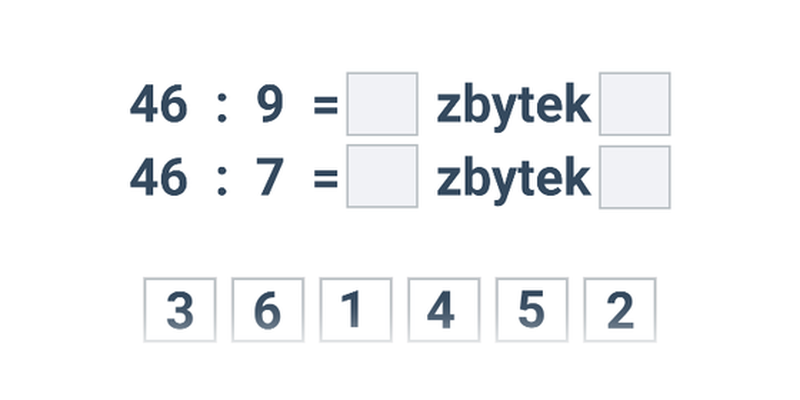
| Slovní úlohy | Dělení se zbytkem | ||
| Přesouvání | Dělení se zbytkem | ||
| Přesouvání | Dělení se zbytkem |
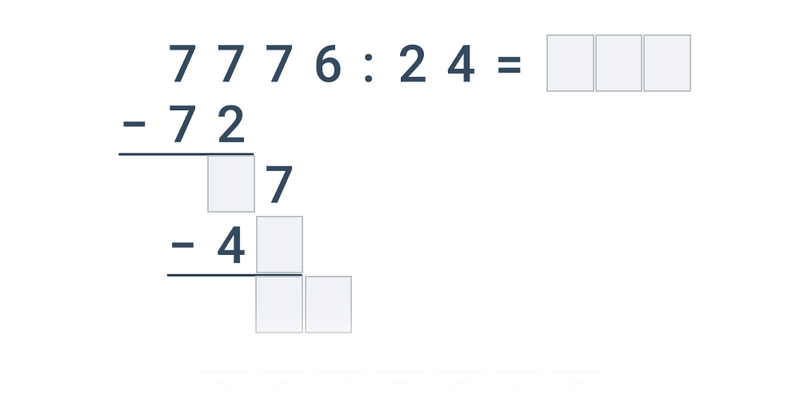
3. Počítání pod sebou
Další důležitá průprava pro složitější příklady.
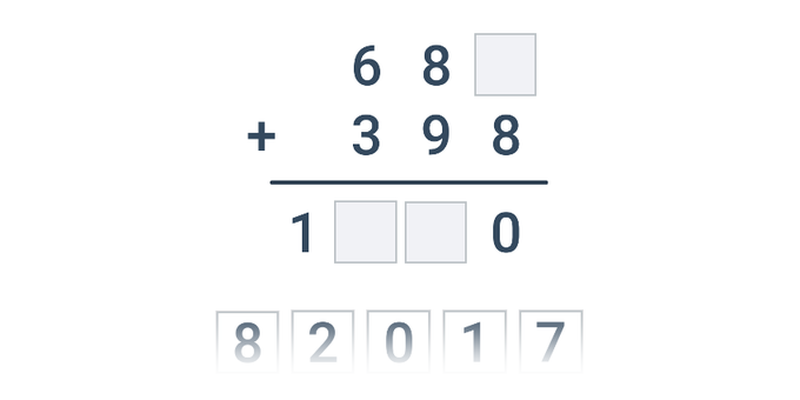
| Přesouvání | Sčítání pod sebou | ||
| Psaná odpověď | Sčítání pod sebou | ||
| Přesouvání | Odčítání pod sebou | ||
| Psaná odpověď | Odčítání pod sebou | ||
| Přesouvání | Písemné násobení pod sebou | ||
| Přesouvání | Písemné násobení pod sebou | ||
| Přesouvání | Písemné dělení jednociferným číslem | ||
| Přesouvání | Písemné dělení dvouciferným číslem |
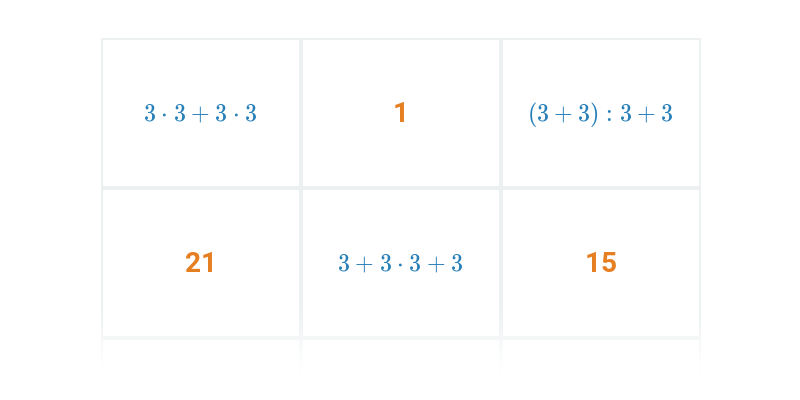
4. Pořadí operací, závorky
Příklady tohoto typu již bývají přímo součástí zkoušek.
| Psaná odpověď | Pořadí operací, závorky | ||
| Psaná odpověď | Pořadí operací, závorky | ||
| Pexeso | Pořadí operací, závorky | ||
| Pexeso | Pořadí operací, závorky |
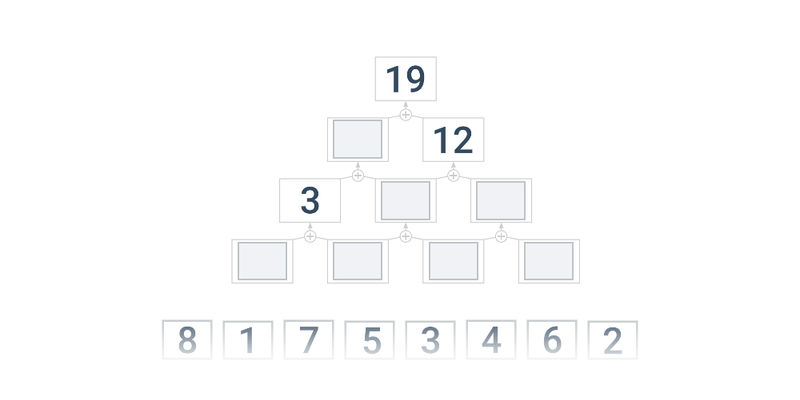
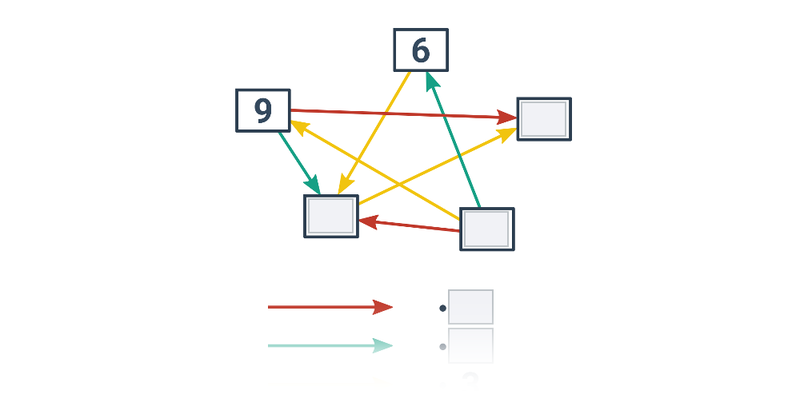
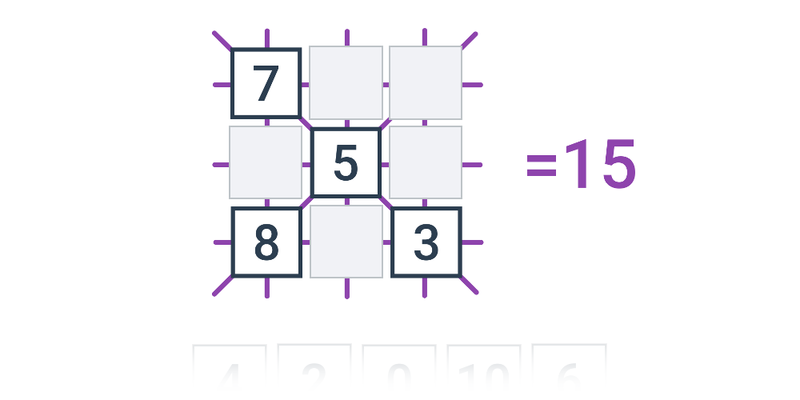
5. Počítání a logické myšlení
Na zkouškách bývají často i úlohy, na které nestačí jen hladké zvládnutí základních počtů, ale vyžadující i zamyšlení nad vhodným postupem. Následující netradiční úlohy na to poskytují dobrý trénink.
| Přesouvání | Sčítací pyramidy | ||
| Přesouvání | Pavučiny s násobením | ||
| Přesouvání | Doplň operaci | ||
| Přesouvání | Doplň operaci | ||
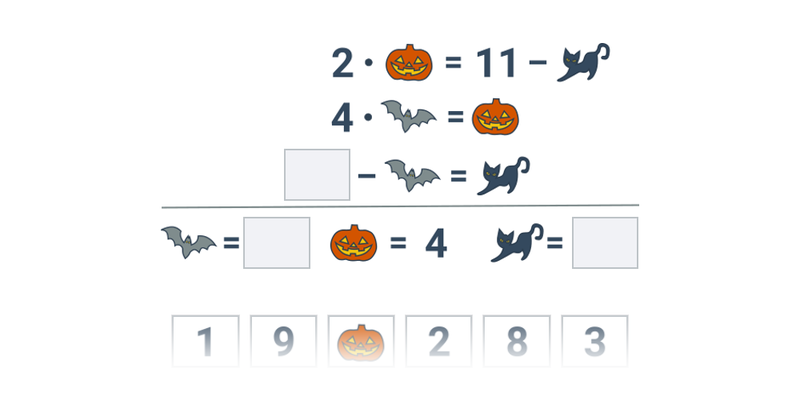
| Přesouvání | Obrázkové rovnice | ||
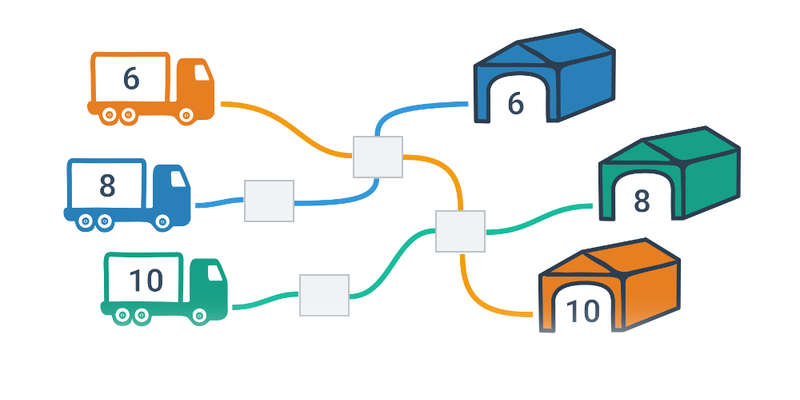
| Přesouvání | Náklaďáky | ||
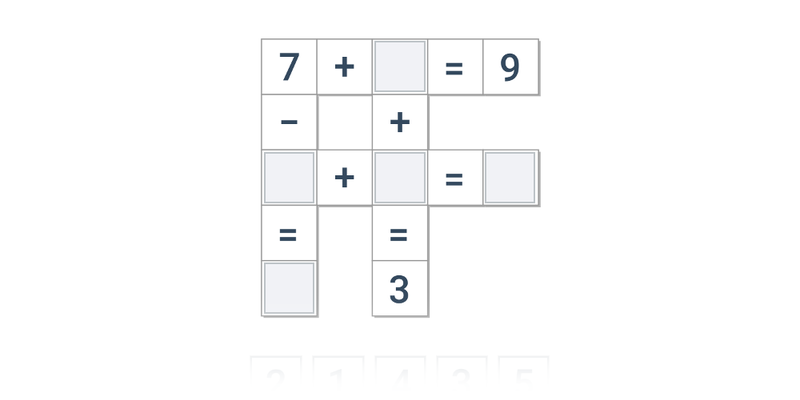
| Přesouvání | Číselné křížovky | ||
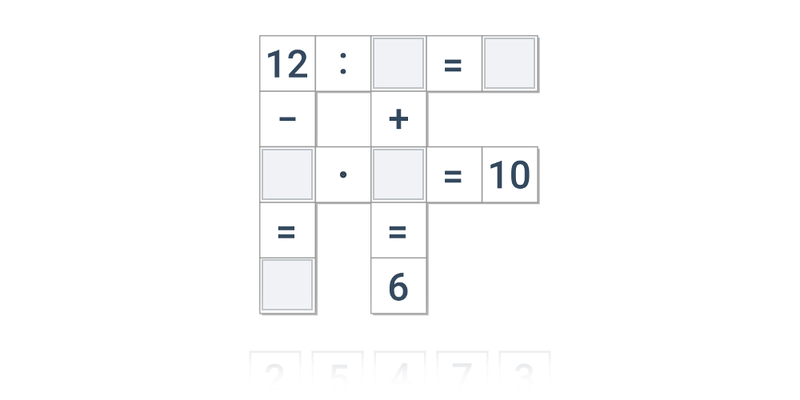
| Přesouvání | Číselné křížovky | ||
| Přesouvání | Magické čtverce |
6. Zlomky a desetinná čísla
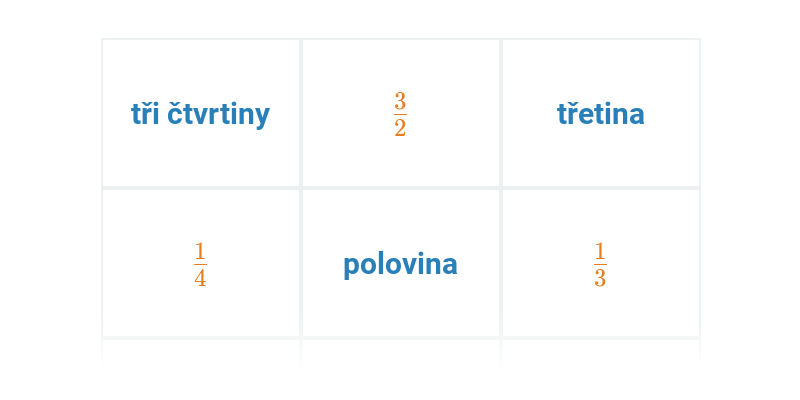
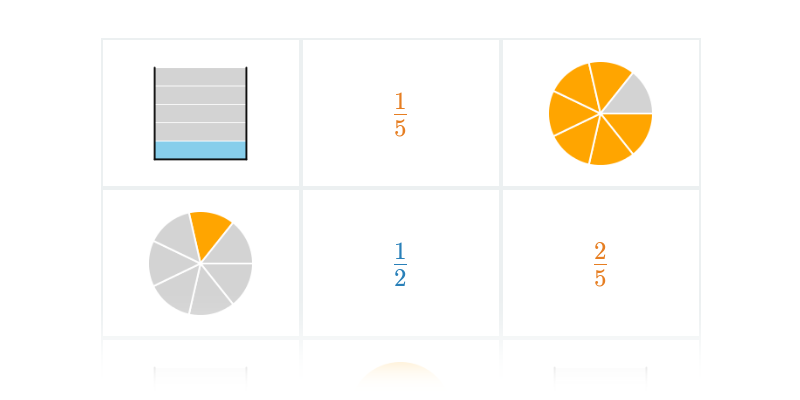
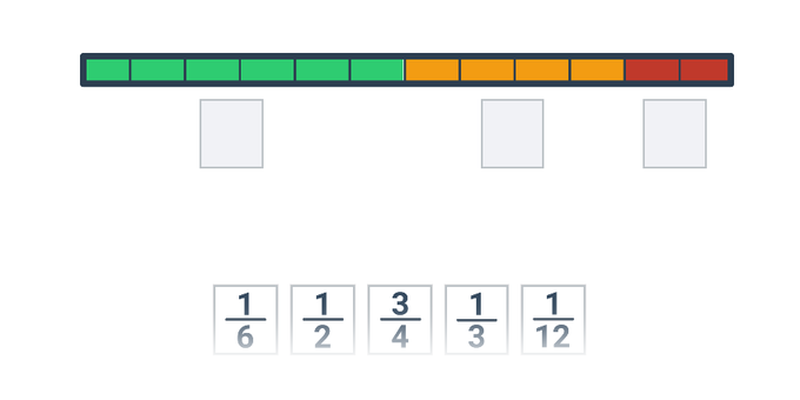
Použití zlomků a desetinných čísel se může vyskytovat v samostatných úlohách i jako součást větších příkladů (např. slovních úloh).
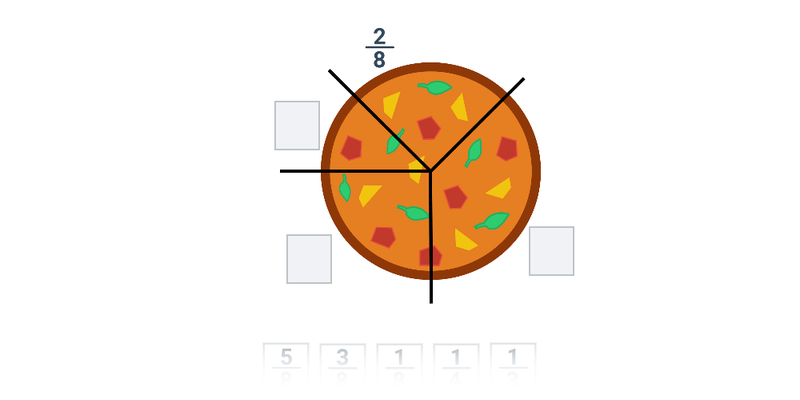
| Pexeso | Zlomky slovně | ||
| Pexeso | Poznávání zlomků | ||
| Psaná odpověď | Poznávání zlomků | ||
| Rozhodovačka | Výpočty se zlomky: mix | ||
| Přesouvání | Poznávání zlomků | ||
| Přesouvání | Poznávání zlomků | ||
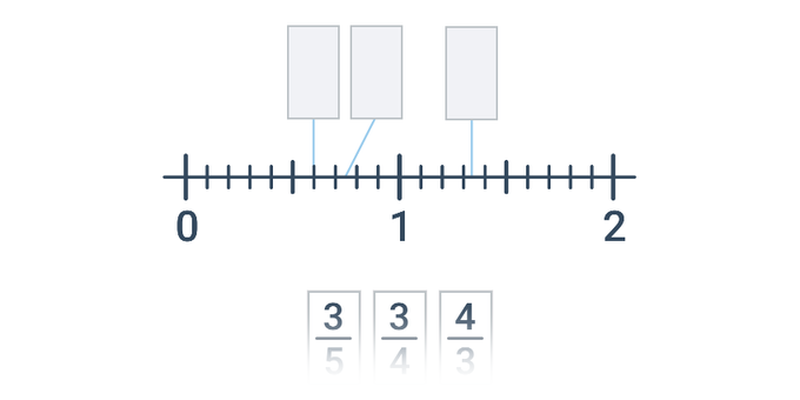
| Přesouvání | Zlomky na číselné ose | ||
| Slovní úlohy | Výpočty se zlomky: mix | ||
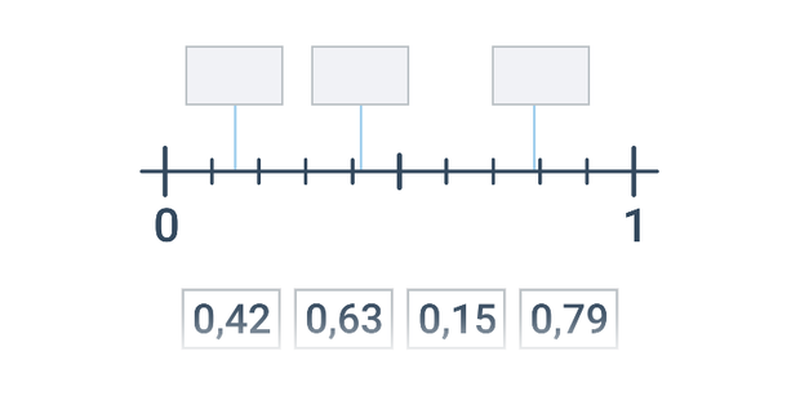
| Přesouvání | Desetinná čísla na číselné ose | ||
| Psaná odpověď | Sčítání a odčítání desetinných čísel | ||
| Slovní úlohy | Výpočty s desetinnými čísly: mix |
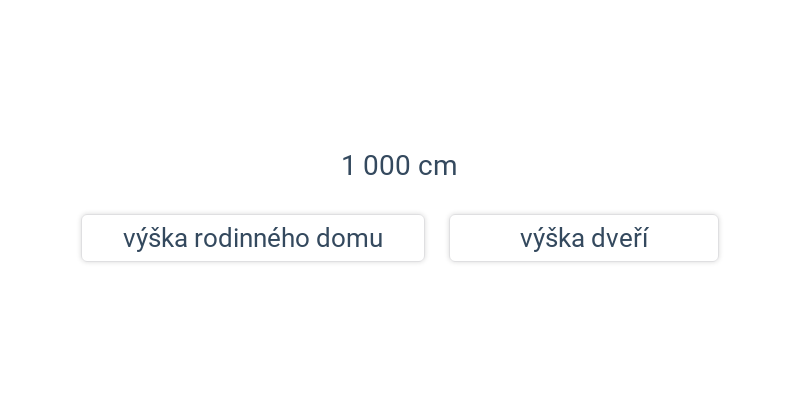
7. Převody jednotek
Převody jednotek jsou další typickou součástí zkoušek, jak samostatně tak v rámci větších příkladů.
| Přesouvání | Jednotky délky | ||
| Psaná odpověď | Jednotky délky | ||
| Krok po kroku | Jednotky délky | ||
| Pexeso | Jednotky hmotnosti | ||
| Psaná odpověď | Jednotky hmotnosti | ||
| Psaná odpověď | Jednotky hmotnosti | ||
| Krok po kroku | Jednotky hmotnosti | ||
| Psaná odpověď | Jednotky času | ||
| Slovní úlohy | Slovní úlohy s časem | ||
| Rozhodovačka | Jednotky: mix |
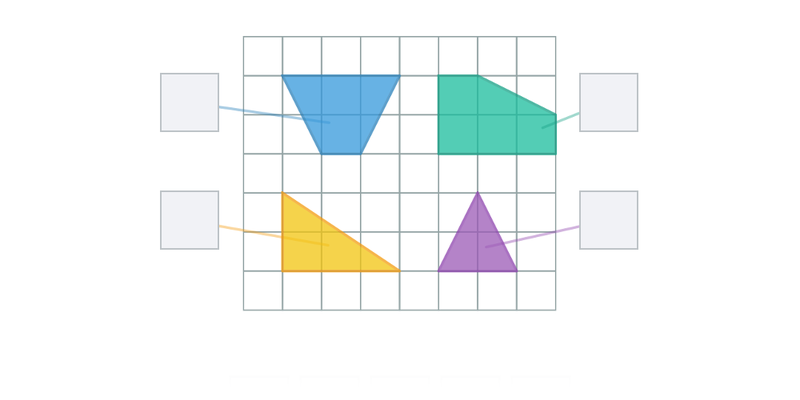
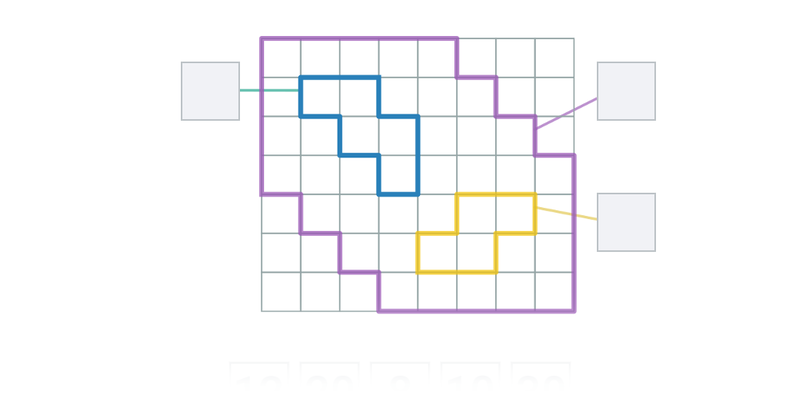
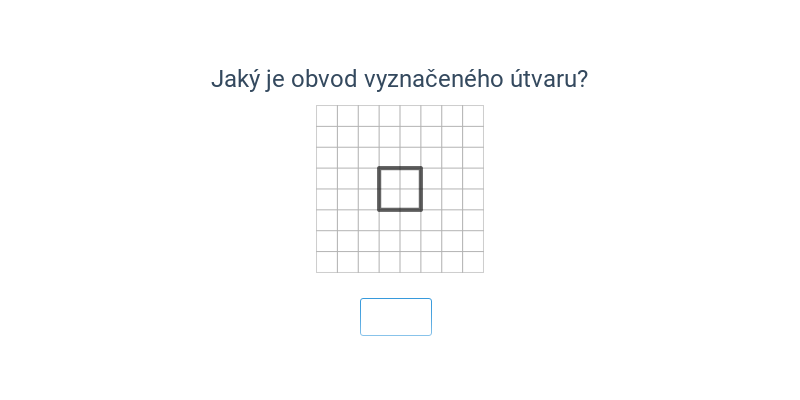
8. Obsah a obvod
Obsah a obvod bývá často na zkouškách ve formě příkladů „na mřížce“, které se soustředí na pochopení hlavního principu, představivost a pečlivost (nikoliv na vzorečky). Současně má určitě smysl procvičovat i obvod a obsah elementárních útvarů (trojúhelník, čtverec, obdélník), které s příklady na mřížce úzce souvisí.
| Psaná odpověď | Obvod čtverce a obdélníku (na mřížce) | ||
| Psaná odpověď | Obvod na mřížce: čtverec, obdélník, trojúhelník | ||
| Přesouvání | Obsah na mřížce: mix | ||
| Psaná odpověď | Obsah, obvod: mix | ||
| Přesouvání | Obvod na mřížce: mix | ||
| Psaná odpověď | Obvod na mřížce: mix | ||
| Mřížkovaná | Obvod | Úlohy | |
| Mřížkovaná | Obsah | Úlohy |
9. Osová souměrnost
Základní princip osové souměrnosti je sice intuitivní („zrcadlo“), ale její důkladné zvládnutí rozhodně není snadné. Zejména v případech, kdy je osa nakloněná, se může člověk snadno splést...
| Rozhodovačka | Osová souměrnost | ||
| Přesouvání | Osová souměrnost | ||
| Přesouvání | Osová souměrnost | ||
| Mřížkovaná | Osová souměrnost | Úlohy | |
| Mřížkovaná | Osová souměrnost těžší | Úlohy |
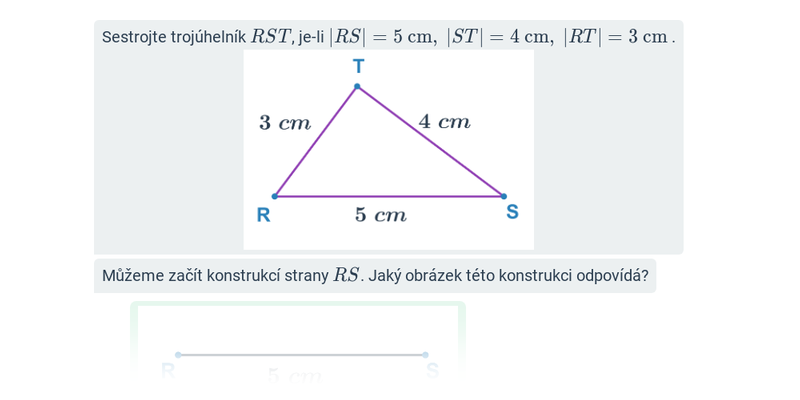
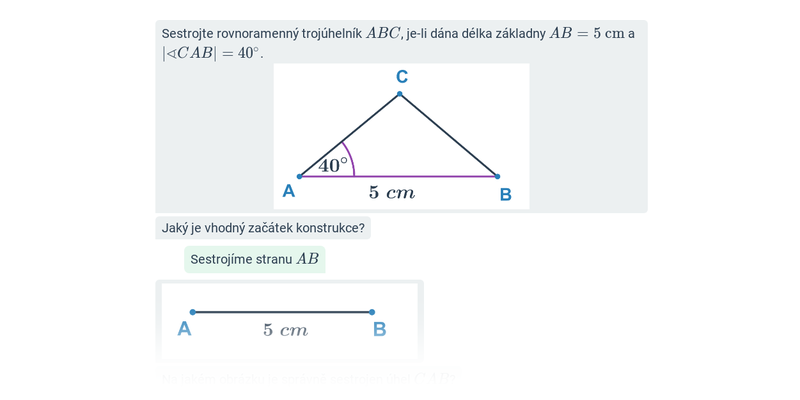
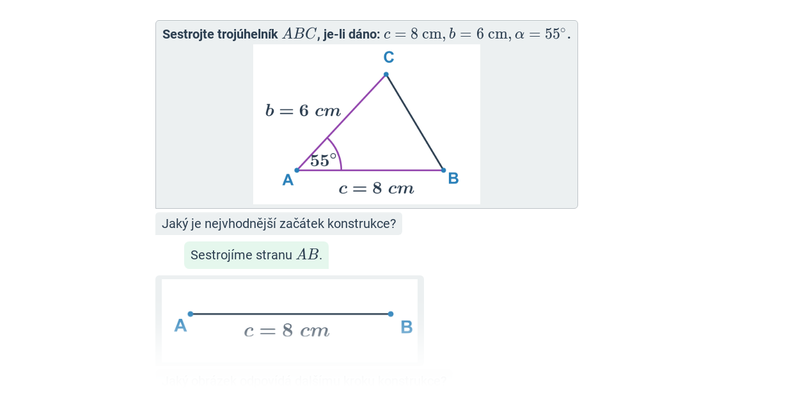
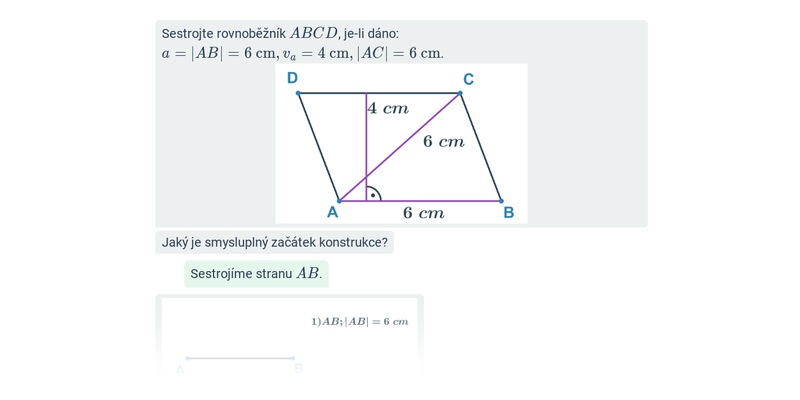
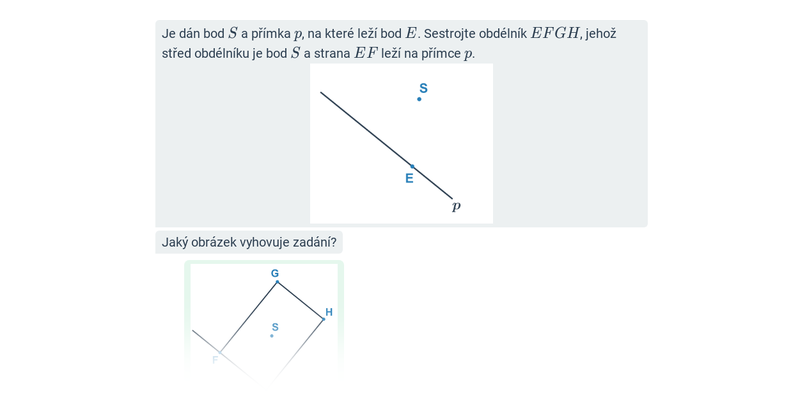
10. Konstrukční úlohy
Před samotným rýsováním se ale vyplatí projít si pojmy a postupy ve cvičeních na počítači. Konstrukční úlohy je pak potřeba trénovat i na papíře, k tomu lze využít například tyto pracovní listy: Konstrukční úlohy: známé délky stran (+ řešení), Konstrukce rovnostraných a rovnoramenných trojúhelníků (+ řešení).
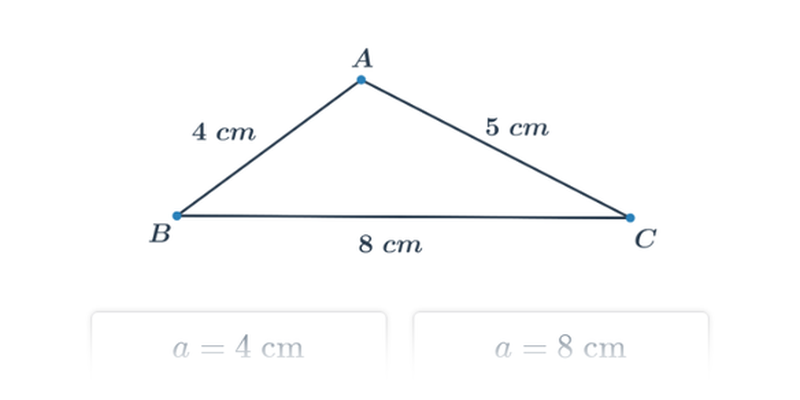
| Rozhodovačka | Konstrukce trojúhelníků: známé délky stran | ||
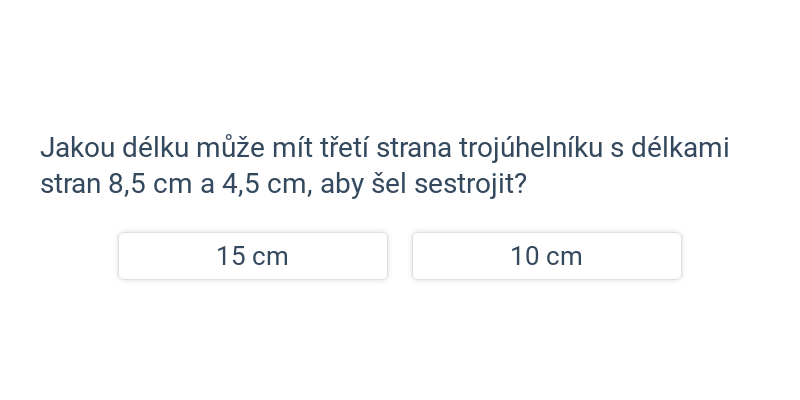
| Rozhodovačka | Trojúhelníková nerovnost | ||
| Krok po kroku | Konstrukce trojúhelníků: známé délky stran | ||
| Krok po kroku | Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky | ||
| Krok po kroku | Konstrukce trojúhelníků: mix | ||
| Krok po kroku | Konstrukce čtyřúhelníků: mix | ||
| Krok po kroku | Konstrukční úlohy průřezově | ||
| Mřížkovaná | Kolmice | Úlohy | |
| Mřížkovaná | Trojúhelníky | Úlohy |
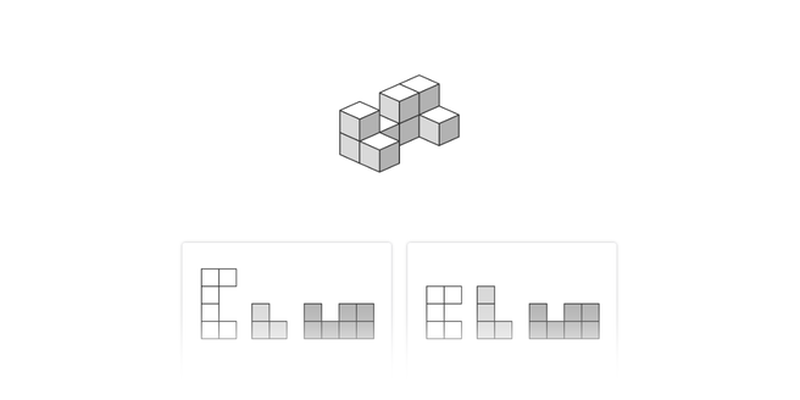
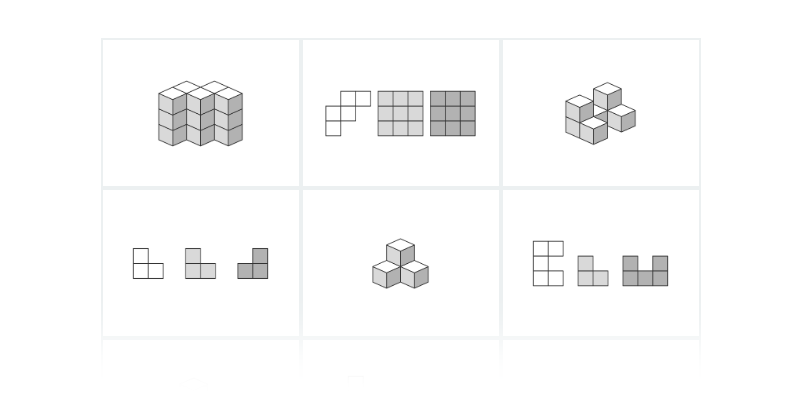
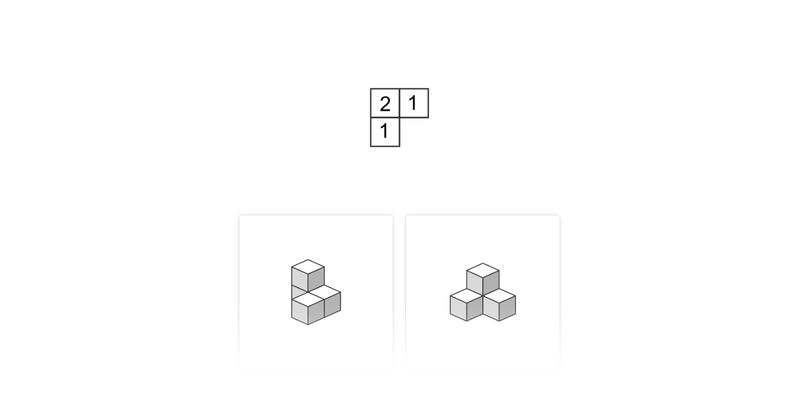
11. Prostorová představivost
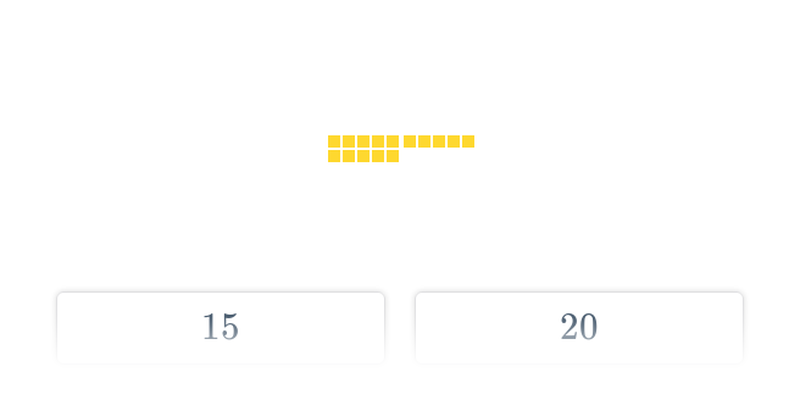
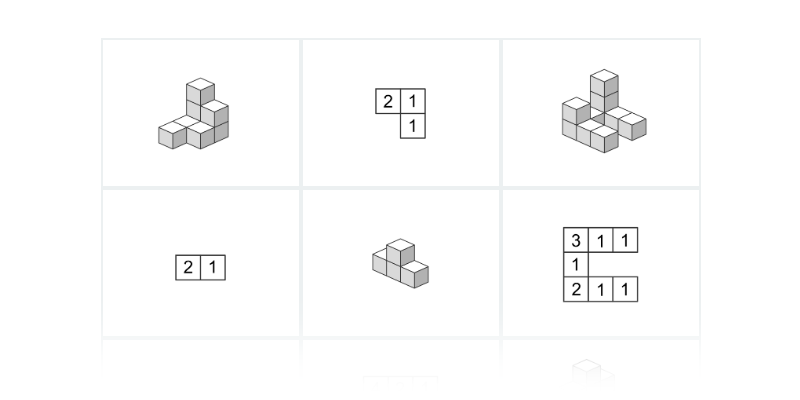
Častou součástí zkoušek bývají úlohy s kostičkami. Je ale rozhodně užitečné trénovat prostorovou představivost obecněji.
| Rozhodovačka | Stavby z kostek: pohled ze stran | ||
| Psaná odpověď | Počet kostek | ||
| Pexeso | Stavby z kostek: pohled ze stran | ||
| Rozhodovačka | Prostorová představivost: mix | ||
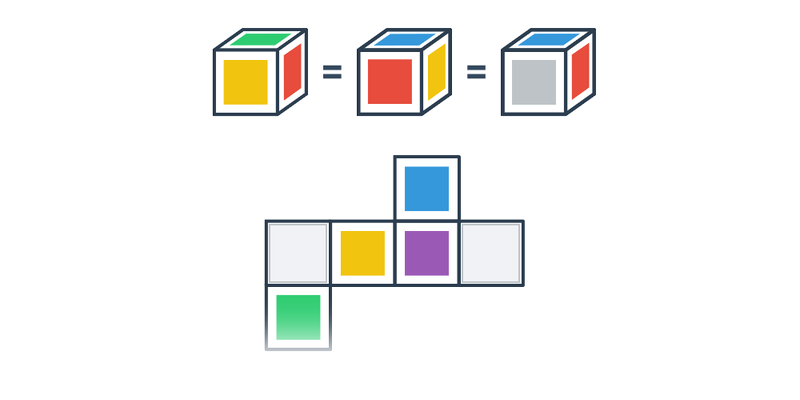
| Přesouvání | Síť krychle | ||
| Pexeso | Kostky: plán stavby | ||
| Rozhodovačka | 3D objekty z různých pohledů | ||
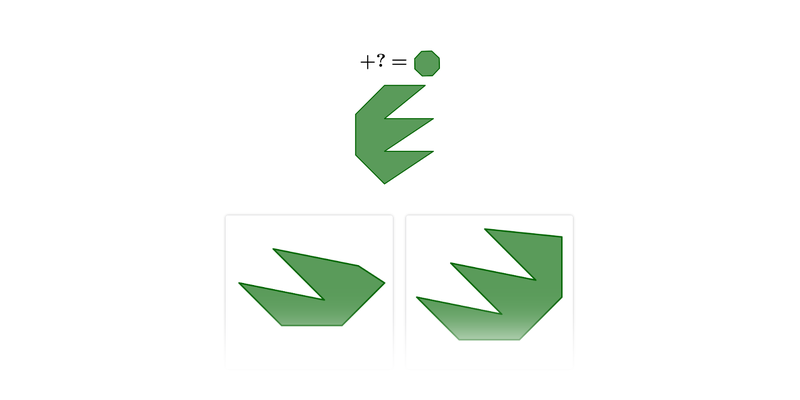
| Rozhodovačka | Doplňování útvarů |