Obsah kruhové výseče

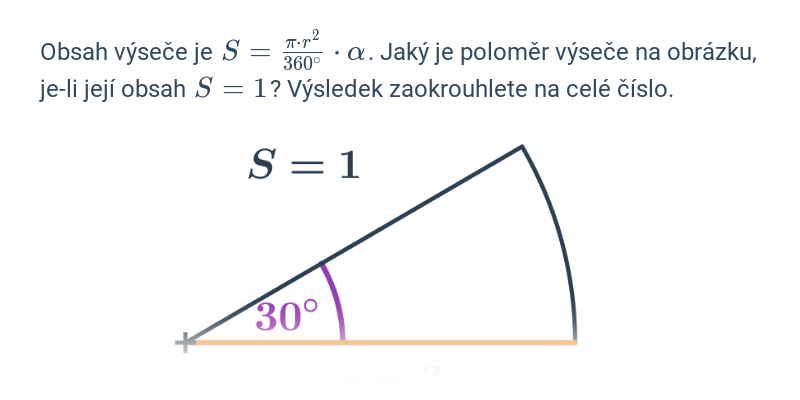
Obsah kruhové výseče

Obsah kruhové výseče se středovým úhlem \alpha a poloměrem r spočítáme jako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2

Příklady

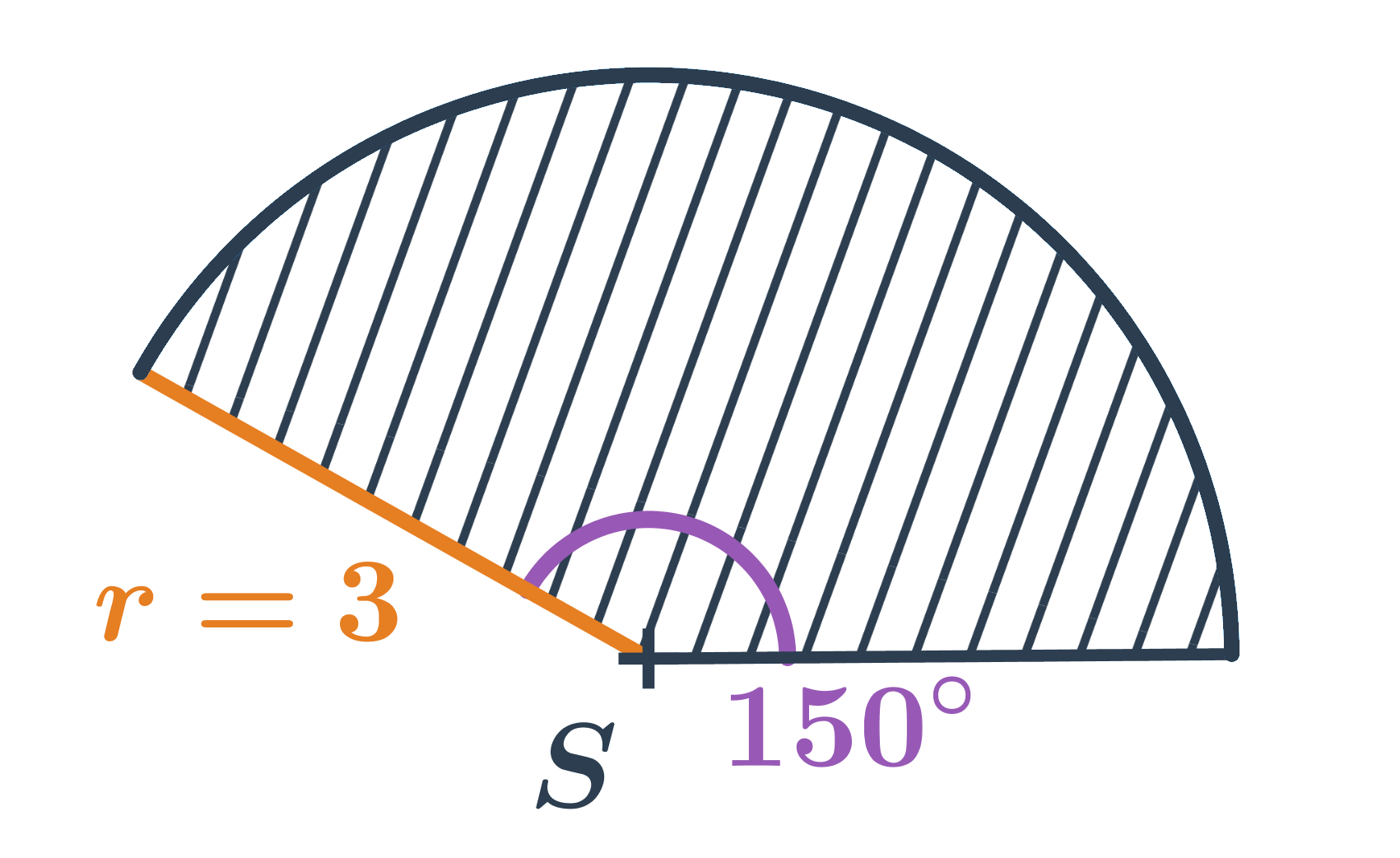
• Kruhová výseč na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi

• Obsah celého kruhu (výseče se středovým úhlem 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2