Jehlan
GDTJehlan je prostorový geometrický útvar, který má jednu podstavu a plášť tvořený trojúhelníky. Podstava jehlanu může být libovolný mnohoúhelník (například čtverec, obdélník nebo trojúhelník) a všechny boční stěny (plášť) se setkávají v jednom společném bodě nazývaném vrchol jehlanu. Příkladem jehlanů jsou pyramidy ze starověkého Egypta, vypadají zhruba jako jehlany se čtvercovou podstavou a čtyřmi trojúhelníkovými bočními stěnami.
Vzorce pro objem a povrch
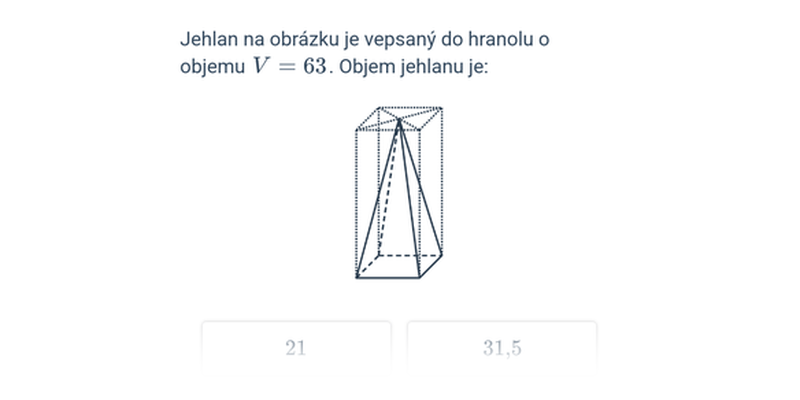
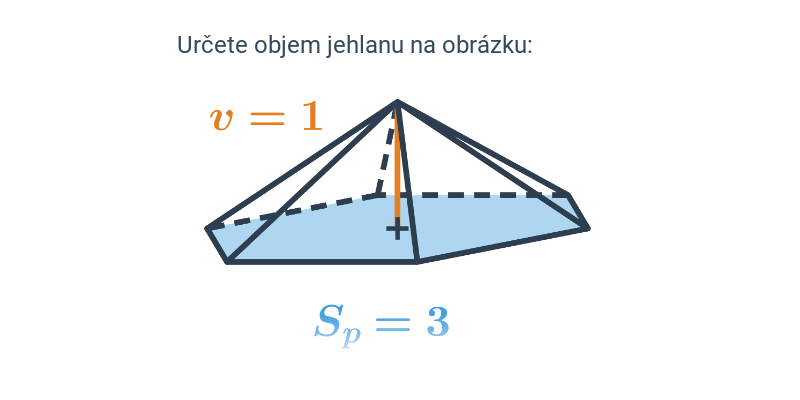
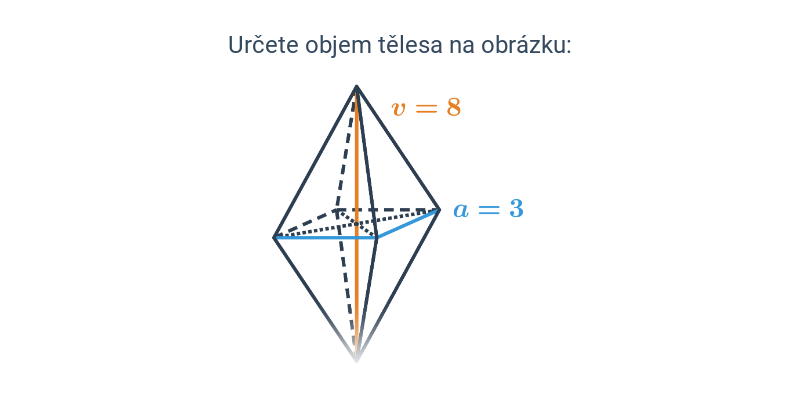
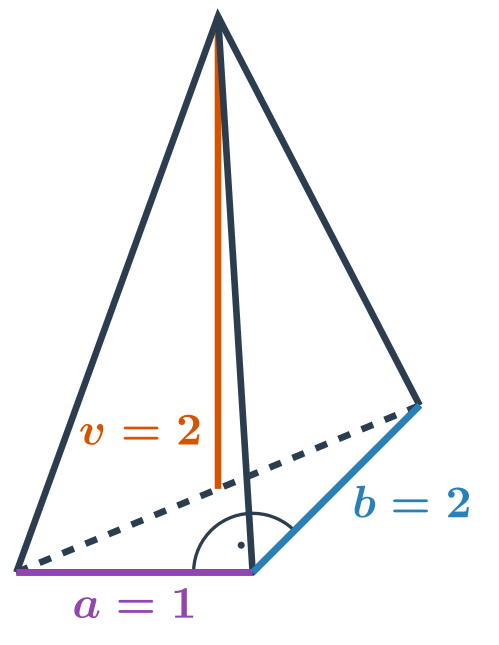
Objem jehlanu V = \frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy a v je výška jehlanu, což je vzdálenost vrcholu od roviny podstavy. (Velikost výšky jehlanu získáme jako délku úsečky, která vede od vrcholu k rovině podstavy a je kolmá na tuto rovinu.)
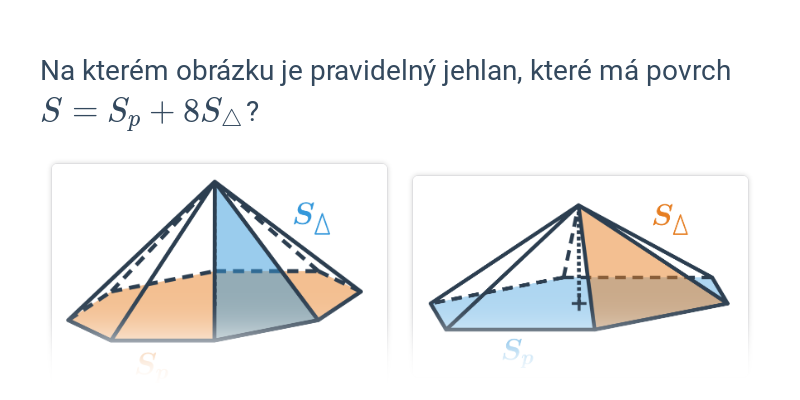
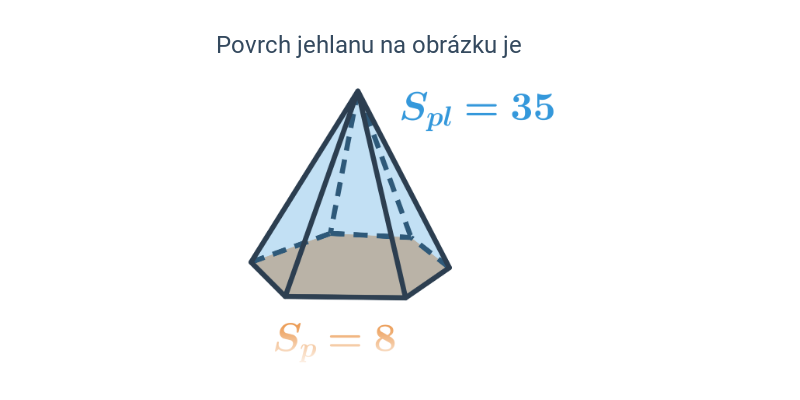
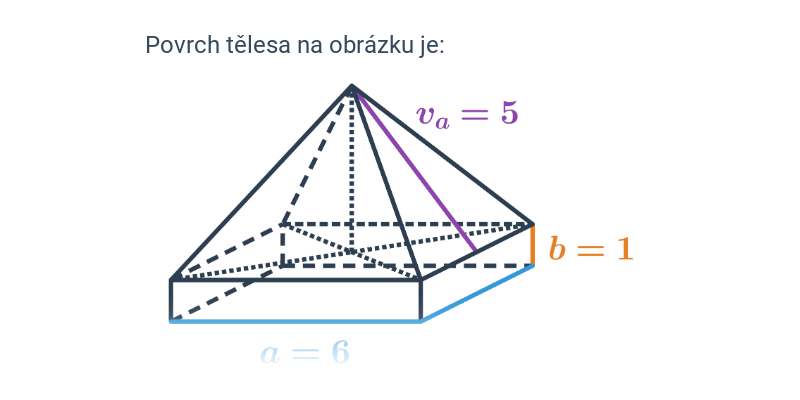
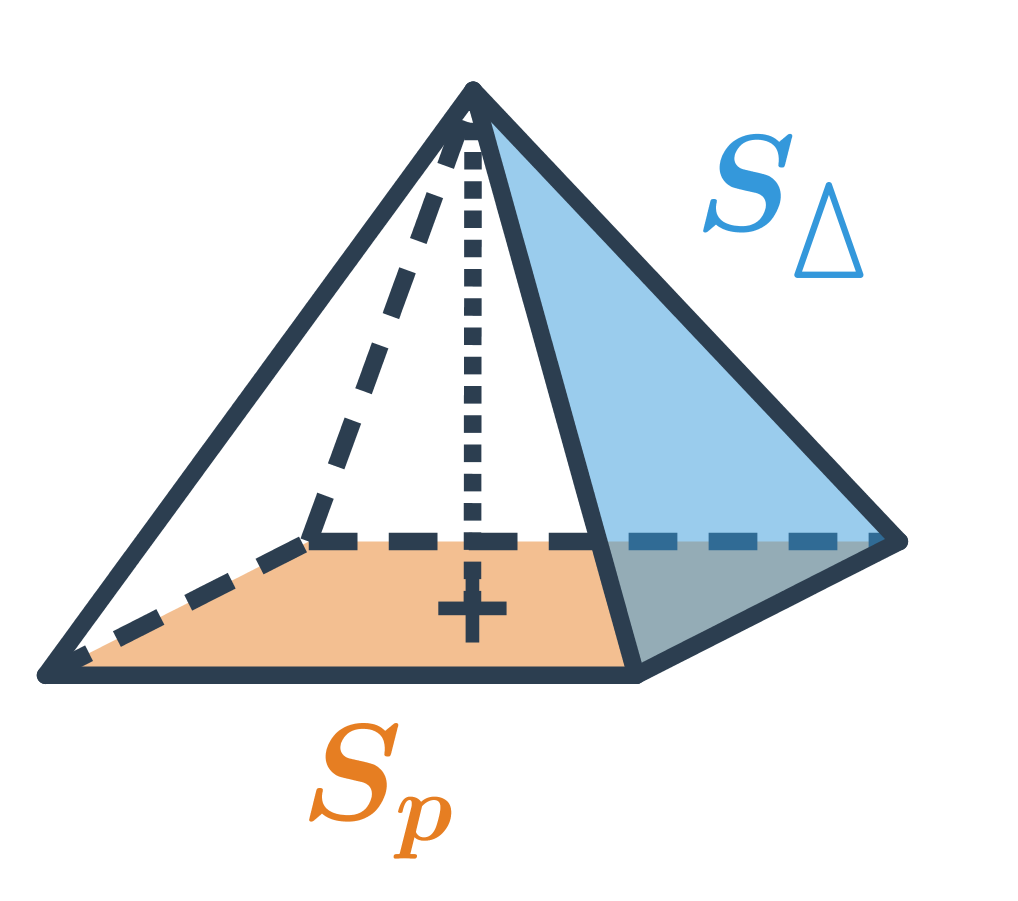
Povrch jehlanu získáme jako součet obsahu podstavy S_p a obsahu pláště S_{pl} (obsah pláště je roven součtu obsahů všech bočních trojúhelníkových stěn jehlanu). Celkově je povrch jehlanu S = S_p + S_{pl}, v případě pravidelného šestibokého jehlanu na obrázku je: S=Sp + 6 \cdot S_{\Delta}
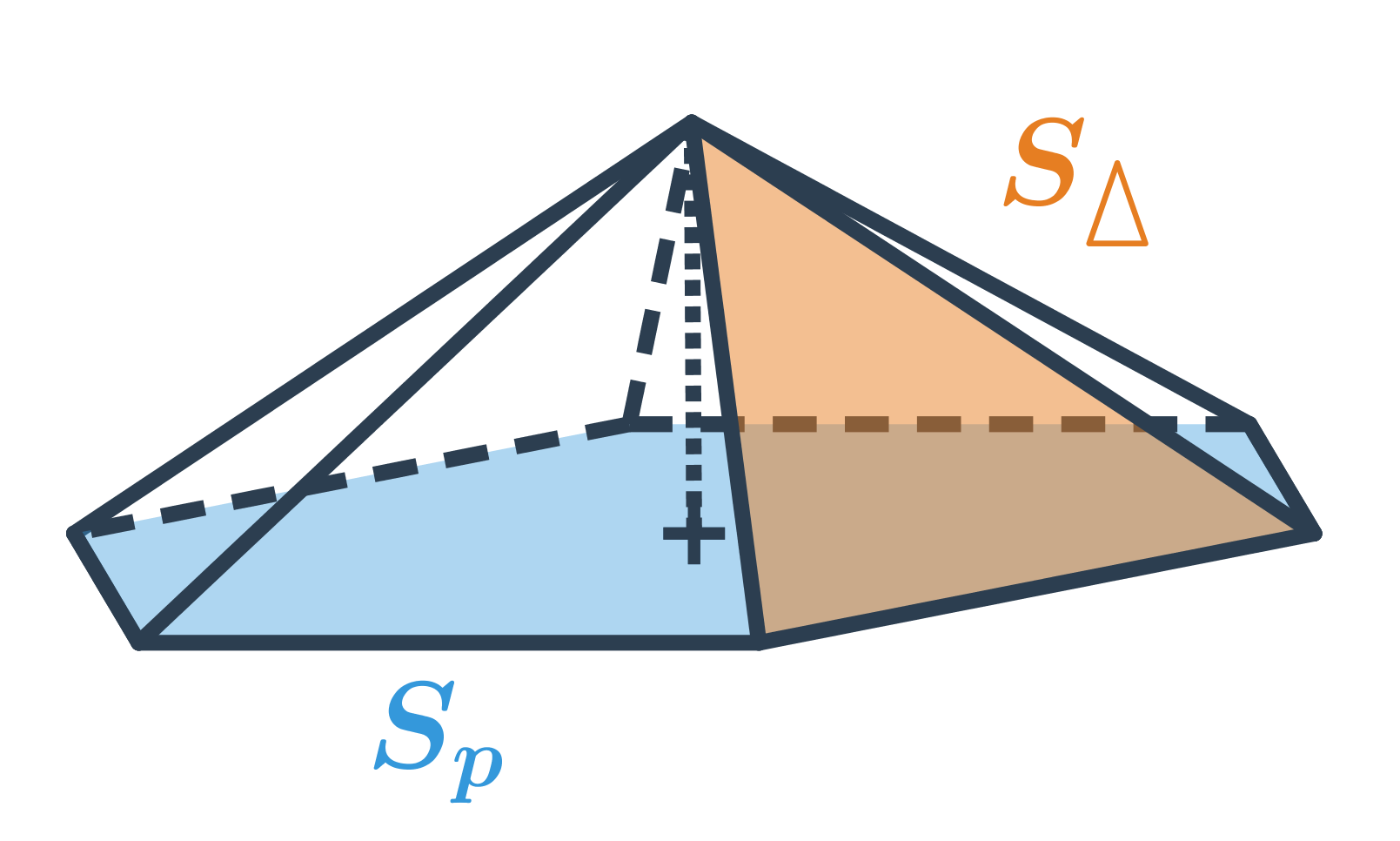
Některé jehlany mají pravidelnou podstavu, vrchol umístěný přímo nad středem podstavy a všechny trojúhelníkové stěny z pláště stejné, ale obecně se může výpočet obsahu každé z těchto trojúhelníkových stěn lišit v závislosti na tvaru podstavy jehlanu.
Speciální případy
Pravidelný čtyřstěn je jehlan, jehož základna i všechny tři boční stěny jsou rovnostranné trojúhelníky. Je jedním z Platónských těles.
Pokud máme pravidelný čtyřstěn, jehož stěny jsou rovnostranné trojúhelníky s délkou každé strany a, umíme si pomocí Pythagorovy věty spočítat výšku každého z těchto rovnostranných trojúhelníků \frac{\sqrt{3}}{2} a.
Povrch pravidelného čtyřstěnu
- Obsah podstavy pravidelného čtyřstěnu se stranou délky a je obsah jednoho ze čtyř stejných rovnostranných trojúhelníků: S_p = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2.
- Povrch pravidelného čtyřstěnu se stranou délky a je: 4 \cdot S_p = \sqrt{3} \cdot a^2
Objem pravidelného čtyřstěnu
- V rovnostranném trojúhelníku leží těžnice na výškách a zároveň na osách vnitřních úhlů. Vrchol pravidelného čtyřstěnu leží na přímce, která je kolmá k jeho podstavě a protíná ji v ortocentru (což je zároveň také těžiště rovnostranného trojúhelníka).
- Můžeme tedy spočítat pomocí Pythagorovy věty nejen výšku trojúhelníků, které tvoří stěny pravidelného čtyřstěnu, ale také výšku celého tělesa:
- v^2 = a^2 - (\frac{2}{3} \cdot \frac{\sqrt{3}}{2} a )^2 = (1-\frac{1}{\sqrt{3}})\cdot a^2
- v = \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a
- Objem pravidelného čtyřstěnu se stranou délky a je:
- \frac{1}{3} S_p \cdot v = \frac{1}{3}\cdot \frac{\sqrt{3}}{4} a^2 \cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a = \frac{1}{4\cdot \sqrt{3}}\cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a^3
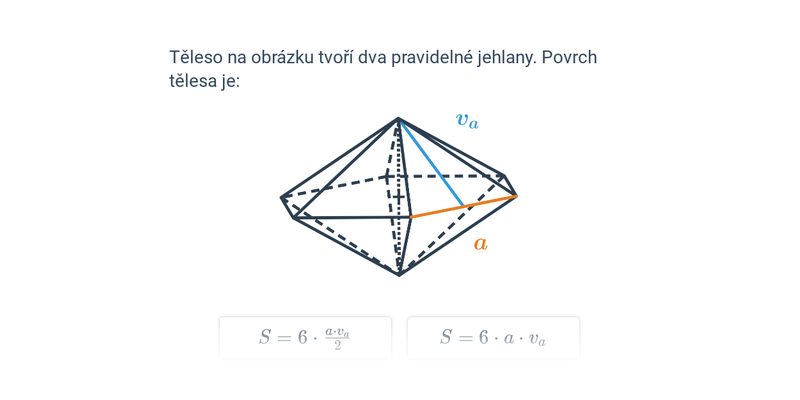
Pravidelný n-boký jehlan má jako podstavu pravidelný n-úhelník, jeho plášť tvoří n rovnoramenných trojúhelníků. Například podstava pravidelného čtyřbokého jehlanu je čtverec, jeho plášť tvoří čtyři rovnoramenné trojúhelníky.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Psaná odpověď
Cvičení, ve kterém píšete odpověď na klávesnici.