Výpis souhrnů
Prostorové útvary
Podtémata
Prostorové útvary
Prostorové útvary jsou množiny bodů v prostoru, tedy jde o třírozměrné útvary. Nejznámější prostorové útvary jsou krychle, kvádr, jehlan, koule, hranol, válec a kužel.
U některých prostorových útvarů umíme jednoduše spočítat jejich objem a povrch.
NahoruKrychle a kvádr
Krychle a kvádr jsou oba prostorové geometrické útvary, které patří mezi mnohostěny, speciálněji jde o zvláštní případy hranolů.
Krychle je prostorový útvar, který má šest stěn, tvar každé stěny je čtverec. Všechny hrany krychle mají stejnou délku a všechny vnitřní úhly jsou pravé, tedy jejich velikost je 90°. Příklady krychlí v běžném životě zahrnují kostky cukru nebo Rubikovu kostku.
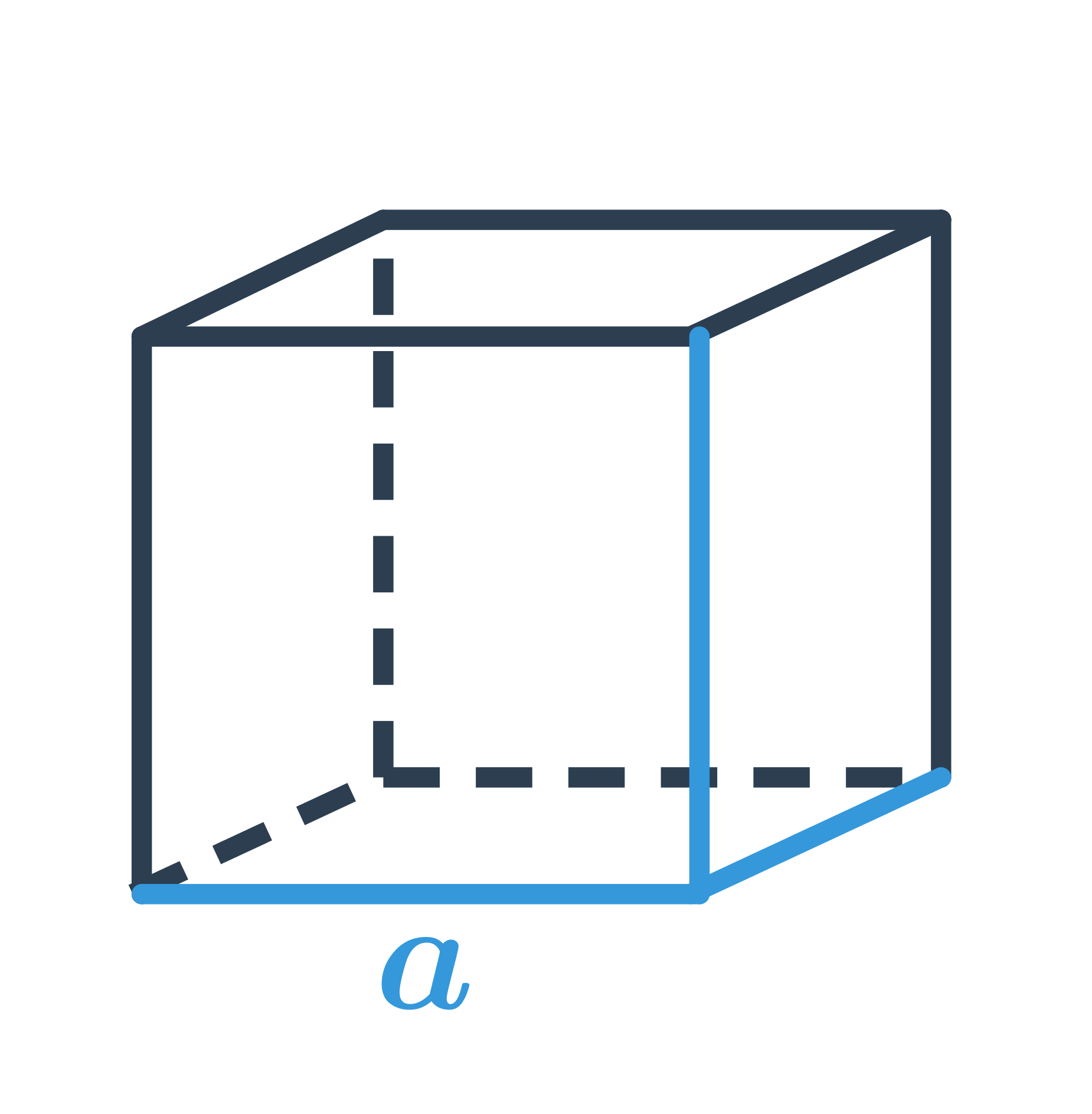
Pro výpočet objemu krychle použijeme vzorec V = a^3, kde a je délka hrany krychle.
Povrch krychle s délkou hrany a se vypočítá pomocí vzorce S = 6a^2.
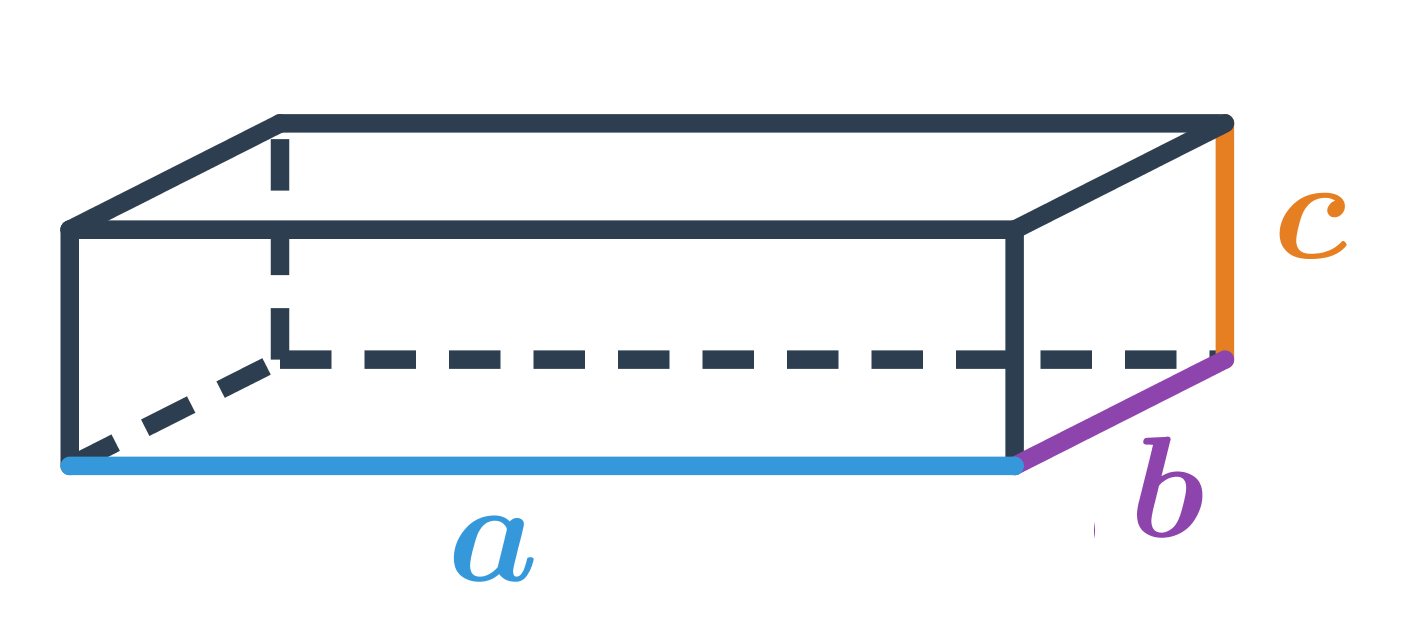
Kvádr je také hranol, ale na rozdíl od krychle mají jeho stěny tvar obdélníků. Kvádr má tři rozměry: šířku, délku a výšku, které nemusí být stejné, jako je tomu u krychle. Kvádr má šest stěn, tvar každé stěny je obdélník nebo čtverec, pokud jsou všechny stěny tvaru čtverce, jde o krychli.
Příklady kvádrů v běžném životě zahrnují krabice, knihy nebo cihly.
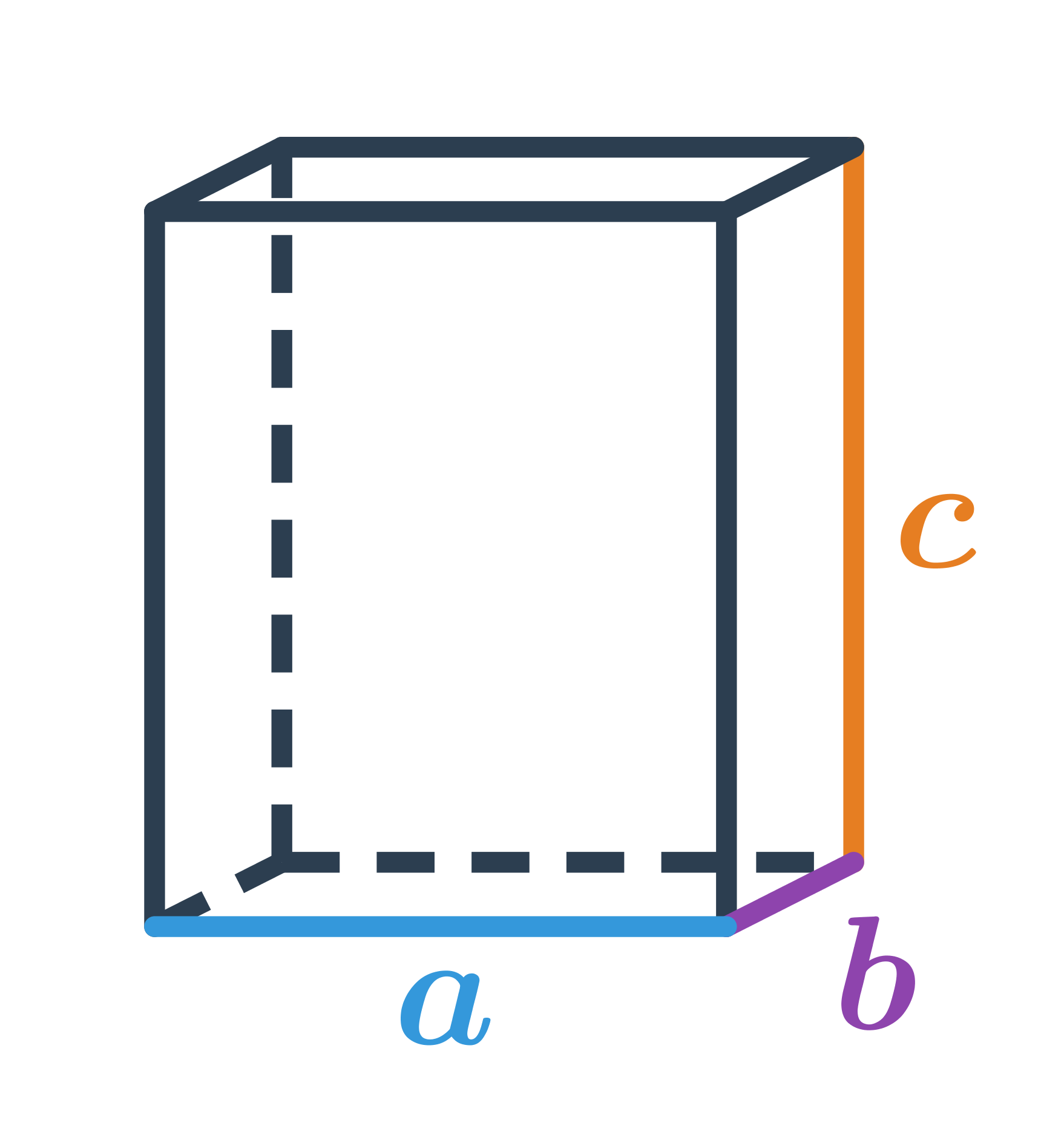
Objem kvádru získáme vzorcem V = a \cdot b \cdot c, kde a,b,c jsou rozměry kvádru.
Povrch kvádru vypočítáme jako součet obsahů všech jeho šesti obdélníkových stěn S = 2(ab + bc + ac). Všechny dvojice protějších stěn jsou dvojice shodných obdélníků, které mají stejné obsahy.
NahoruObjem krychle a kvádru
Objem kvádru s délkami hran a,b,c je: V=a\cdot b\cdot c
Objem krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako objem kvádru s a=b=c, tedy: V=a\cdot a\cdot a=a^3
NahoruPovrch krychle a kvádru
Povrch kvádru s délkami hran a,b,c spočítáme jako součet obsahů všech jeho stěn. Tedy: S=2 (a\cdot b + a\cdot c + b \cdot c)
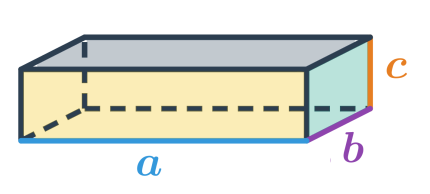
Povrch krychle s délkou hrany podstavy a spočítáme stejným způsobem, jako povrch kvádru s a=b=c, tedy šestkrát obsah jedné čtvercové stěny krychle: S = 6\cdot a\cdot a = 6a^2
NahoruŘezy krychle
Sestrojit řez krychle znamená sestrojit průnik roviny a krychle. Půjde o mnohoúhelník, který leží v rovině řezu a jeho strany jsou okraje řezu, tedy čáry, kudy rovina řízne stěny krychle. Tyto průsečnice řezné roviny se stěnami tělesa chceme sestrojit. Při konstrukci řezů (nejen krychle) můžeme použít tři základní pravidla:
- Pokud leží dva různé body v rovině, pak přímka, která jimi prochází, leží také v této rovině. Když známe ve stěně tělesa dva různé body, které oba leží v rovině řezu, nakreslíme jejich spojnici. Průnik stěny a této spojnice je jednou stranou řezu.
- Dvě rovnoběžné roviny protíná každá další k nim různoběžná rovina ve dvou rovnoběžných přímkách. To znamená, že strany řezu v rovnoběžných stěnách jsou navzájem rovnoběžné.
- Tři navzájem různoběžné roviny se vždy protínají v jednom bodě. Tímto bodem prochází všechny tři průsečnice jednotlivých dvojic rovin. Tedy dvě průsečnice rovin dvou sousedních stěn s rovinou řezu a přímka, na které leží společná hrana stěn, se protínají v jednom bodě.
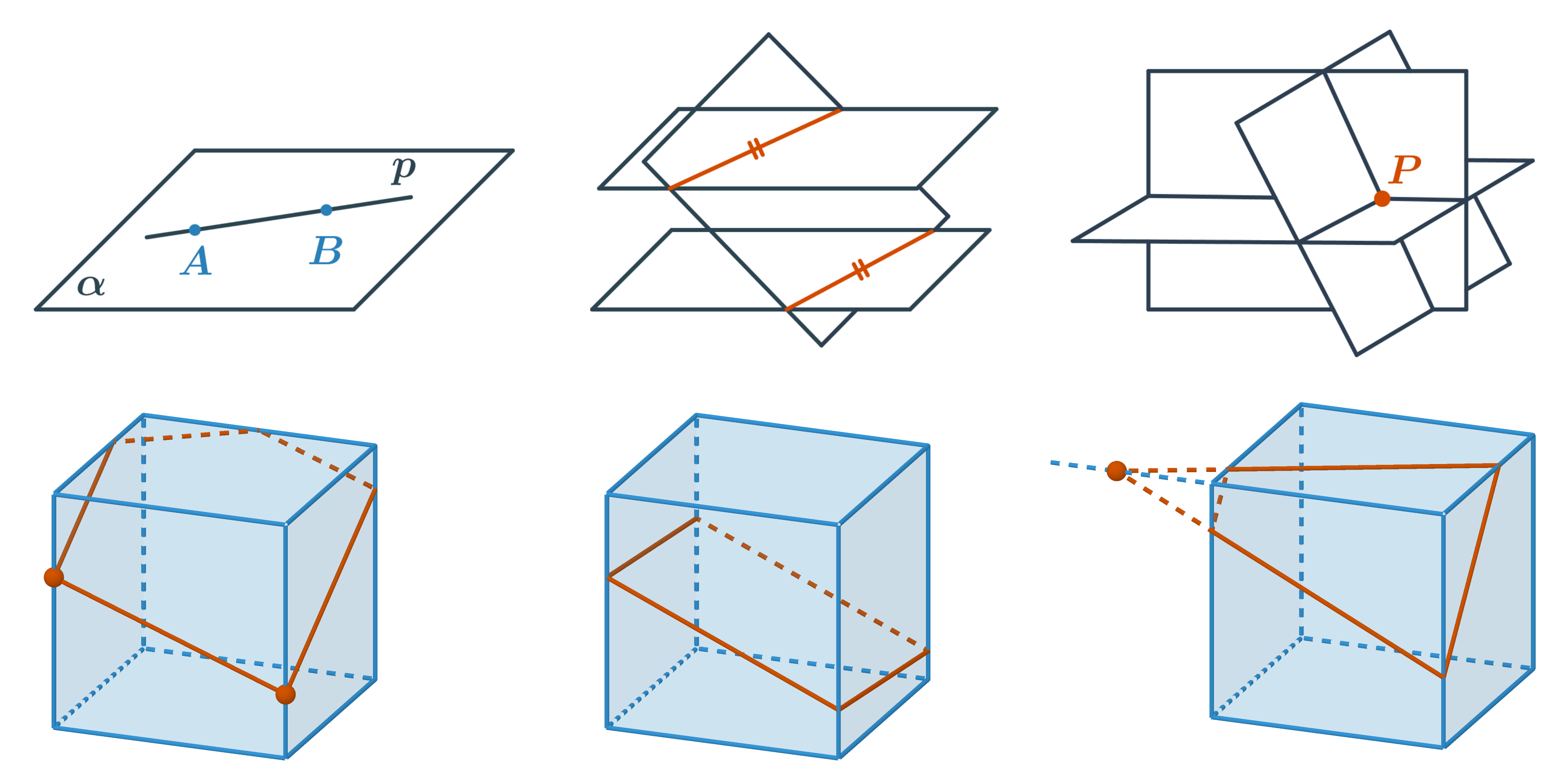
Pozor si dáváme na nejčastější chyby:
- zalomení řezu v jedné stěně (část řezu v jedné stěně musí vždy tvořit jedna úsečka)
- čára řezu jde vnitřkem nebo vnějškem tělesa (okraj řezu musí být celý ve stěnách tělesa)
- čára řezu nekončí na hraně (těleso na hraně končí, řez tělesa také)
Řez krychle rovinou procházející body K, L, M.
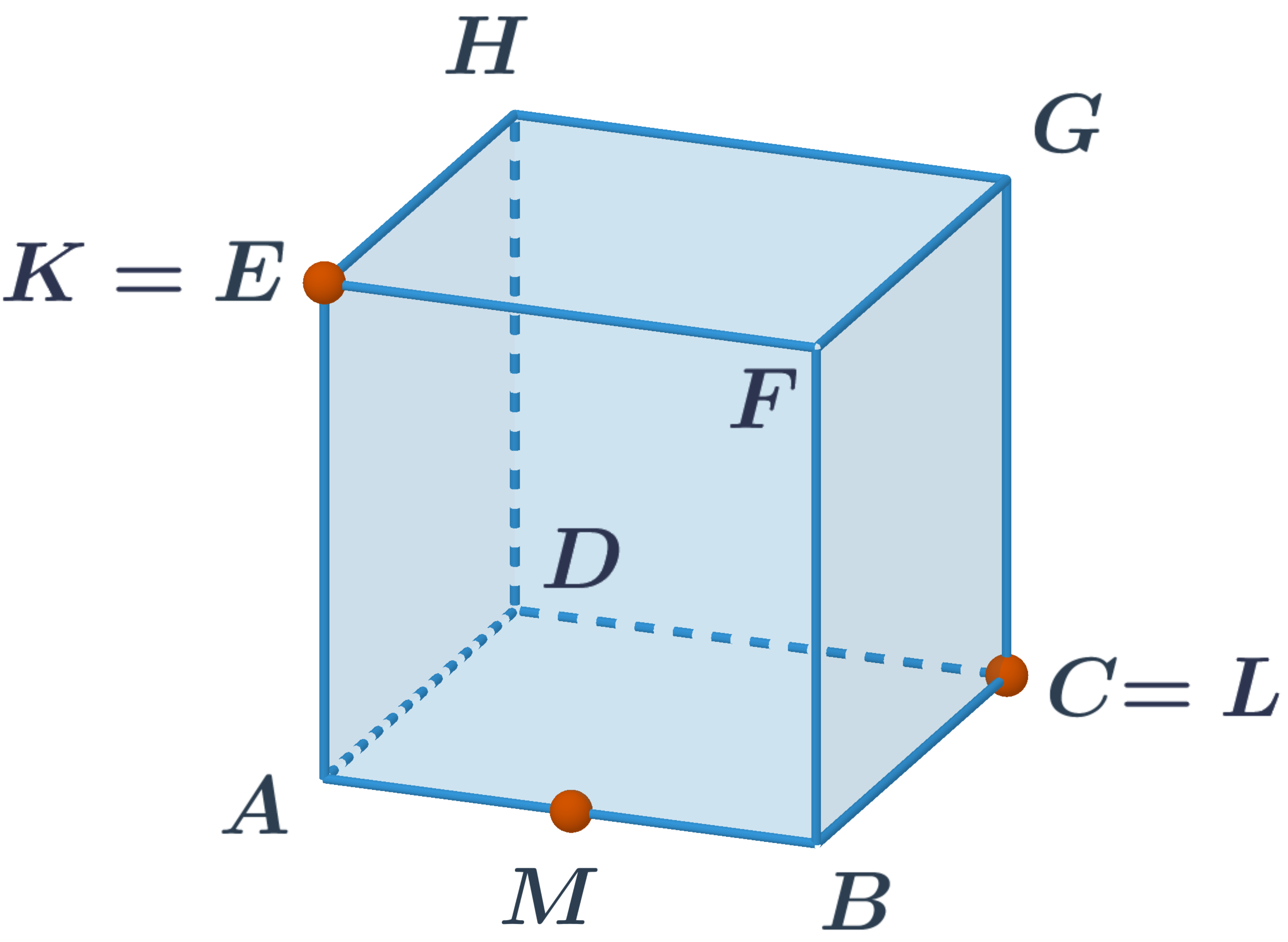
- Body K, M leží v jedné rovině – v přední stěně ABFE. Úsečka KM je tedy první část řezu.
- Stejně tak body L, M leží v jedné rovině – v dolní stěně ABCD. Úsečka LM je tedy druhá část řezu.
- Bod K leží v horní stěně EFGH. Ta je rovnoběžná se stěnou ABCD. Další část řezu KN je tedy rovnoběžná s úsečkou LM.
- Podobně je i poslední část řezu NL v zadní stěně CDHG rovnoběžná s úsečkou KM ve stěně ABFE.
- Řezem je v tomto případě rovnoběžník.
Hranol je prostorový geometrický útvar, který má dvě shodné podstavy umístěné v různých rovinách. Budeme se zabývat kolmými hranoly, ve kterých odpovídající strany podstavy jsou vždy spojené boční stěnou tvaru obdélníka nebo čtverce. (Pro kosé hranoly jsou boční stěny rovnoběžníky.) Podstavy hranolu mohou mít rozličné tvary, například mohou být trojúhelníkové, čtvercové, obdélníkové nebo i mnohoúhelníkové.
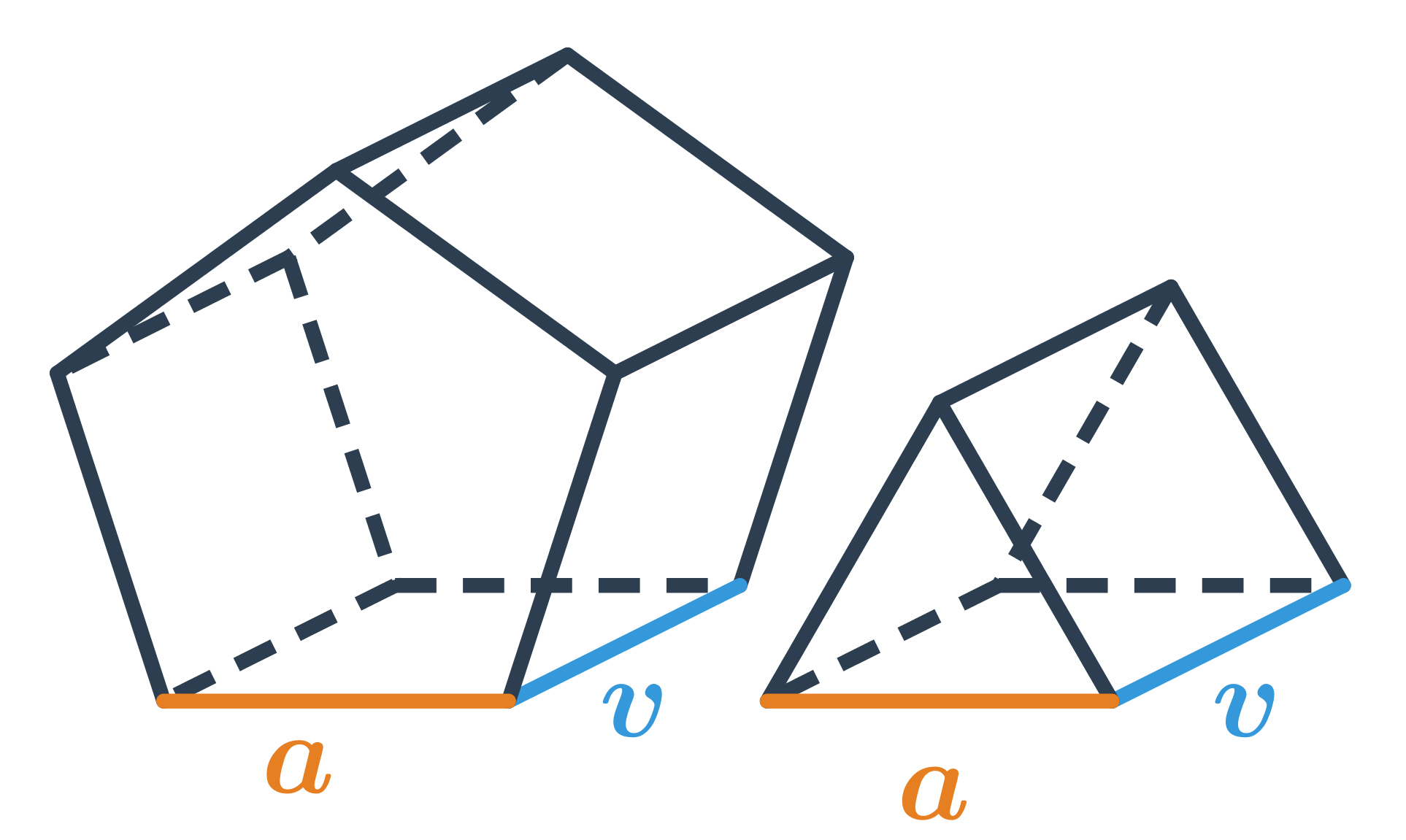
Vzorečky pro objem a povrch hranolu
Pro výpočet objemu hranolu používáme vzorec V = S_p \cdot v, kde S_p je obsah jedné podstavy a v je výška hranolu.
Síť hranolu se skládá ze dvou podstav a pláště, proto jeho povrch vypočítáme jako součet obsahů podstav a obsahu pláště: S = 2S_p + S_{pl}, kde S_{pl} je obsah pláště, což je součet obsahů všech obdélníkových nebo čtvercových stěn tvořících plášť.
Příklady hranolů
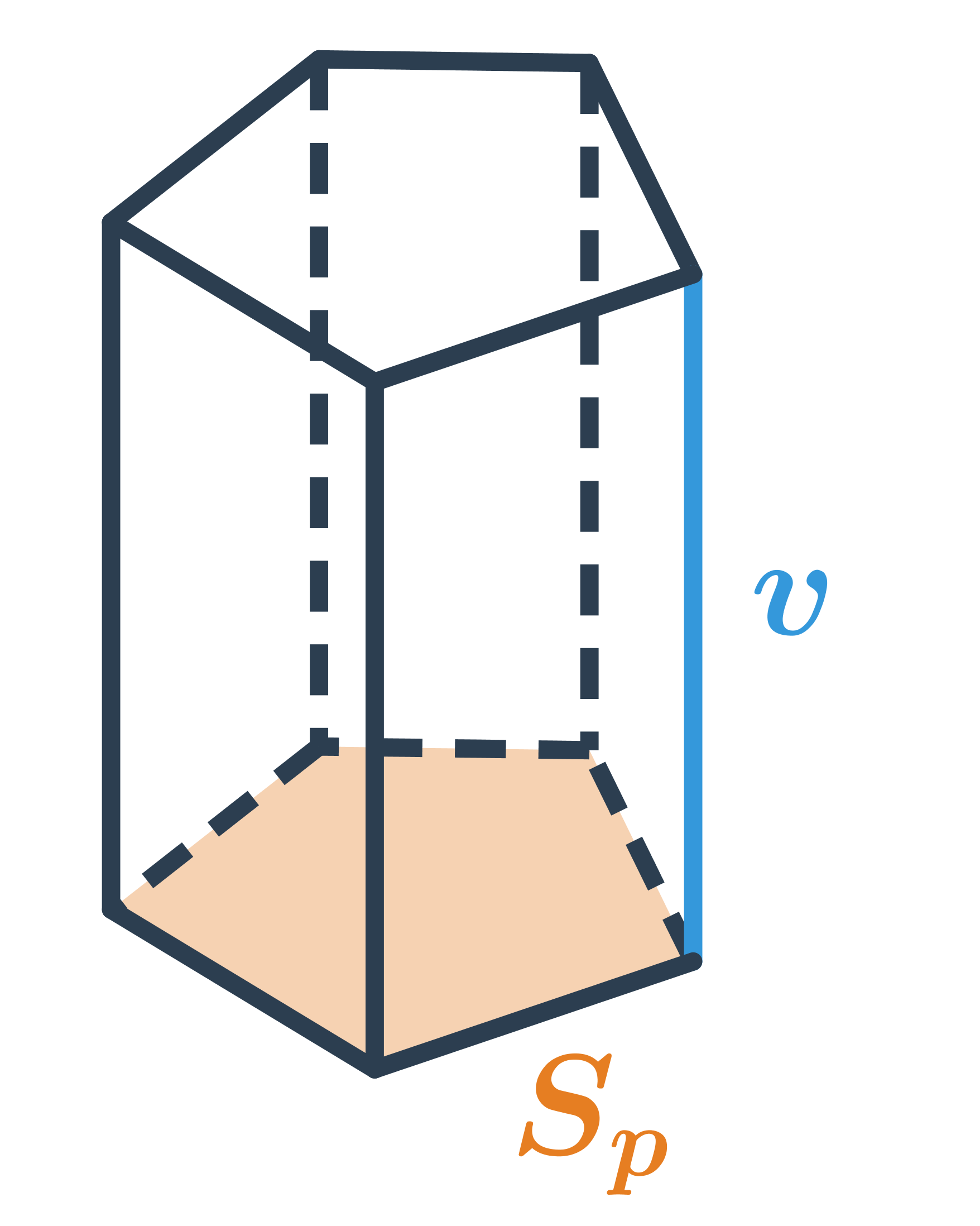
Pravidelný n-boký hranol má jako podstavy dva pravidelné n-úhelníky.
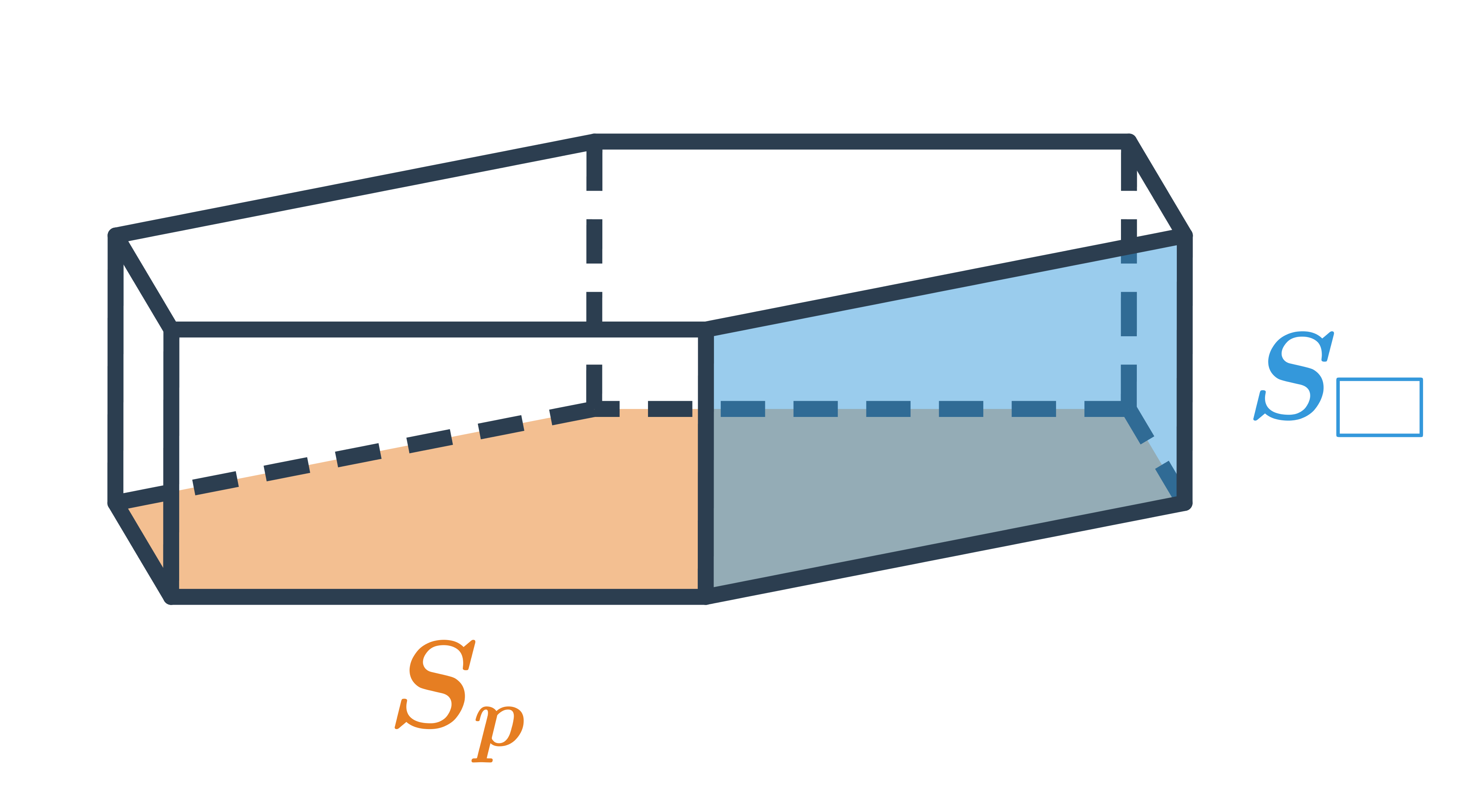
Speciální případy čtyřbokých hranolů jsou kvádr a krychle. Kvádr může a nemusí být pravidelný čtyřboký hranol. Krychle je pravidelný čtyřboký hranol, který navíc splňuje a=v.
Objem hranolu
Objem hranolu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=S_p \cdot v.
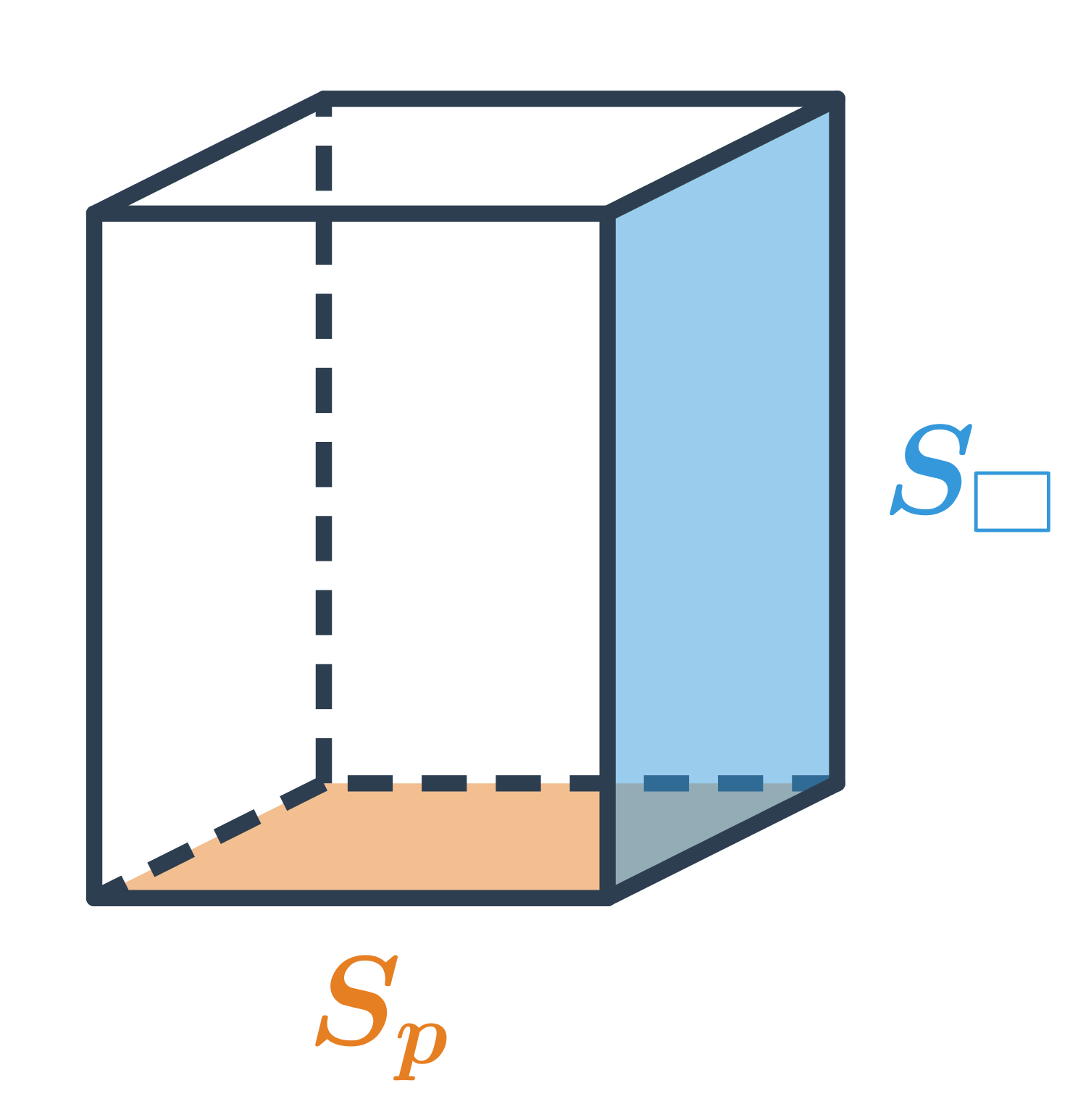
Povrch hranolu
Povrch hranolu, který má podstavu o obsahu S_p plášť o obsahu S_{pl}, spočítáme jako S=2S_p + S_{pl}. Plášť hranolu je tvořen všemi jeho stěnami kromě dvou podstav.
Povrch pravidelného n‑bokého hranolu, který má dvě podstavy ve tvaru pravidelných n‑úhelníků a potom n stejných obdélníkových stěn (obsah jedné označme S_1), spočítáme takto: S=2S_p + n\cdot S_1
NahoruJehlan je prostorový geometrický útvar, který má jednu podstavu a plášť tvořený trojúhelníky. Podstava jehlanu může být libovolný mnohoúhelník (například čtverec, obdélník nebo trojúhelník) a všechny boční stěny (plášť) se setkávají v jednom společném bodě nazývaném vrchol jehlanu. Příkladem jehlanů jsou pyramidy ze starověkého Egypta, vypadají zhruba jako jehlany se čtvercovou podstavou a čtyřmi trojúhelníkovými bočními stěnami.
Vzorce pro objem a povrch
Objem jehlanu V = \frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy a v je výška jehlanu, což je vzdálenost vrcholu od roviny podstavy. (Velikost výšky jehlanu získáme jako délku úsečky, která vede od vrcholu k rovině podstavy a je kolmá na tuto rovinu.)
Povrch jehlanu získáme jako součet obsahu podstavy S_p a obsahu pláště S_{pl} (obsah pláště je roven součtu obsahů všech bočních trojúhelníkových stěn jehlanu). Celkově je povrch jehlanu S = S_p + S_{pl}, v případě pravidelného šestibokého jehlanu na obrázku je: S=Sp + 6 \cdot S_{\Delta}
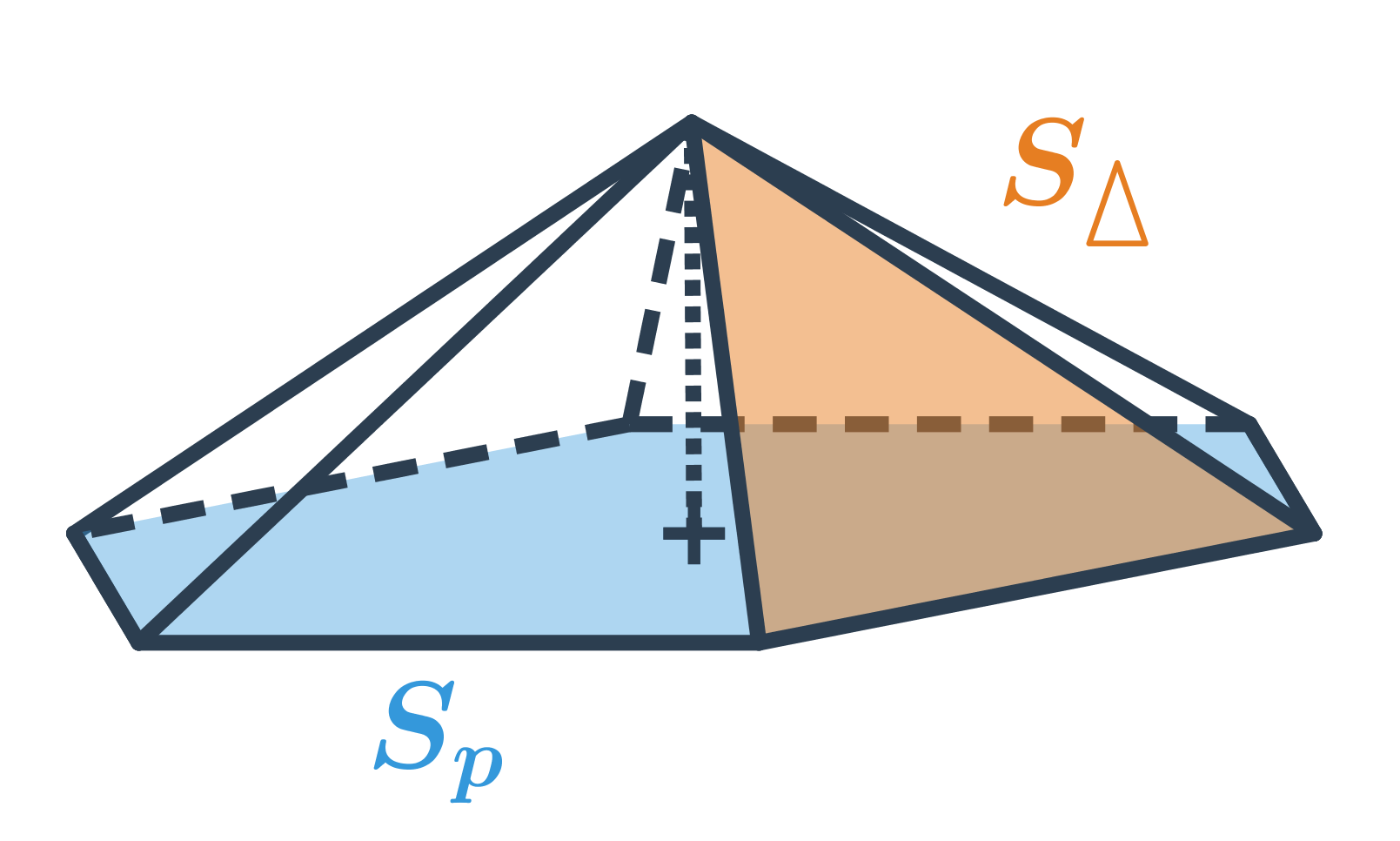
Některé jehlany mají pravidelnou podstavu, vrchol umístěný přímo nad středem podstavy a všechny trojúhelníkové stěny z pláště stejné, ale obecně se může výpočet obsahu každé z těchto trojúhelníkových stěn lišit v závislosti na tvaru podstavy jehlanu.
Speciální případy
Pravidelný čtyřstěn je jehlan, jehož základna i všechny tři boční stěny jsou rovnostranné trojúhelníky. Je jedním z Platónských těles.
Pokud máme pravidelný čtyřstěn, jehož stěny jsou rovnostranné trojúhelníky s délkou každé strany a, umíme si pomocí Pythagorovy věty spočítat výšku každého z těchto rovnostranných trojúhelníků \frac{\sqrt{3}}{2} a.
Povrch pravidelného čtyřstěnu
- Obsah podstavy pravidelného čtyřstěnu se stranou délky a je obsah jednoho ze čtyř stejných rovnostranných trojúhelníků: S_p = \frac{1}{2} \cdot a \cdot \frac{\sqrt{3}}{2} a = \frac{\sqrt{3}}{4} a^2.
- Povrch pravidelného čtyřstěnu se stranou délky a je: 4 \cdot S_p = \sqrt{3} \cdot a^2
Objem pravidelného čtyřstěnu
- V rovnostranném trojúhelníku leží těžnice na výškách a zároveň na osách vnitřních úhlů. Vrchol pravidelného čtyřstěnu leží na přímce, která je kolmá k jeho podstavě a protíná ji v ortocentru (což je zároveň také těžiště rovnostranného trojúhelníka).
- Můžeme tedy spočítat pomocí Pythagorovy věty nejen výšku trojúhelníků, které tvoří stěny pravidelného čtyřstěnu, ale také výšku celého tělesa:
- v^2 = a^2 - (\frac{2}{3} \cdot \frac{\sqrt{3}}{2} a )^2 = (1-\frac{1}{\sqrt{3}})\cdot a^2
- v = \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a
- Objem pravidelného čtyřstěnu se stranou délky a je:
- \frac{1}{3} S_p \cdot v = \frac{1}{3}\cdot \frac{\sqrt{3}}{4} a^2 \cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a = \frac{1}{4\cdot \sqrt{3}}\cdot \sqrt{(1-\frac{1}{\sqrt{3}})}\cdot a^3
Pravidelný n-boký jehlan má jako podstavu pravidelný n-úhelník, jeho plášť tvoří n rovnoramenných trojúhelníků. Například podstava pravidelného čtyřbokého jehlanu je čtverec, jeho plášť tvoří čtyři rovnoramenné trojúhelníky.
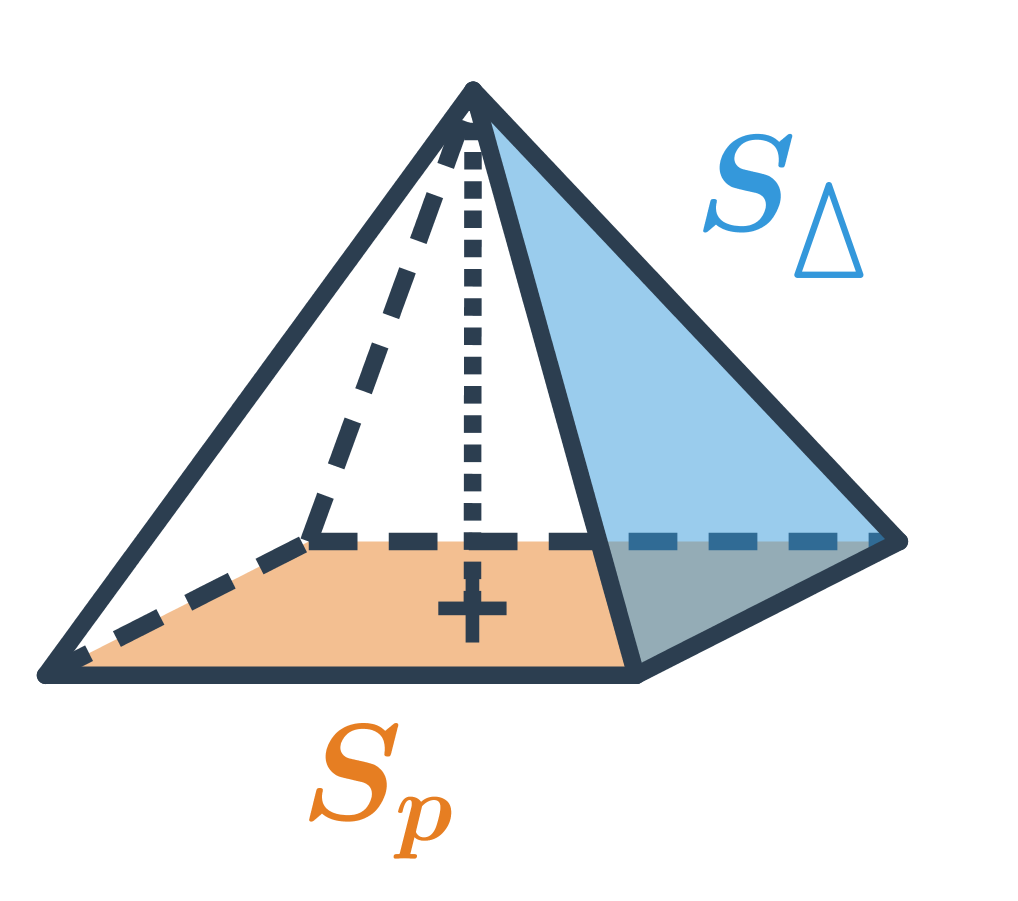
Objem jehlanu
Objem jehlanu, který má podstavu o obsahu S_p a výšku v, spočítáme jako V=\frac{1}{3} S_p \cdot v.
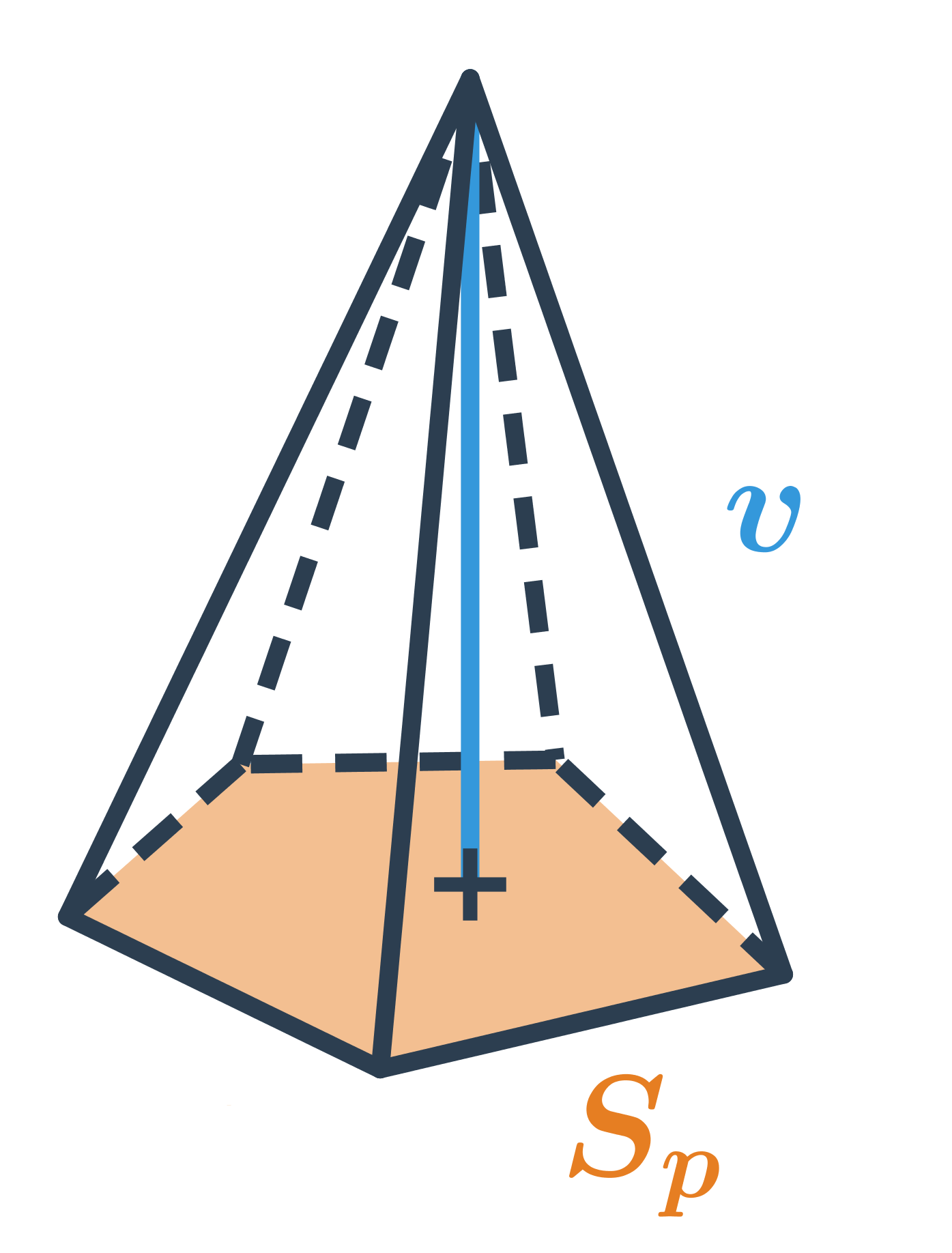
Oproti hranolu se stejnou výškou a tvarem podstavy má jehlan třikrát menší objem.
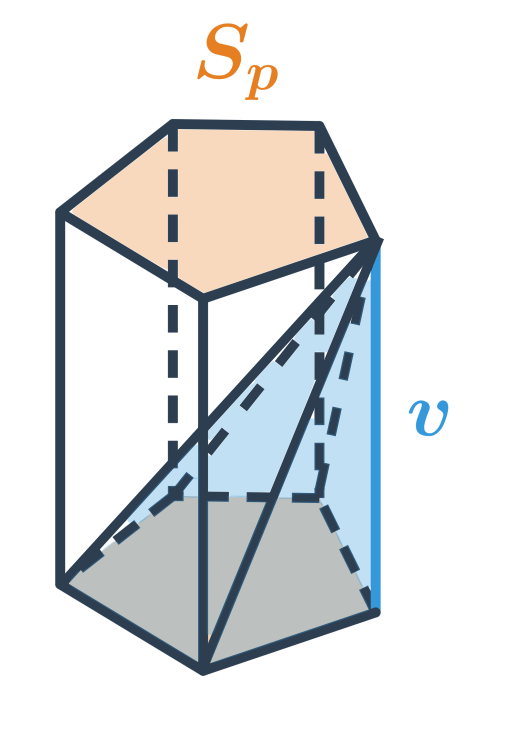
Povrch jehlanu
Povrch jehlanu spočítáme jako součet obsahu jeho podstavy S_p a obsahu jeho pláště S_{pl}. Obsah pláště spočítáme jako součet obsahů stěn jehlanu, které tvoří plášť (tj. všechny stěny jehlanu kromě jeho podstavy).
Povrch pravidelného n‑bokého jehlanu, který má podstavu ve tvaru pravidelného n‑úhelníka a potom n stejných trojúhelníkových stěn (obsah jedné označme S_1), spočítáme takto: S= S_p + n\cdot S_1
NahoruVálec je těleso, které vznikne rotací obdélníku v prostoru okolo jedné strany.
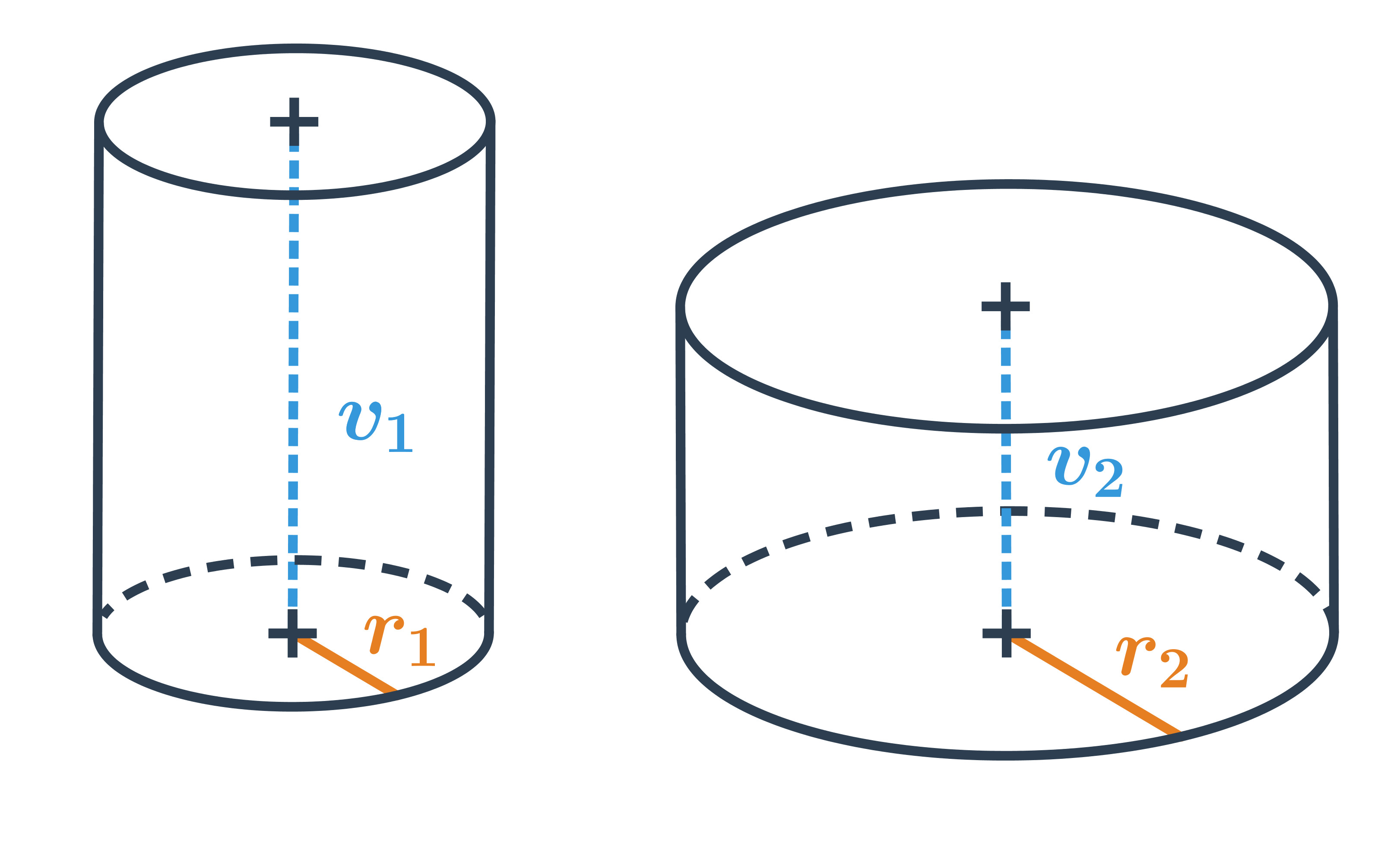
Válec má dvě podstavy tvaru kruhu, je jednoznačně určen poloměrem (nebo průměrem) podstavy a výškou.
Vzorečky pro objem a povrch válce
Objem válce spočítáme podobně jako u hranolu V=S_p \cdot v, kde S_p je obsah kruhové podstavy. Celkově je tedy objem válce: V=\pi \cdot r^2 \cdot v
Povrch válce je součet obsahů jeho dvou podstav a obsahu pláště S = 2\cdot S_p + S_{pl}. Podstavy jsou ve tvaru kruhu a plášť můžeme rozvinout do roviny jako obdélník o rozměrech v a 2\pi \cdot r (výška válce a obvod jeho podstavy). Povrch válce je roven: V = 2\pi \cdot r^2 + 2\pi \cdot r \cdot v = 2\pi r (r+v)
NahoruObjem válce
Objem válce s poloměrem podstavy r a výškou v spočítáme jako: V=\pi \cdot r^2 \cdot v
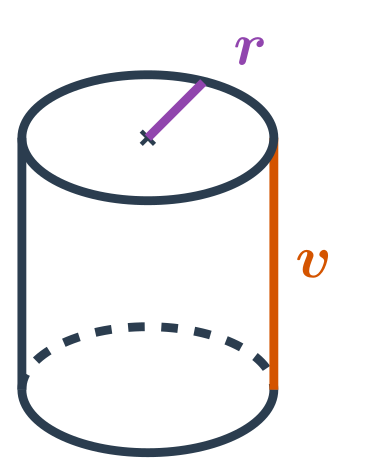
Platí V=S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
NahoruPovrch válce
Povrch válce s poloměrem podstavy r a výškou v spočítáme jako: S = 2\pi r \cdot(r + v)
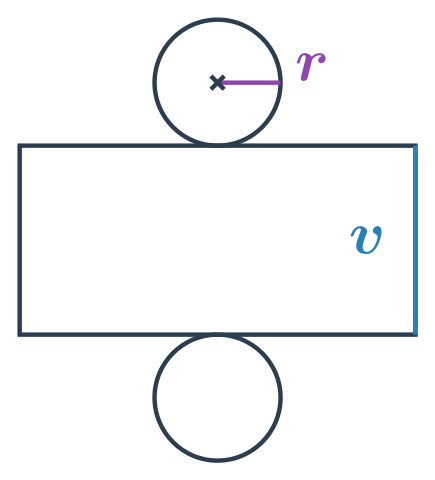
Platí S=2S_p + S_{pl}, kde S_p je obsah podstavy válce a S_{pl} obsah pláště válce. Podstava válce má tvar kruhu s poloměrem r a plášť válce je obdélník o stranách v a 2\pi r. Celkem máme:
- Obsah podstavy: S_p = \pi \cdot r^2
- Obsah pláště: S_{pl}=2\pi r \cdot v
- Povrch válce: S=2\pi r \cdot (r + v)
Koule je prostorový geometrický útvar, který má tvar dokonale kulatého tělesa. Všechny body na povrchu koule jsou stejně daleko od středu, tato vzdálenost se nazývá poloměr koule. Koule je symetrická ve všech směrech, což znamená, že nezáleží na tom, jak ji otočíme, její tvar zůstane stejný.
Příklady koule v běžném životě zahrnují basketbalový míč, zeměkouli nebo kuličku z ložiska.
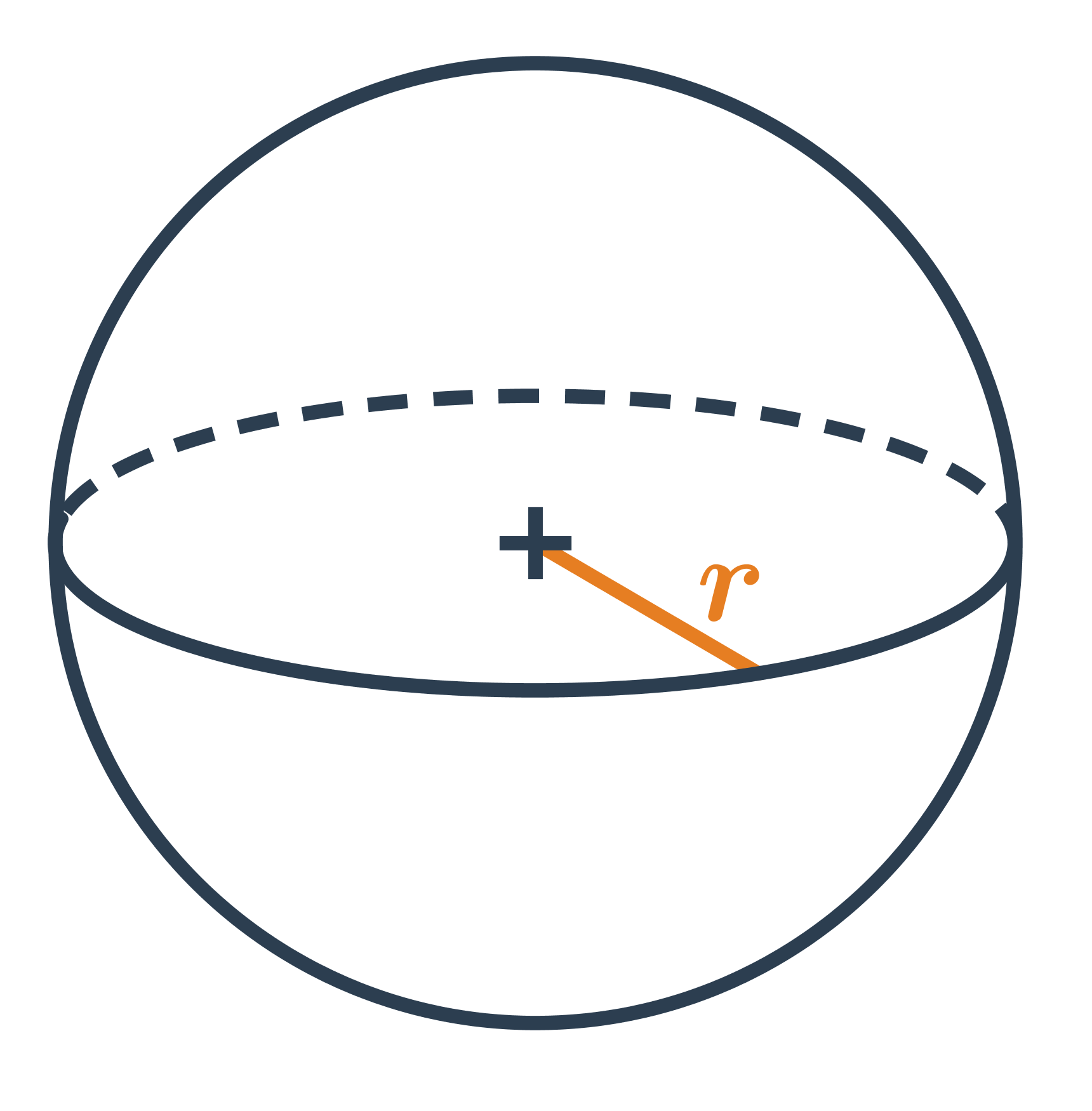
Pro výpočet objemu koule používáme vzorec V = \frac{4}{3} \pi r^3, kde r je poloměr koule.
Povrch koule se vypočítá pomocí vzorce S = 4 \pi r^2, kde opět r značí poloměr koule.
Koule nemá rohy ani hrany, což ji odlišuje od mnoha jiných geometrických útvarů. Tato jedinečná vlastnost dává kouli významnou roli v různých oblastech, včetně fyziky, kde se používá například pro modelování ideálních těles v teorii gravitace. Předmětem studia v neeuklidovské geometrii mohou zase být útvary, které nejsou částí roviny, ale kulové plochy (pak jde o sférickou geometrii, neboli geometrii na sféře).
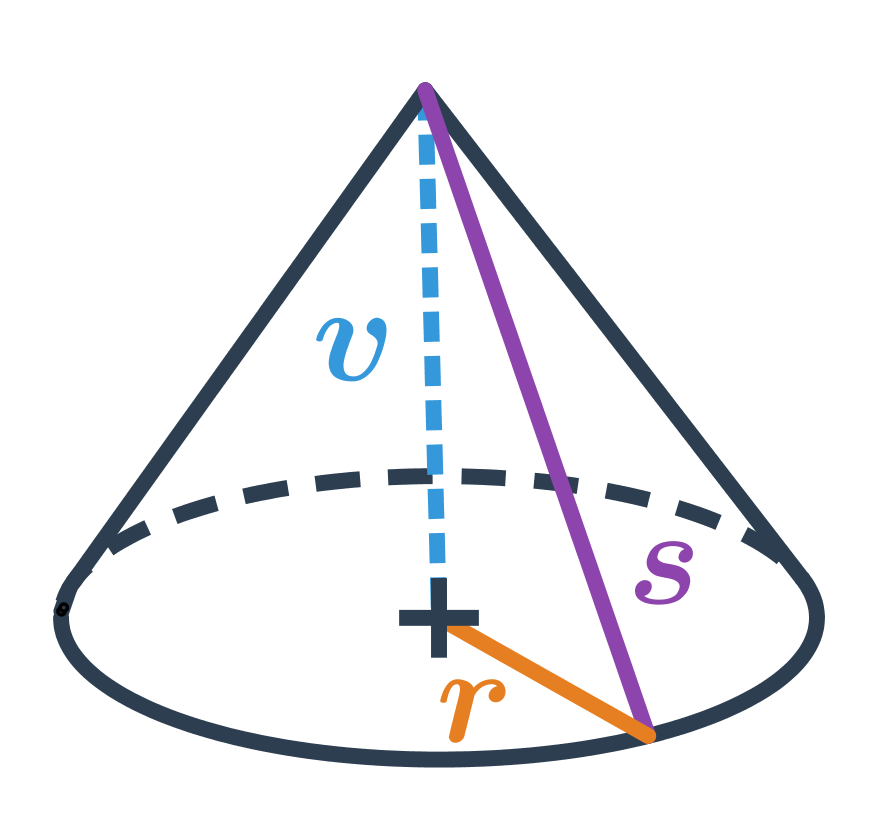
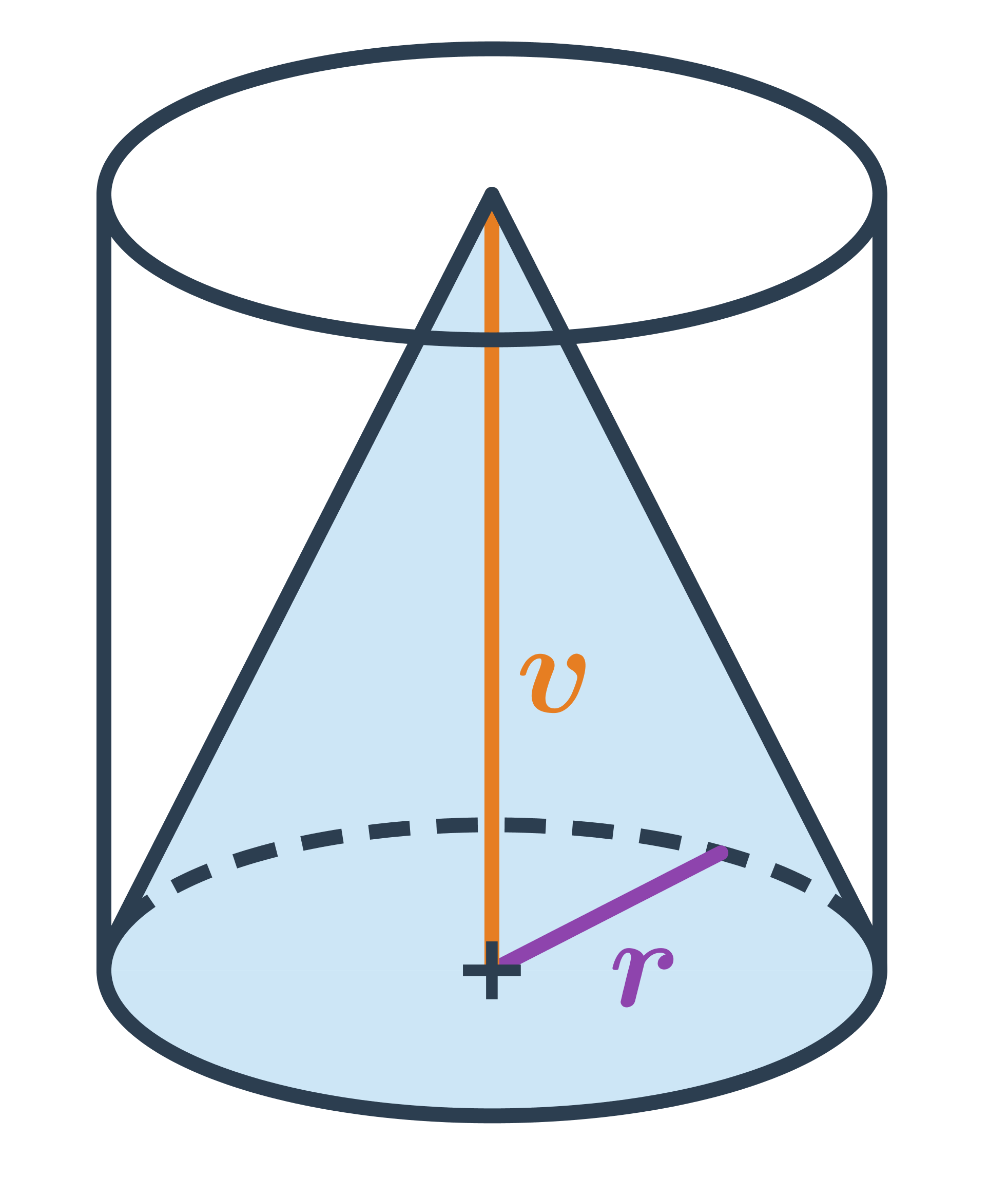
NahoruKužel je prostorový geometrický útvar s kruhovou podstavou. Zužuje se směrem k jednomu bodu zvanému vrchol. Jde o útvar, který vznikne, když se kolem své osy otáčí rovnoramenný trojúhelník. Příkladem kuželu v běžném životě je kornout zmrzliny nebo dopravní kužel.
Vzorce pro objem a povrch
Objem kuželu lze vypočítat pomocí vzorce: V = \frac{1}{3} \pi \cdot r^2 \cdot v, kde r je poloměr podstavy a v je výška kuželu, což je vzdálenost vrcholu od roviny, ve které leží podstava kuželu.
Povrch kuželu získáme sečtením obsahu základny a obsahu pláště S = \pi \cdot r^2 + \pi \cdot r s, kde s je tzv. strana kuželu, což je délka úsečky spojující vrchol kuželu s okrajem jeho základny.
Kuželosečky
Křivky, které vznikají průnikem kuželového povrchu s rovinou, se nazývají kuželosečky. Patří mezi ně například kružnice, elipsa, parabola a hyperbola.
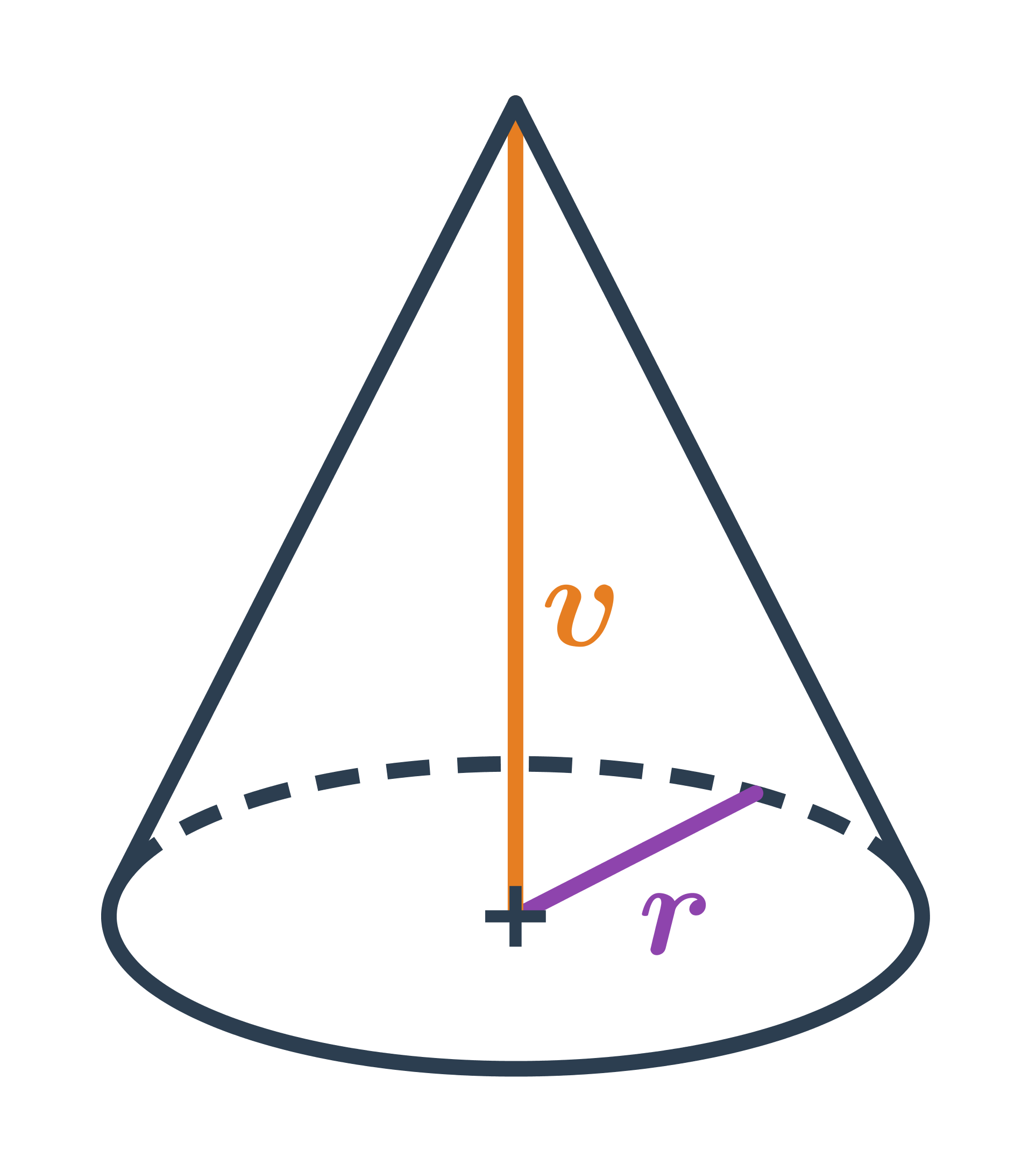
Objem kužele
Objem kužele s poloměrem podstavy r a výškou v spočítáme jako: V=\frac{1}{3} \pi \cdot r^2 \cdot v
Pro kužel platí V=\frac{1}{3} S_p \cdot v, kde S_p je obsah podstavy válce. Podstava válce má tvar kruhu s poloměrem r, takže máme: S_p = \pi \cdot r^2
Oproti válci se stejnou výškou a poloměrem podstavy má kužel třikrát menší objem.
Povrch kužele
Povrch kužele s poloměrem podstavy r a délkou strany s spočítáme takto: V=\pi r^2 + \pi r s = \pi r \cdot (r+s)

Může se stát, že známe poloměr r podstavy kužele a jeho výšku v, ale nemáme zadanou jeho stranu s. Potom si stranu můžeme dopočítat jako přeponu pravoúhlého trojúhelníka s odvěsnami o délkách v a r. Platí: s=\sqrt{v^2+r^2}
- Obsah podstavy kužele: \pi r^2
- Obsah pláště kužele: \frac{1}{2} \cdot 2 \pi r \cdot s = \pi r s