
Grafy kvadratických funkcí

Kvadratickou funkci lze vyjádřit ve tvaru f(x) = ax^2 + bx + c, kde a\neq 0. Grafem kvadratické funkce je parabola. Tento graf zobrazuje funkci 0{,}5 x^2 + x - 4:
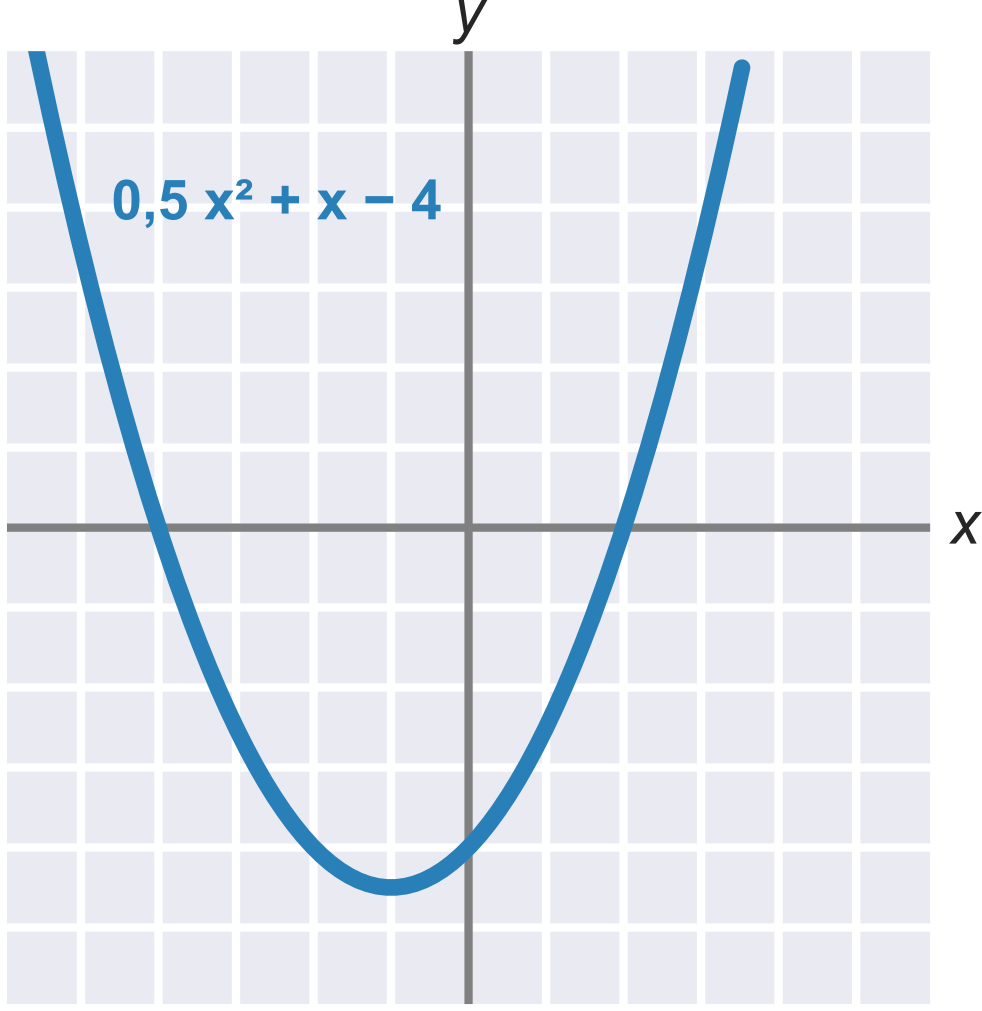
Průsečíky s osou x jsou řešení kvadratické rovnice ax^2 + bx + c = 0. Pro výše uvedený příklad 0{,}5 x^2 + x - 4 jsou těmito řešeními x_1 = -4 a x_2 = 2.
Vliv koeficientů a a c na tvar grafu kvadratické funkce
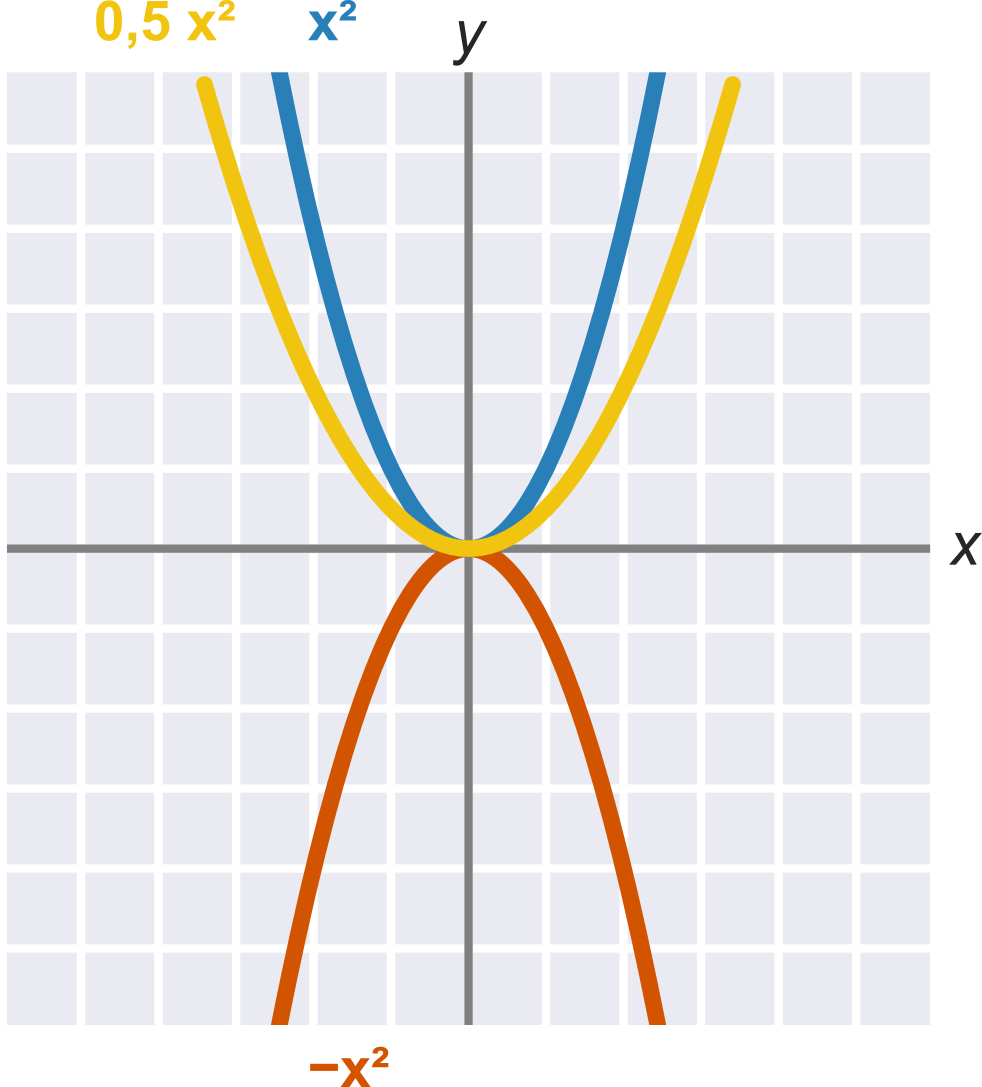
Kvadratický koeficient a ovlivňuje základní podobu paraboly:
- Pokud je a \gt 0, „směřuje parabola nahoru“ (přesněji: je to zdola omezená, konvexní funkce).
- Pokud je a \lt 0, „směřuje parabola dolů“ (přesněji: je to shora omezená, konkávní funkce).
- Velikost kvadratického koeficientu a ovlivňuje, jak je parabola „široká“.
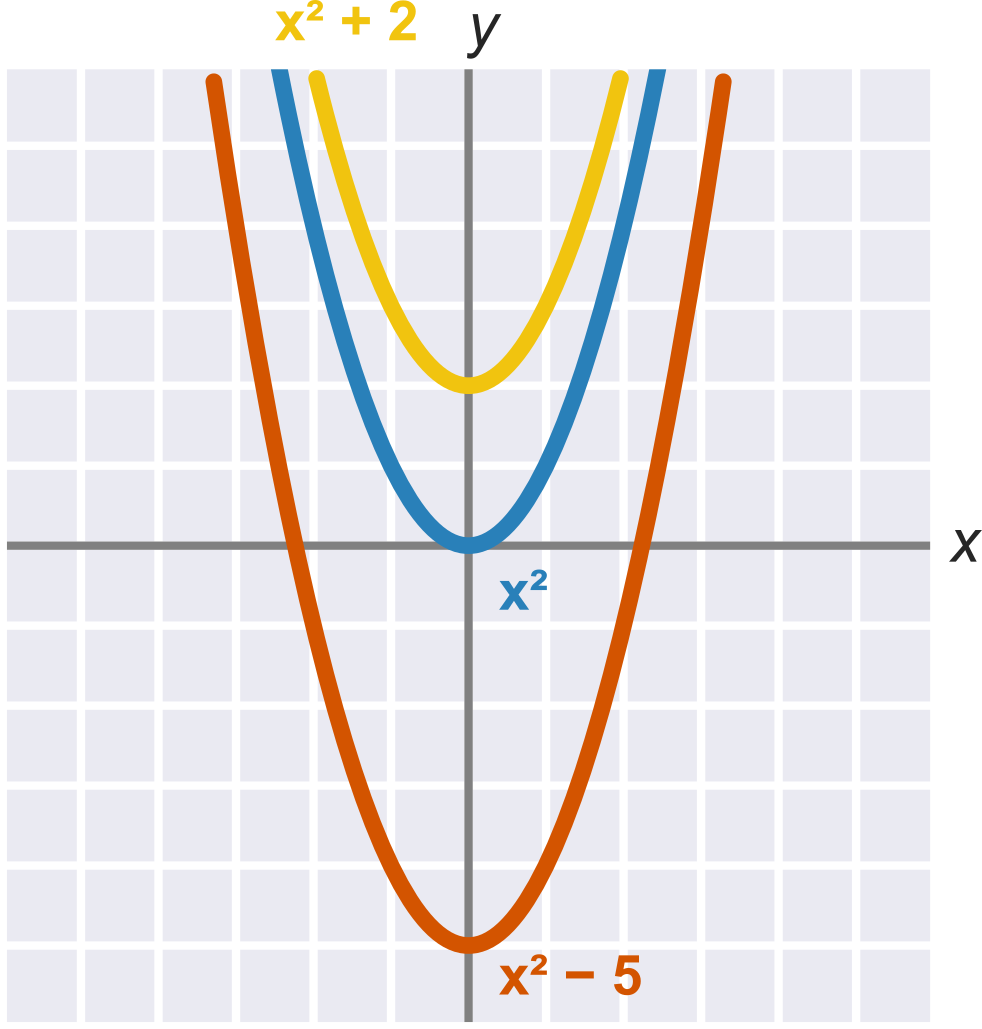
Konstantní člen c ovlivňuje posun paraboly – udává průsečík s osou y.
Určení vrcholu paraboly pomocí úpravy na čtverec
Funkční předpis upravíme tak, aby člen s proměnnou x byl ve tvaru (x-m)^2 (tzv. úprava na čtverec). Souřadnice x vrcholu paraboly je rovna číslu m, souřadnici y získáme jako funkční hodnotu zadané kvadratické funkce v bodě m.
Příklad: určení vrcholu paraboly úpravou na čtverec
Určete vrchol paraboly, která je grafem kvadratické funkce dané předpisem: y=x^2-6x+10
\begin{array}{rrl}y&=&x^2-6x+10\\y&=&x^2-6x+9+1\\y&=&(x-3)^2+1\end{array}
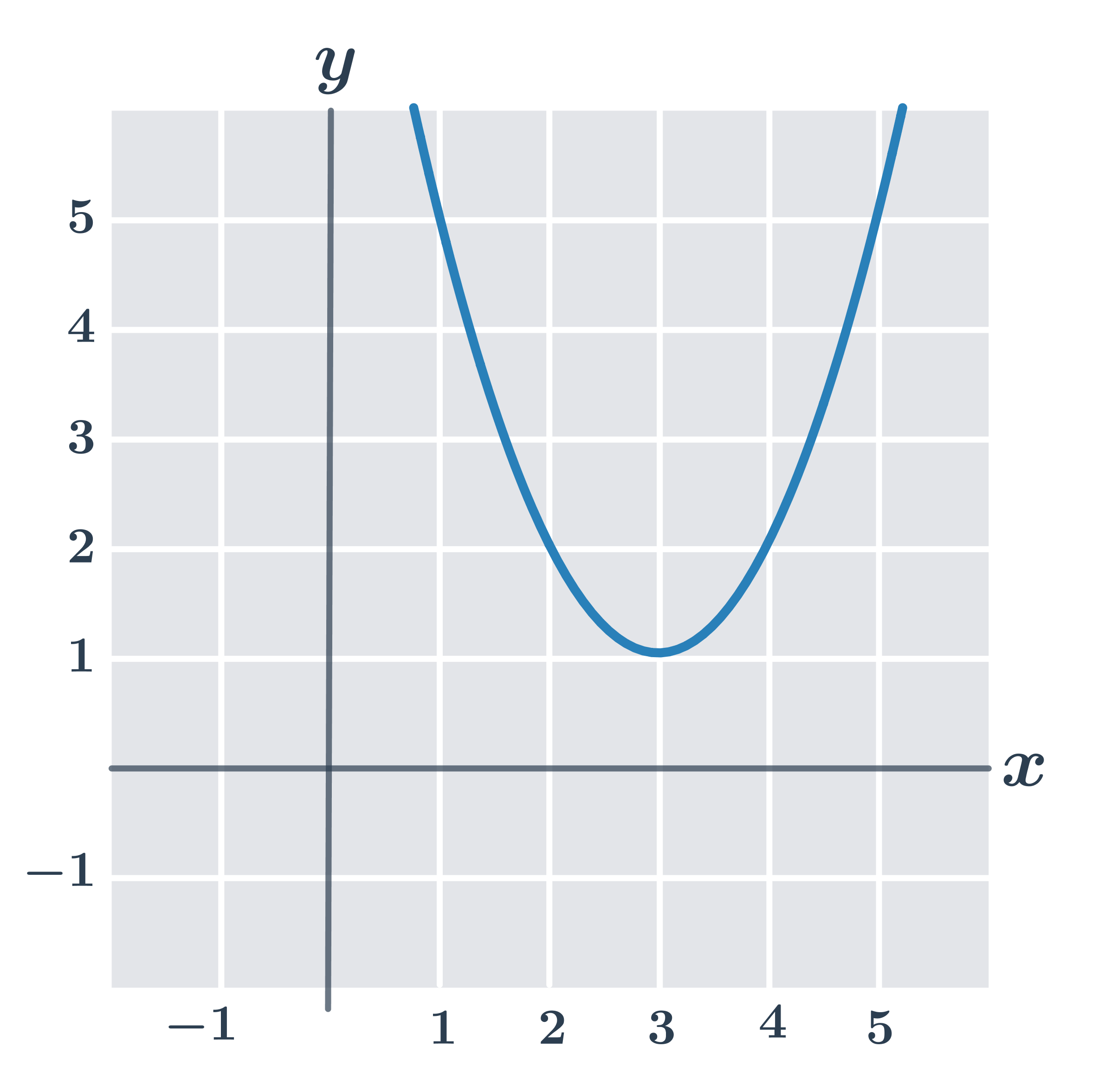
Máme tedy souřadnice vrcholu paraboly x=3 a y=(3-3)^2+1=1.
Zajímavost z analytické geometrie: Převedením konstanty na levou stranu rovnice y=(x-3)^2+1 dostaneme vrcholovou rovnici paraboly y-1=(x-3)^2.
Parabola, která je grafem funkce, má vrchol v bodě [3,1].
Komiks pro zpestření
Zavřít














